2. 东北电力大学 能源与动力工程学院, 吉林 132012;
3. 兰州理工大学 土木工程学院, 兰州 730050;
4. 中石化中原石油工程设计有限公司, 河南 濮阳 457001
2. School of Energy and Power Engineering, Northeast Electric Power University, Jilin 132012, China;
3. School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China;
4. Sinopec Petroleum Engineering Zhongyuan Corporation, Puyang 457001, Henan, China
滑坡碎屑流是滑坡灾害的一种,具有极强的破坏力,当滑坡碎屑流流经城市生命线工程时,势必会造成管线破裂损坏[1]。目前针对滑坡区埋地天然气管道灾变风险研究,主要集中在穿越滑坡体管道力学分析[2-4],滑坡风险下管道风险评价[5-6]、风险监测及预防控制[7-8]等方面。目前,还未见针对滑坡碎屑流作用下,埋地天然气管道灾变风险方面的相关研究。
滑坡区埋地天然气管道灾变风险研究,以穿越滑坡体管道的位移变形、应力应变分布、及各类因素对管道变形和应力应变的影响规律研究为主[9-10]。穿越滑坡体管道受力与滑坡碎屑作用下埋地管道受力存在较大差异,对穿越滑坡体管道而言,所经历的滑坡多数为蠕滑类型,即滑坡体使管道沿滑坡方向,进行微小移动;管道纵向穿越滑坡体时,滑坡体拖拽管道向下移动,坡顶管道受拉伸作用,容易形成拉应力集中区,坡脚管道受压缩作用,多形成压应力集中区,坡顶、坡脚易发生管道屈曲破坏[9];当管道横向穿越滑坡体时,在滑体拖拽下,滑体中心管道容易出现受力集中,滑坡强烈时,中心区域管道会出现弯曲变形,滑体两侧管道会发生剪切破坏[9];而碎屑流在流经埋地管道表面时,埋地管道受力主要是碎屑流本身的压力以及碎屑流摩擦导致作用区土壤对管道的推挤或拖拽作用力,与穿越滑坡体管道受力有较大区别。对穿越滑坡体管道灾变影响研究,目前采用解析法和数值法进行,如文献[11-16]先后采用简单解析方法,利用弹性地基梁理论简化管土作用,分析了横、纵向管道穿越滑坡作用的力学响应,得到纵向滑坡危险性小于横向滑坡;随着计算机技术的提升,由解析法转变到数值法上,相比解析法,数值法可以考虑管土材料弹塑性材料特性、管土相互作用,进而得到管道受土壤性质、管道材料的影响规律,滑坡对埋地管道的影响作用计算结果也更符合实际。目前滑坡区埋地管道灾变风险研究,基本以数值法为主,利用有限元软件进行研究[17-20]。如郝建斌等[21]在考虑管土相互作用过程分析基础上,利用极限平衡法推导了横穿敷设情况下滑坡对管道推力的计算方法,并利用数值模拟验证了该计算方法的合理性。
对滑坡区天然气管道风险评价方法研究,主要为管道环境风险评价和管道力学风险评价两部分[3, 22-27]。许多地质灾害条件下天然气集输管道安全风险评价技术,基本都是基于外部灾害因素的环境风险评价方法[8, 28-30]。目前的管道环境评价技术有定量评价技术、半定量和定性评价技术[31-32]。如基于管道失效故障树的评价方法,剩余强度评价方法、模糊评价等[31, 33-34]。管道力学风险评价,主要在管道的位移变形能力、应力应变能力评价方面。最初管道力学风险评价研究,主要关注管道的位移变形,以及极限工况下管道材料是否发生应力失效;随后较多的研究表明,地震、滑坡等地表大变形特殊情况下,管道虽然承受较大的位移及应变,已经达到或者超过应力判别准则的要求,但管道依旧可以满足输送要求,此时,基于应变的管道风险评价方法更为合适[35]。
滑坡区天然气管道风险监测是通过传感器监测管道位移变形、管道周环向应力、应变变化,与不同失效形式下的管道位移变形、应力、应变限值进行比较,进而实现管道风险的直接监测评价,准确度较高[5-6, 20, 25, 36]。如文献[37]提出了一种基于周向应变测量的间接管道腐蚀监测方法,并在PVC管道上进行了测试实验,模型试验结果表明,光纤光栅环应变传感器在环向应变测量中具有良好的性能,可作为管道健康监测的实用装置[37]。然而,当前埋地天然气管道应变监测存在监测布置方法上的不足,例如基于应变的埋地管道监测,主要通过多个截面的应变监测采集实现,就整条管线而言,监测位移或者应变为离散的数据点,并不能反映整条管道的变形或者应变状况,缺乏管道变形、应变分布函数模型,用于监测评价结果模式识别和监测评价结果修正。
本文将基于热-弹塑性理论,采用管-土耦合方法,建立滑坡碎屑流纵向作用下埋地天然气管道变形分析模型。分析埋地天然气管道的变形分布规律,并基于有限元模拟数据及管道变形分布特征,构建埋地管道变形分布预测模型,确定滑坡碎屑流纵向作用下埋地天然气管道应变分布,为滑坡碎屑流事前应变预警和事后管道安全风险评估奠定基础。
1 有限元模型分析 1.1 物理模型简化小型滑坡碎屑流在土体表面滑动过程中,其堆积形态类似于半椭球体[38],图 1为小型滑坡碎屑流在土壤表层作用示意图,因此本文将土体表面滑坡碎屑流运动过程中的堆积形态近似为半椭球体。同时,依据滑坡碎屑流颗粒流理论,滑坡碎屑流流动是其底部剪力和自身重力共同作用的结果,因此滑坡碎屑流对埋地天然气管道顶层土体表面的作用,可简化等效为其对土体表面的摩擦力和压力的作用。考虑碎屑流对土壤表层作用力,与土壤表层作用对碎屑流作用力为相互作用力,碎屑流对土壤表层等效压力可以利用椭球体积计算公式和重力计算公式求得;而等效摩擦力采用摩擦力计算公式计算;在此基础上,进一步考虑山体坡度,那么滑坡碎屑流对埋地天然气管道顶层土体表面的作用力可依据下式进行计算:

|
图 1 滑坡碎屑在土壤表层作用示意图 Fig. 1 Diagram of landslide debris on soil surface |
| $ \left\{\begin{array}{l} F_y=\frac{1}{6} \pi a b c \rho \cos (\theta) g \eta \\ F_z=\frac{1}{6} \pi a b c \rho \cos (\theta) g \end{array}\right. $ | (1) |
式中: a、b、c分别为埋地管道顶层土体表面滑坡碎屑流椭球体的长度、宽度、高度;g为重力加速度,一般取9.8 m/s2;ρ为滑坡碎屑流密度;θ为坡体与水平夹角;η为滑坡碎屑流与土体表面间的摩擦系数,依照岩土勘查工程手册设定为0.3[39]。
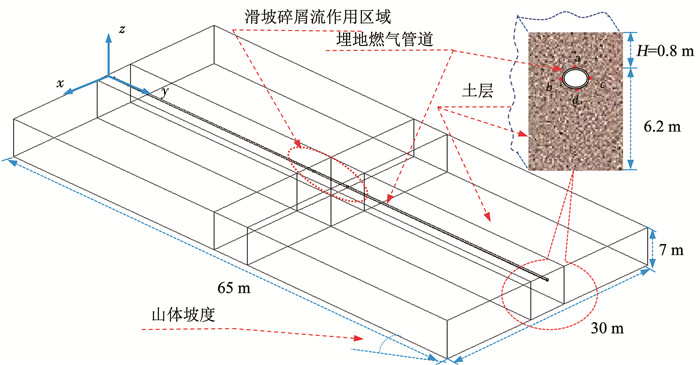
考虑到非滑坡碎屑流影响区管道应变、变形非常小,管道主要变形、应变在碎屑流影响区;在保证不同滑坡碎屑流尺寸、埋土深度状况下模型计算结果不受其边界尺寸影响下,同时保证一定的计算效率,本文在沿管长方向选取65 m,管道两侧选取宽度为30 m的管土区域,埋地管道底层土体厚度确定为6.2 m。图 2为滑坡碎屑流纵向作用下埋地天然气管道变形分析简化模型,其中,a、b、c、d分别为管道外壁面的轴向路径,即管道外壁面管顶轴向路径、管左轴向路径、管右轴向路径、管底轴向路径。
|
图 2 滑坡碎屑流纵向作用下埋地天然气管道变形分析简化模型 Fig. 2 Simplified model on deformation analysis of buried natural gas pipeline under longitudinal action of landslide debris flow |
滑坡碎屑流纵向作用下埋地管道分析模型,主要由管道和土体两部分组成。结合某油田工程实际调研数据,以管道材料为L360钢材,土体为黏土,考虑管土之间的非线性接触作用,进行管-土耦合模拟分析;管道采用双线性弹塑性本构模型,该本构模型需要确定管道弹性模量E、泊松比μ、切线模量Et和屈服强度σ0;土壤采用Drucker-Prager弹塑性模型,D-P本构模型共有4个材料参数: K,G,α,k,可以由黏聚力、摩擦角、弹性模量、泊松比转化确定;其中,土壤黏聚力C为39 kPa,摩擦角φ为24°,其他具体管土材料参数见表 1。
| 表 1 管土材料属性 Tab. 1 Material properties of pipeline and soil |
目前管土相互作用模型有弹性地基梁模型、土弹簧模型、管土非线性接触模型。管土非线性接触模型:一般指有限元中,考虑管道、土壤材料,将管道和土壤交界面定义为接触面,管土之间施加接触约束,可以通过接触面传递接触压力,同时管土模型之间的接触状况,随着外部载荷的作用传递而发生变化,即接触或者分离。
考虑到管道和土壤属于不同的材料,其材料性质大相径庭,管土交界面处的状态是非线性的,并且埋地管道与土的接触面上不仅存在正应力,也存在剪应力;同时,当外力作用时,管土之间必然存在一定程度的滑动。与前两种模型相比采用管土非线性接触模型表征的管土之间关系,更加切合实际。
1.4 边界条件滑坡碎屑流纵向作用下埋地天然气管道的变形,是管内运行压力、温度以及土体共同作用的结果。要准确分析滑坡碎屑流纵向作用下埋地天然气管道的变形,需施加合理的边界条件。依据实际条件,在埋地天然气管道两端的截面,即y=0和y=65 m两截面,施加管长方向固定约束边界,模拟远离滑坡碎屑流区域管土的稳定状态;在埋地天然气管道两侧,即x=±15 m两截面,采用x方向固定约束边界,模拟远离滑坡碎屑流区域土体稳定状态;在土体底层,即z=-7 m截面,采用全自由度固定约束,模拟底层稳定土体。同时,管道运行条件下,内部天然气对管道起到一定的支撑和保护作用,为模拟天然气运行参数对埋地天然气管道的影响,在管道内壁施加正常运行工况时的温度和压力边界[40]。
1.5 网格划分及无关性验证要分析埋地天然气管道变形规律,须对模型进行网格划分,本文ANAYS软件,采用结构化网格进行网格划分,并对网格进行了无关性验证,见表 2。选取4套节点数分别为130 000、270 000、460 000、660 000的网格,对同一工况的计算结果进行对比,当网格节点数超过270 000时计算结果受网格数的影响较小。综合考虑网格节点数对计算效率的影响,最终选取节点数为270 000的网格进行模拟分析。
| 表 2 网格无关性验证 Tab. 2 Mesh-independent validation |
同时,在管道埋深H=0.8 m,坡度角θ=π/9,天然气温度T=328 K,压力P=8.9 MPa条件下,采用普光气田现场监测数据对模型进行了可靠性验证。由于监测过程中,并未出现滑坡碎屑流情况,故而认为滑坡碎屑流作用力Fz、Fy均为零时工况,就是滑坡碎屑流发生时的特殊工况(管道内天然气温度、压力波动的日常运行工况),因而对等效作用力Fz、Fy均为零时的特殊工况进行了验证;在模型验证过程中,选取外部载荷均为零时工况,模拟分析实际运行过程中压力和温度波动对管道应变的影响;实际选择管土模型y=25 m截面处管道轴向应变值与同一位置应变监测值(选取当日管道运行压力波动在1 MPa内,管道运行温度变化差在10 K时的应变)进行比较分析。表 3为埋地天然气管道轴向应变监测值与模拟值对比结果。结果表明,a、b、c位置处的监测应变和数值模拟工况位置处应变之间误差在10%以内,即数值模拟是基本可靠的。
| 表 3 埋地天然气管道轴向应变监测值与模拟值对比(y=25 m) Tab. 3 Relation between test data and simulation results on axial strain of buried natural gas pipeline (y=25 m) |
在管径D=0.323 9 m,壁厚t=0.014 2 m,埋深H=0.8 m,坡度角θ=π/9,天然气温度T=328 K,压力P=8.9 MPa时,模拟分析了管土变形的分布规律。图 3为滑坡碎屑流长度为5 m,宽度5 m,厚度为1 m时,埋地管土模型的管土变形分布;结果表明,土壤变形区域主要为碎屑流作用区及其附近区域,同时沿滑动方向,滑坡碎屑流前部土壤变形区域明显大于后部区域;对于埋地管道而言,管道主要为弯曲变形,管道变形最严重区域同样也是滑坡碎屑流作用下的中心区域。比较管土两者的变形,可以得到滑坡区域土壤的变形量明显大于管道,变形量是不同步的;这是因为滑坡碎屑流灾害发生时,土壤首先承载载荷,部分载荷以土壤变形的方式抵消,且管土之间为有限滑动接触,所以土壤与管道的位移变形将不是同步的。

|
图 3 碎屑流作用下管土变形分布 Fig. 3 Deformation distribution of pipeline and soil under the action of landslide debris flow |
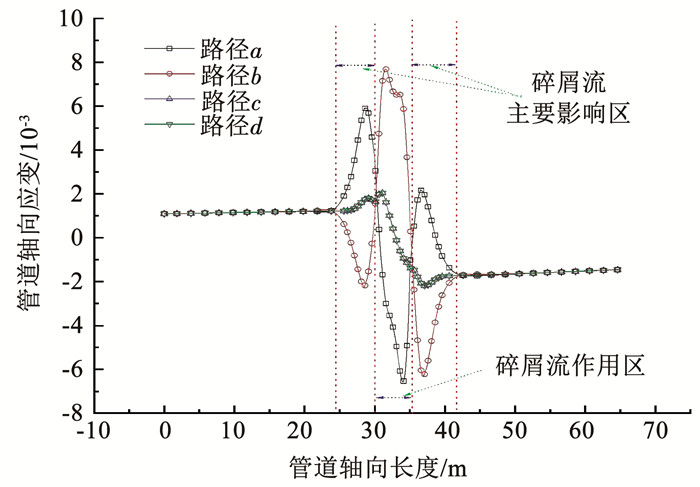
图 4为碎屑流长度L=5 m,宽度W=5 m,厚度TH=1 m时,管道轴向应变在a、b、c、d路径上的分布规律。结果表明,管道沿长度方向各个路径上,既存在拉应变(正),又存在压应变(负),即管道同时受拉力和压力作用;而沿管长方向,碎屑流主要影响区前部管道受压,后部管段受拉,即碎屑流对该区域前部管道起到挤压、对后部拖拽的作用。在滑坡碎屑流作用区域,管道底部取得拉应变极值,管道顶部取得压应变极值,其中拉应变极值要大于压应变极值(a、d分别对应管道顶部和管道底部);因此,滑坡碎屑流作用条件下,碎屑流作用区管道可能最先发生拉裂破坏。
|
图 4 不同路径管道轴向应变分布 Fig. 4 Distribution of axial strain along pipeline with different paths |
为进一步研究不同滑坡碎屑流尺寸条件下,管道轴向应变分布,将管道长度方向每个截面的轴向最大拉应变和压应变分布进行了分析。图 5为碎屑流宽度W=5,厚度TH=1时,不同碎屑流长度条件下的轴向最大拉压应变分布规律。结果表明,沿着轴向长度方向(0~65 m),碎屑流主要影响区前部的轴向应变受滑坡碎屑长度影响显著,应变分布范围随碎屑流长度的增加而逐步扩大,随着滑坡碎屑长度的增加,轴向压应变极大值,由碎屑流作用区转移至碎屑流前部,而轴向拉应变始终在滑坡作用区域内取得极大值;就管道应变分布而言,应变分布具备以下特征:在碎屑流影响区域,管道轴向拉应变分布存在3、4个波峰,而轴向压应变分布存在3、4个波谷,碎屑流影响区域范围是作用区域长度的3倍左右;在远离滑坡碎流的前后区域,管道轴向应变分布为一平滑直线,且沿轴向长度方向,前边为压应变,后边为拉应变。在碎屑流影响区域,管道轴向拉压应变分布出现多个波峰、波谷,这是因为管道壁面已出现褶皱变形,当管道上存在褶皱变形时,拉压应变将同时存在,且变化幅值较大,对应管道轴向拉压应变分布将出现多处波峰和波谷。

|
图 5 不同碎屑流长度下轴向应变εsg和εxg分布 Fig. 5 Distribution of εsg and εxg at different lengths of landslide debris flow |
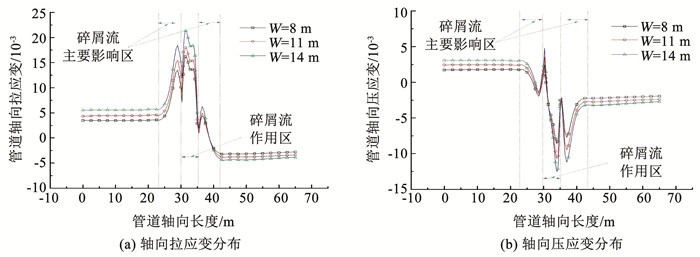
图 6为碎屑流L=5,厚度TH=1时,不同碎屑流宽度条件下的轴向最大拉压应变分布规律。由图 6可知,当碎屑流宽度增大时,碎屑流作用区及主要影响区的轴向应变的波峰和波谷出现微幅增加;就轴向应变的影响区范围而言,相比滑坡长度条件下应变分布范围,管道轴向拉压应变分布范围随滑坡碎屑流宽度的变化并不明显,滑坡宽度对轴向应变影响程度小于滑坡长度;这因为滑坡宽度增加后的扩展区并未直接作用于管道,而是作用于管道两侧。
|
图 6 不同碎屑流宽度下轴向应变εsg和εxg分布 Fig. 6 Distribution of εsg and εxg at different breadths of landslide debris flow |
图 7为碎屑流L=5,宽度W=5时,不同碎屑厚度条件下管道轴向最大拉压应变分布规律。结果表明,滑坡碎屑流厚度对轴向应变分布影响,主要在碎屑流作用区域及影响区;随着碎屑流厚度的增加,轴向应变分布形态迅速扩大,拉应变分布的波峰和压应变分布的波谷幅值显著增加,轴向应变均在滑坡作用区取得拉压应变最值;结合滑坡碎屑长度、宽度条件下的轴向拉压应变分布,轴向拉压应变分布均具备以下特征,滑坡碎屑流作用区和主要影响区的轴向拉压应变基本为几个波峰和波谷组成,而其他区域轴向拉压应变分布基本呈现为一条平滑直线,且沿轴向长度方向,前边为压应变,后边为拉应变。

|
图 7 不同碎屑流厚度下轴向应变εsg和εxg分布 Fig. 7 Distribution of εsg and εxg at different thicknesses of landslide debris flow |
综上所述,不同滑坡碎屑流长度、宽度、厚度条件下,管道轴向拉压应变分布的碎屑流影响区长度基本为碎屑流作用区域长度的3倍左右;随着碎屑流长度的增加,沿管道长度方向,碎屑流主要影响区前部轴向应变分布范围显著扩张,而随着碎屑流宽度和厚度的增加,轴向拉压应变仅在碎屑流作用区增长明显。除此以外,管道轴向应变分布具备以下特征,在滑坡影响区域内,管道轴向拉应变分布由3~4个波峰组成,而轴向压应变分布由3~4个波谷组成,且拉压应变分布基本都在碎屑流作用区的中心波峰或波谷处,取得拉压应变最值;远离滑坡碎屑流影响区域,管道轴向拉压应变分布,沿滑动方向,碎屑流影响区前边为拉应变,后段为压应变,分布基本呈现为一条平滑直线。
2.2 轴向应变分布预测模型研究综合不同碎屑流长度、宽度、厚度下管道轴向应变分布特征,将管道轴向最大拉压应变分布分别划分为3部分区域,滑坡碎屑流影响区及前后部的非碎屑流影响区域;碎屑流影响区域轴向拉压应变可以用正态分布函数关联式来近似表示,而远离碎屑流区域轴向拉压应变分布可用常数函数来表示,假设函数具体形如式(2)所示。
采用Levenber (1944)和Marqurdt (1963)提出的麦夸特(Levenber-Marqurdt method)方法,利用模拟应变分布数据(不同碎屑流长2~11 m、宽5~14 m、厚0.5~3.0 m条件下轴向应变分布,共计24组),对埋地天然气管道轴向应变分布进行非线性拟合计算,确定合适的k1、k2值,得到分布函数通用方程如式(3)、(4)所示。对应变分布预测模型而言,仅需确定μ、σ、a1参数值即可得到管道轴向应变分布,并且这3个参数与滑坡碎屑流规模存在一定关系。也就是说,滑坡碎屑影响区域内,存在3个位置的轴向拉压应变数据,即可得上述3个参数,从而可预测该区域管段轴向最大拉压应变分布。
| $ \left\{\begin{array}{l} \varepsilon_{s g}(x)=k_1 \frac{a_1}{\sigma}[0, \mu-1.50 \sigma] \\ \varepsilon_{s g}(x)=\frac{a_1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{(x-\mu)^2}{2(\sigma)^2}}[\mu-1.50 \sigma, \mu+2.58 \sigma] \\ \varepsilon_{s g}(x)=k_2 \frac{a_1}{\sigma}[\mu+2.58 \sigma, \mu+n \sigma] \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} \varepsilon_{s g}(x)=0.115 \frac{a_1}{\sigma}[0, \mu-1.50 \sigma] \\ \varepsilon_{s g}(x)=\frac{a_1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{(x-\mu)^2}{2(\sigma)^2}}[\mu-1.50 \sigma, \mu+2.58 \sigma] \\ \varepsilon_{s g}(x)=-0.1 \frac{a_1}{\sigma}[\mu+2.58 \sigma, \mu+n \sigma] \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} \varepsilon_{x g}(x)=0.115 \frac{a_1}{\sigma}[0, \mu-2.58 \sigma] \\ \varepsilon_{x g}(x)=-\frac{a_1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{(x-\mu)^2}{2(\sigma)^2}}[\mu-2.58 \sigma, \mu+1.50 \sigma] \\ \varepsilon_{x g}(x)=-0.1 \frac{a_1}{\sigma}[\mu+1.50 \sigma, \mu+n \sigma] \end{array}\right. $ | (4) |
式中:μ、σ、a1分别为管道应变分布预测模型影响参数,其中μ为分布的位置参数,σ为描述分布数据分布的离散程度,a1为常数;x为管道轴向长度位置,m;为保证预测分布模型分段函数划分合理,n≥3。
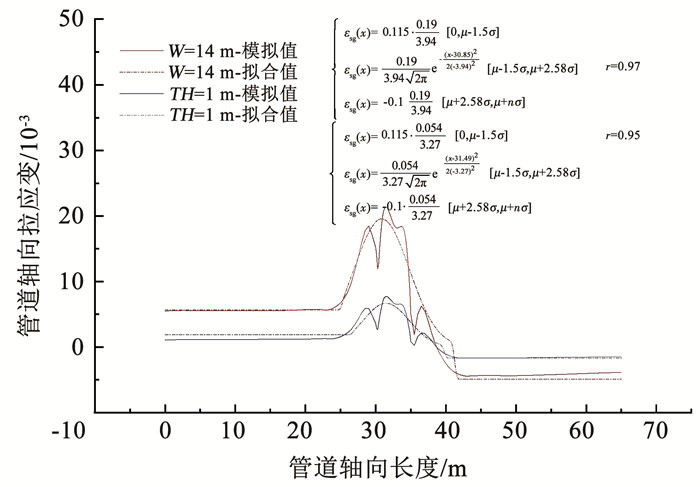
为了验证上述模型可靠性,又在特定规模滑坡碎屑流下,将模拟数据与预测模型计算数据进行了对比。图 8为滑坡碎屑流长度L=5,宽度W=5、W=14,厚度TH=1时,管道拉应变分布与预测模型计算结果对比。结果表明,管道轴向拉应变分布与预测分布模型相关性较好,相关系数均值在0.95以上;碎屑流影响区域及远离碎屑流区域的轴向拉应变分布特征可以被预测模型近似反映。图 9为滑坡碎屑流长度L=5、L=11,宽度W=5,厚度TH=1时,管道轴向压应变分布与预测模型计算结果对比图。结果表明,管道轴向压应变分布与预测分布模型重合度较高,预测分布模型可以表现出管道轴向压应变分布的变化趋势,且两者的相关系数均值在0.92以上,完全满足基本工程要求。
|
图 8 不同碎屑流宽度、厚度下管道轴向εsg分布 Fig. 8 Distribution of εsg at different breadths and thicknesses of landslide debris flow |

|
图 9 不同碎屑流厚度、长度下管道轴向εxg分布 Fig. 9 Distribution of εxg at different thicknesses and lengths of landslide debris flow |
1) 滑坡碎屑流作用下土壤变形区域主要为碎屑流作用区及其附近区域,滑坡碎屑流前部区域土壤变形明显大于后部区域;管道变形最严重区域是滑坡碎屑流中心区域,而管土之间变形并不同步。
2) 碎屑流作用时,沿长度方向,管道在各个路径上,同时受拉力和压力作用;在碎屑流作用区域,管道底部和顶部路径分别取得拉压应变极值,其中拉应变极值要大于压应变极值。
3) 在碎屑流影响区域,管道轴向最大拉压应变由3~4个波峰、波谷组成,碎屑流影响区域范围是作用区域长度的3倍左右;在远离滑坡碎流的前后区域,管道轴向应变分布为一平滑直线,且沿轴向长度方向,前边为压应变,后边为拉应变。
4) 相比碎屑流长度,碎屑流宽度、厚度对管道应变分布范围影响有限,管道应变分布范围随着碎屑流长度增加显著扩张,集中在碎屑流主要影响区前部;不同碎屑流长度、宽度、厚度下管道轴向最大拉压应变基本都在碎屑流作用区最大波峰或波谷处,取得拉压应变最值。
5) 管道应变分布预测模型仅与μ、σ、a13个参数相关,仅需3个位置的轴向拉压应变数据,即可确定该区域管段轴向最大拉压应变分布。
| [1] |
杨扬. 滑坡运动性态及阵列挡板阻挡滑坡碎屑流冲击的数值分析[D]. 合肥: 合肥工业大学, 2019 YANG Yang. Numerical analysis of landslide movement behavior and array baffle blocking landslide debris flow impact[D]. Heifei: Hefei University of Technology, 2019 |
| [2] |
刘金涛. 管道横穿滑坡相互作用大尺度模型试验研究[D]. 成都: 成都理工大学, 2012 LIU Jintao. Study on the large scale model test of the interaction of pipeline across landslide[D]. Chengdu: Chengdu University of Technology, 2012 |
| [3] |
LIU Z Y, WANG X Z, DU C W, et al. Effect of hydrogen-induced plasticity on the stress corrosion cracking of X70 pipeline steel in simulated soil environments[J]. Materials Science and Engineering: A, 2016, 658: 348. DOI:10.1016/j.msea.2016.02.019 |
| [4] |
李璞, 陶燕丽, 周建. 基于应变设计管道局部屈曲应变极限值的计算[J]. 天然气工业, 2013, 33(7): 101. LI Pu, TAO Yanli, ZHOU Jian. A study of the ultimate compressive strain of local buckling in strain-based design of pipelines[J]. Natural Gas Industry, 2013, 33(7): 101. DOI:10.3787/j.issn.1000-0976.2013.07.018 |
| [5] |
JIA Ziguang, REN Liang, LI Hongnan, et al. Experimental study of pipeline leak detection based on hoop strain measurement[J]. Structural Control and Health Monitoring, 2015, 22(5): 799. DOI:10.1002/stc.1718 |
| [6] |
KAHANDAWA G C, EPAARACHCHI J, WANG Hao, et al. Extraction and processing of real time strain of embedded FBG sensors using a fixed filter FBG circuit and an artificial neural network[J]. Measurement, 2013, 46(10): 4045. DOI:10.1016/j.measurement.2013.07.029 |
| [7] |
车福利. 输气管道滑坡段风险评价与监测技术研究[D]. 大庆: 东北石油大学, 2017 CHE Fuli. Study on the risk assessment and monitoring technology of landslide for natural gas pipeline[D]. Daqing: Northeast Petroleum University, 2017 |
| [8] |
WANG Xinhua, SONG Xuting, CHEN Yingchun, et al. Corrosion behavior of X70 and X80 pipeline steels in simulated soil solution[J]. International Journal of Electrochemical Science, 2018, 13: 6436. DOI:10.20964/2018.07.12 |
| [9] |
席莎. 滑坡区埋地管道变形破坏的临界判据与敏感区段研究[D]. 北京: 中国地质大学(北京), 2018 XI Sha. Study on deformation and failure criterion and susceptible zones for buried pipelines across landslides[D]. Beijing: China University of Geosciences, Beijing, 2018 |
| [10] |
张伯君. 山体滑坡区域内长输埋地油气管道强度研究[D]. 杭州: 浙江大学, 2013 ZHANG Bojun. Research on strength behavior of long-distance buried pipe for oil and gas transportation in the landslide area[D]. Hangzhou: Zhejiang University, 2013 |
| [11] |
RAJANI B, ROBERTSON P K, MORGENSTERN N R. Simplified design methods for pipelines subject to transverse and longitudinal soil movements[J]. Canadian Geotechnical Journal, 1995, 32(2): 1094. DOI:10.1139/t95-032 |
| [12] |
O'ROURKE M J, LIU Xuejie, FLORES-BERRONES R. Steel pipe wrinkling due to longitudinal permanent ground deformation[J]. Journal of Transportation Engineering, 1995, 121(5): 443. DOI:10.1061/(ASCE)0733-947X(1995)121:5(443) |
| [13] |
CHAN P D. Soil: Pipeline interaction in slopes[M]. Calgary, AB: University of Calgary, 1999. DOI:10.11575/PRISM/16457
|
| [14] |
梁政. 滑坡地区管线应力和位移的分析[J]. 天然气工业, 1991, 11(3): 55. LIANG Zheng. Analysis of pipeline stress and displacementat landslide-prone areas[J]. Natural Gas Industry, 1991, 11(3): 55. |
| [15] |
张东臣, БыковЛ Й. 滑坡条件下埋地管道受力分析[J]. 石油规划设计, 2001, 12(6): 1. ZHANG Dongchen, Быков Л Й. The force-summing analysis of buried pipeline under landslide condition[J]. Petroleum Planning & Engineering, 2001, 12(6): 1. DOI:10.3969/j.issn.1004-2970.2001.06.001 |
| [16] |
刘慧. 滑坡作用下埋地管线反应分析[D]. 大连: 大连理工大学, 2008 LIU Hui. Response analysis for buried pipelines subjected to the landslide[D]. Dalian: Dalian University of Technology, 2008 |
| [17] |
ZHANG Jie, LIANG Zheng, ZHAO Guanghui. Mechanical behaviour analysis of a buried steel pipeline under ground overload[J]. Engineering Failure Analysis, 2016, 63: 131. DOI:10.1016/j.engfailanal.2016.02.008 |
| [18] |
ZHANG Lisong, XIE Yun, YAN Xiangzhen, et al. An elastoplastic semi-analytical method to analyze the plastic mechanical behavior of buried pipelines under landslides considering operating loads[J]. Journal of Natural Gas Science and Engineering, 2016, 28: 121. DOI:10.1016/j.jngse.2015.11.040 |
| [19] |
ZHANG J, LIANG Z, HAN C J. Numerical modeling of mechanical behavior for buried steel pipelines crossing subsidence strata[J]. Plos One, 2015, 10(6): e0130459. DOI:10.1371/journal.pone.0130459 |
| [20] |
ROFOOEI F R, JALALI H H, ATTARI N K A, et al. Parametric study of buried steel and high density polyethylene gas pipelines due to oblique-reverse faulting[J]. Canadian Journal of Civil Engineering, 2015, 42(3): 178. DOI:10.1139/cjce-2014-0047 |
| [21] |
郝建斌, 刘建平, 荆宏远, 等. 横穿状态下滑坡对管道推力的计算[J]. 石油学报, 2012, 33(6): 1093. HAO Jianbin, LIU Jianping, JING Hongyuan, et al. A calculation of landslide thrust force to transverse pipelines[J]. Acta Petrolei Sinica, 2012, 33(6): 1093. |
| [22] |
MARUSCHAK P, PRENTKOVSKIS O, BISHCHAK R. Defectiveness of external and internal surfaces of the main oil and gas pipelines after long-term operation[J]. Journal of Civil Engineering and Management, 2016, 22(2): 279. DOI:10.3846/13923730.2015.1100672 |
| [23] |
LIU Xiaoben, ZHANG Hong, LI Meng, et al. Failure analysis of oil tubes containing corrosion defects based on finite element method[J]. International Journal of Electrochemical Science, 2016, 11(6): 5180. DOI:10.20964/2016.06.27 |
| [24] |
GAWEDZKI W, TARNOWSKI J. Design and testing of the strain transducer for measuring deformations of pipelines operating in the mining-deformable ground environment[J]. Measurement Science Review, 2015, 15(5): 256. DOI:10.1515/msr-2015-0035 |
| [25] |
GUO Xishui, SHI Taihe, ZHANG Zhi, et al. Stress corrosion cracking behavior of high strength casing steel in working fluids[J]. Journal of Natural Gas Science and Engineering, 2016, 29: 134. DOI:10.1016/j.jngse.2015.12.050 |
| [26] |
WANG Le, LIU Run. The effect of a berm on the lateral resistance of a shallow pipeline buried in sand[J]. Ocean Engineering, 2016, 121: 13. DOI:10.1016/j.oceaneng.2016.05.010 |
| [27] |
GUO Yanbao, MENG Tao, WANG Deguo, et al. Experimental research on the corrosion of X series pipeline steels under alternating current interference[J]. Engineering Failure Analysis, 2017, 78: 87. DOI:10.1016/j.engfailanal.2017.03.003 |
| [28] |
GUO Xiaoyan, ZHANG Laibin, LIANG Wei, et al. Risk identification of third-party damage on oil and gas pipelines through the Bayesian network[J]. Journal of Loss Prevention in the Process Industries, 2018, 54: 163. DOI:10.1016/j.jlp.2018.03.012 |
| [29] |
ZHAO Yafan, SONG Mingda. Failure analysis of a natural gas pipeline[J]. Engineering Failure Analysis, 2016, 63: 61. DOI:10.1016/j.engfailanal.2016.02.023 |
| [30] |
XU Jin, BAI Yunlong, WU Tangqing, et al. Effect of elastic stress and alternating current on corrosion of X80 pipeline steel in simulated soil solution[J]. Engineering Failure Analysis, 2019, 100: 192. DOI:10.1016/j.engfailanal.2019.02.059 |
| [31] |
PORTER M, LOGUE C, SAVIGNY K W, et al. Estimating the influence of natural hazards on pipeline risk and system reliability[C]//International Pipeline Conference. Calgary, Alberta: ASME, 2004, 41766: 2587. DOI: 10.1115/IPC2004-0238
|
| [32] |
MUHLBAUER W K. Pipeline risk management manual[M]. Houston, TX: Gulf Professional Publishing, 1996. DOI:10.1016/B978-0-7506-7579-6.X5000-6
|
| [33] |
VILKYS T, RUDZINSKAS V, PRENTKOVSKIS O, et al. Evaluation of failure pressure for gas pipelines with combined defects[J]. Metals, 2018, 8(5): 346. DOI:10.3390/met8050346 |
| [34] |
XU Qian, FENG Junxiao, ZHANG Shuchen. Combined effects of different temperature and pressure loads on the "L"-type large-diameter buried pipeline[J]. International Journal of Heat and Mass Transfer, 2017, 111: 953. DOI:10.1016/j.ijheatmasstransfer.2017.04.067 |
| [35] |
帅健. 管线力学[M]. 北京: 科学出版社, 2010. SHUAI Jian. Pipeline mechanics[M]. Beijing: Science Press, 2010. |
| [36] |
FENG Xin, WU Wenjing, LI Xingyu, et al. Experimental investigations on detecting lateral buckling for subsea pipelines with distributed fiber optic sensors[J]. Smart Structures and Systems, 2015, 15(2): 245. DOI:10.12989/sss.2015.15.2.245 |
| [37] |
REN Liang, JIA Ziguang, LI Hongnan, et al. Design and experimental study on FBG hoop-strain sensor in pipeline monitoring[J]. Optical Fiber Technology, 2014, 20(1): 15. DOI:10.1016/j.yofte.2013.11.004 |
| [38] |
王忠福, 何思明, 刘汉东, 等. 不同岩崩碎屑颗粒尺寸运移堆积特性试验研究[J]. 岩石力学与工程学报, 2015, 35(S2): 3652. WANG Zhongfu, HE Siming, LIU Handong, et al. Experimental study on accumulation characteristic of different rock avalanche debris particles size[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 35(S2): 3652. DOI:10.13722/j.cnki.jrme.2014.0847 |
| [39] |
林宗元. 简明岩土工程勘察设计手册[M]. 北京: 中国建筑工业出版社, 2003. LIN Zongyuan. Brief geotechnical engineering survey and design manual[M]. Beijing: China Architecture and Building Press, 2003. |
| [40] |
MA Hongqiang, HE Binxian, LUO Xinmei, et al. Investigation on strain characteristic of buried natural gas pipeline under longitudinal landslide debris flow[J]. Journal of Natural Gas Science and Engineering, 2021, 86: 103708. DOI:10.1016/j.jngse.2020.103708 |
 2022, Vol. 54
2022, Vol. 54


