在热机循环和热泵循环基础上构建的联合循环，具有热源利用效率高、输出能力强、能量输出形式多样等诸多优点^[1]。一般而言, 联合循环中的热机子循环部分负责功量输出，热泵子循环部分则是在量(功量、热量)的驱动下，帮助系统进一步获取制热量或制冷量。实际联合循环可以根据不同的输出形式进行分类，如单一的制冷、制热循环、热电联产系统、功冷联供系统和冷热电三联供系统等^[2-7]。

以往研究多采用经典热力学和有限时间热力学方法，将上述复杂热力系统简化为多热源的理想热力学模型^[8-10]。然而，由于热源条件、系统结构、输出形式均不相同，导致不同类型联合循环的热力性能无法对比；关于联合循环热力性能极限的理论研究也十分有限。以张世钢等^[11]提出的吸收式大温差换热技术为例，该系统具有两热源特点(热网一次水和热网二次水)，并能够让一次水出口温度大幅低于二次水进口温度，实现大温差换热。这在宏观上已经突破了传统温驱换热过程的极限换热情况。研究人员^[12-15]提出了两介质换热系统的广义换热过程概念，揭示了两介质换热系统的能量转换机理、热力性能极限、大温差换热过程的判定依据与实际大温差换热系统的构建原则。然而，该理论模型的基本假设之一是热机循环的输出功量与热泵循环的输入功量完全相等，这显然不适用于研究热电联产系统、功冷联供系统等其他形式的联合循环。

本文以两介质热功转换系统为研究对象，提出驱热力过程的基本概念，并根据不同分类准则对驱热力过程进行了分类。构建并求解典型驱热力过程函数，分析其热功转换性能极限，构建评价指标体系。

1 驱热力过程的概念与分类 1.1 驱热力过程的基本概念

本文将具有以下特点的系统称为两介质热功转换系统：1)系统内部包括一个吸热介质和一个放热介质(包括源和汇)、换热设备以及热功转换设备；2)吸热介质与放热介质之间存在能量交换(热量、功量)，但不存在质量交换；3)系统与外界之间可以存在能量交换(热量、功量)，但不存在质量交换。

对于理想两介质热功转换系统而言，忽略系统内的一切不可逆损失，所有热力过程均为可逆过程，即系统中不存在不可逆因素。理想两介质热功转换系统是本文的研究对象，其特点是包含了两个有限热容的热源。

可以通过热量、功量和质量3种形式进行传递^[16]。由于不存在与外界的质量交换，因此在两介质热功转换系统中，只能通过热量和功量的形式进行传递。系统中既有温差驱动的常规换热设备，又有由流驱动的热功转换设备或过程，这使得两换热介质之间的换热能力极限需要被重新定义。本文将两介质热功转换系统内发生的热力过程更加广泛的归结为以流作为驱动力的热力过程，简称驱热力过程。驱热力过程理论模型的特点包括：

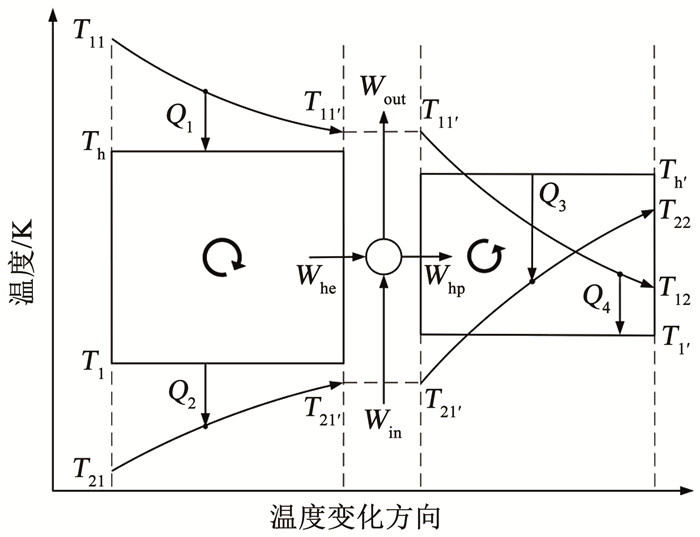
1) 放热介质的高温段设置若干可逆热机循环，并将这个区域称为热机循环区间。在放热介质低温段设置若干可逆热泵循环，并将这个区间称为热泵循环区间，如图 1、2所示。

2) 一部分热机循环输出的功量向系统外界输出；另一部分热机循环输出的功量驱动热泵循环。循环之间的能量传递在更多情况下是以流的形式出现的，故本文将此类热力过程称为驱热力过程。

3) 热泵循环在外部量输入与热机循环流驱动的共同作用下，进一步将放热介质的热量转移至吸热介质，使得系统获得更大的换热能力极限。

4) 在实际驱热力系统中，可以不存在典型的热机循环和热泵循环，但存在相应的热力过程。

5) 本文所定义的驱热力过程可以与外界存在着能量交换，这是和广义换热过程理论模型的本质区别。

1.2 驱热力过程的分类

驱热力过程中最为常见的流形式是功量。根据驱热力过程的实际应用场景，热机循环区间的总输出功量和热泵循环区间的总输入功量之间存在平衡关系，这是驱热力过程的分类依据之一。驱热力过程的功量平衡分类如下：

1) 当热机循环区间输出的总功量超过热泵循环区间的输入功量时，本文定义这种热力过程为功量有富余的驱热力过程，简称正余驱热力过程。在这种工况下，系统对外界输出功量。

2) 当热机循环区间输出的总功量不能满足热泵循环区间的功量需求时，本文定义这种热力过程为功量不足的驱热力过程，简称逆补驱热力过程。这种情况下热泵循环区间需要从外部环境获取额外的功量输入。

3) 当热机循环区间输出的总功量恰好与热泵循环区间所需的功量相等时，本文定义这种热力过程为功量相等的驱热力过程，简称等量驱热力过程。这种情况下，等量驱热力过程与可逆换热过程^[15]等价。

对于以上3种分类，本文提出了输出功量占比这一量纲一的参数，用于定量分析驱热力过程类型。其定义为：驱热力过程中系统对外界输出功量与热机循环产生的功量之比。其表达式为

$ \varphi=\frac{W_{\mathrm{net}}}{W_{\mathrm{he}}}=1-\frac{W_{\mathrm{hp}}}{W_{\mathrm{he}}} $

(1)

式中：φ为输出功量占比，W_net为净输出功量，W_he为热机循环区间的总输出功量，W_hp为热泵循环区间的总输入功量。

根据输出功量占比的不同取值，驱热力过程的定量分类情况如下：

1) 热机循环区间产生的功量全部用于对外界输出时，φ=1，对应于正余驱热力过程(无热泵循环区间的极限情况)，实际系统以有机朗肯循环为例。

2) 热机循环产生的功量一部分用于对外界输出，一部分用于驱动热泵循环，从而获取更多换热量时，φ∈(0, 1)，对应于正余驱热力过程，实际系统以串联型联合循环^[3]、并联型联合循环为例^[17]。

3) 热机循环产生的功量全部用于驱动热泵循环，且外界输入功量为0时，φ=0，对应于等量驱热力过程(广义换热过程)，实际系统以大温差换热系统为例^[15]。

4) 热机循环产生的功量全部用于驱动热泵循环，且外界输入一部分功量同时驱动热泵循环，从而获取更大的换热量，此时φ∈(－∞, 0)，对应于逆补驱热力过程，实际系统以补燃型溴化锂吸收式热泵为例^[18]。

5) 热力过程中不再有热机循环区间，完全由外界输入功量驱动的热泵循环，此时φ=-∞，对应于逆补驱热力过程，实际系统以水源热泵空调系统为例。

除功量平衡分类方法外，还包括其他分类方法。根据两介质热功转换系统中的放热介质与吸热介质的不同流动形式，可将驱热力过程分为不同流型，如连续顺流型、连续逆流型、先顺后逆型、先逆后顺型、离散顺流型、离散逆流型、离散顺逆流结合型^[15]。

当两介质的热容比随热功转换过程而变化时，本文称之为变热容比驱热力过程，如自驱动烟气全热回收系统^[19]。当两介质的热容比恒定时，定义为定热容比驱热力过程，本文以研究定热容比驱热力过程为主。

驱热力过程理论模型适用于分析两介质热功转换系统的任何情况。这显然比其他联合循环理论模型更具有普适性。不同类型的两介质实际系统也可以在驱热力过程理论模型的框架下进行热力性能对比。

2 驱热力过程的数学建模

本文着重研究连续顺流型和连续逆流型两种典型情况。单循环连续顺流型驱热力过程的能流示意图如图 3所示。其中单循环是指在热机循环区间内仅有一个实际热机循环，在热泵循环区间内仅有一个实际热泵循环。将放热介质热容与吸热介质热容之比定义为热容比，并假定在本文所述热功转换系统中的热容比均为固定值，其定义式为

$ k=c_1 m_1 / c_2 m_2 $

(2)

式中：k为热容比，c₁m₁为放热介质热容，c₂m₂为吸热介质热容。

对于连续顺流型驱热力过程^[15]而言，其能量守恒方程可以简化为

$ \mathrm{d} T_2 / \mathrm{d} T_1=-k \cdot T_2 / T_1 $

(3)

式中：T₁为放热介质温度，T₂为吸热介质温度。

假定式(3)的定解条件是给定放热介质进口温度T₁₁和吸热介质进口温度T₂₁，则有

$ T_1^k \cdot T_2=T_{11}^k \cdot T_{21}=H_1 $

(4)

式中H₁为积分常数。

本文规定，热机循环区间的输出功量与系统输出功量为正，热泵循环区间的输入功量与系统输入功量为负。则根据驱热力过程的能量守恒关系，吸热介质与放热介质的能量守恒公式可以表示为:

$ W_{\text {net }}=W_{\text {out }}-W_{\text {in }}=W_{\text {he }}-W_{\mathrm{hp}} $

(5)

$ W_{\text {net }}=c_1 m_1\left(T_{11}-T_{12}\right)-c_2 m_2\left(T_{22}-T_{21}\right) $

(6)

式中：W_out为热机循环向外界输出功量，W_in为热泵循环从外界获取功量，T₁₂为放热介质出口温度，T₂₂为吸热介质出口温度。

联立求解式(4)和式(6)，则可得到放热介质和吸热介质之间的温度关系式：

$ k \cdot T_{12}^{k+1}-\left(k \cdot T_{11}+T_{21}-\Delta T_\text{w}\right) \cdot T_{12}^k+T_{21} \cdot T_{11}^k=0 $

(7)

$ \Delta T_{\mathrm{w}}=W_{\text {net }} /\left(c_2 m_2\right) $

(8)

式中ΔT_w为吸热介质等效温升。

吸热介质等效温升的物理意义为：系统为了向外界输出净功量W_net，而使吸热介质无法进一步升高的温度。在相同工况下，若将W_net全部用于驱动理想条件下的热泵循环，则吸热介质出口温度可以进一步升高ΔT_w。

式(7)确立了放热介质出口温度与放热介质进口温度、吸热介质进口温度、热容比、吸热介质等效温升之间的隐式函数关系，本文将该隐式函数关系定义为连续顺流型驱热力过程函数:

$ T_{12}=I\left(k, T_{11}, T_{21}, \Delta T_\text{w}\right) $

(9)

单循环连续逆流型驱热力过程的能流示意图如图 4所示。与连续顺流型的数学模型相似，其能量守恒公式可表示为

$ T_1^{-k} \cdot T_2=T_{12}^{-k} \cdot T_{21}=H_2 $

(10)

式中H₂为积分常数。

则放热介质与吸热介质之间的温度关系可以表达为

$ k \cdot T_{11}^{1-k}-\left(k \cdot T_{12}-T_{21}+\Delta T_{\mathrm{w}}\right) \cdot T_{11}^{-k}-T_{21} \cdot T_{12}^{-k}=0 $

(11)

式(11)建立了连续逆流型驱热力过程中的放热介质与吸热介质之间的隐函数关系，并与式(7)相似。联立式(10)、(11)，则连续逆流型驱热力过程函数为

$ T_1^{-k} \cdot T_2=\left[I\left(k, T_{11}, T_{21}, \Delta T_\text{w}\right)\right]^{-k} \cdot T_{21} $

(12)

本文与文献[15]中的可逆换热过程最大不同之处在于式(5)，它可以对不同类型的两介质热功转换系统进行分析。采用牛顿-拉夫森单点迭代法即可对理想驱热力过程函数进行求解。其他类型驱热力过程的数学模型与模型验证不再赘述。

3 结果与讨论 3.1 驱热力过程的温度特性

连续顺流型驱热力过程两介质温度关系如图 5所示。以k=0.5为例，随着放热介质温度逐渐降低，吸热介质温度由A点逐渐升高至B点，此时两介质温度相同，达到了传统温驱换热系统的换热极限。当热机循环区间输出的全部量都恰好用于驱动热泵循环区间时，两介质的温度变化极限为D点，此时放热介质由383.00 K降低至285.39 K，吸热介质由308.00 K升高至356.81 K，温度交叉现象明显。对于正余驱热力过程而言，当对外界输出量且ΔT_w=2时，两介质的换热能力极限为图中的C点。此时两介质出口温度分别为307.29 K和343.85 K。理论上，热机循环输出的最大功量出现在B点。对于逆补驱热力过程而言，当有外部量输入且ΔT_w=-2时，两介质的换热能力极限为图中的E点。在外部量的驱动下，两介质进一步交换热量，此时两介质的出口温度极限分别为271.89 K和365.55 K。理论上，持续的外部量输入最终能够将放热介质中的热量全部转移至吸热介质。

在相同计算条件下，连续逆流型驱热力过程两介质温度关系如图 6所示。以k=0.5为例，此时放热介质进口温度与吸热介质出口温度相对应。相对于连续逆流型等量驱热力过程而言，连续逆流型正余驱热力过程两介质温度变化曲线与其近似平行，放热介质出口温度升高，吸热介质出口温度降低。同理，逆补驱热力过程的放热介质出口温度进一步降低，吸热介质出口温度进一步升高。不论是连续顺流型还是连续逆流型，随着热容比k值的不断升高，放热介质的温度变化范围逐渐缩小，吸热介质的温度变化范围则逐渐增加。特别地，当k>1.0时，等量驱热力过程中的吸热介质出口温度将大于放热介质的出口温度。综合图 5、6分析可知，顺流型驱热力过程中的温度交叉现象更为明显。

3.2 过程功量传递特性

在驱热力过程中，热机循环区间与热泵循环区间之间传递的可以是实际的机械功量，也可以是浓度差、压力差等势能所传递的做功能力。

当放热介质出口温度与吸热介质出口温度相等时，此时热机循环区间内的总输出功量最大。本文定义该点温度为分界点温度T^*，顺流型和逆流型驱热力过程的分界点温度表达式分别如下：

$ T^*=T_{11}^{\frac{k}{k+1}} T_{21}^{\frac{1}{k+1}} $

(13)

$ T^*=\left[I\left(k, T_{11}, T_{21}, \Delta T_\text{w}\right)\right]^{\frac{k}{k-1}} T_{21}^{\frac{1}{11-k}} $

(14)

对于k=1.0的特殊情况，逆流型驱热力过程的分界点温度值为放热介质和吸热介质进口温度的平均值。

驱热力过程中的过程功量定义为：当放热介质释放热量至某一温度时，热机循环区间所产生的有用功量、热泵循环区间所消耗的有用功量以及驱热力系统的净输出功量代数和。同时，假设系统外界的输入功量与输出功量只作用于区间分界点处，系统对外输出功量为正，外界向系统输入功量为负。当放热介质温度变化区间为[T₁₁, T₁₂]时，驱热力过程中的过程功量表达式为

$ \left\{\begin{array}{l} W_{\text {process }}=\int_{T_{11}}^{T^*}-c_1 m_1\left(\frac{T_1-T_2}{T_1}\right) \mathrm{d} T_1, \quad T_1 \in\left[T_{11}, T^*\right) \\ W_{\text {process }}=\int_{T^*}^{T_{12}}-c_1 m_1\left(\frac{T_1-T_2}{T_1}\right) \mathrm{d} T_1-W_{\text {net }}, T_1 \in\left[T^*, T_{12}\right] \end{array}\right. $

(15)

式中W_process为过程功量。

为了使分析更具普适性，本文定义了量纲一的过程功量，为驱热力过程的过程功量与总换热量的比值。顺流型和逆流型驱热力过程的量纲一的过程功量表达式如下：

$ \bar{W}_{\text {process }}=\frac{m_1 c_1 \cdot\left[\left(T_{11}-T_{12}\right)+\frac{H_1}{k}\left(\frac{1}{T_{11}^k}-\frac{1}{T_{12}^k}\right)\right]-W_{\text {net }}}{c_2 m_2\left(T_{22}-T_{21}\right)+W_{\text {net }}} $

(16)

$ \bar{W}_{\text {process }}=\frac{m_1 c_1 \cdot\left[\left(T_{11}-T_{12}\right)+\frac{H_2}{k}\left(T_{12}^k-T_{11}^k\right)\right]-W_{\text {net }}}{c_2 m_2\left(T_{22}-T_{21}\right)+W_{\text {net }}} $

(17)

式中W_process为量纲一的过程功量。

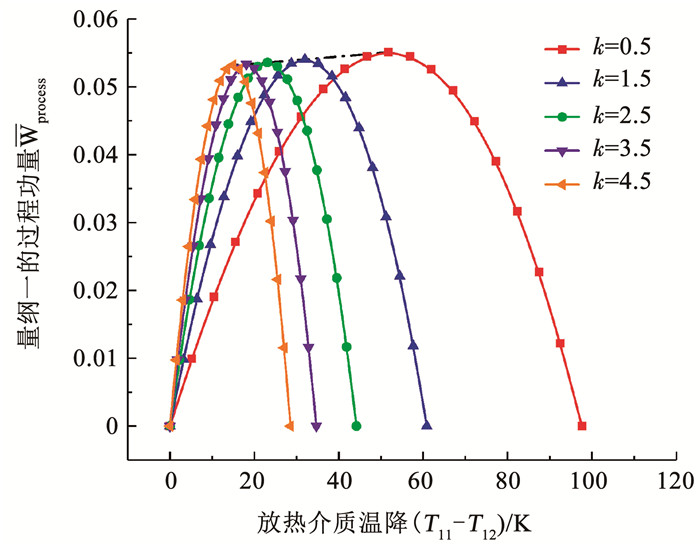
在放热介质进口温度为383.00 K，吸热介质进口温度为303.00 K，净输出功量为零的条件下，图 7分析了顺流型驱热力过程中的量纲一的过程功量随放热介质温降(T₁₁－T₁₂)的变化规律。由图 7可知，随着放热介质温度逐渐降低，量纲一的过程功量先增大后减少。当放热介质温度降低至分界点温度T^*时，量纲一的过程功量达到峰值。对于等量驱热力过程而言，不论其流型如何，热机循环区间输出的总功量与热泵循环区间所需的总功量相等。随着热容比的增加，分界点温度、热机循环区间最大输出功量以及放热介质出口温度均呈现减小趋势。

在上述工况条件下，图 8分析了逆流型驱热力过程中的量纲一的过程功量随放热介质温降(T₁₁－T₁₂)的变化规律。对于逆流型驱热力过程而言，当k < 1.0时，沿放热介质温度降低方向，先经过热机循环区间，再经过热泵循环区间。因此，对于图中k=0.5的工况，量纲一的过程功量呈现先增后减的变化规律。当k>1.0时，逆流过程中吸热介质的出口温度已经高于放热介质进口温度。沿放热介质温度降低方向，先经过热泵循环区间，再经过热机循环区间。因此，对于图中k=1.5的工况，量纲一的过程功量先在泵循环区间中由0开始递减，再在热机循环区间中逐渐递增至0。特别地，当k=1.0时，逆流型驱热力过程的量纲一的过程功量不随放热介质温降而变化。综合分析等量驱热力过程中的量纲一的过程功量变化趋势可知：相同工况下，顺流型驱热力过程比逆流型驱热力过程可以获取更大的量纲一的过程功量。

3.3 吸热介质等效温升

在放热介质进口温度为383.00 K，吸热介质进口温度为303.00 K，两介质热容比k=2.5的工况下，图 9分析了顺流型驱热力过程中量纲一的过程功量随吸热介质等效温升ΔT_w的变化规律。ΔT_w=0对应等量驱热力过程，作为图 9分析的基准曲线。当ΔT_w>0时，系统对外输出功量，此时对应于正余驱热力过程。随着放热介质由A点降温至B点，热机循环区间产生的有用功量逐渐累加，并在放热介质温度达到分界点温度T^*时，热机循环区间最大输出功量达到最大值。在对外输出净功量后，量纲一的过程功量降低至C点，并由此开始进入热泵循环区间。随着放热介质降温至D点，热泵循环区间结束，正余驱热力过程中的功量达到平衡。由于对外界输出了有用功量，使得放热介质出口温度高于基准工况。当ΔT_w < 0时，外界对系统输入功量，此时对应于逆补驱热力过程。热机循环区间输出的最大功量小于基准工况。在外部输入功量的作用下，放热介质出口温度可以进一步降低至更低水平。对于顺流驱热力过程而言，分界点温度并不随着ΔT_w的改变而改变，这与图 5的分析结果一致。

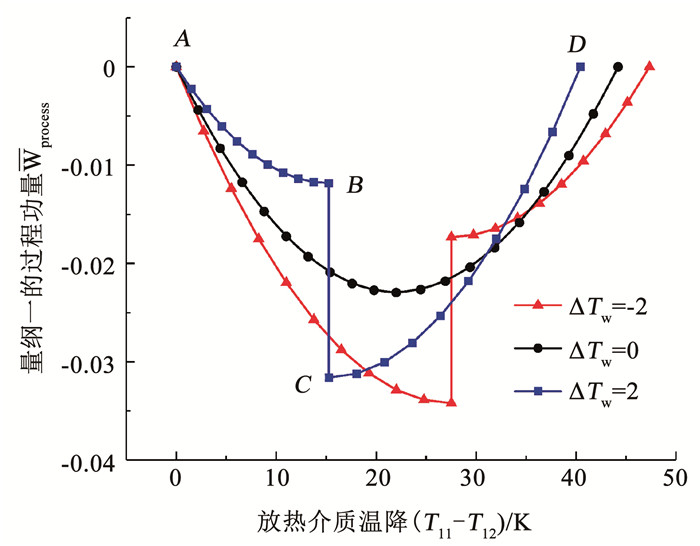
在上述工况条件下，图 10分析了逆流型驱热力过程中量纲一的过程功量随吸热介质等效温升ΔT_w的变化规律。对于正余驱热力过程(ΔT_w>0)，放热介质先流经热泵循环区间，量纲一的过程功量由0开始递减。随着放热介质由A点降温至B点，热泵循环区间所需的过程功量达到最大值。由于对外界输出净功量，故在分界点温度处，量纲一的过程功量由B点降低至C点。随后，放热介质进入热机循环区间，量纲一的过程功量递增至0，最终达到能量平衡。相比于基准工况ΔT_w=0，正余驱热力过程中的热泵循环区间所需过程功量减小，逆补驱热力过程中的热泵循环区间所需过程功量增大。特别地，相比于基准工况，正余驱热力过程中分界点温度减小，逆补驱热力过程中分界点温度增大，这与图 6的分析结果一致。由于顺流型驱热力过程具有更大的量纲一的过程功量，因此其吸热介质等效温升的最大值大于逆流型。

3.4 评价指标与案例

驱热力过程理论模型适用于分析不同类型的实际循环，但仍需要构建合理评价指标体系，才能用于对比分析理想驱热力过程与实际系统性能。

3.4.1 换热完善度

受不可逆因素影响，实际系统所能达到的换热能力必然低于极限情况。换热完善度定义如下：放热介质与吸热介质进口参数相同，且输出功量占比相同的条件下，实际热力过程与理想驱热力过程之间的最大换热量的比值。其表达式为

$ \eta_{\mathrm{h}}=\frac{Q_{\text {real }}}{Q_{\text {iep }}}=\frac{T_{11}-T_{12 \text {, real }}}{T_{11}-T_{12, \text { iep }}} $

(18)

式中：η_h为换热完善度，Q_real为实际热力过程最大换热量，Q_iep为理想驱热力过程最大换热量，T_{12, real}为实际热力过程放热介质出口温度，T_{12, iep}为理想驱热力过程放热介质出口温度。

3.4.2 吸热介质等效温升比

吸热介质等效温升表征了热力过程的类型，也是衡量做功能力的重要指标。吸热介质等效温升比定义如下：在放热介质与吸热介质进口参数相同，且输出功量占比相同的条件下，实际热力过程与理想驱热力过程之间的吸热介质等效温升之比。其表达式为

$ \eta_{\mathrm{w}}=\frac{\Delta T_{\mathrm{w}, \text { real }}}{\Delta T_{\mathrm{w}, \text { iep }}}=\frac{W_{\text {net, real }}}{W_{\text {net }, \text { iep }}} $

(19)

式中：η_w为吸热介质等效温升比，ΔT_w，real、ΔT_w，iep为实际热力过程和理想驱热力过程的吸热介质等效温升，W_{net, real}、W_{net, iep}分别为实际热力过程和理想驱热力过程的净输出功量。

3.4.3 热力完善度

在放热介质与吸热介质进口参数相同，且输出功量占比相同的条件下，实际热力过程净输出功量效率与理想驱热力过程净输出功量效率的比值。其表达式为

$ \mu=\frac{\eta_{\text {net }, \text { real }}}{\eta_{\text {net }, \text { iep }}}=\frac{\eta_{\mathrm{w}}}{\eta_{\mathrm{h}}} $

(20)

式中：μ为热力完善度，η_net，real、η_net，iep分别为实际热力过程和理想驱热力过程的净输出功量效率。

串联型联合循环^[3]是在基本型ORC^[20]的基础上，通过梯级利用热源热量并回收全部冷凝热用于供热，因而具有输出能力强、输出形式多样的优点，适用于同时有用热、用电需求的场合。表 1列出了包括放热介质压力P₁、吸热介质压力P₂、蒸发器过热度ΔT_e、冷凝器过冷度ΔT_c、换热器窄点温差ΔT、泵效率η_p、膨胀机效率η_t在内的对比工况主要参数。在表 1所述工况条件下，采用驱热力过程理论模型对比分析了基本型ORC与串联型联合循环的热力性能，二者都是以R123为有机工质、热容比为1.30的逆流型的正余驱热力过程。

由表 2分析可知，基本型ORC系统对外净输出功量为257 kW，略高于串联型联合循环的244 kW。由于串联型联合循环的实际总换热量是基本型ORC总换热量的1.97倍，使得串联型联合循环的净输出功量效率仅为6.55%，显著低于基本型ORC的13.61%。从热力学第二定律角度分析，基本型ORC的效率(45.73%)显著高于串联型联合循环的效率(26.61%)。相比于各自的理想正余驱热力过程，虽然两个实际系统的换热完善度几乎相同，但基本型ORC的热力完善度为55.73%，显著高于串联型联合循环的36.38%。

分析结果表明，基本型ORC在净发电效率、效率、热力完善度等方面均具有显著优势。而串联型联合循环通过设置喷射式热泵，可在相同热源、冷源条件下获取相对更多的换热量，其输出能力和输出形式更具优势。但其代价是大幅偏离了理想驱热力过程的热力性能极限，仍有较大提升空间。

双热源联合循环实际系统热力性能的提高方法主要包括：1)高性能喷射器和膨胀机的优化设计；2)根据能量梯级利用原则构建多段联合循环系统，减少不可逆程度；3)在热机循环区间与热泵循环区间设置回热器等。

4 结论

1) 在顺流型驱热力过程中，放热介质与吸热介质间的温度交叉现象更为明显。

2) 相同工况下，顺流型驱热力过程可以获取更大的量纲一的过程功量。

3) 吸热介质等效温升可以用于判断驱热力过程类型，其最大值表征了输出功量极限。

4) 尽管热电联产系统的综合输出能力和热源利用效率较优，但其热力完善度仅为36.38%，大幅偏离了理想驱热力过程的热力性能极限。双热源联合循环实际系统的热力性能提高方法值得研究。