火灾是火失去控制而蔓延的一种灾害性燃烧现象,它是各种灾害中发生最频繁且极具毁灭性的灾害之一[1]。若多个起火点位置相近时,由于各火焰之间复杂的相互影响与耦合作用,极有可能形成融合火焰,尤其是在火焰区周围存在切向来流时,甚至可形成融合旋转火焰,进一步增加了火灾破坏性和扑救难度。在上世纪60年代,学者们就曾对多池火燃烧时相互作用与火焰融合等方面展开研究。Putnam等[2]利用天然气阵列形成火源研究了多个湍流浮力扩散火焰的相互作用,并推导了火焰髙度的量纲一的表达式。Thomas等[3]研究了平行放置的火源的火焰融合问题,并进行火焰受力分析,推导火焰融合的临界判据。在此基础上Bladwin[4]将其应用到多油池火源的研究中。Chigier等[5]就环形多池火进行研究,发现火焰高度、稳定性与环形阵列旋流水平、火源间距相关。Huffman等[6]曾通过实验较早地测量了环形池火阵列的燃烧速率随各池火大小及间距的变化情况。Schalike等[7]和Vasanth等[8]对多池火之间的火焰互相融合情况进行了实验研究和理论分析。在国内,刘琼[9]设计了等间距火方阵试验平台,模拟大量火源同时燃烧的情况,分析了空气卷吸和辐射热反馈两种作用机制对多源火燃烧的影响。王佳文等[10]利用多个竖井结构并排时各自内部火源所形成的火旋风试验获得了多个相对独立的火旋风同时发生时的质量燃烧速率及火焰高度的半经验公式。林圣泽等[11]构建了离散可燃物燃烧速率计算模型。焦艳[12]以正庚烷及乙醇作燃料,对正六边形及正方形的阵列进行研究,分析了火点直径D以及间距S等因素对燃烧速率、温度及速度分布、火焰高度、空气卷吸和热量反馈等的影响,揭示了多油池火源的流动、热反馈与燃烧耦合机制。然而,截至目前,国内外学者对多池火研究较多集中在火焰区引射空气没有物理结构约束时的非受限空间的多火源自由燃烧,而对竖井内有侧开缝处引射空气所形成的特殊切向来流作用于多池火时形成的融合旋转火焰研究相对较少。本文通过对竖井内多个池火融合火焰在侧开缝引射切向来流作用下所形成的融合旋转火焰进行试验,对典型多油池融合旋转火焰的燃烧速率与火焰高度进行了分析,所得结果对于此类特殊形式的燃烧速率、融合火焰高度预测等理论模型构建及其灾害防治等均有参考价值。
1 试验装置多池火耦合燃烧试验竖井如图 1所示。顶部开口的试验竖井尺寸为:长0.32 m×宽0.32 m×高2.00 m。竖井左右两侧配有可前、后滑动的侧面板,以便调整形成设定宽度的对称开缝,从而在火源区形成切向引射空气来流。竖井底部按设定摆放形式放置多个直径为0.05 m的圆形油池,燃料质量变化通过BK-D电子称(精度0.01 g)测量和记录。

|
图 1 有侧开缝的试验竖井 Fig. 1 Vertical shaft with side slits in test |
为与竖井内试验结果进行对比,同时还在没有竖井结构约束时进行了相同试验条件下的多池火自由耦合燃烧试验。多池火自由融合燃烧试验装置如图 2所示。

|
图 2 自由融合燃烧时的多池火试验装置 Fig. 2 Multi-pool fire test device during free fusion combustion |
根据试验竖井空间对油池个数的容纳程度,考虑多油池以相对规则的摆放方式融合燃烧场景。试验时,分别对不同油池最外缘间距S的双油池(S为2.50, 5.00, 7.50, 10.00 cm),一字摆放的3油池(S为1.25, 2.50, 5.00 cm)、等边三角形摆放的3油池(S为1.25,2.50,3.75和5.00 cm)及口字型摆放的4油池(S为2.50, 5.00, 7.50 cm)分别以竖井侧开缝宽度d为3.0, 5.0, 7.0, 9.0 cm进行试验,并以相同试验条件进行多油池自由融合燃烧试验。每条次试验的各油池均使用5 ml正庚烷(纯度98%)液态燃料。多油池的各种摆放方式如图 3所示。

|
图 3 各组油池摆放方式 Fig. 3 Arrangement of multi-fuel pools |
试验中由电子称获取的液体燃料质量变化近似为化学反应消耗产生[13],因此本文由燃料质量随时间变化获取燃烧速率以及热释放速率。
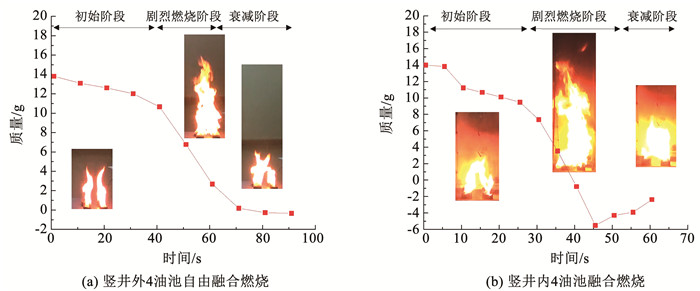
图 4为油池间距为5.00 cm 4油池自由燃烧与相同条件下侧开缝为5.0 cm竖通道内融合旋转火焰燃烧时燃料质量随时间变化曲线。可见多池火均经历了初始阶段、剧烈燃烧阶段和衰减阶段,其中初始阶段和衰减阶段还可能包含火焰间彼此融合以及衰减分离阶段。与自由融合燃烧相比,竖井内多池火融合燃烧过程的各典型阶段对应的融合火焰具有明显更高的亮度,且在剧烈燃烧阶段形成多池火融合旋转火焰的同时,还因剧烈旋转产生向上的抽吸力而使燃料质量出现一定程度的“失重”,致使各阶段持续时间与质量变化速率也与自由融合燃烧明显不同。说明竖井内多池火融合燃烧虽在整体变化趋势上与自由融合燃烧过程相似,但在燃烧过程中(尤其是剧烈燃烧阶段)的燃烧强度发生改变。
|
图 4 燃料质量随时间变化(4油池) Fig. 4 Fuel quality varying with time(four pools) |
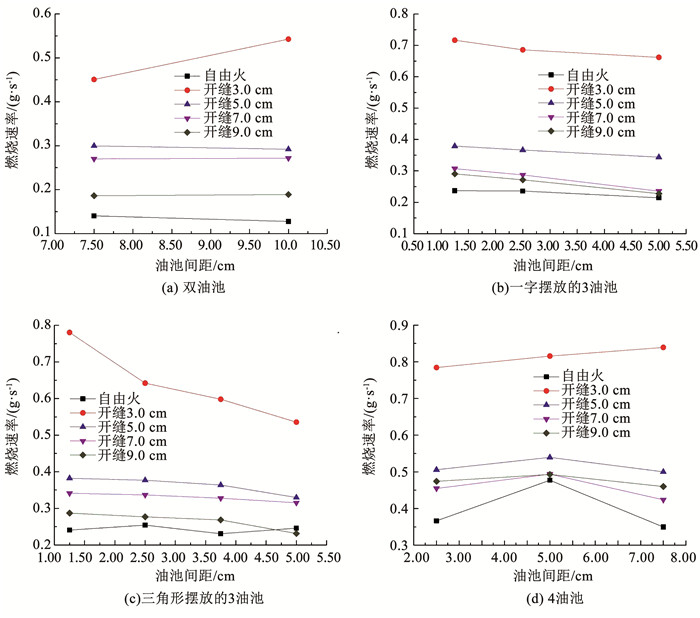
针对剧烈燃烧阶段,不同个数油池和摆放形式时的燃料质量损失速率随油池间距的变化如图 5所示。由图 5可见,与自由融合燃烧相比,竖井内的融合燃烧明显具有更高的燃料质量损失速率,说明竖井内的多池火燃烧被明显强化。同时,竖井侧开缝宽度为3.0 cm时质量损失速率约为自由燃烧时的2.0~3.7倍,而在竖井侧开缝分别为5.0, 7.0, 9.0 cm时约为1.1~2.0倍,说明过大的开缝形成的引射空气来流相对不利于多池火融合旋转火焰形成,从而降低了竖井内的多池火燃烧效率。另外,随着油池数量增加,侧开缝变化带来的质量损失速率增益有所减小,双油池质量损失速率约为自由燃烧时的3.7倍,而4油池时仅为2.0倍。
|
图 5 质量损失速率随油池间距的变化 Fig. 5 Mass loss rate varying with fuel pool spacing |
在获取单位面积燃烧速率ṁ基础上,引入量纲一的单位面积燃烧速率ṁ*:
| $ \dot{m}^*=\frac{\dot{m}}{\dot{m}_0} $ | (1) |
式中ṁ0为间距为2.50 cm的双油池自由燃烧时单位面积质量燃烧速率。同时,考虑到多池火每个火源可以看成是低压、外加辐射热流的独立燃烧火源[11],其质量燃烧速率与火源间距及油池摆放有关。因此参照文献[9],引入燃料面比率rs来表征各火源总燃料表面积与整个燃烧区域面积之比:
| $ r_s=\frac{\text { 火源数量 } \times \text { 油池面积 }}{\text { 燃烧区域面积 }} $ | (2) |
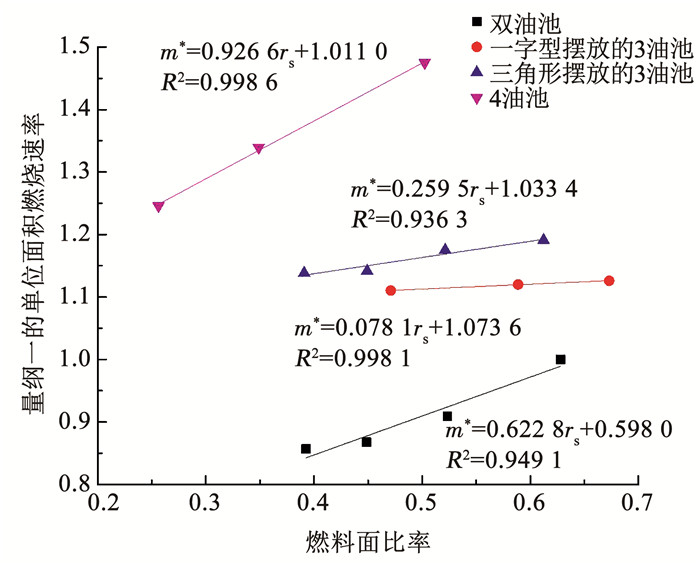
各试验工况的量纲一的单位面积燃烧速率与燃料面比率如图 6所示。可见针对一定摆放形式的多油池来说,其ṁ*与rs之间在一定范围内近似呈线性关系。
|
图 6 量纲一的单位面积燃烧速率随燃料面比率的变化 Fig. 6 Dimensionless burning rate per unit area varying with fuel surface ratio |
王佳文等[10]曾提出多源火旋风质量燃烧速率的半经验公式为
| $ \ln \bar{m}^*=a+b \ln \mathit{\Gamma}^* $ | (3) |
式中: m*为量纲一的单位面积燃烧速率,a,b为拟合常数,Γ*为量纲一的环量,其中
以高度为dz的竖通道微元体为控制体,根据质量守恒,向上流动的热流体质量等于由侧开缝进入的流体质量,即:
| $ \frac{\mathrm{d}}{\mathrm{d} z}\left(\rho u_z L^2\right)=2 \rho_{\infty} u d $ | (4) |
| $ \mathit{\Gamma}^*=\frac{2 \pi u L / \sqrt{2}}{\sqrt{g D_{\text {eq }}^3}}=\frac{\mathrm{d}}{\mathrm{d} z}\left(\rho u_z\right) \frac{\sqrt{2} \pi L^3}{2 \rho_{\infty} d \sqrt{g D_{\mathrm{eq}}^3}}=c\left(\frac{L^3}{d}\right) $ | (5) |
式中:ρ为竖通道内流体密度,ρ∞为竖通道外的环境气体密度,uz为竖通道内流体向上的运动速度,u为竖通道侧开缝入口速度,d为侧开缝宽度,L为竖通道边长,c为待定系数,
将式(5)带入式(3)可得到:
| $ \ln \bar{m}^*=a+b \ln (c)+b \ln \left(\frac{L^3}{d}\right) $ | (6) |
对于竖通道内多池火融合旋转火焰而言,若将其看作为自由浮力池火叠加上旋转环量,则式(6)中系数a可假设是与池火自由燃烧时量纲一的单位面积燃烧速率相关量,即a=pln ṁ*+q,其中p,q为系数。
将燃料质量损失数据带入式(6)中进行拟合得到竖井内多池融合旋转火焰燃料质量消耗关系式:
双油池(R2=0.942 9)
| $ \ln \dot{m}^{\prime *}=2.909\;0+11.690\;0 \ln \dot{m}^*+1.056\;0 \ln \left(\frac{L^3}{d}\right) $ | (7) |
一字摆放的3油池(R2=0.938 7)
| $ \ln \dot{m}^{\prime \prime \prime *}=0.455\;7+3.516\;0 \ln \dot{m}^*+0.762\;2 \ln \left(\frac{L^3}{d}\right) $ | (8) |
三角形摆放的3油池(R2=0.930 8)
| $ \ln \dot{m}^{\prime \prime \prime *}=0.455\;7+3.516\;0 \ln \dot{m}^*+0.762\;2 \ln \left(\frac{L^3}{d}\right) $ | (9) |
4油池(R2=0.810 7)
| $ \ln \dot{m}^{{\prime \prime \prime \prime *}}=0.930\;8+0.031\;0 \ln \dot{m}^*+0.512\;4 \ln \left(\frac{L^3}{d}\right) $ | (10) |
针对竖井内多池火融合旋转火焰剧烈燃烧阶段的燃料质量损失速率,由式(7)~(10)计算结果与试验数据对比如图 7所示。可以看出双油池和3油池场景的吻合相对较好,而4油池时受试验竖井及侧开缝宽度限制,油池间相互竞争空气而相互抑制彼此燃烧反应,导致关系式与试验数据有一定偏差。

|
图 7 竖井内多池火融合旋转火焰的燃料质量消耗速率试验数据与关系式计算结果对比 Fig. 7 Comparison between test data and calculation results of fuel mass consumption rate of multi-pool fusion rotating flame in shaft |
实验中的多池火融合火焰高度H可由获取的图像结果获取。以Zukoski等[15]引入的间歇率0.5时对应的H值来定义平均火焰高度Hc。图 8为油池间距2.50 cm时,自由燃烧火焰与双池融合旋转火焰燃烧过程的对比,图像的时间间隔7 s。由图 8可见,在燃料被引燃后,竖井内的各池火随即展现出比自由融合燃烧时更明显的相互融合趋势;随着时间的推移,竖井内多池火全面融合并发生整体旋转与倾斜,而自由融合燃烧的多池火仅在火焰中部以上区域发生相互融合,底部火焰依然保持各池火相对独立的火焰形式;在燃烧后期阶段,自由融合燃烧的火焰彼此分开保持各自独立,而竖井内多池火融合旋转火焰状态保持则保持至近乎燃料耗尽。

|
图 8 双池融合火焰形态变化(S=2.50 cm) Fig. 8 Morphological change in fusion flame from two fuel pools(S=2.50 cm) |
图 9为侧开缝宽度d为5.0 cm时,竖井内多油池融合旋转火焰与自由融合燃烧火焰高度对比。图 9中同时给出了对应峰值火焰高度Hmax。由图 9可以看出,双油池时,竖井内融合旋转火焰峰值高度约为自由融合燃烧时的1.10倍,但平均高度仅约为自由融合燃烧时的80%,而油池数量增加后,竖井内融合旋转火焰平均高度则与自由融合燃烧时接近或稍高。这是由于竖井内多池火燃烧初始阶段尚未形成剧烈的融合旋转火焰时,此时多池火各自相对独立的火焰在切向来流作用下发生倾斜导致其竖直方向的高度降低,而油池数量较少时相对更易受切向来流影响而发生幅度更大的倾斜;随着竖井内多池火燃烧剧烈程度的增加,引射空气能力增强,使侧开缝进入竖井的空气来流具有更大的切向力而形成剧烈的多池火融合旋转火焰,此时火焰高度较自由融合燃烧时明显增加。对比图 9(b)、(c)可发现,三角形摆放的油池火焰平均约为一字摆放的油池火焰平均高度的1.10倍。这是由于三角形摆放时,各个火源之间彼此更容易相互影响,燃料表面受到相对更多的来自其他两油池火焰的热辐射,因此加速燃料的蒸发速度,进而提升了融合火焰高度。图 9(c)中,油池间距5.00 cm时的竖井内融合旋转火焰峰值高度低于自由融合燃烧火焰,这是由于在此油池间距时竖井内的融合旋转火焰并不稳定,加上由侧开缝进入的气流的影响导致融合旋转火焰整体倾斜且产生明显的进动现象。由此可见,竖井内多池火融合旋转火焰燃烧过程涉及油池个数、油池摆放形式以及竖井侧开缝宽度等多个参数之间的耦合关系。另外,一字摆放的3油池和4油池工况下融合旋转火焰峰值高度约为相同条件下自由融合燃烧时的1.32倍和1.25倍,而双油池及等边三角形摆放的3油池融合旋转火焰峰值高度约为自由融合燃烧时的1.10倍。这说明在竖井结构一定时,油池数量的增加会增大相同条件下融合旋转火焰与自由融合燃烧火焰峰值高度之间的差异。

|
图 9 火焰平均高度及峰值随油池间距的变化 Fig. 9 Average and peak flame heights varying with fuel pool spacing |
针对竖井内单池火旋风,雷佼[13]曾提出火焰高度和热释放速率与外加环量耦合公式为
| $ H / D=k\left(\dot{Q}^* \cdot \mathit{\Gamma}^{* 2}\right)^m $ | (11) |
式中:H为火旋风火焰高度;
| $ H^*=H / H_P=f\left(\mathit{\Gamma}^*\right) $ | (12) |
将式(5)和式(11)带入式(12),可得
| $ \ln H^*=\ln \left(\frac{H}{H_p}\right)=\ln \left(\frac{k D_{ \mathrm{eq}}}{H_p}\right)+m \ln \left[\dot{Q}^* \cdot\left(\frac{L^3}{d}\right)^2\right]+2 m{\ln}\;c $ | (13) |
式中以c(L3/d)代替速度环量,将侧开缝宽度、燃料热释放速率与旋转火焰高度结合在一起。根据前文推导,多池融合旋转火焰的量纲一的单位质量燃烧速率可由自由池火量纲一的单位质量燃烧速率m*及燃料面比率rs求得,故式(13)间接地将自由池火燃烧速率与旋转火焰高度结合在一起。
本文对于式(13)假设与推导都是建立在火焰竖直方向的前提下,未考虑融合火焰在切向力作用下的倾斜影响。对于本文试验,竖井内多池火融合旋转火焰形成后稳定时段对应的平均火焰高度随油池间距的变化数据带入式(13)中进行拟合计算,可得:
双油池(R2=0.985 1)
| $ \ln H^*=0.005\;0 \ln \left[\dot{Q}^* \cdot\left(\frac{L^3}{d}\right)^2\right]+0.070\;8 $ | (14) |
一字摆放的3油池(R2=0.921 2)
| $ \ln H^*=-0.038\;0 \ln \left[\dot{Q}^* \cdot\left(\frac{L^3}{d}\right)^2\right]+0.180\;9 $ | (15) |
三角形摆放的3油池(R2=0.884 6)
| $ \ln H^*=-0.001\;4 \ln \left[\dot{Q}^* \cdot\left(\frac{L^3}{d}\right)^2\right]+0.041\;7 $ | (16) |
4油池(R2=0.898 2)
| $ \ln H^*=-0.003\;4 \ln \left[\dot{Q}^* \cdot\left(\frac{L^3}{d}\right)^2\right]+0.133\;3 $ | (17) |
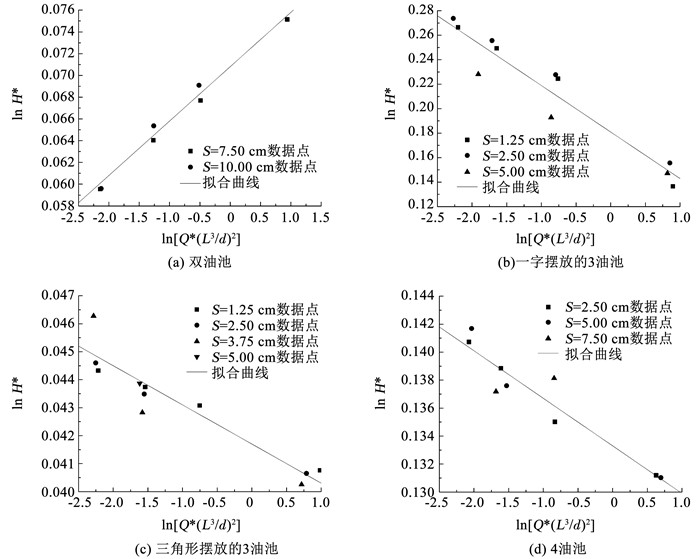
图 10为拟合公式计算结果与试验数据对比。可以看出多油池的融合火焰高度公式计算结果与试验数据吻合较好。另外,双油池拟合直线对应的斜率与其余3个场景时相反,说明对于双油池试验而言,竖井内氧气相对较充足,减小侧开缝宽度不会对燃烧速率有较大影响,即
|
图 10 融合火焰高度试验数据与拟合曲线 Fig. 10 Test data of fusion flame height and its fitting curve |
1) 有侧开缝的竖井所形成的独特引射空气来流改变了多池火之间火焰融合形态以及对燃料液面热反馈,形成的融合旋转火焰在一定程度上强化了燃烧效率并提升了火焰高度。
2) 竖井侧开缝过大可降低竖井内多池火燃烧效率。同时,随着油池数量增加,侧开缝变化带来的质量损失速率增益有所减小,双油池质量损失速率约为自由燃烧时3.7倍,而4油池时仅为2.0倍。
3) 竖井侧开缝和燃料量一定时,多油池燃烧引射空气能力和相对摆放位置决定了融合旋转火焰的形成与持续时间。竖井内双油池时,融合旋转火焰持续时间占总体燃烧过程的时间相对较短,此时融合旋转火焰峰值高度约为自由燃烧融合火焰的1.1倍,但平均高度仅约为自由融合燃烧时的80%。
4) 竖井结构一定时,油池数量增加不仅强化融合旋转火焰的生成能力,而且增大融合旋转火焰与自由融合火焰峰值高度之间的差异。同时,使各池液面均匀接收融合火焰热量反馈的油池摆放方式更有利于形成相对强烈的融合旋转火焰。
5) 基于浮力火焰叠加环量的思想,推导并拟合得到了竖井内典型形式多池火耦合旋转火焰燃烧速率与火焰高度理论模型。
| [1] |
范维澄, 王清安, 姜冯辉, 等. 火灾学简明教程[M]. 合肥: 中国科学技术大学出版社, 1995: 1. FAN Weicheng, WANG Qingan, JIANG Fenghui, et al. A brief course of fire science[M]. Hefei: China University of Science and Technology Press, 1995: 1. |
| [2] |
PUTNAM A A, SPEICH C F. A model study of the interaction of multiple turbulent diffusion flames[J]. Symposium (International) on Combustion, 1963, 9(1): 867. DOI:10.1016/S0082-0784(63)80093-4 |
| [3] |
THOMAS P H, BALDWIN R, HESELDEN A J M. Buoyant diffusion flames: Some measurements of air entrainment, heat transfer, and flame merging[J]. Symposium (International) on Combustion, 1965, 10(1): 983. DOI:10.1016/S0082-0784(65)80241-7 |
| [4] |
BALDWIN R. Flame merging in multiple fires[J]. Combustion and Flame, 1968, 12(4): 318. DOI:10.1016/0010-2180(68)90036-9 |
| [5] |
CHIGIER N A, APAK G. Interaction of multiple turbulent diffusion flames[J]. Combustion Science and Technology, 1975, 10(5/6): 219. DOI:10.1080/00102207508946674 |
| [6] |
HUFFMAN K G, WELKER J R, SLIEPCEVICH C M. Interaction effects of multiple pool fires[J]. Fire Technology, 1969, 5(3): 225. DOI:10.1007/BF02591520 |
| [7] |
SCHALIKE S, MISHRA K B, WEHRSTEDT K D, et al. Limiting distances for flame merging of multiple n-Heptane and Di-tert-Butyl peroxide pool fires[J]. Chemical Engineering Transactions, 2013, 32: 121. DOI:10.3303/CET1332021 |
| [8] |
VASANTH S, TAUSEEF S M, ABBASI T, et al. Mutliple pool fires: Occurrence, simulation, modeling and management[J]. Journal of Loss Prevention in the Process Industries, 2014, 29: 103. DOI:10.1016/j.jlp.2014.01.005 |
| [9] |
刘琼. 多火源燃烧动力学机制与规律研究[D]. 合肥: 中国科学技术大学, 2010 LIU Qiong. Dynamical mechanism and behaviors of multiple fires burning[D]. Hefei: University of Science and Technology of China, 2010 |
| [10] |
王佳文, 江平, 王旭. 多火源火旋风相互作用的实验研究[J]. 中国安全生产科学技术, 2017, 13(9): 144. WANG Jiawen, JIANG Ping, WANG Xu. Experimental research on interaction of fire whirls under multiple fire sources[J]. Journal of Safety Science and Technology, 2017, 13(9): 144. DOI:10.11731/j.issn.1673-193x.2017.09.023 |
| [11] |
林圣泽, 刘琼. 离散分布多火源燃烧速率计算模型研究[J]. 燃烧科学与技术, 2017, 23(3): 274. LIN Shengze, LIU Qiong. Burning rates calculation model of discrete fire[J]. Journal of Combustion Science and Technology, 2017, 23(3): 274. DOI:10.11715/rskxjs.R201606007 |
| [12] |
焦艳. 多油池火源燃烧特性的实验与理论研究[D]. 合肥: 中国科学技术大学, 2018 JIAO Yan. Experimental and theoretical research on combustion characteristics of multiple pool fires[D]. Hefei: University of Science and Technology of China, 2018 |
| [13] |
雷佼. 火旋风燃烧动力学的实验与理论研究[D]. 合肥: 中国科学技术大学, 2012 LEI Jiao. Experimental and theoretical researches on the combustion dynamics of fire whirls[D]. Hefei: University of Science and Technology of China, 2012 |
| [14] |
周魁斌. 火旋风的燃烧规律及其火焰移动机制研究[D]. 合肥: 中国科学技术大学, 2013 ZHOU Kuibin. Combustion behaviors and flame-moving mechanism of fire whirls[D]. Hefei: University of Science and Technology of China, 2013 |
| [15] |
ZUKOSKI E E, KUBOTA T, CETEGEN B. Entrainment in fire plumes[J]. Fire Safety Journal, 1981, 3(2): 107. DOI:10.1016/0379-7112(81)90037-0 |
 2022, Vol. 54
2022, Vol. 54


