给水管道漏损预测模型是给水管网运行维护管理的重要研究内容,本研究的给水管道漏损预测模型是通过分析、统计和学习管道漏失破损事件记录数据,建立管道漏损事件与管道自身因素、环境因素和管网运行因素等参数的显式/隐式函数关系,根据这种函数关系预测管道的未来破损数。基于给水管道漏损预测模型可以制订管道更新改造,可为管道漏损事件发生前的干预工作提供技术支撑,也可为漏损事件发生后的漏失巡检工作提供依据。
漏损预测模型可大致分为3类,即物理模型、统计模型、数据挖掘模型。物理模型旨在发现管道破损现象下的物理机理,多是从材料力学角度出发,计算管道内外环境与管道之间的相互作用,从而判断管道在一定条件下是否发生漏损。该方法的分析过程需要严格精细的控制条件,主要用于漏损成本较高的重要输水管道或管道试验[1-4]。统计模型通过历史数据分析,将管道破裂模式与管道属性参数、环境变量、管网运行参数联系起来[2, 5-7]。赵洪宾等[8]根据实际给水管网的漏损数据,建立了给水管道漏损预测的线性指数平滑模型和二次指数平滑模型;张宏伟等[9]应用多元线性回归分析理论,建立给水管道漏损发生时间为因变量,以管道接口类型、温度、埋深、直径、施工质量、运行压力和管道腐蚀指标为自变量的漏损预测模型,证明多元线性回归方法预测的平均相对误差为21%。数据挖掘模型利用人工智能和机器学习算法建立管道漏损的预测模型,是目前常用的给水管建模方法[5, 10]。根据模型表达形式,又可分为显式模型和隐式模型。Sattar等[1]采用基因表达式编程(gene expression programming, GEP)建立管长、管径、管道保护方式、以前破损数与管道下次破裂发生时间的显式函数关系,误差分析结果表明,GEP模型预测结果稍好于误差反向传播神经网络(back propagation neural network, BPNN)模型。徐强等[4, 11-12]利用遗传编程和进化多项式建立了管道总漏损次数与管龄、管径、管长之间的函数关系,结果表明, 两种模型预测性能相差不大。阎立华等[13]采用BPNN构建了管道安全使用期与管径、压力、埋深、铺设年代、所在地区类型函数关系的预测模型,模型预测结果的相对误差均小于10%。
在相关研究中,管径、管龄、管长被认为是影响管道漏损的重要因素。除这些管道自身影响因素外,天气变化也是导致管道发生漏损的重要因素。Barton等[14]对研究天气变化对管道影响的文章结论进行了综述,认为天气变化对管道漏损存在明显影响,而且铸铁管受天气影响极为明显,具体表现为夏季高温导致土壤水分蒸发致其收缩,然后降雨导致土壤膨胀从而造成管道发生漏损,冬季的极端低温导致土壤水分结冰致其膨胀,挤压管道导致漏损。邓晓婷[15]统计了4个季度的漏损点数,发现一、四季度漏损点数比二、三季度增加16.6%。Rajani等[16]通过定义16种不同的水温和气温变量指标,采用非齐次泊松分布模型分析不同分析步长(5~90 d)内的气温变量指标与管道破损次数之间的关系,结果表明, 最佳分析步长为30 d,对于不同管材需采用不同的气温变量进行分析。Kakoudakis等[17]采用K-means聚类与进化回归多项式结合的算法分别建立了管道破损数与4个自变量(管长、管径、管龄、冰冻指标)、管道破损数与冰冻指标的显式函数关系,结果表明,考虑管道物理属性(管长、管径、管龄)之后的模型预测精度稍有提高。
通过上述文献可知,对于气温变化显著的城市,应建立考虑天气因素的预测模型研究天气因素对管道漏损的影响。由于不同城市气温变化和管网特征的差异,上述研究结论是否适用于中国城市给水管网的漏损预测,仍有待进一步研究。为此,基于中国北方某案例城市的数据,研究了天气因素量化指标与管道漏失事件的相关性,天气影响因素对模型预测精度提升的适用性,显、隐式函数关系构建模型的有效性。
1 研究区域介绍研究对象是北方某城市给水管网干线,给水管网破损数据库记录了2008—2019年管道破损点的管材、管径、抢修类型及发生时间等属性;给水管网地理信息系统数据库记录了给水管道的管材、管径、铺设年份、管长等属性;气温数据库记录了每天的平均气温。案例城市给水管网干线主要由普通铸铁管(CIP)、球墨铸铁管(DIP)、钢管(SP)组成,表 1为该市给水主干管道的基本统计信息。可以看出,普通铸铁管的单位管长破损数最高,破损点的抢修类型分为明漏、暗漏、工程漏,由于工程漏是由管道周边施工导致管道出现破损,与天气变化并无关系,故本研究中主要针对普通铸铁管的明/暗漏破损点建立漏损预测模型。
| 表 1 给水干线基本情况 Tab. 1 Characteristics of water mains |
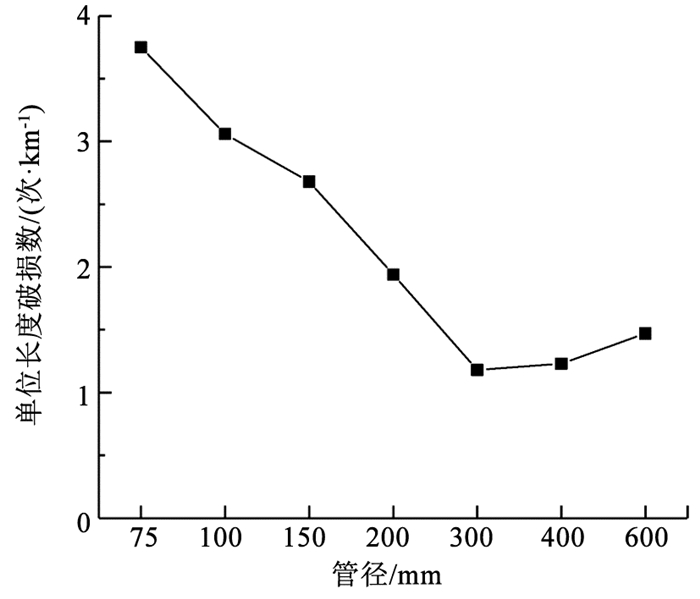
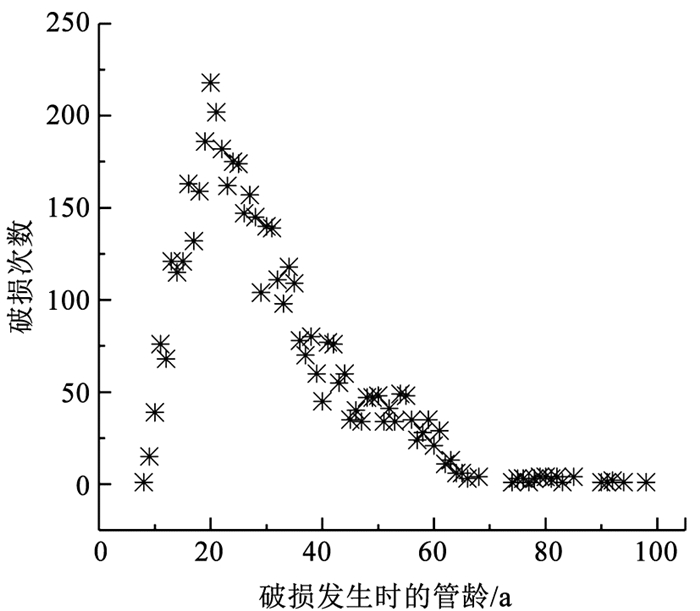
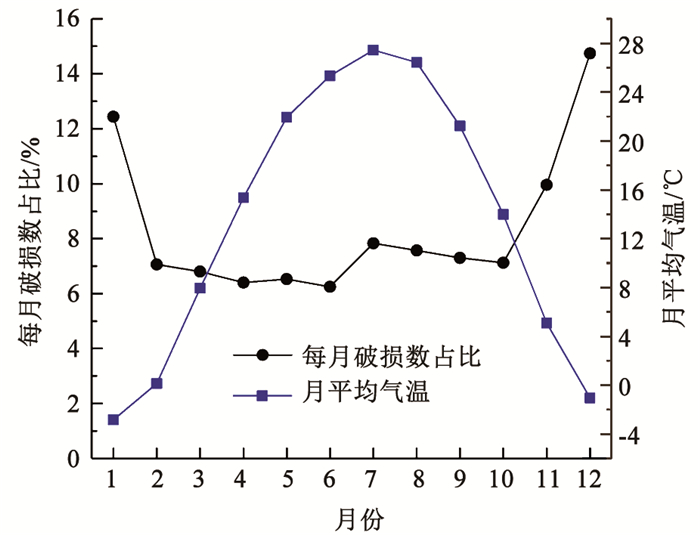
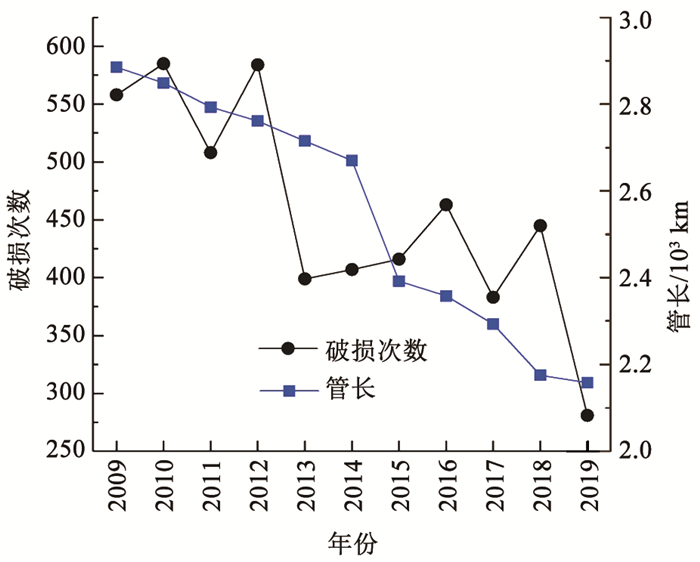
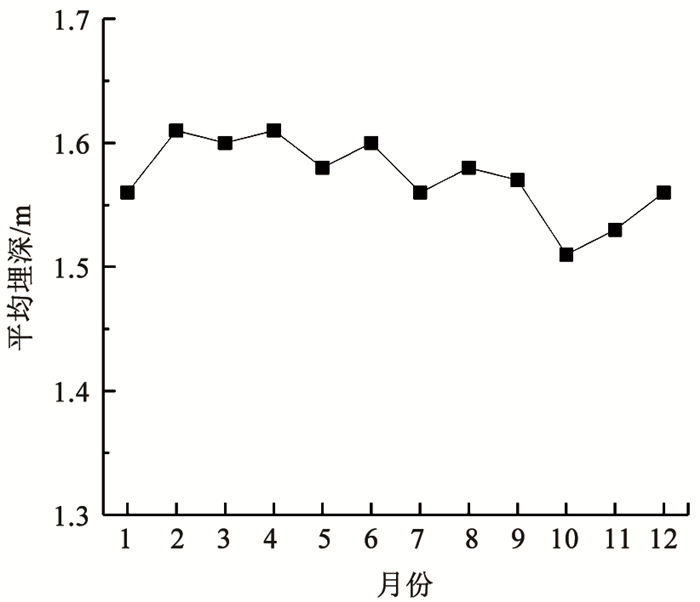
对于普通铸铁管道,单位长度破损数随管径变化趋势见图 1,破损次数随管龄变化见图 2,每月破损数占比及平均气温随月份变化见图 3,破损次数及管长随年份变化见图 4,破损点每月平均埋深如图 5所示。由图 1可知,随着管径减小,单位长度破损数呈现整体降低的趋势。图 2的结果表明,管道漏损次数随管龄变化呈现先上升后下降的趋势,在管龄20 a时管道破损数最大,在管龄65 a后趋于稳定。图 3的结果表明,普通铸铁管漏损次数与寒冷天气存在明显相关性,漏损次数随着气温降低而明显上升,原因可能是秋冬交替期间气温的骤降易导致管道破损数迅速上升,然后持续的低温会进一步导致破损数上升。图 4的统计结果表明,在役普通铸铁管的总长度和年破损数呈现整体下降趋势。图 5的结果表明,在破损数较多的11月至次年1月,这些月份的破损点平均埋深并没有明显小于其他月份。冰冻天气对管道的影响主要体现在土壤水分结冰致其膨胀,埋设在冻土层中的管道结构会受到约束导致漏损。实际中,管道上方土壤冻胀也可能影响位于冰冻线以下的管道,但目前尚缺乏土壤冻胀影响的物理机制、影响深度、管道结构内力和变形的增长率等相关研究。因此,并未根据冰冻线划分管道分组。
|
图 1 单位长度破损数随管径变化 Fig. 1 Variation of number of failures per kilometer with pipe diameter |
|
图 2 破损次数随管龄变化 Fig. 2 Variation of number of failures with pipe age |
|
图 3 每月破损数占比及平均气温随月份变化 Fig. 3 Variation of percentage of failures per month and average temperature in different month |
|
图 4 破损次数及管长随年份变化 Fig. 4 Variation of number of failures and pipe length in different year |
|
图 5 破损点每月平均埋深 Fig. 5 Average buried depth of failures per month |
在漏损影响因素研究方面,管径(D)、管龄(A)、管长(L)是模型较为主要的输入参数。Asnaashari等[2]采用人工神经网络建立管道漏损率与8个变量(管长、管径、管龄、管材、破损类型、土壤类型、水泥砂浆内衬时间、阴极保护法使用时间)的管道漏损率模型。Sattar等[18]采用极限学习机建立年均漏损数与管龄、管长、管径、水泥砂浆保护、阴极保护、历史漏损次数的数学模型。结合图 1、2、4中的统计规律,将D、A、L作为漏损影响因素。
对于天气因素(T)的影响,通过Barton等[14]研究天气变化对管道影响的文章结论的综述可知,在气温变化显著的城市,普通铸铁管受天气影响极为明显。同时, 结合图 3的统计规律可知,该城市漏损次数随着气温降低明显上升,表明普通铸铁管漏损次数与寒冷天气存在明显相关性,故选择天气因素(T)作为漏损影响因素。综上,将D、A、L、T确定为模型输入参数。
确定模型输入参数之后,需要通过数据分组得到模型输入输出数据。Xu等[12]认为建立模型前需考虑数据分组问题,因为不同的数据分组方法会得到不同模型数据。由图 4可知,2008—2019年管道长度逐年下降,故将所有管道先按照年份和管径D进行分组(即认为不同管径、管龄的管道受天气因素的影响存在差异),并计算每组内的总管长Lt和长度加权管龄At。
对于某个自然年份中,不同日期的气温是随时间变化的动态数据,且图 3所示不同月份的管道漏损数差异明显, 因此,在年份、管径分组的基础上,再对1年中的不同月份进行分组,统计不同管径、管龄、月份分组中的天气因素指标、漏损数量。其中按月份分组的日期时间间隔称为时间步长。
由于每日气温数据并不能直接反映天气变化对管道漏损的影响,需要定义天气因素量化指标。采用Rajani等[16]定义的6种天气因素量化指标,具体指标定义和表达式见表 2。Ti, j、Ti, k、Ti, p、Ti, q为时间步长i对应的第j、k、p、q天平均温度; m为时间步长i包含的天数;θ为冰冻阈值,连续2 d(含2 d)温度在θ以下时才可计算为冰冻指标。
| 表 2 天气因素量化指标定义 Tab. 2 Definitions of quantitative indicators of weather factors |
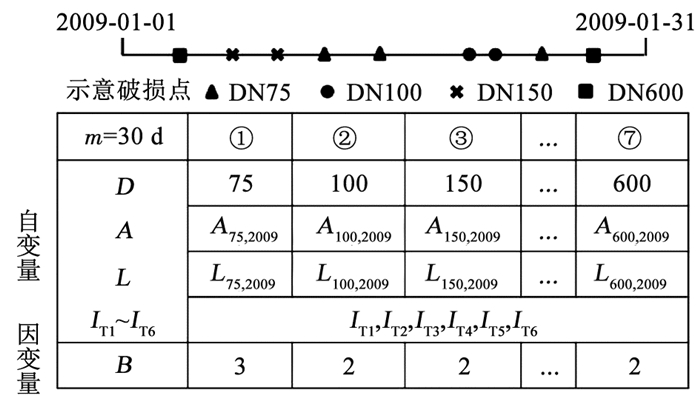
图 6展示了确定模型自变量和因变量的处理方法,其中D、A、L、IT1~IT6、B分别为管径、管龄、管长、6个天气指标、时间步长中的破损数。以时间步长m=30 d为例,在2009-01-01—2009-01-31,根据天气指标定义公式可得该时间步长的6个天气指标IT1~IT6。
|
图 6 模型输入与输出的定义 Fig. 6 Definitions of model input and output |
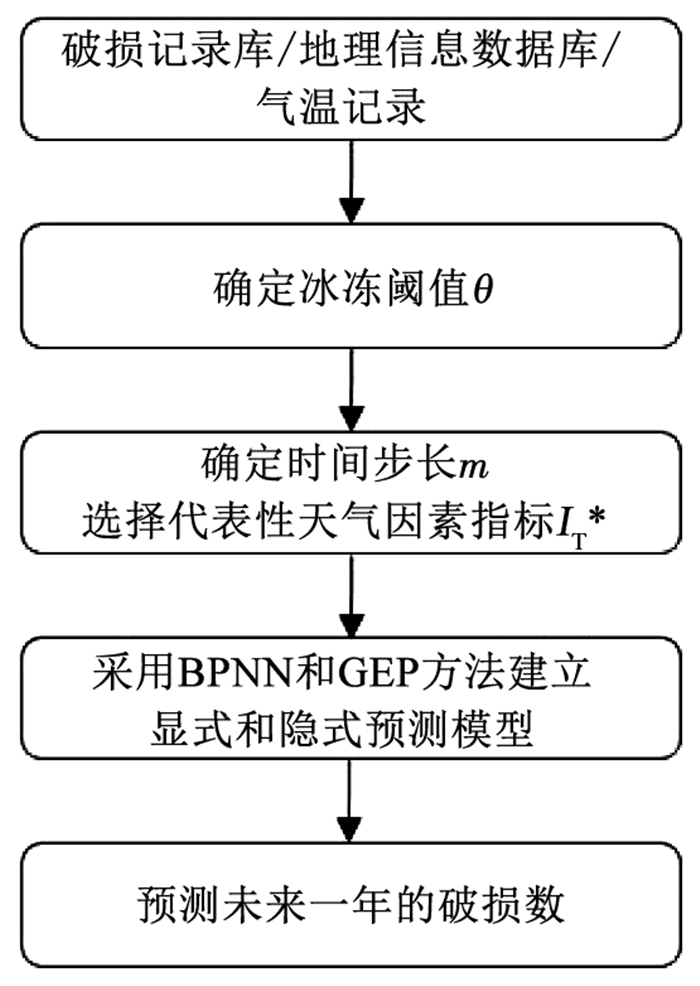
在模型预测流程中,参考Rajani等[16]所采用的分析方法确定天气因素指标的时间步长m以及代表性天气指标IT*,然后采用误差反向传播神经网络(BPNN)和基因表达式编程(GEP)方法建立考虑天气因素的给水管道漏损预测模型。考虑天气因素指标的给水管道漏损预测的具体步骤如下,模型预测流程如图 7所示。
|
图 7 模型预测流程 Fig. 7 Flow chart of prediction model |
1) 收集给水管网破损记录数据库、市政管道地理信息数据库和同期气温记录,对数据库的异常数据、缺失数据进行处理。
2) 统计不同天气温度下对应的管道破损数,确定天气因素冰冻指标的冰冻阈值θ。
3) 确定天气因素指标的时间步长m,选择代表性天气指标IT*。
① 对30、60、90、120 d等不同的时间步长,按照图 6所示的过程计算每个时间步长对应的天气因素指标值,得到不同时间步长对应的建模数据集;
② 对于不同时间步长,采用十重交叉验证技术和BPNN方法,分别建立因变量(破损数)与自变量(管径、管龄、管长和单个天气因素指标)的映射关系(预测模型), 则对于表 2中的6个指标分别建立6个预测模型,比较不同预测模型的决定系数,确定最佳时间步长;
③ 针对最佳时间步长的对应模型,分析天气指标之间相关性,采用枚举法确定余下天气指标的所有组合,对于每种组合模型,共得到500个模型决定系数,比较500个模型决定系数的均值及变异系数,确定代表性气温表征指标。
4) 采用BPNN和GEP方法建立破损数的隐式和显式预测模型。采用2008—2018年的管道破损数据建立模型训练数据集。模型输出(因变量)为管道破损数,模型输入(自变量)包括管径、管龄、管长、代表性天气因素指标。
5) 以未来一年(2018年8月—2019年7月)的管道破损数据作为预测数据,验证预测模型的准确性。
采用决定系数(R2)作为模型预测性能评价指标,定义见式(1)。R2反映因变量的全部变异能通过回归关系被自变量解释的比例,R2越接近1,说明模型性能越好。
| $ R^{2}=1-\frac{\sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}} $ | (1) |
式中yi、ŷi、y分别为预测数据集中第i个预测值、实际值、所有预测值的均值。
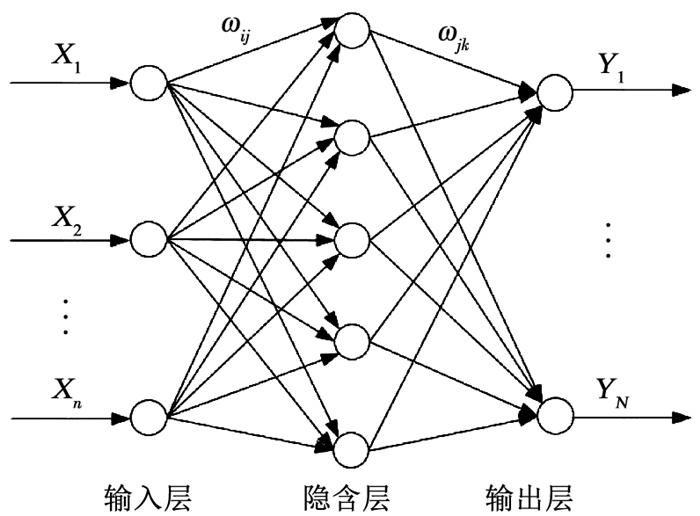
2.3 构建预测模型的方法 2.3.1 误差反向传播神经网络误差反向传播神经网络(BPNN)是一种前向多层反向传播学习算法。在前向传递中,输入信号从输入层经隐含层逐层处理,直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出,则转入反向传播,根据预测误差调整网络权值和阈值,从而使BPNN预测输出不断逼近期望输出。图 8为基于BPNN构建因变量Y与自变量X={X1,X2,…,Xn}函数映射关系的原理示意,ωij和ωjk为BPNN的权值。可以看出,将BPNN看作是一个非线性函数,输入值和输出值分别为函数的自变量和因变量。当输入节点数为n、输出节点数为N时,BPNN就表达了从n个自变量到N个因变量的函数映射关系[19]。BPNN预测流程分为模型构建、模型训练、模型预测3大步骤。
|
图 8 BPNN拓扑结构图 Fig. 8 BPNN topology diagram |
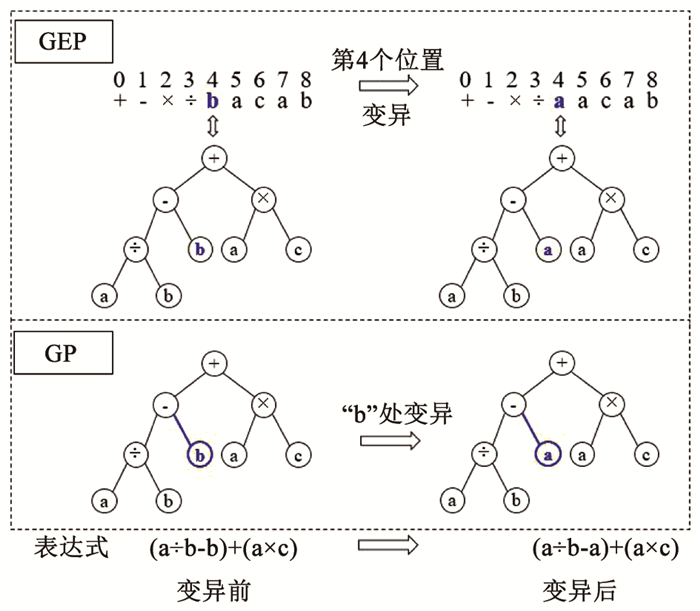
基因表达式编程(GEP)是Ferreira[20]于2001年在传统的遗传算法(genetic algorithm, GA)和遗传编程(genetic programming, GP)的基础上提出的一种新型演化算法,其主要特点在于可以建立因变量与自变量之间的显式函数关系式。在GP中,个体由不同大小和形状的表达式树表示,但其遗传操作是直接作用于GP的树状编码上,随着进化的进行就会出现代码膨胀问题,进化效率越来越低,导致不利于进行遗传操作。GEP的基因具有两种表现形式,即基因型和表现型。任何遗传操作算子的操作都是在基因型上进行(GA优势),而表现型则是基因型的解码,根据求解问题的性质将固定长度的线性结构个体解码成一棵表达式树(GP优势),从而实现了利用简单编码来解决复杂问题。图 9举例展示GEP和GP进行个体“变异”遗传操作时两者的差异。GEP只需在基因第4个位置上进行变异操作,然后解码成表达式树即得新的子代。GP进行变异操作时需要删除表达式树突变点“b”及其以下的树分支,然后用表达式树“a”代替,才得到新子代。
|
图 9 GEP和GP的遗传操作 Fig. 9 Genetic manipulation of GEP and GP |
GEP算法的基本过程和GA与GP相似,首先随机生成含有一定数量个体的染色体(初始种群), 然后染色体解码成表达式树,并评价这些染色体的适应度, 接着通过适应度函数值等指标对解析获得的表达式树进行评价,判断其是否满足进化约束条件。若未满足,则采用复制、变异、重组等方式进行遗传进化处理,从而得到新一代染色体。新一代染色体进入下一轮的生存迭代过程,评价适应度、被选择、经历遗传操作等。这一过程反复进行下去,直到迭代终止条件满足为止[21]。
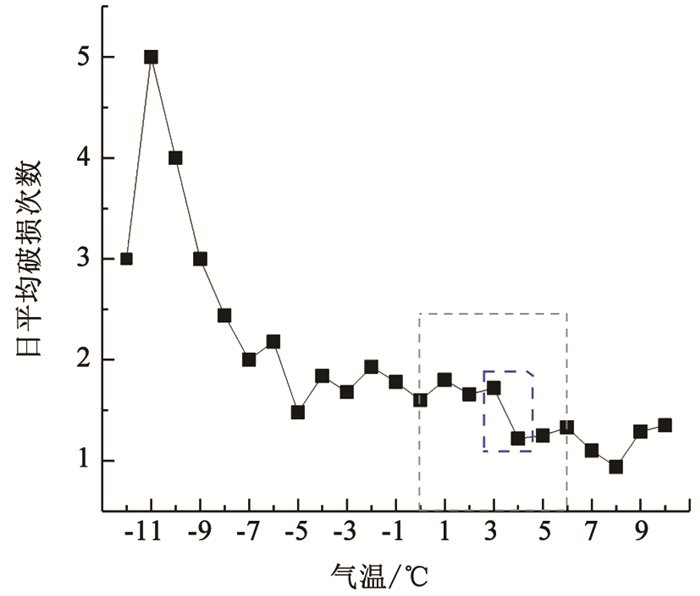
3 实例分析 3.1 冰冻指标阈值根据2.2节步骤建立案例城市给水管道漏损预测模型。对基础数据进行处理后的统计分析, 结果见图 1~5。第2)步确定冰冻指标阈值θ时,图 3中2月份和11月份的气温和破损数变化说明θ取值应该在0~6 ℃。基于11年气温数据,统计不同气温对应天数以及发生的破损数,计算得到不同气温对应日平均破损数,结果如图 10。可以看出,0~6 ℃气温从3 ℃变化为4 ℃时,对应的日平均破损数存在明显下降。综上,将冰冻阈值确定为θ=3 ℃。
|
图 10 日平均破损次数随气温变化 Fig. 10 Variation of average daily failures with temperature |
分别采用m={30, 60, 90, 120} d的时间步长,对于每个时间步长,采用BPNN方法分别建立自变量(管径、管龄、管长、单个天气指标)与因变量(管道破损数)的预测模型,即每个时间步长建立6种预测组合。为避免BPNN建模结果存在偶然性,每次BPNN模型构建时,采用十重交叉验证方法组建模型训练数据集,则可得到10组不同的训练数据集;对每组训练数据,独立运行50次BPNN建模,则每种预测组合最终得到500个隐式预测模型。500个预测模型的拟合结果决定系数的均值(μ)和变异系数(cv)见表 3。其中, μ值越大表明模型预测精度越高,cv越小表明模型预测结果越稳定。
| 表 3 模型决定系数均值和变异系数 Tab. 3 Mean value and variation coefficient of model determination coefficient |
由表 3可知,随着时间步长(m)的增加,预测模型决定系数整体呈现上升趋势,即模型拟合精度提升。但对于部分天气因素指标,该上升趋势并不连续。在m由90 d变为120 d时,天气指标IT1(平均温度)、IT5(最大下降率)对应的模型精度则呈现下降趋势。由于图 3所示管道漏损事件在11月—次年1月有明显增加,且根据表 3中不同模型决策系数均值和变异系数的结果,选取90 d作为案例城市管道预测模型的时间步长。
基于m=90 d,计算案例城市2008—2018年的6个天气因素指标值,这些天因素指标的Pearson相关系数计算结果见表 4。表中平均温度(IT1)与冰冻指标(IT6)的相关系数为-0.89,两指标存在显著的负相关性。因此,在进行预测模型对天气指标的敏感度分析时,剔除平均温度指标,对剩余的5个天气因素指标进行分析。
| 表 4 天气指标的相关系数 Tab. 4 Correlation coefficients of weather variables |
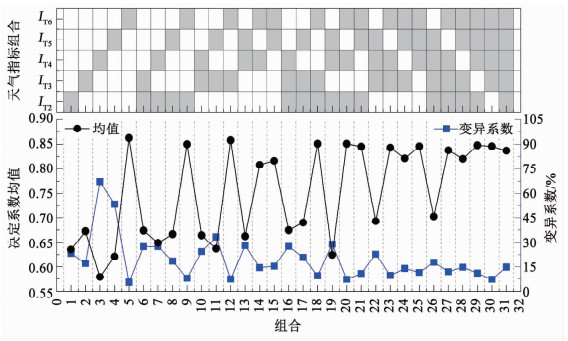
采用枚举法确定5个天气因素指标的所有组合,共得到31种组合方式(C51+C52+C53+C54+C55=31)。对每种天气指标组合,以{D, A, L, 天气指标组合}为自变量,使用十重交叉验证和独立运行50次的方法,基于BPNN分别构建每个组合方式的预测模型。对于每种天气指标组合,预测模型决定系数的均值和变异系数如图 11所示。可以看出,第5、12种天气组合的模型预测精度较高,决定系数平均值均为0.86,决定系数的变异系数分别为5.38%和7.33%。因为两种组合模型精度较接近,优先选择自变量较少的组合(第5种组合,天气指标为IT6)。综上,选择冰冻指标为代表性气温表征指标。
|
图 11 组合模型的决定系数均值及变异系数 Fig. 11 Mean value and variation coefficient of determination coefficient of different combination models |
通过以上分析,最终确定模型时间步长为90 d,模型输入变量(自变量)为管径(D)、管龄(A)、管长(L)、冰冻指标(IF),输出变量(因变量)为时间步长内的管道破损数(B)。将案例城市2008-08-01—2018-07-31的漏损记录数据按照管径、管龄、时间步长进行分组,共得到308组数据,其中280组数据为模型训练数据,其余28组数据为模型测试数据。
建立因变量与自变量之间的隐式函数模型时,采用3层结构的BPNN,其中输入层和输出层节点数分别为4和1,隐含层节点数N由经验公式N=2n+a得出,n为输入层节点数,a为1~10的常数[13, 22]。通过试凑法确定a=7时模型预测误差较小,此时对应隐含层节点数N=15,即最后确定网络模型结构为4-15-1。数据归一化和BPNN模型的构建采用MATLAB机器学习工具箱的内置函数。采用GEP建立因变量与自变量之间的显式函数模型时,参数设置见表 5。
| 表 5 GEP建模参数设置 Tab. 5 Parameters for GEP modeling |
采用BPNN建立隐式预测模型时,采用十重交叉验证和50次独立运行,共生成500个模型,选取模型测试集预测结果决定系数最优的模型作为选定的模型。GEP在建模过程中独立运行5次,共生成774个模型表达式,根据表达式结构和模型测试集预测结果决定系数挑选出5个模型,表达式如表 6所示。RTR2和RTE2分别为模型训练集和测试集决定系数。可以看出,模型②④决定系数相对较低,模型⑤虽然决定系数最好,但模型表达式太过复杂,模型①③表达式结构较相近,但模型①预测精度较高。此外,模型①表达式中漏损数量B与管径D为反比关系,B与管道长度L、冰冻指标IF为正比关系,这些规律与图 1、3、4中的结论一致。故最终选择模型①的表达式为显式预测模型。
| 表 6 GEP模型表达式 Tab. 6 Equations obtained by GEP |
采用BPNN和GEP方法建立的考虑天气影响指标的管道漏损预测隐式(BP-T)和显式(GEP-T)模型,预测案例管网在2018年8月—2019年7月的管道破损数,结果见图 12。此外,图 12还给出了采用BPNN和GEP方法建立的未考虑天气指标的隐式(BP)和显式(GEP)模型预测结果的对比。其中,预测时段的管道破损记录按照管龄、管径、时间步长进行分组,共得到28组实测数据。如图 12所示,每个管径包含4组数据,分别对应时间步长8—10月(T1),11月—次年1月(T2),2—4月(T3),5—7月(T4)。
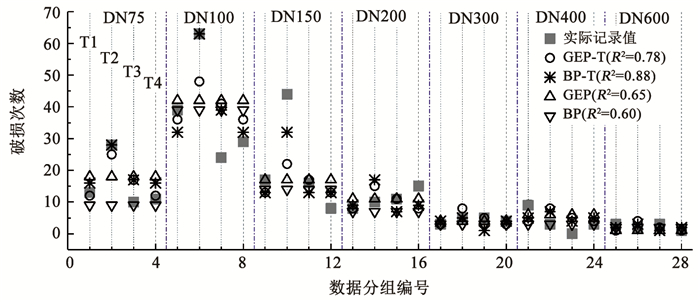
|
图 12 模型预测值与实际值比较 Fig. 12 Comparison between model prediction values and observation values |
由图 12可知,未考虑天气因素指标的显式和隐式模型预测决定系数分别为0.65和0.60,考虑天气因素指标的显式和隐式模型预测结果的决定系数分别为0.78和0.88。考虑天气因素后,显式和隐式模型的预测精度提升率分别为13%和28%。因此,考虑天气因素可有效提升漏损预测模型的整体精度。由图 12中“实际记录值”可知,天气因素对DN75~DN150分组的管道漏损数存在显著影响,即在T2分析步(11月—次年1月)中存在管道漏损数量上升,本研究建立的BP-T模型可以提高预测模型在这些分析步中的预测精度。而对于DN200~DN600分组的分析步中,并未表现出天气因素对T2分析步漏损数的影响,在这些分组中,考虑天气因素的预测模型BP-T和GEP-T并未表现出较高的预测精度。因此,天气因素指标对预测模型精度的提升,适用于实际漏损记录中显著存在天气影响的分组数据。由于实际管网中不同分组类型管道漏损的主要影响因素存在差异,不可简单地预期考虑天气因素指标可以提高所有类型管道漏损预测的精度,也不应仅采用天气因素指标建立预测模型。
图 12在考虑天气因素指标的模型中,BPNN模型的预测精度高于GEP模型, 而在未考虑天气因素指标的模型中,GEP模型的预测精度高于BPNN模型。这说明不同建模方法的适用性随着模型参数数据而变化,在构建给水管道漏损预测模型时,有必要采用不同的建模方法,以获得对于案例管网数据较为客观全面的认知。因此,本研究同时采用显式和隐式方法构建模型的思路是可行的。
4 结论基于北方某城市给水管网破损事件数据和气温记录,分析了不同的天气因素量化指标与管道破损事件的相关性,采用反向传播人工神经网络(BPNN)和基因表达式编程(GEP)算法,建立了考虑天气因素的给水管道漏损预测模型。所建立的模型可预测未来1年不同时段的管道破损数,为管道更新改造、运营维护等管道漏损事件发生前的干预工作提供指导。主要结论如下:
1) 通过模型结果判断最佳时间步长为90 d,结合相关性分析及模型预测结果确定冰冻指标为天气因素代表性指标,考虑冰冻指标后的显式和隐式模型预测精度提升率分别为13%和28%,说明考虑天气因素可明显提高漏损预测模型的拟合精度。
2) 天气因素指标对预测模型精度的提升,适用于实际漏损记录中显著存在天气影响的分组数据,由于实际管网中不同分组类型管道漏损的主要影响因素存在差异,不可简单地预期考虑天气因素指标可以提高所有类型管道漏损预测的精度,也不应仅采用天气因素指标建立预测模型。
3) 在考虑天气因素指标的模型中,BPNN模型的预测精度高于GEP模型, 而在未考虑天气因素指标的模型中,GEP模型的预测精度高于BPNN模型,说明不同建模方法的适用性随着模型参数数据而变化,采用不同的建模方法将有利于获得对管网数据较为客观全面的认知。
| [1] |
SATTAR A M A, GHARABAGHI B, MCBEAN E A. Prediction of timing of watermain failure using gene expression models[J]. Water Resources Management, 2016, 30(5): 1635. DOI:10.1007/s11269-016-1241-x |
| [2] |
ASNAASHARI A, MCBEAN E A, GHARABAGHI B, et al. Forecasting watermain failure using artificial neural network modelling[J]. Canadian Water Resources Journal, 2013, 38(1): 24. DOI:10.1080/07011784.2013.774153 |
| [3] |
DAVIS P, SILVA D D, MARLOW D, et al. Failure prediction and optimal scheduling of replacements in asbestos cement water pipes[J]. Journal of Water Supply: Research and Technology-Aqua, 2008, 57(4): 239. DOI:10.2166/aqua.2008.035 |
| [4] |
XU Q, CHEN Q, LI W. Application of genetic programming to modeling pipe failures in water distribution systems[J]. Journal of Hydroinformatics, 2011, 13(3): 419. DOI:10.2166/hydro.2010.189 |
| [5] |
LIN P, YUAN X. A two-time-scale point process model of water main failures for infrastructure asset management[J]. Water Research, 2019, 150: 296. DOI:10.1016/j.watres.2018.11.066 |
| [6] |
KLEINER Y, RAJANI B. I-WARP: individual water main renewal planner[M]. Boca Raton: CRC Press-Taylor & Francis Group, 2010: 639.
|
| [7] |
ANDREOU S A, MARKS D H, CLARK R M. A new methodology for modelling break failure patterns in deteriorating water distribution systems: theory[J]. Advances in Water Resources, 1987, 10(1): 2. DOI:10.1016/0309-1708(87)90002-9 |
| [8] |
赵洪宾, 陈兵, 伍悦滨. 给水管网漏失预测模型的研究[J]. 给水排水, 2001, 27(10): 94. ZHAO Hongbin, CHEN Bing, WU Yuebin. Research on leakage prediction model of water supply network[J]. Water & Wastewater Engineering, 2001, 27(10): 94. DOI:10.13789/j.cnki.wwe1964.2001.10.033 |
| [9] |
张宏伟, 牛志广, 陈超. 供水管网漏损预测模型研究[J]. 中国给水排水, 2001, 17(6): 7. ZHANG Hongwei, NIU Zhiguang, CHEN Chao. Study on the prediction model for water supply net leakage[J]. China Water & Wastewater, 2001, 17(6): 7. DOI:10.3321/j.issn:1000-4602.2001.06.003 |
| [10] |
邵圆媛. 嵌套BP/GMS神经网络模型在供水管网漏损预测中的研究[D]. 重庆: 重庆大学, 2018 SHAO Yuanyuan. Research on nested BP/GMS neural network models in water supply network leakage prediction[D]. Chongqing: Chongqing University, 2018 |
| [11] |
徐强, 陈求稳, 李伟峰, 等. 基于遗传编程的供水管网漏失模型[J]. 中国给水排水, 2011, 27(1): 45. XU Qiang, CHEN Qiuwen, LI Weifeng, et al. Development of pipe leakage model for water distribution system using genetic programming[J]. China Water & Wastewater, 2011, 27(1): 45. DOI:10.19853/j.zgjsps.1000-4602.2011.01.012 |
| [12] |
XU Q, CHEN Q, LI W, et al. Pipe break prediction based on evolutionary data-driven methods with brief recorded data[J]. Reliability Engineering & System Safety, 2011, 96(8): 942. DOI:10.1016/j.ress.2011.03.010 |
| [13] |
阎立华, 马婷婷, 田昊平. BP神经网络对管网安全使用期的预测[J]. 沈阳建筑大学学报(自然科学版), 2008, 24(5): 845. YAN Lihua, MA Tingting, TIAN Haoping. Research on prediction of safe using dates of water supplying pipes based on BP neural network[J]. Journal of Shenyang Jianzhu University (Natural Science), 2008, 24(5): 845. |
| [14] |
BARTON N A, FAREWELL T S, HALLETT S H, et al. Improving pipe failure predictions: factors affecting pipe failure in drinking water networks[J]. Water Research, 2019, 164: 114926. DOI:10.1016/j.watres.2019.114926 |
| [15] |
邓晓婷. 城市供水管网漏损因素分析及控制[D]. 太原: 太原理工大学, 2012 DENG Xiaoting. Urban water supply pipe network leakage factor analysis and control[D]. Taiyuan: Taiyuan University of Technology, 2012 |
| [16] |
RAJANI B, KLEINER Y, SINK J. Exploration of the relationship between water main failures and temperature covariates[J]. Urban Water Journal, 2012, 9(2): 67. DOI:10.1080/1573062X.2011.630093 |
| [17] |
KAKOUDAKIS K, FARMANI R, BUTLER D. Pipeline failure prediction in water distribution networks using weather conditions as explanatory factors[J]. Journal of Hydroinformatics, 2018, 20(5): 1191. DOI:10.2166/hydro.2018.152 |
| [18] |
SATTAR A M A, ERTUGRUL O F, GHARABAGHI B, et al. Extreme learning machine model for water network management[J]. Neural Computing and Applications, 2019, 31(1): 157. DOI:10.1007/s00521-017-2987-7 |
| [19] |
王小川. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013.
|
| [20] |
FERREIRA C. Gene expression programming: a new adaptive algorithm for solving problems[J]. Complex Systems, 2001, 13(2): 87. |
| [21] |
元昌安. 基因表达式编程算法原理与应用[M]. 北京: 科学出版社, 2010.
|
| [22] |
HECHT-NIELSEN R. Theory of the backpropagation neural network[M]. New York: Academic Press, 1989.
|
 2022, Vol. 54
2022, Vol. 54


