短期需水量预测模型在有限的预测区间(从1个月到1天不等)内进行需水量预测,预测时间步长通常控制在每天到每小时,其在给水系统的优化调度与日常管理中发挥着重要作用[1-2]。以往的短期需水量预测模型一般面向整个城市[3-6],预测步长多以小时和天为时间步长,主要应用于城市水量的供需平衡分析。近年来,随着硬件采集技术的发展,收集步长为1~15 min的观测数据成为可能,物联网、云计算等新技术也不断融入水务行业,期望从供水系统大数据的研究中挖掘出更多工程应用价值。在此背景下,在线调度、压力分区调控、漏损控制、爆管监测等供水系统工程对短期需水量预测提出了新的速度和时间尺度需求。
很多学者对需水量预测方法进行了研究,早期传统的统计学方法因易于理解和实施得到了大量的应用,然而,由于自身的局限性很多时候并不能达到良好的预测效果[2],例如,多元线性回归算法预设了特征与需水量之间的关系;指数平滑算法对其加权系数缺乏客观的识别方法;自回归移动平均算法要求时序数列是平稳的或者经差分处理后是平稳的,且本质上只能捕捉线性关系,而真实需水量的变化是非线性的,且具有随机性。近年来,机器学习方法被更多地应用于短期需水量预测中,机器学习方法是典型的数据驱动算法,通过历史数据来深入挖掘需水量与相关变量之间的关系,从而提高预测模型的稳定性和可靠性。其中,人工神经网络算法(artificial neural network,ANN)和支持向量回归算法(support vector regression,SVR)以及它们的扩展方法在文献中介绍最多[3-5],研究中也多使用二者与新提出的机器学习模型进行性能比较,从而对新模型进行评估。
除ANN与SVR外,极限学习机算法(extreme learning machine,ELM)由于比传统机器学习方法拥有更快的训练速度,近来也被应用于预测模型中,但其实际应用效果表现出一定的差异性[6-8]。Huang等[9]在ELM的基础上提出了核极限学习机(kernel-based extreme learning machine,KELM)算法,该算法继承了ELM较高的训练速度的优点的同时,被证明相比ELM具有更加稳定的性能并且有着与SVR相似的泛化能力[10],但该方法目前尚未在短期需水量预测领域得到更多尝试。
研究人员除了不断追求单独预测模型效率的提高外,近来更多地倾向于组合模型的研究[11-12],通过对两种或多种预测模型进行组合以形成优势互补,来提高整体预测效果。其中,傅里叶级数模型(Fourier series,FS)因实现简单且需要较少的训练数据而常用于与机器学习模型进行组合[13-14]。本研究充分利用数据信息,将短期需水量的预测步长控制在15 min,引入了KELM模型以提高短期需水量预测的速度,同时,提出了以KELM模型为初始预测模块叠加使用FS模块进行残差修正的组合模型(KELM+FS),以进一步提升预测精度。
1 方法原理本研究提出的基于核极限学习机的短期需水量预测模型KELM通过对样本数据进行训练,建立起历史时刻需水量与目标时刻需水量之间的非线性关系,进而根据历史数据实现对目标时刻需水量的预测。模型为多维输入单维输出,输入特征为与目标时刻需水量数据高度相关的历史需水量数据,输出为目标时刻的需水量预测值。KELM+FS模型中的残差修正模块FS则利用傅里叶级数对KELM的预测值与观测值之间的差值进行建模,识别出残差序列中隐含的周期性规律,从而完成对未来时刻残差的推测,其输入为T个历史残差数据,输出为整个预测区间的残差序列。
1.1 极限学习机原理ELM是在单隐含层前馈神经网络的基础上提出的。与传统单隐含层前馈神经网络使用梯度下降法迭代求解网络参数不同,ELM在训练过程中随机生成输入权值ω和偏置b且不再调整,将最优求解问题转化为简单的最小二乘求解问题,这使得ELM具有了更快的学习和运行速度[15]。应用中ELM的训练机理可以简单描述如下[6, 15-16]:
假设给定训练样本{xi, yi|xi∈RD, i=1, …, n}(其中xi表示第i个样本的D维输入向量xi=[xi1, …, xiD],yi对应着第i个样本的观测数据),隐含层神经元数为k,根据ELM网络定义可以写出如下表达式:
| $ \begin{gathered} \sum\limits_{j=1}^{k} g\left(\boldsymbol{\omega}_{j}, b_{j}, x_{i}\right) \beta_{j}=\hat{y}_{i}, \\ i=1,2, \cdots, n, j=1,2, \cdots, k \end{gathered} $ | (1) |
式中:g(*)为显式激活函数; ωj为连接隐含层第j个神经元与输入层神经元的权向量,ωj=[ωj1, …, ωjD]T; bj为隐含层第j个神经元的偏置,偏置向量b=[b1, …, bk]T; βj为隐含层第j个神经元与输出层神经元的连接权值,权值向量β=[β1, …, βk]; ŷi为第i个样本的预测输出结果。
当ELM的输出结果能够以零误差逼近观测数据时,利用矩阵表达可以写为如下形式:
| $ \boldsymbol{H \beta}=\boldsymbol{Y} $ | (2) |
式中:H为隐含层输出矩阵,Y=[y1, …, yn]T为观测向量。
在ELM训练过程中,ω和b采取随机生成的方法确定,为计算网络的输出结果,β是唯一需要求解的参数[17]。
以最小训练误差和最小输出权的范数为求解目标,根据线性代数知识,方程(2)的最小范数最小二乘解为[18]
| $ \boldsymbol{\beta}=\boldsymbol{H}^{+} \boldsymbol{Y}=\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{Y} $ | (3) |
其中H+为隐含层输出矩阵H的Moore-Penrose广义逆矩阵。
1.2 核极限学习机原理为了进一步简化ELM的应用,避免在确定隐含层神经元数时应用耗时的算法和随机分配权重的潜在缺点,Huang等[18]在ELM的基础上提出了KELM,KELM隐含层的映射不再采用g(*)这种简单的显式形式而是采用核矩阵确定,而且隐含层神经元数不再需要指定,在这种情况下KELM比ELM具有更稳定的性能,并且KELM与SVR具有相似的泛化能力[10]。KELM的机制在ELM的基础上可以描述如下[9, 18-19]。
为增加模型的稳定性和泛化能力,在对β的求解中将引入一个正数C,并以最小训练误差和最小输出权的范数为求解目标[20],则有
| $ \begin{array}{c} \min \frac{1}{2}\|\boldsymbol{\beta}\|^{2}+\frac{1}{2} C \sum\limits_{i=1}^{n}\left\|e_{i}\right\|^{2} \\ \text { s. t. } \boldsymbol{h}\left(\boldsymbol{x}_{i}\right) \boldsymbol{\beta}=y_{i}^{\mathrm{T}}-e_{i}^{\mathrm{T}}, i=1, \cdots, n \end{array} $ | (4) |
式中:ei为训练误差,h(x)为隐含层特征映射函数。
| $ \boldsymbol{H}=\left[\begin{array}{c} \boldsymbol{h}\left(\boldsymbol{x}_{1}\right) \\ \vdots \\ \boldsymbol{h}\left(\boldsymbol{x}_{n}\right) \end{array}\right]=\left[\begin{array}{ccc} h_{1}\left(x_{1}\right) & \cdots & h_{k}\left(x_{1}\right) \\ \vdots & & \vdots \\ h_{1}\left(x_{n}\right) & \cdots & h_{k}\left(x_{n}\right) \end{array}\right]_{n \times k} $ | (5) |
此时β被计算为
| $ \boldsymbol{\beta}=\boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{I} / C+\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}\right)^{-1} \boldsymbol{Y} $ | (6) |
对于KELM来说不必知道其映射函数的具体形式,而是构造隐式映射来代替,即构造核矩阵来代替HTH,则有
| $ \begin{gathered} \boldsymbol{\varOmega}_{\mathrm{ELM}}=\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}} \\ \varOmega_{\mathrm{ELM}_{i, j}}=\boldsymbol{h}\left(\boldsymbol{x}_{i}\right) \boldsymbol{h}\left(\boldsymbol{x}_{j}\right)=K\left(x_{i}, x_{j}\right) \end{gathered} $ | (7) |
最终网络输出结果可写为
| $ \begin{gathered} y=f(x)=\boldsymbol{h}(\boldsymbol{x}) \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{I} / C+\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}\right)^{-1} \boldsymbol{Y}= \\ {\left[\begin{array}{c} K\left(x, x_{1}\right) \\ \vdots \\ K\left(x, x_{n}\right) \end{array}\right]^{\mathrm{T}}\left(\boldsymbol{I} / C+\boldsymbol{\varOmega}_{\mathrm{ELM}}\right)^{-1} \boldsymbol{Y}} \end{gathered} $ | (8) |
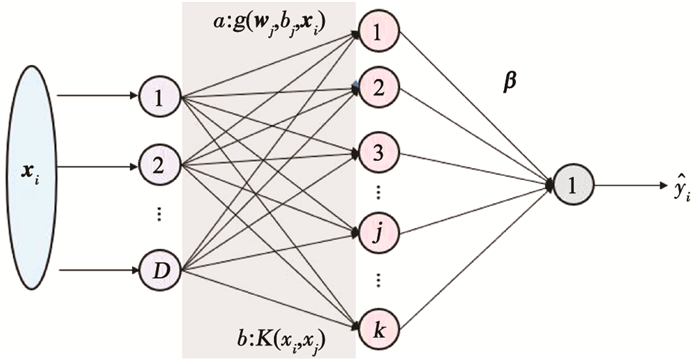
式中:ΩELM为核矩阵,K(xi, xj)为核函数。在KELM中有多种核函数可供选择,比如线性核函数(linear)、多项式核函数(polynomial)、高斯径向基核函数(rbf)等[19]。图 1中给出了ELM与KELM多维输入单维输出的经典结构,其中a为ELM的映射函数,b为KELM的映射函数。
|
图 1 多维输入单维输出的ELM和KELM经典结构 Fig. 1 Typical structures of ELM and KELM with multidimensional input and one-dimensional output |
傅里叶级数能够将周期信号或函数展开为一组不同频率三角函数的和,通过将周期内的历史时间序列数据拟合为傅里叶级数方程来实现对未来时刻数据的推断。假设一个周期由T个时刻组成,将此周期在[0, 2π]区间内进行标准化,则有
| $ t_{q}=\frac{2 {\rm{ \mathsf{ π} }} q}{T}, q=1, \cdots, T $ | (9) |
此时傅里叶级数方程可以定义为
| $ f^{*}\left(t_{\mathrm{q}}\right)=a_{0}+\sum\limits_{p=1}^{M}\left[a_{p} \cos \left(p t_{q}\right)+b_{p} \sin \left(p t_{q}\right)\right] $ | (10) |
式中:tq为经过标准化的时刻;M为傅里叶多项式的级数,M < T/2;a0、ap和bp为可以调整的傅里叶级数方程的系数。
以观测值f(tq)与傅里叶级数方程估计值f*(tq)之间差值的二范数作为目标函数,傅里叶级数方程的系数可以通过最小二乘法确定[13]:
| $ \left\{\begin{aligned} a_{0}=& \frac{\sum\limits_{q=0}^{T-1} f\left(t_{q}\right)}{T} \\ a_{p}=& \frac{2 \sum\limits_{q=0}^{T-1} f\left(t_{q}\right) \cos \left(p t_{q}\right)}{T} \\ b_{p}=& \frac{2 \sum\limits_{q=0}^{T-1} f\left(t_{q}\right) \sin \left(p t_{q}\right)}{T} \end{aligned}\right. $ | (11) |
本研究中,首先选定残差周期,将一个残差周期内的历史时刻进行标准化处理,然后根据式(11)的系数表达式,将周期内的残差序列值f(tq)以及标准化时刻tq依次代入式中,便可计算出相应的系数a0、ap和bp,从而实现傅里叶级数方程的拟合,继而根据残差序列所蕴含的周期性特征,可使用拟合好的傅里叶级数方程推测未来时刻的残差值。
2 建模流程本研究所提出的短期需水量预测模型是在预测区间为24 h,预测步长为15 min的条件下建立的。根据监测条件,观测数据每15 min进行一次采样,每24 h进行一次传输,即历史数据集每24 h进行一次更新。历史数据集的大小始终保持不变,采用移动窗口更新,即当增添最近96个时刻的观测数据的同时会删除最早的96个时刻的数据。
2.1 输入特征选择选择合适的输入特征对模型的建立十分重要。Guo[2]、Bakker[21]、Cutore等[22]在建立短期需水量预测模型时都仅选择历史需水量作为唯一输入特征,并且证明了在这一条件下可以实现可靠的预测。本研究同样使用历史需水量数据作为模型的唯一输入特征。
综合参考Guo[2]、Herrera[3]以及Odan等[13]的输入特征选择方案,并通过相关性分析和模型预测实验,最终选择{当前时刻,前1 d的目标时刻,前2 d的目标时刻,前1周的目标时刻}的用水需求数据作为模型的输入特征,即{Qt, Qt-95, Qt-191, Qt-671}。预测期间Qt-95,Qt-191和Qt-671使用对应的历史观测数据作为输入;在第1个目标时刻时,Qt使用对应的历史观测数据,从第2个目标时刻开始,Qt使用上一时刻的初始预测值作为下一时刻的特征输入。
2.2 KELM模型建立步骤1) 收集并通过数据清洗对历史需水量数据进行预处理。
2) 提取历史需水量数据的输入特征输入到预测模型中,通过KELM训练,建立历史需水量数据与下一时刻需水量数据之间的联系,从而实现KELM模型的建立。
3) 对建立好的模型输入第s个目标时刻(t+s)的特征,得到需水量预测值
4) 重复步骤3),直到获得96个时刻的需水量预测值
KELM+FS的建立主要包括建立需水量初始预测模块和建立残差修正模块两部分。图 2展示了模型建立的流程。其中需水量初始预测模块的构建步骤与KELM模型相同,不再赘述。主要建模步骤如下:

|
图 2 KELM+FS模型建立流程 Fig. 2 Flow chart of KELM+FS model building |
1) 建立需水量初始预测模块。
2) 通过建模训练的历史需水量数据、初始预测模块对训练数据拟合(预测)结果,获得初始预测模型对建模数据的的残差序列e=[e1, e2, …, eT]T。
| $ e_{i}=\hat{Q}_{i}-Q_{i}, i=1, \cdots, T $ | (12) |
式中:ei为建模训练数据中第i时刻对应的模型拟合残差值,Qi为i时刻的需水量观测值,
3) 以T个历史时刻的残差数据作为一个训练窗口拟合傅里叶级数系数,继而预测得到目标时刻对应的初始预测模块的残差值êt+s(s=1, 2, …, 96)。
4) 计算目标时刻的最终需水量预测值:
| $ \hat{Q}_{t+s}^{*}=\hat{Q}_{t+s}-\hat{e}_{t+s}, s=1,2, \cdots, 96 $ | (13) |
式中:
目前已有很多方法应用于需水量预测模型的性能评价,本研究采用已广为接受的指标作为模型的评价指标,其中包括用于评估预测精度的拟合优度(R2)[2, 8, 14]、平均绝对百分比误差(MAPE, EMAP)[2, 14, 23]以及用于评价计算速度的模型计算时间。具体计算公式如下:
| $ R^{2}=1-\frac{\sum\limits_{s=1}^{96}\left(Q_{t+s}-\hat{Q}_{t+s}^{*}\right)^{2}}{\sum\limits_{s=1}^{96}\left(Q_{t+s}-\bar{Q}_{t+s}\right)^{2}} $ | (14) |
| $ E_{\mathrm{MAP}}=\frac{1}{96} \sum\limits_{s=1}^{96} \frac{\left|Q_{t+s}-\hat{Q}_{t+s}^{*}\right|}{Q_{t+s}} \times 100 \% $ | (15) |
式中:
采用某城市3个真实的独立计量区(DMA)历史需水量数据进行预测实验对提出的模型进行验证。这3个DMA的组成结构相似,大部分用户为居民用户,包含少量商业用户,属于典型的城市住宅区DMA。获取数据的时间范围为2019年6月1日—2019年7月30日,采样间隔为15 min。表 1给出收集数据时间范围内这3个DMA的基本数据特征,其中DMA1的平均需水量最高,且相比具有更高的随机波动性;DMA2平均需水量最低;DMA3需水量数据变异系数最低。研究以2019年7月26日96个时刻的需水量数据作为测试数据,将其前55 d的数据通过特征提取后作为模型的建立数据,其中90%作为训练集,10%作为验证集。训练集与验证集用于寻找模型参数并建立模型,测试集则用于测试所建立模型的性能。
| 表 1 3个DMA的基本需水量数据信息 Tab. 1 Basic water demand data for three DMAs |
为了对所提出的模型进行客观评估,引入了已被广泛使用的ANN模型、SVR模型,以及KELM的同源模型——ELM模型和添加了残差修正模块的组合模型一起参与性能测试。所有模型的建立均以MATLAB 2016b为平台,所用计算机CPU型号为Inter Core i7-10510U,内存为16.0 GB。
其中ANN模型采用单层前馈架构构建,并使用广为接受的反向传播算法进行训练,其隐含层神经元数k为该模型主要待定参数,采用log n[24](n为训练样本数)和2D+1[25](D为输入特征维数)确定隐含层神经元的上下限,并通过试错法将产生最小泛化误差的神经元数确定为最优隐含层神经元数[26]。
有关SVR的理论已有很多研究人员进行过详细叙述,具体见文献[4, 27-28]。建立该模型需要确定的主要参数有核函数、不敏感系数ε、惩罚因子C、核函数宽度系数γ。研究中选择径向基函数(RBF)作为核函数。不敏感系数ε选取平台默认值0.1,C和γ的取值分别设为{21, 22, …,25}和{2-5, 2-4, …, 2-1}[19],于建模数据中使用网格搜索和5折交叉验证在取值范围内进行二者的组合寻优。
根据1.1节ELM基础原理,ELM模型待定参数为隐含层神经元数k和激活函数类型。参考Mouatadid等[6]对于ELM模型的训练方案,选取Sig作为激活函数,将k的取值设定为{10, 20, …, 200},使用试错法在泛化误差最小时获取k的最佳取值。
根据1.2节KELM基础原理可知,建立该模型需要确定的参数包括核函数、惩罚因子C。经过试验选定linear作为核函数,将惩罚因子C的取值设为{2-20, 2-19, …, 2-10}[9],使用试错法在泛化误差最小时获取最佳参数取值。
组合模型*+FS由初始预测模块和FS残差修正模块耦合而成,初始预测模块的参数确定方法与前述单独模型的方法一致。对于FS模块,Odan和Reis[13]在建立FS模型时指出按照每7 d为一个周期对傅里叶系数进行计算且每24 h进行一次更新是足够的,本研究采用与之相同的计算和更新策略,将FS模块一周期所包含的时刻数设为T=7×96=672,此时,傅里叶级数M应该满足M < T/2(=336),通过测试确定选用的M为50。
表 2给出了实验中各模型的主要参数取值。
| 表 2 各单独模型的主要参数取值 Tab. 2 Main parameter values of each single model |
表 3给出不同模型对3个DMA进行连续24 h且步长为15 min的短期需水量预测评价结果。
| 表 3 各预测模型在测试集中的评价结果 Tab. 3 Performance indicators of prediction models ontest set |
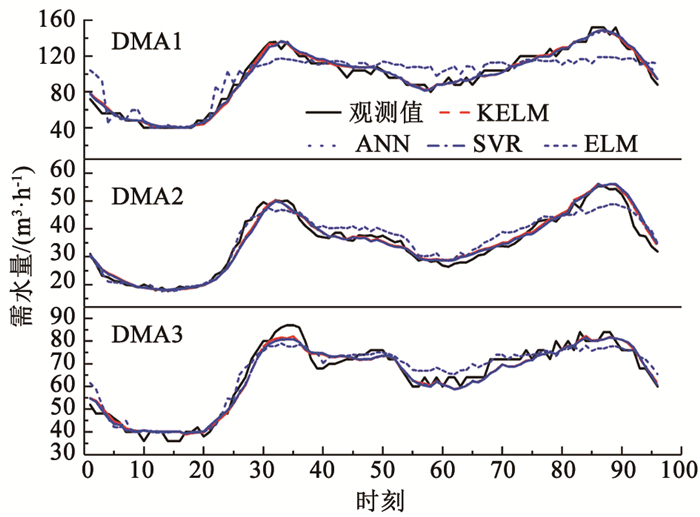
对于预测日,步长为15 min的观测值曲线和各单独模型预测值曲线见图 3。
|
图 3 各单独模型预测值与观测值曲线 Fig. 3 Curves of predicted and observed values of each single model |
KELM模型能够产生与SVR、ANN模型相似的精度。根据表 3统计数据可知,研究所引入的KELM模型在3个DMA的预测测试中都产生了与广为应用的ANN和SVR相近的较高精度。以指标R2为例,ANN、SVR、KELM模型在3个DMA测试中评价结果的均值分别为0.96、0.96和0.97。观察图 3也可以看出, KELM、ANN、SVR的预测曲线非常接近并且与观测值曲线趋势一致,同时较好地捕捉了曲线峰谷变化。
与ELM模型相比,KELM模型的表现更加稳定。ELM模型在3个DMA短期需水量测试中表现出了较大差异,如对历史需水量数据变异系数最高的DMA1进行预测时,其评价指标R2仅为0.76,EMAP也高达12%以上,而对其他两个DMA的测试中R2均达到了0.9以上;KELM模型则始终发挥稳定,R2保持在0.95以上。从图 3中还可观察到相比其他单独模型,ELM在对波峰波谷(时刻30~ 35,时刻85~ 90)的识别中也明显不够准确。此外,从表 3数据可以看出,增加修正模块FS后,原本精度较低的ELM模型,得到的周期性残差补偿更为明显,这也可从侧面说明,KELM模型相比ELM模型能够更多地识别周期性现象并将其耦合到自身的预测过程中。
除了在计算精度和稳定性方面表现优良外,KELM模型的更大优势体现在其计算速度上。KELM与ELM一样,在训练过程中不再调整隐含层参数,使得模型训练所需时间明显下降,其在3个DMA的预测实验中均未超过7 s,这也预示着其在产生与ANN、SVR相似的精度时只需花费二者平均时间的5%左右。
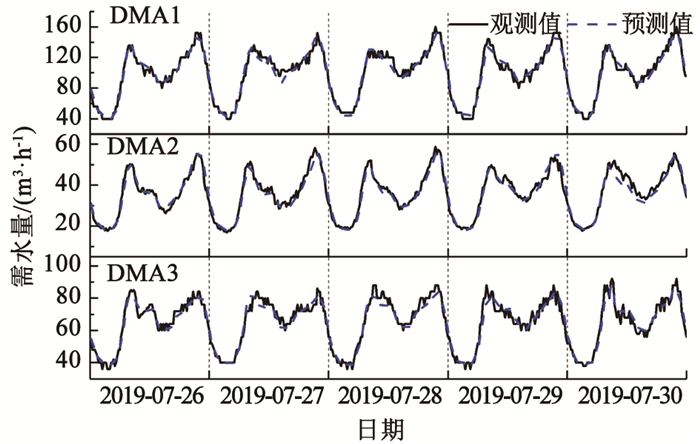
为了测试KELM模型的泛化能力,使用KELM模型对3个DMA分别进行了连续5 d(2019年7月26日—2019年7月30日)的需水量预测实验,其中2019年7月26日、29日和30日为工作日,2019年7月27日和28日为休息日,训练模型时使用每个预测日前55 d数据提取特征后的90%作为训练集,10%作为验证集。表 4给出了对应的评价结果,以R2为例,KELM模型在3个DMA中的平均精度为0.97、0.95和0.95,表现出良好的精度效果。图 4给出了连续预测中步长为15 min的预测值与观测值曲线,预测值始终表现出与观测值非常一致的趋势,也较为准确地捕捉到了峰谷变化。此外,3个DMA工作日和休息日的EMAP平均值分别为4.47% 和4.55%,对于工作日与休息日的预测精度并无较大差别。可见,KELM模型在应对连续预测休息日与工作日的不同时能够表现出良好的泛化能力。
| 表 4 KELM模型连续5 d预测的结果评价 Tab. 4 Performance indicators of KELM prediction model on five consecutive days |
|
图 4 KELM模型连续5 d的预测值与观测值曲线 Fig. 4 Curves of predicted and observed values of KELM model on five consecutive days |
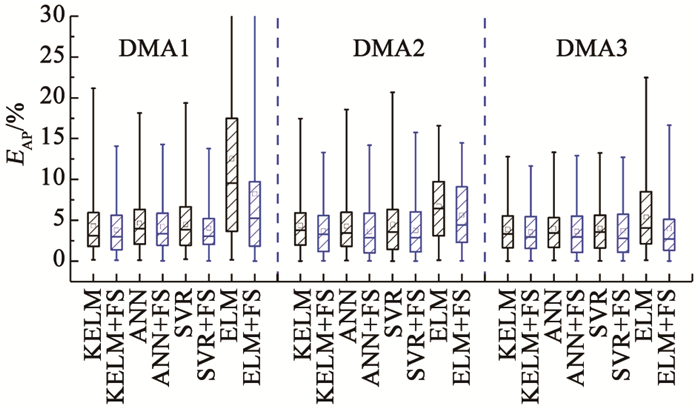
测试结果表明,为KELM模型增加修正模块FS后,其精度得到了一定程度的提升。表 3的统计数据显示,KELM+FS模型在对3个DMA的需水量预测实验中在所有模型中精度表现最佳,相比KELM模型,以EMAP指标为例,KELM+FS模型在3个DMA上的相对降幅分别为12.0%、17.2%和8.4%。事实上,增加修正模块后精度提高不仅限于KELM+FS模型,图 5展示了所有单独模型及其组合模型的绝对百分比误差(APE,EAP)箱线图。可以看出,经过残差修正的模型相比对应的单独模型无论是在EAP的数值范围、平均值,还是中位数方面都有所下降,这也在一定程度上验证了研究中所应用的修正模块的确可以捕捉残差序列中蕴含的周期性特征,并将其补偿到最终预测结果中,发挥进一步降低单独模型误差的作用。
|
图 5 各模型绝对百分比误差箱线图 Fig. 5 Boxplot of absolute percentage error of each model |
综合来看,所提出的KELM+FS组合模型除拥有较高的预测精度外,在完成模型预测所花费的时间上同样极具优势,表现出高效预测性能。图 6给出了所有模型在3个DMA中完成预测范围24 h,预测频率15 min的需水量预测的平均时间柱状图,可见作为耗时最短的KELM模型在添加修正模块后,尽管其时间消耗有所提高,但KELM+FS仍然比目前广为应用的ANN和SVR模型快了大约10倍,这一点使得该模型在需要同时对大量用户进行预测的情况下仍然具有难以忽视的实际应用潜力。

|
图 6 各模型计算所需平均时间柱状图 Fig. 6 Bar chart of the average time required for each model |
1) 对短期需水量进行预测时,KELM模型计算精度与ANN模型、SVR模型相近(相对误差1.8%~ 5.5%),但KELM预测模型的建模时间为ANN、SVR模型建模时间的5%左右;相比极限学习机模型(ELM),KELM的预测性能更加稳定。
2) KELM模型具有较好的泛化能力,能够高效地实现连续日用水量预测,对工作日与休息日的用水量预测结果均达到较高的精度。
3) 核极限学习机模型与傅里叶级数残差修正模块构成的组合预测模型KELM+FS,可以在不显著增加预测时间的前提下,提高KELM预测模型的精度。
| [1] |
PACCHIN E, GAGLIARDI F, ALVISI S, et al. A comparison of short-term water demand forecasting models[J]. Water Resources Management, 2019, 33(4): 1481. DOI:10.1007/s11269-019-02213-y |
| [2] |
GUO G, LIU S, WU Y, et al. Short-term water demand forecast based on deep learning method[J]. Journal of Water Resources Planning and Management, 2018, 144(12): 1. DOI:10.1061/(asce)wr.1943-5452.0000992 |
| [3] |
HERRERA M, TORGO L, IZQUIERDO J, et al. Predictive models for forecasting hourly urban water demand[J]. Journal of Hydrology, 2010, 387(1/2): 141. DOI:10.1016/j.jhydrol.2010.04.005 |
| [4] |
陈磊, 张土乔. 基于最小二乘支持向量机的时用水量预测模型[J]. 哈尔滨工业大学学报, 2006, 38(9): 1528. CHEN Lei, ZHANG Tuqiao. Hourly water demand forecast model based on least squares support vector machine[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1528. DOI:10.3321/j.issn:0367-6234.2006.09.031 |
| [5] |
GHALEHKHOND I, ARDJMAND E, YOUNG W A, et al. Water demand forecasting: review of soft computing methods[J]. Environmental Monitoring & Assessment, 2017, 189(7): 313. DOI:10.1007/s10661-017-6030-3 |
| [6] |
MOUATADID S, ADAMOWSKI J. Using extreme learning machines for short-term urban water demand forecasting[J]. Urban Water Journal, 2016, 14(6): 630. DOI:10.1080/1573062x.2016.1236133 |
| [7] |
殷豪, 董朕, 孟安波. 基于结合混沌纵横交叉的粒子群算法优化极限学习机的短期负荷预测[J]. 计算机应用研究, 2018, 35(7): 2088. YIN Hao, DONG Zhen, MENG Anbo. Short-term load forecasting based on extreme learning machine optimized by particle swarm optimization integrated with chaotic crisscross optimization[J]. Application Research of Computers, 2018, 35(7): 2088. DOI:10.3969/j.issn.1001-3695.2018.07.039 |
| [8] |
VIJAI P, BAGAVATHI S P. Performance comparison of techniques for water demand forecasting[J]. Procedia Computer Science, 2018, 143: 258. DOI:10.1016/j.procs.2018.10.394 |
| [9] |
HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part B, Cybernetics, 2012, 42(2): 513. DOI:10.1109/TSMCB.2011.2168604 |
| [10] |
FU H, VONG C M, WONG P K, et al. Fast detection of impact location using kernel extreme learning machine[J]. Neural Computing and Applications, 2014, 27(1): 121. DOI:10.1007/s00521-014-1568-2 |
| [11] |
AL-ZAHRANI M A, ABO-MONASAR A. Urban residential water demand prediction based on artificial neural networks and time series models[J]. Water Resources Management, 2015, 29(10): 3651. DOI:10.1007/s11269-015-1021-z |
| [12] |
ANELE A, HAMAM Y, ABU-MAHFOUZ A, et al. Overview, comparative assessment and recommendations of forecasting models for short-term water demand prediction[J]. Water, 2017, 9(11): 887. DOI:10.3390/w9110887 |
| [13] |
ODAN F K, REIS L F R. Hybrid water demand forecasting model associating artificial neural network with Fourier series[J]. Journal of Water Resources Planning and Management, 2012, 138(3): 245. DOI:10.1061/(asce)wr.1943-5452.0000177 |
| [14] |
BRENTAN B M, LUVIZOTTO J E, HERRERA M, et al. Hybrid regression model for near real-time urban water demand forecasting[J]. Journal of Computational and Applied Mathematics, 2017, 309: 532. DOI:10.1016/j.cam.2016.02.009 |
| [15] |
CHEN X, DONG Z Y, MENG K, et al. Electricity price forecasting with extreme learning machine and bootstrapping[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2055. DOI:10.1109/tpwrs.2012.2190627 |
| [16] |
YASEEN Z M, SULAIMAN S O, DEO R C, et al. An enhanced extreme learning machine model for river flow forecasting: state-of-the-art, practical applications in water resource engineering area and future research direction[J]. Journal of Hydrology, 2019, 569: 387. DOI:10.1016/j.jhydrol.2018.11.069 |
| [17] |
郑晓芬, 钟旺, 李春祥. 基于核极限学习机的多变量非平稳脉动风速预测[J]. 振动与冲击, 2017, 36(18): 223. ZHENG Xiaofen, ZHONG Wang, LI Chunxiang. Multivariate nonstationary fluctuating wind velocity prediction using kernel-based extreme learning machine[J]. Journal of Vibration and Shock, 2017, 36(18): 223. DOI:10.13465/j.cnki.jvs.2017.18.033 |
| [18] |
HUANG G B. An insight into extreme learning machines: random neurons, random features and kernels[J]. Cognitive Computation, 2014, 6(3): 376. DOI:10.1007/s12559-014-9255-2 |
| [19] |
SHAMSHIRBAND S, MOHAMMADI K, CHEN H L, et al. Daily global solar radiation prediction from air temperatures using kernel extreme learning machine: a case study for city of Bandar Abass, Iran[J]. Journal of Atmospheric & Solar Terrestrial Physics, 2015, 134(105): 109. DOI:10.1016/j.jastp.2015.09.014 |
| [20] |
KONGSOROT Y, HORATA P, MUSIKAWAN P, et al. Kernel extreme learning machine based on fuzzy set theory for multi-label classification[J]. International Journal of Machine Learning and Cybernetics, 2017, 10(5): 979. DOI:10.1007/s13042-017-0776-3 |
| [21] |
BAKKER M, VREEBURG J H G, VAN SCHAGEN K M, et al. A fully adaptive forecasting model for short-term drinking water demand[J]. Environmental Modelling & Software, 2013, 48(3): 141. DOI:10.1016/j.envsoft.2013.06.012 |
| [22] |
CUTORE P, CAMPISANO A, KAPELAN Z, et al. Probabilistic prediction of urban water consumption using the SCEM-UA algorithm[J]. Urban Water Journal, 2008, 5(2): 125. DOI:10.1080/15730620701754434 |
| [23] |
王亮, 张宏伟, 牛志广. 支持向量机在城市用水量短期预测中的应用[J]. 天津大学学报, 2005, 38(11): 1021. WANG Liang, ZHANG Hongwei, NIU Zhiguang. Application of support vector machine in short-term prediction of urban water consumption[J]. Journal of Tianjin University, 2005, 38(11): 1021. DOI:10.3969/j.issn.0493-2137.2005.11.017 |
| [24] |
WANAS N, AUDA G, KAMEL M S, et al. On the optimal number of hidden nodes in a neural network[C]//IEEE Canadian Conference on Electrical & Computer Engineering. Waterloo: IEEE, 1998: 918
|
| [25] |
MISHRA A K, DESAI V R. Drought forecasting using feed-forward recursive neural network[J]. Ecological Modelling, 2006, 198(1/2): 127. DOI:10.1016/j.ecolmodel.2006.04.017 |
| [26] |
JIA Y, CULVER T B. Bootstrapped artificial neural networks for synthetic flow generation with a small data sample[J]. Journal of Hydrology, 2006, 331(3/4): 580. DOI:10.1016/j.jhydrol.2006.06.005 |
| [27] |
朱志宇, 姜长生, 张冰. 基于支持向量回归的混沌序列预测方法[J]. 电工技术学报, 2005, 20(6): 57. ZHU Zhiyu, JIANG Changsheng, ZHANG Bing. Prediction of chaotic time series based on support vector regression[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 57. DOI:10.3321/j.issn:1000-6753.2005.06.012 |
| [28] |
MIRANIAN A, ABDOLLAHZADE M. Developing a local least-squares support vector machines-based neuro-fuzzy model for nonlinear and chaotic time series prediction[J]. IEEE Transactions Neural Network Learn Systems, 2013, 24(2): 207. DOI:10.1109/TNNLS.2012.2227148 |
 2022, Vol. 54
2022, Vol. 54


