2. 武汉众智鸿图科技有限公司,武汉 430223
2. Wuhan Hope Top Technology Co., Ltd., Wuhan 430223, China
供水管网是一个庞大且复杂的系统[1],受限于投资成本等因素,在进行管网设计和运维管理时,管理者需要重点关注管网中的脆弱环节[2]。管段是管网的最重要组成部分之一,进行管段的脆弱性分析,对管网的设计、运维和改造都具有重要意义。管段脆弱性评价研究,主要分为基于水力模拟的方法和基于拓扑结构分析的方法。基于水力模拟的方法通过水力模型模拟所有可能的管段故障后果评价管段对管网正常运行的重要性。由于考虑多管段故障组合计算量十分庞大,通常将故障场景限制为单管段故障,枚举各个管段发生故障后管网的欠缺供应量比评价管段的脆弱性[2]。这类方法的评价结果比较精细,贴合实际工况,但依赖于水力模型的调校精度[3],并且必须针对每根管段执行独立的水力模拟来评估故障影响[4],计算量耗费很高。
由于水力模拟评价方法的计算复杂性,许多学者尝试通过拓扑结构来分析管网组件的重要性。Gutiérrez-Pérez等[5]通过PageRank和HITS两种算法评价和筛选供水管网中的关键节点。Yazdani等[6]采用介数中心性来评价管网中节点的脆弱性,并将各节点介数与最大介数差的平均值作为衡量管网鲁棒性的指标。Agathokleous等[7]在考虑了网络拓扑时序变化的基础上,通过边介数评价管段和管网局部区域的脆弱性。但这些经典的图论方法没有考虑到供水管网中不同节点的角色和地位,以及需求节点与水源节点之间的供需依赖关系,因此,并不完全适用于供水管网的结构分析。为此,Giustolisi等[8]对需求节点和水源节点进行了区分,通过为水源增加虚拟节点等方式增强水源的地位,然后通过边介数评价管段的中心性。但这种方法没有考虑到不同供水路径的重要性,未能精细反映管网真实的结构特征,同时需要修改管网拓扑,不太便于分析。针对上述不足,本研究将供水管网拓扑连接和节点供需关系相结合,考察需求节点的供水路径,提出一种新的评价指标——加权边介数(weighted edge betweenness, WEB)来评价供水管网中管段的脆弱性。
1 边介数中心性介数中心性最早由Freeman[9]于1977年提出,刻画了网络中一节点对于其他节点沿着最短路径传输信息的控制能力,是复杂网络理论中常用的节点重要性衡量指标。Girvan等[10]将其扩展至网络的边,提出了边介数的概念,以衡量网络中边的重要性,其定义为
| $ C_{e}^{\mathrm{B}}=\sum\limits_{s \neq t \in V} \frac{\sigma_{s, t}(e)}{\sigma_{s, t}} $ | (1) |
式中:CeB为边e的介数,σs, t(e)为从节点s到节点t经过边e的最短路径数,σs, t为从节点s到节点t的最短路径总数,V为网络的节点集合。
在社交、生物等网络中,节点是信息共享和交换的主体,因此,重要性评价主要聚焦于网络的节点上。而在供水管网中,管段是管网的最主要组成部分,承载着管网中水的传输,显著影响管网的水力状况和功能[8]。因此,边介数更符合供水管网的可靠性分析需求。管段的中心性越强,其对管网中水的传输控制能力越强,当其发生故障时,对管网的影响越大,即管段的脆弱性越大。
2 加权边介数水源是供水管网供水的基础,需求节点的用水依赖于其与水源间的连通路径,需求节点之间的连通路径并不能保证管网的正常供水,因此,将边介数计算中的节点对修改为需求节点与水源节点组成的节点对,更符合供水管网实际情况。由于求解每一个需求节点与各个水源之间的所有供水路径计算代价过大,将需求节点与水源间的供水路径数量限制为K。实验表明,K通常取为网络节点数的5%~10%就可以达到统计上比较鲁棒的度量结果[4]。本研究使用水源与需求节点间的K最短路径代表实际的供水路径,K取为节点总数的10%。
将供水路径需要克服的阻力作为路径的距离,并采用Herrera等[11]提出的对于供水路径阻力的度量,参考普遍采用的Darcy-Weisbach水头损失公式[12]。水源s与需求节点t之间的第k条最短路径的距离可表示为
| $ d_{s, t}(k)=\sum\limits_{m=1}^{M} \frac{f_{m} L_{m}}{D_{m}} $ | (2) |
式中:M为第k条最短路径上的管段数目,fm为管段m的摩阻系数,Lm为管段m长度,Dm为管段m直径。
另一方面,不同的供水路径其重要性也各不相同。供水路径的重要性主要与其两端连接的水源和需求节点有关。假设需求节点t连接s1和s2两个水源,s2的供应比例大于s1,即节点t的用水更依赖于水源s2,此时s2与节点t之间的路径相比s1与节点t之间的路径更加重要。若水源s连接两个节点t1和t2,节点t2的需求大于节点t1,则节点t2和水源s的连通路径发生故障后,事故的影响更大,节点t2与水源s之间的路径相比节点t1与水源s之间的路径更加重要。因此,根据水源在整个管网中的供应比例和需求节点在整个管网中的需求占比对供水路径进行加权,可以更精细刻画供水路径的重要性。
水源s的供应比例可表示为
| $ c_{s}=\frac{p_{s}}{\sum\limits_{s \in S} p_{s}} $ | (3) |
式中:cs为水源s的供应比例,ps为水源s的供应量,S为水源集合。
需求节点t的需求比例可表示为
| $ q_{t}=\frac{a_{t}}{\sum\limits_{t \in T} a_{t}} $ | (4) |
式中:qt为需水节点t的需求比例,at为节点t的需水量,T为需水节点集合。
水源s和节点t之间供水路径的重要性总权值ws, t可表示为
| $ w_{s, t}=c_{s} q_{t} $ | (5) |
由于水源s与t之间共有K条供水路径,而通常水流总是选择流通阻力更小的路径,水流对路径选择的不确定性本质上是各条路径的流通阻力不同[13]。因此,根据这K条供水路径的距离进行反比例加权。
则水源s和需求节点t之间的第k条路径的权值ws, t, k可表示为
| $ w_{s, t, k}=\frac{g_{s, t}(k)}{\sum\limits_{k=1}^{K} g_{s, t}(k)} w_{s, t} $ | (6) |
式中
| $ g_{s, t}(k)=\frac{1}{d_{s, t}(k)} $ | (7) |
管段e的加权边介数BWE(e)计算公式为
| $ B_{\mathrm{WE}}(e)=\frac{\sum\limits_{s, t \in(S, T)} \sum\limits_{k=1}^{K} w_{s, t, k}(e)}{\sum\limits_{s, t \in(S, T)} \sum\limits_{k=1}^{K} w_{s, t, k}} $ | (8) |
式中:S为水源集合,T为需求节点集合,K为常量,ws, t, k(e)为水源s到需水节点t并且经过管段e的第k条最短路径的权值,ws, t, k为水源s到需水节点t的第k条最短路径的权值。
加权边介数值越大,管段损坏对管网的功能影响越大,即管段脆弱性越大。
3 实验与分析使用Net3和ZJ两个管网作为研究对象。这两个管网规模较为接近,同时分别代表枝状和环状两种不同布局类型的管网。管网Net3是供水管网分析开源库WNTR提供的示例管网数据[14],包含两个水源,环路较少,整体布局呈狭长枝状。管网ZJ是肯塔基大学提供的开放管网数据[15],包含1个水源,环路较多,整体布局呈较均匀网格状。两管网具体特征参数如表 1所示。
| 表 1 两个管网特征 Tab. 1 Characteristics of two WDNs |
首先,使用欠缺供应量比、水龄增长比、经典边介数和WEB对上述两个管网进行管段脆弱性评价,对比其脆弱性分布,然后分别采用经典边介数和WEB作为攻击依据进行供水管网蓄意攻击模拟,验证WEB的敏感度。最后,基于WEB对管网管段进行优化,对比优化前后的管段脆弱性分布。
3.1 脆弱性分布使用经典边介数和WEB对管网Net3和管网ZJ的所有管段进行脆弱性评价,并分别与使用管段欠缺供应量比、水龄增长比的评价相比照。管段欠缺供应量比指的是一管段发生故障后,采用压力驱动的水力模拟方式计算出24 h内管网不能满足的用水需求量占总需求量的比例,因为考虑了延时运行工况,可以认为比较符合实际状况[16]。而水龄增长比是指管段故障后24 h内所有节点总水龄的增量占故障前24 h内所有节点总水龄的比例[17]。
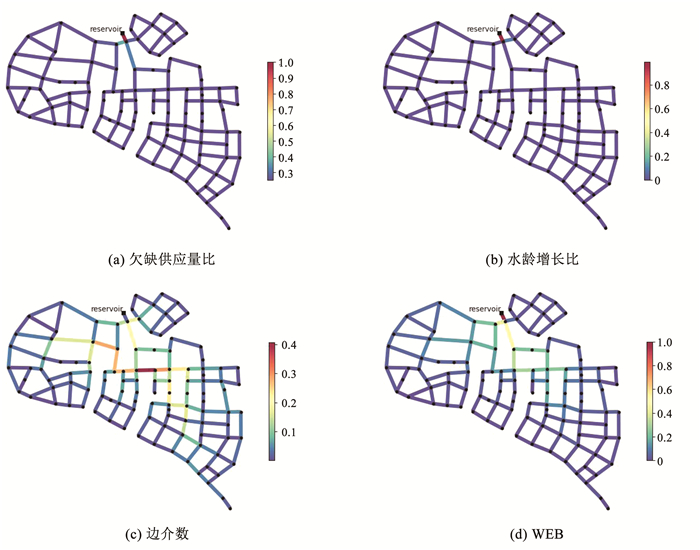
两个管网的管段脆弱性评价结果分级分别见图 1、2。对于管网Net3,按照欠缺供应量比(图 1(a))和水龄增长比评价指标(图 1(b)),存在一条连接水源River的脆弱性显著的路径,该路径上的管段脆弱性明显高于管网其他区域的管段,即发生故障时对管网的影响更大。使用WEB的评价(图 1(d))也识别出一条连接水源River的脆弱性显著的路径,与欠缺供应量比和水龄增长比的评价结果基本一致。而经典边介数评价(图 1(c))识别出的脆弱性最高的管段普遍位于远离水源的管网较末端区域,与欠缺供应量比和水龄增长比的评价结果相差较大。由此也可以看出,越靠近水源的管段其脆弱性往往越大。但图 1中靠近水源River处存在一个三角环,该环中的管段脆弱性小于其直接相连的无环下游管段。这是因为环中的任一管段发生故障时,水流的传输可以经由环中其他管段替代, 而其直接相连的下游管段虽同为大多数节点供水的必经之路但却不存在其他替代路径,因此,该下游管段的脆弱性相对更大。

|
图 1 管网Net3管段脆弱性分布 Fig. 1 Pipe vulnerability distributions of WDN Net3 |
|
图 2 管网ZJ管段脆弱性分布 Fig. 2 Pipe vulnerability distributions of WDN ZJ |
同样,对于管网ZJ,WEB与欠缺供应量比和水龄增长比的评价结果也较为一致,都将连接唯一水源与管网主体的管段评价为最脆弱。而经典边介数识别出的最脆弱管段位于管网中部。管网ZJ虽然整体呈网格状,但只有一个水源通过一根管段与管网主体相连,该管段发生故障后管网将完全失效,WEB和欠缺供应量比的评价结果更符合实际。
两个管网的实验结果都表明,WEB相比经典边介数的评价结果更接近欠缺供应量比和水龄增长比的评价结果,原因主要在于经典边介数将水源与所有需求节点等同看待,没有考虑供水管网的水力特征,在评价中未能体现水源的中心地位。
3.2 敏感度分析在复杂网络中常使用蓄意攻击模拟来分析管网的鲁棒性。蓄意攻击模拟通过逐步移除网络中最脆弱的组件方式对网络进行攻击,然后通过网络性能评价指标的变化衡量网络的鲁棒性。使用不同脆弱性评价指标,网络性能变化幅度不同,体现出评价指标的敏感度差异。敏感度较高的指标更有利于管网鲁棒性分析。
针对实验管网Net3和ZJ,分别采用经典边介数和WEB指标选择最脆弱管段实施蓄意攻击模拟,以最大连通子图规模比和平均节点效率比两个指标衡量供水管网的性能变化。
最大连通子图规模定义为包含至少一个水源节点的最大连通子图的节点数。最大连通子图规模比为
| $ r_{s}=\frac{s^{\prime}}{s} $ | (9) |
式中s和s′分别为攻击前和攻击后的最大连通子图规模。
定义平均节点效率为
| $ c_{\mathrm{avg}}=\frac{1}{n} \sum\limits_{i=0}^{n} \frac{1}{d_{i}} $ | (10) |
式中:n为所有需求节点的总数,di为节点i到任一水源的最短路径距离。
相应地,平均节点效率比定义为
| $ r_{c}=\frac{c^{\prime}}{c} $ | (11) |
式中c和c′分别为攻击前和攻击后的平均节点效率。
将管段按脆弱性评价结果从高到低从管网中移除。表 2为针对管网Net3的实验结果。使用经典边介数指标,移除前5%管段后,最大连通子图规模比和平均节点效率比变化都较小,说明管网性能未受到显著影响,管网仍保持较高服务能力。而使用WEB,移除5%的管段后,最大连通子图规模比已降为0,说明此时管网所有节点都已经与所有水源断开连接,管网已经完全失效。
| 表 2 管网Net3模拟攻击结果 Tab. 2 Attack simulation results of WDN Net3 |
表 3为针对管网ZJ的攻击实验结果。使用经典边介数作为攻击策略,移除前5%管段后,最大连通子图规模比未变化,平均节点效率比变化较小,管网仍保持着较高的服务能力。而使用WEB作为攻击策略,仅移除1%的管段后,上述两个指标即下降为0,管网完全失效。这是因为管网ZJ虽然呈网格状,但只有一个水源与管网主体连接,与水源直接相连的管段为最脆弱管段,移除该管段后,管网中所有节点便与水源失去联系,这与实际情况相符。
| 表 3 管网ZJ模拟攻击结果 Tab. 3 Attack simulation results of WDN ZJ |
从两个管网的实验结果容易看出,WEB相比经典边介数在管网可靠性评价上具有更高敏感度。
3.3 基于WEB的管网优化WEB值较大的管段属于管网的薄弱环节,针对这些管段的优化,可以提升管网整体鲁棒性。本研究以添加平行管段的优化方法为例,印证WEB指标评价对管网优化的作用。具体做法是选择WEB值最大的若干管段,添加管径、管长和管材都相同的平行管段,以形成新的环路,然后重新计算所有管段的WEB指标,通过对比优化前后的管段脆弱性分布考察整体鲁棒性提升状况。
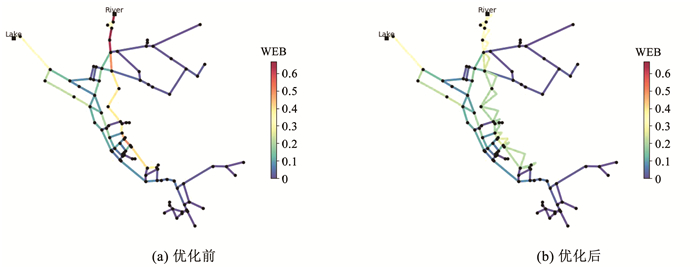
对管网Net3,按WEB值从大到小选取前15%的管段,添加平行管段,优化后的管段脆弱性分布见图 3(b)。可以看出,最脆弱的管段仍主要位于水源附近,但管段脆弱性已经显著降低,全部管段WEB值从0~0.67变为0~0.36。
|
图 3 管网Net3优化前后管段脆弱性分布 Fig. 3 Pipe vulnerability distributions of WDN Net3 before and after optimization |
管网ZJ本身存在很多环状连接,故仅选取WEB值前5%的管段添加平行管段。图 4(b)显示,与水源直接相连的管段仍最脆弱,但脆弱性也显著降低,全局看管段WEB值从0~1变为0~0.5。

|
图 4 管网ZJ优化前后管段脆弱性分布 Fig. 4 Pipe vulnerability distributions of WDN ZJ before and after optimization |
针对两个管网的实验表明,WEB指标对管网优化可以发挥明显指导作用。
4 结语基于需求节点与水源之间的K最短路径,结合供水管网的水力属性和物理属性信息,提出了适用于供水管网的管段脆弱性评价新指标——WEB。WEB考虑了需求节点和水源的供需依赖关系,以及水源节点和需求节点在管网中不同的角色和重要性,能更加精细地反映各个管段在供水管网功能结构稳定性中的作用。实验表明,相比经典边介数指标,WEB更加接近管网实际运行状况,有助于识别管网中脆弱性大的管段。同时可以发现,供水管网中越靠近水源的管段,其脆弱性往往更大,但与水源的距离并不是唯一的影响因素,还与其可替代性有关,若该管段处于一个环中,则其发生故障时管网中将存在其他路径替代,此时其脆弱性反而可能小于其无环的下游管段。WEB可以作为一种较好的供水管网可靠性分析指标,为管网设计验证、加固和改造提供参考依据。
WEB与基于水力模拟的欠缺供应量比、水龄增长比的评价结果较为接近,但属于代理指标法范畴,计算更加简单快捷,更适合于管网优化设计等需要反复迭代计算可靠性的场景。
后续的研究可以进一步挖掘供水管网自身特性,如在计算供水路径时加入部分流向的约束信息,进而基于含有向边和无向边的混合图分析管段脆弱性;还可以进一步考虑水箱、阀门等组件对于管网供水的影响,更精细地评价管段的脆弱性。
| [1] |
DIAO K, FARMANI R, FU G, et al. Clustering analysis of water distribution systems: identifying critical components and community impacts[J]. Water Science and Technology, 2014, 70(11): 1764. DOI:10.2166/wst.2014.268 |
| [2] |
MARLIM M S, JEONG G, KANG D. Identification of critical pipes using a criticality index in water distribution networks[J]. Applied Sciences, 2019, 9(19): 4052. DOI:10.3390/app9194052 |
| [3] |
HERRERA M, ABRAHAM E, STOIANOV I. Graph-theoretic surrogate measures for analysing the resilience of water distribution networks[J]. Procedia Engineering, 2015, 119: 1241. DOI:10.1016/j.proeng.2015.08.985 |
| [4] |
BERARDI L, UGARELLI R, R∅STUM J, et al. Assessing mechanical vulnerability in water distribution networks under multiple failures[J]. Water Resources Research, 2014, 50(3): 2586. DOI:10.1002/2013WR014770 |
| [5] |
GUTIÉRREZ-PÉREZ J A, HERRERA M, PÉREZ-GARCÍA R, et al. Application of graph-spectral methods in the vulnerability assessment of water supply networks[J]. Mathematical and Computer Modelling, 2013, 57(7/8): 1853. DOI:10.1016/j.mcm.2011.12.008 |
| [6] |
YAZDANI A, JEFFREY P. Complex network analysis of water distribution systems[J]. Chaos, 2011, 21(1): 016111. DOI:10.1063/1.3540339 |
| [7] |
AGATHOKLEOUS A, CHRISTODOULOU C, CHRISTODOULOU S E. Topological robustness and vulnerability assessment of water distribution networks[J]. Water Resources Management, 2017, 31(12): 4007. DOI:10.1007/s11269-017-1721-7 |
| [8] |
GIUSTOLISI O, RIDOLFI L, SIMONE A. Tailoring centrality metrics for water distribution networks[J]. Water Resources Research, 2019, 55(3): 2348. DOI:10.1029/2018WR023966 |
| [9] |
FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35. DOI:10.2307/3033543 |
| [10] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821. DOI:10.1073/pnas.122653799 |
| [11] |
HERRERA M, ABRAHAM E, STOIANOV I. A graph-theoretic framework for assessing the resilience of sectorised water distribution networks[J]. Water Resources Management, 2016, 30(5): 1685. DOI:10.1007/s11269-016-1245-6 |
| [12] |
BROWN G O. The history of the Darcy-Weisbach equation for pipe flow resistance[C]//ASCE Civil Engineering Conference and Exposition. Reston: ASCE Press, 2003: 34. DOI: 10.1061/40650(2003)4
|
| [13] |
伍悦滨, 王芳, 田海. 基于信息熵的给水管网系统可靠性分析[J]. 哈尔滨工业大学学报, 2007, 39(2): 251. WU Yuebin, WANG Fang, TIAN Hai. Entropy-based reliability analysis in water distribution systems[J]. Journal of Harbin Institute of Technology, 2007, 39(2): 251. DOI:10.3321/j.issn:0367-6234.2007.02.020 |
| [14] |
KLISE K A, MURRAY R, HAXTON T. An overview of the water network tool for resilience (WNTR)[C]//Proceedings of the 1st International WDSA/CCWI Joint Conference. Kingston: Queen′s University, 2018: 8
|
| [15] |
DANDY G. ZJ Network [EB/OL]. [2020-12-25] http://www.uky.edu/WDST/Systemages/43System_Page_ZJNetwork.html
|
| [16] |
CREACO E, FRANCHINI M, ALVISI S. Evaluating water demand shortfalls in segment analysis[J]. Water Resources Management, 2012, 26(8): 2301. DOI:10.1007/s11269-012-0018-0 |
| [17] |
HERNANDEZ E, ORMSBEE L E. Application of segment based robustness assessment for water distribution networks[C]//Proceedings of the 1st International WDSA/CCWI Joint Conference. Kingston: Queen′s University, 2018: 31
|
 2022, Vol. 54
2022, Vol. 54


