2. 山东电力工程咨询院有限公司,济南 250014
2. Shandong Electric Power Engineering Consulting Institute Co., Ltd., Jinan 250014, China
裂隙岩体渗流是导致水利、土木工程事故的主要原因之一[1-2],还关系到采油、核废料污染的防治、煤田瓦斯危害的防治和填埋垃圾的污水下渗等方面,工程中需要进行细致的考察和分析。
常用的裂隙岩体渗流分析数学模型有离散裂隙网络模型、等效连续介质模型、双重介质模型以及混合渗流模型[3]。因渗流主要在裂隙网络内发生,用离散裂隙网络模型来模拟岩体渗流规律时精度较高,并且由于离散型裂隙网络模型忽略了岩块本身的孔隙系统及裂隙岩体之间的水交替过程,分析时更加简便。二维离散裂隙网络模型由于构造简单发展较为成熟,但计算结果和实际情况相比误差较大。三维离散型裂隙网络模型方面,李新强等[4]使用边界元法计算裂隙网络的渗透张量,并与有限元法流量分析结果比较验证方法的有效性。于青春等[5-7]基于管单元模型通过对裂隙网络的渗透张量进行求解来分析岩体的渗流情况,Ren等[8]提出用统一管网法对裂隙岩体内的渗流情况进行研究,Sun等[9]用3D统一管网法模拟含裂隙的多孔岩石中的裂隙情况。Wang等[6-10]从渗透张量的角度对裂隙网络的REV尺寸进行研究。王振伟等[11]通过岩体的渗透张量来确定渗流的REV尺寸,并研究了裂隙的密度和迹长对裂隙岩体的渗透张量和REV大小的影响。也有研究发现岩体裂隙存在优势水力路径,Zhao等[12-13]发现在裂隙岩体中只有10%~20%的裂隙可以发生渗流,更多的裂隙仅起到存水或持水的作用。Zhang等[14-15]利用数值分析方法以及现场试验测试进行渗流分析,对特定岩体中优势水流的形成机理及其路径进行了相关研究,林宏奕[16]利用质点追踪技术来对岩体裂隙中存在的优势水流路径进行分析,刘华梅等[17]通过对裂隙网络渗流路径进行优化,发现剔除对渗流无贡献的裂隙,可以减少计算量和缩短计算时长,倪绍虎等[18-19]通过对裂隙岩体的渗透特性进行研究发现在裂隙岩体中的渗流的确存在优势水力路径。另外,也有一些学者采用不同的方法对砂岩油藏中优势渗流通道进行识别和分析,如雷霆等[20]提出改进的CRM模型结合生产动态数据来对优势渗透通道进行识别描述。现有研究工作表明,确定渗透张量方面,一维管单元模型可以显著缩减计算工作量,而且由于岩体中存在较大裂隙,沟通岩体范围较大,一定程度也起到优势水力路径作用,因此,在确定渗透张量时,一定程度上可以忽略掉连通范围小的裂隙,但缩减的幅度没有相关研究。
本研究采用三维裂隙网络模型对岩体裂隙渗流进行分析,根据岩体露头裂隙统计参数,用蒙特卡罗法生成岩体的圆盘裂隙网络样本,将渗流通道简化为管单元模型。一定程度上,岩体主干裂隙控制渗透性能,通过对裂隙规模的研究,探索不同缩减规模对渗透张量和岩体REV大小的影响,以及计算规模可缩减的幅度,并通过实际工程案例对此方法进行了验证。
1 三维裂隙网络生成与渗透张量求解 1.1 模型的建立与参数生成采用Baecher模型[21],建立离散网络模型时采用三维整体坐标系,将生成的所有裂隙通过该坐标系确定。将坐标系的主轴方向与地理位置一一对应,即X轴正半轴指向东,Y轴正半轴指向北,Z轴正半轴的方向指向上(与高程一致),按照右手法则来进行方向的角度旋转。生成裂隙所需要确定的几何参数包括裂隙的方向(倾向α, 倾角β)、大小(半径r)、位置(圆盘中心点坐标)、隙宽b,即(α, β, r, x, y, z, b),每个参数变量的生成都遵循其自身的概率密度函数,利用积分法产生随机变量。
裂隙的位置用裂隙面上有代表性的点来描述,在统计过程中用裂隙圆盘圆心来确定裂隙在空间中的位置,在三维空间中即圆心点(x, y, z)。假设圆心点在研究域各处出现的概率是相等的,即裂隙圆盘中心点的生成服从均匀分布。在生成裂隙网络时,应先确定生成域的大小,记录圆心在该生成域内的所有裂隙,然后在生成域内再创建一定范围内的研究域,记录圆心在该研究域内的所有裂隙和与研究域边界相交的裂隙。
生成裂隙三维裂隙网络后,求出各圆盘的交线,传统方法是在此基础上对裂隙圆盘剖分成平面单元进行裂隙网络水力学分析,但是一个研究域的裂隙多达上万条,用平面单元分析会产生十几万的自由度,使求解效率低下。为简化分析计算过程,Tsang[22]和Cacas等[23]提出水流在裂隙面内以沟槽流形态运动,因此,可以对裂隙渗流的分析计算进行简化,如图 1所示。张有天[1]认为可以用一维管单元进行三维裂隙网络水力学分析。具体简化模型为将相交裂隙节理圆盘的圆心和交线中心相互连接起来,然后生成管单元,只在管单元内产生水流,圆心与交线的中点即为节点。对于渗流区域内所有节点建立有限元方程组,用矩阵表示为
| $ \boldsymbol{K H}=\boldsymbol{Q} $ | (1) |

|
图 1 三维裂隙网络简化分析概念简图 Fig. 1 Conceptual simplified analysis diagram of 3D fracture network |
式中:K为总渗透矩阵,在三维空间中有9个分量;H为节点水头矩阵;Q为节点流量矩阵。由于是恒定流,方程可解。
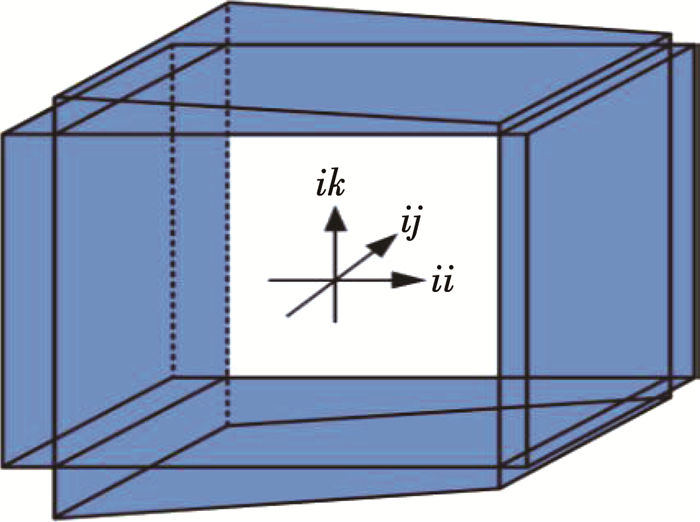
1.2 渗透张量的数值求法数值求法的基本原理为:在模型的某一相对面施加等水头边界,两个面之间存在一定的水头差,另外两对相对面施加变水头边界[24](如图 2所示),渗流边界的节点水头分布情况如图 3所示。利用该模型共模拟了3组实验,第一组实验中令其中一对相对面施加等水头,在另外两对相对面施加变水头,进行计算并保存相应的计算结果。另外两组实验只改变等水头边界施加的方向,其他不变。由于对称性,每组实验的渗流量只计算6个即可,3组实验共产生的流量数据为18个。根据渗透张量的定义得[21]
| $ \left[\begin{array}{lll} k_{x x} & k_{x y} & k_{x z} \\ k_{y x} & k_{y y} & k_{y z} \\ k_{z x} & k_{z y} & k_{z z} \end{array}\right]=\left[\begin{array}{lll} q_{x x} & q_{x y} & q_{x z} \\ q_{y x} & q_{y y} & q_{y z} \\ q_{z x} & q_{z y} & q_{z z} \end{array}\right]\left[\begin{array}{ccc} \frac{1}{\Delta P_{x}} & 0 & 0 \\ 0 & \frac{1}{\Delta P_{y}} & 0 \\ 0 & 0 & \frac{1}{\Delta P_{z}} \end{array}\right] $ | (2) |
|
图 2 模型的边界条件 Fig. 2 Boundary condition of the model |
式中:kij为渗透张量在j方向渗透坡降下产生的i方向分量,qij为渗流量在j方向渗透坡降下产生的i方向分量,ΔPi为在i方向的水力坡降。

|
图 3 裂隙网络渗流水头分布示意 Fig. 3 Schematic of seepage head distribution in fracture network |
对于均质体,在各个方向上的入渗量和出渗量都相等。然而,对于节理岩体,由于岩体中裂隙的分布具有很强的随机性,岩体的入渗流量和出渗流量并不总是相等。
2 计算规模缩减探索于青春等[25]研究发现,渗流主要发生在较大的裂隙中,而较小的裂隙对渗流的影响十分微小,因此,在进行裂隙渗流计算时可以在精度允许的情况下将较小的裂隙删除掉,从而减少计算量,缩短计算时间。本文主要研究了在进行渗流计算时可缩减的规模及其相应的误差,并用实际工程进行了验证,当然在实际工程设计中,应根据工程的精度要求选择合适的缩减量。在此约定:缩减规模为0.1即先将渗流裂隙网络中的裂隙直径按照由小到大的顺序进行排列,然后去掉排在前1/10直径的裂隙,只用剩下的裂隙来进行计算。
规模的缩减一般为全排列缩减,即对裂隙网络空间内所有组数的裂隙从小到大进行整体的规模缩减。例如, 若缩减规模为0.1,则将3组裂隙从小到大排列,删除排在前10%的裂隙,保留剩下的90%进行计算。全排列缩减方式的弊端在于容易较多地删除直径最小的那组裂隙,可能会降低渗透张量的准确性。考虑到力学成因,此组裂隙可能开度较大,渗透能力并不弱,因此,提出另一种缩减方法,即对各组裂隙按指标分别从小到大规模缩减,例如, 若缩减规模为0.1,分别对每组裂隙从小到大排列,再分别删除每组前10%的裂隙,然后将各组的剩余裂隙重新统计在一起,进行渗透张量计算。该方法在计算渗透张量前保证了各组裂隙缩减的平衡性,使各组裂隙数量均匀缩减。
三维裂隙网络的参数信息采用李新强等[4]研究的三维裂隙网络渗流模型,如表 1所示,在该区域共产生的裂隙组数为3。
| 表 1 三维裂隙网络模型参数 Tab. 1 Model parameters of 3D fracture network |
由边界元法计算确定初值,再用现场压水试验校核得到渗透主系数(m/s)和渗透主方向为[4]
| $ \left\{\begin{array}{l} k_{1}=3.08 \times 10^{-7} \text {, 倾向 } 170.0° \text {, 倾角 } 19.8° \\ k_{2}=4.33 \times 10^{-7} \text {, 倾向 } 45.9° \text {, 倾角 } 57.3° \\ k_{3}=4.70 \times 10^{-7} \text {, 倾向 } 269.6° \text {, 倾角 } 24.8° \end{array}\right. $ | (3) |
应用自编的C++有限元渗流程序,控制管径与隙宽的比值为11.506 9[26],应用上述数据进行渗流模拟,选取100 m×100 m×100 m的立方体区域作为生成域,在生成域的中心选择20 m×20 m×20 m的立方体作为研究域。对生成的裂隙进行如上所述两种方式的规模缩减,表 2为每组裂隙分别按相同比例的规模缩减,表 3为3组裂隙全排列情况下的规模缩减。表 2和表 3中渗透主值的误差为
| $ \varepsilon_{i}=\left|\frac{k^{\prime}{}_{i}}{k_{i}}\right|, i=1,2,3 $ | (4) |
| 表 2 每组裂隙分别按相同比例的规模缩减及相应误差 Tab. 2 Scale reduction of each fracture group according to the same proportion and corresponding errors |
| 表 3 3组裂隙全排列规模缩减及相应误差 Tab. 3 Scale reduction of three fracture groups with full arrangement and corresponding errors |
式中:ki为现场压水试验测出的渗透主值,k′i为相应缩减程度下计算所得的对应渗透主值。
表 2和表 3中渗透主方向的误差不可以直接求出,将计算所得渗透主值方向与现场压水试验主值方向的夹角作为主方向的绝对误差。两渗透主值方向的夹角余弦为
| $ \cos \theta=\left|\frac{\left(\boldsymbol{k}_{i j}, \boldsymbol{k}^{\prime}{ }_{i j}\right)}{\left|\boldsymbol{k}_{i j}\right|\left|\boldsymbol{k}^{\prime}{}_{i j}\right|}\right|, i, j=1,2,3 $ | (5) |
式中:kij为现场压水试验渗透主值对应的渗透系数列向量,k′ij为相应缩减程度下计算所得的对应渗透系数列向量。
将未缩减时所得到的渗透主系数和渗透主方向与式(3)进行比较,相应的误差如下:
| $ \left\{\begin{array}{l} \varepsilon_{1}=0.055, \theta_{1}=19.4° \\ \varepsilon_{2}=0.570, \theta_{2}=13.9° \\ \varepsilon_{3}=0.266, \theta_{3}=23.3° \end{array}\right. $ | (6) |
式中:εi为主值相对误差,θi为主方向绝对误差,i=1, 2, 3。
由式(6)模拟可见, 模拟计算的结果与现场压水试验校正结果的误差并不太大,在工程实践可接受的范围内。
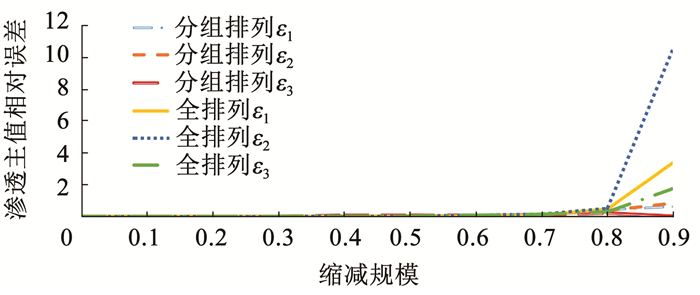
为了便于比较两种排列方式对渗透张量的影响,将表 2和表 3中数据分别绘制两种方式的渗透主值和渗透主方向的误差图像,结果如图 4和图 5所示。
|
图 4 两种缩减方式渗透主值相对误差对比 Fig. 4 Comparison of relative errors of principal permeability for two scale reduction methods |

|
图 5 两种缩减方式渗透主方向绝对误差对比 Fig. 5 Comparison of absolute errors of permeability directions for two scale reduction methods |
由图 4可知,两种缩减方式渗透主值误差在缩减规模0.1~0.7基本一致。当缩减规模达到0.8时,分组排列的误差绝对值为11%,全排列的误差绝对值为9.7%。当缩减规模达到0.8以后,误差绝对值开始骤然增大,分组排列的误差绝对值为32.6%,全排列的误差绝对值为41.3%,此时缩减效果已成病态,不适宜再缩减裂隙规模进行计算。同样根据图 5可知,两种缩减方式渗透主方向均值在缩减规模0.1~0.7波动较小。当缩减规模达到0.7以后,分组排列的角度误差绝对值为2.03°,全排列的误差绝对值为2.60°。当缩减规模达到0.8以后,误差绝对值增幅增大,此时分组排列的误差绝对值为9°,全排列的误差绝对值为4.9°,此时方向误差已经不够准确,不适宜再缩减裂隙规模进行计算。
综上,对于两种缩减方式效果基本一致,实际工程中可以采用任意一种缩减方式。当最大缩减规模为0.7时,最为适宜本例,当缩减规模大于0.7时,裂隙渗流网络中重要的裂隙将被删除,导致渗流分析的结果与裂隙岩体的实际渗流情况差别较大。
3 岩体表征单元体(REV)的确定由于在天然岩体中存在的裂隙是随机分布的,国内外学者在进行岩体力学参数选取时经常会对岩体的表征单元体(REV)进行分析。岩体的各项等效参数具有十分明显的尺寸效应,当岩体的试样体积增加到一定值V0时,各项渗透参数趋于稳定,这一V0称为岩体渗透性代表单元体积(REV),确定岩体REV的尺寸是进行裂隙渗流研究的一个重要方面。目前,国内外学者对于REV尺寸有从等效力学参数进行分析确定的,也有从水力学参数方面对REV进行研究的,还有从裂隙块体几何参数对岩体的REV进行研究的。基于不同岩体参数的尺寸效应而得到的表征单元体的尺寸都不太相同,周创兵等[27]提出了3种确定岩体REV的方法,即数值模拟法、地质统计法和能量叠加法。
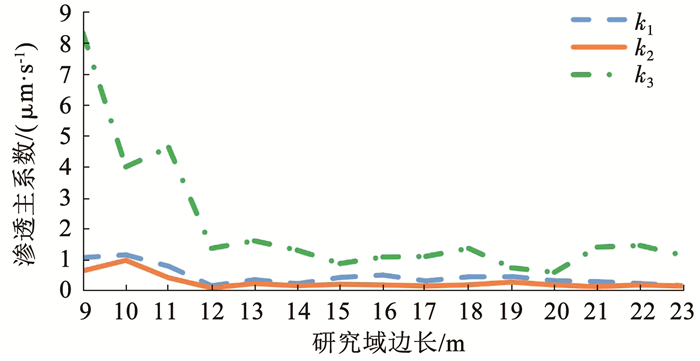
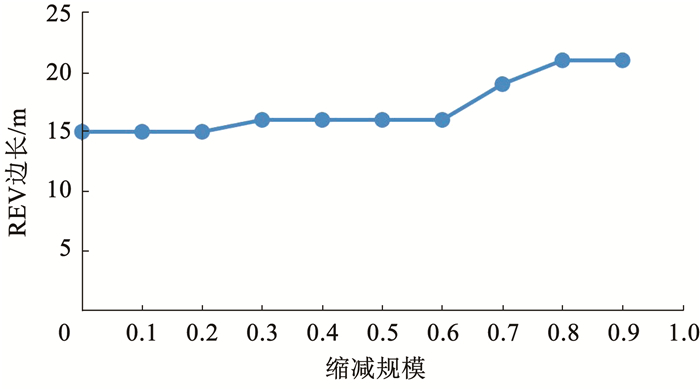
本研究运用数值模拟的方法来计算岩体的渗透张量,根据渗透张量3个渗透主系数的变化情况来确定岩体的REV尺寸,通过对不同缩减规模情况下裂隙网络REV的研究,进一步探索规模缩减对裂隙岩体REV的影响。在缩减规模确定的情况下,对研究域从9 m×9 m×9 m开始逐渐增加到23 m×23 m×23 m,每次研究域的边长增加1 m。以计算规模未进行缩减时的情况为例,管径与隙宽的比值为11.506 9,控制生成域的大小为100 m×100 m×100 m,通过不断改变研究域的大小,得到不同研究域的渗透张量,将所得的裂隙网络渗透主系数绘制成折线图,如图 6所示。可以看出,当所生成的裂隙网络研究域的边长增大到15 m后,随着研究域边长的增大,岩体渗透张量的渗透主系数变化情况基本趋于稳定,故当缩减规模为0时的REV尺寸可取15 m×15 m×15 m。同理,对其他缩减规模下的REV尺寸进行分析,并将得到的REV的边长绘制在折线图上,如图 7所示。可以看出,随着裂隙网络缩减规模数值的增大,岩体的REV尺寸逐渐变大,说明裂隙密度对岩体的表征单元体大小有一定的影响,REV尺寸随裂隙密度减小而增大,该认识与李锦辉等[28]对裂隙数量与REV尺寸关系[11]的研究结论相一致。
|
图 6 计算规模不缩减时的渗透主系数 Fig. 6 Principal permeability curves without calculation scale reduction |
|
图 7 不同缩减规模下的REV边长 Fig. 7 REV side lengths for different scale reductions |
中国水利水电科学研究院的科研人员在新疆对某水利枢纽的左岸边坡岩体进行现场调研后,根据岩体中结构面的分布和组合情况得到如表 4所示的统计结果[29]。
| 表 4 岩体结构面几何参数统计结果 Tab. 4 Statistical results of geometric parameters of rock mass structural surface |
对此工程实例,用自编的程序进行数值模拟,将生成域的大小设为40 m×40 m×40 m,研究域的大小为15 m×15 m×15 m。不缩减时在生成的研究域内裂隙共有8 129条,在裂隙网络中节点数为53 650,单元数为99 659,经过数值仿真模拟得到相应的渗透主系数及渗透主方向为
| $ \left\{\begin{array}{l} k_{1}=6.9349 \times 10^{-6} \text {, 倾向 } 357.1° \text {, 倾角 } 5.9° \\ k_{2}=6.547\ 5 \times 10^{-5} \text {, 倾向 } 89.6° \text {, 倾角 } 48.2° \\ k_{3}=1.029\ 9 \times 10^{-4} \text {, 倾向 } 260.1° \text {, 倾角 } 40.8° \end{array}\right. $ | (7) |
本工程实例采用缩减规模为0.7,经缩减后共剩2 394条裂隙,在裂隙网络中共有15 986个节点、29 716个单元,经数值仿真模拟得到相对应的渗透主系数及渗透主方向为
| $ \left\{\begin{array}{l} k_{1}=6.672\ 5 \times 10^{-6} \text {, 倾向 } 358.0° \text {, 倾角 } 5.5° \\ k_{2}=6.329\ 4 \times 10^{-5} \text {, 倾向 } 93.8° \text {, 倾角 } 46.0° \\ k_{3}=9.667\ 4 \times 10^{-5} \text {, 倾向 } 262.8° \text {, 倾角 } 43.4° \end{array}\right. $ | (8) |
为形象化渗透特性, 根据渗透椭球方程
| $ \frac{x^{2}}{\left(1 / \sqrt{k_{1}}\right)^{2}}+\frac{y^{2}}{\left(1 / \sqrt{k_{2}}\right)^{2}}+\frac{z^{2}}{\left(1 / \sqrt{k_{3}}\right)^{2}}=1 $ | (9) |
将式(7)、(8)用MATLAB软件绘制缩减前后的渗透椭球图,如图 8所示, 由于椭球具有对称性,为更好地显示,取椭球的一半进行观察。
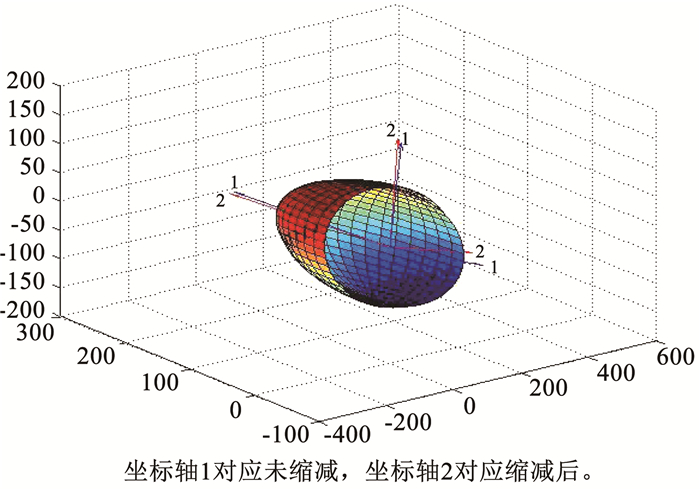
|
图 8 缩减前后渗透椭球对比 Fig. 8 Comparison of permeability ellipsoid before and after reduction |
由式(7)和(8)对比及图 8可以看出,缩减前与缩减规模为0.7的渗透张量及渗透椭球相差不大,说明采用缩减规模为0.7时,计算出的渗透主系数和渗透主方向与未缩减前计算的结果比较接近,这一方法对于工程实际具有一定的参考价值。
对缩减前后裂隙岩体模型的REV尺寸进行计算得:
1) 未缩减时裂隙岩体的REV边长为4 m,相应的渗透主系数和渗透主方向为
| $ \left\{\begin{array}{l} k_{1}=7.315\ 7 \times 10^{-6} \text {, 倾向 } 126.4° \text {, 倾角 } 12.5° \\ k_{2}=6.892\ 4 \times 10^{-5} \text {, 倾向 } 68.4° \text {, 倾角 } 31.9° \\ k_{3}=1.638\ 6 \times 10^{-4} \text {, 倾向 } 204.8° \text {, 倾角 } 29.5° \end{array}\right. $ | (10) |
2) 缩减规模为0.7时的REV边长为6 m,相应的渗透主系数及渗透主方向为
| $ \left\{\begin{array}{l} k_{1}=6.874\ 6 \times 10^{-6} \text {, 倾向 } 142.7° \text {, 倾角 } 10.3° \\ k_{2}=6.547\ 5 \times 10^{-5} \text {, 倾向 } 71.2° \text {, 倾角 } 29.8° \\ k_{3}=1.216\ 8 \times 10^{-4} \text {, 倾向 } 210.3° \text {, 倾角 } 30.6° \end{array}\right. $ | (11) |
将式(11)与(10)进行比较,渗透主系数及渗透主方向的误差分别为
| $ \left\{\begin{array}{l} \varepsilon_{1}=0.066, \theta_{1}=9.18° \\ \varepsilon_{2}=0.050, \theta_{2}=7.59° \\ \varepsilon_{3}=0.257, \theta_{3}=11.62° \end{array}\right. $ | (12) |
式中: εi为主值相对误差,θi为主方向绝对误差,i=1, 2, 3。
由式(12)可知,未缩减时边长为4 m的REV与缩减为0.7时边长为6 m的REV渗透主系数相对误差的最大值为0.257,渗透主方向绝对误差的最大值为4.62°,缩减前后REV的渗透主系数和渗透主方向误差均较小。
5 结论1) 通过删减次要裂隙、保留主干裂隙进行渗透张量计算,结果表明,裂隙网络确实存在优势路径,保留主干裂隙、缩减计算规模0.7时,计算得到的渗透张量仍然具有较好的精度,可以满足工程需要。
2) 对全排列和分组排列两种方法的规模缩减程度与结果精度进行分析,裂隙的渗透主值与主方向与现场压水试验校核后的结果误差在可以接受的范围内,而且两种方法的缩减效果基本一致。
3) 裂隙岩体REV尺寸的大小会随着缩减规模的增大而变大,通过对岩体表征单元体的讨论,发现缩减规模从0变化到0.7时,裂隙岩体的REV体积由15 m×15 m×15 m逐渐增大到21 m×21 m×21 m,说明REV的尺寸受缩减规模的影响。工程实例REV的边长随着缩减规模的增加从4 m增大到了6 m。
4) 通过实例验证缩减计算的实用性。岩体裂隙网络渗流满足逾渗条件,存在REV情况下,对于那些对精度要求不高、地质条件不复杂的情况,渗透张量可以采用缩减规模数为0.7进行计算。对于工程精度要求较高、地质条件复杂的重要工程项目,应结合现场的实测资料与试验,选择合适的缩减规模数进行分析。在误差允许的条件下相对地减少最大缩减量,可以达到减少计算量的目的,提高三维裂隙离散网络模型在工程中的实用性。
| [1] |
张有天. 岩体水力学与工程[M]. 北京: 中国水利水电出版社, 2005: 93. ZHANG Youtian. Rock mass hydraulics and engineering[M]. Beijing: China Water & Power Press, 2005: 93. |
| [2] |
张国新, 武萧峰. 裂隙渗流对岩石边坡稳定的影响: 渗流、变形耦合作用的DDA法[J]. 岩石力学与工程学报, 2003, 22(8): 1269. ZHANG Guoxin, WU Xiaofeng. Influence of seepage on the stability of rock slop-coupling of seepage and deformation by DDA method[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(8): 1269. DOI:10.3321/j.issn:1000-6915.2003.08.008 |
| [3] |
王媛, 速宝玉, 徐志英. 裂隙岩体渗流模型综述[J]. 水科学进展, 1996, 7(3): 93. WANG Yuan, SU Baoyu, XU Zhiying. Review of seepage models for fractured rock masses[J]. Advances in Water Science, 1996, 7(3): 93. DOI:10.14042/j.cnki.32.1309.1996.03.015 |
| [4] |
李新强, 陈祖煜. 三维裂隙网络渗流计算的边界元法及程序[J]. 中国水利水电科学研究院学报, 2006, 49(2): 81. LI Xinqiang, CHEN Zuyu. Boundary element method and program for seepage calculation of 3D fracture network[J]. Journal of China Institute of Water Resources and Hydropower Research, 2006, 49(2): 81. DOI:10.13244/j.cnki.jiwhr.2006.02.001 |
| [5] |
于青春, 武雄, 大西有三. 非连续裂隙网络管状渗流模型及其校正[J]. 岩石力学与工程学报, 2006, 25(7): 1469. YU Qingchun, WU Xiong, OHNISHI Yuzo. Channel model for fluid flow in discrete fracture network and its modification[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1469. DOI:10.3321/j.issn:1000-6915.2006.07.026 |
| [6] |
WANG M, KULATILAKE P, UM J, et al. Estimation of REV size and three-dimensional hydraulic conductivity tensor for a fractured rock mass through a single well packer test and discrete fracture fluid flow modeling[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 887. DOI:10.1016/S1365-1609(02)00067-9 |
| [7] |
王俊奇, 岳潇, 李闯. 三维裂隙网络管单元模型确定岩体渗透张量[J]. 华北电力大学学报(自然科学版), 2015, 42(1): 104. WANG Junqi, YUE Xiao, LI Chuang. Three-dimensional pipe element model in fractured rock mass for determining seepage tensor[J]. Journal of North China Electric Power University, 2015, 42(1): 104. DOI:10.3969/j.ISSN.1007-2691.2015.01.18 |
| [8] |
REN Feng, MA Guowei, WANG Yang, et al. Pipe network model for unconfined seepage analysis in fractured rock masses[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 88: 183. DOI:10.1016/j.ijrmms.2016.07.023 |
| [9] |
SUN Zizheng, YAN Xiao, HAN Weiqi, et al. Simulating the filtration effects of cement-grout in fractured porous media with the 3D unified pipe-network method[J]. Processes, 2019, 7(1): 46. DOI:10.3390/pr7010046 |
| [10] |
ZHANG Wen, CHEN Jianping, LIU Chang, et al. Determination of geometrical and structural representative volume elements at the Baihetan dam site[J]. Rock Mechanics and Rock Engineering, 2012, 45(3): 409. DOI:10.1007/s00603-011-0191-0 |
| [11] |
王振伟, 马克, 田洪圆, 等. 基于RFPA2D-Flow软件对裂隙岩体渗透特性表征单元体的研究[J]. 煤炭学报, 2019, 44(10): 3012. WANG Zhenwei, MA Ke, TIAN Hongyuan, et al. Study on the element volume of permeability characteristics in fractured rock mass based on RFPA2D-Flow[J]. Journal of China Coal Society, 2019, 44(10): 3012. DOI:10.13225/j.cnki.jccs.2018.0988 |
| [12] |
ZHAO J. Rock mass hydraulic conductivity of the Bukit Timah granite, Singapore[J]. Engineering Geology, 1998, 50(1): 211. DOI:10.1016/S0013-7952(98)00021-0 |
| [13] |
SAMANIEGO J, PRIEST S D. Prediction of water flows through discontinuity networks into underground excavations[C]//Proceedings of the ISRM Symposium of Design and Performance of Underground Excavations. London: [s. n.], 1984
|
| [14] |
ZHANG Keni, WU Yushu, BODVARSSON G S, et al. Flow focusing in unsaturated fracture network: a numerical investigation[J]. Vadose Zone Journal, 2004, 3(2): 624. DOI:10.2136/vzj2004.0624 |
| [15] |
SAUSSE J, DEZAYES C, GENTER A, et al. Characterization of fracture connectivity and fluid pathways derived from geological interpretation and 3D modeling of the deep seated EGS reservoir of Soultz (France)[C]//Proceedings of 33rd Workshop on Geothermal Reservoir Engineering. Stanford: [s. n. ], 2008
|
| [16] |
林宏奕. 破裂岩体优势水流路径之研究[D]. 台南: 台湾成功大学, 2009 LIN Hongyi. A study on the dominant water flow path of fractured rock bodies[D]. Tainan: Cheng Kung University, 2009 |
| [17] |
刘华梅, 王明玉. 三维裂隙网络渗流路径识别算法及其优化[J]. 中国科学院研究生院学报, 2010, 27(4): 463. LIU Huamei, WANG Mingyu. Algorithms and their optimization for identification of the connected paths for 3D fracture networks in fractured rocks[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2010, 27(4): 463. |
| [18] |
倪绍虎, 何世海, 汪小刚, 等. 裂隙岩体水力学特性研究[J]. 岩石力学与工程学报, 2012, 31(3): 493. NI Shaohu, HE Shihai, WANG Xiaogang, et al. Hydraulic properties of fractured rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(3): 493. |
| [19] |
倪绍虎, 何世海, 汪小刚, 等. 裂隙岩体渗流的优势水力路径[J]. 四川大学学报(工程科学版), 2012, 44(6): 109. NI Shaohu, HE Shihai, WANG Xiaogang, et al. Preferential flow pathways in fractured rock mass[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 109. DOI:10.15961/j.jsuese.2012.06.035 |
| [20] |
雷霆, 倪天禄, 季岭, 等. 基于生产动态数据的水驱砂岩油藏井间优势渗流通道识别[J]. 复杂油气藏, 2020, 13(2): 38. LEI Ting, NI Tianlu, JI Ling, et al. Identification of predominant seepage channels between wells in waterflooding sandstone reservoirs based on production performance data[J]. Complex Hydrocarbon Reservoirs, 2020, 13(2): 38. DOI:10.16181/j.cnki.fzyqc.2020.02.008 |
| [21] |
BAECHER G B, LANNEY N A, EINSTEIN H H. Statistical description of rock properties and sampling[C]//Proceeding of the 18th U.S. Symposium on Rock Mechanics. Golden: Iohnson Pub Co, 1977: 1
|
| [22] |
TSANGY W, TSANG C F. Channel model of flow through fractured media[J]. Water Resources Research, 1987, 23(3): 467. DOI:10.1029/WR023i003p00467 |
| [23] |
CACASM C, LEDOUX E, DE MARSILY G, et al. Modeling fracture flow with a stochastic discrete fracture network: calibration and validation 1 the flow model[J]. Water Resources Research, 1990, 26(3): 479. DOI:10.1016/0148-9062(90)92855-9 |
| [24] |
李新强, 陈祖煜, 杨昭冬. 利用三维裂隙网络确定岩体渗透张量的方法[C]//中国地质学会2007年生态环境脆弱区工程地质学术论坛. 乌鲁木齐: 中国地质学会, 2007: 6 LI Xinqiang, CHEN Zuyu, YANG Zhaodong. 3D equivalent conductivity method of fracture network and porous media[C]//China Geology Society in 2007 Academic Meeting "Fragile Ecological Environment Area Engineering Geology". Urumqi: China Geology Society, 2007: 6 |
| [25] |
于青春, 刘丰收, 大西有三. 岩体非连续裂隙网络三维面状渗流模型[J]. 岩石力学与工程学报, 2005, 24(4): 662. YU Qingchun, LIU Fengshou, OHNISHI Yuzo. Three-dimensional planar model for fluid flow in discrete fracture network of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 662. DOI:10.3321/j.issn:1000-6915.2005.04.020 |
| [26] |
岳潇. 三维裂隙网络线单元渗流模型确定渗透张量研究[D]. 北京: 华北电力大学, 2015 YUE Xiao. Line element model for fluid flow in three dimensional fracture network[D]. Beijing: North China Electric Power University, 2015 |
| [27] |
周创兵, 陈益峰, 姜清辉. 岩体表征单元体与岩体力学参数[J]. 岩土工程学报, 2007, 29(8): 1135. ZHOU Chuangbing, CHEN Yifeng, JIANG Qinghui. Representative elementary volume and mechanical parameters of fractured rock masses[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1135. DOI:10.3321/j.issn:1000-4548.2007.08.004 |
| [28] |
LI J H, ZHANG L M, WANG Y, et al. Permeability tensor and representative elementary volume of saturated cracked soil[J]. Canadian Geotechnical Journal, 2009, 46(8): 928. DOI:10.1139/T09-037 |
| [29] |
汪小刚, 贾志欣, 张发明, 等. 岩体结构面网格模拟原理及其工程应用[M]. 北京: 中国水利水电出版社, 2010: 311. WANG Xiaogang, JIA Zhixin, ZAHNG Faming, et al. The simulation of rock joint network and its application[M]. Beijing: China Water & Power Press, 2010: 311. |
 2022, Vol. 54
2022, Vol. 54


