2. 建筑安全与节能教育部重点实验室(湖南大学),长沙 410082;
3. 亚热带建筑科学国家重点实验室(华南理工大学),广州 510640
2. Key Laboratory of Building Safety and Energy Efficiency (Hunan University), Ministry of Education, Changsha 410082, China;
3. State Key Laboratory of Subtropical Building Science (South China University of Technology), Guangzhou 510640, China
风能作为一种绿色清洁可再生能源,在缓解能源需求和由于过度使用化石燃料而造成的全球气候变化问题上具有较大潜力[1]。中国南海地区海上风能资源丰富,但由于深海环境条件较为恶劣,海上风电基础的设计和安装将面临诸多挑战[2]。
近几年,由传统基础形式结合而成的复合基础被许多学者提出并应用在陆上工程[3]和海洋工程[4]。针对海上风机发展面临的问题,一种新型的桩盘复合基础被提出,该基础结合了单桩基础与重力式基础的优点,可同时发挥桩基础与重力式基础的承载优势。对于V-H联合受荷下桩盘复合基础的承载特性,许多学者进行了研究。Arshi等[4]基于室内模型实验,研究了桩盘复合基础的摩擦盘盘径、盘下土体的强度和摩擦盘与泥面之间的初始接触状态对基础在砂土中水平承载力的影响;Stone等[5]通过离心机实验,探究了桩盘复合基础中桩基础和摩擦盘在被固定和非固定两种状态下的水平承载特性;El-Marassi[6]基于离心机实验和数值模拟,发现桩盘复合基础在V-H组合荷载作用下,基础的水平承载力在V/Vmax ≈0.4时达到最大值;Wang等[7-8]通过离心机实验和数值模拟证明在砂土中,桩盘复合基础的水平承载力比对应单桩基础的水平承载力提高了50%~350%;Trojnar[9]基于室内模型实验和数值模拟,得到了桩盘复合基础在砂土中的水平受荷破坏机制;Anastasopoulos等[10]从工程实际的角度提出了桩盘复合基础的安装方法,即首先将中间留有孔位的重力式基础浮运并安装到位,然后将单桩基础在对应孔位打桩至设计深度。打桩完成后,在桩基础和重力式基础的连接部件之间灌浆,以此实现桩基础与重力式基础的完全固定,从而完成桩盘复合基础的安装。
目前,关于在上层砂土下层黏土地层中V-H联合受荷状态下桩盘复合基础的承载特性研究十分有限,而中国南海地区许多海域均呈上硬下软的地层分布状态[11]。由于在上砂下黏地层中,桩盘复合基础的V-H联合受荷承载特性和破坏机制与其在纯砂土和纯黏土地层中是完全不同的。因此,开展桩盘复合基础在上层砂土下层黏土地层中的V-H承载特性研究十分必要。鉴于此,通过自行设计制作的V-H联合加载装置,完成了对桩盘复合基础在上层砂土下层黏土地层中的加载测试,其中水平荷载H等效为作用在泥面处桩中心的水平力H和弯矩M(M=H×e, e为加载点高度到泥面的距离),据此探讨了不同摩擦盘盘径对于桩盘复合基础V-H联合受荷承载特性的影响,得到了不同工况下桩盘复合基础的水平荷载- 位移曲线及桩身弯矩分布。经无量纲化处理和拟合,得到了不同盘径下复合基础的V-H承载力包络线及简化计算公式。此外,结合工程实际进行了一系列的数值模拟计算,探究了摩擦盘盘径和加载点高度对于复合基础V-H承载力包络线的影响,并通过拟合得到了桩盘复合基础水平及弯矩承载力公式,可供工程应用参考。
1 模型实验 1.1 桩基础与摩擦盘几何尺寸及参数针对海上风机基础桩径为3 m、入土深度为40 m的桩基础原型,以及盘径为24 m、盘高为1.6 m的重力式基础原型,根据相似比原理,按照1∶ 65的几何缩尺比确定桩盘复合基础的几何尺寸。对于桩基础,选取桩长L为620 mm、外径Dp为48 mm、内径为44 mm的6061-T6铝合金管桩作为模型桩。模型桩底部采用实心铁质圆锥封底,形成底部封闭式管桩。模型桩表面使用砂纸沿与圆周呈±45°的方向交叉打磨,以增加桩身表面的粗糙度。桩身外表面对称粘贴9对BF120-3AA型弯矩应变片,应变片电阻为(120±0.5) Ω,灵敏度系数为2.08±0.01,其布置如图 1所示。应变片四周及表面涂抹环氧树脂进行保护和防水处理。应变片导线由应变片旁边小孔引入桩身内部,然后统一通过靠近桩头处的预留圆孔引出。应变片采用1/4桥接法连接在DH3816型应变箱上,试验过程中通过采集应变片的应变变化,经式(1)换算得到桩身不同深度处的弯矩:
| $M = \frac{{EI \times \Delta \varepsilon }}{{{D_{\rm{p}}}}} $ | (1) |

|
图 1 模型桩桩身应变片布置及摩擦盘示意(mm) Fig. 1 Layout of strain gauges for model piles and diagram of friction wheels(mm) |
式中: EI为模型桩的抗弯刚度; Δε=ε1-ε2,为同一深度处桩身两侧应变差。采用简支梁法对模型桩进行了标定,测得模型桩抗弯刚度为5.49 kN·m2。
对于重力式基础,选用盘径Dw分别为267、322、366 mm,盘高为25 mm的实心铝制摩擦盘,其中铝盘中间预留一略大于模型桩外径的圆孔,并且固定有一高60 mm、外径78 mm的盘领,作为桩基础与摩擦盘基础固定的过渡结构(在盘领一侧开有螺纹孔)。摩擦盘尺寸如图 1所示。
1.2 模型箱及联合加载和测量装置实验模型箱尺寸为1 600 mm×1 400 mm×1 000 mm(长×宽×高),模型箱的剖面及平面布置如图 2、3所示。模型箱两侧面为可视化钢化玻璃,可在土体填筑过程中观察土层分布情况。当水平荷载施加到桩头上时,桩盘复合基础会挤压周围土体。为消除边界效应及基础间的相互影响,使桩盘复合基础与模型箱壁在水平荷载加载方向上的距离大于1.4Dw[7], 在平面垂直加载方向上, 基础间的距离大于0.8Dw和6Dp。桩底与模型箱底的距离取大于7Dp,此距离可认为足以避免由桩体传递下来的竖向应力引起的边界效应[12]。

|
图 2 试验加载装置示意(mm) Fig. 2 Schematic of test loading system(mm) |

|
图 3 桩盘复合基础布置示意(mm) Fig. 3 Layout of monopile-friction wheel hybrid foundation(mm) |
水平向和竖向荷载采用气动加载的方式施加,该联合加载装置包括水平和竖向反力架、气泵、调压表、气压表、力传感器、气缸和桩头球铰等。为保证桩身在受水平荷载发生偏转和受竖向荷载发生沉降时保持V和H的相互关系不变,水平加载气缸和竖向加载气缸均通过螺栓固定在可滑动导轨上,并且将V与H通过桩头球铰施加到桩身,从而保证了竖向和水平荷载的施加方向始终保持不变。水平位移由一台激光位移传感器测定,其安装在水平加载点高度处。竖向位移由在桩头上方沿水平加载方向平行安装的两台激光位移传感器测定(如图 2、4所示)。

|
图 4 加载装置布置 Fig. 4 Loading device layout |
本研究模拟的是上层砂土下层黏土的地层分布形式。黏土采用湘江枯水期淤泥质软土,首先在桶形容器中将土加水搅拌得到均匀的淤泥质黏土,之后将土样摊开风干备用,保证黏土的含水率控制在合适的范围内。每组实验的黏土层填筑深度为700 mm,分为5层填筑,每层140 mm。黏土填筑过程中,采用5 kg的砝码从60 cm的高度自由落下进行夯实。黏土填筑完毕后,在重塑黏土层表面压重进行排水固结并将其长时间静置,以满足正常固结的要求。静置完成后,使用十字板剪切仪测得饱和黏土层不同深度开挖面表层不同区域的不排水抗剪强度su,计算得到其平均不排水抗剪强度,并在黏土层不同深度开挖面表层的不同区域取样,测量并计算得到其平均含水率。由试验测试结果可知,黏土层不同深度开挖面表层黏土的su和含水率相差不大,因此,选取黏土层不同深度开挖面表层黏土su和含水率的平均值来代表黏土层的不排水抗剪强度和含水率,试验所用黏土的土体参数如表 1所示。
| 表 1 黏土参数 Tab. 1 Properties of clay |
本实验所用砂土为中国福建标准砂。填筑的砂土层厚度为300 mm,采用砂雨法进行均匀填筑, 填筑过程中控制砂土层的相对密实度为65%左右。经取样测试,砂土的土体参数如表 2所示。
| 表 2 砂土参数 Tab. 2 Properties of sand |
桩盘复合基础的安装过程如下:首先将摩擦盘安放在设计桩位,然后用铁锤将模型桩沿摩擦盘中间预留孔位缓慢匀速贯入至设计埋深(过程中确保模型桩匀速下沉并且保持垂直),最后使用螺栓将摩擦盘盘领和模型桩固定,使其不能相对滑动。
1.4 加载方案加载方案共分为4组,如表 3所示,第①、②组试验首先测试单桩及不同盘径的桩盘复合基础的水平极限承载力Hu及竖向极限承载力Vu; 第③、④、⑤组试验测试单桩及两种不同盘径下桩盘复合基础在桩顶分别预先施加竖向力为0.3Vu、0.6Vu和0.9Vu情况下的水平极限承载力(Vu分别取不同基础对应的竖向极限承载力)。
| 表 3 联合加载方案 Tab. 3 Combined loading schemes |
加载方法:本研究的试验目的是得到桩盘复合基础的V-H承载力包络线,且由于是V-H联合加载,水平荷载不宜采用循环加载法,采用慢速维持法进行加载。加载过程中以每5 min的加载点变形量小于等于0.01 mm为每级荷载的加载稳定标准。桩盘复合基础的竖向极限承载力及水平极限承载力均取其荷载- 位移曲线发生明显陡降的起始点对应的荷载。
2 模型试验结果 2.1 盘径对桩盘复合基础承载力的影响图 5展示了单桩及3种不同盘径下桩盘复合基础的水平荷载- 位移曲线。可以看出,在荷载- 位移曲线的线性部分,桩盘复合基础的水平刚度明显大于单桩基础。对于单桩基础(Dw=0 cm),在加载点位移达到大约0.75 cm时,其荷载- 位移曲线达到拐点,得到单桩基础的水平承载力为209.72 N。对于桩盘复合基础,当复合基础达到水平极限状态时,其对应的加载点水平位移分别为0.7 cm(Dw=26.7 cm)、0.69 cm(Dw=32.2 cm)和0.65 cm(Dw=36.6 cm),即随着摩擦盘盘径的增加,复合基础水平极限承载状态下的水平位移会减小。而对于不同盘径的桩盘复合基础,其水平极限承载力Hu相对于单桩基础,分别提高了33.14%(Dw=26.7 cm)、47.73%(Dw=32.2 cm)和60.33%(Dw=36.6 cm)。因此,增加摩擦盘的盘径对于基础水平极限承载力的提高作用是明显的。
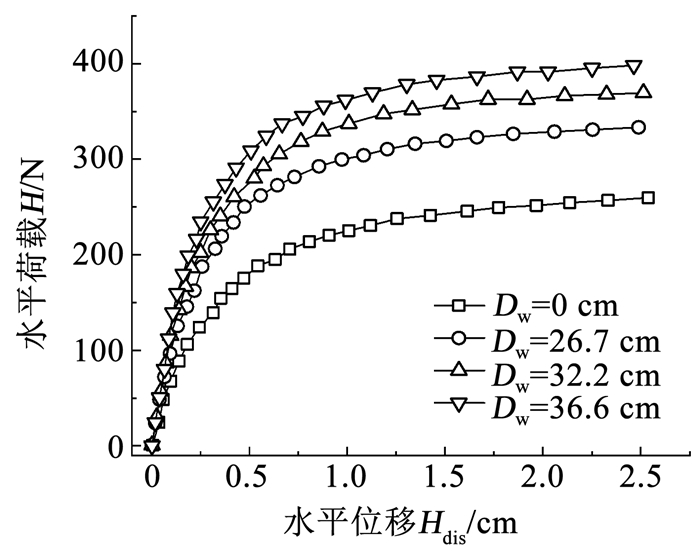
|
图 5 桩顶水平荷载- 位移曲线 Fig. 5 Horizontal load-displacement curves of pile head |
图 6为盘径Dw=32.2 cm的桩盘复合基础在水平极限承载状态下的破坏示意。可以看出,在加载方向前侧,桩盘复合基础摩擦盘的右侧边陷入泥面,挤压盘后侧土体从而导致泥面隆起和裂开。而在水平加载方向后侧,摩擦盘与泥面脱开形成间隙。由桩盘复合基础的破坏模式可知,当复合基础抵抗水平荷载时,摩擦盘的后侧挤压盘下和盘后土体,从而使土体产生与加载方向相反的摩擦力和垂直接触面的被动土抗力,由此产生的水平抗力和恢复力矩提高了复合基础的水平与弯矩承载力。

|
图 6 基础周围土破坏形态 Fig. 6 Soil failure patterns around the foundation |
为研究竖向荷载对桩盘复合基础承载力的影响,分别对单桩基础和两种不同盘径的桩盘复合基础预先施以不同的竖向荷载,然后施加水平荷载直至破坏,得到其对应的桩身水平及弯矩承载特性(实验组③、④、⑤)。试验过程中,首先对不同盘径的桩盘复合基础进行单一作用V的载荷试验(实验组②),得到对应的Vu分别为605 N(Dw=0 cm)、2 796 N(Dw=26.7 cm)和5 571 N(Dw=36.6 cm)。在此基础上进行V-H组合加载测试。
图 7(a)为单桩基础在桩顶预加竖向荷载分别为0、182 N(0.3 Vu(P))、363 N(0.6Vu(P))和545 N(0.9 Vu(P))时的加载点水平荷载(H)-位移(Hdis)曲线。可以看出,竖向荷载对单桩基础的水平承载特性影响较为有限,随着V的增大,单桩基础水平极限承载力仅有较小幅度的提高。出现此现象的原因在于在上硬下软的地层中,预施加竖向荷载会使桩身发生沉降,桩身侧摩阻力得到发挥,但其对桩身水平抗力的提高作用较为有限。

|
图 7 不同竖向荷载下的桩顶水平荷载- 位移曲线 Fig. 7 Horizontal load-displacement curves at pile head under different vertical loads |
图 7(b)为盘径为26.7 cm的桩盘复合基础在桩顶预施加竖向荷载为0、839 N(0.3Vu(PW1))、1 677 N (0.6Vu(PW1))和2 516 N(0.9Vu(PW1))时,桩盘复合基础的桩顶水平荷载(H)-位移(Hdis)曲线。可以看出,当V从0增加到839 N(0.3 Vu(PW1))时,复合基础的初始水平刚度有了明显提高,水平极限承载力从319.3 N增加到369.7 N,提高了大约15.8%。而当V增加到1 677 N(0.6 Vu(PW1))时,水平极限承载力从369.7 N增加到409.7 N,提高了大约10.8%。然而当V增加到2 516 N(0.9 Vu(PW1))时,水平极限承载力从409.7 N减小到302.2 N。出现此现象的原因在于当预加竖向荷载传递到摩擦盘上时,盘下土体会在摩擦盘的挤压作用下产生较大的被动土压力,且此被动土压力随着预加竖向力的增加而增大。当桩头产生水平位移时,盘下土体将产生较大的水平摩阻力和作用在泥面处桩身中心的恢复力矩,从而提高复合基础的承载力。当竖向荷载接近极限承载力时,竖向荷载的P-Δ效应增强,导致基础的水平承载力下降。Arshi等[3]通过一系列砂土中桩盘复合基础的承载特性室内模型试验,得到了类似的结论,即在砂土中,初始的摩擦盘与盘下土体的接触状态将显著影响桩盘复合基础的水平承载特性。
图 7(c)为盘径为36.6 cm的桩盘复合基础在预加竖向荷载V=0、1 671 N(0.3Vu(PW2))、3 343 N (0.6Vu(PW2))和5 014 N(0.9Vu(PW2))时,桩顶的水平荷载- 位移曲线。可以看出, 在V从0增加到0.6Vu(PW2)的过程中,桩盘复合基础的水平承载力和水平刚度均有较大幅度的提高,然而随着竖向力V的增加,其会降低桩盘复合基础的水平承载力。例如,当V从0增加到0.3Vu(PW2)时,桩盘复合基础的水平极限承载力从336.24 N增加到了534.86 N,提高了大约59%;而当V从0.3Vu(PW2)增加到0.6Vu(PW2),桩盘复合基础的水平极限承载力从534.86 N减小到了497.49 N;而当V从0.6Vu(PW2)增加到0.9Vu(PW2)时,桩盘复合基础的水平极限承载力从534.86 N减小到了198.14 N。出现此现象的原因在于当桩盘复合基础的竖向预荷载增加时,摩擦盘提供的水平抗力和恢复力矩随之增大,从而提高了桩盘复合基础的水平极限承载力。而随着竖向荷载V的进一步提高,基础周围的土体逐渐进入弹塑性阶段,在水平和竖向荷载的双重作用下,桩盘复合基础周围的土体快速进入塑性阶段,同时P-Δ效应在此时发挥作用,因此,桩盘复合基础的水平极限承载力被削弱,且由于此时的V较大, 水平承载力的削弱作用比图 7(b)中的现象更加明显。El-Marassi[6]通过一系列数值模拟和离心机试验,证明了在砂土中,预加竖向力对于桩盘复合基础水平承载特性的影响是一个由增强到减弱的过程,即存在一个提高桩盘复合基础水平承载力的最优竖向荷载值。
2.3 单桩与桩盘复合基础桩身弯矩分布单桩基础与不同盘径下的桩盘复合基础在单向水平受荷后的桩身弯矩分布如图 8所示。由图 8(a)与8(b)对比可知,在相同水平荷载下,桩盘复合基础中靠近泥面处的桩身弯矩值比单桩基础明显减小,同时, 桩身最大弯矩值也有明显降低,并且随着盘径的增加,桩身最大弯矩值的位置会有所上升,但均保持在泥面下2~4倍桩径附近。图 9为不同竖向荷载下,两种不同盘径(Dw = 26.7和36.6 cm)桩盘复合基础的桩身弯矩分布。由图 9(a)可知,当V由0 N增加到1 677 N (0.6VPW1(ult))时,桩身最大弯矩在较小水平荷载状态(100 N)和较大水平荷载状态(300 N)时均有明显的减小,桩身的水平承载力得以提高。而当V由1 677 N增加到2 516 N(0.9VPW1(ult))时,桩身弯矩整体呈现增加的趋势,同样的结论也可以由图 9(b)得出。由此可见, 桩盘复合基础在上硬下软的地层中,随着预加竖向力的增加,水平受荷状态下的桩身弯矩先减小后增加。

|
图 8 无竖向荷载时桩身弯矩分布 Fig. 8 Bending moment curves of pile shaft without vertical load |

|
图 9 不同竖向荷载下桩身弯矩分布 Fig. 9 Bending moment curves of pile shaft under different vertical loads |
选取图 7中单桩及不同盘径下桩盘复合基础的水平荷载- 位移曲线拐点处的水平反力,并结合海上桩基0.1Dp的竖向变形控制标准[13],确定基础的水平极限承载力,将其无量纲化处理后拟合,得到了无量纲的V-H联合受荷桩盘复合基础的承载力包络线。由图 10可知,竖向荷载V对复合基础的水平承载力先是正向的增强作用,在竖向荷载增加到某一定值时,其会对桩盘复合基础的水平承载力产生消极的削减作用。

|
图 10 单桩与不同盘径桩盘复合基础V-H承载力包络线 Fig. 10 V-H bearing capacity envelopes of monopile and hybrid foundations with different wheel diameters |
为便于工程设计应用,对图 10中的基础无量纲承载力包络线进行拟合,得到对应的基础在上层砂土下层黏土地层中的承载力计算公式,如式(2)所示。式(2a)为单桩基础承载力计算公式,式(2b)为Dw/L=0.43时的复合基础承载力计算公式,式(2c)为Dw/L=0.59时的复合基础承载力计算公式。在实际应用中,首先分别确定水平和竖向力单独作用下的桩盘复合基础极限承载力Hu和Vu, 然后将基础实际受到的等效水平及竖向荷载代入式(2)中,若等式左侧小于1,则表明满足设计要求,相反若等式左侧大于1,则说明桩盘复合基础处于不可靠状态,应该调整设计。
| $\left\{ {\begin{array}{*{20}{l}} {\frac{H}{{{H_{{\rm{u}}({\rm{P}})}}}} - 1.25 \times {{\left( {\frac{V}{{{V_{{\rm{u}}({\rm{P}})}}}}} \right)}^{0.83}} \times \left[ {1.12 - 1.95 \times {{\left( {\frac{V}{{{V_{{\rm{u}}({\rm{P}})}}}}} \right)}^{2.73}}} \right] = 1} & (2{\rm{a}})\\ {\frac{H}{{{H_{{\rm{u}}({\rm{PW}}1)}}}} - 0.38 \times {{\left( {\frac{V}{{{V_{{\rm{u}}\left( {{\rm{P}}{{\rm{W}}_1}} \right)}}}}} \right)}^{0.8}} \times \left[ {1.42 - 4.1 \times {{\left( {\frac{V}{{{V_{{\rm{u}}({\rm{PW}}1)}}}}} \right)}^{8.1}}} \right] = 1}& (2{\rm{b}})\\ {\frac{H}{{{H_{{\rm{u}}({\rm{PW}}2)}}}} - 0.26 \times {{\left( {\frac{V}{{{V_{{\rm{u}}({\rm{PW}}2)}}}}} \right)}^{0.81}} \times \left[ {0.82 - 4.8 \times {{\left( {\frac{V}{{{V_{{\rm{u}}({\rm{PW}}2)}}}}} \right)}^{6.9}}} \right] = 1}& (2{\rm{c}}) \end{array}} \right. $ |
为进一步探究不同参数对桩盘复合基础V-H承载力包络线的影响,使用大型通用有限元软件ABAQUS[14]进行数值分析,模拟上层砂土下层黏土地层中V-H组合荷载作用下桩盘复合基础的承载特性。如图 11所示,首先依据模型试验的尺寸和参数建立数值模型,基础结构采用线弹性本构模型,砂土和黏土均采用Mohr-Coulomb准则[15]进行模拟,采用的砂土和黏土的参数如表 1、2所示。基础与土层之间摩擦系数取为0.4,并允许基础与土体脱开。数值模拟计算中,桩端的位移并未被约束,桩端与土体的接触形式与模型试验中的一致,即自由接触且允许脱开。桩端和桩侧与土体之间通过设置接触对,定义了法向和切向接触属性。砂土层和黏土层的模拟是通过将一个整体土层Part切分为两个部分,并分别将两个部分赋予砂土和黏土的土体参数而建立。土体模型水平向边界为2Dw, 桩底与模型底部的边界为L, 以此来消除边界效应。通过对比模型试验结果与数值模型结果,对数值模型的建模方法和所采用参数的合理性进行了验证。由图 12可知,数值模型的计算结果与模型试验结果较为一致,因此,可认为数值模型选取的建模方法和采用的土体参数是符合实际的。

|
图 11 有限元计算模型 Fig. 11 Finite element model |

|
图 12 试验与数值模型水平荷载- 位移曲线对比 Fig. 12 Comparison between horizontal load-displacement curves of model test results and numerical model results |
在此基础上,参照海上风机的工程实际,建立了桩盘复合基础数值模型。桩基础的桩长为L, 桩径为Dp, 摩擦盘盘径为Dw, 加载点高度为e。桩基础和摩擦盘均采用钢材材质,重度为78.5 kN/m3, 弹性模量为210 GPa,泊松比为0.17。砂土和黏土采用的参数如表 4所示, 砂土和黏土弹性模量等参数的选取根据室内三轴试验的结果和参考文献所推荐的计算方法确定[11, 16-18],其中黏土层的不排水抗剪强度根据实际海床黏土层分布特点设定为su=sum+ kz,式中sum为黏土层上表层黏土的不排水抗剪强度,z为深度, k为不排水抗剪强度随深度增加的梯度,取k=1 kPa/m [19-20]。
| 表 4 数值模型土体参数 Tab. 4 Properties of soil in numerical models |
参照海上风机的工程实际,模型选取的桩径Dp为4 m,桩长L为40 m, 盘径Dw为20~26 m(Dw/L= 0.5~0.65),盘高为2.5 m, 加载点高度e为60~100 m(e/Dp=15~25)。据此,研究了不同盘径和不同加载点高度对桩盘复合基础V-H承载力包络线的影响。其中对水平和竖向荷载分别进行了归一化处理,即H/(2πR3γ′s)和V/(2πR3γ′s), 其中R为桩半径,γ′s为砂土有效重度。
图 13(a)为不同盘径下桩盘复合基础的V-H承载力包络线,可以看出,随着盘径的增加,其V-H承载力包络线逐渐扩大,且扩大的速度呈增加趋势。桩盘复合基础的承载力包络线上最大水平承载力对应的竖向力相对值V/Vu随着盘径的增加而增加,并且V/Vu保持在0.5~0.6。

|
图 13 桩盘复合基础V-H联合承载力包络线 Fig. 13 V-H bearing capacity envelopes of the hybrid foundations |
图 13(b)为不同水平加载点高度下的桩盘复合基础V-H承载力包络线。可以看出,随着水平加载点高度的增加,V-H承载力包络线逐渐缩小,同时,包络线上最大水平承载力对应的预加竖向荷载也呈现递减的趋势。原因在于当水平加载点提高时,基础在承受相同大小水平力的情况下,其泥面处的弯矩荷载随e的增加而增大,从而使得基础周围的土体更加容易进入塑性破坏状态。
3.2 经验公式及验证基于上文的数值分析与研究,选取参数如加载点高度e,摩擦盘盘径Dw和竖向荷载V为主要影响桩盘复合基础水平及弯矩承载力的因素,并将参数归一化为e/Dp、Dw/L和V/(2πR3γ′s)的形式。由数值模拟计算得到桩盘复合基础水平承载力与几种影响因素的关系,通过变量之间的运算和拟合,得到了如下的经验公式:
| $\begin{array}{l} \frac{H_{\mathrm{u}}}{2 \pi R^{3} \gamma_{\mathrm{s}}^{\prime}}=-6.57+\left(123.73-3.28 \times \frac{e}{D_{\mathrm{p}}}\right) \times \\ \qquad\qquad \frac{D_{\mathrm{w}}}{L}+0.08 \times \frac{V}{2 \pi R^{3} \gamma_{\mathrm{s}}^{\prime}}\end{array} $ | (3) |
为验证公式的实际应用价值,选取了两个符合实际海上风机基础受力特征的工况[21]进行验证。工况1为3.6 MW的海上风机,选取的模型参数为盘径Dw=22 m, 桩径Dp=4 m, 加载点高度e=80 m, 竖向荷载V=3 MN, 桩长L=40 m。由公式计算得到的桩盘复合基础水平承载力为13.15 MN, 对应的数值模拟计算结果为13.07 MN, 相对误差为0.61%。工况2为5 MW的海上风机塔,选取的模型参数为盘径Dw=26 m, 桩径Dp=4 m, 加载点高度e=90 m, 竖向荷载V=7 MN, 桩长L=40 m。由公式计算得到的桩盘复合基础水平承载力为13.71 MN, 对应的数值模拟计算结果为13.79 MN, 相对误差为0.58%。由此说明此经验公式是可靠的,可根据实际情况用于估计桩盘复合基础在上硬下软地基中V-H联合荷载下的水平承载能力。
4 结论1) 桩盘复合基础由于在泥面处添加了摩擦盘,其水平及弯矩承载力相对于单桩基础提高了30%~60%。桩盘复合基础水平承载机制为:桩盘复合基础的摩擦盘挤压盘下及盘后土体,使泥面处砂土被挤密并产生相应的被动土压力,由此产生盘下水平摩阻力和作用在桩中心的恢复力矩,从而提高了基础的水平及弯矩承载力。
2) 在V-H共同作用下,桩盘复合基础的水平承载力随着竖向荷载的增加先增强然后减小。表明在上硬下软的地层中,预加竖向荷载V对桩盘复合基础的水平承载力提高存在一个最优值, 为(0.5~0.6)Vu。
3) 桩盘复合基础的泥面处弯矩值和桩身最大弯矩值相对于单桩基础有明显的减小。桩盘复合基础的桩身最大弯矩位置相较单桩基础有所提升,但基本位于泥面下2~4倍桩径范围内。在V-H共同作用下,随着V的增加,桩盘复合基础的桩身弯矩最大值首先减小,在V达到最优值时,桩身弯矩又呈现增大的趋势。
4) 通过对试验结果拟合得到了无量纲化的V-H联合受荷桩盘复合基础承载力包络线,发现桩盘复合基础的盘径对承载力包络线的影响主要体现在基础的水平承载力大小及最优竖向荷载V/Vu大小上。同时给出了考虑盘径对承载力包络线影响的简化计算公式。通过数值模拟进行的一系列参数分析,得到了考虑竖向荷载、加载点高度及盘径的桩盘复合基础水平承载力计算公式。
| [1] |
季欣洁, 唐友刚, 李焱, 等. 湍流风对铰接式海上风力机动力响应的影响[J]. 哈尔滨工业大学学报, 2020, 52(12): 178. JI Xinjie, TANG Yougang, LI Yan, et al. Influence of turbulent wind on dynamic response of articulated wind turbine[J]. Journal of Harbin Institute of Technology, 2020, 52(12): 178. DOI:10.11918/201905221 |
| [2] |
周涛, 何炎平, 孟龙, 等. 二阶波浪力下6MW单柱浮式风力机动态响应分析[J]. 哈尔滨工业大学学报, 2018, 50(4): 145. ZHOU Tao, HE Yanping, MENG Long, et al. Dynamic response analysis of a 6 MW spar-type floating offshore wind turbine under second-order wave forces[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 145. DOI:10.11918/j.issn.0367-6234.201706105 |
| [3] |
毕俊伟, 高广运, 张建经. 下覆倾斜地层软土桩- 网复合地基破坏机理试验[J]. 哈尔滨工业大学学报, 2020, 52(2): 1. BI Junwei, GAO Guangyun, ZHANG Jianjing. Model test study on the failure mechanisms of the geogrid-reinforced and pile-supported foundation on soft soil with overlying sloping base[J]. Journal of Harbin Institute of Technology, 2020, 52(2): 1. DOI:10.11918/201809061 |
| [4] |
ARSHI S. Physical and numerical modelling of hybrid monopiled-footing foundation systems[D]. Brighton: University of Brighton, 2016
|
| [5] |
STONE K L, ARSHI S, ZDRAVKOVIC L. Use of a bearing plate to enhance the lateral capacity of monopiles in sand[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2018, 144(8): 04018051. DOI:10.1061/(ASCE)GT.1943-5606.0001913 |
| [6] |
El-MARASSI M. Investigation of hybrid monopile-footing foundation systems subjected to combined loading[D]. Ontario: Western University, 2011
|
| [7] |
WANG X, ZENG X, LI J, et al. Lateral bearing capacity of hybrid monopile-friction wheel foundation for offshore wind turbines by centrifuge modelling[J]. Ocean Engineering, 2018, 148: 182. DOI:10.1016/j.oceaneng.2017.11.036 |
| [8] |
YANG X, ZENG X, WANG X, et al. Performance and bearing behavior of monopile-friction wheel foundations under lateral-moment loading for offshore wind turbines[J]. Ocean Engineering, 2019, 184: 159. DOI:10.1016/j.oceaneng.2019.05.043 |
| [9] |
TROJNAR K. Multi scale studies of the new hybrid foundations for offshore wind turbines[J]. Ocean Engineering, 2019, 192: 106506. DOI:10.1016/j.oceaneng.2019.106506 |
| [10] |
ANASTASOPOULOS I, THEOFILOU M. Hybrid foundation for offshore wind turbines: environmental and seismic loading[J]. Soil Dynamics and Earthquake Engineering, 2016, 80: 192. DOI:10.1016/j.soildyn.2015.10.015 |
| [11] |
ZOU X, HU Y, HOSSAIN M, et al. Capacity of skirted foundations in sand-over-clay under combined V-H-M loading[J]. Ocean Engineering, 2018, 159(1): 201. DOI:10.1016/j.oceaneng.2018.04.007 |
| [12] |
LEBLANC C, HOULSBY G, BYRNE B. Response of stiff piles in sand to long-term cyclic lateral loading[J]. Géotechnique, 2010, 60(2): 79. DOI:10.1680/geot.7.00196 |
| [13] |
WANG X, ZENG X, LI J. Assessment of bearing capacity of axially loaded monopiles based on centrifuge tests[J]. Ocean Engineering, 2018, 167: 357. DOI:10.1016/j.oceaneng.2018,8.063 |
| [14] |
Abaqus analysis user′s manual[R]. Johnston: Dassault Systèmes Simulia, Inc, 2016
|
| [15] |
GOURVENEC S, BARNETT S. Undrained failure envelope for skirted foundations under general loading[J]. Géotechnique, 2011, 61(3): 263. DOI:10.1680/geot.9.T.027 |
| [16] |
LI X, HU Y, WHITE D. A large deformation finite element analysis solution for modelling dense sand[C]//18th International Conference on Soil Mechanics and Geotechnical Engineering. Paris: Presses des Ponts, 2013: 2359
|
| [17] |
ZHOU M, HOSSAIN M, HU Y, et al. Behaviour of ball penetrometer in uniform single- and double-layer clays[J]. Géotechnique, 2013, 63(8): 682. DOI:10.1680/geot.12.P.026 |
| [18] |
GOURVENEC S, BARNETT S. Undrained failure envelope for skirted foundations under general loading[J]. Géotechnique, 2011, 61(3): 263. DOI:10.1680/geot.9.T.027 |
| [19] |
VULPE C, GOURVENEC S, LEMAN B, et al. Failure envelope approach for consolidated undrained capacity of shallow foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 142(8): 04016036. DOI:10.1061/(ASCE)GT.1943-5606.0001498 |
| [20] |
GOURVENEC S, RANDOLPH M. Offshore geotechnical engineering[M]. New York: Taylor and Francis Spon Press, 2011.
|
| [21] |
MALHOTRA S. Selection, design and construction of offshore wind turbine foundations[M]. .
|
 2022, Vol. 54
2022, Vol. 54


