2. 浙江大学 建筑工程学院悬浮隧道研究中心, 杭州 310058
2. Research Center for Submerged Floating Tunnel, College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
连续梁在桥梁、建筑、海洋工程等土木工程基础设施领域得到了广泛的应用,其不仅受恒载及静力荷载的作用,而且有些结构设施还受移动荷载等的作用,边界条件不仅有纵向可伸缩滑移的滚轴或铰支座,而且还有弹性支撑的支座(包括竖向的弹性支撑及平面内的转动弹性支撑)等。为了便于分析,在研究连续梁的动力响应问题时,大多学者将支撑边界简化为铰支座,如:Cheung等[1]将多跨梁的模态假设为单跨梁模态与三次样条函数的叠加,分析了多跨梁在移动车辆作用下的振动响应。Zakęś等[2]将多跨梁转换为单跨梁,研究了一般支撑下多跨均匀连续梁在移动荷载作用下的动力特性。Martínez-Rodrigo等[3]研究了两跨一般支撑连续梁在移动荷载作用下的振动响应,研究了最大共振和消振现象。
然而,实际结构的支撑条件并非完全刚性,因而需要引入弹性支撑来反应梁的实际振动情况。晏麓晖等[4]针对单跨两端弹簧支撑的弹性支撑梁的力学模型,建立并推导了其在爆炸荷载下动力响应的理论解。Ding等[5]通过对比刚性竖向支承的黏弹性梁和带有竖向弹性支承的刚性杆,证明了考虑弹性支撑对于研究结构的力传递的必要性。Wattanasakulpong等[6]基于三阶剪切变形理论和切比雪夫配置法,给出了弹性边界条件下功能梯度梁的弹性约束端固有频率的数值结果。Chen等[7]推导了弹性边界欧拉梁横向振动分析的解析解,分析了转动弹簧刚度和平移弹簧刚度对振型变化的影响机理。Aydin等[8]研究了悬臂梁在不同的简谐振动下的最佳弹性支撑位置和最佳刚度系数设计。Froio等[9]研究了黏弹性支承下无限欧拉-伯努利弹性梁上移动荷载问题的计算。Wang等[10]采用静力位移和刚体位移的叠加位移作为振型函数,推导了简支弹性地基梁基频的计算公式。对于多跨梁的分析,文献[11-13]基于传递矩阵法,推导了两端固定、铰支或竖向弹性支撑边界条件下多跨弹性支撑连续梁的频率特征方程。Tan等[14]研究了带竖向弹性支承的非均匀Timoshenko梁的动力响应问题,并采用龙格-库塔法和三次样条插值法计算了非均匀Timoshenko梁的固有频率和振型。Leontiev[15]讨论了弹性基底支撑条件变化时自由边界的梁的固有横向振动问题。叶茂等[16]则建立了两端铰支、中间带弹性支撑的多跨连续梁车-桥耦合动力分析模型,研究了耦合系统的随机演变响应。Froio等[17]研究了竖向弹性支座上均匀拉紧弦在集中横向移动荷载作用下的稳态响应问题的数值解。
上述研究在引入弹性支撑时仅考虑了连续梁中间支座的弹性,未考虑两端边界条件的任意性,尚不能为实际结构建立一个统一的分析模型。比如桥梁与隧道相接时,桥梁两端就会受到一个平面内转动的约束,相比与直接简化为固结,将这一约束简化为转动弹簧支撑则更为合理。为此,本文以两端具有竖向弹簧支撑及平面内转动弹性支撑的多跨弹性支撑梁为研究对象,推导其在移动荷载作用下的动力响应方程,同时与有限元法分析方法的结果进行对比,验证所提出方法的正确性,并讨论转动弹簧刚度、线弹簧刚度以及荷载移动速度对梁体动力响应的影响规律,在实际工程应用中可适用于任意不同边界情况。
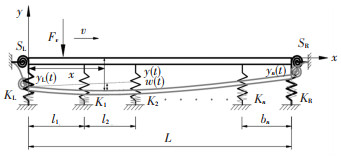
1 力学模型图 1为两端具有竖向弹簧支撑及平面内转动弹性支撑的多跨弹性支撑连续梁,即连续梁左右两端分别有竖向刚度为KL、KR的线弹簧和平面内刚度为SL、SR的转动弹簧作为边界约束支撑,中间包含n个弹簧刚度分别为K1、K2、…、Kn的弹性支撑,其间距分别为l1、l2、…、ln, 根据Euler-Bernoulli梁理论[18], 其在移动荷载Fv(x, t)作用下的运动微分方程为
| $ \begin{aligned} &E I \frac{\partial^{4} w(x, t)}{\partial x^{4}}+m \frac{\partial^{2} y(x, t)}{\partial t^{2}}+c \frac{\partial y(x, t)}{\partial t}= \\ &\ \ \ \ -F_{v} \delta(x-v t) \end{aligned} $ | (1) |
|
图 1 两端任意约束中间弹性支撑的多跨连续梁 Fig. 1 Multi-span continuous beam with elastic supports under arbitrary constraints at two ends |
式中:EI为梁的抗弯刚度;m为梁体单位长度的质量;c为梁的阻尼;δ(x-vt)为Dirac函数;y(x, t)为梁上任意点在荷载作用下的竖向位移,由两部分组成,一部分为只考虑梁为刚体,在荷载Fv(x, t)作用下由两端的弹簧支撑分别下挠yL(t)、yR(t),另一部分为梁体产生的弹性变形,即梁体的竖向挠度w(x, t),如图 1所示。于是有
| $ y(x, t)=\left(1-\frac{x}{L}\right) y_{\mathrm{L}}(t)+\frac{x}{L} y_{\mathrm{R}}(t)+w(x, t) $ | (2) |
其中yL(t)、yR(t)分别为梁左端和右端的竖向位移。
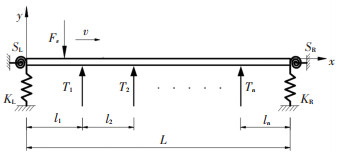
对多跨的弹性支撑连续梁,可将中间弹性支撑转化为支反力Ti,得到中间作用有n个弹性支撑反力(T1,T2,…,Tn)的等价模型,如图 2所示,当在任意时间t的第i个弹性支撑处xi的梁体位移为y(xi, t),则各中间支反力的大小为
| $ T_{i}=-K_{i} y\left(x_{i}, t\right) $ | (3) |
|
图 2 两端多重弹簧支撑约束的多跨弹性支撑连续梁等价模型 Fig. 2 Equivalent model of multi-span continuous beam with elastic supports under multiple spring support restraints at both ends |
由此得到梁的运动微分方程为
| $ \begin{gathered} E I \frac{\partial^{4} w(x, t)}{\partial x^{4}}+m \frac{\partial^{2} y(x, t)}{\partial t^{2}}+c \frac{\partial y(x, t)}{\partial t}= \\ -F_{v} \delta(x-v t)-\sum\limits_{i=1}^{n} K_{i} y\left(x_{i}, t\right) \delta\left(x-x_{i}\right) \end{gathered} $ | (4) |
式(4)中,多个离散弹簧的支反力与梁体振动位移相关,因此要进行多次的迭代求解,其收敛性和算法均难度较大。Sato等[19]曾对比研究发现,当弹性支撑间距相等(l1=l2=…=ln= l)、弹性支撑刚度相同(K1=K2=…=Kn=K),且梁体的支撑刚度K、抗弯刚度EI以及弹性支撑间距(或跨径)l满足式(5)时,可以将离散弹性支撑近似等效为弹性地基支撑,即将弹性支撑刚度K转化为弹性地基的分布刚度k(k=K/l)。在式(5)条件下,弹性地基梁的一阶频率与离散弹性支撑梁的一阶频率之比大于98%,能够满足实际工程的精度要求。
| $ \frac{K l^{3}}{24 E I} \leqslant 0.05 $ | (5) |
根据这一条件,可将式(4)进一步转化为
| $ \begin{gathered} E I \frac{\partial^{4} y(x, t)}{\partial x^{4}}+m \frac{\partial^{2} y(x, t)}{\partial t^{2}}+c \frac{\partial y(x, t)}{\partial t}+ \\ k y(x, t)=-F_{v} \delta(x-v t) \end{gathered} $ | (6) |
对两端任意弹簧支撑约束的多跨弹性支撑连续梁等价模型,其左右两端的边界条件分别为
| $ \left\{\begin{array}{l} y_{\mathrm{L}}(t)=y(0, t) \\ \theta_{\mathrm{L}}(t)=\frac{\partial y(0, t)}{\partial x} \\ E I \frac{\partial^{2} y(0, t)}{\partial x^{2}}=S_{\mathrm{L}} \theta_{\mathrm{L}}(t) \\ E I \frac{\partial^{3} y(0, t)}{\partial x^{3}}=-K_{\mathrm{L}} y_{\mathrm{L}}(t) \end{array}\right. $ | (7) |
| $ \left\{\begin{array}{l} y_{\mathrm{R}}(t)=y(L, t) \\ \theta_{\mathrm{R}}(t)=\frac{\partial y(L, t)}{\partial x} \\ E I \frac{\partial^{2} y(L, t)}{\partial x^{2}}=-S_{\mathrm{R}} \theta_{\mathrm{R}}(t) \\ E I \frac{\partial^{3} y(L, t)}{\partial x^{3}}=K_{\mathrm{R}} y_{\mathrm{R}}(t) \end{array}\right. $ | (8) |
对于两端任意弹簧支撑约束的近似等效为弹性地基支撑梁,根据分离变量法,在外荷载作用下梁的位移y(x, t)可表示为模态的级数形式:
| $ y(x, t)=\sum\limits_{n=1}^{N} \varphi_{n}(x) q_{n}(t) $ | (9) |
其中:φn(x)为梁的各阶模态函数,qn(t)为对应的广义坐标。
因此需要确定两端任意弹簧支撑的弹性地基连续梁的模态函数。根据任意弹簧支撑约束边界条件,可设其模态函数为
| $ \varphi(x)=C_{1} \cos \alpha x+C_{2} \sin \alpha x+C_{3} \cosh \alpha x+C_{4} \sinh \alpha x $ | (10) |
式中:
| $ \left[\begin{array}{cccc} \mu_{\mathrm{L}} & 1 & -\mu_{\mathrm{L}} & 1 \\ 1 & -\eta_{\mathrm{L}} & 1 & \eta_{\mathrm{L}} \\ \sin \alpha L+\mu_{\mathrm{R}} \cos \alpha L & \mu_{\mathrm{R}} \sin \alpha L-\cos \alpha L & -\left(\mu_{\mathrm{R}} \cosh \alpha L+\sinh \alpha L\right) & -\left(\mu_{\mathrm{R}} \sinh \alpha L+\cosh \alpha L\right) \\ \eta_{\mathrm{R}} \sin \alpha L-\cos \alpha L & -\left(\sin \alpha L+\eta_{\mathrm{R}} \cos \alpha L\right) & \eta_{\mathrm{R}} \sinh \alpha L-\cosh \alpha L & \eta_{\mathrm{R}} \cosh \alpha L-\sinh \alpha L \end{array}\right] \cdot\left[\begin{array}{l} C_{1} \\ C_{2} \\ C_{3} \\ C_{4} \end{array}\right]=0 $ | (11) |
其中:
式(11)存在非零解的条件为行列式等于零,即得到梁的固有频率方程,求解固有频率方程的各个根为αn,进而求得梁的各阶固有频率ωn。将获得的αn再代入式(11)并进行归一化处理后求得模态函数的各项系数,将其代入式(10)得
| $ \varphi_{n}(x)=\frac{A_{1} \cos \alpha_{n} x+A_{2} \sin \alpha_{n} x+A_{3} \cosh \alpha_{n} x+A_{4} \sinh \alpha_{n} x}{B_{1} \cos \alpha_{n} L+B_{2} \sin \alpha_{n} L+B_{3} \cosh \alpha_{n} L+B_{4} \sinh \alpha_{n} L}, n=1, 2, 3, \cdots $ | (12) |
式中:
| $ \left[\begin{array}{l} A_{1} \\ A_{2} \\ A_{3} \\ A_{4} \end{array}\right]=\left[\begin{array}{cccc} -\mu_{\mathrm{L}}-\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} & \mu_{\mathrm{L}} \eta_{\mathrm{L}}+1 & 2 \eta_{\mathrm{L}}-\mu_{\mathrm{R}}+\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} & \mu_{\mathrm{L}} \eta_{\mathrm{L}}+2 \mu_{\mathrm{R}} \eta_{\mathrm{L}}-1 \\ \mu_{\mathrm{L}} \eta_{\mathrm{L}}+1 & \mu_{\mathrm{R}}+\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} & 2 \mu_{\mathrm{L}} \mu_{\mathrm{R}}-\mu_{\mathrm{L}} \eta_{\mathrm{L}}+1 & 2 \mu_{\mathrm{L}}+\mu_{\mathrm{R}}-\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} \\ \mu_{\mathrm{R}}+2 \eta_{\mathrm{L}}-\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} & \mu_{\mathrm{L}} \eta_{\mathrm{L}}+2 \mu_{\mathrm{R}} \eta_{\mathrm{L}}-1 & \mu_{\mathrm{R}}+\mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}} & \mu_{\mathrm{L}} \eta_{\mathrm{L}}+1 \\ 2 \mu_{\mathrm{L}} \mu_{\mathrm{R}}+\mu_{\mathrm{L}} \eta_{\mathrm{L}}-1 & \mu_{\mathrm{L}} \mu_{\mathrm{R}} \eta_{\mathrm{L}}-\mu_{\mathrm{R}}-2 \mu_{\mathrm{L}} & -\mu_{\mathrm{L}} \eta_{\mathrm{L}}-1 & -\mu_{\mathrm{R}}-\mu_{\mathrm{L}} \mu_{\mathrm{R}} \mu_{\mathrm{L}} \end{array}\right]\left[\begin{array}{l} \sin \alpha L \\ \cos \alpha L \\ \sinh \alpha L \\ \cosh \alpha L \end{array}\right] $ | (13) |
| $ \left[\begin{array}{l} B_{1} \\ B_{2} \\ B_{3} \\ B_{4} \end{array}\right]=\left[\begin{array}{c} \mu_{R}+\mu_{L} \mu_{R} \eta_{L} \\ \mu_{L} \eta_{L}+1 \\ 2 \mu_{L}+\mu_{R}-\mu_{L} \mu_{R} \eta_{L} \\ 2 \mu_{L} \mu_{R}-\mu_{L} \eta_{L}+1 \end{array}\right] $ | (14) |
将式(9)代入式(6),得
| $ \begin{aligned} &\ \ \ \ \sum\limits_{n=1}^{N} \frac{\mathrm{d}^{2}}{\mathrm{~d} x^{2}}\left[E I \frac{\mathrm{d}^{2} \varphi_{n}(x)}{\mathrm{d} x^{2}}\right] q_{n}(t)+\sum\limits_{n=1}^{N} m \varphi_{n}(x) \ddot{q}_{n}(t)+ \\ &\sum\limits_{n=1}^{N} c \varphi_{n}(x) \dot{q}_{n}(t)+k \sum\limits_{n=1}^{N} \varphi_{n}(x) q_{n}(t)=F_{v} \delta(x-v t) \end{aligned} $ | (15) |
利用模态函数关于刚度和质量的正交性可得
| $ \ddot{q}_{\mathrm{n}}(t)+2 \beta \dot{q}_{n}(t)+\omega^{2} q_{n}(t)=Q_{n}(t), n=1, 2, 3, \cdots $ | (16) |
式中:
根据式(16)可求得广义坐标qn(t),将其代入式(9)得到梁在移动荷载作用下的竖向振动位移y(x, t)。
由于弹性支撑边界条件下梁的模态函数(式(12))十分复杂,因此本文通过MATLAB编写计算程序来计算上述求解过程。
3 数值算例分析为了说明本文方法的应用及所提出方法的正确性,这里选取一个算例,用所编制的程序进行计算,并用有限元计算结果进行对比分析。
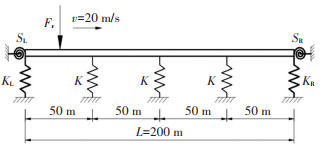
计算模型参考文献[20],如图 3所示,为四跨弹性支撑连续梁。其中梁总长L=200 m;支撑间距l=50 m;截面为管状断面,截面外径D=15 m,截面内径d=13 m;截面惯性矩I=1 083 m4;材料密度ρ=2 550 kg/m3;弹性模量E=3.45×104 MPa;中间弹性支撑刚度Ki=1.28×105 kN/m;两端线弹簧支撑刚度取KL=KR=3×106 kN/m;转动弹簧支撑刚度取SL=SR=109 kN/m。移动荷载参数:荷载大小Fv=1 176 kN;移动速度v=20 m/s。
|
图 3 算例的计算模型 Fig. 3 Calculation model of the example |
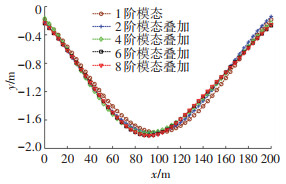
为了验证模态叠加法的收敛性,计算不同模态叠加后梁的竖向位移和弯矩值。图 4为当荷载移动到跨中时前8阶模态叠加后该梁各处的竖向位移。可以发现,前4阶至前8阶模态叠加后得到的位移结果基本一致,说明计算结果具有收敛性,且取前4阶模态叠加就具备较高的精度。
|
图 4 各阶模态叠加后梁的位移 Fig. 4 Displacements of beam after mode superposition |
表 1列出了弹性支撑连续梁利用本文的理论方法及有限元法分析的前3阶固有频率。理论计算得到的1阶固有频率为8.12 rad/s,其与有限元分析结果非常接近,两者的差异仅为0.16 rad/s(1.96%)。而随模态阶数的增加,两者计算的固有频率差异有所增加。这说明,两种模型在低阶频率上有较好的一致性,但在高阶频率上仍存在一定的差异。换句话说,弹性支撑连续梁的振动特性可以通过弹性地基边界和离散弹性支座边界来反映,但这种假设在结构高阶振动分析中会产生一定的误差,需要进一步分析。
| 表 1 结构固有圆频率 Tab. 1 Natural vibration frequency of the structure |
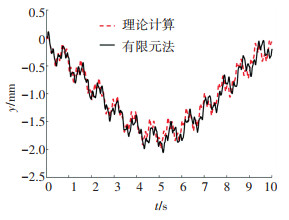
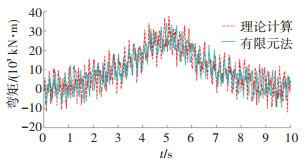
图 5及图 6则进一步给出了该弹性支撑连续梁跨中位置处的位移和弯矩的时程曲线,可以观察到本文理论计算得到的位移和弯矩的时程变化曲线与有限元法计算得到的结果,两者之间具有很好的一致性,但存在微小的相位差,且本文方法的理论计算值与有限元分析值有一定的误差,这与理论推导中将离散弹性支撑连续梁理想化为“弹性地基支撑梁”模型有关,导致两者的结构计算得到的频率有所差异,而使计算结果存在一定的偏差,且这个偏差与弹性支撑的刚度K和结构的抗弯刚度EI及弹性支撑的间距l有关,通过分析,当其满足式(5)条件时,误差可以控制在5%以内。同时可以发现,由于结构的边界条件为弹性支撑,其上各点的位移和弯矩变化均较为剧烈,说明边界条件的设定对结构的疲劳分析将会产生较大影响。
|
图 5 跨中位置处的竖向位移时程曲线 Fig. 5 Time history curves of vertical displacement at mid-span |
|
图 6 跨中位置处弯矩时程曲线 Fig. 6 Time history curves of bending moments at mid-span |
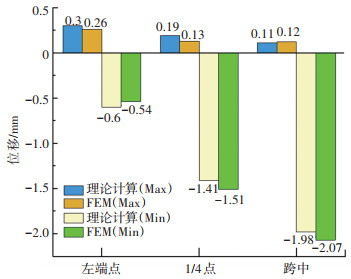
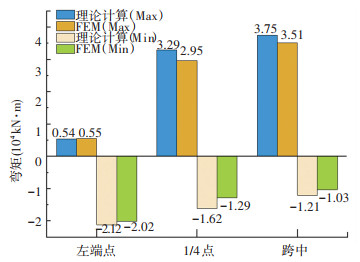
图 7及图 8分别为不同位置处(左端点、1/4点、跨中)位移和弯矩最大值和最小值,通过对计算结果和有限元结果进行比较发现两者结果比较接近。在动荷载作用下,梁体向下动位移的最大值出现在跨中,而向上动位移的最大值出现在梁端。同时在各个截面处均交替出现了正弯矩和负弯矩,其中跨中位置处的正弯矩和端点处的负弯矩最为显著。
|
图 7 不同位置处位移的最大值和最小值 Fig. 7 Maximum and minimum values of displacements at different positions |
|
图 8 不同截面处弯矩的最大值和最小值 Fig. 8 Maximum and minimum values of bending moments at different sections |
图 9进一步讨论了两端弹簧刚度不同对前6阶模态函数的影响。当两端竖向弹簧刚度KL=KR=∞, 平面内转动刚度SL=SR=0时,两端的支撑条件即转化为铰支座;当两端竖向弹簧刚度KL=KR=∞,平面内转动刚度SL=SR=∞时,两端的支撑条件即转化为固定支承。在图 9中,对于第1阶振型,两端为弹性支撑的连续梁与两端简支的连续梁振型比较接近,但随着频率的增加,弹性支撑的高阶振型与刚性支撑(两端简支和两端固支)的振型区别越来越明显。与两端刚性支撑的振型不同,由于边界条件为弹性,其高阶模态曲线边界处的幅值反而更大。
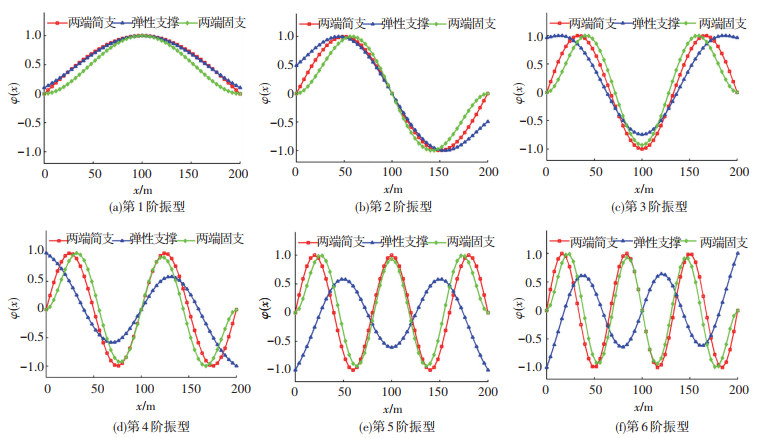
|
图 9 边界条件对振型的影响 Fig. 9 Effect of boundary conditions on mode shapes |
表 2则给出了梁两端简支、固支及弹性支撑边界条件下等效弹性地基梁的前6阶频率。由此可看出边界条件对频率的影响。对于第1阶频率,弹性支撑的频率介于两端简支和两端固支之间,从第2阶频率开始,弹性支撑的频率均小于两端简支,且随着阶数的增加,两者的差距逐渐增大。说明将边界条件简化为刚性支撑,会使结构的高阶计算频率增大。
| 表 2 不同边界条件对等效弹性地基梁频率的影响 Tab. 2 Effect of different boundary conditions on frequency of equivalent elastic foundation beam |
图 10给出了梁两端简支、固支及弹性支撑边界条件对等效弹性地基梁跨中挠度的影响。在本算例条件下,边界为两端简支的连续梁跨中挠度幅值最大,边界为弹性支撑的连续梁跨中挠度位于简支边界和固支边界之间。
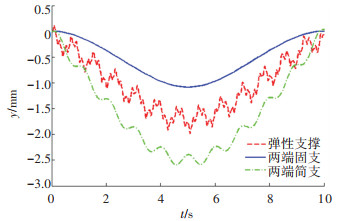
|
图 10 不同边界条件对等效弹性地基梁跨中竖向位移的影响 Fig. 10 Effect of different boundary conditions on mid-span vertical displacement of equivalent elastic foundation beam |
从图 10可以发现,在两端固支的边界条件下,跨中挠度的振动幅度最不明显,而两端弹性支撑连续梁的跨中挠度的高频振动最为明显,说明当边界条件为弹性支撑时,连续梁的高阶振型的振型参与系数更大。图 11、12分别分析了两端转动弹簧刚度和线弹簧刚度对移动荷载作用下跨中位移的影响机理。由图 11可知,当两端竖向支撑刚度KL=KR=∞时,随着转动弹簧刚度的增加,跨中最大位移减小,振动幅度也减弱,当转动刚度增加至完全刚性时(即达到固支状态),由于两端支点强大的约束刚度,使梁的振动明显减弱。由图 12可知,当两端转动弹簧刚度SL=SR=∞时,随着线支撑刚度的减小,跨中位移的振动幅度明显增大,振动位移的平均值也略有增加。结合图 10~12可以发现,两端线弹簧刚度对结构的振动幅度影响更大,而转动弹簧刚度则对结构的最大振动位移影响更为明显。
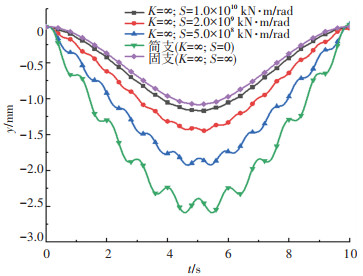
|
图 11 两端转动弹簧刚度对跨中位移响应的影响 Fig. 11 Effect of rotational spring stiffness on mid-span displacement response |
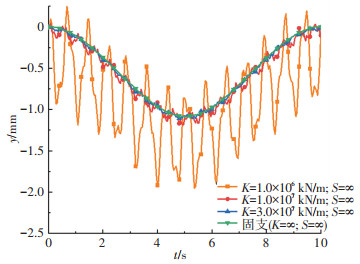
|
图 12 两端线弹簧刚度对跨中位移响应的影响 Fig. 12 Effect of line spring stiffness on mid-span displacement response |
为探讨移动荷载速度变化对该类结构位移响应的影响,图 13进一步分析了移动荷载以20 m/s,30 m/s,40 m/s运动时,两端弹性支撑梁跨中位移的变化规律。从图中可以看出,在荷载经过梁体时,移动速度越大,位移波动的周期就越长;跨中位移的最大值随速度增加而略有减小。
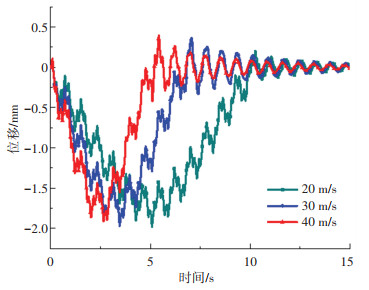
|
图 13 移动荷载速度对结构跨中位移响应的影响 Fig. 13 Effect of moving load velocity on mid-span displacement response |
针对两端任意约束中间弹性支撑的多跨连续梁,通过将弹性支撑间距相等、弹性支撑刚度相同的离散弹性支撑连续梁等效为两端任意约束的具有均匀弹性地基支撑的等价模型梁,推导建立了其在移动荷载作用下结构振动响应的微分方程,并根据相应的边界条件,给出了梁体在以一定速度移动的荷载作用下的动力响应,编制了相应的计算程序,通过研究可以得出以下结论:
1) 两端边界条件为弹性支撑时的连续梁的高阶模态与两端简支和两端固支的高阶模态明显不同,由于边界条件为弹性,其高阶模态曲线边界处的幅值反而更大。同时两端弹性支撑的一阶频率与两端简支情况相近,而高阶频率则均小于两端简支情况。
2) 在移动荷载作用下,梁体向下动位移的最大值出现在跨中,而向上动位移的最大值出现在梁端。同时在各个截面处均出现了正弯矩和负弯矩,跨中位置处的正弯矩和端点处的负弯矩最为显著。
3) 两端弹性支撑的连续梁的跨中挠度变化幅值介于两端固支和两端简支之间,但高频振动更加明显。改变两端弹簧支撑刚度将会对结构位移产生明显影响,转动弹簧刚度越大,结构振动的竖向位移越小;线弹簧支撑刚度越大,结构往复振动的幅度越小。
4) 跨中位移响应与荷载的移动速度有关,移动速度越大,位移波动的周期就越长,位移响应的最大值略有减小。
| [1] |
CHEUNG Y K, AU F T K, ZHENG D Y, et al. Vibration of multi-span non-uniform bridges under moving vehicles and trains by using modified beam vibration functions[J]. Journal of Sound and Vibration, 1999, 228(3): 611. DOI:10.1006/jsvi.1999.2423 |
| [2] |
Zakęś F, ŚNIADY P. Application of volterra integral equations in dynamics of multispan uniform continuous beams subjected to a moving load[J]. Shock and Vibration, 2016, 2016: 1. DOI:10.1155/2016/4070627 |
| [3] |
MARTÍNEZ-RODRIGO M D, ANDERSSON A, PACOSTE C, et al. Resonance and cancellation phenomena in two-span continuous beams and its application to railway bridges[J]. Engineering Structures, 2020, 222: 111103. DOI:10.1016/j.engstruct.2020.111103 |
| [4] |
晏麓晖, 曾首义, 陈斌. 弹性支承梁动力响应分析[J]. 工程力学, 2003, 20(增刊1): 381. YAN Luhui, ZENG Shouyi, CHEN Bin. The dynamic analysis of elastic supported beam[J]. Engineering Mechanics, 2003, 20(S1): 381. |
| [5] |
DING H, ZHU M, CHEN L. Nonlinear vibration isolation of a viscoelastic beam[J]. Nonlinear Dynamics, 2018, 92(2): 325. DOI:10.1007/s11071-018-4058-8 |
| [6] |
WATTANASAKULPONG N, BUI T Q. Vibration analysis of third-order shear deformable FGM beams with elastic support by Chebyshev collocation method[J]. International Journal of Structural Stability and Dynamics, 2018, 18(5): 1850071. DOI:10.1142/S0219455418500712 |
| [7] |
CHEN Q, DU J. A Fourier series solution for the transverse vibration of rotating beams with elastic boundary supports[J]. Applied Acoustics, 2019, 155: 1. DOI:10.1016/j.apacoust.2019.05.008 |
| [8] |
AYDIN E, DUTKIEWICZ M, ÖZTVRK B, et al. Optimization of elastic spring supports for cantilever beams[J]. Structural and Multidisciplinary Optimization, 2020, 62(1): 55. DOI:10.1007/s00158-019-02469-3 |
| [9] |
FROIO D, RIZZI E, SIMÕES F M F, et al. A true PML approach for steady-state vibration analysis of an elastically supported beam under moving load by a DLSFEM formulation[J]. Computers & Structures, 2020, 239: 106295. DOI:10.1016/j.compstruc.2020.106295 |
| [10] |
WANG S, QIN X, YU L, et al. Stiffness identification method of simply elastic supported beam based on first-order modal Rayleigh solution[J]. Journal of Physics: Conference Series, 2020, 1670: 012037. DOI:10.1088/1742-6596/1670/1/012037 |
| [11] |
叶茂, 谭平, 任珉, 等. 中间带弹性支承各种边界条件连续梁模态分析[J]. 工程力学, 2010, 27(9): 80. YE MAO, TAN PING, REN MIN, et al. Modal analysis of multi-span beams with intermediate flexible constraints and different boundary conditions[J]. Engineering Mechanics, 2010, 27(9): 80. |
| [12] |
LIN H, CHANG S C. Free vibration analysis of multi-span beams with intermediate flexible constraints[J]. Journal of Sound and Vibration, 2005, 281(1/2): 155. DOI:10.1016/j.jsv.2004.01.010 |
| [13] |
姚佐球. 各种支承连续梁的振动频率方程[J]. 华南理工大学学报(自然科学版), 1991, 19(4): 63. YAO Zuoqiu. The vibration frequency equations of various supporting continuous beams[J]. Journal of South China University of Techno-logy (Natural Science), 1991, 19(4): 63. DOI:10.3321/j.issn:1000-565X.1991.04.009 |
| [14] |
TAN G, WANG W, CHENG Y, et al. Dynamic response of a nonuniform timoshenko beam with elastic supports, subjected to a moving spring-mass system[J]. International Journal of Structural Stability and Dynamics, 2018, 18(5): 1850066. DOI:10.1142/S0219455418500669 |
| [15] |
LEONTIEV Y. Transverse oscillations of the beam on an elastic base if the boundary conditions change[J]. International Journal for Computational Civil and Structural Engineering, 2020, 16(3): 35. DOI:10.22337/2587-9618-2020-16-3-35-46 |
| [16] |
叶茂, 张鹏, 傅继阳, 等. 带弹性支撑多跨连续梁桥的车桥耦合演变随机振动[J]. 振动与冲击, 2014, 33(3): 76. YE Mao, ZHANG Peng, FU Jiyang, et al. Coupled vehicle-bridge evolutionary random vibration for a multi-span continuous bridge with elastic bearings[J]. Journal of Vibration and Shock, 2014, 33(3): 76. DOI:10.3969/j.issn.1000-3835.2014.03.016 |
| [17] |
FROIO D, RIZZI E, SIMÕES F M F, et al. DLSFEM-PML formulation for the steady-state response of a taut string on visco-elastic support under moving load[J]. Meccanica, 2020, 55(4): 765. DOI:10.1007/s11012-019-01047-7 |
| [18] |
宋一凡. 公路桥梁动力学[M]. 北京: 人民交通出版社, 2000. SONG Yifan. Highway bridge dynamics[M]. Beijing: China Communications Press, 2000. |
| [19] |
SATO M, KANIE S, MIKAMI T. Mathematical analogy of a beam on elastic supports as a beam on elastic foundation[J]. Applied Mathematical Modelling, 2008, 32(5): 688. DOI:10.1016/j.apm.2007.02.002 |
| [20] |
LIN H, XIANG Y, YANG Y. Vehicle-tunnel coupled vibration analysis of submerged floating tunnel due to tether parametric excitation[J]. Marine Structures, 2019, 67: 102646. DOI:10.1016/j.marstruc.2019.102646 |
 2022, Vol. 54
2022, Vol. 54


