2. 桥梁结构抗风技术交通运输行业重点实验室(同济大学),上海200092;
3. 省部共建山区桥梁及隧道工程国家重点实验室(重庆交通大学), 重庆 400074
2. Key Laboratory of Transport Industry of Wind Resistant Technology for Bridge Structures (Tongji University), Shanghai 200092, China;
3. State Key Laboratory of Mountain Bridge and Tunnel Engineering (Chongqing Jiaotong University), Chongqing 400074, China
随着大跨桥梁建设的日益增多及桥位日趋复杂的风场环境,风荷载已成为桥梁建造运营的主要控制荷载。较高的桥面风速不仅会增加大跨桥梁行车的风荷载敏感性,对行车舒适度产生影响,在车辆行驶过程中出现风致行车安全问题[1-2],甚至造成严重的经济损失和社会影响。减少在不利风环境下的大跨桥梁的行车风险,提高桥梁在恶劣天气条件下的利用率,并保障桥上行车安全是值得深入研究的课题。为了在不利风的环境下能保障大跨桥梁行车安全,相较于改变车辆自身的外形参数降低其风荷载敏感性以提高行车安全性的方式[3],采用在桥面设置具有遮挡效应的风障等附属结构,不仅能够有效地降低横风作用下的桥面风速,改善行驶车辆在侧风作用下的气动效应[4],也为行车安全与驾乘安全性和舒适度提供了保障。目前在桥面加设风障以降低桥面侧向风速、改善桥面行车风环境并增加驾乘舒适性的研究与应用日益增多,如英国Severn悬索桥、中国杭州湾跨海大桥及中国青马大桥等均是成功案例[5-6]。
关于风障阻风效果和其对大跨桥梁桥面减风效应方面的研究仍然以风洞试验[7-12]和数值模拟[13-14]手段为主,其中风障有效阻风面积和风障最优透风率仍是备受关注的话题。文献[15]通过风洞试验和数值模拟的方法讨论了最优风障型式及其应用。文献[16]通过数值模拟的方法比选了曲线型风障对桥面风速的影响。从已有研究可以发现,桥面安装风障在改善桥面行车风环境的同时,会对主梁所受风荷载或其抗风性能有一定影响,但考虑风障作为重要的能够有效降低桥面来流风速的附属结构,对保障在大风等恶劣天气条件下的大跨桥梁行车安全性至关重要。因此对桥面风障的合理优化选型是值得研究的课题。目前已有风障对桥面行车风环境的改善作用等相关研究成果仍缺乏必要的现场实测验证工作。随着计算流体力学的发展,越来越多的数值模拟方法被提出并应用于工程实践。合理选用数值计算模型、计算域离散化方法和边界条件是保障数值模拟结果准确性的前提,同时能够有效提升数值模拟方法在桥面风环境分析等领域的应用。为保障采用数值模拟方法应用于桥面行车风环境分析结果的精度,开展相关风洞试验与实桥现场实测等验证工作是十分必要的。因此,本文以西堠门大桥为研究背景,采用CFD模拟了设置风障前后的桥面风场绕流变化情况,结合试验和实测结果对其结果进行了验证。在此基础上开展了桥面风障的选型优化工作,研究分析了风障对桥面风环境改善的主要影响因素,为桥面风障安装应用和保障大跨桥梁行车安全和舒适度提供了理论基础。
1 桥面风环境桥梁受风荷载作用时,桥面风速会随离桥面的高度变化而变化,为衡量桥面以上一定范围内侧向风速的大小,根据总风压相等的原则定义桥面等效风速[17]为
| $ V_{\mathrm{eff}}=\sqrt{\frac{1}{Z_{\mathrm{r}}} \int_{0}^{Z_{\mathrm{r}}} V^{2}(z) \mathrm{d} z} $ | (1) |
式中:Zr为等效高度范围,与车辆在桥面上行驶时受侧风影响的高度范围相对应,对集装箱卡车和小轿车分别取4.5 m和2.0 m;V为桥面风速;z为垂直桥面高度。
为反映风障对来流风速的干扰作用,定义等效风速与参考风速(来流风速)的比值为风障的侧风折减系数β,表达式为
| $ \beta=\frac{V_{\text {eff }}}{V_{\mathrm{R}}} $ | (2) |
式中VR为参考风速。
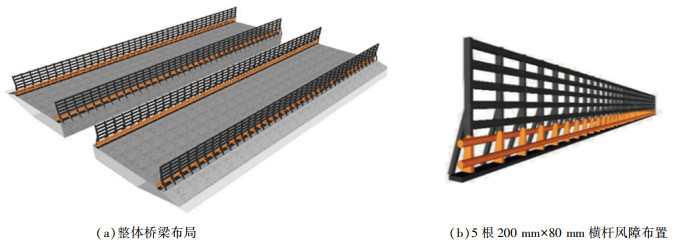
2 风环境数值模拟 2.1 方案设置以西堠门大桥开槽箱梁为研究背景,分析了设置风障条件下侧向来流时桥面风环境的变化情况。桥梁为中央开槽的分体式钢箱梁,梁高3.5 m,宽36.0 m,开槽宽6.0 m。主梁断面和计算车道位置如图 1所示。考虑来流风向为从左向右即自A车道向F车道,风攻角为0°。图 2给出了风障设置型式为5根200 mm×80 mm横杆时桥梁整体布局和风障局部示意图。

|
图 1 桥梁断面及计算车道示意图(mm) Fig. 1 Schematic diagram of Xihoumen Bridge cross-section and calculation lanes (mm) |
|
图 2 桥梁及风障示意图 Fig. 2 Schematic diagram of bridge and wind barriers |
为避免阻塞率对桥面风环境数值模拟结果的影响,计算域大小设置为282 m×124 m(x×y),其中x为来流方向,y为竖直方向。图 3给出了桥面设置风障时整体计算域的设置型式,无风障桥面风环境计算时边界条件与计算域的设置与之相同。来流入口区域为20倍梁高,尾流区域为50倍梁高,上下边界均为17倍梁高,阻塞率为0.023。桥梁周围绕流考虑为不可压缩流,计算域流动入口条件为速度边界条件,取入口速度为来流风速为27 m/s,出口条件为自由流边界条件;桥梁结构断面,栏杆及风障断面,上下边界均采用无滑移固壁边界条件。流场求解采用已在大气边界层成熟应用的SIMPLE压力速度耦合方法对压力-速度耦合场进行求解[18],计算中残差值设置为1×10-5以满足收敛条件。除此之外,本文后续分析过程中对不同风障类型进行优化比选,因此可认为雷诺数对各个风障方案的影响是有限的。

|
图 3 边界条件与计算域的设置型式 Fig. 3 Boundary conditions and computation domain setting |
流场的数值模拟是以绕流的连续性方程及动量守恒方程的Navier-Stokes方程作为基本控制方程,并进行离散化的数值模拟方法对流场进行求解。工程分析中应用较多的为大涡模拟(LES)[19]与Reynolds平均法等方法[20]。基于Reynolds平均法(RANS)的双参数k-ε湍流模型均已成熟应用于工程实践中,其中Realizable k-ε模型作为目前验证最为广泛的计算模型[21-22]。由于其对充分发展的湍流计算有效,对于近壁区以黏性力为主导的边界层即湍流不充分发展区域,需结合壁面函数对流场进行模拟计算能显著降低计算量的同时也能保证计算精度[23]。目前主要有多区域模拟法和近似壁面边界条件模拟法等。前者对流场近壁面离散化要求较高,需采用尺度非常小的网格捕捉近壁面的流场变化特征,因此计算效率普遍不高。相关研究表明后者能够解决高雷诺数下的主梁断面绕流问题[24],即壁面函数法,能够提供黏性底层和充分发展的湍流层之间的相关关系以模拟近壁面流体的发展。文献[25]表明雷诺平均双参数模型能够较好地和壁面函数结合,求解黏性底层流动并能够提升计算效率。本文采用Realizable k-ε湍流模型并结合标准壁面函数法对桥梁断面二维绕流进行数值模拟,对加设风障前后桥面以上不同高度处的风速变化情况进行模拟,研究风障对桥面风环境的影响情况。
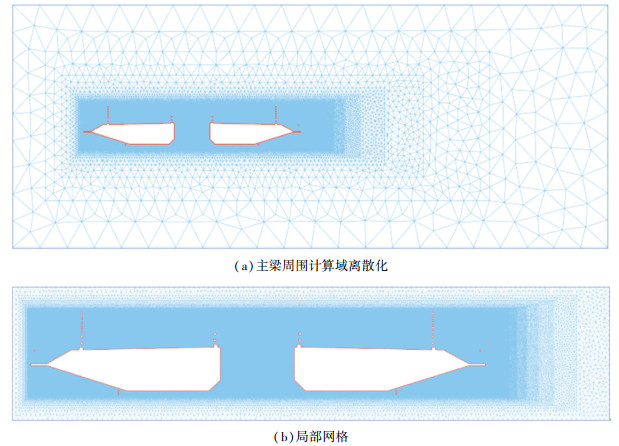
流场离散化处理是保障数值模拟方法求解流场正确性与精确度的基础。高质量网格能够有效减少计算过程的数值耗散并保障结果精确性的同时,还能有效减少计算过程中的非物理解[26]。对流场进行求解时采用非结构化三角形网格进行离散化,并对主梁周围加密的网格划分以有效减少由于网格质量造成的结果精度不足[27-28]。数值模拟分析中对比了4种不同密度网格计算所得结构阻力系数与风洞试验结果,如图 4(a)所示。可以看出随着近壁面网格加密程度增加,数值模拟精度也随网格数量增加而提升。进一步对流场离散化方案进行网格独立性检验(参考点P1、P2见图 3),计算收敛后结果对比如图 4(b)所示,可以看出当网格数量达到1 157 100时,继续增加网格数量计算结果变化甚微。考虑节约计算成本最终计算域流场划分整体离散化共计1 157 100个三角形网格单元,整体网格划分见图 5。文献[29]采用局部加密的非结构化网格,并取分析对象表面网格尺寸为0.15~0.40 m的流场离散化方式分析了风障对列车及简支梁桥气动性能的影响,其分析结果满足精度要求。文献[30]也采用了局部加密的非结构化网格方式分析了风障对周围风场的影响,结果表明其网格划分方式在保障结果精度与节省计算时间方面符合要求。综上,采取局部加密的非网格划分方式对近壁面区的流动处理更为精细,且在能保证数值模拟计算结果精度的基础上既能兼顾计算效率又在一定程度上避免了计算资源的浪费。

|
图 4 不同网格对比 Fig. 4 Comparison of different types of meshes |
|
图 5 流场离散化示意图 Fig. 5 Schematic diagram of flow-field discretization |
为验证数值模拟所得结果的精确性,在同济大学TJ-2风洞进行了比例为1/40的主梁节段模型表面风环境试验,如图 6所示。试验测试了未设置风障和设置风障(5根200 mm×80 mm矩形横杆)工况下且风攻角为0°时,垂直于桥面上方4.5 m高度处各不同计算车道位置处(AB车道分界,B车道,BC车道分界与D车道)的桥面侧向等效风速演变规律,图 7给出了试验时各测点的布置。试验时横桥向的均匀来流风速为10 m/s,采用皮托管测量方法对不同车道位置来流风速进行测量,并以模型前方2 m处的风速作为参考风速计算折减系数。

|
图 6 风洞试验 Fig. 6 Wind tunnel test |

|
图 7 风速测点布置 Fig. 7 Layout of wind speed measuring points |
桥面安装风障相较于未安装风障时,安装风障后桥面风速显著降低。图 8展示了设置风障前后桥面上方各计算车道4.5 m高度处的风速变化趋势。从图中可以看出,有无风障情况下桥面来流风速自迎风向至背风侧呈逐渐降低的趋势,风洞试验结果与CFD结果具有相同的变化趋势。安装风障后风洞试验结果趋势性相较于CFD结果稍有偏差,这体现了附加格栅产生特征紊流的影响。数值模拟与风洞试验所得桥面风速演变规律具有相同的趋势,仍存在稍许偏差(在可接受范围之内)。究其原因,在于数值模拟时模型采用全尺模型与风洞试验中节段比例模型存在尺度效应差异。与实际桥面风场相比较,无论风洞试验中还是数值模拟,初始条件的设置均在一定程度上与实际桥面风场存在偏差,但目前既有风洞试验与CFD条件下,可认为结合数值模拟方法开展桥面风环境模拟具有较可靠的精度。

|
图 8 风洞试验与数值模拟结果比对 Fig. 8 Comparison of wind tunnel test and numerical simulation results |
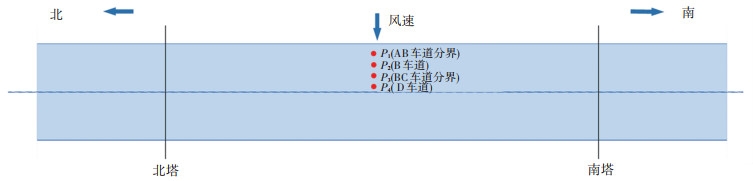
为进一步检验数值模拟结果精度和风障的实际阻风效果,采用风杯式风速计在成桥状态下,对安装5根200 mm×80 mm风障时桥面上方1.8 m和4.5 m高度处的来流风速变化情况进行测量。风速测量采用美国NRG#40风杯式风速计,测试最小风速为0.78 m/s,最大风速为96 m/s,精确度为±0.1 m/s。实测时采样频率为0.5 Hz。测试位置设置竖立的6 m高度直杆,竖杆外径为0.12 m,且保证风向角相对正北变化,即正北为0°风向角。为尽量降低竖杆对来流风速干扰,将风速计采用专用横向水平支架固定于竖杆上,风速仪离开竖杆水平距离1.2 m。桥面测点位置布置如图 9所示,P1~P4测点依次分别对应于AB车道分界处、B车道中间位置处、BC车道分界处以及C车道中间位置处,风速测量仪器安装与实测情况如图 10所示。
|
图 9 实测位置布置图 Fig. 9 Layout of field measurement |

|
图 10 风速计安装与风环境现场实测 Fig. 10 Anemometer installation and field measurement of wind environment |
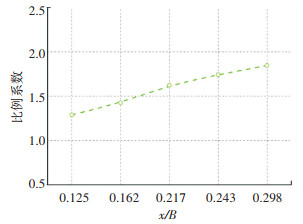
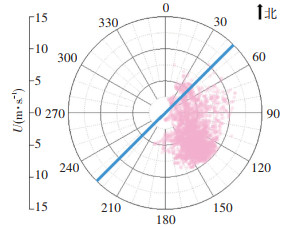
现场实桥状态实测时,桥梁结构自身对周围风场存在干扰使得在桥面附近难以准确测得实际来流风速的大小,根据CFD所得结果对桥面流场及不同车道风速剖面分析可知,风障对桥面风场与来流风速的影响范围约为2倍梁高之内。因此数值模拟时对桥面设置风障情况下计算域中距主梁断面前缘10 m位置处作为速度监测点,开槽位置的分流作用会导致下游桥梁表面风速较低,因此仅对上游桥面各车道(A、AB分界、B、BC分界、C)4.5 m高度位置处作为速度监测点(见图 3参考点P1),对比监测分析前缘与桥面4.5 m高度位置处风速关系。可以发现随着距主梁前缘距离的增加各车道4.5 m高度位置处风速呈降低的趋势,其比例关系见图 11。因此比例系数取前缘10 m位置处与迎风侧各车道4.5 m高度位置处风速比值的均值,偏安全取值约为1.59。确定来流风速后,根据侧向风速分布可计算各测试位置的桥面等效风速和侧风折减系数。图 12给出了实测时B车道4.5 m高度位置处平均风速和风向时程,可以看出平均风速和风向随时间变化而变化,由于桥轴线与正北方向约为45°角,来流风向基本垂直于桥轴线,因此可忽略斜风带来的局部流场三维特性。
|
图 11 监测点与各车道4.5 m高度处风速关系 Fig. 11 Relationship between monitoring points and wind speed at 4.5 m height of each lane |
|
图 12 风速风向图 Fig. 12 Wind speeds and directions |
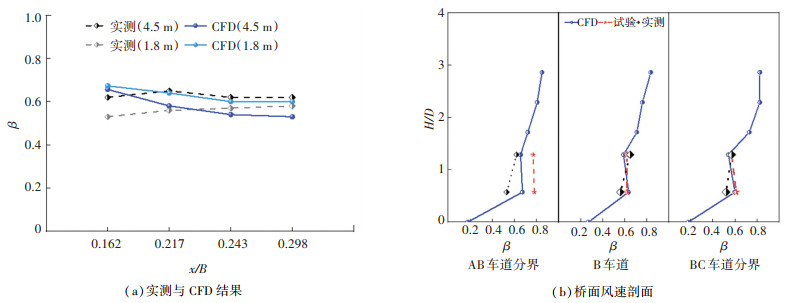
图 13给出了采用3种不同分析方法对迎风侧车道风速变化的对比分析结果。3种不同分析方法得到的桥面风速演变规律稍有偏差但具有相同的变化趋势。由图 13(a)可以看出在AB车道分界处实测结果相较于风洞试验与数值模拟结果偏低,在其他计算车道位置处两者结果略有偏高但风速变化趋势相同。原因在于实测时实际来流风向并不与风洞试验或数值模拟时简化的理想的与桥轴线完全垂直且不发生变化的风向,导致实测所得风速沿高度不同风向角也会存在变化。图 13(b)给出了桥面部分计算车道的风剖面图,可以看出CFD所得结果与成桥状态的实测结果接近,两种方法所得结果相差不大(约为9.1%)。由此可知,采用既有网格划分策略及数值求解模型能够成功再现实际桥面风场的变化情况并得到工程适用精度较高的计算结果。另外,由于黏性力作用桥面近地面风速基本为零,随着离桥面高度的增加来流惯性力的作用使得桥面风速随高度呈逐渐增加的状态,但在桥面向上2.0 m至5.0 m左右风速变化缓慢,这是由于风障的遮挡效应使得来流风速降低,桥面高度超过风障的有效遮挡高度时,风障对风速的折减效果明显减弱因而桥面风速变化较小。
|
图 13 桥面风环境比对分析 Fig. 13 Comparison of wind environment around bridge deck |
为实现更优的风障挡风效果,对主梁上不同类型风障进行了优化比选,采用数值模拟分析的手段计算不同风障设置型式下的桥面绕流和不同车道处风速变化情况。图 14为部分主梁上风障设置方案示意图。表 1给出了12种风障设置型式和透风率及高度的变化情况,其中除第10种风障为4根200 mm×80 mm的矩形横杆,高度为3.6 m,其余高度均为3.0 m。

|
图 14 部分风障设置代表方案细部示意图 Fig. 14 Layout of details of wind barrier examples |
| 表 1 不同风障设置方案 Tab. 1 Different wind barrier setting schemes |
表 2给出了12种不同风障设置型式下桥面各车道位置4.5 m高度位置处的侧风折减系数计算结果。可以看出,随着风障横杆数目的增多,桥面风速呈逐渐降低的趋势,也即风障对桥面风速的改善作用越明显。风障设置型式为5根200 mm×80 mm横杆且位于桥面栏杆上侧时折减效果最佳。各风障型式下,桥面各计算车道的风速变化规律相似,呈从来流方向至下游区逐渐降低的趋势,且变化幅度逐渐趋于平缓。即风障对来流具有一定的遮挡屏蔽效应和桥面开槽部位对来流的疏导分流作用,使得桥面来流风速呈逐渐降低的趋势。
| 表 2 不同风障设置方案下桥面4.5 m处各计算车道位置侧风折减系数 Tab. 2 Crosswind reduction factors of different lanes at 4.5 m of bridge deck under different wind barrier setting schemes |
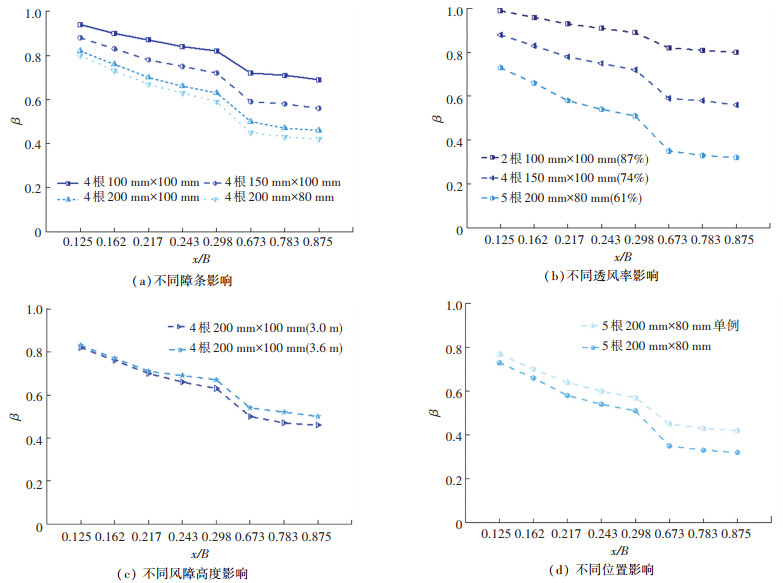
图 15对比不同计算车道的风速变化情况,对不同横条高宽比、透风率、高度及其设置位置对风障挡风效果的影响程度进行了分析。风障横杆断面型式是决定其挡风效果的主要因素。图 15(a)给出了在风障横条均为4根时但横杆高宽比不同时的侧风折减效应,随着横杆高宽比逐渐增大也即风障横条越窄高,其对侧风的遮挡效应越显著,在相同高度范围内随着横杆高宽比的增加其有效阻风面积也会随之增加,提高风障的遮风效应。
|
图 15 不同类型风障折减效果对比 Fig. 15 Comparison of reduction effects of different types of wind barriers |
透风率为风障孔洞/间隙之间与风障总面积的比值,过大的透风率会显著降低风障的有效遮风面积,造成风障遮风效应减弱,也即桥面风速与风障透风率呈反比的关系。图 15(b)给出了风障设置位置和高度相同但透风率不同(分别为87%、74%、61%)时各车道风速变化情况,随着透风率的降低,风障对来流风速的折减效果愈为显著,风障透风率每降低13%,风障折减效应相应提高16%左右。
当风障横杆数目和横杆断面型式相同时,风障高度的改变势必会造成风障透风率的改变,致使风障对来流风速的折减效果发生变化。图 15(c)给出了风障高度发生变化时,桥面计算车道位置处的风速的变化情况。研究结果表明横杆数目相同时,随着风障的高度增加,风障对桥面风速的折减效应显著降低。
不同的风障布置位置对其侧风折减效应也存在较大的影响。图 15(d)给出了风障型式和高度都相同,位置不同时对桥面风环境的影响情况。风障位于栏杆上侧时侧风折减效果要优于风障单列设置。风障单独布置一列时,挡风区域与栏杆挡风区域存在相互重叠的部分,透风率相较于风障位于栏杆上侧稍大,造成风障挡风效果降低。
综上所述,通过对不同风障影响因素对其侧风折减效应的影响程度分析,结果表明风障的侧风折减效应与其设置型式、横杆断面、高度、透风率等因素密切相关。影响其侧风折减效应的最主要因素为透风率,包括风障横杆型式、高度和位置因素的改变都在一定程度上反应了风障透风率变化对其挡风效应的影响。
图 16为设置5根200 mm×80 mm风障与未设置风障时的桥面各车道风剖面对比。有无风障时的各车道风速沿高度变化规律相接近,由于风障对来流的遮风效应,设置风障时桥面各车道沿高度在0~6.0 m之间风速大小相差都较明显,设置风障后桥面各车道风速降低约30%~50%,风障减风效果显著且实际遮风有效区域略大于风障实际高度,但在高出风障高度一定范围内随着距风障顶部高度的增加,屏蔽效应逐渐减弱。与未设置风障时桥面风速变化趋势相比,设置风障后在垂直桥面约6~7 m高度之外,桥面风速都趋于稳定不再发生明显变化,可得出风障对桥面的影响范围约为2倍梁高左右,在此范围之外桥梁风场不再受风障等附属构件的扰动并趋于稳定。

|
图 16 桥面各车道风剖面 Fig. 16 Wind profiles at different lanes |
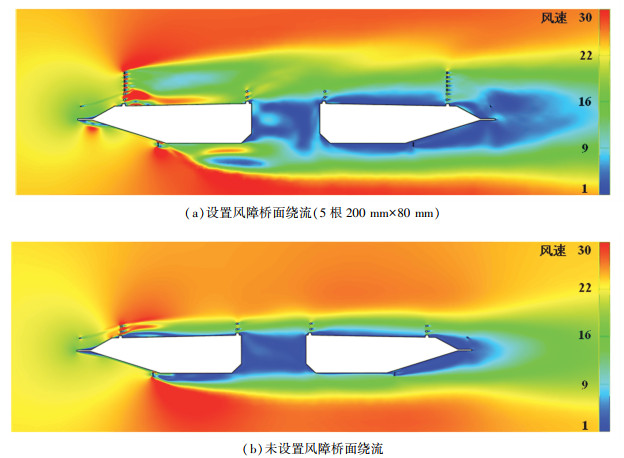
由上分析结果可见,相较于未设置风障时,安装风障后由于风障对桥面来流的干扰作用,桥面风速相较于未安装风障时明显降低。设置风障前后(5根200 mm×80 mm)的流场速度云图见图 17。桥面未安装风障时,来流在迎风侧翼缘被自然分流,在桥面形成较为均匀的压力分布,桥面流场分布较为均匀。桥面安装风障后,来流经过桥面翼缘的分流后由于风障横杆的扰动分离作用,来流再次在横杆端部发生分离,并在桥面上形成横向发展的旋涡导致桥面压力分布的不均匀性产生压力差,使得风障后风场分布发生变化,在风障高度内桥面风速相较于未安装风障时明显降低。除此之外,上游风障对来流的屏蔽干扰作用也会造成下游桥面风速变化较上游逐渐趋于平缓且风速逐渐降低,这说明在来流方向安装风障不仅可以有效降低桥面风速,对背风侧桥面风环境也有一定的改善作用。分离式断面开槽部分对来流也具有显著的疏导分泄作用,导致下游桥面风速明显低于上游。
|
图 17 设置风障前后流场速度云图分析 Fig. 17 Wind flow-field analysis with or without wind barriers |
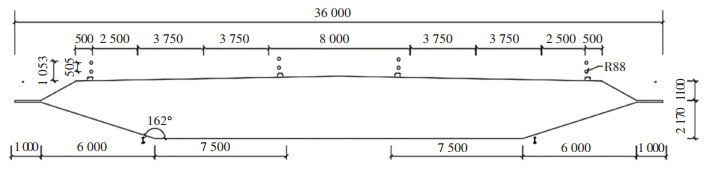
综合以上数值模拟结果,主梁中央开槽部位对桥面绕流有一定的影响。为探究中央开槽部位对桥面风环境的影响,分别对整体式箱梁断面和分体式双箱梁的绕流形态和桥面不同高度位置处风速变化情况进行了模拟。整体式箱梁断面如图 18所示,主梁表面各车道分布和来流方向与分体式箱梁断面相同。
|
图 18 整体式箱梁断面示意(mm) Fig. 18 Schematic of integrated box girder cross-section (mm) |
图 19为分体式断面和整体式箱梁断面绕流示意图。来流经过分体式箱梁中央开槽部位在上游梁上下表面尾部形成新的交替脱落的漩涡,表现为上表面形成在中央开槽部位向下发展的漩涡,下表面形成向上发展的漩涡,两者相互作用对下游梁周围绕流产生影响,使得下游梁表面风环境与整体式箱梁不同。上游主梁上表面尾部形成的漩涡逐渐向下发展并穿过开槽部位,但由于上游下表面形成的漩涡并未能完全发展至下游主梁上表面,最终上游主梁上表面尾部形成的漩涡与下表面形成的漩涡交汇进入下游主梁梁底,削弱了来流自上游向下游主梁上表面的发展,造成分体式箱梁下游主梁上表面风速低于于上游。文献[31]对箱型分体式双幅桥之间的气动干扰进行了研究,结果表明中央开槽部位是流动干扰的最主要位置,且上下游主梁之间气动干扰与桥面间距有关。文献[32]采用表面压力测试和主梁断面绕流测试方法分析了分体式双主梁模型相互气动影响和上下主梁绕流特性对槽间距敏感性。结果表明随着槽间距的增加上下游主梁相互气动影响增强,超过一定的临界值之后,下游主梁断面绕流形态受上游主梁影响又会减弱。综上,分体式箱梁下游主梁绕流形态受上游主梁影响较大,开槽位置对来流的分流作用导致分体式箱梁下游主梁表面风速相较于上游表面风速较低。开槽间距的大小也对下游主梁风环境受上游主梁的影响程度起重要作用,也是本文中分体式箱梁下游表面风速虽低于整体式箱梁但并不十分显著的原因。

|
图 19 主梁断面绕流 Fig. 19 Flow parttens around bridge girder |
通过采用CFD数值模拟方法对桥面风环境进行了模拟计算,为校验CFD数值模拟计算精度,开展了风洞验证试验与现场实测等验证工作,可以得出以下结论:
1) 本文所采用的数值模拟求解方法及流场离散化策略经风洞试验所得气动力结果校验,可成功再现实桥成桥状态桥面绕流,分析误差介于3%~9%之间,能够精确模拟风障对来桥面来流风速的屏蔽遮挡效应,揭示了桥面局部风场绕流特性和风障对来流遮挡干扰效应机理,可成功应用于桥面行车风环境等工程应用。
2) 桥面风障对来流的干扰屏蔽作用使得风障后风场重新分布从而有效改善桥面风环境,安装风障后对桥面侧向来流风速的折减介于30%~50%之间。风障有效减风区域不仅与风障高度相关,其布置位置与设置型式都是重要的影响因素,但其中风障透风率是影响有效阻风效应的最主要因素。
3) 相较于整体式箱梁断面,中央开槽部位对桥面来流的分流作用是开槽断面下游主梁上表面风速低于上游桥面风速的主要原因。除此之外,开槽间距大小也对下游主梁风环境受上游主梁的影响程度起重要作用。本文中未量化讨论槽间距的影响,仍需要后续进行深入研究和探讨。
| [1] |
GAWTHORPE R G. Wind effects on ground transportation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 52: 73. DOI:10.1016/0167-6105(94)90040-X |
| [2] |
CHEN Ning, LI Yongle, WANG Bin, et al. Effects of wind barrier on the safety of vehicles driven on bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 143: 113. DOI:10.1016/j.jweia.2015.04.021 |
| [3] |
CHELI F, CORRADI R, ROCCHI D, et al. Wind tunnel tests on train scale models to investigate the effect of infrastructure scenario[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6/7): 353. |
| [4] |
周蕾, 何旭辉, 陈争卫, 等. 风屏障对桥梁及车桥系统气动特性影响的数值研究[J]. 中南大学学报(自然科学版), 2018, 49(7): 1742. ZHOU Lei, HE Xuhui, CHEN Zhengwei, et al. Numerical study of effect of wind barrier on aerodynamic of bridge and train-bridge system[J]. Journal of Central South University (Sciencce and Technology), 2018, 49(7): 1742. |
| [5] |
CHU C R, CHANG C Y, HUANG C J, et al. Windbreak protection for road vehicles against crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 116(5): 61. |
| [6] |
庞加斌, 王达磊, 陈艾荣, 等. 桥面侧风对行车安全性影响的概率评价方法[J]. 中国公路学报, 2006, 19(4): 59. PANG Jiabin, WANG Dalei, CHEN Airong, et al. Probability evaluating method of bridge deck side wind effects on driving safety[J]. China Journal of Highway and Transport, 2006, 19(4): 59. DOI:10.3321/j.issn:1001-7372.2006.04.011 |
| [7] |
MCANENEY J, JUDD J A H. Multiple windbreaks: an aeolean ensemble[J]. Boundary-Layer Meteorology, 1991, 54(1/2): 129. |
| [8] |
FRANK C, RUCK B. Double-arranged mound-mounted shelterbelts: influence of porosity on wind reduction between the shelters[J]. Environmental Fluid Mechanics, 2005, 5(3): 267. DOI:10.1007/s10652-004-3820-2 |
| [9] |
JUDD J A H, RAUPACH M R, FINNIGAN J. A wind tunnel study of turbulent flow around single and multiple windbreaks, part Ⅰ: velocity fields[J]. Boundary-Layer Meteorology, 1996, 80(1): 127. DOI:10.1007/BF00119015 |
| [10] |
HONG S W, LEE I B, SEO I H. Modelling and predicting wind velocity patterns for windbreak fence design[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 142: 53. DOI:10.1016/j.jweia.2015.03.007 |
| [11] |
DONG Zhibao, LUO Wanyin, QIAN Guanqiang, et al. A wind tunnel simulation of the mean velocity fields behind upright porous fences[J]. Agricultural and Forest Meteorology, 2007, 146(1/2): 82. |
| [12] |
KOZMAR H, PROCINO L, BARTOLI G, et al. Sheltering efficiency of wind barriers on bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 107-108: 274. DOI:10.1016/j.jweia.2012.04.027 |
| [13] |
SANTIAGO J L, MARTIN F, CUERVA A, et al. Experimental and numerical study of wind flow behind windbreaks[J]. Atmospheric Environment, 2007, 41(30): 6406. DOI:10.1016/j.atmosenv.2007.01.014 |
| [14] |
项超群, 郭文华, 张佳文. 双线高速铁路桥最优风障高度及作用机理的数值研究[J]. 中南大学学报(自然科学版), 2014, 8: 2891. XIANG Chaoqun, GUO Wenhua, ZHANG Jiawen. Numerical study on optimal height of wind barriers and mechanism on high-speed railway bridge with double lines[J]. Journal of Central South University (Science and Technology), 2014, 8: 2891. |
| [15] |
WANG Dalei, CHEN Airong, ZHOU Zhiyong. Aerodynamic characters of a trans-oceanic cable-stayed bridge with wind barrier[C]//Proceedings of the 12th International Conference on Wind Engineering. Cairns: ICWE, 2007
|
| [16] |
周奇, 朱乐东, 郭震山. 曲线风障对桥面风环境影响的数值模拟[J]. 武汉理工大学学报, 2010, 32(10): 38. ZHOU Qi, ZHU Ledong, GUO Zhenshan. Numerical simulation for curve windshield barrier effects on wind environment around bridge deck[J]. Journal of Wuhan University of Technology, 2010, 32(10): 38. DOI:10.3963/j.issn.1671-4431.2010.10.009 |
| [17] |
夏锦林, 李珂, 葛耀君, 等. 不同风障形式下桥梁断面行车风环境及颤振性能[J]. 哈尔滨工业大学学报, 2017, 49(3): 98. XIA Jinlin, LI Ke, GE Yaojun, et al. Crosswind environemnt and flutter performances of bridge deck with different wind barriers[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 98. |
| [18] |
赖锡军, 汪德爟, 傅源方. 非结构同位网格SIMPLE类算法收敛性能比较[J]. 空气动力学学报, 2004, 22(3): 289. LAI Xijun, WANG Deguan, FU Yuanfang. Convergence performance of SIMPLE-like algorithm on unstructured grids[J]. Acta Aerodynamic Sinica, 2004, 22(3): 289. DOI:10.3969/j.issn.0258-1825.2004.03.009 |
| [19] |
GOPALAN H, HEINZ S, STOLINGER M K. A unified RANS-LES model: computational development, accuracy and cost[J]. Journal of Computational Physics, 2013, 249: 249. DOI:10.1016/j.jcp.2013.03.066 |
| [20] |
RICHARDS P J, NORRIS S E. Appropriate boundary conditions for computational wind engineering models revisited[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 257. DOI:10.1016/j.jweia.2010.12.008 |
| [21] |
LATEB M, MASSON C, STATHOPOULOS T, et al. Comparison of various types of k-ε models for pollutant emissions around a two-building configuration[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 115: 9. DOI:10.1016/j.jweia.2013.01.001 |
| [22] |
TOMINAGA Y, STATHOPOULOS T. Numerical simulation of dispersion around an isolated cubic building: comparison of various types of k-ε models[J]. Atmospheric Environment, 2009, 43(20): 3200. DOI:10.1016/j.atmosenv.2009.03.038 |
| [23] |
BLOCKEN B, STATHOPOULOS T, SAATHOFF P, et al. Numerical evaluation of pollutant dispersion in the built environment: comparisons between models and experiments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1817. |
| [24] |
CHENG S Y, TSUBOKURA M, NAKASHIMA T, et al. A numerical analysis of transient flow past road vehicles subjected to pitching oscillation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(5): 511. DOI:10.1016/j.jweia.2011.02.001 |
| [25] |
FU Chen, UDDIN M, ROBINSON A C. Turbulence modeling effects on the CFD predictions of flow over a NASCAR Gen 6 racecar[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 176: 98. DOI:10.1016/j.jweia.2018.03.016 |
| [26] |
WILSON J D. Numerical studies of flow through a windbreak[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1985, 21(2): 119. DOI:10.1016/0167-6105(85)90001-7 |
| [27] |
周宇, 钱炜祺, 邓有奇, 等. k-ω SST两方程湍流模型中参数影响的初步分析[J]. 空气动力学学报, 2010, 28(2): 213. ZHOU Yu, QIAN Weiqi, DENG Youqi, et al. Introductory analysis of the influence of Menter's k-ω SST turbulence model's parameters[J]. Acta Aerodynamic Sinica, 2010, 28(2): 213. DOI:10.3969/j.issn.0258-1825.2010.02.015 |
| [28] |
BRADLEY E F, MULHEAARN P J. Development of velocity and shear stress distribution in the wake of a porous shelter fence[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 15(1): 145. |
| [29] |
何旭辉, 杜风宇, 冉瑞飞, 等. 侧风下挡风墙对CRH2列车-简支梁桥气动性能的影响[J]. 铁道科学与工程学报, 2013, 10(6): 1. HE Xuhui, DU Fengyu, RAN Ruifei, et al. Influence of wind-break wall on aerodynamic performance of CRH2 train-simply supported bridge under crosswind[J]. Journal of Railway Science and Engineering, 2013, 10(6): 1. DOI:10.3969/j.issn.1672-7029.2013.06.001 |
| [30] |
BENDJEBBAS H, EI-HADJ A A, ABBAS M. Numerical simulation of wind barrier openings effect on high wind speed flow around heliostats field[J]. Applied Mathematical Modelling, 2018, 61(3): 443. |
| [31] |
朱乐东, 周奇, 郭震山, 等. 箱形双幅桥气动干扰效应对颤振和涡振的影响[J]. 同济大学学报(自然科学版), 2010, 38(5): 12. ZHU Ledong, ZHOU Qi, GUO Zhenshan, et al. Aerodynamic interference effects on flutter and vortex-excited resonance of bridges with twin-separate parallel box decks[J]. Journal of Tongji University (Natural Science), 2010, 38(5): 12. |
| [32] |
LAIMA Shuijin, LI Hui. Effects of gap width on flow motions around twin-box girders and vortex-induced vibrations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 139: 37. DOI:10.1016/j.jweia.2015.01.009 |
 2022, Vol. 54
2022, Vol. 54


