2. 同济大学 交通运输工程学院,上海 201804
2. College of Transportation Engineering, Tongji University, Shanghai 201804, China
孔扩张理论早在1972年应用到岩土工程中[1],用于解决隧道开挖、静力触探[1]、旁压试验[2]、沉桩挤土、注浆扩孔等工程问题的应力分析。国内外学者从不同方面对其进行了研究,在屈服准则方面,文献[1, 3]基于M-C屈服准则,推导了圆孔扩张问题近似解析解;文献[4]分别将土体看作Tresca材料和M-C材料,给出了柱孔扩张过程中孔周土体应力和位移场计算公式;文献[5-6]等基于广义SMP破坏准则分析柱孔扩张问题的弹塑性应力解;文献[7]结合修正剑桥模型,将扩孔桩桩周土体分为流动破坏区、塑性变形区和弹性变形区,推导出应力、位移解析解;文献[8]采用了统一强度准则。在影响因素方面,大量成果多集中于剪胀[9]、应变软化[10]、结构性[11]、排水固结[12]、初始应力状态的各项异性[13]等因素的研究,但考虑地下水渗流对注浆扩孔方面影响的研究则较少。
已有研究表明,作为岩土工程重要的环境因素,地下水的存在对坝体、水工隧道、坡体稳定性等的影响很大[14-16],特别是富水岩土体中注浆或沉桩扩孔,地下水渗流作用对孔周土体应力场和位移场的影响不可忽视。文献[17]基于SMP准则,研究了考虑渗流作用下沉桩过程中桩端球孔扩张引起的土体力学响应,分析了渗流体积力对扩孔压力、塑性区半径的影响规律;文献[18]将渗流作用以超孔隙水压力的形式体现,给出了渗流影响球孔扩张问题的弹塑性应力解答;文献[19]仅考虑孔周有限范围内的渗流体积力的作用,并对渗流体积力作了大量假设,推导出同时考虑各向异性、渗流和剪胀影响的柱孔扩张问题统一解。以上皆是基于达西渗流定律开展的研究,其渗流规律是在特定水力条件下的实验结果,因此只在特定范围内适用,当描述岩土体处于高速或低速渗流状态时,其有效性备受质疑,此时通常选用非线性渗流定律更为合理。
此外,对于压密注浆机理的研究也大多基于小孔扩张理论。文献[20-21]考虑压滤效应对压密注浆的影响,给出了压密注浆球柱孔扩张应力和位移解;文献[22]建立盾构隧道壁后注浆压密模型,推导了压密注浆浆体扩张率、土体塑性扩张率及注浆对管片产生的压力,在研究中未充分考虑地下水渗流对计算结果的影响。鉴于此,本文对饱和软黏土地层压密注浆柱孔扩张问题进行理论分析,考虑非达西渗流和应变软化等影响因素,推导出孔周土体弹塑性区的应力场和位移场解析式,并分析渗流和应变软化特性对扩孔压力和塑性区半径的影响规律。
1 力学模型及基本理论 1.1 力学模型及基本假设考虑具有初始孔径为R0的圆柱形孔,在内压力Pa作用下不断扩张,当Pa较小时,孔周围土体处于弹性状态,当Pa达到某一量值时,孔周土体进入塑性区,产生塑性应变,形成软化区,随着扩孔压力Pa的不断增加,孔周土体出现流动状态,从孔中心由内向外依次形成流动区、软化区、弹性区3个区域,其中流动区和软化区统称为塑性区。R0为初始孔径,Ra为扩孔半径,Rf、Rp分别为流动区、软化区外半径,P0为初始扩孔应力,Pa为扩孔压力,Py为临塑扩张压力,uf、up分别为流动区与软化区、软化区与弹性区交界面处的径向位移,σr、σθ分别为孔周任意一点径向应力和切向应力。孔扩张理论计算模型如图 1所示。
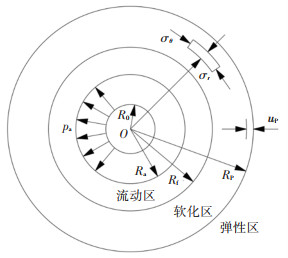
|
图 1 柱孔扩张理论计算模型 Fig. 1 Theoretical model for expansion of cylindrical cavity |
针对上述压密注浆柱孔扩张问题,作以下几点假设:1)土体为均质、各向同性的理想弹塑性材料;2)浆液、孔隙水和土颗粒都不可压缩;3)弹性区土体服从线弹性和小变形假定,应力和变形符合广义Hooke定律,在塑性区采用广义Tresca屈服准则描述应力和变形;4)孔周土体处于饱和状态,且在整个注浆过程中未发生劈裂注浆;5)忽略重力对渗流和土体压缩的影响,不考虑土体渗透率的变化。
1.2 土体特性模型根据常规三轴试验的结果,岩土材料的应力-应变关系曲线可用图 2的三折线应变软化模型来描述[10],其中,ε1、ε3为大、小主应变;εv为体积应变;ε1p、ε3p、εvp、ε1f、ε3f和εvf分别为软化区和流动区在局部坐标系中对应的塑性应变,以压或缩为正、拉或胀为负。图 2中,参数β、h和f的值可由三轴压缩试验测得,根据受力特征,本文按平面应变问题求解,σr、σθ分别对应图中的σ1、σ3,其他参数和符号对应关系类同[10]。
根据广义Tresca屈服准则,结合上述简化的土体应变软化模型,得到考虑应变软化特性的Tresca屈服准则为
| $ \sigma_{r}-\sigma_{\theta}=\sigma_{0}=\left\{\begin{array}{cc} 2 c_{0} & \text { (初始屈服点) } \\ 2 c_{0}-\lambda \cdot \varepsilon_{r}^{\mathrm{p}} & \text { (软化区) } \\ 2 \kappa \cdot c_{0} & \text { (流动区) } \end{array}\right. $ | (1) |
式中:c0为土体黏聚力;λ为软化区应力应变曲线斜率,
根据文献[23],对于具有应变软化和剪胀特性的岩土类材料,由试验得出的塑性应变增量的方向往往并不与屈服面正交,可采用非相关联流动法则,其塑性应变增量的方向完全取决于应力全量,而与应力增量无关。结合文中图 2中塑性区各应变增量分量间的关系,确定在软化阶段和流动阶段的流动法则分别为
| $ \frac{\mathrm{d} \varepsilon_{r}{ }^{\mathrm{p}}}{\mathrm{d} \varepsilon_{\theta}{ }^{\mathrm{p}}}=-\frac{1}{h} $ | (2) |
| $ \frac{\mathrm{d} \varepsilon_{r}{ }^{\mathrm{f}}}{\mathrm{d} \varepsilon_{\theta}{ }^{\mathrm{f}}}=-\frac{1}{f} $ | (3) |
式中:h、f分别为软化区和流动区的剪胀系数,当考虑土体剪胀特性时h = f > 1,否则h = f = 1[10]。
1.3 非线性渗流理论水在土体中流动时,将会引起水头的损失。而这种水头损失是由于水在土体孔隙中流动时,力图拖曳土粒而消耗能量的结果。自然,水流在拖曳土粒时将给予土粒以某种拖曳力,将渗透水流施于单位土体内土粒上的拖曳力称为渗流力[23]。忽略土体内水的自重的影响,本文采用Izbash非线性渗流公式[24],其数学表达形式为
| $ J=\frac{1}{k} v^{m}, m \neq 1 $ | (4) |
式中:J为水力梯度;v为渗流速度;k为渗透系数,可由试验测得;m为非线性渗流系数。
上式属于经验拟合公式,幂指数m为经验常数,与流体流态有关,而流体流态可通过雷诺数Re来确定[25]。一般地,m的取值小于2,当m=1时,该式为线性渗流达西定律,当m=2时,流体处于高速纯紊流流速状态[26],当m=0~1时,其适用于描述非达西低速非线性渗流情况,当m=1~2时,其适用于描述非达西高速非线性渗流情况[27]。
根据渗流力学理论,平面二维渗流场径向渗流连续方程为
| $ \frac{\partial v}{\partial r}+\frac{v}{r}=0 $ | (5) |
式中r为平面上任意一点到圆心的距离。
求解式(5),可得径向渗流速度为
| $ v=\frac{c_{1}}{r} $ | (6) |
式中c1为待定系数,由渗流边界条件确定。
联立式(4)和式(6),可得Izbash径向渗流水力坡度计算公式为
| $ J=\frac{1}{\gamma_{\mathrm{w}}} \frac{\partial P_{\mathrm{i}}}{\partial r}=\frac{1}{k}\left(\frac{c_{1}}{r}\right)^{m} $ | (7) |
式中γw为地下水容重,取10 kN·m-3。
对式(7)进行积分,边界条件分别取孔壁和无限远(即αRa,α一般取20~50即可)处的渗透水压力Pi|r=Ra=Pw、Pi|r=α·Ra=Pw0,求出在非线性渗流场作用下的渗透水压力为
| $ \begin{gathered} P_{\mathrm{i}}=\frac{\left[P_{\mathrm{w}}\left(\alpha \cdot R_{\mathrm{a}}\right){}^{1-m}-P_{\mathrm{w}_{0}} R_{\mathrm{a}}^{1-m}\right]-\Delta P_{\mathrm{w}} \cdot r^{1-m}}{\left(\alpha \cdot R_{\mathrm{a}}\right)^{1-m}-R_{\mathrm{a}}{ }^{1-m}}= \\ P_{\mathrm{w}_{0}}+\Delta P_{\mathrm{w}} \cdot \frac{\alpha^{1-m}-\left(\frac{r}{R_{\mathrm{a}}}\right)^{1-m}}{\alpha^{1-m}-1} \end{gathered} $ | (8) |
式中:Pw、Pw0分别为孔壁和无限远处渗透水压力; ΔPw为渗透水压力差,ΔPw=Pw-Pw0。
2 非线性渗流作用下的柱孔扩张土体应力场、位移场求解 2.1 基本方程柱孔扩张过程中,在考虑渗流体积力的作用下,距离孔中心为r的土体应力,满足平衡微分方程,即
| $ \frac{\partial \sigma_{r}}{\partial r}+\frac{\sigma_{r}-\sigma_{\theta}}{r}-\xi \frac{\partial P_{\mathrm{i}}}{\partial r}=0 $ | (9) |
式中ξ为孔隙水压力系数。
几何方程和本构方程分别为
| $ \left\{\begin{array}{l} {\varepsilon}_{r}=-\frac{\mathrm{d} u_{r}}{\mathrm{~d} r} \\ {\varepsilon}_{\theta}=-\frac{u_{r}}{r} \end{array}\right. $ | (10) |
| $ \left\{\begin{array}{l} \varepsilon_{r}^{\mathrm{e}}=\frac{1-\mu^{2}}{E}\left(\sigma_{r}-\frac{\mu}{1-\mu} \sigma_{\theta}\right) \\ \varepsilon_{\theta}^{\mathrm{e}}=\frac{1-\mu^{2}}{E}\left(\sigma_{\theta}-\frac{\mu}{1-\mu} \sigma_{r}\right) \end{array}\right. $ | (11) |
式中:εr、εθ、εre、εθe分别为总径向应变、总切向应变、弹性径向应变、弹性切向应变;ur为径向位移;E为土体弹性模量;μ为泊松比。
2.2 弹性区应力、位移解答(即r≥Rp)根据弹性力学三大方程的关系,联立式(9)~(11),整理后得
| $ \frac{\mathrm{d}^{2} \sigma_{r}}{\mathrm{~d} r^{2}}+\frac{3}{r} \frac{\mathrm{d} \sigma_{r}}{\mathrm{~d} r}=A \cdot r^{-m-1} \cdot\left(\frac{\mu}{1-\mu}+2-m\right) $ | (12) |
其中
解式(12)可得,径向应力表达式为
| $ \sigma_{r}=\frac{c_{2}}{r^{2}}+c_{3}+\frac{\frac{1}{1-\mu}+1-m}{(m-1)(m-3)} \cdot A \cdot r^{1-m} $ | (13) |
式中c2、c3为待定系数,可进一步结合边界条件σr|r=Rp =py,σr|r→∞=p0求得。
由此可知,弹性区应力场和位移场表达式分别为
| $ \left\{\begin{array}{l} \sigma_{r}=p_{\mathrm{y}} \cdot \frac{R_{\mathrm{p}}{}^{2}}{r^{2}}+p_{0} \cdot\left(1-\frac{R_{\mathrm{p}}{}^{2}}{r^{2}}\right)+N \cdot A \cdot r^{1-m} \\ \sigma_{\theta}=-p_{\mathrm{y}} \cdot \frac{R_{\mathrm{p}}{}^{2}}{r^{2}}+p_{0} \cdot\left(1+\frac{R_{\mathrm{p}}{}^{2}}{r^{2}}\right)-A \cdot r^{1-m} \cdot(M+N) \end{array}\right. $ | (14) |
| $ \begin{aligned} u_{r}=& \frac{1+\mu}{E}\left[\left(p_{\mathrm{y}}-p_{0}\right) \cdot \frac{R_{\mathrm{p}}{}^{2}}{r}-p_{0} \cdot r \cdot(1-2 \mu)+\right.\\ &\left.A \cdot r^{2-m} \cdot\left(N+\frac{1}{m-1}\right)\right] \end{aligned} $ | (15) |
式中:
| $ N=\frac{\frac{1}{1-\mu}+1-m}{(m-1)(m-3)} \cdot\left(1-\frac{R_{\mathrm{p}}{}^{3-m}}{r^{3-m}}\right)。$ |
在r=Rp处,结合式(1)中的屈服条件σr-σθ=2c0和式(14),可得弹塑性交界面处的临塑扩张压力py为
| $ p_{\mathrm{y}}=\left.\sigma_{r}\right|_{r=R_{\mathrm{p}}{}^+}=c_{0}+p_{0}-\frac{1}{2} \cdot B $ | (16) |
其中
根据式(15),令r=Rp,得弹性区与软化区交界面处的径向位移up为
| $ \begin{aligned} &\ \ \ \ u_{\mathrm{p}}=\left.u_{r}\right|_{r=R_{\mathrm{p}}{ }^{+}}= \\ &\frac{R_{\mathrm{p}} \cdot(1+\mu)}{E}\left[c_{0}-p_{0} \cdot(1-2 \mu)+\frac{1-2 \mu}{2} \cdot B\right] \end{aligned} $ | (17) |
在弹性区与软化区交界面处(即r=Rp),径向应力和径向位移满足连续性条件:
| $ \left.\sigma_{r}\right|_{r=R_{\mathrm{p}}{}^{+}}=\left.\sigma_{r}\right|_{r=R_{\mathrm{p}}{}^{-}} $ | (18) |
| $ \left.u_{r}\right|_{r=R_{\mathrm{p}}{}^+}=\left.u_{r}\right|_{r=R_{\mathrm{p}}{ }^{-}} $ | (19) |
该区内的总应变可表示为
| $ \left\{\begin{array}{l} \varepsilon_{r}=\left.\varepsilon_{r}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{ }^-}+\varepsilon_{r}{ }^{\mathrm{p}} \\ {\varepsilon}_{\theta}=\left.\varepsilon_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{ }^-}+\varepsilon_{\theta}{ }^{\mathrm{p}} \end{array}\right. $ | (20) |
由式(2)和式(20)可得
| $ h \cdot \varepsilon_{r}+\varepsilon_{\theta}=\left.h \cdot \varepsilon_{r}{}^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{}^-}+\left.\varepsilon_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{}^-} $ | (21) |
根据式(10)、(15)和式(19),在r = Rp处有
| $ \left.\varepsilon_{r}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{}^-}=\frac{1+\mu}{E}\left[c_{0}+p_{0} \cdot(1-2 \mu)+\frac{2 \mu-1}{2} \cdot B\right] $ | (22) |
| $ \left.\varepsilon_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}{}^-}=\frac{1+\mu}{E}\left[-c_{0}+p_{0} \cdot(1-2 \mu)+\frac{2 \mu-1}{2} \cdot B\right] $ | (23) |
软化区总体变形不考虑弹性变形增量,即在软化区,弹性变形保持不变,且为弹塑性交界面处的弹性变形。将式(10)、(22)、(23)代入到式(21)中,整理得
| $ h \cdot \frac{\mathrm{d} u_{r}}{\mathrm{~d} r}+\frac{u_{r}}{r}=G_{1} \cdot(1+h) $ | (24) |
其中
| $ G_{1}=\frac{1+\mu}{E} \cdot\left[\frac{1-h}{1+h} \cdot c_{0}-p_{0} \cdot(1-2 \mu)+\frac{1-2 \mu}{2} \cdot B\right] $ |
对式(24)求解,可得
| $ u_{r}=c_{4} \cdot r^{-\frac{1}{h}}+G_{1} \cdot r $ | (25) |
其中c4为待定系数,可结合式(17)、(19)求得,由此可得软化区径向位移表达式为
| $ u_{r}=h \cdot G_{2} \cdot R_{\mathrm{p}} \cdot\left(\frac{R_{\mathrm{p}}}{r}\right)^{\frac{1}{h}}+G_{1} \cdot r $ | (26) |
其中
将式(26)对r求导并取负数,得到软化区径向应变εr、弹性区与软化区交界面处径向应变ε1e表达式分别为
| $ \varepsilon_{r}=G_{2} \cdot\left(\frac{R_{\mathrm{p}}}{r}\right)^{\frac{1}{h}+1}-G_{1} $ | (27) |
| $ \varepsilon_{1}^{\mathrm{e}}=\left.\varepsilon_{r}\right|_{r=R_{\mathrm{p}}{}^-}=G_{2}-G_{1} $ | (28) |
根据关系式β·ε1e= εr|r=Rf+可得,软化区半径与流动区半径之比:
| $ \eta_{1}=\frac{R_{\mathrm{p}}}{R_{\mathrm{f}}}=\left[\beta+\frac{G_{1} \cdot(1-\beta)}{G_{2}}\right]^{\frac{h}{1+h}} $ | (29) |
令r = Rf,根据式(26)可得软化区与流动区交界面处的径向位移uf为
| $ u_{\mathrm{f}}=\left.u_{r}\right|_{r=R_{\mathrm{f}}{}^+}=G_{3} \cdot R_{\mathrm{f}} $ | (30) |
其中G3=G1·(1+h)-β·h·(G1-G2)。
联立式(1)、(9)和式(10),可得该区应力和应变的关系式为
| $ \frac{\mathrm{d} \sigma_{r}}{\mathrm{~d} r}-\frac{2 c_{0}-\lambda \cdot\left(\varepsilon_{r}-\varepsilon_{1}\right)}{r}=A \cdot r^{-m} $ | (31) |
将式(27)和式(28)代入式(31),求解可得
| $ \begin{aligned} \sigma_{r}=& \frac{h \cdot \lambda \cdot G_{2}}{1+h} \cdot\left(\frac{R_{\mathrm{p}}}{r}\right)^{\frac{1}{h}+1}+\frac{A}{1-m} \cdot r^{1-m}+\\ &\left(2 c_{0}+\lambda \cdot G_{2}\right) \cdot \ln r+c_{5} \end{aligned} $ | (32) |
其中c5为待定系数,结合式(16)、(18)求得软化区径向应力表达式为
| $ \begin{aligned} \sigma_{r}=& \frac{h \cdot \lambda \cdot G_{2}}{1+h} \cdot\left[\left(\frac{R_{\mathrm{p}}}{r}\right)^{\frac{1}{h}+1}-1\right]+\frac{A \cdot r^{1-m}}{1-m} \cdot \\ & {\left[1-\left(\frac{R_{\mathrm{p}}}{r}\right)^{1-m}\right]-\left(2 c_{0}+\lambda \cdot G_{2}\right) \cdot \ln \frac{R_{\mathrm{p}}}{r}+} \\ & c_{0}+p_{0}-\frac{1}{2} B \end{aligned} $ | (33) |
在软化区与流动区交界面处(即r=Rf),径向应力和径向位移满足连续性条件:
| $ \left.\sigma_{r}\right|_{r=R_{\mathrm{f}}{ }^{+}}=\left.\sigma_{r}\right|_{r=R_{\mathrm{f}}{ }^{-}} $ | (34) |
| $ \left.u_{r}\right|_{r=R_{\mathrm{f}}{ }^{+}}=\left.u_{r}\right|_{r=R_{\mathrm{f}}{ }^{-}} $ | (35) |
该区内的总应变可表示为
| $ \left\{\begin{array}{l} \varepsilon_{r}=\left.\varepsilon_{r}{}^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{ }^{-}}+\varepsilon_{r}{ }^{\mathrm{p}} \\ \varepsilon_{\theta}=\left.\varepsilon_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{ }^{-}}+\varepsilon_{\theta}{ }^{\mathrm{p}} \end{array}\right. $ | (36) |
结合式(3)和式(36)可得
| $ f \cdot \varepsilon_{r}+\varepsilon_{\theta}=\left.f \cdot \varepsilon_{r}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{ }^{-}}+\left.\varepsilon_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{ }^{-}} $ | (37) |
假设在流动区内径向弹性应变和切向弹性应变都为0,即
| $ \left.\boldsymbol{\varepsilon}_{r}{}^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{}^-}=\left.\boldsymbol{\varepsilon}_{\theta}{ }^{\mathrm{e}}\right|_{r=R_{\mathrm{f}}{}^-}=0 $ | (38) |
将式(10)、(38)代入式(37)中,整理得
| $ f \cdot \frac{\mathrm{d} u_{r}}{\mathrm{~d} r}+\frac{u_{r}}{r}=0 $ | (39) |
对式(39)求解,可得
| $ u_{r}=c_{6} \cdot r^{-\frac{1}{f}} $ | (40) |
其中c6为待定系数,可结合式(30)、(35)求得,由此得到流动区径向位移表达式为
| $ u_{r}=G_{3} \cdot R_{\mathrm{f}} \cdot\left(\frac{R_{\mathrm{f}}}{r}\right)^{\frac{1}{f}} $ | (41) |
联立式(1)和式(9)得流动区平衡方程为
| $ \frac{\mathrm{d} \sigma_{r}}{\mathrm{~d} r}+\frac{2 \kappa \cdot c_{0}}{r}=A \cdot r^{-m} $ | (42) |
对式(42)求解,可得
| $ \sigma_{r}=\frac{A}{1-m} \cdot r^{1-m}-2 \kappa \cdot c_{0} \cdot \ln r+c_{7} $ | (43) |
其中c7为待定系数,结合应力边界条件σr|r=Ra=pa,可得流动区径向应力表达式为
| $ \sigma_{r}=\frac{A \cdot r^{1-m}}{1-m}\left[1-\left(\frac{R_{\mathrm{a}}}{r}\right)^{1-m}\right]+2 \kappa \cdot c_{0} \cdot \ln \frac{R_{\mathrm{a}}}{r}+p_{\mathrm{a}} $ | (44) |
根据在扩孔前后土体体积保持不变的原则,孔扩张的体积等于弹性区、软化区和流动区体积变化量之和[4, 10],即
| $ {\rm{ \mathsf{ π} }} R_{\mathrm{a}}^{2}-{\rm{ \mathsf{ π} }} R_{0}^{2}={\rm{ \mathsf{ π} }}\left[R_{\mathrm{p}}^{2}-\left(R_{\mathrm{p}}-u_{\mathrm{p}}\right)^{2}\right]+\varDelta_{1}+\varDelta_{2} $ | (45) |
式中Δ1、Δ2分别表示软化区和流动区体积变化量,略去up的高阶次幂,上式可简化为
| $ {\rm{ \mathsf{ π} }} R_{\mathrm{a}}^{2}-{\rm{ \mathsf{ π} }} R_{0}^{2}=2 {\rm{ \mathsf{ π} }} \cdot R_{\mathrm{p}} \cdot u_{\mathrm{p}}+\varDelta_{1}+\varDelta_{2} $ | (46) |
一般地,上式中的塑性区平均体积应变量为已知量,与实际情况存在差别,根据其表达式Δ1=
| $ \begin{gathered} \varDelta_{1}=-2 {\rm{ \mathsf{ π} }} \cdot R_{\mathrm{p}}{ }^{2} \cdot\left(G_{1}+h \cdot G_{2}\right)+ \\ 2 {\rm{ \mathsf{ π} }} \cdot R_{\mathrm{f}}{}^{2}\left[G_{1}+h \cdot G_{2} \cdot\left(\frac{R_{\mathrm{p}}}{R_{\mathrm{f}}}\right)^{\frac{1}{h}+1}\right] \end{gathered} $ | (47) |
| $ \varDelta_{2}=-2 {\rm{ \mathsf{ π} }} \cdot G_{3} \cdot\left[R_{\mathrm{f}}{}^{2}-R_{\mathrm{a}}{}^{2} \cdot\left(\frac{R_{\mathrm{f}}}{R_{\mathrm{a}}}\right)^{\frac{1}{h}+1}\right] $ | (48) |
将式(47)、(48)代入式(46)中,化简可得
| $ \frac{R_{\mathrm{f}}}{R_{\mathrm{a}}}=\left[\frac{1-\left(\frac{R_{0}}{R_{\mathrm{a}}}\right)^{2}}{2 G_{3}}\right]^{\frac{h}{1+h}} $ | (49) |
| $ \eta_{2}=\frac{R_{\mathrm{p}}}{R_{\mathrm{a}}}=\eta_{1} \cdot\left[\frac{1-\left(\frac{R_{0}}{R_{\mathrm{a}}}\right)^{2}}{2 G_{3}}\right]^{\frac{h}{1+h}} $ | (50) |
联立式(29)、(33)、(34)、(44)和式(50),并令r = Rf,化简可得扩孔压力Pa为
| $ \begin{aligned} p_{\mathrm{a}}=& c_{0} \cdot\left(\frac{1+3 h-2 \kappa \cdot h}{1+h}-2 \ln \eta_{1}-\frac{2 \kappa \cdot h}{1+h} \cdot\right.\\ &\left.\ln \frac{2 G_{3}}{1-\left(R_{0} / R_{\mathrm{a}}\right)^{2}}\right)-\lambda \cdot G_{2} \ln \eta_{1}+\xi \cdot \frac{\Delta P_{\mathrm{w}}}{1-\alpha^{1-m}} \cdot\\ & {\left[1-\frac{1-2 \mu}{2(1-\mu)} \cdot \eta_{2}{}^{1-m}\right]+p_{0} } \end{aligned} $ | (51) |
令Ra = Rf,此时η1 = η2,代入式(51)中,可得临界扩孔压力Py1为
| $ \begin{gathered} p_{\mathrm{y}_{1}}=c_{0} \cdot\left(\frac{1+3 h-2 \kappa \cdot h}{1+h}-2 \ln \eta_{1}\right)-\lambda \cdot G_{2} \ln \eta_{1}+ \\ \xi \cdot \frac{\Delta P_{\mathrm{w}}}{1-\alpha^{1-m}} \cdot\left[1-\frac{1-2 \mu}{2(1-\mu)} \cdot \eta_{1}{ }^{1-m}\right]+p_{0} \end{gathered} $ | (52) |
当Pa = Py1时,孔壁处刚好进入流动区,当扩孔压力Pa继续增大,即Pa > Py1时,以上解答皆适用。
文中通过扩孔压力条件确定交界面位置,具体过程:由式(51)可以看出,扩孔压力Pa与扩孔半径Ra之间存在一一对应的关系,当给定扩孔压力Pa,在实际工程中可通过注浆压力计算求得,即可得到扩孔半径Ra,之后通过式(49)、(50)分别确定流动区、软化区与弹性区之间相邻两区交界面位置。
以上是考虑非达西渗流和应变软化的Tresca材料柱孔扩张时的全部解析解。
3 算例验证为进一步说明柱孔扩张过程中土体受到非线性渗流作用的影响,将由式(51)得到的柱孔扩张扩孔压力解答,与文献[28]给出的扩孔压力计算结果进行对比分析。文献中采用的基本参数如下:初始半径R0 =1 m,扩孔半径Ra=2 m,初始土压力P0=150 kPa,土体弹模E=24×103 kPa,泊松比μ=0.3,黏聚力c0=20 kPa,文献未考虑土体应变软化和胀缩性,因此分别取κ=1、β=1.55,孔隙水压力系数ξ=1。根据本文所提供的理论计算公式,当m分别取1.0、1.2、1.4、1.6、1.8时,求得孔周注浆扩孔压力依次为344.66、338.51、336.86、336.26、336.03 kPa,而文献[28]给出的扩孔压力为286.9 kPa。
通过对比不难发现,在不考虑地下水渗流作用时的孔扩张所需压力值相较于有地下水影响下的扩孔压力值偏低,两者的差值与孔壁处的渗透水压力基本相当,说明地下水的存在对扩孔过程起到一定的抑制作用,且扩孔压力值随着非线性渗流系数的增加略有降低,从而验证了本文理论解答的正确性。
通过以上扩孔压力值的比较也充分说明,在解决饱和软黏土地层压密注浆扩孔实际工程问题时,地下水渗流的影响不容小觑,特别是要结合实际工程环境,选择较为合理的渗流模式,尽可能地使计算结果更加符合实际,为工程设计提供合理的理论依据。
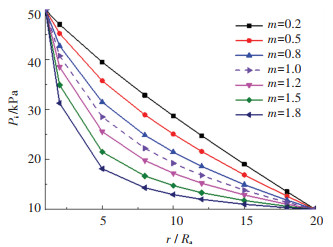
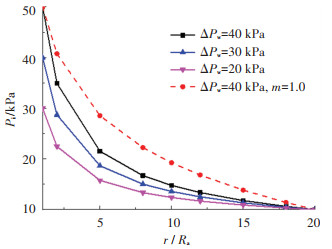
4 非线性渗流影响作用分析 4.1 非达西渗流对孔周土体渗流场的影响图 3、4分别为不同非线性渗流系数m和渗透水压力差ΔPw取值下,孔周土体渗透水压力沿半径方向变化曲线,m分别取0.2、0.5、0.8、1.2、1.5、1.8,渗透水压力差ΔPw分别取20、30、40 kPa,并与m=1.0时(即Darcy渗流,下同)进行对比分析。其中α=20,Pw0=10 kPa,初始半径R0=0.05 m,扩孔半径Ra=0.1 m,黏聚力c0=40 kPa,κ=0.25,其他参数取值与前文相同。
|
图 3 不同m取值时渗透水压力沿孔径分布情况(ΔPw=40 kPa) Fig. 3 Distribution of seepage water pressure along cavity radius with different m values (ΔPw=40 kPa) |
|
图 4 不同ΔPw下渗透水压力沿孔径分布情况(m=1.5) Fig. 4 Distribution of seepage water pressure along cavity radius with different ΔPw values (m=1.5) |
从图 3、4中可以看出,渗透水压力总体上沿径向呈不断减小的趋势,这与注浆扩孔过程中土体内部超孔隙水压力随着距离的增加不断消散的情况相符,衰减速度先增大后减小,并趋于稳定。非线性渗流系数m越大,渗透水压力差ΔPw越大,其非线性变化程度越明显,渗透水压力衰减速度也越快,但随着距离孔中心位置的增大,衰减速度逐渐放缓。与达西渗流相比,高速非线性渗流状态下的渗透水压力沿程压降较为明显,而低速非线性渗流状态下的渗流水压力沿程压降较小。从以上分析可以看出,非达西渗流具有惯性效应,且渗透性越好、渗透水压力差越大,非达西惯性效应也越明显。
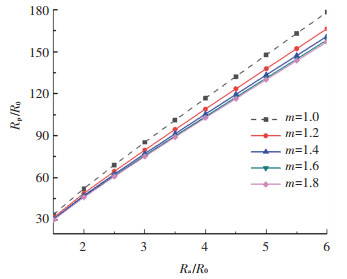
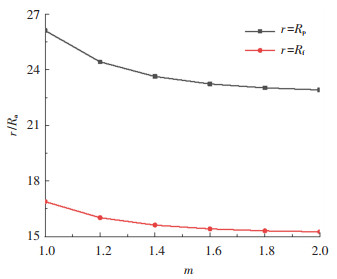
4.2 非达西渗流对塑性区半径的影响图 5、6分别给出了不同非线性渗流系数m取值下,塑性区半径随扩孔半径的变化曲线及非线性渗流系数对塑性区半径的影响曲线。令m分别取1.2、1.4、1.6、1.8,并与m=1.0时进行对比分析。其中α→∞、ΔPw=40 kPa,其他参数取值与前文相同。
|
图 5 扩孔半径对塑性区半径的影响曲线 Fig. 5 Influence of cavity radius on radius of plastic zone |
|
图 6 非线性渗流系数m对塑性区半径的影响 Fig. 6 Influence of nonlinear seepage coefficient m on radius of plastic zone |
结合图 5、6可见,塑性区半径随扩孔半径的增大而增大,总体上呈现线性增长的趋势,两者的比值基本上为一定值,且随着m值不断增大,其线性增长率逐渐减小。流动区半径与扩孔半径的比值大致在15~17之间,软化区半径与扩孔半径的比值大致在22~27之间,且m值越大,其比值也越小,并逐渐趋近于一定值,呈现出明显的非线性减小的特点。相较于达西渗流模式,非达西渗流状态下的塑性区半径与扩孔半径比值略小。由此可以看出,高速非线性渗流对土体扩孔有一定的抑制作用,但效果不明显。
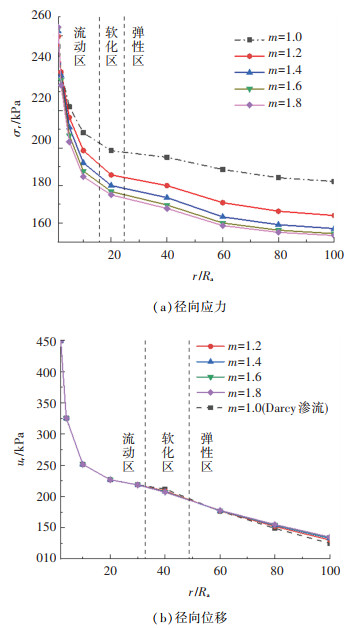
4.3 非达西渗流对孔周应力场和位移场的影响算例中给出扩孔半径Ra=0.5 m,渗透水压力差ΔPw=40 kPa,其余参数取值与前文相同。令m分别为1.2、1.4、1.6、1.8,并与m=1.0时进行对比分析,研究孔周土体径向应力和径向位移沿径向变化规律。图 7给出了非线性渗流系数m取不同值时,孔周土体径向应力和径向位移沿径向分布情况。
|
图 7 孔周土体径向应力和径向位移沿径向的分布情况 Fig. 7 Distribution of radial stress and radial displacement of soil around cavity along radial direction |
由图 7可知,孔壁处径向应力(即扩孔压力)在250~270 kPa之间,孔周土体内部径向应力随远离孔中心的方向先迅速衰减后趋于平缓,并最终趋近于定值,且m值越小,该值越大。从图中可以看出,在距离孔中心10 m的位置,m=1.8时的径向应力为175.01 kPa,比达西渗流状态下的径向应力降低了20.57 kPa,由此可知,径向应力受非线性渗流系数m的影响较为明显。从图中不难看出,孔周土体内的径向位移变化规律与径向应力的变化规律一致,与注浆位置的距离越大,径向位移越小。孔壁处产生的位移最大,为450 mm左右,这也与实际扩孔半径相同,但其受非线性渗流系数m的影响较小,几乎不受影响,其解释为前文中假设土体为不可压缩且处于饱和状态,其孔壁处径向位移为一定值,只会随着扩孔半径的增大而增大,与处于何种渗流模式无关。
需要说明的是,从图 6中不难看出,流动区、软化区半径随非线性渗流系数m的不同而有所不同,而非定值,图中所示的用于划分弹塑性区的分区线只是取了大致位置,方便读者理解,不具有实际意义。
5 结论1) 在考虑地下水非线性渗流的情况下,基于Tresca屈服准则,推导饱和软黏土地层压密注浆柱孔扩张过程中孔周土体应力场、位移场解析解,并给出扩孔压力和塑性区半径的表达式。
2) 在分析孔周土体渗流场变化时,考虑非达西渗流与渗透水压力差的影响下,孔周土体渗流场沿径向都变现出明显的衰减现象,且随非线性渗流系数m与渗透水压力差ΔPw的增大衰减现象越明显。
3) 通过分析发现,在饱和软黏土地层中进行压密注浆过程中,非线性渗流系数m对孔周土体应力场、位移场和塑性区半径都产生了不同程度的影响,其影响作用不容忽略。当均质土体处于饱和状态且保证土颗粒、孔隙水都不可压缩时,在地下水高速非线性渗流(即1<m<2)和达西线性渗流(即m=1)两种模式下的压密注浆柱孔扩张孔周土体径向应力分布有所不同,m越大,径向应力越小,塑性区半径越大,径向位移基本无差别,因此在以后针对此类柱孔扩张问题进行理论分析时应考虑因渗流状态的不同而造成的不同结果。
| [1] |
VESIC A S. Expansion of cavities in infinite soil mass[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(3): 265. DOI:10.1061/JSFEAQ.0001740 |
| [2] |
CAO L F, TEH C I, CHANG M F. Undrained cavity expansion in modified Cam clay I: theoretical analysis[J]. Géotechnique, 2001, 51(4): 323. DOI:10.1680/geot.2001.51.4.323 |
| [3] |
CARTER J P, BOOKER J R, YEUNG S K. Cavity expansion in cohesive frictional soils[J]. Geotechnique, 1986, 36(3): 349. DOI:10.1680/geot.1986.36.3.349 |
| [4] |
蒋明镜, 沈珠江. 考虑材料应变软化的柱形孔扩张问题[J]. 岩土工程学报, 1995, 17(4): 10. JIANG Mingjing, SHEN Zhujiang. Expansion of cylindrical cavity of materials with strain-softening behaviour[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(4): 10. DOI:10.3321/j.issn:1000-4548.1995.04.003 |
| [5] |
李波, 栾茂田. 基于SMP破坏准则的柱形孔扩张问题理论分析[J]. 大连理工大学学报, 2006, 46(2): 246. LI Bo, LUAN Maotian. Theoretical analysis of expansion of cylindrical cavity based on SMP criterion[J]. Journal of Dalian University of Technology, 2006, 46(2): 246. DOI:10.3321/j.issn:1000-8608.2006.02.018 |
| [6] |
郝冬雪, 栾茂田, 陈榕, 等. 基于广义SMP准则的线性软化柱形孔扩张分析[J]. 大连理工大学学报, 2010, 50(1): 103. HAO Dongxue, LUAN Maotian, CHEN Rong, et al. Analysis of cylindrical expansion withlinear softening behavior based on extended SMP criterion[J]. Journal of Dalian University of Technology, 2010, 50(1): 103. |
| [7] |
宋勇军, 胡伟, 王德胜, 等. 基于修正剑桥模型的挤密桩挤土效应分析[J]. 岩土力学, 2011, 32(3): 811. SONG Yongjun, HU Wei, WANG Desheng, et al. Analysis of squeezing effect of compaction piles based on modified Cam-clay model[J]. Rock and Soil Mechanics, 2011, 32(3): 811. DOI:10.3969/j.issn.1000-7598.2011.03.028 |
| [8] |
邹金锋, 吴亚中, 李亮, 等. 考虑大变形和排水条件时柱孔扩张问题统一解析[J]. 工程力学, 2010, 27(6): 1. ZOU Jinfeng, WU Yazhong, LI Liang, et al. Unified elastic plastic solution for cylindrical cavity expansion considering large strain and drainage condition[J]. Engineering Mechanics, 2010, 27(6): 1. |
| [9] |
李林, 李镜培, 孙德安, 等. 剪胀性砂土中球孔扩张弹塑性解[J]. 岩土工程学报, 2017, 39(8): 1453. LI Lin, LI Jingpei, SUN Dean, et al. Elastoplastic solution to expansion of a spherical cavity in dilatant sand[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(8): 1453. |
| [10] |
梁发云, 陈龙珠. 应变软化Tresca材料中扩孔问题解答及其应用[J]. 岩土力学, 2004, 25(2): 261. LIANG Fayun, CHEN Longzhu. Analytical solution to cavity expansion in strain-softening soils with Tresca yield criterion and its applications[J]. Rock and Soil Mechanics, 2004, 25(2): 261. DOI:10.3969/j.issn.1000-7598.2004.02.020 |
| [11] |
李镜培, 周攀, 李亮, 等. 饱和结构性黄土不排水柱孔扩张问题弹塑性解[J]. 同济大学学报(自然科学版), 2021, 49(2): 163. LI Jingpei, ZHOU Pan, LI Liang, et al. Elastic-plasticsolution for undrained expansion of cylindrical cavity in saturated structured loess[J]. Journal of Tongji University (Natural Science), 2021, 49(2): 163. |
| [12] |
李林, 李镜培, 龚卫兵, 等. K0固结天然饱和黏土中柱孔扩张弹塑性解[J]. 哈尔滨工业大学学报, 2017, 49(6): 90. LI Lin, LI Jingpei, GONG Weibing, et al. Elasto-plastic solution to expansion of a cylindrical cavity in K0-consolidated natural saturated clay[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 90. |
| [13] |
章定文, 刘松玉, 顾沉颖. 各向异性初始应力状态下圆柱孔扩张理论弹塑性分析[J]. 岩土力学, 2009, 30(6): 1631. ZHANG Dingwen, LIU Songyu, GU Chenying. Elastoplastic analysis of cylindrical cavity expansion with anisotropic initial stress[J]. Rock and Soil Mechanics, 2009, 30(6): 1631. DOI:10.3969/j.issn.1000-7598.2009.06.017 |
| [14] |
周建, 蔡键, 杨帆, 等. 注浆、衬砌作用下非线性渗流隧洞弹塑性解[J]. 哈尔滨工业大学学报, 2021, 53(3): 58. ZHOU Jian, CAI Jian, YANG Fan, et al. Elastoplastic solution of tunnel with non-linear seepage under grouting and lining support[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 58. |
| [15] |
刘忠玉, 徐传永, 朱新牧, 等. 考虑非Darcy渗流的砂井地基弹黏塑性固结分析[J]. 哈尔滨工业大学学报, 2021, 53(5): 113. LIU Zhongyu, XU Chuanyong, ZHU Xinmu, et al. Elasto-viscoplastic consolidation analysis of ground with sand drains considering non-Darcian flow[J]. Journal of HarbinInstitute of Technology, 2021, 53(5): 113. |
| [16] |
卢玉林, 陈晓冉. 地下水渗流作用下土坡稳定性的简化Bishop法解[J]. 应用力学学报, 2018, 35(3): 524. LU Yulin, CHEN Xiaoran. Solution for stability of soil slopes subjected to seepage of groundwater via simplified Bishop Method[J]. Chinese Journal of Applied Mechanics, 2018, 35(3): 524. |
| [17] |
李雨浓, 李伟. 考虑渗流影响的球孔扩张理论解答[J]. 应用力学学报, 2020, 37(5): 1980. LI Yunong, LI Wei. An analytical solution for spherical cavity expansion considering the influence of seepage[J]. Chinese Journal of Applied Mechanics, 2020, 37(5): 1980. |
| [18] |
梅毕祥, 杨敏, 贾尚华. 基于摩尔库伦准则考虑渗流影响的孔扩张理论[J]. 同济大学学报(自然科学版), 2017, 45(3): 309. MEI Bixiang, YANG Min, JIA Shanghua. Mohr-Coulomb criterion-based theoretical solutions of spherical cavity expansion considering seepage[J]. Journal of Tongji University (Natural Science), 2017, 45(3): 309. |
| [19] |
饶平平, 李镜培, 张常光. 考虑各向异性、剪胀和渗流的柱孔扩张问题统一解[J]. 岩土力学, 2010, 31(增刊2): 79. RAO Pingping, LI Jingpei, ZHANG Changguang. Unified solutions of cylindrical cavity expansion considering anisotropy, shear dilation and seepage[J]. Rock and Soil Mechanics, 2010, 31(S2): 79. |
| [20] |
张忠苗, 邹健, 何景愈, 等. 考虑压滤效应下饱和黏土压密注浆柱扩张理论[J]. 浙江大学学报(工学版), 2011, 45(11): 1980. ZHANG Zhongmiao, ZOU Jian, HE Jingyu, et al. Cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(11): 1980. DOI:10.3785/j.issn.1008-973X.2011.11.015 |
| [21] |
邹健, 张忠苗. 考虑压滤效应饱和黏土压密注浆球孔扩张理论[J]. 哈尔滨工业大学学报, 2011, 43(12): 119. ZOU Jian, ZHANG Zhongmiao. Spherical cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Harbin Institute of Technology, 2011, 43(12): 119. |
| [22] |
叶飞, 陈治, 苟长飞, 等. 基于球孔扩张的盾构隧道壁后注浆压密模型[J]. 交通运输工程学报, 2014, 14(1): 35. YE Fei, CHEN Zhi, GOU Changfei, et al. Back-filled grouting compaction model of shield tunnel based on spherical cavity expansion[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 35. DOI:10.3969/j.issn.1671-1637.2014.01.007 |
| [23] |
殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007. YIN Zongze. Geotechnical principles[M]. Beijing: China Water & Power Press, 2007. |
| [24] |
张丙强, 王启云, 臧万军. 非达西渗流效应对深埋圆形隧洞弹塑性解的影响[J]. 铁道学报, 2018, 40(8): 139. ZHANG Bingqiang, WANG Qiyun, ZANG Wanjun. Influence of non-Darcy seepage effect on elastoplastic solution of a deep-buried circular opening[J]. Journal of the China Railway Society, 2018, 40(8): 139. DOI:10.3969/j.issn.1001-8360.2018.08.018 |
| [25] |
孟如真, 胡少华, 陈益峰, 等. 高渗压条件下基于非达西流的裂隙岩体渗透特性研究[J]. 岩石力学与工程学报, 2014, 33(9): 1756. MENG Ruzhen, HU Shaohua, CHEN Yifeng, et al. Permeability of non-Darcian flow in fractured rock mass under high seepage pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1756. |
| [26] |
XIAO Liang, YE Ming, XU Yongxin, et al. A simplified solution using Izbash's equation for non-Darcian flow in a constant rate pumping test[J]. Groundwater, 2019, 57(6): 962. DOI:10.1111/gwat.12886 |
| [27] |
和晓楠, 周晓敏, 郭小红, 等. 深埋隧道注浆加固围岩非达西渗流场及应力场解析[J]. 中国公路学报, 2020, 33(12): 200. HE Xiaonan, ZHOU Xiaomin, GUO Xiaohong, et al. Analysis of non-Darcy seepage field and stress field of surrounding rock strengthened by grouting in deep buried tunnel[J]. China Journal of Highway and Transport, 2020, 33(12): 200. DOI:10.3969/j.issn.1001-7372.2020.12.016 |
| [28] |
李雨浓, 李伟. 球(柱)孔扩张问题的扩孔压力与扩孔半径分析[J]. 应用力学学报, 2020, 37(1): 142. LI Yunong, LI Wei. Theoretical analysis of expanded radius and internal expanding pressure of the spherical (cylindrical) cavity expansion[J]. Chinese Journal of Applied Mechanics, 2020, 37(1): 142. |
 2022, Vol. 54
2022, Vol. 54



