科学合理的公交时刻表有利于提高公交系统运营效率、增加公交出行吸引力。针对公交时刻表优化问题,国内外学者进行了大量研究,目前研究主要集中在单线路调度和区域调度两方面。单线路调度方面,文献[1-2]主要以乘客出行时间和公交企业运营成本最小为优化目标,对发车频率进行优化;文献[3]提出了“满意度的概念”,对乘客候车时间、车厢拥挤程度及公交企业利润之间的量纲进行了统一,建立了发车间隔优化模型,并采用一维搜索法进行求解;文献[4-5]采用遗传算法对公交调度优化问题进行了求解。区域调度方面,公交协同换乘研究引起了很多学者的关注,主要以乘客同步换乘概率最大或乘客换乘候车时间最小为优化目标,构建优化模型,文献[6]首次提出了同步换乘的概念,文献[7]在文献[6]基础上以车辆驻站时间和发车间隔为优化变量,车辆在换乘站点相遇次数最大为优化目标建立了优化模型;文献[8]引入换乘站点重要度和线路换乘吸引度两个指标来研究公交乘客时刻表优化问题,以乘客换乘过程中候车时间最短为优化目标对发车时刻表进行优化;文献[9]在考虑车辆容量限制的条件下,以换乘点之间平均换乘时间最小为优化目标构建了优化模型。
近几年,随着城市公交线网规模的扩大,线路重叠现象非常普遍,部分学者对公交线路重叠区段运行车辆优化调度研究进行了尝试,文献[10-11]针对重叠区段上乘客选择行为,基于乘客选择概率分布理论构建了客流分配模型;文献[12]对重叠线路进行联合调度,使各线路车辆在重叠区段载客量均衡;文献[13]基于双层规划、Logit模型等基础理论,建立了考虑重叠区段客流特征的车辆配置协同优化模型;文献[14]研究了多运营商在重叠区间公交调度优化问题,并对重叠区间线路客流竞争关系进行了深入研究;文献[15]通过调整发车频率同步多组公交线路到站时刻,使同步站点的乘客候车时间和公交运营成本降到最低,引入时间索引将其转化混合整数线性规划问题进行求解;文献[16-17]基于重叠线路间的竞争关系,分别提出了基于全程车和跨站车的混合公交调度方法和基于乘客出行数据的多车型调度方法。
通过以上文献梳理发现,对单线路公交调度和区域公交调度的研究已较为成熟,对重叠线路系统内公交协同调度研究较少,且现有研究仅主要集中在重叠线路间客流竞争关系,较少涉及重叠区间乘客协同换乘。基于此,以乘客总出行时间最短和公交运营成本最小为优化目标,建立考虑乘客换乘的重叠线路公交调度优化模型。以哈尔滨市3条重叠公交线路为案例,运用提出的优化模型对重叠区段运行的公交车辆进行优化调度,设计遗传算法对模型进行求解,验证模型的可行性。
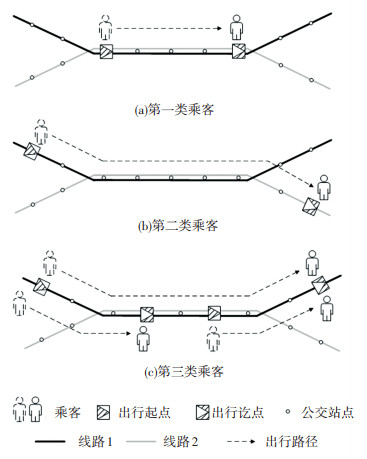
1 乘客分类为了便于对乘客的候车行为进行数学描述,根据乘客乘车起讫站点与重叠区段的相对位置关系,将乘客划分为三类:1)出行起讫点均位于重叠区段内的为第一类乘客,如图 1(a)所示,第一类乘客可乘坐重叠区段内任一线路的车辆完成出行任务,针对该类乘客,重叠区段内的线路之间存在竞争关系;2)需要在重叠区段内站点进行换乘的乘客为第二类乘客,如图 1(b)所示,第二类乘客的出行起讫点分别位于不同线路的非重叠区段,需要通过在重叠区段内换乘才能完成出行任务,重叠区段内的线路间存在合作关系;3)出行起讫点位于同一线路上且起点和讫点至少一个不在重叠区段上的乘客为第三类乘客,如图 1(c)所示,第三类乘客只能乘坐该特定线路的车辆完成出行任务,针对该类乘客,重叠区线路间既不存在竞争也不存在合作关系。
|
图 1 乘客出行路线示意图 Fig. 1 Schematic diagram of passenger travel routes |
由于存在容量限制,当车辆到站后,站点的候车乘客包括两部分:1)当前候车时段内到达的乘客,即前一车辆离开站点后到达站点的乘客;2)上一候车时段滞留乘客,即由于容量限制,未能乘坐前车而在车站滞留的乘客。
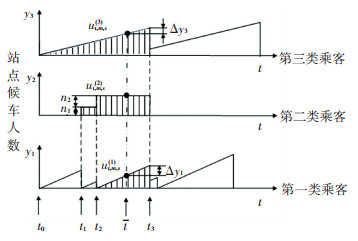
重叠区段内站点候车人数变化曲线如图 2所示,用于描述三类乘客在站点的上车和滞站情况,站点候车人数总人数由三类乘客候车人数组成。其中,曲线斜率为乘客到达率,第一、第三类候车乘客满足均匀到达,第二类乘客为集中到达。另外,图中还可反映各线路车辆到站时刻(如图中线路j、k、i车辆到站时刻分别为t1、t2、t3)、发车间隔(如图中线路i的发车间隔为t3-t0)、不同线路车辆到达重叠区段站点的时间间隔(线路j、k车辆的到站时间间隔为t2-t1)及换乘乘客数量(t1时刻线路j车辆上需要换乘到线路i的乘客数量为n1)等信息。引入车辆剩余容量曲线(x=t,t为三类乘客累积到站人数之和为车厢剩余容量Bi, m, s对应的时刻),可用于计算三类乘客的上车和滞站人数,以第一类乘客为例,t3时刻共有ui, m, s(1)人被线路i车辆接载,其他Δy1为滞留乘客数量。
|
图 2 三类乘客站点候车人数变化曲线 Fig. 2 Variation of numbers of wating passengers at stations for three passenger categories |
以线路i车辆m在站点s接载乘客为例,基于“先到先服务”原则的站点乘客滞留人数计算过程如下。
输入:每条线路的发车间隔和首车发车时间、各类乘客在各站点的到达率及下车比例等数据。
步骤1 计算车厢剩余容量Bi, m, s。Bi, m, s=B-
步骤2 计算线路i第m辆车到达时在站点s的候车总人数Ui, m, s。
步骤3 判断站点是否存在滞留乘客。若Ui, m, s≤Bi, m, s,则滞留人数为0,转步骤6;若Ui, m, s > Bi, m, s,存在滞留人数,转步骤4。
步骤4 计算t。
步骤5 计算三类乘客实际上车人数ui, m, s(1)、ui, m, s(2)、ui, m, s(3)。
步骤6 根据三类乘客的实际上车人数计算其对应的滞留人数。如wi, m, s(2)=Ui, m, s(2)-ui, m, s(2)。
输出:三类乘客实际上车人数、下车人数、滞留人数ui, m, s(1)、ui, m, s(2)、ui, m, s(3)、vi, m, s(1)、vi, m, s(2)、vi, m, s(3)、wf(i, m), s(1)、wi, m, s(2)、wi, m, s(3)。
2 问题描述与建模 2.1 问题描述及参数定义以I条重叠线路为建模研究对象,以乘客总出行时间(包括候车时间和车上时间)最小和公交运营成本最小为优化目标,以线路首车发车时刻和发车间隔为决策变量,建立重叠线路公交发车间隔协同优化模型。通过对决策变量进行优化,调整各线路车辆到达重叠站点的顺序和时间差,以此提高公交服务水平和降低公交运营成本。基于实际场景,作如下简化和假设:1)在研究时段内,乘客均匀到达站点;2)不同线路公交车车型、票价均相同;3)在研究时段内,公交车辆匀速运行。
模型中涉及的符号定义如下:1)集合。I为公交线路i的集合;S(i)为线路i的站点集;S1(i)为线路i从起始站至重叠区段前所包含的所有站点集合;S2(i)为线路i的重叠区段站点集合;N(i)为线路i发车车辆的集合。2)参数。Ni, m, s线路i车辆m由站点s-1到站点s前车厢内人数;ti, m, s线路i车辆m到达站点s的时刻;λi, s(h)线路i站点s第h类乘客的到达率,人/min,h∈{1, 2, 3};pi, js为由线路i在站点s换乘至线路j的乘客比例;Ci线路i车辆单位距离运营成本,元/km;θ乘客单位时间成本,元/min; vi线路i公交平均运行速度;Li表示线路i的总长度;tmax为线路最大发车间隔;tmin为线路最小发车间隔。3)决策变量。ti表示线路i(i∈I)发车间隔;t0(i)表示线路i始发站首车发车时间。
2.2 乘客总出行时间分析乘客总出行时间由候车时间和乘客车内时间构成。乘客车内时间为
| $ W_{\mathrm{OC}}=\sum\limits_{i \in I} \sum\limits_{m \in N(i) } \sum\limits_{s \in S(i)} N_{i, m, s}\cdot \left(t_{i, m, s}-t_{i, m, s-1}\right) $ | (1) |
式中:当s=1时,Ni, m, s=0,ti, m, s-ti, m, s-1=0;当s>1时,
乘客候车时间与站点乘客到达规律有关,当乘客均匀到达时,每位乘客的平均候车时间为连续公交车头时距的一半[18],三类乘客候车总时间计算表达式如下。
1) 第一类乘客候车总时间为
| $ \begin{gathered} W_{1}=\sum\limits_{i \in I} \sum\limits_{s \in S_{2}(i) } \sum\limits_{m \in N(i)} 0.5 \cdot \lambda_{i, s}^{(1)} \cdot\left(\Delta t_{i, m, s}\right)^{2}+\\ \sum\limits_{i \in I} \sum\limits_{s \in S_{2}(i) } \sum\limits_{m \in N(i)} w_{f(i, m)-1, s}^{(1)}\cdot \Delta t_{i, m, s} \end{gathered} $ | (2) |
式中:Δti, m, s指线路i车辆m在站点s与前车的车头时距,所有线路车辆按同一站点到站时间进行升序排列,线路i车辆m在站点s的新车序可通过映射f(i, m)得到,则Δti, m, s=tf(i, m), s-tf(i, m)-1, s。
2) 第二类乘客候车时间W2包括在非重叠区段等候需要搭乘的第一辆公交的候车时间W2(1)及在重叠区段换乘站点的换乘候车时间W2(2),即
| $ W_{2}=W_{2}^{(1)}+W_{2}^{(2)} $ | (3) |
| $ \begin{aligned} W_{2}^{(1)}=& \sum\limits_{i \in I} \sum\limits_{m \in N(i) } \sum\limits_{ s \in S_{1}(i)}0.5 \cdot \lambda_{i, s}^{(2)} \cdot\left(t_{i, m, s}-t_{i, m-1, s}\right)^{2}+\\ & \sum\limits_{i \in I} \sum\limits_{m \in N(i)} \sum\limits_{s \in S_{1}(i)} w_{i, m-1, s}^{(2)} \cdot\left(t_{i, m, s}-t_{i, m-1, s}\right) \end{aligned} $ | (4) |
| $ \begin{aligned} W_{2}^{(2)}=& \sum\limits_{i \in I} \sum\limits_{j \in I} \sum\limits_{m \in N(i)} \sum\limits_{ n \in N(j)}\sum\limits_{s \in S_{2}(i)} N_{i, m}^{(2)} P_{i, j}^{s}\left(t_{j, n, s}-\right.\\ &\left.t_{i, m, s}\right) X_{m, n} X_{i, j}+\sum\limits_{j \in I} \sum\limits_{n \in N(j) }\sum\limits_{s \in S_{2}(i)} w_{i, n-1, s}^{(2)} \cdot t_{j} \end{aligned} $ | (5) |
式中:当m=1时,ti, m, s-ti, m-1, s=t0(i);当m > 1时,ti, m, s-ti, m-1, s=ti;Ni, m(2)为线路i车辆m上需要在重叠区段进行换乘的总人数,Ni, m(2)=
3) 第三类乘客候车时间及换乘乘客等候第一辆车的时间为
| $ \begin{aligned} W_{3}=& \sum\limits_{i \in I} \sum\limits_{m \in N(i)} \sum\limits_{s \in S(i)} 0.5 \cdot \lambda_{i, s}^{(3)} \cdot\left(t_{i, m, s}-t_{i, m-1, s}\right)^{2}+\\ & \sum\limits_{i \in I} \sum\limits_{m \in N(i)} \sum\limits_{s \in S(i)} w_{i, m-1, s}^{(3)} \cdot\left(t_{i, m, s}-t_{i, m-1, s}\right) \end{aligned} $ | (6) |
式中:当m=1时,ti, m, s-ti, m-1, s=t0(i);当m > 1时,ti, m, s-ti, m-1, s=ti。
2.3 发车间隔协同优化模型的构建以乘客总出行时间最小和公交运营成本最小为优化目标构建重叠线路发车间隔协同优化模型为
| $ \min W=W_{1}+W_{2}+W_{3}+W_{\text {OC }} $ | (7) |
| $ \min C=2 \sum\limits_{i \in I} N_{i} C_{i} L_{i} $ | (8) |
s.t.
| $ t_{\min } \leqslant t_{i} \leqslant t_{\max }, \forall i \in I $ | (9) |
| $ 0 \leqslant t_{0}^{(i)} \leqslant t_{i}, \quad \forall i \in I $ | (10) |
| $ X_{i, j}=\left\{\begin{array}{l} 1, i \neq j, \forall i, j \in I \\ 0, i=j, \forall i, j \in I \end{array}\right. $ | (11) |
| $ X_{m, n}= \begin{cases}1, & t_{j, n-1, s}<t_{i, m, s} \leqslant t_{j, n, s}, \forall i, j \in I, m \in N(i), n \in N(j), s \in S_{2}(i) \\ 0, & \text { 其他 }, \forall i, j \in I, m \in N(i), n \in N(j), s \in S(i)\end{cases} $ | (12) |
式(7)、(8)是问题的目标函数,式(7)表示乘客总出行时间最小化;式(8)表示公交运营成本最小化,Ci为线路i单位里程运营成本,包括固定折旧维修成本、人员工资成本、停靠怠速成本及运行能耗成本[19]。式(9)~(12)为约束条件,式(9)为发车间隔约束,公交发车间隔须满足最大和最小发车间隔限制;式(10)为始发站首车发车时间约束,公交线路首车发车时间作为优化变量时须小于发车间隔取值;式(11)为0-1变量约束,用于判断两线路是否构成换乘关系,线路i与线路j表示不同线路时Xi, j为1,否则为0;式(12)为0-1变量约束,当满足tj, n-1, s < ti, m, s≤tj, n, s时定义车辆m和车辆n间形成有效接续,即Xm, n=1,否则为0。
3 模型求解所提出的考虑乘客换乘的重叠线路发车间隔协同优化模型属于非线性整数规划问题,是一类典型的NP-hard问题,其计算量随着重叠线路数量的增多而呈指数形式增长。因此,该类问题通常采用可同时保证计算速度和计算精度的启发式算法求解。遗传算法具有过程简单、计算时间少、鲁棒性高、延展性强等优点,故采取遗传算法对本模型进行求解。
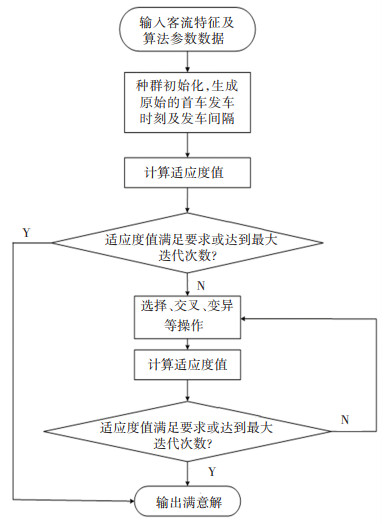
本模型采用遗传算法进行求解,算法流程如图 3所示,决策变量为重叠线路的发车间隔和首车发车时间,采取多参数级联编码的方式进行组合编码,其求解步骤如下。
|
图 3 遗传算法流程图 Fig. 3 Flow chart of genetic algorithm |
步骤1 输入客流特征数据及算法参数数据。
步骤2 生成原始线路首车发车时刻及发车间隔,得到初始种群。
步骤3 评价个体适应度。引入权重系数,计算系统总成本,将多目标规划转化为单目标优化,构造适应度函数,如式(13)所示。α、β分别为乘客出行总成本和公交运营成本的期望权重,满足α+β=1,0≤α≤1,0≤β≤1。
| $ \min Z_{\text {total }}=\alpha \cdot \theta \cdot\left(W_{1}+W_{2}+W_{3}+W_{\mathrm{OC}}\right)+\beta \cdot C $ | (13) |
步骤4 判断是否满足迭代终止条件。若满足,跳到步骤6;若不满足,转至步骤5。
步骤5 进行选择、交叉、变异等操作形成新个体,操作完成后转步骤3。
步骤6 程序结束,输出满意解。
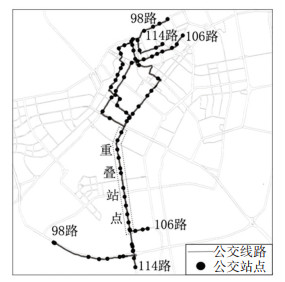
4 算例分析 4.1 算例简述选取哈尔滨市98路、106路、114路公交为仿真研究对象,图 4展示了这3条线路的重叠区段分布情况,重叠区段内共有12个重叠站点。以11:00—12:00为调查时段,采用人工调查法获得各站点的上下车乘客数,根据上车客流和乘客下车概率表推算各公交线路的OD客流数据表,根据三类乘客的起讫点特征,分别得到各类乘客的上车乘客数,进而可得到其到达率,经统计三类乘客的客流比例为0.18∶0.05∶0.77。参数设置如下:最小发车间隔tmin和最大发车间隔tmax分别取3 min和20 min,研究时段内的总时间T为60 min,乘客候车平均成本θ为0.32元/min,权重系数α=0.6、β=0.4,各线路车辆单位距离运营成本为13.6 km/h,公交车额定载客数B为100人,其他公交线路信息见表 1。
|
图 4 重叠区段示意图 Fig. 4 Schematic diagram of overlapping sections |
| 表 1 公交线路信息 Tab. 1 Bus line information |
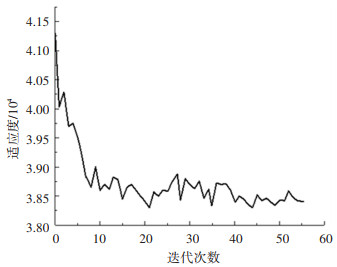
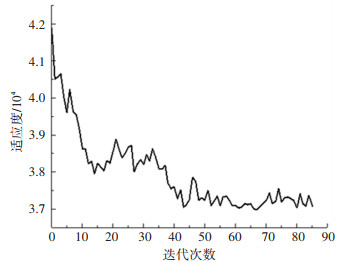
以所建立的发车间隔协同优化模型为依据,结合3条公交线路的相关数据,利用遗传算法进行求解。为了确定遗传算法基本参数进行了大量的实验,最终得到如下较好的参数取值,其中种群规模为20、交叉概率为0.7、变异概率为0.1、最大迭代次数为150。优化方案1发车间隔不变,以首车发车时间为优化变量;优化方案2以首车发车时间和发车间隔为优化变量。对两种优化方案进行求解并与原方案对比,其中乘客出行时间指标对比结果见表 2,调度方案成本指标对比结果见表 3,遗传算法迭代过程如图 5、6所示。
| 表 2 乘客出行时间指标对比 Tab. 2 Comparison of passenger travel time indexes |
| 表 3 调度方案成本指标对比 Tab. 3 Cost indexes comparison of scheduling schemes |
|
图 5 优化方案1遗传算法迭代过程 Fig. 5 Genetic algorithm iteration process of optimization plan 1 |
|
图 6 优化方案2遗传算法迭代过程 Fig. 6 Genetic algorithm iteration process of optimization plan 2 |
由表 2和表 3可知,优化方案1仅以线路首车发车时间为优化变量,优化效果有限,第二、三类乘客候车时间分别下降12.9%和7.7%,第一类乘客候车时间上升8.5%,这是由于第一乘客所占比重较小,在优化过程中未能起到决定性作用;优化方案2以首车发车时间和发车间隔为优化变量,可寻求到更佳满意解,优化效果较为明显,公交运营成本降低了15.2%,第一、二、三类乘客候车总时间分别减少了3.2%、33.2%、18.6%,乘客车上时间变化不大,优化后的发车时刻表见表 4。
| 表 4 优化方案2发车时刻表 Tab. 4 Departure schedule of optimization plan 2 |
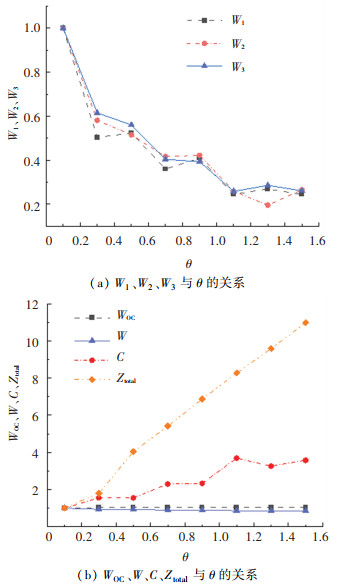
不同城市人均收入水平存在差距,乘客的单位时间价值也不相等。研究以线路首车发车时间和发车间隔为优化变量时乘客单位时间价值θ变化对各类乘客候车时间、乘客车上时间、乘客出行总时间、公交运营成本和系统总成本的影响。θ以0.2的步长由0.1逐渐增加至1.5,其余输入参数取值不变,决策变量为常数且为最优解。图 7展示了不同θ值下各指标的变化情况(θ=0.1时各项指标值为基数1,取其他θ值时各项指标值进行相应换算)。由图 7可知:1)随着θ逐渐增大,三类乘客候车时间及乘客候车总时间呈下降趋势,公交运营成本及系统总成本呈上升趋势;2)由于线路站间距、车辆速度、乘客到达率不变,仅第一类乘客在重叠线路上的客流分配发生了变化,故乘客车上时间变化不大;3)三类乘客候车时间的变化趋势基本相同,在其他条件不变的情况下,乘客总出行时间成本占系统总成本的比例与θ值正相关,随着θ值增大,优化结果中各线路发车间隔取值减小,各类乘客的候车时间随之减小。
|
图 7 θ值敏感性分析 Fig. 7 Sensitivity analysis of θ value |
1) 建立了一种考虑乘客换乘行为的重叠区公交车辆调度优化模型,通过哈尔滨市3条重叠公交线路对模型进行了验证,采用两种优化方案,将两种优化方案中乘客出行时间与优化前对比可得,同时优化首车发车时刻和车辆发车间隔,可以减少乘客出行时间,降低公交运营成本,乘客总出行时间降低了6.7%,公交运营成本降低了15.2%。
2) 考虑到乘客换乘过程中乘客候车时间计算的复杂性,根据公交乘客出行起讫点与重叠区域的位置关系,将乘客分为三类,基于三类乘客各自换乘行为特性,分别构建了三类乘客各自候车时间的数学表达式,使乘客出行时间的计算更加合理,同时结合公交实际运营成本需求,完成公交车辆调度合理优化,减低了公交运营成本,改善了公交运营现状。
3) 考虑到模型的可移植性,对乘客单位时间成本进行敏感性分析,结果表明,三类乘客候车时间的敏感性变化趋势大体相同,三类乘客候车时间对乘客单位时间的变化均表现为弹性,乘客车上时间及乘客总出行时间则表现为非弹性。
| [1] |
KOUTSOPOULOS H N, ODONI A, WILSON N H M. Determination of headways as a function of time varying characteristics on a transit network[M]//Computer Scheduling of Public Transport 2. Amsterdam: Elsevier, 1985: 391
|
| [2] |
NIU Huiming. Determination of the skip-stop scheduling for a congested transit line by bilevel genetic algorithm[J]. International Journal of Computational Intelligence Systems, 2011, 4(6): 1158. DOI:10.1080/18756891.2011.9727864 |
| [3] |
牛学勤, 陈茜, 王炜. 城市公交线路调度发车频率优化模型[J]. 交通运输工程学报, 2003, 3(4): 68. NIU Xueqin, CHEN Qian, WANG Wei. Optimal model of urban bus frequency determination[J]. Journal of Traffic and Transportation Engineering, 2003, 3(4): 68. DOI:10.3321/j.issn:1671-1637.2003.04.016 |
| [4] |
CHAKROBORTY P, DEB K, SUBRAHMANYAM P S. Optimal scheduling of urban transit systems using genetic algorithms[J]. Journal of Transportation Engineering, 1995, 121(6): 544. DOI:10.1061/(ASCE)0733-947X(1995)121:6(544) |
| [5] |
PATTNAIK S B, MOHAN S, TOM V M. Urban bus transit route network design using genetic algorithm[J]. Journal of Transportation Engineering, 1998, 12(4): 368. DOI:10.1061/(ASCE)0733-947X(1998)124:4(368) |
| [6] |
CEDER A, GOLANY B, TAL O. Creating bus timetables with maximal synchronizations[J]. Transportation Research Part A: Policy and Practice, 2001, 35(10): 913. DOI:10.1016/S0965-8564(00)00032-X |
| [7] |
田启华, 陈艳艳. 区域公交协调调度优化算法研究[J]. 交通运输系统工程与信息, 2011, 11(4): 160. TIAN Qihua, CHEN Yanyan. Coordinated scheduling optimization for public transport hub[J]. Journal of Transportation System Engineering and Information Technology, 2011, 11(4): 160. DOI:10.3969/j.issn.1009-6744.2011.04.025 |
| [8] |
QUAK C B. A passenger-oriented approach of the construction of a global line network and an efficient timetable[D]. Delft: Delft University of Technology, 2003
|
| [9] |
赵航, 安实, 金广君, 等. 考虑车辆运输能力限制的公交换乘优化[J]. 吉林大学学报(工学版), 2012, 42(3): 606. ZHAO Hang, AN Shi, JIN Guangjun, et al. Optimization of transit transfer with vehicle capacity constraints[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(3): 606. |
| [10] |
GUIDO G, SANG N, STEFANO P. Route choice on transit networks with online information at stops[J]. Transportation Science, 2005, 39(3): 289. DOI:10.1287/TRSC.1040.0109 |
| [11] |
MARGUIER P H J. Optimal strategies in waiting for common bus lines[D]. Cambridge: Massachusetts Institute of Technology, 1981
|
| [12] |
王贵平, 吴奇. 重复公交线路公交车的发车间隔协同优化[J]. 交通运输工程与信息学报, 2017, 15(2): 35. WANG Guiping, WU Qi. Research on repeat-route bus departure interval synchro optimization[J]. Journal of Transportation System Engineering and Information Technology, 2017, 15(2): 35. DOI:10.3969/j.issn.1672-4747.2017.02.006 |
| [13] |
洪豆. 考虑公交线路重复路段的车辆配置协同优化研究[D]. 重庆: 重庆交通大学, 2018 HONG Dou. Research on collaborative optimization of vehicle configuration considering repeat sections of bus routes[D]. Chongqing: Chongqing Jiaotong University, 2018 |
| [14] |
宋现敏, 张明业, 姜景玲. 考虑区间重叠的多运营商公交调度优化[J]. 交通运输系统工程与信息, 2020, 20(5): 142. SONG Xianmin, ZHANG Mingye, JIANG Jingling. Bus dispatching optimization of multi-operators considering overlapping interval[J]. Journal of Transportation System Engineering and Information Technology, 2020, 20(5): 142. DOI:10.16097/j.cnki.1009-6744.2020.05.021 |
| [15] |
SILVA-SOTO Y I, IBARRA-ROJAS O J. Timetabling with flexible frequencies to synchronise groups of bus lines at common stops[J]. Transportmetrica A: Transport Science, 2021, 17(4): 978. DOI:10.1080/23249935.2020.1822952 |
| [16] |
BIE Yiming, TANG Ruru, WANG Linhong. Bus scheduling of overlapping routes with multi-vehicle types based on passenger OD data[J]. IEEE Access, 2020, 8: 1406. DOI:10.1109/ACCESS.2019.2961930 |
| [17] |
BIE Yiming, TANG Ruru, LIU Zhiyuan, et al. Mixed scheduling strategy for high frequency bus routes with common stops[J]. IEEE Access, 2020, 8: 34442. DOI:10.1109/ACCESS.2020.2974740 |
| [18] |
CEDER A, MARGUIER M. Passenger waiting time at transit stops[J]. Traffic Engineering and Control, 1985, 26(6): 327. |
| [19] |
张思林, 袁振洲, 曹志超. 考虑容量限制的多公交车型运行计划优化模型[J]. 交通运输系统工程与信息, 2017, 17(1): 150. ZHANG Silin, YUAN Zhenzhou, CAO Zhichao. Optimization model of bus operation plan based on hybrid bus sizes with constraints on vehicle capacity[J]. Journal of Transportation System Engineering and Information Technology, 2017, 17(1): 150. DOI:10.16097/j.cnki.1009-6744.2017.01.022 |
 2022, Vol. 54
2022, Vol. 54


