2. 大连海事大学 交通运输工程学院,辽宁 大连 116000
2. College of Transportation Engineering, Dalian Maritime University, Dalian 116000, Liaoning, China
随着经济的发展,物流业地位的不断提高,想要为企业带来更多经济收益,就需要以更低的物流成本来响应客户的需求。产品的生产过程以零部件的组装和配送为主,因此物料配送方法的合理选择能够更好地发挥企业生产的优势,进而为企业的高效生产提供有效的保障[1]。国内外学者已在物料配送方式领域进行了一定的研究。文献[2]以线边物料的堆存成本最小为目标建立模型,并设计反向动态规划算法和人工蜂群算法进行仿真与求解。文献[3]以配送时间最短和配送成本最低为目标建立大数据平台下的物料配送模型。文献[4]以物料配送成本最小为目标,建立基于智能感知网的动态物料配送优化模型,设计基于禁忌搜索的改进蚁群算法进行求解。文献[5]以搬运车辆最少、运输时间最短为目标构建了车辆路径优化模型并设计遗传算法求解。文献[6]提出一种适用于卫星总装数字孪生车间的基于灰色理论和多模型交互机制的物料准时配送方法。文献[7]以相关成本最小化为目标,对稳定的随机装配系统进行动态的性能分析。文献[8]分别设计了kit供应(指根据生产计划和物料清单,把某个工位需要的单辆份零件组装成kit,放入料箱中,然后通过牵引车或AGV小车将料箱供给到线边堆放区的供应方式)、连续供应和批量供应下相关成本的计算公式,并对不同的组合物料供应方式的总成本进行效果评估。文献[9]定性研究了物料数量、种类、尺寸、物料存储面积、操作效果对物料配送方式选择的影响。文献[10]以成本最小为目标,建立基于批量配送和kit配送的选择决策模型。文献[11]以能源消耗最小为目标,建立混流装配线物料配送多目标优化模型,并设计禁忌增强粒子群算法求解。文献[12]采用数据包络分析法,将集件系统(SPS)模型与传统模型进行比较,系统分析其优势。国内研究侧重于针对传统的单一配送方式进行优化建模并设计相关算法进行求解,国外研究多从物流成本入手设计合理有效的物料配送方案,在系统性能的定量评估及影响因素的定性分析方面做出诸多贡献,然而从降低成本的角度对不同物料配送方式进行组合优化的相关研究尚需要深入。
基于上述分析,针对生产车间亟待优化的单一物料配送方式所导致的成本过高问题,本文改进了传统物料配送方式优化模型,建立了基于批量配送和kit配送的物料配送方式组合优化模型,并通过实例验证了模型的鲁棒性。本文研究的物流作业仅为物料配送环节,且本文研究的生产线物料配送范围是从物料存储区到生产线,故未考虑装卸、拆包、交接等环节。影响物料配送方式选择的因素有很多,如配送成本、配送路径、配送时间、车辆及人员安排等,其中物料配送成本对方式选择的影响相对较强。因此本文模型以生产车间物料配送总成本最优为物流作业需求,配送方式选择的合理性仅考虑配送成本,不考虑配送时间、配送路径等因素。本文所建立的物料配送方式组合优化模型对于降低物流成本,指导制造企业完成成本最优化的物流配送,提升企业竞争力具有重要作用。
1 问题描述传统的配送方法有两种,批量配送和kit配送。批量配送方式简单易懂,便于操作,但企业需准备大量库存以应对市场需求变化带来的风险,工作人员需耗费较多时间找到所需物料[13]。kit配送方式有效减少了对于线边堆放区的空间需求,较好地实现了生产车间的机械化处理,但kit的组装、运输和存储增加了非生产性的物料处理工作,产生额外成本[14]。由于批量配送和kit配送方式的优缺点互补,将二者结合使用可以发挥各自的长处,优化企业的物流成本,更加符合生产发展需求。
1.1 批量配送运作流程从物料存储区到线边堆放区的批量配送方式流程图如图 1所示。图 1中,物料存储区Ⅰ和Ⅱ分别表示存放的是以纸箱形式和托盘形式装载的物料;G表示生产线的工位;①表示搬运人员用牵引车将以纸箱包装的物料通过循环配送至生产线边堆放区,并空车返回的过程,在图中用实线表示;②表示搬运人员用叉车将以托盘包装的物料,单个配送至生产线边堆放区的过程,在图中用虚线表示;③和④表示生产线装配人员前往线边堆放区取料并返回工位的过程,在图中用点划线表示。

|
图 1 批量配送流程图 Fig. 1 Flow chart of batch distribution |
kit译为“工具箱”,其有固定型kit和移动型kit[15]两种类型。kit配送的特点是多批次、小批量,线边堆放的kit料箱依据组装周期和生产节拍对kit进行补充。从物料存储区到线边堆放区的批量配送和kit配送的组合配送过程如图 2所示。

|
图 2 批量配送和kit配送的组合配送流程图 Fig. 2 Combinatorial distribution flow chart of batch distribution and kit distribution |
图 2中,组装区是负责对kit进行组装的区域。①和⑥表示搬运人员用牵引车将以纸箱包装的和不易组装成kit的物料通过循环配送至生产线边堆放区,并空车返回的过程,在图中用点线表示;②表示搬运人员用牵引车将以纸箱形式包装和需要组装的物料运至组装区的过程,在图中用较粗的点线表示;③表示搬运人员用叉车将以托盘形式包装的和需要组装的物料运至组装区的过程,在图中用虚线表示;④表示搬运人员用叉车将以托盘包装的和不易组装成kit的物料,单个配送至生产线边堆放区的过程,在图中用较细的虚线表示;⑤和⑦表示牵引车将组装好的kit料箱循环配送至生产线边堆放区并空车返回的过程,在图中用实线表示;⑧和⑨表示生产线装配人员前往线边堆放区取料并返回工位的过程,在图中用较细的点线表示;⑩表示组装区内挑选所需物料组装成kit的过程,在图中用点划线表示。
1.3 假设条件运用0-1规划的思想,以配送总成本最小为目标,构造基于批量配送和kit配送的物料配送方式组合优化模型,生产过程中需要满足以下假设:1)为节约线边堆放区的空间,规定线边堆放区内的物料包装先按竖直方向来摆放,堆满3层后再按水平方向来摆放,且不同的物料包装不能堆在同一列,如图 3所示;2)为方便kit的装载,规定kit料箱被分成4层,即每个kit料箱可以装载4个kit;3)牵引车和叉车只能在物料存储区和组装区外使用,物料存储区和组装区内部需靠人力完成相关操作。

|
图 3 线边堆放区物料存储示意图 Fig. 3 Material storage of stacking area at the edge of production line |
本文研究的kit为固定型kit,其被运至线边堆放区后,只能供给单一工位,不同工位之间不能共享或转赠。以一个工作周为研究时长,以U型生产线上的某一种产品为研究对象。为便于后续数据的收集,将N个产品归为一组进行研究(N根据实际生产计划可取任意值,本文取N=20)。
2 物料配送方式组合优化模型论文改进了传统物料配送方式优化模型,所建立的模型包括改进的批量配送成本模型、改进的kit配送成本模型和组合优化模型,其改进之处如下:1)建模成本项。考虑生产车间内物料配送的实际流程,模型增加了批量配送和kit配送下线边堆放区的存储成本。2)向上取整。为使求解结果更符合实际,所建立的模型对于非整数的纸箱数、托盘数和kit数均进行了向上取整。3)参数补充。增加了生产线工作人员在线边堆放区拿起物料或kit所需的时间,减小了求解结果误差。
2.1 改进的批量配送成本模型批量配送过程会产生4项成本:线边堆放区的存储成本、从物料存储区到线边堆放区的搬运成本、生产线工作人员的拣料成本和理货人员的供料成本。
2.1.1 线边堆放区的存储成本在批量配送中,线边堆放区存储的是以纸箱形式包装的物料和以托盘形式包装的物料。生产N个产品时,工位j对应的线边堆放区内存放物料i的纸箱和托盘数量分别为
| $ Q_{i j}^{\mathrm{b}}=\left\lceil\frac{W_{i j}^{b}}{T_{i}^{\mathrm{b}}}\right\rceil $ | (1) |
| $ Q_{i j}^{\mathrm{p}}=\left\lceil\frac{W_{i j}^{\mathrm{p}}}{T_{i}^{\mathrm{p}}}\right\rceil $ | (2) |
式中:Qijb、Qijp分别为生产N个产品时,工位j对应的线边堆放区内存放物料i的纸箱数量或托盘数量;Wijb、Wijp分别为生产N个产品时,工位j对以纸箱或托盘装载的物料i的需求数量;Tib、Tip分别为单个纸箱或托盘能够装载物料i的数量。
批量配送下,线边堆放区的存储成本C1为
| $ \begin{aligned} C_{1}=& C^{\mathrm{m}} \sum\limits_{j=1}^{J}\left[\sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left\lceil Q_{i j}^{\mathrm{b}} \cdot \frac{R}{3 N}\right\rceil \cdot S_{\mathrm{b}} \cdot\left(1-x_{i j}\right)+\right.\\ &\left.\sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}}\left\lceil Q_{i j}^{\mathrm{p}} \cdot \frac{R}{3 N}\right\rceil \cdot S_{\mathrm{p}} \cdot\left(1-x_{i j}\right)\right] \end{aligned} $ | (3) |
式中:Cm为线边堆放区内单位存储面积的成本,元/m2;φb、φp分别为以纸箱形式或托盘形式装载的物料的集合;φj为生产线的工位j使用的物料的集合;J为生产线的工位总数量;Sb、Sp分别为单个纸箱或托盘所需的存储面积,m2;R为生产线每周生产该产品的平均数量。
2.1.2 从物料存储区到线边堆放区的搬运成本在搬运过程中,以纸箱形式装载的物料采用牵引车以循环配送的方式配送到对应工位的线边堆放区,以托盘形式装载的物料采用叉车进行搬运,每次向对应工位的线边堆放区配送一个托盘,配送完毕空叉车返回物料存储区Ⅱ。因此,从物料存储区到线边堆放区的搬运成本C2为
| $ \begin{aligned} C_{2}=& C_{2}^{\mathrm{b}}+C_{2}^{\mathrm{p}}=C^{\mathrm{b}} \cdot\left[\frac { D ^ { \mathrm { b } } } { \overline { v } _ { 2 } } \cdot \left\lceil\frac{1}{A^{\mathrm{b}}} \cdot\right.\right.\\ &\left.\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left\lceil\frac{W_{i j}^{\mathrm{b}} \cdot R}{T_{i}^{\mathrm{b}} \cdot N}\right\rceil \cdot\left(1-x_{i j}\right)\right\rceil+\\ &\left.\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}} \frac{2 D_{j}^{\mathrm{p}}}{\overline{v_{1}}} \cdot\left\lceil\frac{W_{i j}^{\mathrm{p}} \cdot R}{T_{i}^{\mathrm{p}} \cdot N}\right\rceil \cdot\left(1-x_{i j}\right)\right] \end{aligned} $ | (4) |
式中:C2b、C2p分别为批量配送下,以纸箱和托盘装载的物料从物料存储区Ⅰ到线边堆放区的搬运成本,元;Cb为搬运人员每小时的成本,元/h;Db为循环配送以纸箱形式装载的物料的距离,km;v2为牵引车循环配送纸箱装载的物料时的速度,km/h;v1为叉车的行驶速度,km/h;Djp为物料存储区Ⅱ与工位j的线边堆放区之间的距离,km;Ab为一次循环配送能够装载的纸箱平均数量。
2.1.3 生产线人员的拣料成本批量配送下,生产线工作人员拣取物料的过程实质是生产线工作人员从工位前往对应的线边堆放区存放所需物料处,拿起单个物料,再原路返回工位的过程。因此,生产线工作人员的拣料成本C3为
| $ \begin{aligned} C_{3}&=C_{3}^{\mathrm{b}}+C_{3}^{\mathrm{p}}=C^{\mathrm{s}} \cdot\left[\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left(\frac{2 d_{\mathrm{b}}}{1\ 000 \bar{v}_{3}}+\frac{t_{\mathrm{b}}}{60}\right)\cdot\right. \\ &W_{i j}^{\mathrm{b}} \cdot \frac{R}{N} \cdot\left(1-x_{i j}\right)+\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}}\left(\frac{2 d_{\mathrm{p}}}{1\ 000 \overline{v_{3}}}+\frac{t_{\mathrm{p}}}{60}\right) \cdot\\ &\left.W_{i j}^{\mathrm{p}} \cdot \frac{R}{N} \cdot\left(1-x_{i j}\right)\right] \end{aligned} $ | (5) |
式中:C3b、C3p分别为批量配送下,生产线工作人员拣取所需的以纸箱或托盘装载的物料时的成本,元;Cs为生产线工作人员每小时的成本,元/h;db、dp分别为生产线工作人员到对应工位的线边堆放区所需的以纸箱或托盘装载的物料处的距离,m;tb、tp分别为拣取一个以纸箱装载的物料所需的时间,s;v3为人的行走速度,km/h。
2.1.4 理货人员的供料成本批量配送下,理货人员在物料存储区的供料过程实质是理货人员前往所需物料处,拿取规定数目的纸箱或托盘后,再原路返回物料存储区的入口处等待搬运的过程。因此,理货人员的供料成本C4为
| $ \begin{aligned} &C_{4}=C_{4}^{\mathrm{b}}+C_{4}^{\mathrm{p}}=C^{\mathrm{L}} \cdot\left[\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left(\frac{2 d_{1}}{1\ 000 \bar{v}_{3}}+\frac{t_{1}}{60} \cdot U_{i}\right) \cdot\right. \\ &\left\lceil\frac{W_{i j}^{\mathrm{d}} \cdot R}{T_{i}^{\mathrm{b}} \cdot U_{i} \cdot N}\right\rceil \cdot\left(1-x_{i j}\right)+\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}}\left(\frac{2 d_{2}}{1\ 000 \bar{v}_{3}}+\frac{t_{2}}{60}\right) \cdot \\ &\left.\left\lceil\frac{W_{i j}^{\mathrm{p}} \cdot R}{T_{i}^{\mathrm{p}} \cdot N}\right\rceil \cdot\left(1-x_{i j}\right)\right] \end{aligned} $ | (6) |
式中:C4b、C4p分别为批量配送下,理货人员在物料存储区Ⅰ和Ⅱ的供料成本,元;CL为理货人员每小时的成本,元/h;Ui为理货人员每次能够拿起存放物料i的纸箱的数量;d1、d2分别为理货人员在物料存储区Ⅰ和Ⅱ寻找物料的行走距离,m;t1、t2分别为在物料存储区Ⅰ和Ⅱ内拣取一个存放物料的纸箱或托盘的时间,s。
2.2 改进的kit配送成本模型kit配送过程产生5项成本:线边堆放区的存储成本,从组装区到线边堆放区的搬运成本,生产线工作人员的拣料成本,理货人员的供料成本和kit的组装成本。
2.2.1 线边堆放区的存储成本kit配送下,线边堆放区存储的是各个工位需要的kit料箱。所以线边堆放区的存储成本Cβ1为
| $ C_{\beta 1}=C^{\mathrm{m}} \cdot \sum\limits_{j=1}^{J}\left\lceil W_{j}^{\mathrm{k}} \cdot \frac{R}{4 N}\right\rceil \cdot S_{\mathrm{kit} \ \mathrm{lx}} $ | (7) |
式中:Wjk为生产N个产品时工位j对kit的需求数量;Skit lx为单个kit料箱所需的存储面积,m2。
2.2.2 从组装区到线边堆放区的搬运成本组装人员将物料组装成所需的kit后,由牵引车载着kit料箱向生产线的线边堆放区进行循环配送,而后空车返回组装区,等待下一轮的配送。在kit配送下,从组装区到线边堆放区的搬运成本Cβ2应表示为
| $ C_{\beta 2}=C^{\mathrm{b}} \cdot \frac{D^{\mathrm{kit}}}{\bar{v}_{4}}\left\lceil\frac{\sum\limits_{j=1}^{J}\left\lceil W_{j}^{\mathrm{k}} \cdot \frac{R}{N}\right\rceil}{A^{\mathrm{kit}}}\right\rceil $ | (8) |
式中:Dkit为循环配送kit料箱的距离,km;v4为牵引车循环配送kit料箱时的速度,km/h;Akit为一次循环配送能够装载的kit料箱的平均数量。
2.2.3 生产线工作人员的拣料成本在kit配送下,生产线工作人员拣取kit的过程,实质是生产线工作人员从工位前往对应的线边堆放区存放kit处,拿起kit中的某个零件,再原路返回工位的过程。生产线工作人员的拣料成本Cβ3为
| $ \begin{aligned} C_{\beta 3}=& C_{\beta 3}^{\mathrm{b}}+C_{\beta 3}^{\mathrm{p}}=C^{\mathrm{s}} \sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left(\frac{2 d_{\mathrm{kit}}}{1\ 000 \bar{v}_{3}}+\frac{t_{\mathrm{kit}}}{60}\right) \cdot W_{j}^{\mathrm{k}} \cdot\\ & P_{i}^{\mathrm{b}} \cdot \frac{R}{N} \cdot x_{i j}+C^{\mathrm{s}} \sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}}\left(\frac{2 d_{\mathrm{kit}}}{1\ 000 \bar{v}_{3}}+\frac{t_{\mathrm{kit}}}{60}\right) \cdot\\ & W_{j}^{\mathrm{k}} \cdot P_{i}^{\mathrm{p}} \cdot \frac{R}{N} \cdot x_{i j} \end{aligned} $ | (9) |
式中:Cβ3b、Cβ3p分别为批量配送下,理货人员在物料存储区Ⅰ和Ⅱ的供料成本,元;dkit为生产线工作人员到对应工位的线边堆放区的所需kit处的距离,m;tkit为在线边堆放区拣取一个kit所需的时间,s;Pib和Pip分别为一个kit中以纸箱和托盘装载的物料i的数量。
2.2.4 理货人员的供料成本kit配送下,理货人员需要从物料存储区的入口处前往所需物料处,拿取一定数目的物料后,原路返回,再使用牵引车将从物料存储区Ⅰ拿取的物料运送至组装区;或使用叉车将从物料存储区Ⅱ拿取的物料运送至组装区。kit配送下理货人员的供料成本Cβ4为
| $ \begin{aligned} &C_{\beta 4}=C_{\beta 4}^{\mathrm{b}}+C_{\beta 4}^{\mathrm{p}}=C^{\mathrm{L}}\left\{\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left[\frac{2}{M_{i}^{\mathrm{b}}}\left(\frac{d_{1}}{\bar{v}_{3}}+\frac{D_{\mathrm{z} 1}}{\bar{v}_{2}}\right)+t_{\mathrm{b}}\right] .\right. \\ &W_{j}^{\mathrm{k}} \cdot P_{i}^{\mathrm{b}} \cdot \frac{R}{N} \cdot x_{i j}+\sum\limits_{j=1}^{J} \sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left[\frac{2}{M_{i}^{\mathrm{p}}}\left(\frac{d_{2}}{\bar{v}_{3}}+\frac{D_{z 2}}{\bar{v}_{1}}\right)+t_{\mathrm{p}}\right] \cdot \\ &\left.W_{j}^{\mathrm{k}} \cdot P_{i}^{\mathrm{p}} \cdot \frac{R}{N} \cdot x_{i j}\right\} \end{aligned} $ | (10) |
式中:Cβ4b、Cβ4p分别为物料存储区Ⅰ和Ⅱ至kit组装区的供料成本,元;Dz1、Dz2分别为物料存储区Ⅰ和Ⅱ与组装区之间的距离,km;Mib、Mip分别为理货人员在物料存储区Ⅰ和Ⅱ中平均每次能够拿取物料i的数量。
2.2.5 kit的组装成本kit的组装成本Cβ5为
| $ C_{\beta 5}=C^{\mathrm{z}} \cdot \frac{Z_{\mathrm{k}}}{60} \cdot \sum\limits_{j=1}^{J}\left\lceil W_{j}^{\mathrm{k}} \cdot \frac{R}{N}\right\rceil $ | (11) |
式中:Cz为组装kit的工作人员每小时的成本,元/h;Zk为组装一个kit所需要的时间,s。
2.3 组合优化模型对传统物料配送方式优化模型进行改进,以配送总成本最优为目标,考虑批量配送和kit配送两种方式,构建物料配送方式组合优化模型,其约束条件的改进之处:增加生产线物料供应量≥需求量约束,避免出现生产中断的现象;增加了运输车辆额定载重限制,减小了运输途中车辆因超载发生侧翻的风险;从线边堆存区的面积角度进行限制。
所述物料配送方式组合优化模型的目标函数为
| $ \min Z=\left(C_{1}+C_{2}+C_{3}+C_{4}+C_{\beta 1}+C_{\beta 2}+C_{\beta 3}+C_{\beta 4}+C_{\beta 5}\right) $ | (12) |
约束条件为
| $ Q_{i j}^{\mathrm{b}} \cdot T_{i}^{\mathrm{b}} \geqslant W_{i j}^{\mathrm{b}}\left(1-x_{i j}\right), i \in \varphi_{\mathrm{b}} \cap \varphi_{j}, j=1, 2, \ldots, J $ | (13) |
| $ Q_{i j}^{\mathrm{p}} \cdot T_{i}^{\mathrm{p}} \geqslant W_{i j}^{\mathrm{p}}\left(1-x_{i j}\right), i \in \varphi_{\mathrm{p}} \cap \varphi_{j}, j=1, 2, \ldots, J $ | (14) |
| $ \max \left\{T_{i}^{\mathrm{b}} \cdot A^{\mathrm{b}} \cdot B_{i}^{\mathrm{b}} \cdot\left(1-x_{i j}\right)\right\} \leqslant B_{\mathrm{r}} $ | (15) |
| $ \max \left\{T_{i}^{\mathrm{p}} \cdot B_{i}^{\mathrm{p}} \cdot\left(1-x_{i j}\right)\right\} \leqslant B_{\mathrm{u}} $ | (16) |
| $ \begin{gathered} \sum\limits_{j=1}^{J}\left(\sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}} W_{j}^{\mathrm{k}} \cdot P_{i}^{\mathrm{b}} \cdot B_{i}^{\mathrm{b}} \cdot x_{i j}+\sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}} W_{j}^{\mathrm{k}} \cdot P_{i}^{\mathrm{p}} \cdot B_{i}^{\mathrm{p}} \cdot x_{i j}\right) \leqslant \\ \sum\limits_{j=1}^{J} W_{j}^{\mathrm{k}} \cdot B^{\mathrm{k}} \end{gathered} $ | (17) |
| $ \begin{gathered} \sum\limits_{j=1}^{J}\left[\sum\limits_{i \in \varphi_{\mathrm{b}} \cap \varphi_{j}}\left\lceil Q_{i j}^{\mathrm{b}} \cdot \frac{R}{3 N}\right\rceil \cdot S_{\mathrm{b}}\left(1-x_{i j}\right)+\sum\limits_{i \in \varphi_{\mathrm{p}} \cap \varphi_{j}}\left\lceil Q_{i j}^{\mathrm{p}} \cdot \frac{R}{3 N}\right\rceil \cdot\right. \\ \left.S_{\mathrm{p}}\left(1-x_{i j}\right)+\left\lceil W_{j}^{\mathrm{k}} \cdot \frac{R}{4 N}\right\rceil \cdot S_{\mathrm{kitlx}}\right] \leqslant S \end{gathered} $ | (18) |
式中:决策变量xij=1时,工位j的物料i是通过kit配送的;xij=0时,工位j的物料i是通过批量配送的;Bk为单个kit的质量,kg;Bib和Bip分别为单个以纸箱或托盘装载的物料i的质量,kg;Br和Bu分别为牵引车和叉车的额定载重量,kg;S为线边堆放区的总面积,km2。式(13)表示生产N件产品时,工位j对应的线边堆放区内的以纸箱装载的物料i的存储数量≥工位j对纸箱装载的物料i的需求数量;式(14)表示生产N件产品时,工位j对应的线边堆放区内的以托盘装载的物料i的存储数量≥工位j对托盘装载的物料i的需求数量;式(15)表示牵引车一次循环配送时,所装载的kit或各种物料的质量之和≤牵引车的额定承重量;式(16)表示叉车一次运送所装载的物料的质量≤叉车的额定载重量;式(17)表示各个工位所需的kit内各种物料的质量之和≤各个工位所需的kit的总质量;式(18)表示线边堆放区内各类物料和kit料箱的存储面积之和≤线边堆放区的总面积。
3 算例验证以某型号汽车为研究对象,对某汽车制造公司进行实地调研并获得相关数据。生产车间物料配送涉及的物料品项数为451种,生产线呈“U”型,涉及27个工位。固定参数取值如下:Sb=1.5 m2,Sp=2 m2,Br=800 kg,Ab=25箱,Cb=24元/h,Akit=32,tb=0.12s,Cs=27元/h,CL=25元/h,t1=0.09 s,t2=0.108 s,Db=2.6 km,Skit lx=1 m2,Dkit=2.8 km,v1=5.4 km/h,v2=4.2 km/h,d1=8 m,d2=12 m,tkit=0.06 s,dkit=2.5 m,Dz1=0.28 km,Dz2=0.17 km,db=3 m,dp=3 m,v3=3.6 km/h,tp=0.12 s,v4=4 km/h,Czz=26元/h,Zk=13.2 s,Bk=3.5 kg,S=400 m2,Bu=350 kg,Cm=4元/m2。
3.1 求解结果以收集的实际数据为基础设计算例,由于解空间较小,采用枚举算法可获得准确的最优解,单一配送方式下的算例计算结果见表 1,不同约束条件下的组合优化模型最优解计算结果见表 2。
| 表 1 单一配送方式下的算例计算结果 Tab. 1 Calculation results of the example under the single material distribution mode |
| 表 2 不同约束条件下的组合优化模型最优解结果 Tab. 2 Calculation results of the example under different constraints |
全约束条件是指考虑全部约束条件,即考虑式(13)~(18)的情况;部分约束条件是指考虑一部分约束条件,即仅考虑式(13)、(14)、(17)的情况。由表 1、2可知,在4种不同的情况下,物料全部进行批量配送所花费的成本最大,其次是物料全部采用kit配送的成本。部分约束条件下的组合优化模型最优解虽然能够最大程度节约成本,但没有考虑线边堆放区的空间限制以及运载车辆的载重限制,与实际生产存在一定差异,故在后续研究中不加以分析,仅考虑全约束条件下的组合优化模型最优解方式(后文简称“组合优化模型最优解”)。
在本算例中,与单一的批量配送和kit本着方式相比,改进的物料配送方式组合优化模型可以分别节约83.6%和70.8%的物流成本。为进一步验证所建立的组合优化模型在成本节约方面的鲁棒性,引入另外两组数据进行求解。当i=322、j=22时,组合优化模型最优解为36 171元,相比于单一的批量配送方式,可节约81.5%的成本,相比于单一的kit配送方式,可节约72.4%的成本;当i=384、j=24时,组合优化模型最优解为38 475元,相比于单一的批量配送方式,可节约84.5%的成本,相比于单一的kit配送方式,可节约70.7%的成本。
由此可知,针对物料全部采用批量配送和全部采用kit配送的情况,在物料种类数和工位数不同的条件下,组合优化模型最优解节约的成本百分比能够维持在一定范围内,无明显变化,说明所建立的模型对于配送成本节约效果良好,且具有较好的鲁棒性。单一的物料配送方式导致较高成本的原因为:单一批量配送方式需要大量线边堆存区空间来存储纸箱和托盘,且生产线人员寻找物料较为耗时;单一kit配送方式对物料进行二次处理,增加了工作人员的任务量、区域间的供料成本以及额外的仓储面积。改进的物料配送方式组合优化模型根据每种物料的特性为其选择最适合的配送方式,因此能够大幅度降低成本。算例求解结果中, 组合优化模型最优解中各成本项依次为C1=4 214.0元;C2=445.8元;C3=2 452.0元;C4=72.3元;Cβ1=92.0元;Cβ2=50.4元;Cβ3=1 143.1元;Cβ4=42 042元;Cβ5=514.8元。单一配送方式下的各成本见表 3。
| 表 3 单一配送方式下的各成本项 Tab. 3 Each cost item under the single material distribution mode |
由此可见,无论采用单一的批量配送还是kit配送,都有缺点,无法成为最佳的配送方式。只有将两种配送方式结合起来考虑,才能有效降低配送成本。
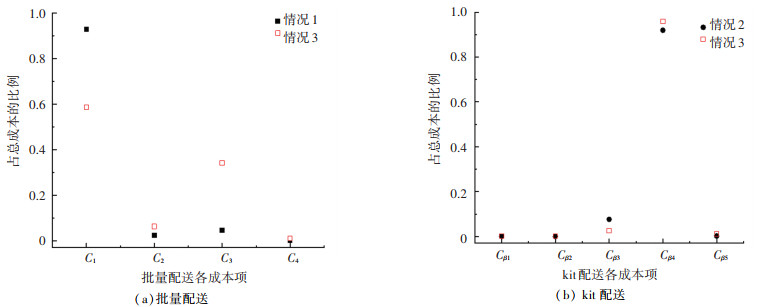
3.2 对比分析批量配送和kit配送中各成本所占的比例如图 4所示。图 4中情况1为物料均选择批量配送;情况2为物料均选择kit配送;情况3为组合优化模型最优解。如图 4(a)所示,由于批量配送对于线边堆放区储存空间的需求较高,且生产线人员会在工位和线边堆放区之间频繁往返,所以物料在线边堆放区的存储成本和生产线工作人员的拣料成本占据了较大的比重。如图 4(b)所示,由于物料配送过程多了组装kit这一环节,物料存储区至kit组装区的供料成本会占据较大比重。选择批量配送和kit配送的物料种类数情况如图 5所示,情况5为物料采用托盘形式进行配送,情况6为物料采用纸箱形式进行配送。因为装载物料的托盘重量通常比纸箱的重量大得多,所以以托盘形式装载的物料有更大概率会采取kit配送的方式。
|
图 4 批量配送和kit配送中各成本所占百分比 Fig. 4 Percentage of each costitem of batch distribution and kit distribution |
|
图 5 选择批量配送和kit配送的物料种类数 Fig. 5 Situations of the number of material types corresponding to batch distribution and kit distribution |
生产车间内有两种运输车辆:叉车和牵引车。不同的牵引车额定载重下的各成本项见表 4,不同的叉车额定载重下各成本项见表 5,Br表示牵引车额定载重,Bu表示叉车额定载重。从表 4和表 5可知,各成本项对于叉车额定载重的改变并不敏感,而批量配送下的线边存储成本和生产线人员的供料成本以及kit配送下的供料成本受牵引车额定载重变化的影响较大,其变化均呈现先慢后快的趋势。
| 表 4 不同Br下的各项成本 Tab. 4 Costs under different Br |
| 表 5 不同Bu下的各项成本 Tab. 5 Costs under different Bu |
不同线边堆放区面积下各成本项见表 6。与改变牵引车额定载重时各成本项受到的影响相同,批量配送下线边存储成本和生产线人员的拣料成本以及kit配送下的供料成本对于存储总面积的变动较为敏感。
| 表 6 不同S下的各项成本 Tab. 6 Costs under different S |
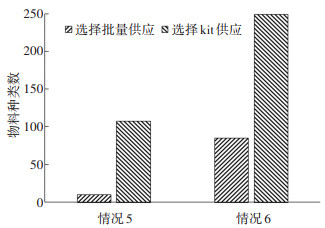
运输车辆额定载重和线边堆放区面积对配送方式选择的影响如图 6所示。由图 6(a)可知,改变叉车的额定载重对物料配送方式选择所造成的影响十分微弱;随着牵引车额定载重量的定量增长,选择kit配送方式的物料种类数并未随之线性下降,而是呈现先慢后快的下降趋势,在超过某一特定的额定载重量后,对配送方式的选择不再产生影响。
|
图 6 运输车辆额定载重和线边堆放区面积对配送方式选择的影响图 Fig. 6 Influence of rated loading capacity of transport vehicles and proportions of line stacking area on the choice of distribution modes |
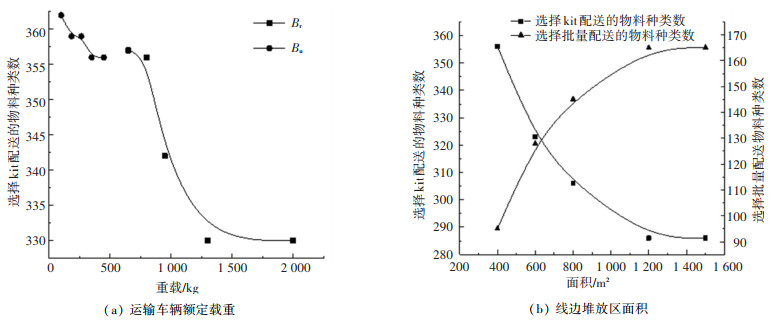
当线边堆放区的存储面积逐渐增大时,由于对空间限制的减弱,更多物料倾向于批量配送,如图 6(b)所示。随着存储面积的定量增加,选择两种方式的物料种类数均呈现先快后慢的变化趋势,超过特定值后,不再对决策变量x的取值和各成本项产生影响。运输车辆额定载重对于批量配送下线边堆放区的存储成本和kit配送下的供料成本的影响如图 7所示。线边堆放区总面积对于批量配送下线边堆放区的存储成本和kit配送下的供料成本的影响如图 8所示。

|
图 7 运输车辆额定载重对于两种成本的影响 Fig. 7 Influence of rated loading capacity of transport vehicles on the two costs |

|
图 8 线边堆放区面积对于两种成本的影响 Fig. 8 Influence of proportions of line stacking area on the two costs |
由图 7和图 8可知,无论是改变运输车辆额定载重还是线边堆放区面积,C1和Cβ4都呈现出较大的变化,将每个变化项的两种成本放在一起考虑,得到影响配送方式选择的因素的优先级顺序:线边堆放区总面积 > 牵引车额定载重 > 叉车额定载重。
5 结论1) 本文以配送总成本最小为目标,基于批量配送和kit配送方式,构建了改进的物料配送方式组合优化模型,并设计算例对模型进行了有效性验证,结果表明,与单一批量配送或kit配送方式相比,改进后的物料配送方式组合优化模型可以分别节约83.6%和70.8%的物流成本,具有较好的鲁棒性。相比于纸箱装载的物料,以托盘形式装载的物料有更大概率会选择kit配送方式。在有约束条件限制的情况下,更倾向于采用kit配送方式。
2) 敏感性分析表明,改变运输车辆额定载重和线边堆放区面积情况下,批量配送下线边堆放区的存储成本和kit配送下的供料成本都呈现出较大的变化,影响配送方式选择的因素优先级顺序:线边堆放区总面积 > 牵引车额定载重 > 叉车额定载重。研究结果可为物流配送过程提供优化决策建议。
3) 为了提升模型的易用性,本文建立的物料配送方式组合优化模型为线性优化模型,虽能在一定程度上解决配送成本过高的问题,但其适用性有待提高。后续研究将在此基础上建立非线性模型,增强其可行性,使模型更贴近实际。本文所建立的模型是单目标优化模型,配送方式选择的合理性仅考虑了配送成本,后续研究将致力于建立以配送总成本最优和配送总时间最短的双目标优化模型,以提升模型的实用性。
| [1] |
江林燕. 基于系统仿真的离散型制造企业生产线物料配送优化研究[D]. 南京: 东南大学, 2017 JIANG Linyan. Study on the improvement of material delivery for discrete manufacturing enterprises based on system simulation[D]. Nanjing: Southeast University, 2017 |
| [2] |
周炳海, 彭涛. 混流装配生产线准时化物料补给调度方法[J]. 控制与决策, 2017, 32(6): 976. ZHOU Binghai, PENG Tao. Scheduling methods of just-in-time material replenishment in mixed-model assembly lines[J]. Control and Decision, 2017, 32(6): 976. |
| [3] |
徐君翔, 郭静妮. 基于大数据平台下的物流配送车辆路径问题研究[J]. 交通运输系统工程与信息, 2018, 18(增刊1): 86. XU Junxiang, GUO Jingni. Research onlogistics vehicle routing problem based on big data framework[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(S1): 86. |
| [4] |
葛妍娇, 郭宇, 黄少华, 等. 基于智能感知网的物料配送动态优化方法[J]. 计算机工程与应用, 2019, 55(22): 212. GE Yanjiao, GUO Yu, HUANG Shaohua, et al. Dynamic optimization method for material delivery based on intelligent sensing network[J]. Computer Engineering and Applications, 2019, 55(22): 212. DOI:10.3778/j.issn.1002-8331.1808-0103 |
| [5] |
彭慧杰, 李成松, 李景彬, 等. 穴播器混流装配线动态物料配送方法优化研究[J]. 机械设计与制造, 2020(11): 246. PENG Huijie, LI Chengsong, LI Jingbin, et al. Optimization of dynamic material distribution method for dibbler mixed-model assembly line[J]. Machinery Design & Manufacture, 2020(11): 246. DOI:10.3969/j.issn.1001-3997.2020.11.061 |
| [6] |
张连超, 刘蔚然, 程江峰, 等. 卫星总装数字孪生车间物料准时配送方法[J]. 计算机集成制造系统, 2020, 26(11): 2897. ZHANG Lianchao, LlU Weiran, CHENG Jiangfeng, et al. Just-in-time material distribution method for satellite assembly digital twin shop-floor[J]. Computer Integrated Manufacturing Systems, 2020, 26(11): 2897. |
| [7] |
RAMACHANDRAN S, DELEN D. Performance analysis of a kitting process in stochastic assembly systems[J]. Computers & Operations Research, 2005, 32(3): 449. |
| [8] |
CAPUTO A C, PELAGAGGE P M. A methodology for selecting assembly systems feeding policy[J]. Industrial Management & Data Systems, 2011, 111(1): 84. |
| [9] |
HUA S Y, JOHNSON D J. Research issues on factors influencing the choice of kitting versus line stocking[J]. International Journal of Production Research, 2010, 48(3): 779. DOI:10.1080/00207540802456802 |
| [10] |
LIMÈRE V, LANDEGHEM H V, GOETSCHALCKX M. A decision model for kitting and line stocking with variable operator walking distances[J]. Assembly Automation, 2015, 35(1): 47. DOI:10.1108/AA-05-2014-043 |
| [11] |
ZHOU Binghai, SHEN Chengyi. Multi-objective optimization of material delivery for mixed model assembly lines with energy consideration[J]. Journal of Cleaner Production, 2018, 192: 293. DOI:10.1016/j.jclepro.2018.04.251 |
| [12] |
WU Qun, LIAO Ying, LIAO Kun, et al. Optimisation evaluation on material distribution systems: from the perspective of automobile manufactures[J]. International Journal of Technology, Policy and Management, 2020, 20(2): 104. DOI:10.1504/IJTPM.2020.108747 |
| [13] |
SCHMID N A, LIMÈRE V. A classification of tactical assembly line feeding problems[J]. International Journal of Production Research, 2019, 57(24): 7588. |
| [14] |
HANSON R, BROLIN A. A comparison of kitting and continuous supply in in-plant materials supply[J]. International Journal of Production Research, 2013, 51(4): 979. DOI:10.1080/00207543.2012.657806 |
| [15] |
KHAJAVI S H, BAUMERS M, HOLMSTRÖM J, et al. To kit or not to kit: analysing the value of model-based kitting for additive manufacturing[J]. Computers in Industry, 2018, 98: 102. |
 2022, Vol. 54
2022, Vol. 54


