2. 哈尔滨工业大学(威海) 汽车工程学院,山东 威海 264209;
3. 陕西省公安厅交通管理局,西安 710061
2. School of Automotive Engineering, Harbin Institute of Technology, Weihai, Weihai 264209, Shandong, China;
3. Traffic Administration of Shaanxi Public Security Department, Xi'an 710061, China
冰雪天气导致高速公路路面平整度和抗滑性能显著下降,是引发交通事故的重要因素。文献[1]对1967—2005年相关文献分析后发现:降雪可导致事故率和受伤率平均分别增加84%和75%。中国受冰雪影响的区域约占国土面积的一半,冬季是高速公路事故多发期,恶劣的路面条件与之密切相关,每百万公里冰雪路面事故率高达20.8%,是正常道路环境下的两倍[2]。鉴于冰雪路面下事故的高发特征,准确识别其影响因素,挖掘各因素对事故的影响规律,从而为制定有效的安全改善措施提供决策依据,对提高冰雪路面下的行车安全性至关重要。
高速公路交通系统中人、车、路及环境等因素间存在复杂的交互作用,某方面因素的失衡就可能导致交通事故。以往对事故影响因素的定量分析,大多是根据事故分布特点,构建统计模型[3-5]。随着研究的深入,交通事故的成因分析已由早期的单因素或多因素分析发展到系统致因分析。故障树分析法是一种典型的系统致因理论方法,其模型结构直观明了、简单易行,应用较为广泛,文献[6]对西弗吉尼亚州12起矿运卡车死亡事故分别建立故障树模型,分析诱发事故的高风险因素;文献[7]依据事件链原理,建立山区高速公路伤亡事故故障树模型,分析事故成因;文献[8]将故障树和模糊集理论相结合进行定量分析,将其应用到高铁安全管理中。贝叶斯网络也是交通安全领域常用的分析方法,文献[9]分别建立西班牙乡村公路轻伤、重伤和死亡事故的贝叶斯网络模型,基于贝叶斯推理,鉴别事故严重程度影响因素;文献[10]基于昆山市两年的交通事故数据,建立基于贝叶斯网络的事故严重程度预测模型,研究各指标对事故严重程度的影响及各因素之间的交互作用。传统模型中的事件只有两种状态,即故障和正常,难以描述具有多种状态的事件(如本文中事故严重程度),且假设事故因素间相互独立。贝叶斯网络通过调整模型结构和节点间条件概率表,可描述事件的多态性和逻辑关系的不确定性,但网络结构的构建较为复杂。故障树可简化贝叶斯网络结构的构建过程,而贝叶斯网络推理又可弥补故障树的缺陷,提高其定量分析的精度,因此,已有研究将两者结合应用到机械领域及航海领域等[11-12],并取得了较好的应用效果。但目前,将故障树与贝叶斯网络相结合的模型在交通安全领域的应用较少,仍需进一步研究以验证该模型的适用性。
综上,本文在构建故障树模型的基础上进一步引入贝叶斯网络,为克服故障树中事故因素间相互独立和事故只有两态的缺陷,在转化后的贝叶斯网络中增设了3条表征因素间相关性的有向弧,并根据事故严重程度,将叶节点分为3种状态T1、T2、T3,对叶节点条件概率表进行了更新。通过贝叶斯网络逆向推理和敏感性分析,在识别事故致因因素的同时,进一步分析事故严重程度影响因素。本文提出的故障树和贝叶斯网络相结合的方法可为事故因素分析提供新视角。
1 数据来源数据来源于黑龙江省高速公路数据管理系统,从中提取了2010—2018年省内高速公路冰雪路面下的交通事故,删除记录信息不全的事故,共计367起。每条事故数据均包含事故类型、事故发生时间、地点、事故形态、事故认定原因、驾驶员性别、驾龄、受伤部位、车辆类型、路表状况、道路线型和天气等信息,模型涉及的驾驶员、车辆、道路及环境因素见表 1。
| 表 1 模型事件信息汇总 Tab. 1 Information summary for crash events |
本文定义的“冰雪路面”包括各种冰雪凝结物理状态,如松雪、冰板、冰膜、雪浆等,此外,将连续变量“能见度小于等于200 m”和“驾龄小于等于3年”分别归类为“能见度低”[13]和“驾驶经验不足”[14]。
2 事故影响因素分析方法 2.1 故障树故障树(fault tree, FT)分析法是将定性和定量分析相结合的图形演绎及逻辑推理方法,具体是以某个不希望发生的事件为起点,自上而下分析其发生原因,并将引发该事件的原因用树形图进行表述[15]。故障树中事件类型分为顶事件、中间事件和基本事件:顶事件,不希望发生的某类事件(本文交通事故);中间事件,位于顶事件和基本事件之间的结果事件;基本事件,导致顶事件发生的最基本原因(事故因素)。事件间逻辑关系用逻辑门表示,常用的逻辑门包括与门和或门:与门,输出事件必须在所有输入事件都发生时才发生;或门,只要有一个输入事件发生,输出事件就能发生。
2.2 贝叶斯网络贝叶斯网络(Bayesian network, BN)由网络结构和条件概率表组成,即BN=〈G, Θ〉。其中,G表示网络结构(有向无环图),由节点和有向弧构成,节点代表随机变量,有向弧代表节点间因果关系,由父节点指向子节点;Θ表示节点间条件概率表,Θ=P{Xi|Val(Parents(Xi))}(1≤i≤n),其中Val(Parents(Xi))表示节点Xi的父节点集,n表示父节点的个数。贝叶斯网络结构中,无父节点的节点称为根节点,无子节点的节点称为叶节点。贝叶斯网络结构示意见图 1,其中X2和X3为M1的父节点,M1为X2和X3的子节点,X1、X2、X3为根节点,M1为中间节点,T为叶节点。
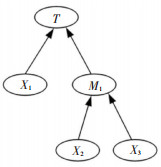
|
图 1 贝叶斯网络结构示意 Fig. 1 Schematic of Bayesian network structure |
基于贝叶斯原理,设A、B为两个基本事件,则
| $ P(B \mid A)=\frac{P(A \mid B) \times P(B)}{P(A)} $ | (1) |
若E为样本空间,B1, B2, …, Bn为样本空间的完备事件组,则
| $ P(A)=\sum\limits_{i=1}^{n} P\left(A \mid B_{i}\right) P\left(B_{i}\right) $ | (2) |
进一步推理,得
| $ P\left(B_{i} \mid A\right)=\frac{P\left(B_{i} \mid A\right) \times P\left(B_{i}\right)}{\sum\limits_{i=1}^{n} P\left(B_{i} \mid A\right) P\left(B_{i}\right)} $ | (3) |
式中:P(Bi)为事件Bi的先验概率,P(Bi|A)为事件Bi的后验概率。
基于式(3)可进行简单的贝叶斯网络逆向推理,即假设事故发生的风险水平已知(事件发生),逆向推理可得到各根节点的后验概率(P(Bi|A)),通过观察节点风险等级状态概率的变化情况(如节点先验概率与后验概率的差异),逆向分析并寻找原因。
贝叶斯网络还可进行敏感性分析,通过分析数值参数(如根节点先验概率)的微小变化对输出参数(如叶节点先验概率)的影响,鉴别出对目标节点影响较大的指标。在安全管理中,基于各因素的敏感性大小,可迅速识别对结果(事故风险)影响较大的因素,予以重点关注。本文基于文献[16]提出的敏感性分析算法进行贝叶斯网络敏感性分析。
2.3 故障树向贝叶斯网络的转化故障树和贝叶斯网络均可用于事故因素分析。传统故障树主要基于布尔代数法定性分析求解最小割集,进而进行定量分析,定量分析对定性分析的全面性和精确度要求较高,否则会有较大的数据偏差。贝叶斯网络的构建是一个不确定知识的获取过程,包括结构学习和参数学习,其中结构学习方法主要包括专家意见法、机器学习法和专家意见与机器学习相结合的办法,参数学习方法包括最大似然估计法、SEM算法和贝叶斯方法等,整体上模型构建过程较为复杂。综上,故障树模型虽简单易用,但难以准确地进行定量分析;贝叶斯网络在定量分析方面具备优势,但其网络结构构建相对复杂。鉴于二者的模型图和推理机制相似,可将故障树转换为贝叶斯网络形式,以简化贝叶斯网络建模过程,同时弥补故障树定量分析的不足。具体步骤:1)将故障树中基本事件、中间事件和顶事件分别转换为贝叶斯网络的根节点、中间节点和叶节点;2)根据故障树事件间的逻辑关系将贝叶斯网络中所有节点连接起来,有向弧的方向对应故障树中逻辑门的输入或输出关系;3)将故障树中各基本事件的概率作为贝叶斯网络中对应根节点的先验概率,根据故障树中逻辑门类型,确定中间节点和叶节点的条件概率表。故障树逻辑门与贝叶斯网络条件概率表间的转换规则见图 2,其中“1”表示事件发生,“0”表示事件不发生。
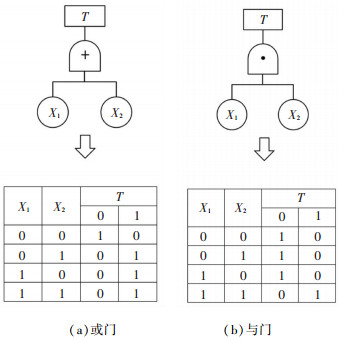
|
图 2 FT逻辑门与BN条件概率表间转换规则 Fig. 2 Conversion rules between FT logic gate and BN conditional probability table |
传统的故障树方法只能对事故的两种状态(如:“发生事故”与“不发生事故”,“严重事故”与“非严重事故”等)进行分析,当事故状态超过两种时,故障树方法不再适用,而贝叶斯网络中节点可设置为多种状态,弥补了故障树的不足。本文的事故状态(或事故类型)分为财产损失、受伤和死亡3种,分别以贝叶斯网络中叶节点的3种状态T1、T2、T3表示。
故障树模型中各事故因素间相互独立,然而在实际情况中,部分因素之间存在一定联系,如:驾驶经验不足可能导致驾驶员操作不当,超载的车辆大多是货车,雨、雪、雾等不良天气会影响驾驶员视野,导致能见度降低。根据因素间的因果关系,在故障树结构的基础上,转化后的贝叶斯网络中增设3条有向弧,见图 4。此有向弧子节点X2、X12和X19的条件概率表根据事故数据中因素间的条件概率确定。
转换后的贝叶斯网络中,叶节点表示交通事故,其父节点为M1、M2、M3、M4,分别代表人、车、路及环境4种因素。基于事故数据,可得到3种状态在各父节点发生时的条件概率P(Tm|Mi, …, Mj)(1≤m≤3, 1≤i≤j, 1≤j≤4),计算公式为
| $ P\left(T_{m} \mid M_{i}, \cdots, M_{j}\right)=\sum\limits_{n=i}^{j} P\left(T_{m} \mid M_{n}\right) $ | (4) |
| $ \sum\limits_{m=1}^{3} P\left(T_{m} \mid M_{i}, \cdots, M_{j}\right)+P\left(0 \mid M_{i}, \cdots, M_{j}\right)=1 $ | (5) |
式中P(0|Mi, …, Mj)为事件不发生的概率。式(5)归一化后可得叶节点的条件概率,见表 2。
| 表 2 叶节点条件概率 Tab. 2 Conditional probability table of leaf nodes |
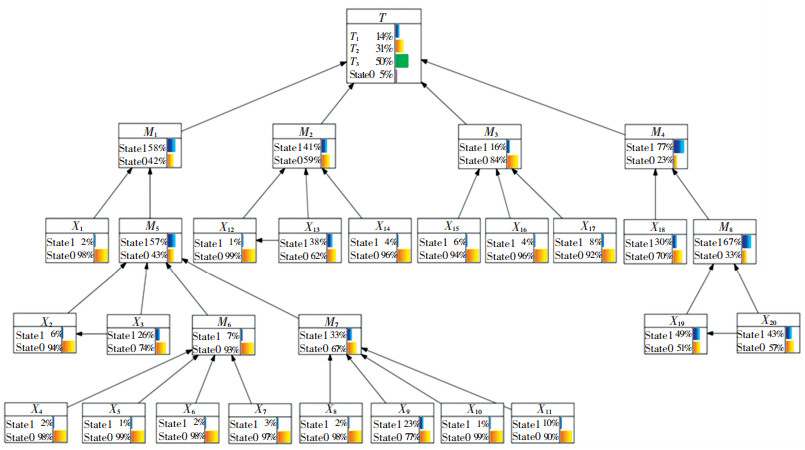
以冰雪路面下高速公路交通事故为顶事件,19个具体因素为基本事件,构建故障树模型,从上到下逐级分析事故发生原因。构建的故障树模型见图 3,转换修正后的贝叶斯网络见图 4。
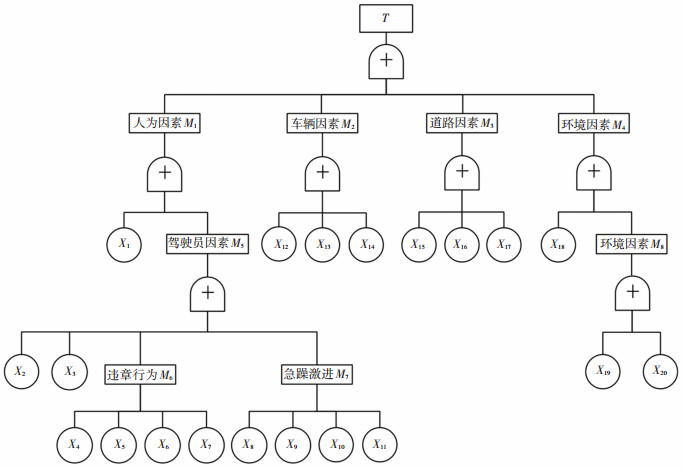
|
图 3 冰雪路面下高速公路事故故障树模型 Fig. 3 Fault tree crash model for ice-snow covered freeways |
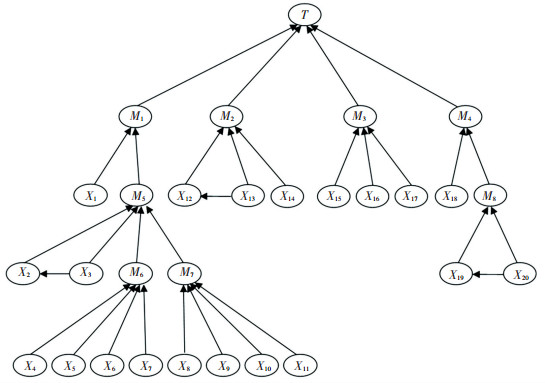
|
图 4 冰雪路面下高速公路事故贝叶斯网络模型 Fig. 4 Bayesian network crash model for ice-snow covered freeways |
有向弧子节点X2、X12和X19的条件概率表根据事故数据中因素间的条件概率确定,其余根节点的先验概率为故障树中基本事件的概率,中间节点的条件概率表由故障树逻辑门转换得到,叶节点的条件概率由表 2直接得到。根据贝叶斯网络推理,计算各非根节点的先验概率,见图 5。分别假定财产损失事故(T1)、受伤事故(T2)和死亡事故(T3)发生的概率为100%,根据贝叶斯网络逆向推理,算得各节点的后验概率。
|
图 5 先验概率计算结果 Fig. 5 Calculation results of prior probability |
事故数据中3种事故状态的比例分别为17%、39%和44%,本模型预测事故状态比例分别为14%、31%和50%,基本与实际相符。故障树概率统计的基本假设为“事故已发生”,即P(T)=1,图 5中冰雪路面下高速公路交通事故的先验概率为0.95,可能原因是故障树建模时某些事故因素未被识别。由于建模过程中不可避免地存在一定误差,且本模型误差小于10%,故认为该模型可有效反映事故因素特征。
随机抽取30%的事故数据,以其中的受伤事故为例,由模型计算得到的各因素后验概率与样本中的实际概率趋势基本相符,见图 6。与样本实际概率相比,受伤事故模型后验概率平均绝对误差(MAE)为4.84%,均方根误差(RMSE)为6.25%,表明贝叶斯网络推理分析精度较高,可用于事故致因因素分析。

|
图 6 受伤事故后验概率与样本实际概率曲线 Fig. 6 Posterior probability and actual probability curves of injury crashes |
根节点后验概率分布见图 7,图 7表明,除X13外,其他节点在3种事故状态下的后验概率相差不大,后验概率较高的节点依次为X19、X20、X13、X18、X3、X9、X11,表明这些基本事件是诱发交通事故的主要因素,在风险管理中应优先和重点关注。以上因素分别表示:能见度低、不良天气(雨、雪、雾)、货车、夜间无照明、驾驶经验不足、超速行驶、未保持安全距离。其潜在原因:低能见度和夜间无照明直接影响驾驶员视野,遇到突发情况时,可导致驾驶员采取延迟制动或无效的避让动作;“雨、雪、雾”环境下驾驶员视线受阻,水滴、雪颗粒和光的共同作用将显著降低驾驶员对物体的辨认能力,且不良天气造成能见度降低,影响驾驶员的判断;缺乏经验的驾驶员,行车场景经历较少,在复杂路面状况下行驶时往往过度紧张,从而做出错误判断,增加了事故发生风险;冰雪路面下,道路与车辆间摩擦系数降低,刹车距离显著增加,超速行驶与车距保持不足均极易导致车辆追尾及连环相撞事故,且货车的制动性能远不及小轿车,在湿滑的路面条件下,更容易导致追尾事故,使得货车成为主要肇事车型之一。

|
图 7 根节点后验概率分布 Fig. 7 Posterior probability distribution of root nodes |
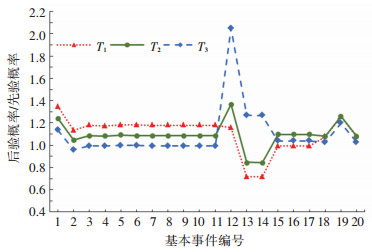
后验概率与先验概率的比值可用来衡量各根节点与叶结点之间的关系,比值越大表明该根节点对叶节点的影响越大。图 8为给定状态下各根节点后验概率与先验概率的比值,可见,X12、X13、X14在T3状态下的后验概率增长率较大,明显高于T1和T2状态,表明这些因素更容易加重事故发生后的严重程度。
|
图 8 根节点后验概率与先验概率的比值 Fig. 8 Ratios of posterior probability to prior probability of root nodes |
上述加重事故严重程度的因素分别代表超载、货车、违法上路。其潜在原因:超载的车型大多为货车,货车本身制动性能较差,超载使得车辆惯性增大、制动距离变长,导致紧急情况下不能及时减速停车,加之冰雪路面十分湿滑,紧急制动容易导致车辆倾翻等事故,车辆自身的重量及洒落的货物,会影响自身及其他车辆的安全;涉及货车的多为追尾事故,当追尾车辆为小汽车时,两种车型的速度差、质量差和货车尾部的防护装置等均会加重对小汽车驾驶员的伤害程度;机件(如:转向、制动及安全辅助系统等)质量不符合要求的车辆违法上路时,可导致驾驶员采取的转向等避让动作无法有效执行,高速公路车速较高,事故一旦发生,后果必然十分严重。
4.2 贝叶斯网络敏感性分析3种事故状态发生概率为100%时,人、车、路和环境四要素的后验概率见表 3。3种状态下,M1和M4的后验概率明显高于M2和M3,且4个节点的概率之和均大于100%,这表明人和环境要素对事故影响较大,且各要素之间存在复杂的交互作用。
| 表 3 3种事故状态下四要素的后验概率 Tab. 3 Posteriori probability of four major factors for three crash states |
将中间节点M1、M4设置为目标节点,对其进行敏感性分析,得到各因素的敏感值,结果见表 4。节点X3、X9的敏感值明显高于其他节点,为M1的高敏感度因素;节点X20、X19的敏感值明显高于X18,为M4的高敏感度因素。结果表明,两要素中驾驶经验不足、超速行驶、不良天气(雨、雪、雾)和能见度低为诱发冰雪路面高速公路事故的高敏感因素。
| 表 4 敏感性分析结果 Tab. 4 Sensitivity analysis results |
基于贝叶斯网络逆向推理和敏感性的分析结果,为提高冰雪路面下高速公路行车安全性,在常年受冰雪影响的高速公路上,应增加轮廓标等低能见度视线诱导设施,优化夜间照明装置;加强电子监控和执法力度,减少超速、违章驾驶、车辆违法上路等现象;对于车辆超载,应采取“联合治超”手段,从根本上解决超载问题;加强对货运公司及货车驾驶员的监管,随时查询货车行驶状态,当周边环境及路面状态不宜行车时,应及时到服务区停车休息;建议相关部门对高速公路实行动态监管,制定冰雪路面和不良天气下高速公路限速及关闭标准,并严格实施;对高寒地区,尽可能采用功能性路面建设材料,提升道路自身的融雪及抗冰防滑能力。
5 结论1) 针对冰雪路面下高速公路交通事故,构建了基于故障树和贝叶斯网络的综合模型,该模型克服了传统故障模型中事件只有两态和因素间相互独立的缺陷,同时提高了故障树定量分析的精度。
2) 贝叶斯网络逆向推理结果表明:能见度低、不良天气(雨、雪、雾)、货车、夜间无照明、驾驶经验不足、超速行驶、未保持安全距离等,是诱发事故的高风险因素,在风险防控中应予以重点关注;根节点概率变化趋势表明:超载、货车、违法上路等因素在冰雪路面下,更易加重事故发生后的严重程度;贝叶斯网络敏感性分析结果表明:人和环境要素对事故影响较大,且各要素之间存在复杂的交互作用,两要素中,驾驶经验不足、超速行驶、不良天气(雨、雪、雾)和能见度低敏感性较强,极易诱发事故。
3) 本文数据来源于交警事故记录系统,数据量偏少,未来可综合更多冰雪路面事故数据进行分析,增加分析结果的普适性;此外,还可针对非冰雪路面交通事故构建模型,并与本文结果进行对比,以便更准确地掌握冰雪条件对交通安全的影响。
| [1] |
QIU Lin, NIXON W A. Effects of adverse weather on traffic crashes: systematic review and meta-analysis[J]. Transportation Research Record, 2008, 2055(1): 139. DOI:10.3141/2055-16 |
| [2] |
刘小高, 许书红, 潘凌峰, 等. 冰雪天气高速公路行车安全预警等级标定[J]. 黑龙江交通科技, 2018, 41(11): 165. LIU Xiaogao, XU Shuhong, PAN Lingfeng, et al. The calibration of freeway traffic safety warning level under snow and ice conditions[J]. Communications Science and Technology Heilongjiang, 2018, 41(11): 165. DOI:10.3969/j.issn.1008-3383.2018.11.095 |
| [3] |
HOU Qinzhong, HUO Xiaoyan, LENG Junqiang, et al. Examination of driver injury severity in freeway single-vehicle crashes using a mixed logit model with heterogeneity-in-means[J]. Physica A: Statistical Mechanics and its Applications, 2019, 531: 121760. DOI:10.1016/j.physa.2019.121760 |
| [4] |
HUO Xiaoyan, LENG Junqiang, HOU Qinzhong, et al. Assessing the explanatory and predictive performance of a random parameters count model with heterogeneity in means and variances[J]. Accident Analysis & Prevention, 2020, 147: 105759. DOI:10.1016/j.aap.2020.105759 |
| [5] |
HOU Qinzhong, HUO Xiaoyan, LENG Junqiang. A correlated random parameters tobit model to analyze the safety effects and temporal instability of factors affecting crash rates[J]. Accident Analysis & Prevention, 2020, 134: 105326. DOI:10.1016/j.aap.2019.105326 |
| [6] |
ZHANG Meng, KECOJEVIC V, KOMLJENOVIC D. Investigation of haul truck-related fatal accidents in surface mining using fault tree analysis[J]. Safety Science, 2014, 65: 106. DOI:10.1016/j.ssci.2014.01.005 |
| [7] |
孟祥海, 柳昕汝. 山区高速公路伤亡事故故障树模型及事故成因分析[J]. 公路交通技术, 2018, 34(5): 118. MENG Xianghai, LIU Xinru. Fault tree analysis model for fatal and injury crashes on mountainous freeways and causes analysis of crashes[J]. Technology of Highway and Transport, 2018, 34(5): 118. |
| [8] |
LIU Pei, YANG Lixing, GAO Ziyou, et al. Fault tree analysis combined with quantitative analysis for high-speed railway accidents[J]. Safety Science, 2015, 79: 344. DOI:10.1016/j.ssci.2015.06.017 |
| [9] |
De OÑA J, MUJALLI R O, CALVO F J. Analysis of traffic accident injury severity on Spanish rural highways using Bayesian networks[J]. Accident Analysis & Prevention, 2011, 43(1): 402. DOI:10.1016/j.aap.2010.09.010 |
| [10] |
SONG Yaochao, KOU Siyuan, WANG Chen. Modeling crash severity by considering risk indicators of driver and roadway: a Bayesian network approach[J]. Journal of Safety Research, 2020. DOI:10.1016/j.jsr.2020.11.006 |
| [11] |
DONGIOVANNI D N, IESMANTAS T. Failure rate modeling using fault tree analysis and Bayesian network: DEMO pulsed operation turbine study case[J]. Fusion Engineering and Design, 2016, 109-111: 613. DOI:10.1016/j.fusengdes.2016.02.036 |
| [12] |
LANDQUIST H, ROSEN L, LINDHE A, et al. Bayesian updating in a fault tree model for shipwreck risk assessment[J]. Science of the Total Environment, 2017, 590-591: 80. DOI:10.1016/j.scitotenv.2017.03.033 |
| [13] |
张甜甜, 陈永. 雾霾天气低能见度下的交通流仿真研究[J]. 黑龙江交通科技, 2018, 41(10): 167. ZHANG Tiantian, CHEN Yong. Traffic flow simulation study under low visibility in haze and haze[J]. Communications Science and Technology Heilongjiang, 2018, 41(10): 167. DOI:10.3969/j.issn.1008-3383.2018.10.087 |
| [14] |
刘雪梅, 向往. 不同驾龄新手驾驶员感知能力认知偏差分析[J]. 黑龙江科学, 2020, 11(22): 162. LIU Xuemei, XIANG Wang. Analysis of perception ability cognitive bias of green hands divers of different driving years[J]. Heilongjiang Science, 2020, 11(22): 162. DOI:10.3969/j.issn.1674-8646.2020.22.076 |
| [15] |
KABIR S. An overview of fault tree analysis and its application in model based dependability analysis[J]. Expert Systems with Applications, 2017, 77: 114. DOI:10.1016/j.eswa.2017.01.058 |
| [16] |
KJAERULFF U, Van Der GAAG L C. Making sensitivity analysis computationally efficient[C]// Sixteenth Conference on Uncertainty in Artificial Intelligence. Stanford: UAI, 2013
|
 2022, Vol. 54
2022, Vol. 54


