2. 深圳市市政设计研究院有限公司,广东 深圳, 518000
2. Shenzhen Municipal Design & Research Institute Co., Ltd., Shenzhen 518000, Guangdong, China
预弯预应力组合梁(简称预弯组合梁或预弯梁)是在预弯工字形钢梁上浇筑一期混凝土及腹板、桥面板等二期混凝土,以利用钢梁的反弹作用对处于受拉区的一期混凝土施加预压应力,由此得到的组合结构[1-2],相比与其用钢量相近的钢结构,其刚度明显增加,抗疲劳性能增强,振动噪音降低;与使用广泛的钢筋混凝土结构相比,当其外形尺寸相似时,其承载力大幅提高,且抗裂性能好;与预应力混凝土结构相比,其截面尺寸减小。正是由于预弯预应力组合梁与钢结构、钢筋混凝土结构以及预应力混凝土结构相比有其独特的优越性,并考虑其在桥梁经济性方面的优势,故可被广泛用于多层以上立交桥或公路城市高架桥[2]。
预弯梁是20世纪40年代后期由比利时工程师A. Lipski(利普斯基)等提出的[3]。国外对预弯组合梁的设计方法研究比较完善的主要是日本,日本对预弯组合梁应力及挠度计算的弹性计算方法进行了研究,并推出了设计规范及标准化设计[4]。韩国对预制预弯组合梁的施工方法和完全预制的预弯组合梁桥的弹塑性性能等方面展开了研究[5]。
在预弯组合梁这一结构引入国内后,国内的桥梁设计者和科研人员在试验及总结工程经验的基础上,对预弯组合梁桥的应力、挠度及裂缝计算上,主要采用以换算截面为基础的弹性设计方法[6-7]。陆亚芳等[8]对预弯组合梁正截面极限强度,给出了一种粗略的计算方法,并使用试验进行验证。黄侨等[9]通过对10根梁的极限承载力试验对预弯预应力混凝土简支梁桥的抗弯及抗剪极限承载力进行研究,并提出建议的计算方法,最终用于工程实践。张光波等[10]基于对5根预弯梁的加载试验结果,提出了抗弯承载力计算公式,计算时认为钢梁下缘及部分腹板达到塑性,而钢梁上缘还未屈服,而受压区混凝土采用矩形应力分布图形计算。郑一峰等[11]基于10片预弯组合试验梁试验,并在预弯组合梁弹塑性极限状态的破坏机理提出了基于弹塑性理论的预弯组合梁抗弯和抗剪强度的实用计算方法,且该计算方法的计算值与试验值吻合良好。在此之后,国内关于预弯组合梁极限承载能力的研究开展较少。直至2018年,中国住房与城乡建设部颁布了《预弯预应力组合梁桥技术标准》(CJJ/T 276—2018)[7],标准中基于弹塑性理论,给出了预弯组合梁的抗弯承载力计算方法。相关研究表明,采用该方法计算预弯组合梁的抗弯承载力精度较高。
中国其他相关组合结构规范,如住房和城乡建设部颁布的《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[12]和《钢结构设计规范》(GB 50017—2017)[13]等,计算钢混组合梁截面抗弯承载力均采用了塑性方法,并对钢梁尺寸进行了限定。《预弯预应力组合梁桥技术标准》(CJJ/T 276—2018)[7]中,抗弯承载力计算所用的弹塑性方法与现行规范中的计算方法有所不同。为方便工程技术人员的理解与应用,本文基于塑性理论,对预弯预应力组合梁的抗弯承载力计算方法进行再研究。力图对《预弯预应力组合梁桥技术标准》(CJJ/T 276—2018)[7]中计算较为繁琐的抗弯承载力计算方法进行简化,同时使得其与住房与城乡建设部其他相关规范计算理论相一致。
1 预弯组合梁的截面抗弯承载力的基本表达式与基本假设现行《预弯预应力组合梁桥技术标准》(CJJ/T 276—2018)[7]中给出了基于弹塑性理论的截面抗弯承载力计算公式,该计算方法是基于预弯组合梁弹塑性极限状态的破坏机理而提出的。具体验算公式[7]为
| $ \gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{ud}} $ | (1) |
式中:Md为承载能力极限状态下作用效应基本组合的截面弯矩设计值,Mud为截面按照弹塑性理论方法计算的抗弯承载力设计值, γ0为桥梁结构重要性系数。
该计算方法给出以下基本假定[7]: 1)截面变形符合平截面假定,即钢梁与混凝土间抗剪连接件连接良好、且无滑移,混凝土的极限压应变取为εu=3 500 με;2)一期混凝土及二期混凝土的受拉区开裂后均退出工作,全部拉力由钢梁承担;3)钢梁上下翼板厚度相等且均可达到屈服,认为钢腹板上存在弹性区域,腹板下部部分钢板达到屈服,其应力分布为矩形,且应力均达到钢材的抗拉强度设计值;4)二期混凝土受压区应力分布为矩形,其应力图高度为x。
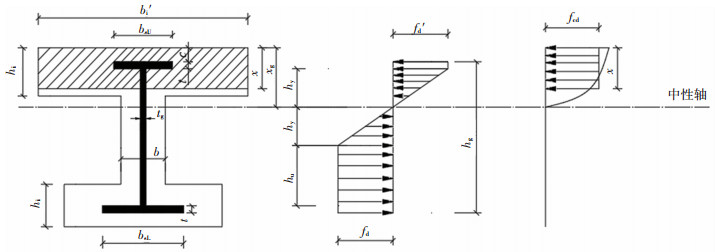
根据上述假定,基于弹塑性理论的预弯组合梁抗弯承载力计算采用如图 1所示的计算图式[7]。
|
图 1 弹塑性抗弯承载能力计算图式 Fig. 1 Schematic of calculation of elastoplastic bending capacity |
| $ \Delta b_{\mathrm{s}}=b_{\mathrm{sL}}-b_{\mathrm{sU}} $ | (2) |
| $ h_{\mathrm{y}}=\frac{x}{0.8}-c-t $ | (3) |
| $ h_{\mathrm{u}}=h_{\mathrm{g}}-2 h_{\mathrm{y}}-2 t=h_{\mathrm{g}}-\frac{2 x}{0.8}+2 c $ | (4) |
| $ x_{\mathrm{s}}=\frac{x}{0.8} $ | (5) |
式中:hy为钢梁腹板弹性区高度,hu为钢梁腹板塑性区高度,bsL、bsU分别为钢梁上、下缘宽度,hg为预弯钢梁高度,t分别为钢梁翼板厚度,x、xs分别为混凝土矩形应力块高度和实际受压区高度,c为上缘混凝土保护层厚度。
根据中性轴位置的不同,需要考虑两种情况[7]:
1) 混凝土等效矩形应力块高度位于二期混凝土上翼缘(x≤h′i),由∑N=0,得
| $ f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x=f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (6) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{ud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}\left(\frac{h_{\mathrm{u}}}{2}+\frac{x}{0.8}-c-t\right)+ \\ &\frac{2}{3} f_{\mathrm{d}} t_{\mathrm{w}}\left(\frac{x}{0.8}-c-t\right)^{2}+f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (7) |
2) 混凝土等效矩形应力块高度位于二期混凝土腹板内(x≥h′i),由∑N=0,得
| $ f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)+f_{\mathrm{cd}} b x=f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (8) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{ud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}\left(\frac{h_{\mathrm{u}}}{2}+\frac{x}{0.8}-c-t\right)+ \\ &\frac{2}{3} f_{\mathrm{d}} t_{\mathrm{w}}\left(\frac{x}{0.8}-c-t\right)^{2}+f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)\left(\frac{x}{0.8}-\frac{h_{\mathrm{i}}^{\prime}}{2}\right)+ \\ &f_{\mathrm{cd}} b x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (9) |
在实际应用时,按式(6)、(8)计算中性轴的位置,按式(7)、(9)确定截面弹塑性抗弯承载力[7]。
2 基于塑性理论的预弯组合梁抗弯承载力计算方法 2.1 塑性抗弯承载力的基本概念目前,国内外钢筋混凝土结构设计规范中的受弯梁承载力多采用塑性方法[12]。而钢结构和钢-混凝土组合结构受弯梁则既有采用弹性方法计算截面抗弯承载力的,也有采用塑性方法进行计算的[13-17]。住房与城乡建设部颁布的现行《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[13]和《钢结构设计规范》(GB 50017—2017)[14]中均给出了基于塑性理论的建筑钢结构和钢-混凝土组合结构的承载力计算方法。在相关规范中,为保证受弯梁破坏阶段钢梁可以产生足够的拉应变,对所设计的受弯梁(钢或钢-混凝土组合梁)给出了具体的构造要求限制。
规范GB 50917—2013[13]规定:1)钢梁必须为软钢,且其力学性能应符合一定的条件;2)要求组合截面的受压翼板及腹板在进入全塑性状态之前,不会出现局部失稳,因此规范规定了板件宽厚比的要求。
参照钢-混凝土组合梁塑性承载力计算方法的构造要求限制,由于预弯组合梁钢梁部分由混凝土完全包裹,故钢梁受压翼板及腹板在进入全塑性状态前,不会发生局部失稳,所以无需考虑板件的宽厚比要求,钢梁材料也必然满足要求。因而预弯组合梁塑性计算方法是可适用于任何预弯组合梁截面的。
《预弯预应力组合梁桥技术标准》(CJJ/T 276—2018)[7]中给出的抗弯承载力计算方法则认为钢梁腹板局部仍处于弹性工作区,但是由于钢腹板弹性部分的存在,使得截面承载力计算公式项数多,且计算过程复杂。
以下采用塑性理论,对预弯组合梁的抗弯承载力进行推导。基于塑性理论,假定钢梁截面全部进入塑性阶段,即其截面拉压应力分布为矩形,于是式(1)可改写为
| $ \gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{pud}}{}^{[12]} $ | (10) |
式(10)与式(1)具有相同的表达形式,等式左端为设计荷载,右端为塑性承载力设计值。
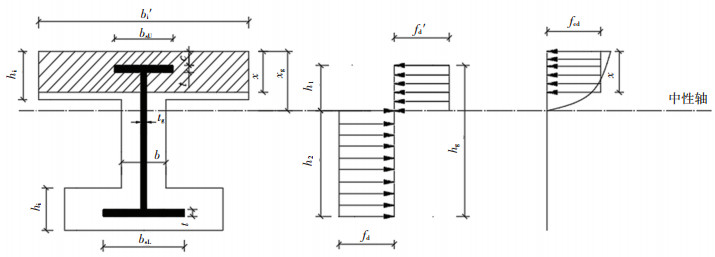
2.2 塑性抗弯承载力计算方法预弯组合梁塑性抗弯承载力计算假定除式(3)外,其他假定均与弹塑性抗弯承载力计算基本假定一致。对于式(3),认为钢梁上下翼板厚度相等且均可达到屈服,钢梁腹板也已全部进入塑性状态,其应力分布为矩形,且应力均达到钢材的抗拉强度设计值。由基本假定和图 2塑性抗弯承载力计算图式可得
| $ h_{1}=x_{\mathrm{s}}-c=\frac{x}{0.8}-c $ | (11) |
| $ h_{2}=h_{\mathrm{g}}-h_{1}=h_{\mathrm{g}}-\frac{x}{0.8}+c $ | (12) |
式中h1、h2分别为钢梁受压区高度和受拉区高度。
|
图 2 塑性抗弯承载力计算图式 Fig. 2 Schematic of calculation of plastic bending capacity |
根据中性轴位置的不同,需要考虑以下两种情况:
1) 混凝土等效矩形应力块高度位于二期混凝土上翼缘内(x≤h′i),由∑N=0,得
| $ f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x=f_{\mathrm{d}}\left(h_{2}-h_{1}\right) t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (13) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{pud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+\frac{1}{2} f_{\mathrm{d}} t_{\mathrm{w}}\left(\frac{x}{0.8}-c-t\right)^{2}+ \\ &\frac{1}{2} f_{\mathrm{d}} t_{\mathrm{w}}\left(h_{\mathrm{g}}-\frac{x}{0.8}+c-t\right)^{2}+f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (14) |
2) 混凝土等效矩形应力块高度位于二期混凝土腹板内(x≥h′i),由∑N=0,得
| $ f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)+f_{\mathrm{cd}} b x=f_{\mathrm{d}}\left(h_{2}-h_{1}\right) t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (15) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{pud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+\frac{1}{2} f_{\mathrm{d}} t_{\mathrm{w}}\left(\frac{x}{0.8}-c-t\right)^{2}+\\ &\frac{1}{2} f_{\mathrm{d}} t_{\mathrm{w}}\left(h_{\mathrm{g}}-\frac{x}{0.8}+c-t\right)^{2}+f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)\left(\frac{x}{0.8}-\right. \\ &\left.\frac{h_{\mathrm{i}}^{\prime}}{2}\right)+f_{\mathrm{cd}} b x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (16) |
完全塑性计算方法式(14)或式(16)与弹塑性计算方法式(7)或式(9)对比,可发现:公式计算项数未有减少,计算仍较为复杂;完全塑性计算方法计算所得截面抗弯承载力大于弹塑性计算方法所得值,安全储备略减少,属于承载能力计算上限值,对于工程使用偏于不安全。
2.3 抗弯承载力简化计算方法结合以上推导,本文对弹塑性方法计算公式进行简化,并提出以下抗弯承载力简化计算方法。
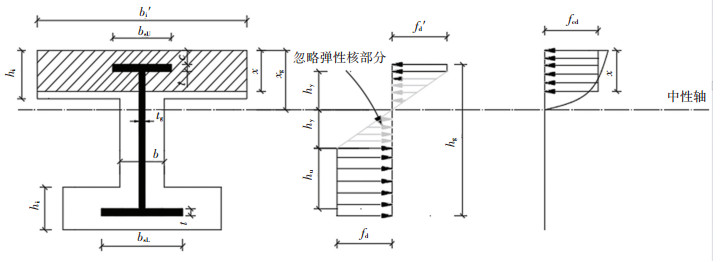
该抗弯承载力简化计算方法基于弹塑性计算方法,对钢梁腹板承载力进一步简化,忽略钢梁腹板中原弹性核高度内弹性承载力,腹板其他部分认为均达到屈服,上下翼板厚度相等且均可达到屈服,其压应力达到钢材强度设计值。图 3为实用截面抗弯承载力简化计算图式,虚化部分为舍弃的截面弹性核高度内的腹板提供的抗弯承载力。
|
图 3 抗弯承载力简化计算图式 Fig. 3 Schematic of simplified calculation of bending capacity |
同理,根据中性轴位置的不同,也需要考虑两种情况:
1) 混凝土等效矩形应力块高度位于混凝土上翼缘内(x≤h′i),由∑N=0,得
| $ f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x=f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (17) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{pud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}\left(\frac{h_{\mathrm{u}}}{2}+\frac{x}{2}-c-t\right)+ \\ &f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime} x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (18) |
将式(4)代入式(17)有
| $ x=\frac{\left(h_{\mathrm{g}}+2 c\right) t_{\mathrm{w}}+\Delta b_{s} t}{f_{\mathrm{cd}} b_{\mathrm{i}}^{\prime}+2.5 f_{\mathrm{d}} t_{\mathrm{w}}} f_{\mathrm{d}} \leqslant h_{\mathrm{i}}^{\prime} $ | (19) |
2) 混凝土等效矩形应力块高度位于二期混凝土腹板内(x≥h′i),由∑N=0,得
| $ f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)+f_{\mathrm{cd}} b x=f_{\mathrm{d}} h_{\mathrm{u}} t_{\mathrm{w}}+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t $ | (20) |
由∑M=0,得
| $ \begin{aligned} &\gamma_{0} M_{\mathrm{d}} \leqslant M_{\mathrm{pud}}=f_{\mathrm{d}} b_{\mathrm{sU}} t\left(\frac{x}{0.8}-c-\frac{t}{2}\right)+f_{\mathrm{d}} b_{\mathrm{sL}} t\left(h_{\mathrm{g}}-\right. \\ &\left.\frac{x}{0.8}+c-\frac{t}{2}\right)+f_{\mathrm{d}} t_{\mathrm{w}} h_{\mathrm{u}}\left(\frac{h_{\mathrm{u}}}{2}+\frac{x}{0.8}-c-t\right)+ \\ &f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)\left(\frac{x}{0.8}-\frac{h_{\mathrm{i}}^{\prime}}{2}\right)+f_{\mathrm{cd}} b x\left(\frac{x}{0.8}-\frac{x}{2}\right) \end{aligned} $ | (21) |
将式(4)代入式(20)有
| $ x=\frac{f_{\mathrm{d}} t_{\mathrm{w}}\left(h_{\mathrm{g}}+2 c\right)+f_{\mathrm{d}} \Delta b_{\mathrm{s}} t-f_{\mathrm{cd}} h_{\mathrm{i}}^{\prime}\left(b_{\mathrm{i}}^{\prime}-b\right)}{f_{\mathrm{cd}} b+2.5 f_{\mathrm{d}} t_{\mathrm{w}}} $ | (22) |
在这两种情况下,其所求得的中性轴位置xs还应满足以下条件[6]:1)按式(19)得到的中性轴位置xs应满足xs>c+t的条件,从而满足钢梁上翼缘板应力可达到其抗压设计强度f′d;2)按式(22)得到的中性轴位置xs应满足xs≤ξjs(hs+c)条件,从而满足钢梁下翼缘能够进入屈服阶段,其中ξjs为截面界限受压区高度系数,可按式(23)进行计算。
| $ \xi_{\mathrm{js}}=\frac{\beta \varepsilon_{\mathrm{u}}}{\frac{f_{\mathrm{d}}}{E_{\mathrm{s}}}+\varepsilon_{\mathrm{u}}} $ | (23) |
在式(6)~(23)中,Mpud为预弯组合梁的塑性抗弯承载力设计值,fcd、fd分别为混凝土和钢材的材料强度设计值,hi、bi、h′i、b′i分别为一期和二期混凝土板的厚度及宽度。
3 基于试验梁实测数据的验证为了验证本文方法的可靠性和计算准确性,使用本文提出方法对文献[9]中7根试验梁的抗弯承载力进行试算,并与实测值、弹塑性抗弯承载力进行对比分析。同时根据这7根试验梁的原始尺寸,采用通用有限元软件Abaqus建立三维空间模型进行计算分析,对试验梁进行原始尺寸建模,充分考虑其对称性,建立半梁模型,一共建立21个有限元模型,用以对比理论计算结果和试验结果。
3.1 试验梁尺寸及材料参数根据文献[4]7根试验梁中W3-3、W3-4为3 m试验梁,W5-1、W5-3、W5-4为5 m试验梁,W7-2、W7-3为7 m试验梁,这7根梁均用于抗弯破坏试验。各个梁的尺寸及材料参数有所区别:试验梁一期混凝土材料实测抗压立方体强度为30~40 MPa,二期混凝土实测抗压立方体强度为20~37 MPa,混凝土密度为2 500 kg/m3;试验梁钢材力学性能按厚度进行实测取值:6 mm钢板实测屈服强度为360 MPa;8 mm钢板实测屈服强度为410 MPa;10 mm钢板实测屈服强度为380 MPa。图 4为试验梁截面尺寸示意图,7根试验梁截面具体尺寸参数见表 1[4]。

|
图 4 试验梁截面尺寸示意图 Fig. 4 Schematic of cross-sectional dimensions of experimental beam |
| 表 1 7根试验梁尺寸参数 Tab. 1 Dimensions of seven experimental beams |
表 1中钢梁上下翼板厚度均为t,一期混凝土等效高度he是将一期混凝土承托部分基于混凝土面积不变的原则等效为一期混凝土高度。7根试验梁预弯力的加载与抗弯强度试验均采取四分点加载的形式[9],加载立面图见图 5。

|
图 5 试验梁加载立面示意图 Fig. 5 Loading elevation diagram of experimental beam |
使用2.3节计算方法对W3-3、W3-4等共7根试验梁跨中截面的理论抗弯承载力进行计算,结果见表 2。为了更直观地反应简化抗弯承载力与弹塑性抗弯承载力计算差值的来源,对计算截面不同的钢梁腹板弹性核区域高度与两种理论计算差值进行列表统计并分析,见表 3。
| 表 2 实测与计算的xs和Mu对比 Tab. 2 Comparison between measured and calculated values of xs and Mu |
| 表 3 弹性核高度对截面极限承载能力大小的影响 Tab. 3 Influence of elastic core height on cross-sectional ultimate bending capacity |
对比分析中,未计入钢材与混凝土的材料安全系数,均取材料的实测强度平均值进行计算[18]。
表 2中,xs为预弯组合梁受压区高度;Mu为预弯组合梁的抗弯承载力,其中实测值为文献[4]中试验得到的抗弯承载力值,弹塑性计算值为采用预弯组合梁弹塑性抗弯承载力计算方法重新求得的结果,完全塑性计算值为塑性抗弯承载力计算方法求得的结果,简化计算值为本文抗弯承载力简化计算方法求得的结果。由表 2可见,在不计材料安全系数的情况下,塑性抗弯承载力计算方法计算所得截面抗弯承载力大于弹塑性计算方法所得值,安全储备略减少;简化计算方法与实测结果吻合很好,且小于弹塑性计算方法所得值,Mu的实测值/塑性计算值的统计平均值为1.076,均方差为σn=0.056, 离散系数Cv=0.052 144 7。
表 3中hy为弹性核高度,相对差值为塑性计算值减去弹塑性计算值。结合预弯组合梁弹塑性极限抗弯强度计算方法,从表 3的对比中可知,简化计算方法计算结果均小于弹塑性计算方法计算值,且与弹塑性计算方法差值主要是由于原弹性核高度部分腹板提供的弹性抗弯承载力;简化计算方法假定钢梁腹板部分受拉区已达到完全塑性状态,忽略腹板其他弹性核提供承载力,故当跨径大小相同时,其弹性核高度越大,对应弹塑性及简化方法计算值差值越大,而弹性核高度与截面尺寸、材料等因素相关。
故在表 3中可以看到,以W3-3梁与W3-4梁为例,由于其截面尺寸相似,W3-4梁混凝土材料强度低于W3-3梁,故其理论计算实际受压区高度大于W3-3梁,W3-4梁的弹性核高度大于W3-3梁,W3-4梁对应弹塑性与简化方法计算值差值也大于W3-3梁。但差值占弹塑性计算值的比例很小,说明二期混凝土受压部分,钢梁顶底板及腹板塑性区域提供了截面承载力的主要部分,忽略弹性核部分承载力,对截面承载力影响不大。
经过比较,7根试验梁使用2.3节计算方法与弹塑性计算方法计算结果相差均小于2%。
3.3 有限元对比分析根据以上试验梁原始尺寸,采用通用有限元软件Abaqus建立三维空间模型进行非线性分析。其中,混凝土部分采用8节点减缩积分实体单元(C3D8R)。为了更好地观察及获取钢梁截面正应力分布,故钢梁采取实体单元建模,采用8节点减缩积分实体单元(C3D8R)。
由于预弯组合梁施工阶段的特殊性,需考虑初始预应力场对其截面抗弯承载能力的影响。因此,预弯力的加载采取与试验相同的方式,即在钢梁四分点处施加集中力,并在一期混凝土结硬后释放预弯力以施加预应力;有限元中具体采用model change生死单元及initial stress初始应力场等功能通过应力场的导入及构件的失效激活来模拟实际试验中梁体预弯力施加、一期混凝土结硬释放预弯力及恒载施加等阶段带来的全梁应力场的变化,且有限元模拟中不考虑各施工阶段梁体线形的变化及混凝土的收缩徐变[19]。
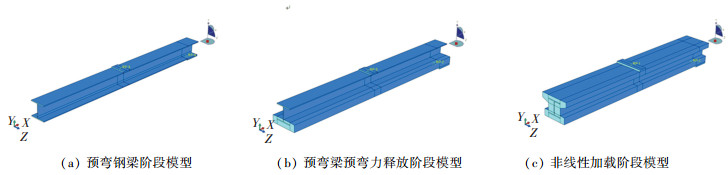
本文一共建立21个有限元半梁模型用以各阶段应力场的模拟施加及非线性加载计算,并将有限元计算结果与理论计算结果以及试验结果进行比较分析,有限元计算模型如图 6所示。
|
图 6 各阶段试验梁模型 Fig. 6 Models of experimental beams in different stages |
结果表明:模拟所得预弯组合梁各阶段控制点应力与理论计算及试验实测值吻合良好;当达到抗弯极限承载力时,一期混凝土及二期混凝土的受拉区开裂,破坏原因主要是二期混凝土顶板压碎;钢梁上下翼板厚度相等且均可达到屈服,其压应力达到钢材强度实测值,钢腹板存在部分弹性核,与试验所得结果一致。
图 7为7根试验梁非线性有限元加载得到的试验梁荷载位移曲线,由于预弯组合梁中预弯钢梁的存在,使梁体在达到其极限承载力后,没有直接发生突降,而是保持一定的承载力缓慢下降,具有较好的延性。7根试验梁有限元模拟计算抗弯承载力见表 4,从表 4中可以看到,7根试验梁使用2.3节计算方法计算得到的承载力值与有限元计算得到的截面抗弯承载力统计平均值为1.123,吻合较好;且简化方法计算值始终低于实测值与有限元模拟承载力,说明使用2.3节计算方法计算得到的理论承载力具有足够的安全储备,其计算精度能够满足实际工程需要。

|
图 7 7根试验梁有限元模拟荷载位移曲线 Fig. 7 Load-displacement curves of seven experimental beams in finite element simulation |
| 表 4 截面实测、有限元模拟、理论计算承载力 Tab. 4 Comparison between measured, simulated, and calculated cross-section bending capacity |
经过3.1节、3.2节的对比,可以认为简化计算方法计算精度满足工程需要,因而简化计算方法可代替弹塑性计算方法进行设计。
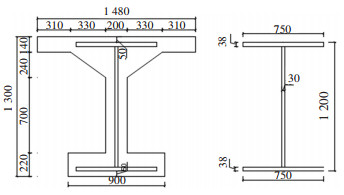
4 计算实例文献[2]第9章对一跨径为42 m的预弯组合梁桥进行了弹塑性抗弯承载能力的计算,跨中截面形状及尺寸如图 8所示。该桥结构重要性系数γ0=1.1,按基本组合计算的跨中截面弯矩组合设计值Md=9 863.9 kN·m。采用材料参数:顶底板采用38 mm厚钢板,腹板采用30 mm厚钢板,fd=270 MPa;一期混凝土采用C50混凝土,fcd=22.4 MPa;二期混凝土采用C30混凝土,fcd=13.8 MPa。
|
图 8 预弯梁截面尺寸(mm) Fig. 8 Cross-sectional dimensions of preflex beam (mm) |
该预弯组合梁截面的加腋截面按照混凝土截面面积不变的原则,将其原混凝土翼板及加腋截面的厚度进行简化计算,而其宽度不变,即h′i=0.226 m。
假设混凝土等效矩形应力块高度处于混凝土腹板内,根据式(4)计算腹板塑性受拉区高度hu=590 mm, 根据式(21)计算其截面抗弯承载力Mpud=12 759.384 kN·m,按照CJJ/T 276—2018中给出的弹塑性公式计算,可得Mud= 13 145.2 kN·m,其值均大于γ0Md=1.1×9 863.9 kN·m=10 850.3 kN·m。两种方法计算得到的截面抗弯承载力相差为385.816 kN·m,是简化方法计算抗弯承载力的3.02%,所占比例较小,而抗弯承载力简化计算公式更为简便,且安全储备充足。
5 结论1) 采用塑性理论,对预弯组合梁的塑性抗弯承载力计算公式进行了推导。在理论推导的基础上,对弹塑性方法进行适当合理的简化,提出了一种抗弯承载力简化计算方法,并给出了相应的计算公式。
2) 采用文献[4]中的7根预弯组合梁抗弯承载力试验结果对所提出方法进行了验证。计算结果表明,简化计算方法与现行标准中公式计算结果及试验实测值均较为接近。简化计算方法与现行标准规定公式计算结果受弹性核高度参数影响较为明显,弹性核高度越高,二者相对差越大。但差值占弹塑性计算值的比例很小,说明二期混凝土受压部分,是钢梁顶底板及腹板塑性区域提供了截面承载力的主要部分,忽略弹性核部分承载力,对截面承载力影响不大。对于7根试验梁,可发现二者相对差不超过2%。
3) 采用通用有限元软件Abaqus建立非线性三维空间模型进行数值计算模拟仿真研究,7根试验梁使用本文提出的简化计算方法计算得到的承载力与有限元计算得到的截面抗弯承载力吻合较好,且简化方法计算值始终低于实测值与有限元模拟承载力,说明使用简化计算方法计算得到的承载力具有足够的安全储备,其计算精度能够满足实际工程需要。
4) 本文提出的简化计算方法较现行标准的计算方法有所简化,而且计算精度良好,可供预弯组合梁桥设计时参考。
| [1] |
张士铎. 预弯预应力混凝土梁介绍[J]. 公路, 1987(3): 4. ZHANG Shiduo. Introduction of preflexed composite beam[J]. Highway, 1987(3): 4. |
| [2] |
黄侨. 桥梁钢-混凝土组合结构设计原理[M]. 2版. 北京: 人民交通出版社, 2017: 185. HUANG Qiao. Design theory of steel-concrete composite structure in bridge[M]. 2nd ed. Beijing: China Communications Press, 2017: 185. |
| [3] |
BASE L, LIPSKI A. Prestressed beams of steel and concrete[J]. Concrete and Constructional Engineer, 1953, 48(12): 402. |
| [4] |
黄侨. 预弯组合梁桥的设计理论及试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2000 HUANG Qiao. Design theory and experimental study of preflexed composite beam bridge[D]. Harbin: Harbin Institute of Technology, 2000 |
| [5] |
郭赵元. 预弯组合梁开裂荷载试验及理论研究[D]. 南京: 东南大学, 2017 GUO Zhaoyuan. Experiment and theoretical study on cracking load of preflexed beam[D]. Nanjing: Southeast University, 2017 |
| [6] |
杨明, 黄侨. 预弯组合梁收缩、徐变计算方法解析[J]. 公路交通科技应用技术版, 2005(8): 119. YANG Ming, HUANG Qiao. Analysis of calculation method for shrinkage and creep of preflex beam bridge[J]. Journal of Highway and Transportation Research and Development, 2005(8): 119. |
| [7] |
中华人民共和国住房与城乡建设部. 预弯预应力组合梁桥技术标准: CJJ/T 276—2018[S]. 北京: 中国建筑工业出版社, 2018 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical standard for preflexed composite beam bridges: CJJ/T 276—2018[S]. Beijing: China Architecture & Building Press, 2018 |
| [8] |
陆亚芳, 张士铎. 预弯梁及其正截面强度[J]. 土木工程学报, 1989, 22(3): 84. LU Yafang, ZHANG Shiduo. Preflexed beam and the cross-section bending capacity[J]. China Civil Engineering Journal, 1989, 22(3): 84. |
| [9] |
黄侨, 郑一峰. 预弯预应力混凝土简支梁桥的极限承载力研究[C]//全国城市桥梁青年科技学术会议论文集. 上海: 中国土木工程学会市政工程学会, 1996: 737 HUANG Qiao, ZHENG Yifeng. Research on ultimate beading capacity of preflexed simply-supported beam bridge[C]// Proceedings of National Urban Bridge Youth Science and Technology Academic Conference. Shanghai: China Civil Engineering Society Municipal Engineering Society, 1996: 737 |
| [10] |
张克波, 李素平. 预弯预应力混凝土受弯构件正截面受弯承载力[J]. 长沙交通学院学报, 1998, 14(2): 33. ZHANG Kebo, LI Suping. The cross-section bending capacity of preflexed beam[J]. Journal of Changsha Communications University, 1998, 14(2): 33. |
| [11] |
郑一峰, 黄侨, 冷曦晨, 等. 预弯组合梁桥的弹塑性极限承载能力研究[J]. 中国公路学报, 2005, 18(4): 54. ZHENG Yifeng, HUANG Qiao, LENG Xichen, et al. Research on elastic ultimate capacity of preflex beam bridges[J]. China Journal of Highway and Transport, 2005, 18(4): 54. |
| [12] |
黄侨, 郭赵元, 万世成, 等. 钢-混凝土组合梁桥的截面弹性抗弯承载力计算方法研究[J]. 中国公路学报, 2017, 30(3): 167. HUANG Qiao, GUO Zhaoyuan, WAN Shicheng, et al. Research on calculation method of elastic bending capacity for steel-concrete composite beam bridges[J]. China Journal of Highway and Transport, 2017, 30(3): 167. |
| [13] |
中华人民共和国住房与城乡建设部. 钢-混凝土组合桥梁设计规范: GB 50917—2013[S]. 北京: 中国计划出版社, 2013 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of steel and concrete composite bridges: GB 50917—2013[S]. Beijing: China Planning Press, 2013 |
| [14] |
中华人民共和国住房与城乡建设部. 钢结构设计规范: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [15] |
中华人民共和国交通运输部. 公路钢混组合桥梁设计与施工规范: JTG /T D64-01—2015[S]. 北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. Specifications for design and construction of highway steel-concrete composite bridge: JTG/T D64-01—2015[S]. Beijing: China Communication Press, 2015 |
| [16] |
中华人民共和国交通运输部. 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG 3362—2018[S]. 北京: 人民交通出版社, 2018 Ministry of Transport of the People's Republic of China. Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG 3362—2018[S]. Beijing: China Communication Press, 2018 |
| [17] |
中华人民共和国交通运输部. 公路钢结构桥梁设计规范: JTG D64—2015[S]. 北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. Specifications for design of higway steel bridge: JTG D64—2015[S]. Beijing: China Communication Press, 2015 |
| [18] |
中华人民共和国交通运输部. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. General specifications for design of highway bridges and culverts: JTG D60—2015[S]. Beijing: China Communication Press, 2015 |
| [19] |
袁鹏飞. 波形钢腹板组合槽型梁桥静动力学性能研究[D]. 南京: 东南大学, 2019 YUAN Pengfei. Study on static and dynamic performances of composite trough girder with corrugated steel webs[D]. Nanjing: Southeast University, 2019 |
 2022, Vol. 54
2022, Vol. 54


