2. 广西交通投资集团, 南宁 530029;
3. 绍兴文理学院 土木工程学院, 浙江 绍兴 312000;
4. 广西新发展交通集团有限公司, 南宁 530029
2. Guangxi Communications Investment Group Co., Ltd., Nanning 530029, China;
3. School of Civil Engineering, Shaoxing University, Shaoxing 312000, Zhejiang, China;
4. Guangxi Xinfazhan Communications Group Co., Ltd., Nanning 530029, China
水中悬浮隧道是一种全封闭新型交通结构形式[1-2]。由于悬浮在水中,相比于桥梁、沉管隧道等其他结构,具有跨越能力大、纵向坡度小、布线灵活、受外界干扰小、绿色环保等优点,使其成为21世纪最具竞争力的跨海结构之一[3]。全世界范围内时有发生的水下爆炸事故为悬浮隧道的安全运营带来了极大威胁。这方面现有研究包括:文献[4]将悬浮隧道简化为等截面的弹性支撑梁,研究了水下爆炸冲击波作用下管体的位移和弯矩响应;文献[5-6]通过LS-DYNA对悬浮隧道水下爆炸冲击作用下的动力过程进行模拟,分析了爆炸参数、支撑体系对其结构响应的影响;文献[7-8]将数值模拟和激波管爆炸试验相结合研究了悬浮隧道的混凝土性能和截面形式对抗爆的影响。上述研究大多集中于数值模拟,鲜有理论方面的研究,且在计算中对爆炸荷载作了较大简化,没有考虑气泡荷载。车辆荷载是悬浮隧道作为交通结构物所面临的常规荷载,这方面的研究包括:文献[9-10]将车辆荷载简化为单自由度系统,研究了悬浮隧道车-隧耦合的动力响应问题;文献[11-13]将车辆荷载简化为移动荷载序列,研究了悬浮隧道在不同形式移动荷载作用下的动力响应问题。考虑到悬浮隧道在运营期间必然受到车辆荷载的作用,因此有必要考虑车辆荷载和其他荷载共同作用下悬浮隧道的动力响应。
基于悬浮隧道在水下爆炸方面现有研究的不足,本文一方面通过Cole冲击波半经验公式和Vernon气泡运动方程考虑完整的冲击波及气泡爆炸荷载,另一方面通过建立任意移动荷载序列模型模拟公路I级车辆荷载的作用。在此基础上,建立能考虑悬浮隧道水平、垂直振动的动力学模型,最终对爆炸和移动荷载参数进行分析,得到水下爆炸-移动荷载作用下悬浮隧道的响应规律,为悬浮隧道及同类水下结构的相关研究提供参考。
1 水下爆炸及移动荷载模型悬浮隧道依靠管体自身的浮力和锚索的张力而悬浮在水下一定深度,主要由水下基础、锚索支撑、隧道管体等部分组成,具体如图 1所示,本节将建立悬浮隧道受到的主要荷载模型,隧道运动方程将在第2节中建立。水下爆炸荷载主要由冲击波和气泡脉动两部分组成,大约各占爆炸总能量的一半。水下爆炸荷载压力变化曲线可简化为两个阶段,如图 2所示。第Ⅰ阶段为冲击波荷载的正压衰减阶段;第Ⅱ阶段为气泡膨胀-收缩运动形成的流场脉动压力阶段。
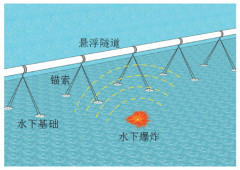
|
图 1 悬浮隧道形象图 Fig. 1 Image of SFT |
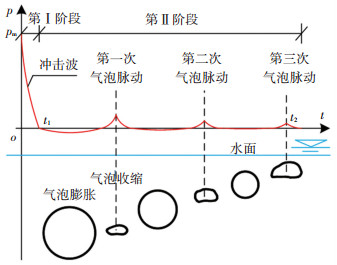
|
图 2 水下爆炸荷载的简化 Fig. 2 Simplification of underwater explosive load |
水下爆炸冲击波荷载的计算较为成熟,通常可采用Cole综合大量水下爆炸实验数据提出的半经验公式[14]来计算:
| $ p_{\mathrm{i}}(t)=p_{\mathrm{m}} \exp \left(\frac{-t}{t_{1}}\right), 0<t \leqslant t_{1} $ | (1) |
式中:pi为入射波压力;pm=52.4 (W1/3/R)1.13为TNT炸药发生水下爆炸的冲击波超压值,MPa;R为爆心距;W为炸药量;t1为冲击波压力的衰减常数,ms,t1=0.084 W1/3 (W1/3/R)-0.23。
如图 3所示,由水下爆炸作用产生的冲击波相对于结构而言可称为入射波,当入射波作用在水下结构上,会使结构发生运动从而产生散射波,作用在结构上的压力也会因两种波的共同作用发生变化。许多学者对冲击波的这种瞬态流固耦合效应进行了研究[15-16],其中泰勒平板理论应用较为广泛,是一种计算荷载总压力的简便方法:
| $ p_{1}(t)=2 p_{\mathrm{i}}(t)-\rho_{\mathrm{w}} s v_{p} $ | (2) |
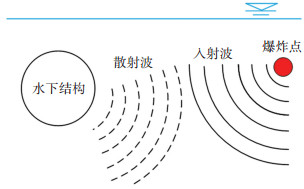
|
图 3 水下爆炸流固耦合 Fig. 3 Fluid-solid interaction of underwater explosion |
式中:p1为冲击波对水下结构造成的总压力;ρw为水的密度;s为波在水中传播的速度,可取1 500 m/s;vp为结构的振动速度。
为了对式(2)进行化简,考虑结构的受力和运动,可以建立其瞬态平衡方程如式(3)所示。进一步,根据vp(0)=0的初始条件,解得结构的速度vp的表达式如式(4)所示。
| $ m_{\mathrm{s}} \dot{v}_{p}+\rho_{\mathrm{w}} s v_{p}=2 p_{\mathrm{m}} \exp \left(-\frac{t}{t_{1}}\right) $ | (3) |
| $ v_{p}=\frac{2 p_{\mathrm{m}} t_{1}}{m_{\mathrm{s}}(1-\beta)}\left[\exp \left(-\frac{\beta t}{t_{1}}\right)-\exp \left(-\frac{t}{t_{1}}\right)\right] $ | (4) |
式中:ms为单位面积结构的质量,对于梁而言可取为单位长度管体的质量;β为冲击波扰动的水体质量与结构质量的比值,β=ρwst1/ms。
将vp代入式(2)可得作用在结构上的总压力为水下爆炸第Ⅰ阶段的荷载[17], 即
| $ p_{1}(t)=\frac{2 p_{\mathrm{m}}}{1-\beta}\left[\exp \left(-\frac{t}{t_{1}}\right)-\beta \exp \left(-\frac{\beta t}{t_{1}}\right)\right] $ | (5) |
气泡脉动荷载的求解相对复杂,可以通过气泡的运动方程或气泡荷载经验公式来计算,前者在计算精度方面优于后者,因此本文采用气泡运动方程来计算,气泡脉动荷载的具体求解步骤如图 4所示。

|
图 4 气泡荷载计算步骤 Fig. 4 Calculation steps of bubble load |
为了求解气泡脉动作用下的流体加速度
考虑气泡的迁移效应和气泡阻力的影响,气泡模型如图 5所示。在此假设基础上,气泡的运动可采用Vernon无量纲微分方程组描述[18]:
| $ \left\{\begin{array}{l} \sigma=\dot{\chi} \\ \lambda=\dot{\zeta} \\ \dot{\lambda}=\dot{\zeta}=-\frac{3}{2}\left[\frac{\sigma^{2}}{\chi}-\frac{\lambda^{2}}{\sigma \chi}+\frac{\zeta}{\chi \zeta_{0}}-\frac{(\gamma-1) k}{\chi^{3 \gamma+1}}\right] \\ \dot{\lambda}=-3\left[\frac{1}{\zeta_{0}}+\frac{\sigma \lambda}{\chi}-C_{\mathrm{d}} \frac{\lambda^{2}}{4 \chi}\right] \end{array}\right. $ | (6) |
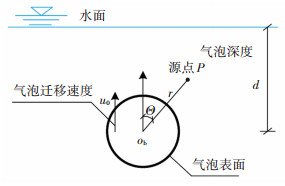
|
图 5 气泡运动示意图 Fig. 5 Schematic diagram of bubble motion |
式中:χ为无量纲气泡半径;ζ为无量纲压头;ζ0为无量纲初始压头;k为无量纲能量系数,对于TNT炸药,k≈0.074 3z01/4,其中z0为初始压头;γ为绝热气体系数取1.25;Cd为气泡阻尼经验系数, 取2.5。
定义长度尺度因子L= [3E0/ (4πρwgz0)]1/3与时间尺度因子T=1.428W1/3/z05/6,E0为爆炸的总能量(对于TNT,可取E0=2.056×106W)。这样便可以得到上述方程中的无量纲参数:
| $ \left\{\begin{array}{l} \chi=\frac{a}{L} \\ \zeta=\frac{z}{L} \\ \zeta_{0}=\frac{z_{0}}{L} \\ \tau=\frac{t}{T} \end{array}\right. $ | (7) |
式中:a为气泡半径,z为压力水头,τ为无量纲时间。
只要给定初始条件,式(6)便可以通过Runge-Kutta法进行求解。选定初始条件为χ=χ0,ζ=ζ0,σ=0,λ=0。其中χ0为无量纲气泡初始半径,可由不考虑气泡迁移效应的能量守恒方程[19]得到,
通过式(6)解得无量纲气泡半径χ(t)和压头函数ζ(t)等气泡参数后,便可采用势流理论来计算气泡运动产生的流体加速度。球形气泡脉动压力下的流场速度势函数可设为拉普拉斯方程对于球坐标已知解的形式。基于势流理论,流体速度为速度势的负梯度,对速度势函数进行梯度运算即可得到气泡脉动作用下的流体速度u:
| $ \left\{\begin{array}{l} \varphi=\frac{e_{1}}{r}+\frac{e_{2}}{r^{2}} \cos \varTheta \\ u=-\nabla \varphi=\frac{e_{1}}{r^{2}}+\frac{2 e_{2} \cos \varTheta}{r^{3}} \end{array}\right. $ | (8) |
式中:
确定了气泡脉动压力下的流体速度后,可对其求导得到流体加速度
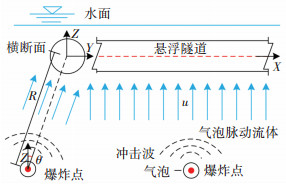
|
图 6 水下爆炸荷载简化示意图 Fig. 6 Simplified diagram of underwater explosive load |
这样计算的精度与切片理论的精度相同,最终作用在隧道管体的气泡脉动荷载[21]可以写为
| $ p_{2}(t)=\left(m_{\mathrm{a}}+m_{\mathrm{w}}\right) \dot{u}-m_{\mathrm{a}} \frac{\partial^{2} w}{\partial t^{2}}, t_{1}<t \leqslant t_{2} $ | (9) |
式中:ma为圆柱体切片理论的附加质量,ma=πρwD2/4;D为悬浮隧道的直径;mw为单位长度隧道的排水质量;
通过以上的步骤建立了能够考虑爆炸冲击波和气泡脉动的爆炸荷载两阶段时程函数。至此,作用在悬浮隧道上的爆炸荷载时域分布可以表示为
| $ P_{t}(t)=\left\{\begin{array}{l} p_{1}(t), 0<t \leqslant t_{1} \\ p_{2}(t), t_{1}<t \leqslant t_{2} \end{array}\right. $ | (10) |
爆炸荷载的大小和方向可以通过爆心距R和入射角θ进行控制。除此之外,因为悬浮隧道的管体长度较长, 还需要考虑水下爆炸荷载沿悬浮隧道纵向的空间分布[22],将式(10)与之相乘后得到最终作用在悬浮隧道的水下爆炸荷载为
| $ \left\{\begin{array}{l} P_{x}(x)=\left(\frac{R}{\sqrt{R^{2}+(x-0.5 l)^{2}}}\right)^{1.13} \\ P(x, t)=P_{t}(t) P_{x}(x) \end{array}\right. $ | (11) |
式中:x为悬浮隧道长度方向上的坐标,l悬浮隧道的长度。
1.3 移动荷载序列悬浮隧道作为交通结构物,车辆荷载的作用不可忽略。不同形式的车辆荷载都可采用移动荷载序列来模拟。图 7给出了单个移动荷载作用在管体上的示意图,如图 7第i个移动荷载Fi在t=ti时刻进入管体,此时它的荷载作用位置在管端(x=0)则可用狄拉克函数表示为Fiδ(x-0)。经过T秒后在t=ti+T时刻,移动荷载的作用位置为x=vT,则其表达式等价于Fiδ[x-v(t-ti)]。同时在移动荷载未驶入和驶出管体期间,其作用应该消失,这里利用阶跃函数H(t)构建出Ci(t)来控制第i个移动荷载在ti到ti+l/v时间内出现,最终将多个移动荷载叠加得到移动荷载序列的表达式为
| $ F(x, t)=\sum\limits_{i=1}^{N} F_{i} \delta_{i}\left[x-v\left(t-t_{i}\right)\right] C_{i}(t) $ | (12) |
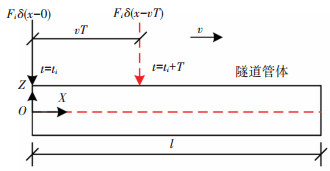
|
图 7 单一移动荷载示意图 Fig. 7 Schematic diagram of single moving load |
式中:Fi为第i个移动荷载的大小;N为移动荷载的数量;δi(t)为狄拉克函数,用来控制移动荷载的作用位置;v为移动荷载的速度;ti为第i个移动荷载进入管体的时间,
为了使移动荷载的计算结果更具参考意义,参考现行的《公路工程技术标准》(JTG B01—2014)[23],本文选用公路I级车辆荷载作为悬浮隧道内的移动荷载,规范中的车辆荷载要求采用标准车辆荷载来进行布置,如图 8所示,双车道隧道在横向需布置两个标准车辆荷载。为了简化此处将标准移动荷载的荷载值乘以2来考虑作用在悬浮隧道上的移动荷载。
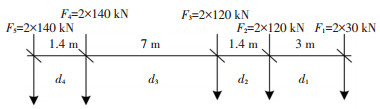
|
图 8 公路I级荷载 Fig. 8 Grade I vehicle load of highway |
在建立悬浮隧道运动方程时,为了便于计算在此作出以下假定:1)采用连续的弹性地基刚度简化离散的锚索支撑[9];2)悬浮隧道的长度远大于其径向尺寸,满足简化为梁的条件;3)悬浮隧道的驳岸接头满足简支支撑条件。
2.1 流体作用式(13)为Morison方程,常常被用来求解作用在单位长度管体上的流体作用,方程右边第1项为流体的附加阻尼力,第2项为流体的附加惯性力。考虑管体Y、Z两个方向的运动后得到其流体作用:
| $ \left\{\begin{array}{l} f_{z D}=\frac{1}{2} C_{D} \rho_{\mathrm{w}} D \frac{\partial z}{\partial t}\left|\frac{\partial z}{\partial t}\right|+\frac{1}{4} C_{m} {\rm{ \mathsf{ π} }} D^{2} \rho_{\mathrm{w}} \frac{\partial^{2} z}{\partial t^{2}} \\ f_{y D}=\frac{1}{2} C_{D} \rho_{\mathrm{w}} D \frac{\partial y}{\partial t}\left|\frac{\partial y}{\partial t}\right|+\frac{1}{4} C_{m} {\rm{ \mathsf{ π} }} D^{2} \rho_{\mathrm{w}} \frac{\partial^{2} y}{\partial t^{2}} \end{array}\right. $ | (13) |
式中:CD为拖拽力系数,此处CD取0.7;Cm为附加质量系数[24],此处Cm取0.7或1,其他参数同上。
2.2 微分方程的建立与求解考虑到悬浮隧道的跨度远大于截面尺寸,可将锚索简化为地基弹簧,将悬浮隧道简化为等间距的连续支撑梁来分析整体动力响应[25]。如图 9所示,在考虑爆炸荷载、移动荷载、流体作用后,可以根据D′Alembert原理建立悬浮隧道Z、Y方向的动力平衡方程:
| $ \left\{\begin{array}{l} E I_{y} \frac{\partial^{4} z}{\partial x^{4}}+m \frac{\partial^{2} z}{\partial t^{2}}+c_{z} \frac{\partial z}{\partial t}+k_{z} z= \\ \ \ \ \ \ \ \ \ P_{z}(x, t)-F(x, t)-\frac{1}{2} \rho_{\mathrm{w}} C_{D} \frac{\partial z}{\partial t}\left|\frac{\partial z}{\partial t}\right| \\ E I_{z} \frac{\partial^{4} y}{\partial x^{4}}+m \frac{\partial^{2} y}{\partial t^{2}}+c_{y} \frac{\partial y}{\partial t}+k_{y} y= \\ \ \ \ \ \ \ \ \ P_{y}(x, t)-\frac{1}{2} \rho_{\mathrm{w}} C_{D} \frac{\partial y}{\partial t}\left|\frac{\partial y}{\partial t}\right| \end{array}\right. $ | (14) |
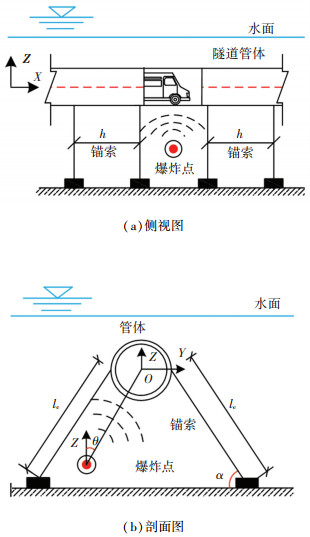
|
图 9 悬浮隧道荷载-结构模型 Fig. 9 Load-structure model of SFT |
式中:EIy、EIz分别为悬浮隧道管体竖直方向和水平方向上的弯曲刚度;m为等效质量,m=ms+ma;cz、cy分别为管体竖直方向和水平方向上的黏滞阻尼系数,此处取cz=cy;kz、ky分别为锚索在竖直方向和水平方向上的刚度,
对于式(14)可采用分离变量法进行解耦,管体竖直和水平两个方向的位移函数可以表示为
| $ \left\{\begin{array}{l} z(x, t)=\sum\limits_{n=1}^{\infty} Z_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l} \\ y(x, t)=\sum\limits_{n=1}^{\infty} Y_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l} \end{array}\right. $ | (15) |
式中Zn(t)、Yn(t)分别为管体第n阶振型的广义坐标。
根据振型正交性进行化简,可得到便于计算的常微分方程组:
| $ \left\{\begin{array}{l} \ddot{Z}_{n}(t)+\frac{c_{z}}{m} \dot{Z}_{n}(t)+\left[\frac{E I_{y}}{m}\left(\frac{i {\rm{ \mathsf{ π} }}}{l}\right)^{4}+\frac{k_{z}}{m}\right] Z_{n}(t)= \\ \ \ \ \ \ \ \ \ \frac{2}{m l}\left(P_{I z}(t)-\sum\limits_{i=1}^{N} F_{i} C_{i}(t)-D_{z n}\right) \\ \ddot{Y}_{n}(t)+\frac{c_{y}}{m} \dot{Y}_{n}(t)+\left[\frac{E I_{z}}{m}\left(\frac{i {\rm{ \mathsf{ π} }}}{l}\right)^{4}+\frac{k_{y}}{m}\right] Y_{n}(t)= \\ \ \ \ \ \ \ \ \ \frac{2}{m l}\left(P_{I y}(t)-D_{y n}\right) \end{array}\right. $ | (16) |
式中:Dzn、Dyn分别为管体在竖直和水平方向上受到的流体非线性阻尼力,PIz、PIy分别为管体在竖直和水平方向受到的爆炸荷载积分后的结果,表达式分别为
| $ \begin{aligned} D_{z n}=& \frac{1}{2} \rho_{\mathrm{w}} C_{D} \int_{0}^{L} \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\left[\sum\limits_{i=1}^{n} \dot{Z}_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\right] \\ &\left|\sum\limits_{i=1}^{n} \dot{Z}_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\right| \mathrm{d} x \end{aligned} $ |
| $ P_{I z}(t)=\int_{0}^{l} P_{z}(x, t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l} \mathrm{d} x $ |
| $ \begin{aligned} D_{y n}=& \frac{1}{2} \rho_{\mathrm{w}} C_{D} \int_{0}^{L} \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\left[\sum\limits_{i=1}^{n} \dot{Y}_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\right] \\ &\left|\sum\limits_{i=1}^{n} \dot{Y}_{n}(t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l}\right| \mathrm{d} x \end{aligned} $ |
| $ P_{I y}(t)=\int_{0}^{l} P_{y}(x, t) \sin \frac{n {\rm{ \mathsf{ π} }} x}{l} \mathrm{~d} x $ |
由式(16)可以发现,振动系统中存在非线性项Dzn和Dyn,流体作用中附加阻尼项将多阶振型耦合,使得该方程的无法求得解析解,在后续计算中将采用四阶Runge-Kutta法数值积分求解微分方程组。
3 参数分析目前悬浮隧道尚处于研究阶段,国内外没有已建成的,参考国内外各待建悬浮隧道的设计参数,本文中数值算例所采用的参数[9-11]如下所列。
悬浮隧道的管体参数:长度l=500 m,管体外径D=14.26 m,管体厚度tk=1.43 m,弹性模量E=32 GPa,管体密度ρ=2 018 kg/m3,管体深度H0=30 m,管体黏滞阻尼cs=10-4 N·s/m。悬浮隧道锚索的参数:锚索间距h=100 m,弹性模量Ec=190 GPa,长度lc=161 m,外径dc=0.35 m,倾角α=45°。流体计算参数:密度ρw=1 028 kg/m3,水中波速s=1 500 m/s。后续计算中所采用的一般移动荷载的速度v=90 km/h,一般爆炸荷载的炸药量W=50 kg,爆心距R=20 m。
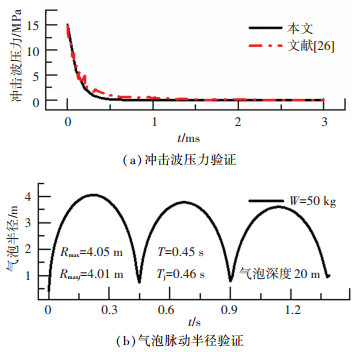
3.1 模型验证文献[26]通过爆炸试验测得了水下爆炸的冲击波的压力,本文冲击波计算结果与文献[26]结果如图 10所示。由图 10(a)可知两者具有相同的冲击波压力峰值和相似的变化规律,只是后者在曲线中伴有细微局部波动,这主要是现场测试结果还包括了气泡在冲击波阶段产生的部分压力。图 10(b)中还给出了本文计算出的气泡半径时程曲线,可采用Cole提出的气泡最大半径Rmax, j=3.38[W/(d+10.3)]1/3和周期Tj=2.11W1/3/(d+10.3)5/6经验公式进行验证,经验证得到本文计算的气泡最大半径和周期的误差分别为1.0%和2.2%。
|
图 10 水下爆炸荷载验证 Fig. 10 Validation of underwater explosive load |
文献[9]研究了单独移动荷载作用下悬浮隧道的动力响应,为了验证本文移动荷载模型和结构模型的可靠性,图 11(a)和11(b)分别为移动荷载下隧道的跨中竖向位移时程曲线和移动荷载在跨中时的竖向位移分布曲线。由图 11可知本文和文献[9]中的结果基本一致。由此可见,本文中建立的荷载模型和结构模型是较为可靠的。

|
图 11 移动荷载验证 Fig. 11 Validation of moving load |
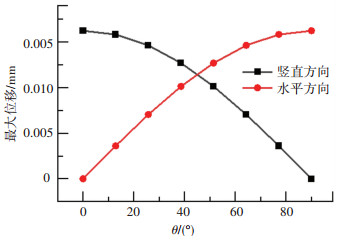
本小节将讨论爆炸荷载参数对悬浮隧道动力响应的影响。为了单独分析爆炸荷载的作用,此处暂不考虑车辆荷载的作用。图 12给出了不同爆炸荷载入射角下悬浮隧道竖直和水平方向上的最大位移。可以看出两个方向上的最大位移分布相似,随荷载入射角的增大竖直位移呈抛物线下降,水平位移呈抛物线上升,在入射角接近45°时相等。两者相似的原因在于本文选择了各向同性的管体参数及锚索刚度。为了避免冗杂,此处选择0°荷载入射角(即爆炸发生在隧道跨中正下方),讨论竖直方向上的动力响应。
|
图 12 不同荷载入射角下隧道最大位移 Fig. 12 Maximum displacement of tunnel under different load incidence angles |
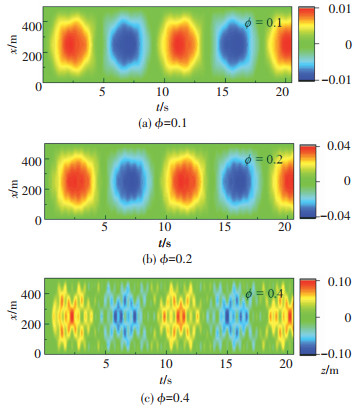
冲击波超压值与炸药量W和爆心距R距离有关,定义冲击因子ϕ=W1/3/R可综合考虑炸药量和爆心距的影响[27]。图 13给出了3种冲击因子下隧道的位移云图。可以看出ϕ=0.1与ϕ=0.2两种冲击因子下隧道位移分布较为相似,表现为正负位移的交替出现,而当ϕ=0.4时位移分布有所改变,峰值明显增大,且不同隧道位置处的位移差值显著增大。与ϕ=0.1相比冲击因子增大2倍和4倍,最大位移分别增大4倍和10倍。由此可见冲击因子能够极大促进悬浮隧道最大位移的增加。
|
图 13 不同冲击因子下隧道位移 Fig. 13 Unnel displacement under different impact factors |
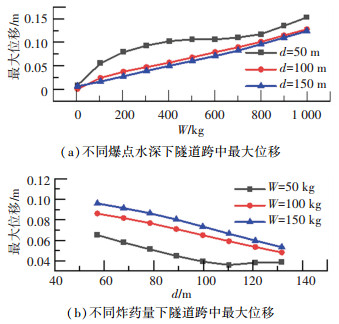
与冲击波荷载不同,气泡荷载除受炸药量W影响外还受爆点水深d的影响。图 14(a)和14(b)给出了不同炸药量、爆点水深与隧道跨中最大位移的关系。由图 14(a)可以看出在3种d值下随炸药量的增大,隧道最大位移基本呈线性增大,仅当d=50 m时曲线有所上浮。由图 14(b)可以看出,在3种W值下随爆点水深的增大,隧道最大位移基本呈线性减小,但当W=50 kg时曲线末端逐渐平缓。这说明爆点水深只能在一定范围内抑制水下爆炸。
|
图 14 不同爆点水深和炸药量下跨中位移 Fig. 14 Mid-span displacement under different explosion depth and explosive amount |
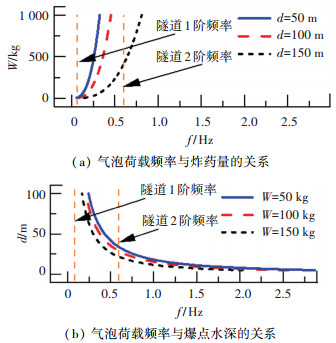
图 15(a)和15(b)给出了隧道频率与气泡频率的关系曲线。可以看出随炸药量的增大气泡荷载频率成指数增大,随爆点水深的增大气泡荷载频率成反比例减小。另外,在不同炸药量和水深情况下气泡荷载频率均小于3 Hz,而隧道的1阶和2阶固有频率分别为0.079、0.594 Hz,因此隧道有发生共振的可能性,由图中也可看出隧道的频率直线与气泡荷载频率曲线存在交点。
|
图 15 气泡荷载频率与隧道频率关系 Fig. 15 Relationship between bubble load and tunnel frequency |
本小节分析移动荷载耦合效应对悬浮隧道动力响应的影响。为了一般地分析爆炸时移动荷载位置的影响,定义隧道纵向无量纲位置变量ξ=x/l。
选择炸药量W=500 kg,移动荷载速度为v=50 m/s进行计算分析。图 16(a)给出了3种移动荷载位置下(1/8跨、1/4跨、1/2跨,分别对应ξ为0.125、0.25、0.5)爆炸后的跨中位移时程曲线。可以看出爆炸前管体位移在车辆荷载作用下缓慢增大,爆炸发生后位移出现剧烈的震荡,并由负向转为正向。ξ为0.125、0.25、0.5时对于的位移峰值分别为0.127、0.148、0.152 m。由此可知移动荷载在管体边缘(1/8跨)时发生爆炸的位移峰值最小,其余两种情况的位移峰值相近。

|
图 16 移动荷载位置对悬浮隧道位移的影响 Fig. 16 Effect of moving load position on SFT displacement |
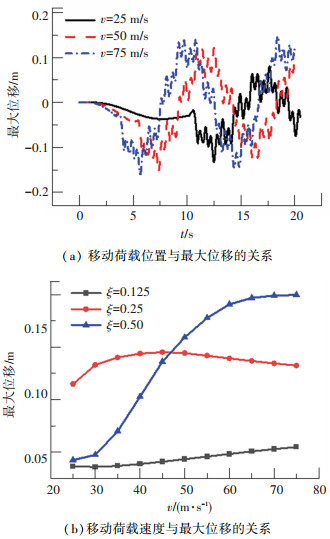
为了进一步分析,图 16(b)给出了移动荷载位置与隧道最大位移的关系曲线。可以看出在3种移动速度下(对于一般车辆是难以达到75 m/s车速的,此处选择较大的车速是从理论上分析车速的影响规律),随移动荷载位置参数ξ的增大最大位移都呈先增后减的变化趋势,且移动速度越大,曲线峰值越大,横坐标ξ越接近0.5。同时曲线表现出极强的非对称性,当ξ接近于1(即车辆即将驶出隧道)最大位移出现明显的下降。这说明移动荷载将要驶出隧道时发生爆炸对隧道危害性较小,跨中移动荷载接近跨中时发生爆炸对隧道危害性较大。
选择炸药量W=500 kg,移动荷载位置参数ξ=0.5进行计算分析。图 17(a)给出了3种移动荷载速度下(25、50、75 m/s)爆炸后的跨中位移时程曲线。可以看出3种情况下的位移分布整体相近。移动荷载速度为25、50、75 m/s对应的隧道最大位移分别为0.13、0.15、0.16 m。由此可知,隧道位移在移动荷载速度最小时位移峰值最小,移动荷载速度最大时位移峰值最大。
为了进一步分析,图 17(b)给出了移动荷载速度与隧道最大位移的关系曲线。可以看出在3种移动荷载位置下图中关系曲线的分布各不相同。其中当ξ≠0.5时,移动荷载速度对最大位移的影响不大。当ξ=0.5时,随移动荷载速度的增大隧道最大位移整体呈抛物线上升趋势。总体而言,爆炸移动耦合作用下悬浮隧道的最大位移受到移动荷载位置和速度的综合影响,车辆以最快速度行驶至跨中时刻发生爆炸对隧道危害性较大。
|
图 17 移动荷载速度对悬浮隧道位移的影响 Fig. 17 Effect of moving load speed on SFT displacement |
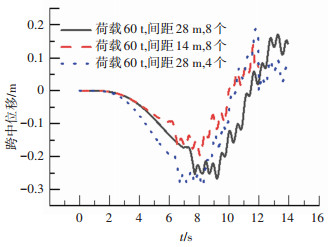
为了讨论移动荷载分布对悬浮隧道的影响,采用与上文不同移动荷载形式——等间距移动荷载(列车荷载)进行计算,单个移动荷载大小取6×105 N,炸药量W取500 kg,移动荷载速度v取50 m/s。由图 18可以看出不同荷载数量和间距下管体的位移整体变化相似,由于选择跨中加载爆炸,情况1(间距为28 m,8个移动荷载)到达跨中时间稍大于其他两种情况。3种情况下(间距为28 m,8个移动荷载;间距为14 m,8个移动荷载;间距为28 m,4个移动荷载)的位移峰值分别为0.26、0.29、0.20 m,由此可以看出当荷载间距较小时位移稍大,减小移动荷载间距对管体爆炸动力响应具有一定促进作用。另一方面当荷载数量由4个增加至8个后,管体的位移有小幅增加。由于可以看出在移动和爆炸耦合作用下增加移动荷载的数目对于管体位移也具有一定促进作用。
|
图 18 移动荷载分布对悬浮隧道位移的影响 Fig. 18 Effect of moving load distribution on SFT displacement |
1) 本文建立的悬浮隧道爆炸-移动模型能够考虑水下爆炸荷载的作用阶段和空间位置、悬浮隧道管体的水平、竖直两方向运动状态以及隧道内的移动荷载,较为符合悬浮隧道的实际受力情况。
2) 冲击因子能够极大促进悬浮隧道最大位移的增加。在仅水下爆炸荷载作用下与ϕ=0.1相比,冲击因子增大2倍和4倍时,隧道最大位移分别增大了4倍和10倍。
3) 随炸药量的增大气泡荷载频率成指数增大,随爆点水深的增大气泡荷载频率成反比例下降,不同炸药量和水深情况下,气泡荷载频率均小于3 Hz,与悬浮隧道低阶频率相近容易导致共振。
4) 在水下爆炸和移动荷载作用下,悬浮隧道的最大位移受到移动荷载位置和速度的综合影响,其中车辆以最快速度行驶至跨中时刻发生爆炸对隧道危害性较大。
5) 本文在计算冲击波的瞬态流固耦合效应时采用了较为简便的泰勒平板理论,在一定程度上降低了计算的精度,后续可通过数值模拟或试验对水下爆炸荷载进行修正以进一步提高计算准确性。
| [1] |
项贻强, 陈政阳, 杨赢. 悬浮隧道动力响应分析方法及模拟的研究进展[J]. 中国公路学报, 2017, 30(1): 69. XIANG Yiqiang, CHEN Zhengyang, YANG Ying. Research development of method andsimulation for analyzing dynamic response of submerged floating tunnel[J]. China Journal of Highway and Transport, 2017, 30(1): 69. |
| [2] |
DONNA A. Chapter 10 submerged floating tunnels—a concept whose time has arrived[J]. Tunnelling and Underground Space Technology, 1997, 12(2): 317. DOI:10.1016/S0886-7798(97)90022-5 |
| [3] |
丁浩, 程亮, 李科. 悬浮隧道结构动力响应研究进展与展望[J]. 隧道建设(中英文), 2019, 39(6): 901. DING Hao, CHENG Liang, LI Ke. Research progress and prospect on dynamic response of SFT structures[J]. Tunnel Construction, 2019, 39(6): 901. |
| [4] |
SEO S I, SAGONG M, SON S W. Global response of submerged floating tunnel against underwater explosion[J]. KSCE Journal of Civil Engineering, 2015, 19(7): 2029. DOI:10.1007/s12205-015-0136-3 |
| [5] |
HONG K Y, LEE G H, LEE S L. Dynamic behavior of submerged floating tunnel by underwater explosion[J]. Journal of the Computational Structural Engineering Institute of Korea, 2018, 31(5): 215. DOI:10.7734/COSEIK.2018.31.5.215 |
| [6] |
LUO Gang, ZHOU Xiaojun, CHEN Jianxun. The dynamic response of an experimental submerged floating tunnel with different cross sections under explosive impact[J]. Journal of Coastal Research, 2018, 82(S1): 212. DOI:10.2112/SI82-031.1 |
| [7] |
KRISTOFFERSEN M, MINORETTI A, BØRVIK T. On the internal blast loading of submerged floating tunnels in concrete with circular and rectangular cross-sections[J]. Engineering Failure Analysis, 2019, 103: 462. DOI:10.1016/j.engfailanal.2019.04.074 |
| [8] |
TØMTE A. Energy absorption and damage prevention in a submerged floating tunnel during internal blast loading[D]. Trondheim: Norwegian University of Science and Technology, 2015
|
| [9] |
项贻强, 林亨, 陈政阳. 移动荷载作用下悬浮隧道动力响应分析[J]. 振动与冲击, 2018, 37(4): 82. XIANG Yiqiang, LIN Heng, CHEN Zhengyang. Dynamic response analysis of a submerged floating tunnel subjected to moving load[J]. Journal of Vibration and Shock, 2018, 37(4): 82. |
| [10] |
LIN Heng, XIANG Yiqiang, YANG Ying, et al. Dynamic response analysis for submerged floating tunnel due to fluid-vehicle-tunnel interaction[J]. Ocean Engineering, 2018, 166: 290. DOI:10.1016/j.oceaneng.2018.08.023 |
| [11] |
董满生, 张嫄, 唐飞, 等. 等间距移动荷载作用下水中悬浮隧道管体的位移响应[J]. 应用力学学报, 2016, 33(5): 34. DONG Mansheng, ZHANG Yuan, TANG Fei, et al. Characteristic comparison of energy absorbing and dissipating of honeycomb panel and Whipple structure in hypervelocity impact[J]. Chinese Journal of applied mechanics, 2016, 33(5): 34. |
| [12] |
TARIVERDILO S, MIRZAPOUR J, SHAHMARDANI M, et al. Vibration of submerged floating tunnel due to moving loads[J]. Applied Mathematical Modelling, 2011, 35(11): 5413. DOI:10.1016/j.apm.2011.04.038 |
| [13] |
JIN C, KIM M. Dynamic responses of a moored submerged floating tunnel under moving loads and wave excitations[C]// Proceedings of the Twenty-Eighth International Ocean and Polar Engineering Conference. Sapporo: International Society of Offshore and Polar Engineers, 2018: 278
|
| [14] |
COLE R H. Underwater explosion[M]. Princeton: Princeton University Press, 1948.
|
| [15] |
张阿漫, 戴绍仕. 流固耦合动力学[M]. 北京: 国防工业出版社, 2011. ZHANG Aman, DAI Shaoshi. Fluid-structure interaction dynamics[M]. Beijing: Nation Defense Industry Press, 2011. |
| [16] |
罗泽立, 周章涛, 毛海斌, 等. 水下爆炸强冲击波与平板结构相互作用的理论分析方法[J]. 高压物理学报, 2017, 31(4): 94. LUO Zeli, ZHOU Zhangtao, MAO Haibin, et al. Theoretical analysis of the interaction between the plate structure and strong shock wave in underwater explosion[J]. Chinese Journal of High Pressure Physics, 2017, 31(4): 94. |
| [17] |
谌勇, 唐平, 汪玉, 等. 刚塑性圆板受水下爆炸载荷时的动力响应[J]. 爆炸与冲击, 2005, 25(1): 90. CHEN Yong, TANG Ping, WANG Yu, et al. Dynamic response analysis of rigid-plastic circular plate under underwater blast loading[J]. Explosion and Shock Waves, 2005, 25(1): 90. |
| [18] |
VERNON T A. Whipping response of ship hulls from underwater explosion bubble loading[R]. Dartmouth: Defence Research Establishment Atlantic, 1986
|
| [19] |
张弩, 宗智, 张文鹏, 等. 基于双渐进方法的水下爆炸气泡载荷作用下舰船的动态响应分析[J]. 振动与冲击, 2012, 31(23): 50. ZHANG Nu, ZONG Zhi, ZHANG Wenpeng, et al. Dynamic response of a ship hull stucture subjected to an underwater explosion bubble based on doubly asymptotic approximation method[J]. Journal of Vibration and Shock, 2012, 31(23): 50. |
| [20] |
姚熊亮, 陈建平. 水下爆炸二次脉动压力下舰船抗爆性能研究[J]. 中国造船, 2001, 42(2): 48. YAO Xiongliang, CHEN Jianping. A study on anti-underwater explosion performance of ship subjected to gas bubble impulsive pressure[J]. Ship Building of China, 2001, 42(2): 48. |
| [21] |
张弩. 水下爆炸气泡作用下船体总纵强度估算方法[J]. 中国舰船研究, 2014(6): 14. ZHANG Nu. Theevaluation method of the longitudinal strength of a ship hull subjected to the bubble load in underwater explosion[J]. Chinese Journal of Ship Research, 2014(6): 14. |
| [22] |
李海涛, 张振华, 牟金磊, 等. 水下爆炸作用下弹塑性船体梁整体运动模型及损伤特性[J]. 工程力学, 2019, 36(1): 241. LI Haitao, ZHANG Zhenhua, MOU Jinlei, et al. Hydro-elastic-plastic dynamic response of a ship hull girder subjected to underwater explosion: a simplified theoretical model[J]. Engineering Mechanics, 2019, 36(1): 241. |
| [23] |
公路工程技术标准: JTG B01—2014[S]. 北京: 交通运输部, 2014. Technical Standard of Highway Engineering: JTG B01—2014[S]. Beijing: Ministry of Transport of the People's Republic of China, 2014. |
| [24] |
项贻强, 张科乾. 基于Morison方程分层积分计算悬浮隧道的波浪力[J]. 浙江大学学报(工学版), 2011, 45(8): 1399. XIANG Yiqiang, ZHANG Keqian. The layered integrating method for calculating wave force of submerged floating tunnel based on Morison equation[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(8): 1399. |
| [25] |
XIANG Yiqiang, YANG Ying. Spatial dynamic response of submerged floating tunnel under impact load[J]. Marine Structures, 2017, 53: 20. DOI:10.1016/j.marstruc.2016.12.009 |
| [26] |
LI Jian, RONG Jili. Experimental and numerical investigation of the dynamic response of structures subjected to underwater explosion[J]. European Journal of Mechanics-B/Fluids, 2012, 32: 59. DOI:10.1016/j.euromechflu.2011.09.009 |
| [27] |
姚熊亮, 许维军, 梁德利. 水下爆炸时舰船冲击环境与冲击因子的关系[J]. 哈尔滨工程大学学报, 2004, 25(1): 9. YAO Xiongliang, XU Weijun, LIANG Deli. The relation of impulsive environment and impulsive factor on underwater explosion of ship[J]. Journal of Harbin Engineering University, 2004, 25(1): 9. |
 2022, Vol. 54
2022, Vol. 54


