混杂纤维混凝土(hybrid fiber reinforced concrete, HFRC) 是在混凝土基体内掺入不同类型的纤维,在利用纤维抗拉和抗剪能力的同时发挥不同纤维的协同工作效应,增强混凝土基体的抗裂、抗压强度,改善混凝土基体的各项性能[1]。将HFRC应用到深梁构件中,可以显著的提高深梁构件的承载能力、延性和刚度。
国内外学者已对HFRC深梁进行了试验研究。文献[2]通过试验发现,在HFRC试件中,短纤维主要起到延缓裂缝形成的作用,而长纤维则主要“桥接”裂缝、提高试件的延性。文献[3]进行了混杂纤维高性能混凝土深梁抗弯及抗剪性能试验,研究了两种不同类型的纤维掺量及分布钢筋配筋率对高性能混凝土深梁抗剪能力的影响。结果表明,混杂纤维对高性能混凝土深梁抗弯、抗剪承载能力及延性改善效果显著。文献[4]对比分析了钢纤维混凝土深梁和聚酯纤维混凝土深梁,发现钢纤维混凝土的流动性虽然较差,但可以为构件提供更高的承载能力。此外,国内外学者也对纤维混凝土(fiber reinforced concrete, FRC)深梁承载能力的计算方法进行了相关研究。文献[5]利用人工神经网络对FRC深梁的抗剪承载能力进行了预测,并研究了不同设计参数对抗剪承载能力的影响。文献[6]提出了一种改进的基于遗传算法的FRC深梁抗剪承载力计算方法。
钢纤维是常用的纤维之一,可以明显地增强混凝土基体的基本性能[4],进而改善混凝土构件的力学性能。然而,现有研究主要集中于单一纤维混凝土构件,对混杂钢纤维混凝土(hybrid steel fiber reinforced concrete, HSFRC)深梁的试验研究较少[7];此外,现有的基于拉压杆模型(softened strut and tie model, SSTM)的深梁抗剪承载力计算方法中未考虑钢纤维的影响。为此,本文在考虑HSFRC材料特性的基础上,建立了适用于HSFRC深梁的抗剪承载力计算方法。之后,设计制作了4根HSFRC深梁试件,对其进行抗剪性能试验,验证计算方法的合理性,并分析混合钢纤维体积掺量和分布钢筋配筋率对试件抗剪性能的影响。
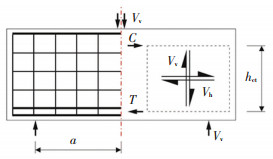
1 HSFRC深梁软化拉压杆模型 1.1 宏观模型集中荷载作用下,深梁的受力如图 1所示。图 1中Vv和Vh分别表示水平和竖向剪力;C表示受压区混合钢纤维混凝土合力;T表示受拉纵筋合力;hct为C和T间的距离;a为剪跨,即加载点至支座中点的距离。
|
图 1 HSFRC深梁的受力简图 Fig. 1 Force diagram of HSFRC deep beam |
对于中、低纤维掺量构件,其中性轴位置的变化可忽略不计,近似与普通混凝土构件相同[8]。参考文献[9-10],由图 1可得
| $ \frac{V_{\mathrm{v}}}{V_{\mathrm{h}}} \approx \frac{h_{\mathrm{ct}}}{a} $ | (1) |
| $ h_{\mathrm{ct}}=h_{\mathrm{t}}-\frac{k h_{\mathrm{t}}}{3} $ | (2) |
| $ k=\sqrt{\left(n \rho_{\mathrm{f}}\right)^{2}+2 n \rho_{\mathrm{f}}}-n \rho_{\mathrm{f}} $ | (3) |
| $ \rho_{\mathrm{f}}=\frac{A_{\mathrm{s}}+\varOmega A_{\mathrm{sh}}}{b h} $ | (4) |
式中:ht为截面有效高度;kht表示深梁受压区高度,系数k可由经典弯曲理论计算;n为钢筋弹性模量和混合钢纤维混凝土弹性模量之比;ρf为抗弯配筋率;As和Ash分别为受拉纵筋和水平分布钢筋横截面面积;Ω为水平分布钢筋贡献有效系数,可近似取0.2[11];b为截面宽度。
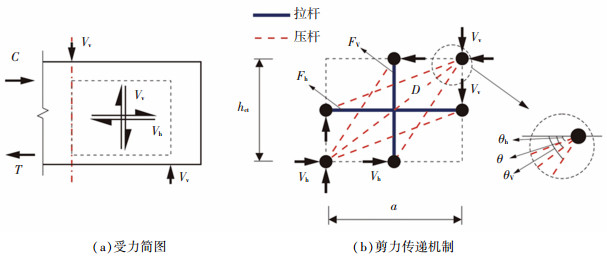
现有研究[3]表明,深梁在开裂前,斜向拉力主要由混合钢纤维混凝土承担,分布钢筋作用相对较小。当斜向拉力大于混合钢纤维混凝土的抗拉强度时,初始斜裂缝开始发展;此时,钢纤维会贯穿斜裂缝,并提供一定的抗拉强度,深梁的斜向拉力主要由受拉纵筋、分布钢筋及钢纤维承担。钢纤维在混凝土基体中呈三维随机乱向分布,为简化分析,可将裂缝处乱向分布的钢纤维等效为等量的水平微筋和垂直微筋。则开裂后深梁的抗拉体系可分为受拉纵筋,水平分布钢筋和等效水平向钢纤维,竖向分布钢筋和等效竖向钢纤维三部分。因此,深梁的软化拉压杆模型可分为斜向机构、水平机构和竖向机构三部分,如图 2所示。

|
图 2 HSFRC深梁的软化拉压杆模型 Fig. 2 SSTM of HSFRC deep beam |
斜向机构由受拉纵筋和一个对角斜压杆组成[12],如图 2(a)所示,斜压杆与水平轴之间的夹角可表示为
| $ \theta=\arctan \frac{h_{\mathrm{ct}}}{a} $ | (5) |
深梁开裂后,混合钢纤维混凝土主压应力方向与斜压杆方向一致,斜压杆有效面积可表示为
| $ A_{\mathrm{str}}=a_{\mathrm{s}} \cdot b_{\mathrm{s}} $ | (6) |
| $ a_{\mathrm{s}}=\sqrt{(k h)^{2}+\left(\frac{a_{\mathrm{b}}}{2}\right)^{2}} $ | (7) |
式中:as为斜压杆的高度,与深梁边界条件(即加载支座)和受压区高度有关;bs为斜压杆的宽度,可近似取深梁宽度;ab为加载支座截面宽度。
水平机构由水平拉杆和两个缓压杆组成[12],如图 2(b)所示,缓压杆与水平轴之间的夹角可表示为
| $ \theta_{\mathrm{h}}=\arctan \frac{h_{\mathrm{ct}}}{2 a} $ | (8) |
水平拉杆由水平分布钢筋和等效水平向钢纤维组成,其抗拉强度可表示为
| $ F_{\mathrm{h}}=F_{\mathrm{s}, \mathrm{h}}+F_{\mathrm{sf}, \mathrm{h}}=A_{\mathrm{s}, \mathrm{h}} f_{\mathrm{s}, \mathrm{h}}+A_{\mathrm{sf}, \mathrm{h}} f_{\mathrm{sf}} $ | (9) |
| $ A_{\mathrm{sf,h}}=\eta_{\mathrm{sf}} A_{\mathrm{sf}}=\eta V_{\mathrm{sf}} \frac{b h_{\mathrm{ct}}}{\sin \theta} $ | (10) |
式中:Fs, h为水平分布钢筋拉力;Fsf, h为等效水平向钢纤维拉力;fs, h为水平分布钢筋抗拉强度;As, h为水平分布钢筋横截面面积;fsf为钢纤维抗拉强度;Asf, h为等效水平向钢纤维面积;ηsf为等效钢纤维数量;η为等效系数,可近似取为0.41[13];Vsf为钢纤维体积率;Asf为单根钢纤维横截面面积。
竖向机构由竖向拉杆和两个陡压杆组成[12],如图 2(c)所示,陡压杆与水平轴之间的夹角可表示为
| $ \theta_{\mathrm{v}}=\arctan \frac{2 h_{\mathrm{ct}}}{a} $ | (11) |
竖向拉杆由竖向分布钢筋和等效竖向钢纤维组成,其抗拉强度Fv的计算方法与水平拉杆强度的计算方法相同,此处不再赘述。
1.2 力的平衡深梁软化拉压杆模型的内力如图 3所示,根据平衡条件,水平剪力和竖向剪力可分别表示为
| $ V_{\mathrm{h}}=-D \cos \theta+F_{\mathrm{h}}+2 F_{\mathrm{v}} \cot \theta_{\mathrm{v}} $ | (12) |
| $ V_{\mathrm{v}}=-D \sin \theta+2 F_{\mathrm{h}} \tan \theta_{\mathrm{h}}+F_{\mathrm{v}} $ | (13) |
|
图 3 HSFRC深梁软化拉压杆模型的内力 Fig. 3 Internal force of SSTM for HSFRC deep beam |
式中D为斜压杆中的压力。
文献[14]提出,拉杆内拉力与深梁剪力存在以下关系:
| $ F_{\mathrm{h}}=\gamma_{\mathrm{h}} \cdot V_{\mathrm{h}} $ | (14) |
| $ \gamma_{\mathrm{h}}=\frac{2 \tan \theta-1}{3} $ | (15) |
| $ F_{\mathrm{v}}=\gamma_{\mathrm{v}} \cdot V_{\mathrm{v}} $ | (16) |
| $ \gamma_{\mathrm{v}}=\frac{2 \cot \theta-1}{3} $ | (17) |
式中:γh为水平拉杆的拉力与水平剪力的比值;γv为竖向拉杆的拉力与竖向剪力的比值。
根据现有研究[14],斜压杆中的压力、水平拉杆和竖向拉杆中的拉力存在以下比例关系:
| $ (-D \sin \theta):\left(F_{\mathrm{h}} \tan \theta\right): F_{\mathrm{v}}=R_{\mathrm{d}}: R_{\mathrm{h}}: R_{\mathrm{v}} $ | (18) |
| $ R_{\mathrm{d}}=\frac{\left(1-\gamma_{\mathrm{h}}\right)\left(1-\gamma_{\mathrm{v}}\right)}{1-\gamma_{\mathrm{h}} \gamma_{\mathrm{v}}} $ | (19) |
| $ R_{\mathrm{h}} =\frac{\gamma_{\mathrm{h}}\left(1-\gamma_{\mathrm{v}}\right)}{1-\gamma_{\mathrm{h}} \gamma_{\mathrm{v}}} $ | (20) |
| $ R_{\mathrm{v}} =\frac{\gamma_{\mathrm{v}}\left(1-\gamma_{\mathrm{h}}\right)}{1-\gamma_{\mathrm{h}} \gamma_{\mathrm{v}}} $ | (21) |
式中Rd、Rh、Rv分别为3种内力之间的比例系数,满足以下关系:
| $ R_{\mathrm{d}}+R_{\mathrm{h}}+R_{\mathrm{v}}=1 $ | (22) |
联立以上各式,可得
| $ D=-\frac{1}{\sin \theta} \cdot \frac{R_{\mathrm{d}}}{R_{\mathrm{d}}+R_{\mathrm{h}}+R_{\mathrm{v}}} \cdot V_{\mathrm{v}} $ | (23) |
| $ F_{\mathrm{h}}=-\frac{1}{\tan \theta} \cdot \frac{R_{\mathrm{h}}}{R_{\mathrm{d}}+R_{\mathrm{h}}+R_{\mathrm{v}}} \cdot V_{\mathrm{v}} $ | (24) |
| $ F_{\mathrm{v}}=\frac{R_{\mathrm{v}}}{R_{\mathrm{d}}+R_{\mathrm{h}}+R_{\mathrm{v}}} \cdot V_{\mathrm{v}} $ | (25) |
3种机构共同作用下,深梁压杆范围内混合钢纤维混凝土的最大压应力可表示为
| $ \begin{aligned} \sigma_{\mathrm{c}, \max }=& \frac{1}{A_{\mathrm{str}}}\left[-D+\frac{\cos \left(\theta-\arctan \frac{h_{\mathrm{ct}}}{2 a}\right)}{\cos \left(\arctan \frac{h_{\mathrm{ct}}}{2 a}\right)} F_{\mathrm{h}}+\right.\\ &\left.\frac{\cos \left(\arctan \frac{2 h_{\mathrm{ct}}}{a}-\theta\right)}{\sin \left(\arctan \frac{2 h_{\mathrm{ct}}}{a}\right)} F_{\mathrm{v}}\right] \end{aligned} $ | (26) |
混合钢纤维混凝土受压应力-应变关系[15]可表示为
| $ \sigma_{\mathrm{c}}=\left\{\begin{array}{l} \lambda f_{\mathrm{c}}{}^{\prime}\left[2 \frac{\varepsilon_{\mathrm{c}}}{\lambda \varepsilon_{0}}-\left(\frac{\varepsilon_{\mathrm{c}}}{\lambda \varepsilon_{0}}\right)^{2}\right], \varepsilon_{\mathrm{c}} \leqslant \lambda \varepsilon_{0} \\ \lambda f_{\mathrm{c}}{}^{\prime}\left(\frac{\frac{\varepsilon_{\mathrm{c}}}{\varepsilon_{0}}-\lambda}{2-\frac{1}{\lambda}}\right), \varepsilon_{\mathrm{c}}>\lambda \varepsilon_{0} \end{array}\right. $ | (27) |
| $ \lambda=\frac{1}{\sqrt{1+600 \varepsilon_{\mathrm{t}}}} $ | (28) |
式中:ε0为混合钢纤维混凝土峰值压应变;εc和εt为混合钢纤维混凝土主压应力和主拉应力分别对应的应变;fc′为混合钢纤维混凝土圆柱体抗压强度,参照《钢纤维混凝土结构技术规程》[16],其与立方体抗压强度的换算可参考相关混凝土结构规范的相应规定;λ为混合钢纤维混凝土软化系数,可参考文献[17]计算。
钢筋应力-应变关系可表示为
| $ f_{\mathrm{s}}=\left\{\begin{array}{c} E_{\mathrm{s}} \varepsilon_{\mathrm{s}}, \varepsilon_{\mathrm{s}}<\varepsilon_{\mathrm{y}} \\ f_{\mathrm{y}}, \varepsilon_{\mathrm{s}} \geqslant \varepsilon_{\mathrm{y}} \end{array}\right. $ | (29) |
式中:Es为钢筋弹性模量;fs和εs分别为钢筋的应力和应变;fy和εy分别为钢筋的屈服应力和屈服应变。
钢纤维应力-应变关系可表示为
| $ f_{\mathrm{sf}}=E_{\mathrm{sf}} \varepsilon_{\mathrm{sf}} $ | (30) |
式中:Esf为钢筋弹性模量,εsf为钢纤维的应变。
由于钢纤维抗拉强度较高,深梁剪切破坏时,钢纤维通常是被拔出而非拉断。因此,混合钢纤维混凝土的抗拉强度主要取决于钢纤维与混凝土基体的黏结强度。此外,相关研究[18]表明短纤维主要抑制微裂缝的产生与发展。而荷载在达到峰值时,深梁的裂缝宽度已发展到一定程度,此时短纤维对深梁抗剪承载力的贡献已减弱,为简化计算过程,忽略短纤维的影响。则钢纤维黏结强度可按下式计算:
| $ A_{\mathrm{s}} f_{\mathrm{sf}} \leqslant d_{\mathrm{sf}} A_{\mathrm{spf}} \tau_{\mathrm{sf}, \max } $ | (31) |
| $ A_{\mathrm{spf}}=\frac{1}{4} {\rm{ \mathsf{ π} }} D_{\mathrm{sf}} l_{\mathrm{sf}} $ | (32) |
| $ \tau_{\mathrm{sf}, \max }=2.5 f_{\mathrm{c}}{}^{\prime} $ | (33) |
式中:τsf, max为长钢纤维与混凝土的黏结强度,可参考文献[19]计算;dsf为钢纤维类型影响因数,对长直形、波浪形、弯钩形钢纤维分别取0.5、0.75、1.0[20];Aspf为钢纤维表面积;Dsf为钢纤维直径;lsf为钢纤维长度。
将式(31)~(33)代入到式(30)中,并进行简化,可得
| $ f_{\mathrm{sf}} \leqslant \frac{d_{\mathrm{sf}} l_{\mathrm{sf}} \tau_{\mathrm{sf}, \max }}{D_{\mathrm{sf}}} $ | (34) |
则水平拉杆和竖向拉杆内的拉力满足以下条件:
| $ F_{\mathrm{h}} \leqslant F_{\mathrm{yh}}=A_{\mathrm{s}, \mathrm{h}} E_{\mathrm{s}} \varepsilon_{\mathrm{h}}+A_{\mathrm{sf}, \mathrm{h}} \frac{d_{\mathrm{sf}} l_{\mathrm{sf}} \tau_{\mathrm{sf}, \max }}{D_{\mathrm{sf}}} $ | (35) |
| $ F_{\mathrm{v}} \leqslant F_{\mathrm{yv}}=A_{\mathrm{s}, \mathrm{v}} E_{\mathrm{s}} \varepsilon_{\mathrm{v}}+A_{\mathrm{sf}, \mathrm{v}} \frac{d_{\mathrm{sf}} l_{\mathrm{sf}} \tau_{\mathrm{sf}, \max }}{D_{\mathrm{sf}}} $ | (36) |
式中Fyh和Fyv分别为水平拉杆和竖向拉杆屈服时的拉力。
1.4 协调方程根据莫尔圆应变协调准则,可得
| $ \varepsilon_{\mathrm{c}}+\varepsilon_{\mathrm{t}}=\varepsilon_{\mathrm{h}}+\varepsilon_{\mathrm{v}} $ | (37) |
式中:εc和εt分别为混合钢纤维混凝土的主压应变和主拉应变;εh和εv分别为混合钢纤维混凝土水平向和竖向的平均应变。
1.5 求解过程本文在计算方法的建立过程中,相关的假定和公式推导是基于混合钢纤维混凝土深梁处于峰值点时的受力状态,将上述平衡方程、本构方程和协调方程联立求解,可得到深梁的抗剪承载力。计算流程如图 4所示,主要计算步骤:1) 根据已知条件,整理数据,计算θ、θh、θv、ε0、Astr、As, h、As, v、Asf, h、Asf, v。2)利用式(15)、(17)计算γh和γv,利用式(19)~(21)计算Rd、Rh和Rv。3)合理给定Vv,利用式(23)~(25)计算D、Fh、Fv,利用式(26)、(35)、(36)计算σc, max、εh和εv。4)确定混合钢纤维混凝土的软化作用,合理给定εc,利用式(37)计算εt(当tan θ≤1/2时,令εh=0;当tan θ≥2时,令εv=0;当无腹筋或腹筋屈服时,采用屈服应变,即εh=0.002或εv=0.002)。5)计算软化系数λ,利用式(27)计算σc。6)比较σc与σc, max,若σc, max < σc,则重新给定Vv,重复步骤3~5,直至σc, max≥σc。7)比较εc与λε0,若εc<λε0,则重新给定εc,重复步骤4~6,直至εc≥λε0计算停止。

|
图 4 计算流程 Fig. 4 Calculation procedure |
上述计算步骤可通过MATLAB编制计算程序,代入相关参数进行计算。
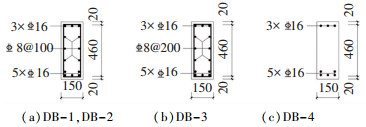
2 HSFRC深梁抗剪承载力试验以混合钢纤维体积掺量和分布钢筋配筋率为变量,设计了4个矩形截面深梁,对其进行抗剪性能试验研究,试件的设计参数及配筋见表 1和图 5。钢筋采用HRB400,纵筋直径为16 mm,分布钢筋直径为8 mm。混合钢纤维混凝土配合比参考文献[21]中的相关内容,具体见表 2。根据已有研究结果[22],当长钢纤维掺量达到1.5%(钢纤维总掺量为2%)之后,继续增加其掺量对混凝土强度的提升已不在显著,且容易造成混凝土流动性的降低。综合比较下,长钢纤维与短钢纤维掺量分别为1.5%和0.5%时,混凝土具有较高的抗压强度和抗拉强度,且流动性较好,故本文选择此种配比。同时,为了研究钢纤维掺量对深梁抗剪性能的影响,选取长钢纤维与短钢纤维掺量为0.75%和0.25%的配比。试验中采用的长、短两种钢纤维基本参数:长钢纤维为长度30 mm、直径0.55 mm的端弯型纤维,短钢纤维为长度13 mm、直径0.20 mm的平直型纤维。试件制作过程中,对相关材料性能进行测试,测试结果:HSFRC-1和HSFRC-2的立方体抗压强度分别为85.3、89.7 MPa,轴心抗拉强度分别为3.85、5.28 MPa;C16和C8钢筋的屈服强度分别为474、568 MPa,极限强度分别为622、723 MPa。
| 表 1 试件参数 Tab. 1 Parameters of specimens |
|
图 5 试件配筋图(mm) Fig. 5 Reinforcement details of specimens(mm) |
| 表 2 HSFRC材料配合比 Tab. 2 Material proportions of HSFRC |
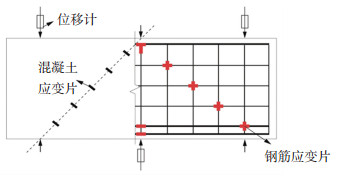
试验过程中,在加载点和支座的对应位置布置位移计,在加载点和支座连线的位置粘贴钢筋应变片和混凝土应变片,在受拉纵筋中点粘贴钢筋应变片,如图 6所示。加载过程中,采用ZBL-F101裂缝观测仪量测裂缝宽度。试验在5 000 kN的长柱试验机上进行,加载装置如图 7所示。加载点为试件跨中,支座设置在距梁端120 mm处。加载速度为0.1 mm/min,当试件承载力下降至极限荷载的85%时,试验结束。
|
图 6 量测布置 Fig. 6 Measurement arrangement |

|
图 7 加载装置 Fig. 7 Test device |
试件的最终破坏形态如图 8所示。加载过程中,试件跨中底部首先出现垂直受弯裂缝。之后,试件剪跨区出现受剪斜裂缝,裂缝宽度较小且发展缓慢。随着荷载的增加,斜裂缝宽度逐渐增大并向加载点和支座处延伸,裂缝处可以观察到部分短钢纤维被拔出。当达到峰值荷载后,主裂缝形成,其余裂缝缓慢发展,并伴有钢纤维拔出的“吱吱”声,在主裂缝处可以观察到端部带有弯勾的长钢纤维被拔出。对比试件破坏现象,试件DB-2的裂缝最为细密,试件DB-1与DB-3的裂缝分布形态相当,试件DB-4的裂缝较为稀疏,宽度较大。

|
图 8 破坏形态 Fig. 8 Failure modes |
从试验现象可以看出,大部分短钢纤维在裂缝出现不久后就被拔出,对试件开裂后承载能力的发展贡献较小;而长钢纤维多在峰值荷载后被拔出,全程参与了试件的受力。试件承载力计算中可忽略短钢纤维的影响,但应计入长钢纤维的贡献。
3.2 HSFRC应变试件加载点与支座连线处的混合钢纤维混凝土应变情况如图 9所示,其总体呈不均等增长趋势,裂缝处的应变增长较快,而其他位置的应变变化较小。在加载初期,混合钢纤维混凝土应变增长缓慢。试件DB-1在150 kN左右,应变出现明显增大,而试件DB-2在200 kN左右,应变才出现明显增大。钢纤维体积掺量对应变的增长幅度有一定的影响,掺量越大,混凝土基体中钢纤维分布越密集,裂缝受到的抑制作用越明显,应变增长越慢。随着荷载的增大,混凝土基体中微裂缝逐渐发展,部分短钢纤维被拔出,混合钢纤维混凝土应变急剧增加,但其最大值受到钢纤维体积掺量的影响。对比试件DB-1和DB-2,当钢纤维体积掺量从1%增至2%时,应变最大值提高64.7%。在整个加载过程中,分布钢筋配筋率对混合钢纤维混凝土应变的影响相对较小。混凝土基体中的钢纤维会“桥接”裂缝,当钢纤维掺量提高后,裂缝间的钢纤维变得更密集,这在一定程度上延缓了混凝土基体应变的增长、增强了其抗拉能力,提高了其在试件受剪过程中承担的剪力。

|
图 9 HSFRC应变 Fig. 9 Strain of HSFRC |
试件水平、竖向分布钢筋应变随荷载变化情况如图 10(a)、10(b)所示。在斜裂缝出现前,水平分布钢筋应变增长缓慢,而竖向分布钢筋应变增长相对较快。在斜向裂缝出现后,分布钢筋应变迅速增加。对比试件DB-1、DB-2和DB-3,钢纤维体积掺量及分布钢筋配筋率的提高均会降低分布钢筋应变的增长幅度。混凝土开裂后,钢纤维会“桥接”裂缝,承担裂缝处的部分拉力。当钢纤维体积掺量增大后,裂缝处的钢纤维变得更密集,可以承担更多的拉力,使分布钢筋承担的拉力减小;而分布钢筋配筋率的增大会增加钢筋的受力面积,使每根钢筋的应力得以减小。

|
图 10 钢筋应变 Fig. 10 Strain of reinforcement |
试件受拉纵筋应变随荷载变化情况如图 10(c)所示。在跨中受弯裂缝出现前,纵筋应变增加缓慢,且近似与荷载呈线性关系;裂缝出现后,纵筋应变增长幅度增大。钢纤维体积掺量和分布钢筋配筋率的增加均会降低纵筋应变的增长幅度。对于试件DB-4,当试件中未配置分布钢筋时,纵筋应变在裂缝出现后急剧增大,远超于试件DB-2与DB-3。
对比试件DB-1和DB-2,在加载的全过程中,试件DB-2分布钢筋和受拉纵筋的应变增长幅度始终低于试件DB-1,这说明钢纤维对钢筋应变增长的延缓作用是始终存在的。钢纤维在裂缝出现后没有被全部拔出,与钢筋共同承担了裂缝处的拉力,软化拉压杆模型中拉杆由钢筋和钢纤维共同组成的假设是合理的。
3.4 承载能力和变形能力加载过程中,短钢纤维主要延缓微裂缝在混凝土基体中的扩展,作为增强混凝土基体的“微筋”存在;当构件局部产生较大裂缝时,长钢纤维由于端部带有弯钩,抗拔出性能优异,可以在构件承载过程中耗散更多能量,延缓裂缝发展,进而抑制混凝土受拉区扩展,提高受压区高度。同时,钢纤维的掺入也提高了混凝土的抗拉强度,延迟钢筋受拉屈服。两种钢纤维在试件加载过程中协同作用,提高了试件的承载能力和变形能力。试件的荷载-跨中挠度曲线如图 11所示。试件DB-2的初始刚度比试件DB-1提高了24.6%;但两者均在跨中挠度达到3.3 mm时出现退化,且退化速率基本相同。钢纤维体积掺量的增加可以明显提高试件的刚度,但对刚度退化速率的影响较小。对比试件DB-2、DB-3和DB-4,试件DB-2在加载位移达到3.45 mm时,刚度开始退化;而试件DB-4在加载位移达到2.7 mm时,刚度开始退化,且退化速率较快。分布钢筋配筋率的增加可以延缓试件的刚度退化,并降低刚度退化速率,但对试件初始刚度的影响较小。

|
图 11 荷载-挠度曲线 Fig. 11 Load-deflection curves |
试件的承载能力和变形能力见表 3,表中Vc和Δc分别为开裂点的荷载和位移,Vp和Δp分别为峰值点的荷载和位移,Vu和Δu分别为极限点的荷载和位移。对比试件DB-1和DB-2,随着钢纤维体积掺量的增加,试件的承载能力和变形能力得到提高。当钢纤维体积掺量从1%增至2%时,试件的开裂荷载和峰值荷载分别提高了42.4%和26.9%,开裂位移和极限位移分别增加了10.1%和9.6%。对比试件DB-2、DB-3和DB-4,随着分布钢筋配筋率的提高,试件的承载能力逐渐增大,变形能力呈先增大后轻微降低的趋势。当分布钢筋配筋率从0增至0.68%时,试件的开裂荷载和峰值荷载分别增加了23.2%和24.5%;而其开裂位移和极限位移先分别提高了32.9%和28.1%,后分别降低了7.2%和2.9%。值得注意的是,试件DB-1和DB-4的峰值荷载相近,表明钢纤维在一定程度上可以弥补分布钢筋缺失的缺陷。
| 表 3 试件承载能力和变形能力 Tab. 3 Bearing and deformation capacities of specimens |
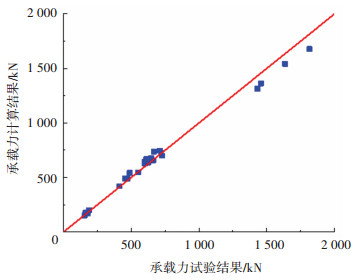
选取本文建立的承载力计算方法,收集试验及相关文献[7, 23]中的实测数据进行计算,结果见图 12和表 4,表中Vu和Vc, u分别为抗剪承载力的试验值和计算值。由计算结果可知,试验结果与计算结果之比的平均值为0.98,标准差为0.054,变异系数为0.055,符合较好。
|
图 12 试验结果与计算结果比较 Fig. 12 Comparison between calculation and test results |
| 表 4 抗剪承载力试验值与计算值比较 Tab. 4 Comparison between calculation and test results of shear bearing capacity |
基于软化拉压杆理论,提出了HSFRC深梁抗剪承载力计算方法,并对4根HSFRC深梁进行了抗剪性能试验,验证了计算方法的合理性,研究了混合钢纤维体积掺量和分布钢筋配筋率对HSFRC深梁抗剪性能的影响,得到以下主要结论:
1) 基于软化拉压杆模型,考虑钢纤维混凝土抗拉强度对深梁抗剪承载力的贡献,将钢纤维并入到深梁的抗拉体系中,对相关公式进行了改进,并结合HSFRC受压和受拉本构方程,对计算过程中的平衡方程进行了修正,最终给出了HSFRC深梁抗剪承载力计算方法,计算结果较为准确。
2) 在混凝土开裂后,钢纤维会“桥接”裂缝,承担裂缝处的拉力,并延缓裂缝处混凝土应变和钢筋应变的发展,且钢纤维体积掺量越大效果越明显。分布钢筋配筋率的增大会延缓钢筋应变的发展。
3) 钢纤维体积掺量的增加会提高试件的初始刚度,但对刚度的退化速率影响较小。分布钢筋配筋率对试件初始刚度的影响相对较小,但会延缓试件刚度的退化。
4) 随着钢纤维体积掺量的增加,试件的承载能力和变形能力得到提高。随着分布钢筋配筋率的增加,试件的承载能力得到提高,但变形能力呈现先增大后轻微降低的趋势。
| [1] |
QIAN C X, STROEVEN P. Development of hybrid polypropylene-steel fibre-reinforced concrete[J]. Cement & Concrete Research, 2000, 30(1): 63. |
| [2] |
ADEBAR P, MINDESS S, St PIERRE D, et al. Shear tests of fiber concrete beams without stirrups[J]. ACI Structural Journal, 1997, 94(1): 68. DOI:10.1109/CITCON.1997.599414 |
| [3] |
刘胜兵, 徐礼华. 混杂纤维高性能混凝土深梁受剪性能[J]. 土木工程学报, 2013, 46(3): 29. LIU Shengbing, XU Lihua. Shear behavior of hybrid fiber reinforced high performance concrete deep beams[J]. China Civil Engineering Journal, 2013, 46(3): 29. |
| [4] |
SHAH D L. Evaluation of shear strength in self-com parting fiber-reinforced concrete and conventional concrete deep beams[J]. Magazine of Concrete Research, 2012, 64(6): 527. DOI:10.1680/macr.11.00028 |
| [5] |
NAIK U, KUTE S. Span-to-depth ratio effect on shear strength of steel fiber-reinforced high-strength concrete deep beams using ANN model[J]. International Journal of Advanced Structural Engineering, 2013, 5(1): 29. DOI:10.1186/2008-6695-5-29 |
| [6] |
SHAHNEWAZ M, ALAM M S. Improved shear equations for steel fiber-reinforced concrete deep and slender beams (with appendix)[J]. ACI Structural Journal, 2014, 111(4): 851. |
| [7] |
周家亮, 陈宝春, 马熙伦, 等. 超高性能混凝土深梁受剪性能[J]. 交通运输工程学报, 2020, 20(6): 117. ZHOU Jialiang, CHEN Baochun, MA Xilun, et al. Shear performance of ultra-high performance concrete deep beams[J]. Journal of Traffic and Transportation Engineering, 2020, 20(6): 117. |
| [8] |
CAMPIONE G. Flexural response of FRC corbels[J]. Cement and Concrete Composites, 2009, 31(3): 204. DOI:10.1016/j.cemconcomp.2009.01.006 |
| [9] |
RUSSO G, VENIR R, PAULETTA M, et al. Reinforced concrete corbels shear strength model and design formula[J]. ACI Structural Journal, 2006, 103(1): 3. |
| [10] |
HWANG S J, LU W Y, LEE H J. Shear strength prediction for reinforced concrete corbels[J]. ACI Structural Journal, 2000, 97(4): 543. |
| [11] |
HE Z Q, LIU Z, MA Z J. Investigation of load-transfer mechanisms in deep beams and corbels[J]. ACI Structural Journal, 2012, 109(4): 467. |
| [12] |
LU W Y. Shear strength prediction for steel reinforced concrete deep beams[J]. Journal of Constructional Steel Research, 2006, 62(10): 933. DOI:10.1016/j.jcsr.2006.02.007 |
| [13] |
ROMUALDI J P, MANDEL J A. Tensile strength of concrete affected by uniformly distributed and closely spaced short lengths of wire reinforcement[J]. ACI Materials Journal, 1964, 61(6): 657. |
| [14] |
SCHÂFER K. Strut-and-tie models for the design of structural concrete[J]. Tainan: Cheng Kung University, 1996, 32(10): 1376. |
| [15] |
TAN K H, MURUGAPPAN K, PARAMASIVAM P. Shear behavior of steel fiber reinforced concrete beams[J]. ACI Structural Journal, 1993, 90(1): 3. |
| [16] |
钢纤维混凝土结构技术规程: CECS 38: 2004[S]. 北京: 中国计划出版社, 2004 Technical specification for fiber reinforced concrete structures: CECS 38: 2004[S]. Beijing: China Planning Press, 2004 |
| [17] |
祝明桥, 方志, 程火焰, 等. 配筋钢纤维高强混凝土薄壁箱梁受扭性能分析[J]. 建筑结构学报, 2005, 26(1): 108. ZHU Mingqiao, FANG Zhi, CHENG Huoyan, et al. Torsional behavior of reinforced SFHSC thin-walled box girder[J]. Journal of Building Structures, 2005, 26(1): 108. DOI:10.3321/j.issn:1000-6869.2005.01.017 |
| [18] |
马恺泽, 刘亮, 刘伯权. 混合钢纤维活性粉末混凝土力学性能研究[J]. 硅酸盐通报, 2017, 36(8): 2725. MA Kaize, LIU Liang, LIU Boquan. Mechanical properties of hybrid steel fiber reactive powder concrete[J]. Bulletin of the Chinese Ceramic Society, 2017, 36(8): 2725. |
| [19] |
VOO J Y L, FOSTER S J. Variable engagement model for fobre reinforced concrete in tension[R]. Sydney: The University of New South Wales, 2003: 1
|
| [20] |
KHUNTIA M, STOJADINOVIC B, GOEL S C. Shear strength of normal and high-strength fiber reinforced concrete beams without stirrups[J]. ACI Structural Journal, 1999, 96(2): 282. |
| [21] |
马恺泽, 刘亮, 刘超, 等. 高强混合钢纤维混凝土的力学性能[J]. 建筑材料学报, 2017, 20(2): 261. MA Kaize, LIU Liang, LIU Chao, et al. Mechanical properties of hybrid steel fiber reinforced high strength concrete[J]. Journal of Building Materials, 2017, 20(2): 261. DOI:10.3969/j.issn.1007-9629.2017.02.018 |
| [22] |
MA K, QI T, LIU H, et al. Shear behavior of hybrid fiber reinforced concrete deep beams[J]. Materials, 2018, 11(10): 1. |
| [23] |
MADAN S K, RAJESH KUMAR G, SIHGH S P. Steel fibers as replacement of web reinforcement for RC deep beams in shear[J]. Asian Journal of Civil Engineering (Building and Housing), 2007, 8(5): 479. |
 2022, Vol. 54
2022, Vol. 54


