《国家新型城镇化规划(2014—2020)》[1]中提出,要满足城市群范围内旅客快速增加的出行需求,必须加快城市群交通一体化规划建设, 强化城市群之间的交通联系。城市群多方式协同运营是提高城市群交通运输供给能力,满足出行需求的重要手段。现阶段各运输方式仍处于独立运营、互不干涉状态,协同多方式运输面临着基础设施规范、数据标准和共享、票源开放共享等难题,需要耗费大量的建设与管理成本。为了节约成本,要以需求为导向对协同模式进行优化。
国内外对多方式多路线协同运输的研究较多,主要包括对多方式协调运营规划的研究和设施枢纽布局的研究。在多方式运营规划方面,文献[2]从多方式运营时间协调的角度出发,考虑铁路列车到达情况,建立了换乘时间最小的地铁列车发车时刻协同优化模型;文献[3]考虑不同方式的运能匹配,以运能匹配度为约束,对不同交通方式的分配比例进行优化;文献[4]以乘客换乘延迟成本最小为目标,制定与地铁站点接驳的社区公交发车时刻。在设施枢纽布局方面,文献[5]针对铁路主导型客运枢纽,建立以换乘时间和冲突最少为目标的双层规划模型;文献[6]借助CAD和CG制图,仿真分析换乘设施布局的合理性;文献[7]探讨了衔接轨道交通枢纽的交通方式的选择问题,以解决交通方式规划不合理带来的效率低下问题。此外,学者们还关注与协同运输有关的体制机制及利益分配问题,如文献[8-9]探讨了多式联运利益分配的公平性;文献[10-11]研究了公路和铁路运输一体化的协调机制。综上,一方面现有研究多围绕着如何通过多方式衔接规划、协同运营组织等策略提高运输供给能力,而很少从兼顾经济和社会效益的角度出发,对多方式协同运输能力的供给进行合理性规划;另一方面,现有研究对于多方式的协同多围绕着城市范围内方式间的协同,专注于城市群范围内的多方式协同问题的探讨不多。此外,对于协同运输模式的多样化及其适应性的探讨也不多。
本文提出了以线路为导向的协同运营模式。首先从规模经济的角度分析协同线路规模的合理性;其次,建立城市群出行超网络并从在乘和换乘两个阶段来量化出行广义成本;在此基础上,以系统效益最大化为目标构建协同线路优选的双层规划模型,对上层和下层模型分别设计求解算法;最后以京津冀城市群部分区域为实例对模型进行求解,并从边际效益的视角探讨城市群协同线路设置规模的合理性与适应性。本文设计了城市群范围内多方式衔接运输线路的协同运营模式,研究了协同运营线路的布设优化方法,并以帕累托最优为原则对协同线路规模进行探讨,为城市群一体化建设提供理论指导。
1 协同线路规模的合理性任何行业的经济活动都存在一定的规模经济性,只是表现程度、表现方式不同而已。一般情况下,城市群协同线路越多,由于换乘衔接时间的缩短,旅客节约的出行成本就越多。但是为实现协同运输,而在基础社会建设和使用过程中人、财、物的投入并非总能获得比投入要素价值更大的社会劳动节约,即城市群的协同线路存在规模效益或规模经济性。
发展规模的研究多应用于公路网规划、货运场站等设施建设的适应性规划等领域[12-14]。文献[15]基于“扩展适应行动周期”的概念框架,对城市道路基础设施进行适应规划。文献[16]基于DEA对高速公路建设与社会经济的适应性进行评价。文献[17]针对部分客站客流超饱和、部分客站客流欠饱和等发展不平衡不充分的问题提出铁路客运站规模的适应性规划方法。
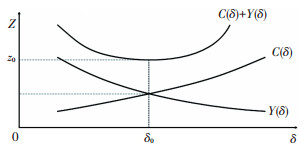
借鉴公路网合理发展规模的概念,首先从规模经济的视角分析城市群合理的协同线路规模。如图 1所示,横坐标为协同线路数量即规模δ,纵坐标为费用Z。旅客运输费用随着城市群范围内协同线路的增加而降低,表示为函数Y(δ);而运营、维护等管理费用随着协同线路的增加而增加,表示为函数C(δ)。合理的协同规模必须考虑建设、管理、维护费用与运输费用这两方面的因素,使这两方面费用之和最小,即min Z=C(δ)+Y(δ)。根据帕累托最优原理,可以看出这两个函数在某一规模δ0值处达到综合费用最小z0,故δ0为城市群协同线路的合理规模。
|
图 1 旅客节约运输费用与线路协同的管理费用函数曲线 Fig. 1 Function curve of transportation cost saved by passengers and management cost of collaborative routes |
由于运营、管理等成本难以测算,因此本文借鉴帕累托边际效益递减理论来判断协同线路规模的适应性。边际效益的计算式为
| $ D=\frac{\Delta U}{\Delta Q} $ | (1) |
式中:D为边际效益,ΔU为效益的变化量,ΔQ为投入的变化量,在本文中投入即为协同线路的数量。根据边际效益递减理论,随着城市群协同线路数量的增多,客运系统效益逐渐增大,但当协同线路的数量达到某一阈值时,效益不再增加,或增加很少可认为不再增加,该阈值即为适合于当前需求的最佳的城市群范围内的协同线路规模。
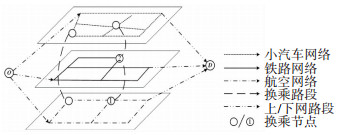
2 基于多方式换乘的超网络模型城市群客运出行的超网络由各个交通方式的子网络组成,每个子网络代表一种交通方式,不同子网络之间通过换乘节点以换乘弧连接,如图 2所示。城市群客运出行超网络可表示为G=(M, N, A),其中M为超网中交通方式的集合;N为节点的集合,分为两类,一类为出行的起终点,另一类为换乘节点;A=A1+A2+A3+A4={a1, a2, …, an}为区段的集合,其中A1为在乘段集合,A2为换乘段集合,A3与A4分别为上网与下网段集合。本文只关注枢纽之间的出行路径,即在乘段与换乘段。
|
图 2 超网络结构 Fig. 2 Structure of super network |
城市群多方式交通的超网络结构如图 2所示,出行者从出发地O到目的地D,可选择的交通方式有航空、铁路、小汽车3种方式,出行者可以选择直达方式,如选择小汽车直达;也可以选择多方式换乘,例如在节点1换乘至节点2,实现航空到铁路的换乘。
本文中所涉及的协同线路描述的是指通过多方式协调调度、“一票制”等手段精简旅客换乘流程的路线,其优势主要体现在换乘段对旅客出行时间的节约。协同线路的设置除需满足基础设施条件外(具体参照交通运输部《关于加快推进旅客联程运输发展的指导意见》[18]对于基础设施的要求),还需要有一定的关联强度。若线路换乘客流量过小,建成协同线路后线路利用率低,不仅无法发挥协同线路的优势,还会造成资源的浪费。在此设置协同线路的客流量阈值ql,当线路客流量q≥ql时,认为线路具备协同运输的条件。
3 出行广义费用广义费用函数是对出行有影响的各种因素的综合作用,描述了乘客出行过程中付出的代价。基于城市群城际出行的出行特征,给出在乘段和换乘段的区段广义费用计算方法。
3.1 在乘段广义出行费用从乘客的角度出发,在乘段乘客所支付的乘车费用多少、在乘时间长短与乘车舒适性这三者是最能给予乘客直观感受的3个影响因素,对乘客的路径与方式选择起到了决定性的作用。
1) 乘车费用。由交通方式的票价和区段长度决定,假设各种交通方式的单位票价固定,则在乘段的乘车费用Ea1m计算式为
| $ E_{a_{1}}^{m}=L_{a_{1}}^{m} \cdot C_{a_{1}}^{m}, m \in M, a_{1} \in A_{1} $ | (2) |
式中:La1m为方式m区段a1的长度;Ca1m为区段a1上方式m的票价。
2) 在乘时间。由区段的长度和交通方式的速度计算得到,在乘时间Ta1m可表示为
| $ T_{a_{1}}^{m}=\frac{L_{a_{1}}^{m}}{V_{a_{1}}^{m}}, m \in M, a_{1} \in A_{1} $ | (3) |
式中Va1m为区段a1上方式m的速度。
3) 不舒适度。舒适程度主要与在途时间及车辆满载程度有关,给定疲劳恢复需要的极限时间B,则不舒适度Sa1m的计算式为
| $ S_{a_{1}}^{m}=\frac{B}{1+\alpha \mathrm{e}^{-\beta T_{a_{1}}^{m}}} \cdot \frac{f_{a_{1}}^{m}}{r_{a_{1}}^{m} \omega_{a_{1}}^{m}}, m \in M, a_{1} \in A_{1} $ | (4) |
式中:fa1m为区段a1上方式m的客流量;ra1m为区段a1上方式m的发车频率;ωa1m为区段a1上方式m的容量;恢复疲劳极限时间B=12 h;α、β为不舒适度计算参数,根据已有研究[19]对各种交通方式舒适度参数的取值,本文针对不同方式参数取值见表 1。
| 表 1 α、β参数取值表 Tab. 1 Value of α and β |
综合考虑乘车费用、在乘时间和不舒适度,得到在乘段的广义费用函数为
| $ \begin{gathered} f\left(a_{1}\right)=\varphi_{1} E_{a_{1}}^{m}+W\left(\varphi_{2} T_{a_{1}}^{m}+\varphi_{3} S_{a_{1}}^{m}\right)=\varphi_{1} L_{a_{1}}^{m} \cdot C_{a_{1}}^{m}+ \\ W\left(\frac{\varphi_{2} L_{a_{1}}^{m}}{V_{a_{1}}^{m}}+\frac{\varphi_{3} B}{1+\alpha \mathrm{e}^{-\beta T_{a_{1}}^{m}}} \cdot \frac{f_{a_{1}}^{m}}{r_{a_{1}}^{m} \omega_{a_{1}}^{m}}\right), m \in M, a_{1} \in A_{1} \end{gathered} $ | (5) |
式中:W为乘客时间价值,可通过地区国民生产总值与地区人口和平均劳动时间乘积的比值计算;φ1、φ2、φ3分别为乘车费用、在乘时间和不舒适度对应的系数。
3.2 换乘段广义出行费用在乘客出行换乘过程中,影响乘客出行的因素主要包括换乘时间和换乘便利性两方面。
换乘时间仅考虑换乘时的换乘行走时间,换乘便利性则考虑到换乘时的候车时间和购票时间。则换乘段的广义费用函数为
| $ \begin{aligned} f\left(a_{2}\right)=& W\left(\varphi_{4} H_{a_{2}}^{m_{1}, m_{2}}+\varphi_{5} R_{a_{2}}^{m_{1}, m_{2}}+\varphi_{6} J_{a_{2}}^{m_{1}, m_{2}}\right), \\ & m_{1}, m_{2} \in M, a_{2} \in A_{2} \end{aligned} $ | (6) |
式中:Ha2m1, m2为换乘段a2由方式m1换乘到方式m2的换乘行走时间;Ra2m1, m2为换乘段a2由方式m1换乘到方式m2的换乘等待时间;Ja2m1, m2为换乘段a2由方式m1换乘到方式m2的购票时间;φ4、φ5、φ6分别为换乘行走时间、换乘候车时间和购票时间对应的系数。协同线路的优势在于对换乘时间的节约,在此对协同线路的换乘候车时间φ5和购票时间φ6对应的系数进行调整,取极限值为0。
综上,普通出行超路径与协同超路径的广义费用为各段的广义费用之和,最终得到出行路径i的广义费用函数表达式为
| $ \begin{aligned} &U_{i}=\sum\limits_{a_{1} \in A_1^i} f\left(a_{1}\right)+\sum\limits_{a_{2} \in A_{2}^i} f\left(a_{2}\right)=\sum\limits_{a_{1} \in A_1^i}\left[\varphi_{1} L_{a_{1}}^{m} \cdot C_{a_{1}}^{m}+\right. \\ &\left.W\left(\frac{\varphi_{2} L_{a_{1}}^{m}}{V_{a_{1}}^{m}}+\frac{\varphi_{3} B}{1+\alpha \mathrm{e}^{-\beta T_{a_{1}}^{m}}} \cdot \frac{f_{a_{1}}^{m}}{r_{a_{1}}^{m} \omega_{a_{1}}^{m}}\right)\right]+\sum\limits_{a_{2} \in A_{2}^i} W\left(\varphi_{4} H_{a_{2}}^{m_{1}, m_{2}}+\right. \\ &\left.x_{i} \cdot \varphi_{5} R_{a_{2}}^{m_{1}, m_{2}}+x_{i} \cdot \varphi_{6} J_{a_{2}}^{m_{1}, m_{2}}\right) \end{aligned} $ | (7) |
式中:A1i为路径i上在乘段的集合;A2i为路径i上换乘段的集合;xi为0-1变量,当路径i为协同路径时xi=0,否则xi=1。
4 城市群协同线路选择的优化模型运输管理部门通过设置线路协同服务来提高客运系统的整体效益,而出行者则根据不同线路的广义出行成本,基于最小费用原则来进行出行方式和路径选择。因此,本文构建的双层规划模型中,上层目标是城市群客运系统的效益最大化,下层目标是弹性需求下的多方式交通网络的随机用户均衡。
4.1 上层模型 4.1.1 目标函数系统效益由客运系统运行的利润和乘客的时间节约效益两部分组成。客运系统运行的利润为收入和成本的差值,收入主要为票价收入,成本主要分为运输成本和协同运输管理成本。其中,普通线路主要为运输成本,而协同线路需要额外的支付服务和管理费用。乘客的时间节约效益是指乘客出行过程中节省的时间所产生的效益。则最大系统效益的目标函数为
| $ \begin{aligned} &\ \ \ \ \max Z=G-C+E=\sum\limits_{m \in M }\sum\limits_{a_{1} \in A_{1}} f_{a_{1}}^{m} \cdot L_{a_{1}}^{m} \cdot C_{a_{1}}^{m}-n \cdot Y- \\ &\sum\limits_{m \in M} K^{m} \cdot r^{m} \cdot I^{m}+W\left\{t-\sum\limits_{m_{1}, m_{2} \in M }\sum\limits_{a_{2} \in A_{2}}\left[f_{a_{2}}^{m_{1}, m_{2}} \cdot H_{a_{2}}^{m_{1}, m_{2}}+\right.\right.\\ &\left.\left.x_{a_{2}}\left(R_{a_{2}}^{m_{1}, m_{2}}+J_{a_{2}}^{m_{1}, m_{2}}\right)\right]-\sum\limits_{m \in M } \sum\limits_{a_{1} \in A_{1}} f_{a_{1}}^{m}\cdot T_{a_{1}}^{m}\right\} \end{aligned} $ | (8) |
式中:Z为系统效益;G为票价收入;C为运输成本;E为乘客的时间节约效益;fa1m为区段a1上方式m的客流量;Km为方式m的单位运输成本;rm为方式m的发车频率;Im为方式m的车辆循环时间周期;n为协同线路数量;Y为协同线路的运营和管理成本,可根据运营和管理成本支出框架,以运营支出法确定[20];t为初始乘客出行总时间,可以根据初始条件下的客流分配结果计算得到;fa2m1, m2为换乘段a2上由方式m1换乘到方式m2的客流量;xa2为0-1变量,若换乘段a2在协同路径上时xa2=0,否则xa2=1。
4.1.2 约束条件模型的约束包括枢纽能力约束、区间能力约束和客流关联约束等,上层模型的约束条件如下:
1) 枢纽换乘能力约束,fa2m1, m2≤ha2m1, m2,枢纽的各种方式间换乘量fa2m1, m2不大于枢纽各种方式间最大换乘能力ha2m1, m2。
2) 区段运输能力约束,fa1m≤pa1m,区段a1方式m的客流量不大于区段a1方式m的运输能力pa1m。
3) 枢纽客流平衡,
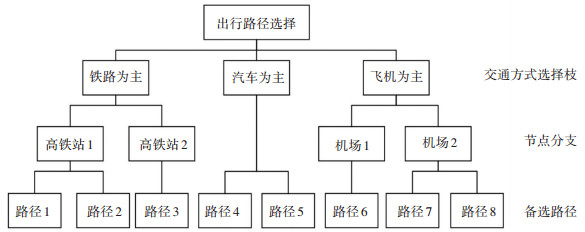
乘客由自身感知到的广义出行费用,依据效用理论选择出行路径。基于效用理论的选择行为建模,国内学者大都采用多项Logit模型,但是由于该模型独立不相关特性(ⅡA)的局限性,很容易造成客流分配结果的不准确。因此在城市群的客流分配中,将出行者的路径选择行为划分为3个层次的决策过程:选择枝为交通方式选择;每个选择枝都对应着不同的分支,即超网络的节点选择;每个分支对应着相应的备选路径,3层巢式Logit模型的结构示意图如图 3所示。
|
图 3 3层Logit模型结构 Fig. 3 Structure of three-tier Logit model |
乘客在OD点对k间选择某一路径的概率计算式为Psdlk=Psk·Pd|sk·Pl|dsk,其中Psdlk为最终选择路径l的概率,Psk为选择交通方式s的概率,Pd|sk为选择交通方式s的条件下选择换乘节点d的概率,Pl|dsk为选择交通方式s和换乘节点d的条件下选择路径l的概率。Pl|dsk计算式为
根据Logit效用模型,乘客在进行路径选择时,总是倾向于选择广义费用最小的路径。当某路径的广义费用较小时,将吸引较多的乘客选择该路径,而随着该路径的客流量增大,又会引起该路径广义费用的增加,阻碍乘客继续选择此路径而选取其他广义费用更小的路径,最终各条路径的客流量将达到平衡点。在随机平衡分配模型中,平衡状态下OD点对k之间路径l的交通量应满足以下条件:
| $ \begin{gathered} F_{l}^{k}=P_{s d l}^{k} \cdot Q=P_{s}^{k} \cdot P_{d | s}^{k} \cdot P_{l | d s}^{k} \cdot Q= \\ \frac{\mathrm{e}^{\theta_{1} v_{s}}}{\sum\limits_{m} \mathrm{e}^{\theta_{1} v_{m}}} \cdot \frac{\mathrm{e}^{\theta_{2} v_{d | s}}}{\sum\limits_{i} \mathrm{e}^{\theta_{2} v_{i | s}}} \cdot \frac{\mathrm{e}^{\theta_{3} v_{l |d s}}}{\sum\limits_{j} \mathrm{e}^{\theta_{3} v_{j | d s}}} \cdot Q \\ \text { s.t. }\left\{\begin{array}{c} \sum\limits_{l} F_{l}^{k}=Q, \forall l \in I, k \in K \\ F_{l}^{k} \geqslant 0, \forall l \in I, k \in K \\ f_{a}=\sum\limits_{k} \sum\limits_{l} F_{l}^{k} \xi_{a, l}^{k}, \forall a \in A \end{array}\right. \end{gathered} $ | (9) |
式中:Flk为OD点对k之间路径l的客流量;Q为k之间的总客流量;a为超网络中的区段;A为区段集;l为超网络中的路径;I为路径集;K为OD点对集合;ξa, lk为0-1变量,若区段a在k之间路径l上,则ξa, lk=1,否则ξa, lk=0。
5 模型求解 5.1 下层模型求解相继平均法(MSA)是求解网络均衡问题的经典算法,本文基于相继平均法设计下层模型的求解算法,具体步骤如下:
步骤1 初始化。根据路径的广义费用函数进行随机分配,得到初始乘客流量集F。迭代次数n=1。
步骤2 辅助流量计算。根据当前的流量集更新区段的广义出行费用并进行路径客流分配,进而进行方向搜索,得到辅助流量集f′。
步骤3 更新区段流量。区段流量集F(n+1)=
步骤4 收敛判定。判断误差是否满足收敛条件,若满足,算法结束;若不满足,令n=n+1,返回步骤2。
其中,在分配之前需要确定有效路径集合并在此基础上再次确定可协同超路径集合,具体搜索算法如下:
步骤1 以起点O作为当前节点i,并从起点O开始搜索。
步骤2 判断当前节点i的下游节点集合中的节点是否已经全部标记,若是,转步骤7;否则,转步骤3。
步骤3 选择当前节点i和下游节点集合中的未检查节点j,若路段(i, j)为换乘段,则换乘次数ψ=ψ+1,同时更新路径出行时间TODl;否则,只更新路径出行时间TODl。
步骤4 检验ψ≤λ,TODl≤(1+ρ)TODmin是否同时成立,若成立,转步骤5;否则,返回上层节点i,还原ψ和TODl,并将节点j标记为已检查,转步骤2。
步骤5 判断节点j是否为终点D,若是,记录路径为有效超路径,将节点j标记为已检查,转步骤6;否则,将节点j作为当前节点,转步骤2。
步骤6 判断当前有效超路径是否同时满足ψ≥1,q≥ql和基础设施条件,若满足,记录路径为可协同超路径,转步骤7;否则,路径仍然记为有效超路径,转步骤7。
步骤7 判断当前节点i是否为起点O,若是,算法结束;否则,标记当前节点已检查并返回上层节点,并以上层节点为当前节点,返回步骤2。
5.2 上层模型求解本文所研究的线路优选问题属于典型的组合优化问题,适合采用遗传算法求解,但传统遗传算法交叉概率和变异概率固定,可能会导致算法收敛过慢或者过早收敛陷入局部最优,因此对于上层的优化模型,本文采用改进的自适应遗传算法进行求解,具体步骤如下:
步骤1 初始化。采取二进制编码形式进行编码,染色体代表协同线路选择方案,染色体上不同位置的基因代表不同的线路,并以1代表线路为协同线路,0代表线路不为协同线路,如110001代表有6条线路且线路一、二、六为协同线路,其他线路为非协同线路。遗传算法的最优解理论上不受到初始解的影响,因此采用MATLAB函数随机生成0-1向量,每个向量代表一个个体Si,即一种线路优选方案,向量的长度为线路总数量。设置种群规模Psize、交叉概率pc、变异概率pm、最大迭代次数N和迭代次数n=1,随机生成Psize个0-1向量,作为初始种群。
步骤2 适应度计算。对每个个体,在其所代表的协同线路选择方案下进行下层模型的客流分配计算,得到每个个体对应的系统效益值,作为个体的适应度f(Si)。
步骤3 交叉概率pc和变异概率pm的自适应化。交叉概率pc和变异概率pm的计算公式分别为
| $ p_{c}=\left\{\begin{array}{c} k_{1} \mathrm{e}^{\frac{f_{\max }-f^{\prime}}{f_{\max }-f_{\text {avg }}}}, f^{\prime} \geqslant f_{\mathrm{avg}} \\ k_{2}, f^{\prime}<f_{\mathrm{avg}} \end{array}\right. $ |
| $ p_{m}=\left\{\begin{array}{c} k_{3} \mathrm{e}^{\frac{f_{\max }-f}{f_{\max } f_{\text {avg }}}, f \geqslant f_{\text {avg }}} \\ k_{4}, f<f_{\text {avg }} \end{array}\right. $ |
式中:fmax为种群中个体的最大适应度;favg为种群中的个体平均适应度;f ′为待交叉个体中较大的适应度;f为变异个体的适应度。当算法接近收敛时,交叉概率pc和变异概率pm仍然不为0,保证了遗传算法不会陷入局部最优。k1、k2、k3、k4为自适应控制参数,为了使适应度较小的个体能够进行交叉操作,k1=1、k2=1、k3=0.5、k4=0.5。
步骤4 种群进化。选择操作是通过轮盘赌选择法进行种群的选择。计算每个个体Si被选择的概率
步骤5 终止判定。判断迭代次数n是否大于最大迭代次数N,若大于,算法结束;否则,令n=n+1,返回步骤2。
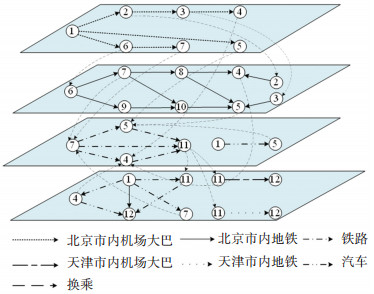
6 案例分析 6.1 京津冀城市群客运枢纽超网络建立以京津冀城市群范围内北京市客运枢纽到天津市客运枢纽的乘客出行为例,进行模型的应用和结果分析。考虑到首都机场和天津滨海国际机场没有铁路连接方式,因此建立首都机场到铁路网的北京市市内接驳子网络,天津滨海国际机场到铁路网的天津市市内接驳子网络,与枢纽间的铁路子网络及枢纽间的公路子网络,共同构成城市群的客运出行超网络,城市群客运出行超网络的基本结构如图 4所示,各个节点对应的枢纽见表 2。
|
图 4 京津冀城市群部分节点超网络结构 Fig. 4 Example nodes of super network in Beijing-Tianjin-Hebei Urban Agglomeration |
| 表 2 节点编号对应枢纽表 Tab. 2 Node numbers corresponding to transportation hubs |
以北京首都机场到天津站和北京南站到天津滨海国际机场的出行为例,根据有效超路径的搜索,两组OD间出行的有效超路径分别见表 3和表 4。
| 表 3 北京首都机场—天津站线路表 Tab. 3 Routes from Beijing Capital International Airport to Tianjin Railway Station |
| 表 4 北京南站—天津滨海国际机场线路 Tab. 4 Routes from Beijingnan Railway Station to Tianjin Binhai International Airport |
根据已有研究[21]对京津冀城市群乘客出行属性、客流特征和交通方式间连接情况的研究,对模型参数进行取值,各参数取值见表 5。
| 表 5 模型中的各参数值 Tab. 5 Value of model parameters |
在上述获取的18条出行超路径的基础上搜索满足协同条件的超路径。其中,路径14和路径18为汽车直达线路,不具备设置协同运输的条件,可排除。通过对2019年5月1日京津冀地区的手机信令数据进行处理,提取出北京首都机场—天津站、北京南站—天津滨海国际机场的总的出行OD量分别为1 000人/d和500人/d,各条线路的客流量见表 6,受调查工具的限制,所获得的客流量数据必然与现实存在一定的偏差。考虑到客流关联强度并结合表 6中各条线路的客流量,设置协同线路客流设置阈值ql为60人。通过5.1节的搜索算法,按客流量由大到小的顺序,得到协同路径备选集为{15,7,10,13,17,16,1,2,11}。
| 表 6 各线路客流量 Tab. 6 Passenger flow of different routes |
基于筛选得到的协同线路备选集中共有9条线路,根据优化模型确定合理的协同线路规模。如表 7所示,不同规模下的协同线路设置方案并不相同,这是由于线路之间并不相互独立,每条线路的影响范围不同,表中协同线路方案对应的是模型求解得到的不同规模下的最佳协同线路选择方案。此外,系统效益随着协同线路规模的增加而增加,乘客平均出行时间、乘客平均换乘时间随着协同线路规模的增加而减少,由此可见,协同能够提高客运网络系统的运行效率,协同是城市群枢纽发展方向。
| 表 7 不同规模下最佳协同线路方案 Tab. 7 Optimal scheme of collaborative routes under different scales |
但是,在线路协同规模到达7以后,这种协同所带来的变化就明显降低。为了进一步优化协同线路规模,基于边际效益计算公式(2),计算协同线路的边际效益,即计算协同线路每增加一条,系统效益的变化情况,将边际效益的计算结果绘制成曲线,如图 5所示。
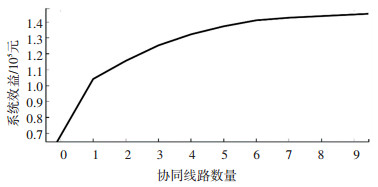
|
图 5 随协同线路数量增加的边际效益变化曲线 Fig. 5 Marginal benefit curve with increasing numbers of collaborative routes |
根据边际效应的基本原理,每增加一条协同线路,客运系统的效益将随之增加,但是成本也会相应地增加。当协同线路数量增加到一定程度时,系统效益将达到最大化,如果再增加协同线路,协同管理与运营成本的增加将削弱系统效益,系统效益达到最大化时的边际效益为零,达到帕累托最优状态。
由图 5可知,在协同线路较少时,每增加一条协同线路,系统效益的增加幅度较大,尤其表现在协同数量为1和2时,系统效益增量分别达到52.3%与11%;而从协同线路数为5条开始,系统效益增加幅度变得缓慢;帕累托最优状态出现在协同线路为6时。此外,从表 7中的效益增量来看,也基本印证了这样的结果,当协同线路数量增加至8与9时,系统效益的增幅很小,如果再考虑到协同管理与运营成本,系统边际效益将呈现下降趋势。因此,最优的线路选择方案为{15,7,10,17,1,2},协同线路网络设置如图 6所示。
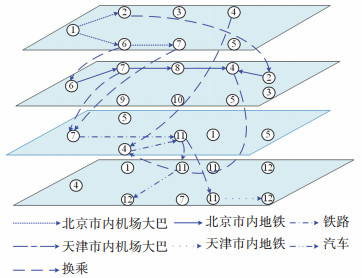
|
图 6 京津冀城市群协同线路设置方案 Fig. 6 Setting schemes of collaborative routes in Beijing-Tianjin-Hebei Urban Agglomeration |
需要说明的是,本文假定客运系统中的客流需求是一定的,协同线路设置后,随着客流向协同线路的转移必然会降低旅客出行成本, 从而带来系统效益的增加,但是当所有旅客出行都达到最优状态后,再增加协同线路也不会引起大量的客流转移,产生明显的效益改善。而如果考虑到协同线路运营与管理成本,那么更需要找到合适的协同规模,使得投入成本能获得明显的收益。
对比协同优化前后的效果:协同优化前的系统效益为68 407元,协同优化后为141 100元;协同优化前乘客平均出行时间为2.289 2 h,协同优化后为1.825 h;协同优化前乘客平均换乘时间为0.658 1 h,协同优化后为0.238 5 h。计算分析可知最优协同线路方案下的系统效益提升了106.27%,乘客平均出行时间降低了20.28%,乘客平均换乘时间降低了63.76%,该优化方案对于提高城市群出行效率效果明显。从表 7可知,优选出的这6条线路承担了城市群近80%的客流量,表明选择的协同线路与客流需求基本相适应。
7 结论针对城市群运输能力供给规划问题,从边际效益的视角提出城市群协同运输线路选择优化方法,并以京津冀城市群范围内的部分枢纽为实例进行验证,得出主要结论如下:
1) 借鉴公路网合理规模的思路,基于边际效益理论对城市群协同线路范围进行合理性规划。应用双层规划模型,以系统效益最大为目标对不同协同线路规模下的最优线路方案进行选择。
2) 将旅客的路径选择描述为方式层、节点层、路径层,利用3层巢式Logit模型构建城市群旅客出行路径选择行为模型,并应用于下层规划的路网均衡分配模型中。
3) 结合京津冀多方式换乘路网,对模型构建的合理性进行验证,结果表明,当协同线路的设置规模大于6条时,系统效益的增幅将不再明显。优选出的这6条线路分别为线路15、7、10、17、1、2。从结果可知,这6条线路承担了城市群近80%的客流量,表明选择的协同线路与客流需求基本相适应。相比于初始方案,客运系统乘客平均出行时间降低了20.28%,乘客平均换乘时间降低了63.76%,该优化方案对于提高城市群出行效率效果明显。
| [1] |
国家新型城镇化规划(2014—2020年)[M]. 北京: 人民出版社, 2014 National new urbanization plan (2014—2020)[M]. Beijing: People's Publishing House, 2014 |
| [2] |
庄黄蕊, 柏赟, 明先俊, 等. 考虑铁路换乘客流的地铁列车发车时刻与限流方案协同优化研究[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(5): 779. ZHUANG Huangrui, BAI Yun, MING Xianjun, et al. Study on collaborative optimization of subway train departure time and current limiting scheme considering railway transfer passenger flow[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2020, 44(5): 779. DOI:10.3963/j.issn.2095-3844.2020.05.002 |
| [3] |
张琦琳, 姜志侠, 刘东晓, 等. 综合客运枢纽接驳运能协调调度的多目标优化问题[J]. 长春理工大学学报(自然科学版), 2018, 41(1): 134. ZHANG Qilin, JIANG Zhixia, LIU Dongxiao, et al. The multi-objective optimization problem of the comprehensive passenger transport hub connecting transport coordination scheduling[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2018, 41(1): 134. DOI:10.3969/j.issn.1672-9870.2018.01.032 |
| [4] |
XIONG J, HE Z, GUAN W. Optimal timetable development for community shuttle network with metro stations[J]. Transportation Research: Part C, 2015, 60: 540. DOI:10.1016/j.trc.2015.10.007 |
| [5] |
沈瑞光. 综合客运枢纽换乘设施布局优化模型研究[J]. 北方交通, 2018(8): 82. SHEN Ruiguang. Study on optimal layout model of transfer facilities in integrated passenger transport hub[J]. Beifang Jiaotong, 2018(8): 82. |
| [6] |
YATSKIV I, SAVRASOVS M, GROMUL V, et al. Passenger terminal safety: simulation modelling as decision support tool[J]. Procedia Engineering, 2016, 134: 459. DOI:10.1016/j.proeng.2016.01.068 |
| [7] |
PUGH D, EKROTH D, ALLEN B G, et al. Comprehensive plan & state of the city Lorena, TX[R]. College Station: Texas A&M University, 2001
|
| [8] |
贺政纲, 黄娟, 帅宇红. 基于蚁群劳动分工的多式联运利益分配研究[J]. 铁道学报, 2018, 40(11): 19. HE Zhenggang, HUANG Juan, SHUAI Yuhong. Research on benefit allocation of multimodal transport based on ant colony's labor division[J]. Journal of the China Railway Society, 2018, 40(11): 19. DOI:10.3969/j.issn.1001-8360.2018.11.003 |
| [9] |
张德超. 基于shapley值的多式联运收益分配研究[J]. 交通科技与经济, 2015, 17(6): 35. ZHANG Dechao. The benefit assignment mechanism research on multimodal transport based on shapley value[J]. Technology and Economy in Areas of Communications, 2015, 17(6): 35. DOI:10.3969/j.issn.1008-5696.2015.06.009 |
| [10] |
LI G, TAMURA K, MUTO M. Fundamental analyses for constructing road-rail intermodal freight transport system[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(6): 1. DOI:10.1016/S1570-6672(13)60143-9 |
| [11] |
YANG K, YANG L, GAO Z. Planning and optimization of intermodal hub-and-spoke network under mixed uncertainty[J]. Transportation Research Part E: Logistics & Transportation Review, 2016, 95: 248. |
| [12] |
MA C, YE Q. An improved genetic algorithm for the large-scale rural highway network layout[J]. Mathematical Problems in Engineering, 2014, 2014(9): 1. |
| [13] |
张然. 公路网发展适应性评价研究[D]. 武汉: 华中科技大学, 2017 ZHANG Ran. Research on adaptability evaluation of highway network development[D]. Wuhan: Huazhong University of Science and Technology, 2017 |
| [14] |
史焕杰, 许薛军, 汤左淦. 新时代普通国省干线公路网规模结构研究[J]. 公路交通科技, 2019, 36(12): 127. SHI Huanjie, XU Xuejun, TANG Zuogan. Study on scale structure of ordinary national and provincial trunk highway network in new era[J]. Journal of Highway and Transportation Research and Development, 2019, 36(12): 127. |
| [15] |
HERRER J S C, MACASKILL K, HAIGH S. Identifying interactions between policy, accountability and outcomes for adaptation of urban roads[J]. Transportation Research Part D: Transport and Environment, 2020, 88: 10. |
| [16] |
汪威. 基于DEA的贵州高速公路建设与社会经济适应性的评价[J]. 营销界, 2020(51): 98. WANG Wei. Assessing of Guangxi harmonious development between transportation and economy based on DEA Model[J]. Marketing Industry, 2020(51): 98. |
| [17] |
武赞. 铁路客站规模适应性研究[J]. 铁道标准设计, 2021, 65(8): 1. WU Zan. Study on the scale adaptability of railway station[J]. Railway Standard Design, 2021, 65(8): 1. |
| [18] |
中华人民共和国交通运输部. 关于加快推进旅客联程运输发展的指导意见[EB/OL]. (2018-02-01)[2021-01-16]. http://www.gov.cn/xinwen/2018-02/01/content_5262782.htm Ministry of Transport of the People's Republic of China. Guiding opinions on accelerating the development of passenger interline transportation[EB/OL]. (2018-02-01)[2021-01-16]. http://www.gov.cn/xinwen/2018-02/01/content_5262782.htm |
| [19] |
韦凌翔, 陈红, 蒋金亮. 基于广义费用函数的高铁票价双层规划模型研究[J]. 铁道科学与工程学报, 2015, 12(2): 250. WEI Lingxiang, CHEN Hong, JIANG Jinliang. Study on bi-level programming model of high-speed rail fares based on generalized cost function[J]. Journal of Railway Science and Engineering, 2015, 12(2): 250. DOI:10.3969/j.issn.1672-7029.2015.02.005 |
| [20] |
杨洋, 陈进杰, 郑钰馨. 城市轨道交通运营成本计算方法研究[J]. 石家庄铁道大学学报, 2017, 30(3): 93. YANG Yang, CHEN Jinjie, ZHENG Yuxin. Research on urban rail transit operation cost calculation method[J]. Journal of Shijiazhuang Tiedao University, 2017, 30(3): 93. |
| [21] |
陈琳. 京津冀城市群枢纽间旅客联程出行行为研究[D]. 北京: 北京交通大学, 2020 CHEN Lin. Research on the intermodal behavior of passengers between the hubs of the Beijing-Tianjin-Hebei urban agglomeration[D]. Beijing: Beijing Jiaotong University, 2020 |
 2022, Vol. 54
2022, Vol. 54


