轮轨噪声是地铁噪声的主体部分，它同时包含低频分量和高频分量。因为低频声在传播时的衰减速率较慢，且容易透射或绕射过传播路径上的阻挡结构，所以只依靠布设声屏障难以将其消减。对于声影区内的剩余轮轨噪声，因为其经历了声屏障的消减作用，所以其中低频声的占比很高。因为低频次级声能消减噪声的低频分量，并且不会干扰声屏障消减高频声，所以本文令有源消声系统只释放低频声波，并将该系统和声屏障相结合，可见该有源声屏障的总声压级插入损失比传统声屏障的强。

目前铁路声屏障降噪方面已有大量研究。文献[1]对比了吸声边界引起的T形、圆形、Y形声屏障降噪量变化；文献[2]研究了改变T型声屏障顶端宽、声屏障位置、声屏障高、受声点位置引起的顶端降噪量变化；文献[3]分析了声屏障降噪量变化机理；文献[4]比较了不同轨下基础情况下的降噪量。相关成果主要为改变频率、吸声系数、形状尺寸所引起的降噪量变化，而极少研究有源声屏障的消声规律。文献[5]分析了传感器位置对消声的影响；文献[6]模拟了室内环境下有源声屏障对低频声的消减；文献[7]分析了有源声屏障对电厂低频声的消减效果。相关成果均是针对单频点声源进行消声，很少有针对轮轨声源的研究。由于地铁声源主要集中在轮轨处，故能在声源附近设次级源，以确保消声显著^[8]。

本文将理论分析同仿真结合，研究次级源最合理位置、消声频段、消声区界线、消声量、有源声屏障降噪区界线、有源声屏障降噪量，从而为有源声屏障设计提供参考。

1 声学仿真模型建立

采用间接边界元法，来计算考虑车身透射的半自由场。轮轨声源为两条具有指向性的、与列车等长的线声源，无指向性的次级源沿轨道纵向等间距分布。由列车附近全部次级源的辐射声和噪声叠加，即可计算出瞬时声场。通过实测信息设置声源及完成模型验证。

1.1 间接边界元法

间接边界元法既适于计算半自由场，又可模拟车体的透射作用。本文通过构建多个声学网格面，来实现对列车、声屏障、轨道、大地的模拟。每个节点内外侧之间速度差σ_i和声压差μ_i由系数矩阵B、C、D及系数向量f_σ、f_μ来确定，即

$ \left[\begin{array}{ll} \boldsymbol{B} & \boldsymbol{C} \\ \boldsymbol{C}^{\mathrm{T}} & \boldsymbol{D} \end{array}\right]\left[\begin{array}{l} \boldsymbol{\sigma}_{i} \\ \mu_{i} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{f}_{\sigma} \\ \boldsymbol{f}_{\mu} \end{array}\right] $

(1)

各单元内部的速度差σ_j和声压差μ_j，由网格上所有节点的σ_i、μ_i及其全局形函数N_σi、N_μi来确定，即

$ \sigma_{j} =\sum\limits_{i=1}^{n} N_{\sigma i} \sigma_{i} $

(2)

$ \mu_{j} =\sum\limits_{i=1}^{n} N_{\mu i} \mu_{i} $

(3)

由全部节点的σ_i、μ_i及其系数A_σi、A_μi计算出声场内的各处声压p_i，即

$ p_{i}=\left\{A_{\sigma i}\right\}^{\mathrm{T}}\left\{\sigma_{i}\right\}+\left\{A_{\mu i}\right\}^{\mathrm{T}}\left\{\mu_{i}\right\} $

(4)

1.2 边界元模型参数

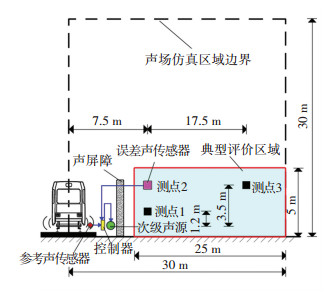
基于规范^[9]令声场仿真区域的面积取30 m×30 m，见图 1。由于仿真波长需大于6倍的最大网格边长以保证结果准确，而本文仿真声频段为50~5 000 Hz，故令10 mm作为网格边长限值。

模型中的主体结构(见图 2)为6节B型车及纵连式整体道床。其具体尺寸：列车长度取116 m，车体宽度取2.8 m，车内净高取2.1 m，车地板距轨面高度取1.1 m，车顶距轨面高度取3.6 m，转向架长度取2.995 m，转向架宽度取2.635 m，位于同节车辆上的两个转向架之间的距离取12.6 m，位于同一转向架上的两个轮轴之间的距离取2.2 m，位于同个轮轴上的两个车轮之间的内侧距取1.353 m，车轮直径取0.84 m，轨枕长度取2.4 m，轨枕宽度取0.297 m，轨枕超过道床高度取0.02 m，道床厚度取0.3 m，道床宽度取2.8 m。

在声场仿真区域内构建平面坐标系，其竖轴为轨道竖向对称轴，其横轴为地面线，轨道轴线同大地相交处为坐标原点。采用1.5节中的现场声屏障布设尺寸，声屏障高4 m，其安装位置离轨道竖向对称轴(以下简称“对称轴”)3 m。声速取344 m/s，传播介质密度取1.21 kg/m³。

1.3 噪声源的设置

令线声源位于轨顶面处，并和列车等长，其所引起的声压P与角频ω、声速c之间的关系为

$ \nabla^{2} P+\frac{\omega^{2} P}{c^{2}}=0 $

(5)

当辐射方向和地面间夹角φ确定后，可确定此角度上的声压级折减量C_φ^[10]。

当-10°≤φ≤21.5°时，

$ C_{\varphi}=-0.02\left(21.5^{\circ}-\varphi\right)^{1.5} $

(6)

当21.5°＜φ≤50°时，

$ C_{\varphi}=-0.016\ 5\left(\varphi-21.5^{\circ}\right)^{1.5} $

(7)

当φ＜-10°时，按照φ为10°来确定C_φ；当φ＞50°时，按照φ为50°来确定C_φ。

1.4 有源消声系统的设置

噪声场会随列车行驶而移动，为使次级声波只出现在临近列车的区域，令有源消声模块沿纵向等间隔排列。如图 1所示，单个独立模块由1个次级源、1个参考传声器、1个误差传声器、1个控制器组成，其运行规则：1)临近轨道的参考传声器将接收到的轮轨声波数据实时传给控制器；2)只有等足够强的轮轨信号传至控制器时，其才会产生并传递消声信号；3)次级源基于消声信号进行声波辐射；4)误差传声器(根据文献[10]确定其位置)将收到的干涉声数据传至控制器；5)控制器获得两传声器传来数据后，由自适应算法形成消声信号。

确定消声信号的依据是使误差传声器处声能达最小，评价指标为

$ J=\left(\boldsymbol{Z}_{\mathrm{pe}} \boldsymbol{q}_{\mathrm{p}}+\boldsymbol{Z}_{\mathrm{se}} \boldsymbol{q}_{\mathrm{s}}\right)^{\mathrm{H}}\left(\boldsymbol{Z}_{\mathrm{pe}} \boldsymbol{q}_{\mathrm{p}}+\boldsymbol{Z}_{\mathrm{se}} \boldsymbol{q}_{\mathrm{s}}\right) $

(8)

式中：J是声压的平方；Z_pe、Z_se分别是声源、次级源至场点的传递函数；q_p、q_s分别是声源、次级源的强度。

1.5 现场实测及模型验证

在北京地铁13号线路基段沿线采集声信息，周围区域空旷，当列车抵达测点所在横断面时开始采集声波，当列车离开测点所在横断面时结束采集声波，基于规范^[9]将所得频谱中的各个A计权声压级进行背景噪声折减。

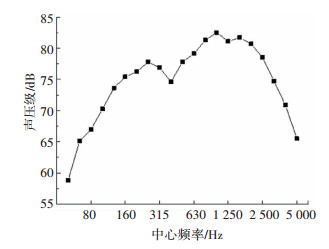
令测点与轨顶等高，且其同轨道轴线相隔1.5 m^[11]。采集车速达70 km/h时的声源频谱，横轴采用三分之一倍频程频率，见图 3，从而确定仿真所需声源强度。

当列车以70 km/h速度驶过设有地面声屏障的区段时，基于相关规范^[11-12]布设测点见图 1。近场的噪声采集位置为测点1、测点2，远场的噪声采集位置为测点3，基于这3处位置的噪声信息进行模型验证。针对三分之一倍频程频谱，比较数值计算与实测结果，由图 4可知，计算误差普遍未超过3 dB，其极值为6.75 dB，可见模型计算合理。

1.6 轮轨噪声超限区

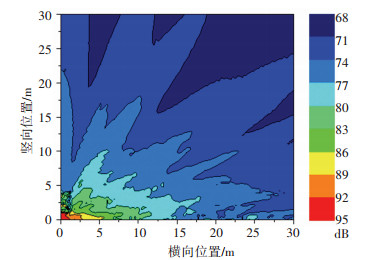
轮轨噪声总声压级场见图 5，由规范^[13]可知地铁沿线噪声限值为70 dB，且由图 5可知超限区基本位于本文的声场仿真区域以内，所以1.2节中所设置的计算范围是合理的。

2 确定次级源的合理布设参数

基于仿真模拟和理论推导，确定出有源消声效果达最强时的次级源布设参数。为了同时实现消减效果的显著性和稳定性，本文构建只能在某频率范围内产生广域消声的系统。令次级声和采样声具有相同初相位。

2.1 基于仿真模拟的次级源消声特性研究

确定出消声频率范围，以及令消声评价指标达极值情况下次级源布设地点。

2.1.1 基于平均声压级改变量进行评价

经仿真发现，消声区形状与声影区相似，且临近地面区域的降噪效果相对更好，故依据规范测点^[11-12]设置“典型评价区”，见图 1。因为单个受声点处的降噪量无法代表区域的整体降噪效果，故基于能量等效提出式(9)，可将评价区中全部节点声压级进行等效平均。在原声场基础上增加次级源，会使“平均声压级值”产生变化。当该平均声压级增大时表明次级源引起增噪效果，当该平均声压级减小时表明次级源引起消声效果。

$ L_{\mathrm{Aeq}}=10 \lg \left[\frac{1}{m_{1}} \sum\limits_{i=1}^{m_{1}} 10^{0.1 L_{\mathrm{J} i}}\right] $

(9)

式中：L_Aeq为平均声压级，dB；L_Ji为区域中某节点声压级，dB；m₁为区域中节点数。

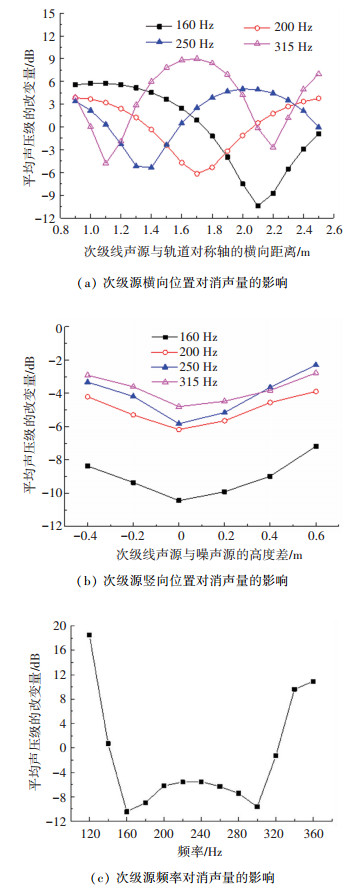
暂且忽略次级点源纵距，布设单侧次级线源。当次级源的竖向位置坐标值等于声源高度时，次级源横向位置对消声量的影响规律见图 6(a)；当次级源的横向位置坐标值等于声波长度时，次级源竖向位置对消声量的影响规律见图 6(b)；当次级源位于最合理布设位置时，次级源频率对消声量的影响规律见图 6(c)。由图 6(a)、6(b)可知，其最合理位置和对称轴间隔一个声波长度，且和声源等高；由图 6(c)可知，次级声对150~320 Hz噪声消减显著。当车两侧均布设次级线源时，所得结论同上。

有源消声系统必须处在地铁限界以外，且由图 6(b)可知，其与轮轨声源等高，故由相关规范^[14]可知，其与对称轴间隔不能小于1.04 m。由图 6(a)可知，令频率取160 Hz或200 Hz，则当次级源位置与其最合理位置之间的距离小于0.1 m时，消声显著；令频率取250 Hz或315 Hz，则当次级源位置与其最合理位置之间的距离小于0.05 m时，消声显著。所以应同时布设9条次级线源，具体参数见表 1，以消减150~320 Hz噪声。

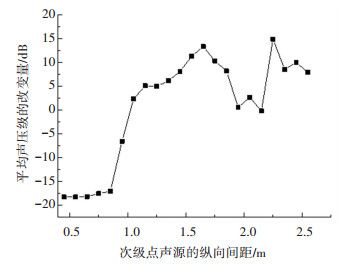
以次级点源列代替次级线源，使其处在最合理位置。由图 7可知，当纵向间隔达到半个声波长度以下时，消声效果尤为显著(类似次级线源的效果)。这与文献[8]中所介绍的单点噪声源情况下次级源最佳纵距一致。由于本文系统可消减150~320 Hz噪声，故后文模型中的纵距均被设置成0.5 m。

2.1.2 基于最高边界点高度进行评价

当次级源处在最合理位置时，在车两侧会出现消声区，见图 8。消声区形似以本文坐标原点为顶点的三角形。

由图 8可知，采用对称布设方式能引起更大的消声面积和消声量。针对本文仿真所得消声区，存在离地最高的边界点。将最高边界点高度简写成“边界高”。当次级源的竖向位置坐标值等于声源高度时，次级源横向位置对边界高的影响规律见图 9(a)。当次级源的横向位置坐标值等于声波长度时，次级源竖向位置对边界高的影响规律见图 9(b)。通过图 9所得的次级源最合理位置和通过图 6所得的一致。

2.2 基于理论推导的次级源消声特性研究

次级源纵列释放的声波，会与线声源释放的低频声波形成干涉。因为低频声具有较大波长，故近似认为声场不随纵向改变，从而推导计算二维场。分析次级源合理参数和消声边界特性，从而验证相应仿真结论是否合理。

2.2.1 双侧布设次级源

令两个轮轨声源、两个次级源分别关于轨道轴线对称。并令所有点源所处的高度、频率一致。首先建立单点声源辐射声压模型^[15]，即

$ p=\frac{A}{r_{1}} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r_{1}}{c}\right)} $

(10)

式中：p为任意场点声压，Pa；r₁为场点与声源间隔，m；A为声源振幅；t为时间，s；ω为角频率，rad/s；c为声速，m/s。

相距l的两点声源辐射声压模型为

$ p=\frac{A}{r_{1}} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r_{1}}{c}\right)}+\frac{A}{r_{2}} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r_{2}}{c}\right)} $

(11)

式中r₂为场点与声源间隔，m。

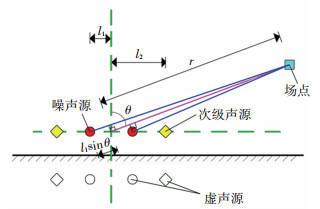
如图 10所示，对于r≫l的远场点，将r₁、r₂分别简化为r+0.5lsin θ、r-0.5lsin θ。

故可将式(11)简化为

$ \begin{array}{l} p=\frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\left[\mathrm{e}^{\frac{-\mathrm{j} \omega l \sin \theta}{2 c}}+\mathrm{e}^{\frac{\mathrm{j} \omega l \sin \theta}{2 c}}\right]= \\ \ \ \ \ \ \ \ \frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)} \cdot 2 \cos \left(\frac{\omega l \sin \theta}{2 c}\right) \end{array} $

(12)

由式(12)推导出关于次级声和噪声干涉相消的数学模型，即

$ \begin{aligned} p=&\frac{2 A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\left[\cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\alpha \cos \left(\frac{\omega l_{2} \sin \theta}{c}\right)\right]= \\ &\frac{2 A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\left[\cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\alpha-2 \alpha \sin ^{2}\left(\frac{\omega l_{2} \sin \theta}{2 c}\right)\right] \end{aligned} $

(13)

式中：l₁为轨头半距, l₁=0.75 m；l₂为次级源与对称轴间隔，m；α为次级源与声源振幅比。

对于式(13)，由于临近地面场点可使sin θ近似等于1，则得到如下规律：1)当声频取150~320 Hz时，$ \cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right) < 0$。为实现最佳消声效果，需令$ \alpha \cos \left( {\frac{{\omega {l_2}\sin \theta }}{c}} \right) = \alpha $，则l₂必须等于波长，此规律符合图 6(a)中的结论。2)令α取1，l₂等于波长，则$ \alpha \cos \left( {\frac{{\omega {l_2}\sin \theta }}{c}} \right) = 1 $。为实现消声效果，需令干涉相消后的声压低于噪声压，即$ \cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right) + 1 < \left| {\cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right)} \right|$，则声频应取151~302 Hz，该频率范围与图 6(c)中的消声频率范围相近。3)对于消声边界上的场点，需令干涉相消后的声压等于噪声压，即$ \alpha \cos \left( {\frac{{\omega {l_2}\sin \theta }}{c}} \right) = 0$。令声频取150~320 Hz，l₂等于波长。故当sin θ=0.75时的场点线即是消声边界，其倾角较固定。

通过镜像原理实现大地反射，在每个声源的正下方且关于地面对称的位置增设1个虚源，虚源的频率、初相位及振幅与其所对应声源的一致，参考式(13)的建立和分析思路，则其消声规律和式(13)的一致。

2.2.2 单侧布设次级源

同理，只在两个噪声源的单侧布设1个次级源，则噪声源两侧的干涉模型分别为

$ \begin{aligned} p=& \frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)} \cdot 2 \cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\frac{\alpha A}{r-l_{2} \sin \theta} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)} \cdot \mathrm{e}^{\frac{\mathrm{j} \omega l_{2} \sin \theta}{c}}=\frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\\ &\left[2 \cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\frac{\alpha r}{r-l_{2} \sin \theta} \mathrm{e}^{\frac{\mathrm{j} \omega l_{2} \sin \theta}{c}}\right] = \\ & \frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\left\{2 \cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\frac{\alpha r}{r-l_{2} \sin \theta}\left[\cos \left(\frac{\omega l_{2} \sin \theta}{c}\right)+\sin \left(\frac{\omega l_{2} \sin \theta}{c}\right) \mathrm{j}\right]\right\} \end{aligned} $

(14)

$ \begin{aligned} p=& \frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\left[2 \cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\frac{\alpha r}{r+l_{2} \sin \theta} \mathrm{e}^{\frac{-\mathrm{j} \omega l_{2} \sin \theta}{c}}\right]=\frac{A}{r} \mathrm{e}^{\mathrm{j}\left(\omega t-\frac{\omega r}{c}\right)}\\ &\left\{2 \cos \left(\frac{\omega l_{1} \sin \theta}{c}\right)+\frac{\alpha r}{r+l_{2} \sin \theta}\left[\cos \left(\frac{\omega l_{2} \sin \theta}{c}\right)-\right.\right.\left.\left.\sin \left(\frac{\omega l_{2} \sin \theta}{c}\right) \mathrm{j}\right]\right\} \end{aligned} $

(15)

同式(13)的分析思路，使sin θ近似等于1，则得到如下规律：1)当声频取150~320 Hz时，$ 2\cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right) < 0$。为实现最佳消声效果，需令$ \alpha \cos \left( {\frac{{\omega {l_2}\sin \theta }}{c}} \right) = \alpha $，则l₂必须等于波长。2)令α取1，l₂等于波长。对于消声边界上的场点，需令干涉相消后的声压等于噪声压，即满足$ 2\cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right) + 1 = \left| {2\cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right)} \right|$。故当$ \cos \left( {\frac{{\omega {l_1}\sin \theta }}{c}} \right)=-0.25$时的场点线即是消声边界，其倾角和频率呈正相关。3)当声频取150~320 Hz时，单侧布设次级源情况下的消声边界倾角小于双侧布设次级源情况。

3 分析有源声屏障的降噪效果

由于吸声系数和插入损失之间关系的规律已知^[15]，故将该因素忽略。经数值模拟，确定了布置声屏障并不影响次级源最合理参数值。当次级源处在最合理位置时，研究有源声屏障与次级源或声屏障相比的优越性。

3.1 有源声屏障与次级源的低频消减能力比较

比较不同布设方式的消减量，如图 11所示。发现双侧布设有源声屏障比单侧优越，有源声屏障比次级源优越。

比较各布设方式所产生的降噪区面积。由数值模拟确定，双侧布设次级源情况下的边界高与双侧布设有源声屏障情况类似。如图 12所示，双侧布设次级源所引起边界线倾角随频率改变而变化不显著，符合式(13)的相应结论。单侧布设次级源所引起边界线倾角和频率呈正相关，符合式(14)的相应结论。双侧布设有源声屏障所引起边界线倾角大于单侧布设情况；单侧布设有源声屏障所引起边界线倾角大于单侧布设次级源情况。

3.2 有源声屏障与声屏障的总声级消减能力比较

仿真声频取50~5 000 Hz，步长取5 Hz，布设双侧有源声屏障，按表 1中参数设置次级源纵列。人耳易识别高于3 dB的声压级变化^[16]，如图 13所示，在声屏障的基础上布置次级源纵列，能令声影区内总声压级普遍降低3~12 dB，且令声影区外的放大值基本不超过3 dB，并且可确保列车内声场变化不大。

4 结论

1) 本文构建了用于消减地铁轮轨噪声的有源声屏障模型。有源消声系统针对低频分量，声屏障主要针对高频分量。

2) 次级声对150~320 Hz噪声消减显著。消声区面积和频率呈正相关。

3) 在列车左右两侧对称布设次级源纵列的消声效果优于在列车一侧布设的效果。次级源最合理位置与轨道对称轴间隔一个声波长度，与声源等高，具有短于半个声波长度的纵向间隔。

4) 在声屏障的基础上布置次级源纵列，能令声影区内总声压级普遍降低3~12 dB, 且令声影区外的放大值基本不超过3 dB，并且可确保列车内声场变化不大。