2. 北京市轨道工程重点实验室(北京交通大学),北京 100044;
3. 新疆铁道勘察设计院 地质路基设计分处,乌鲁木齐 830011
2. Beijing Key Laboratory of Track Engineering(Beijing Jiaotong University), Beijing 100044, China;
3. Geological Subgrade Design Branch, Xinjiang Railway Survey and Design Institute, Urumqi 830011, China
风吹雪是雪粒在气流的作用下发生蠕移、跃移及悬移等运动的一种自然现象[1]。随着寒区铁路网的日益完善,风吹雪现象带来的积雪灾害对铁路运营安全的影响成为亟待解决的问题。现场监测是获取风吹雪特征最直接有效的方法,但交通线路延伸长,风吹雪灾害往往出现在高寒边疆地区,难以长时间全面进行实地的风吹雪观测,且风吹雪灾害具有明显的区域特征,而现场监测难以控制风雪场条件,所得结果也具有随机性[2]。
通过数值计算是获取积雪分布信息的有效方法之一,根据天气条件、地理特征等多因素总结各种不易积雪的公路路基断面型式和不同防护措施,提取不同断面流场的风速变化情况[3],从流场变化的角度分析积雪的变化特征[4];陈凤箴[5]考虑防雪栅对公路风吹雪灾害的防治作用,总结了公路风吹雪灾害防治的防雪栅类型,吴鹏等[6]通过改变路堤高度及边坡坡率等参数,对不同路基结构形式下的防雪栅作用进行了研究,并总结了防雪栅栏、挡雪墙、导风板和防雪林等4种目前用于新疆公路风吹雪的防治措施的相关设置参数[7]。
目前风吹雪灾害的防治一般通过改变风雪场流向以达到目的,其中主要包括应用防雪栅(墙)、防雪林及防雪走廊等,实践表明防雪林在风吹雪易发区域种植条件要求较高且难以维护[8],防雪走廊入口处易产生积雪[9],采用防雪栅来减轻积雪对道路的影响是相对简便有效的方法[10]。怀俄明公路自设置防雪栅以来, 栅栏防护区域事故率减少了75%,每年减少近9 d因积雪封闭道路的时间[11],国内近年来已将防雪栅较多地应用在滨绥线、图佳线、两伊线等风雪灾害易发区域,但由于早期工程建设的忽视,往往是出现灾害后才考虑采取防治措施,所采用的方法与布置形式也较多基于经验选择。
精伊霍铁路是中国首次大规模在铁路工程设计时考虑了风吹雪灾害的防护,并选用了包括防雪墙和防雪栅在内的组合设施,十余年来发挥了显著的防雪作用,但由于两种防雪设施距离较近,防雪墙作用效果没有充分发挥,同时因为防雪栅栏距离路基结构过近,也未能充分发挥防雪栅效果[12];在新建克塔铁路则主要从铁路选线设计原则和路基结构形式(包括设计积雪平台和对比不同边坡坡率)方面对风吹雪灾害进行了重点防护,对所设置的防雪栅效果则需要进一步进行观察[13]。
综上所述,目前交通领域风吹雪灾害防治成果主要以公路工程为代表,但铁路路基形式与公路路基有较大不同,而且铁路线路难以像公路可以灵活绕避雪害区域,铁路沿线风吹雪灾害呈现“点多面广危害大”的特点,但目前关于铁路路堑结构形式的积雪量以及防雪栅作用下两侧堆积雪量和对路堑内外雪量的影响尚无统一定论。因此,本文以新建铁路工程背景为建模基础,采用实际所测风雪场参数为计算条件,定量分析风吹雪作用下铁路路堑内外和不同形式防雪栅两侧的积雪分布。
1 数值模型的建立基于ANSYS中Fluent计算模块,并采用user-defined-function自定义加载运动模型和边界条件,建立三维多相流风吹雪分析模型。
1.1 风雪场运动模型采用欧拉多相流模型来描述雪粒在空气中的运动,其中空气的运动受雷诺时均方程(RANS)支配,并采用RNG k-ε湍流模型使RANS方程封闭后求解,其中k为湍流动能,ε为湍流耗散率[14]。在多相流计算中认为雪粒为连续流体,运动方程[15]为
| $\frac{{\partial {\rho _{\rm{s}}}f}}{{\partial t}} + \frac{{\partial {\rho _{\rm{s}}}f{u_{\rm{j}}}}}{{\partial {x_{\rm{j}}}}} = \frac{\partial }{{\partial {x_{\rm{j}}}}}\left[ {\frac{{{v_{\rm{t}}}}}{{{S_{\rm{c}}}}}\left( {\frac{{\partial {\rho _{\rm{s}}}f}}{{\partial {x_{\rm{j}}}}}} \right)} \right] - \frac{{\partial {\rho _{\rm{s}}}fw}}{{\partial {x_\varepsilon }}}$ | (1) |
式中:ρs为雪的密度;f为雪的体积分数(ρs与f的乘积表示雪粒体积浓度);Sc为施密特数,取值为1[16];w为雪粒降落速度。
驱使雪粒运动的最小摩擦速度称为“阈值速度u* t”,当雪粒表面受到的摩擦速度u*大于自身运动的阈值速度u* t时便产生运动,雪粒表面的摩擦速度u*由其剪切力计算得出,如式(2)所示。雪表面的堆积和侵蚀运动取决于摩擦速度u*[17],当u*大于u* t时,雪粒开始运动并发生雪量减少的侵蚀作用,侵蚀减少雪量为qero;u*小于u* t时雪粒无法运动产生堆积,堆积增加雪量为qero,如式(3)~(4)所示,并根据式(5)计算某一点处的总雪量变化。
| ${u_*} = \sqrt {\frac{\tau }{{{\rho _{\rm{s}}}}}} $ | (2) |
| ${q_{{\rm{dep }}}} = {\rho _{\rm{s}}}fw\frac{{u_{*{{\rm{t}}}}^2 - u_*^2}}{{u_{*{\rm{t}}}^2}}$ | (3) |
| ${q_{{\rm{ero }}}} = {A_{{\rm{ero }}}}\left( {u_*^2 - u_{*{{\rm{t}}}}^2} \right)$ | (4) |
| ${q_{{\rm{total }}}} = {q_{{\rm{dep }}}} + {q_{{\rm{ero }}}}$ | (5) |
式中:τ为雪粒受到的剪切力;qdep为雪粒堆积量;qero为雪粒侵蚀量;qtotal表示雪粒总流量;Aero为雪粒间黏结强度,取值为7×10-4。
在上述运动方程和堆积-侵蚀模型中,雪粒密度139 kg/m3来源于线路区域降雪后连续3 d实测的平均值;风吹雪灾害现场测得3 m高处的雪粒宏观起动风速为6 m/s,根据近地层风场对数率剖面模型算得阈值速度u* t为0.15 m/s,雪粒降落速度w为0.1 m/s,雪粒粒径为200 μm[18]。
1.2 计算域参数基于现场风吹雪灾害防治试验段路基形式,并根据TB 10098—2017《铁路线路设计规范》要求[19],建立路基面宽度为8 m、路基边坡坡度为1∶1.75、路基两侧均有宽度为5 m积雪平台的单线铁路路基,计算中来流风向垂直于线路方向。
计算域如图 1所示,其中为保证来流风速与出流风速的充分发展,并且减小计算域壁面对积雪分布的影响,流场方向长度为所有计算工况中防雪栅到铁路路堑上风侧边坡顶部的最大距离的10倍,高度为所有计算工况中最高模型高度的10倍,线路方向则尽可能地延长,最终计算域为800 m(流场方向)×600 m(线路方向)×50 m(高度)。

|
图 1 计算域整体示意图 Fig. 1 Schematic diagram of overall computing domain |
计算域边界条件中入流面设置为速度入口(velocity-inlet),以监测数据建立近地层风场对数率剖面模型[20],其中3 m高处来流风速为6 m/s,地面粗糙度为2×10-4 m;出流面设置为自由流出口(outflow),该边界不定义任何参数;计算域顶面与两侧面设置为对称边界,该边界上的剪应力为0,各物理量的梯度为0,不影响区域内计算;地面、防雪栅和路基模型表面设置为流体不可穿过的wall边界。
1.3 求解器参数计算采用非定常流,初始设置雪颗粒体积分数vs为0.01,与雪量变化相关的参数α和输出结果r分别用式(6)和式(7)表示。计算步长设置为0.01 s,总计算时长为1 800 s(30 min)。
| $ \alpha=\frac{r-r_{0}}{r_{0}-1}$ | (6) |
| $r = \frac{{{v_{\rm{f}}}}}{{{v_{\rm{s}}}}}$ | (7) |
式中:r0为无防雪栅时计算前后的雪粒体积分数比值,r为有雪防雪栅时计算前后的雪粒体积分数比值;r0-1为无防雪栅作用下雪粒体积分数的变化量;α为雪量变化率,表示防雪栅作用下雪量的变化程度,正值表示雪量减少,负值表示雪量增加;vf为计算结束时的测点雪粒体积分数,数值越大,表示雪量越多。
2 模型验证为验证数值模拟结果的合理性,在新建铁路试验段设置气象站和防雪栅,在降雪后对试验段进行雪深测量,并与数值模拟计算结果进行比较。
2.1 工程背景本段以新建阿勒泰—富蕴铁路为研究对象,线路全长154.5 km,所经区域地势平坦开阔,沿线植被主要为低矮杂草,山坡相对平缓,有发达的丘陵平原。该地区气候干燥,区域内历史最大瞬时风速达到22.1 m/s, 最大雪深940 mm,是新疆雪灾较严重的地区之一。根据全线调查和前期自建气象站的风场监测数据,选择某来流风向垂直于线路,并出现风吹雪现象的区域作为试验段,试验段全长400 m,分成两段长度相等的区域Ⅰ和区域Ⅱ,其中区域Ⅰ线路外预设防雪栅,防雪栅孔隙率20%,高度3 m,与路堑距离40 m;区域Ⅱ无防雪栅。试验段沿线路堑深度在0.8~1.2 m之间,路基两侧积雪平台宽度为5 m。试验段防雪栅与雪深测量点位如图 2所示。

|
图 2 试验段防雪栅与测量点位示意图 Fig. 2 Locations of snow fence and measurement points in test section |
2018年12月16日至17日自然降雪后,2018年12月18日使用精度为1 mm的钢尺对试验段内积雪分布进行测量。图 3为试验段内雪深测量结果等高线图。由图 3可以看出区域Ⅰ雪粒在栅两侧形成堆积,栅两侧雪深最大值为430 mm,在远离防雪栅区域雪深逐渐减小;区域Ⅱ路堑外雪深波动较小,整体分布较为平均。试验段区域自然降雪深度为135 mm,区域Ⅰ路堑外平均雪深为215 mm,区域Ⅱ路堑外平均雪深为193 mm,即防雪栅作用下路堑外平均雪深较无防雪栅区域增加了37.93%;路堑内雪深与路堑外的雪深呈相反的趋势。区域Ⅰ路基顶面平均雪深为218 mm, 区域Ⅱ平均雪深为231 mm,即防雪栅作用下路基顶面平均雪深较无防雪栅区域减少约13.61%。

|
图 3 试验段实际测量雪深等高线图 Fig. 3 Contour map of measured snow depths in test section |
本文以无人机航测获得的地形图数据为基础,建立地形分辨率为5 m的模型。计算采用的多相流模型、堆积-侵蚀条件与边界条件均与第1节保持一致。
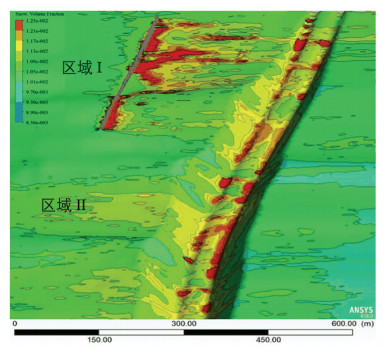
图 4为对试验段铁路路堑内外进行风吹雪数值计算得到的雪粒体积分数等高线图。由图 4可以看出,区域Ⅰ雪粒体积分数平均值为1.032,比区域Ⅱ高69.96%。路基顶面雪粒体积分数为1.109,防雪栅对路基顶面的雪量减少率为25.93%,计算得到的雪量变化趋势与现场实测结果有较好的一致性。
|
图 4 试验段雪粒体积分数等高线图 Fig. 4 Contour map of snow volume fraction in test section |
通常高度过低(小于2 m)的防雪栅难以发挥阻雪作用,高度过大(大于6 m)的防雪栅在大风条件下稳定性存在问题并且造价较高[10]。结合孔隙率为0的防雪墙和存在孔隙结构的防雪栅,并考虑防雪栅与路堑间的不同布置距离,本文对防雪栅不同结构形式和布置距离对路基内外积雪分布变化的影响进行了分析,计算变量和工况见表 1。
| 表 1 计算变量和工况 Tab. 1 Calculation variables and cases |
对各工况的不变量,防雪栅的高度和距离分别选择5 m和80 m,使栅两侧尽可能多地积雪,孔隙率选择中间值50%。试验同时进行了无防雪栅工况的计算。
3.1 孔隙率图 5为不同孔隙率作用下路堑内外沉积雪量。由图 5可见,不同孔隙率防雪栅的栅前与栅后积雪分布形态明显不同,也导致了路堑内的雪量差异。孔隙率为0时(无孔隙挡雪墙),栅两侧雪粒体积分数比值最大分别为1.208,出现在栅前;孔隙率为25%、50%、75%时,栅两侧雪粒体积分数比值最大分别为1.173、1.168、1.126,且75%孔隙率时该值出现在栅后,即孔隙率从0增至75%的过程中栅两侧积雪峰值逐渐减小,积雪堆积趋势从栅前向栅后转移。

|
图 5 不同孔隙率作用下路堑内外沉积雪量 Fig. 5 Deposited snow amounts inside and outside the cutting under different porosities |
利用曲线拟合多项式方程,得到不同工况下路堑外栅前、栅后和栅两侧影响长度内的雪粒体积分数比值的变化情况。防雪栅孔隙率为50%时的计算公式如式(8)~(12)所示,其中防雪栅栅前影响长度按20 m计算,多项式方程的曲线拟合度均在0.9以上。
| $\begin{array}{l} {r_{{\rm{f}}50}} = 28.316 + 7.65 \times {10^{ - 2}}x + 7.15 \times {10^{ - 3}}{x^2} + \\ \;\;\;\;\;\;\;2.228 \times {10^{ - 5}}{x^3} \end{array}$ | (8) |
| $\begin{array}{l} {r_{{\rm{b}}50}} = 0.99 - 5.28 \times {10^{ - 3}}x - 1.32 \times {10^{ - 4}}{x^2} - \\ \;\;\;\;\;\;\;9.935 \times {10^{ - 7}}{x^3} \end{array}$ | (9) |
| ${{\bar r}_{{\rm{f}}50}} = \frac{{\int {{r_{{\rm{f}}50}}} }}{{{l_{\rm{f}}}}} = 1.041$ | (10) |
| ${{\bar r}_{{\rm{b}}50}} = \frac{{\int {{r_{{\rm{b}}50}}} }}{{{l_{\rm{b}}}}} = 1.053$ | (11) |
| ${{\bar r}_{50}} = \frac{{\int {{r_{{\rm{f}}50}}} + \int {{r_{{\rm{b}}50}}} }}{{{l_{\rm{f}}} + {l_{\rm{b}}}}} = 1.048$ | (12) |
式中:x为路堑内外横断面距离,以路基顶面中心处为零点,对应图 5横坐标;rf50为50%孔隙率防雪栅栅前雪粒体积分数比值;lf为栅前雪量影响长度,取值为20 m; rb50为50%孔隙率防雪栅栅后雪粒体积分数比值;lb为栅后雪量影响长度,取值为栅栏到路堑距离;rf50为50%孔隙率防雪栅栅前各点位雪粒体积分数比值的平均值;rb50为50%孔隙率防雪栅栅后各点位雪粒体积分数比值的平均值;r50为50%孔隙率防雪栅两侧各点位雪粒体积分数比值的平均值。
图 6为不同防雪栅孔隙率作用下不同位置的沉积雪量,其中折线图对应左纵轴,柱状图对应右纵轴。从图 6中可以看出,栅前雪粒体积分数比值的平均值与孔隙率成反比,说明栅前雪量随着孔隙率的增加而减少,栅后雪粒体积分数比值的平均值先增大后减小,即随着孔隙率的增加栅后雪量先增多后减小。50%孔隙率防雪栅作用下路堑外雪粒体积分数比值的平均值最大,为1.049。与无防雪栅工况相比,孔隙率为0、25%、50%、75%时,路堑外雪粒体积分数比值的平均值分别增加了51.45%、74.55%、92.95%、45.50%,即随着孔隙率从0增加到75%,路堑外雪量先增大后减小。

|
图 6 不同孔隙率作用下不同位置沉积雪量对比 Fig. 6 Deposited snow amounts at different locations under different porosities |
铁路路堑内积雪变化趋势与路堑外相反。无防雪栅时路基顶面测点的雪粒体积分数比值为1.096,当孔隙率为0、25%、50%、75%时,路基顶面雪粒体积分数比值分别为1.077、1.082、1.073、1.085,雪量减少率分别为19.44%、14.42%、23.52%、10.98%,即防雪栅孔隙率为50%时路基顶面雪量最少,防雪栅对路基顶面的雪量减少作用最明显。
3.2 作用距离防雪栅与路基距离除了影响防雪栅两侧流场和积雪分布外,也涉及占地规划问题,使得该因素成为防雪栅设计乃至铁路工程初期设计重要的考虑因素之一。
图 7为防雪栅与路基不同作用距离时沉积雪量。由图 7可以看出,防雪栅与路基距离变化时栅后的积雪形态和路堑内雪量明显不同。随着防雪栅与路基距离的减小,靠近路堑区域的雪粒体积分数比值越来越大,栅两侧积雪峰值也逐渐增加。当防雪栅和路基相距20 m时,路基顶面雪粒体积分数比值沿风向逐渐减小,说明此时路基顶面处于栅后的积雪沉积区,路基顶面雪量甚至大于无防雪栅时的雪量。

|
图 7 不同防雪栅作用距离时路堑内外沉积雪量 Fig. 7 Deposited snow amounts inside and outside the cutting with different distances of snow fence |
图 8为不同防雪栅与路基间距离作用下不同位置的雪量对比,其中折线图对应左纵轴,柱状图对应右纵轴。从图 8可以看出,作用距离60 m时,路堑外雪粒体积分数比值的平均值达到最大,同时路基顶面测点的雪粒体积分数比值最小,这说明使用5 m高、孔隙率为50%的防雪栅对路基顶面的最优防护距离约在60 m左右;在作用距离从80 m减小到20 m过程中,路基顶面雪量减少率先从23.52%增大到24.69%,后减小到-9.57%,负值说明雪量相对无防雪栅时增加。

|
图 8 不同防雪栅作用距离时不同位置雪量对比 Fig. 8 Deposited snow amounts at different locations with different distances of snow fence |
防雪栅与路基距离较远时防雪栅下风侧积雪沉积区得到充分发展,路堑外雪量增加,但此时防雪栅与路堑距离过远,防雪栅对路堑内雪量影响较弱;随着作用距离的减小,防雪栅对路基顶面雪量的影响逐渐增加,而在过近时路基顶面会处于栅后积雪沉积区,使得路基顶面雪量相对无防雪栅时增大,此时雪量减少率为负值。
3.3 高度选定防雪栅距离为80 m,栅栏孔隙率为50%,图 9为不同高度防雪栅作用下的沉积雪量对比。由图 9可以看出,防雪栅高度为2、3、4、5 m时栅两侧的雪粒体积分数比值最大分别为1.106、1.112、1.120、1.168,随栅高增大而增大,同时防雪栅两侧积雪沉积距离也增大。防雪栅高度为2 m时,栅后雪粒沉积长度为15~20 m;防雪栅高度为3、4、5 m时,栅后雪粒沉积长度分别为20~25 m、30~35 m、40~50 m,即栅后雪粒沉积长度约为防雪栅高度的10~12倍。

|
图 9 不同高度时路堑内外沉积雪量 Fig. 9 Deposited snow amounts inside and outside the cutting with different heights |
表 2为用相同的多项式拟合方法得到的不同栅高下雪量对比结果。由表 2可以看出5 m高时铁路路堑外雪粒体积分数比值最大达到1.047,与无防雪栅工况相比,2、3、4、5 m高度下铁路路堑外雪粒体积分数比值分别增加了49.92%、70.90%、87.53%和92.95%。路堑内积雪变化趋势与路堑外积雪变化趋势相反。栅高为2、3、4、5 m时,路基顶面的雪量减少率分别为10.42%、13.54%、19.79%和23.52%,即防雪栅高度为5 m时,路基顶面雪量最少,防雪栅对路基顶面的雪量减少作用最明显。
| 表 2 不同高度时各位置处雪量对比 Tab. 2 Deposited snow amounts at different locations with different heights |
根据上节计算采用的防雪栅孔隙率、高度和布置距离,建立L16(45)的正交试验。计算采用的多相流模型、堆积-侵蚀条件与边界均与上节保持一致。计算工况与结果见表 3,路堑外栅栏的影响距离内为区域1,其中栅前取值为20 m,栅后取值为防雪栅到路堑的距离;路基顶面为区域2。
| 表 3 计算条件与计算结果 Tab. 3 Calculation conditions and obtained results |
本文采用极差分析方法对影响防雪栅两侧与路基顶面雪量的因素进行分析,孔隙率、高度和作用距离为极差分析的3项因素。在极差分析中,Kjm为第j列因素第m水平所对应的试验目标的和,Kjm为Kjm的平均值,极差R如式(13)所示,即某列因素各水平下的目标值的最大值与最小值的差,极差R越大说明该因素对实验目标越敏感,影响越剧烈,根据极差R的大小,可以判断影响因素的主次。
| $R = \max \left( {{{\bar K}_{j1}}, {{\bar K}_{j2}}, \cdots , {{\bar K}_{j{\rm{m}}}}} \right) - \min \left( {{{\bar K}_{j1}}, {{\bar K}_{j2}}, \cdots , {{\bar K}_{jm}}} \right)$ | (13) |
表 4为路堑外栅栏影响长度内(区域1)雪粒体积分数比值的极差分析,由表 4算得防雪栅孔隙率、高度和作用距离的极差R值分别为3.81×10-3、1.743×10-2和3.047×10-3,即防雪栅高度是影响路堑外积雪沉降量的主要因素,防雪栅的孔隙率和作用距离主要影响防雪栅两侧积雪的分布形态和堆积位置,所以对路堑外整体的雪量影响较小。
| 表 4 区域1雪粒体积分数比值的极差分析 Tab. 4 Range analysis of ratio of snow volume fraction in Region 1 |
表 5为路基顶面(区域2)雪粒体积分数比值的极差分析,由表 5算得防雪栅孔隙率、高度和作用距离的极差R值分别为7.55×10-3、7.36×10-3和1.36×10-3,即防雪栅的作用距离是影响路基顶面沉积雪量主要因素。当防雪栅与路基距离过近时,防雪栅对路基顶面的雪量减少率为负值,随着作用距离的增加,雪量减少率逐渐增加,路基顶面雪量减少,因此作用距离会对路基顶面的雪量产生较明显的影响;栅高和孔隙率主要影响路堑外积雪分布和沉积雪量,并间接改变了路基顶面的雪量。
| 表 5 区域2雪粒体积分数比值的极差分析 Tab. 5 Range analysis of ratio of snow volume fraction in Region 2 |
1) 铁路路堑外设置的防雪栅可以改变流场分布并影响雪粒运动,使雪粒沉积在防雪栅两侧;当路堑位于防雪栅下风侧时,路堑外沉积雪量增多,路堑内雪量较无防雪栅时减少,可达到风吹雪灾害防治的目的。
2) 防雪栅孔隙率主要影响栅两侧积雪分布形态,随着孔隙率的增加,栅两侧的沉积雪量从小范围的剧烈变化向大范围的平缓分布转变,孔隙率为50%时栅两侧的沉积雪量最大。
3) 栅栏高度增加时,防雪栅两侧最大沉积雪量和防雪栅影响范围均增加;当孔隙率为50%时,防雪栅下风侧积雪沉积区长度约为防雪栅高度的10~12倍。
4) 影响路堑外沉积雪量的主要因素是防雪栅结构形式,影响路堑内沉积雪量的主要因素是防雪栅作用距离。16组正交试验中,防雪栅所致的路堑外雪量增加17.14% ~ 79.80%,对路基顶面的雪量最大减少率为26.17%。
| [1] |
施佳誉, 徐冬英, 夏才初, 等. 公路风吹雪雪阻分布规律及雪灾形成机理研究[J]. 公路, 2020, 65(1): 257. SHI Jiayu, XU Dongying, XIA Caichu, et al. Research on the distribution law of snow blockage of snow drift on road and the formation mechanism of snow disaster[J]. Highway, 2020, 65(1): 257. |
| [2] |
李博. 铁路工程风吹雪监测方法研究[J]. 现代交通技术, 2019, 16(4): 77. LI Bo. Research on monitoring method of snow drifting disaster in railway engineering[J]. Modern Transportation Technology, 2019, 16(4): 77. DOI:10.3969/j.issn.1672-9889.2019.04.016 |
| [3] |
席建锋, 李江, 朱光耀, 等. 公路风吹雪积雪力学原理与积雪深模型[J]. 吉林大学学报(工学版), 2006, 36(增刊2): 152. XI Jianfeng, LI Jiang, ZHU Guangyao, et al. Hydromechanical mechanism of road snowdrift deposit and its depth model[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(S2): 152. |
| [4] |
郑黎黎, 席建锋, 丁同强, 等. 公路风吹雪流场测定及仿真分析[J]. 长春理工大学学报(自然科学版), 2009, 32(2): 260. ZHENG Lili, XI Jianfeng, DING Tongqiang, et al. Flow field observation and simulation of road snow-drift[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2009, 32(2): 260. DOI:10.3969/j.issn.1672-9870.2009.02.026 |
| [5] |
陈凤箴. 防雪栅栏对公路风吹雪灾害的防治技术研究[J]. 内蒙古公路与运输, 2009(1): 1. CHEN Fengzhen. Study on the prevention and control technology of snow barrier to highway wind-blown snow disaster[J]. Highways Transportation in Inner Mongolia, 2009(1): 1. DOI:10.3969/j.issn.1005-0574.2009.01.001 |
| [6] |
吴鹏, 陈发明, 刘健, 等. 基于Fluent防雪栅栏数值仿真研究[J]. 交通科技与经济, 2016, 18(6): 57. WU Peng, CHEN Faming, LIU Jian, et al. Research on numerical simulation of snow fence based on Fluent[J]. Technology & Economy in Areas of Communications, 2016, 18(6): 57. DOI:10.19348/j.cnki.issn1008-5696.2016.06.011 |
| [7] |
吴鹏. 新疆公路风吹雪雪害防治措施的研究[J]. 西部交通科技, 2019(6): 54. WU Peng. Study on prevention measures of snowdrift disasters in Xinjiang highway[J]. Western China Communications Science & Technology, 2019(6): 54. DOI:10.13282/j.cnki.wccst.2019.06.016 |
| [8] |
MCCLURE S, KIM J J, LEE S J, et al. Shelter effects of porous multi-scale fractal fences[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 163: 6. DOI:10.1016/j.jweia.2017.01.007 |
| [9] |
杨旭. 玛依塔斯交通走廊风吹雪特点研究[J]. 铁道工程学报, 2018, 35(12): 1. YANG Xu. Research on the characteristics of drifting snow disaster in Xinjiang Mayitas traffic corridor[J]. Journal of Railway Engineering Society, 2018, 35(12): 1. DOI:10.3969/j.issn.1006-2106.2018.12.001 |
| [10] |
SAÑUDO-FONTANEDA L A. Classification and comparison of snow fences for the protection of transport infrastructures[J]. Journal of Cold Regions Engineering, 2011, 25(4): 162. DOI:10.1061/(ASCE)CR.1943-5495.0000031 |
| [11] |
TABLER R, MEENA J. Effects of snow fences on crashes and road closures: a 34-year study on Wyoming Interstate-80[C]// 13th International Conference on Cold Regions Engineering. Orono: American Society of Civil Engineers, 2006. DOI: 10.1061/40836(210)74
|
| [12] |
王廷亮. 铁路风吹雪灾害数值模拟及防治技术研究[D]. 兰州: 兰州大学, 2009 WANG Tingliang. Study on numerical simulation and prevention measures of the drifting snow disaster along railway[D]. Lanzhou: Lanzhou University, 2009 |
| [13] |
祁延录. 考虑风吹雪灾害的新疆克塔铁路选线研究[J]. 铁道科学与工程学报, 2018, 15(11): 2813. QI Yanlu. Strategies of railway alignment selection for Karamay-Tacheng railway in Xinjiang considering snow drifting disasters[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2813. |
| [14] |
王晓晶, 沈志琦, 满国佳. 液压锥阀气穴现象两相流仿真及实验[J]. 哈尔滨工业大学学报, 2019, 51(7): 144. WANG Xiaojing, SHEN Zhiqi, MAN Guojia. Simulation and experiment of cavitation phenomenon two-phase flow of hydraulic cone valve[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 144. |
| [15] |
TOMINAGA Y, OKAZE T, MOCHIDA A. CFD modeling of snowdrift around a building: an overview of models and evaluation of a new approach[J]. Building & Environment, 2011, 46(4): 899. |
| [16] |
TOMINAGA Y, STATHOPOULOS T. Numerical simulation of dispersion around an isolated cubic building: model evaluation of RANS and LES[J]. Building Environmental, 2010, 45(10): 2231. DOI:10.1016/j.buildenv.2010.04.004 |
| [17] |
ZHOU X, ZHANG Y, KANG L, et al. CFD simulation of snow redistribution on gable roofs: impact of roof slope[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 185: 16. DOI:10.1016/j.jweia.2018.12.008 |
| [18] |
桑嘉宾. 混合粒径风雪流运动的数值模拟[D]. 兰州: 兰州大学, 2012 SANG Jiabin. Numerical simulations of blowing snow with mixed diameter[D]. Lanzhou: Lanzhou University, 2012 |
| [19] |
铁路线路设计规范: TB 10098—2017[S]. 北京: 中国铁道出版社, 2017 Code for railway line design: TB 10098—2017[S]. Beijing: China Railway Publishing House, 2017 |
| [20] |
YAN K, CHENG T, ZHANG Y. A new method in measuring the velocity profile surrounding a fence structure considering snow effects[J]. Measurement, 2018, 116: 373. DOI:10.1016/j.measurement.2017.11.032 |
 2022, Vol. 54
2022, Vol. 54


