2. 桂林电子科技大学 建筑与交通工程学院, 广西 桂林 541004;
3. 长春工程学院 土木工程学院, 长春 130012
2. School of Architecture and Transportation Engineering, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China;
3. School of Civil Engineering, Changchun Institute of Technology, Changchun 130012, China
为了满足日益增长的货运需求,港珠澳大桥、莲塘口岸等地相继启用了公路货运通道,用于跨境货物分流。伴随着公路货运的发展,货车参与的交通事故数量逐年增加。根据《2018年度道路交通事故统计年报》[1]显示,中国货运车辆参与的道路交通事故约4万起,导致约2万人死亡,分别占全年总事故数和死亡人数的21%和22%,直接经济损失高达5亿元。由于货车总重大、车身长、加减速性能差等相关因素,货运通道事故中重、特大事故比例高,其中货车冲出路外事故(路侧事故)占比较大且致死率较高,严重影响了人们的生命和财产安全。
货车事故的发生暴露出货运行业存在的不足和问题。为了提高公路运输安全水平,各国学者相继开展了公路线形设计研究。例如,文献[2]提出一种新的缓和曲线类型—回旋对称投影缓和曲线(SPTC),通过分析SPTC曲率变化与其在x轴上投影长度之间的线性关系,研究得出:SPTC可以代替立方抛物线,当需要较长的缓和曲线时,SPTC可以有效连接两个同向曲线。通过将西班牙高速公路划分为具有相同特征的路段,文献[3]分析了不同线形指标与交通事故率的关系,由此确定了评价道路设计一致性的最佳指标,以及相应评价指标阈值。文献[4]提出了一种基于操作系统的公路平面线形优化模型,以达到最佳的线形设计一致性,并通过应用实例和灵敏度分析,证明了该模型在评估改进策略方面的能力。文献[5]利用州际路段的事故数据建立道路设计特征与行车安全性之间的关系,并使用非相关负二项式(SUNB)技术探索分析了不同碰撞严重程度之间未观察到的共享效应。文献[6]通过分析道路线形、交通状况和交通事故之间的相关性,并比较了四车道和两车道曲线段交通事故率。结果显示:双车道道路的事故率较高,且曲率半径越小,事故率越高。文献[7]通过总结前人关于圆曲线半径与相邻曲线距离对事故风险的相互作用研究,分析得出:曲线之间的平均距离越短,相邻曲线越尖锐,给定曲线半径的事故风险增加越小。
与西方发达国家相比,中国公路货运普遍存在安全隐患高、效率低等问题。为了改善货运环境,文献[8]采用DHS-130XL红外观测仪测量车辆制动毂温度,建立了货车制动毂温度预测模型,确定了长大下坡路段合理平均纵坡指标值及对应坡长值,提出了长大下坡安全设计与评价程序。文献[9]统计了山区公路的交通事故数据与平面线形数据,采用角度变化率作为平面线形的表征参数,利用最小二乘法拟合了事故率与角度变化率之间的曲线关系。文献[10]运用Stata9.0统计软件对2003—2005年甘肃省某山区双车道公路发生的尾随相撞事故与8个道路设计要素进行了广义负二项回归分析,研究表明:山区双车道公路上的尾随相撞事故与累计坡长呈显著的正相关关系,累计坡长越长,尾随相撞的事故数越多。文献[11-12]从公路三维线形本质出发,利用SPSS分别建立了高速公路和双车道公路相邻路段平均曲率差、挠率差与事故率之间的关系模型;随后以三维空间线形的曲率和挠率作为公路线形几何特征描述参数,以车道偏移量作为侧向行车安全的表征指标,剖析了线形在空间层面发生的几何突变对车道偏离的影响。
纵观当前道路交通安全研究领域,鲜有涉及到专门针对公路货运通道的线形设计理论与方法。与常规混合车道相比,在不同交通特性和行车环境的影响下,货运通道事故致因机理往往存在差异性,这同时给货运通道线形设计提出了新的要求。鉴于此,本文利用PC-Crash仿真软件获取公路货运通道路侧事故数据,通过二元Logistic回归分析构建基于显著性风险因素的货运通道路侧事故概率预测模型,基于模型预测结果,借助传统交通事故多发点判别方法——“累计频率曲线法”的思想,提出货运通道路侧事故多发路段判别方法;针对路侧事故多发路段,采用分类树CART算法开展货运通道线形优化设计研究,并提出相应改善措施。研究成果有助于丰富公路货运通道安全设计、交通管理等理论,为交管部门完善货运通道交通基础建设提供决策依据。
1 数据收集通过大量的路侧事故致因调查,并考虑到PC-Crash事故仿真软件的功能性,本文选取公路线形指标(圆曲线半径、纵坡坡度、超高横坡度、硬路肩宽度、圆曲线加宽)、路面条件(路面附着系数)、交通特性(车速、车型)8个风险因素作为自变量,车辆最终状态(正常行驶、驶离行车道)作为因变量,利用仿真软件收集研究数据,其中车型包括载重货车和铰接列车,车辆正常行驶代表未发生路侧事故,驶离行车道代表发生路侧事故。首先调取Avia-A30 L-A30作为载重货车的代表车型,MAN-19.372和Avia-A30 L-A30分别作为拖车和挂车的代表车型,由此组成铰接列车;随后建立了行车道宽度为3.75 m,边坡坡度为1∶3.5,边坡高度为4 m的双向四车道公路货运通道模型,如图 1所示。

|
图 1 试验场景 Fig. 1 Test scenario |
根据《公路路线设计规范》[13]相关规定,各个风险因素的取值:车速分别取40、60、80、100 km/h;圆曲线半径分别取200、400、600、800、1 000 m;纵坡坡度分别取0、2%、4%、6%;超高横坡度分别取0、2%、4%、6%;硬路肩宽度分别取0.75、1.5、2.25、3 m;路面附着系数分别取0.2、0.4、0.6、0.8。针对圆曲线加宽,根据规范[13]规定,当圆曲线半径为200 m时,进行加宽值设置,其中,载重货车对应加宽值为0.6 m,铰接列车对应加宽值为0.8 m。此外,考虑到车辆行驶至弯道路段时驾驶人的转向操作,故在每次试验前通过对车辆转弯半径的设置来实现车辆转向轮的偏转,以匹配不同圆曲线半径。
根据每种风险因素的取值,首先建立了5×4×4×4×4=1 280种道路线形组合。通过对载重货车和铰接列车施加4种速度,并进行对应车型的圆曲线加宽设置,共开展1 280×4×2=10 240组仿真试验,其中未发生路侧事故8 938组,占87.3%;发生路侧事故1 302组,占12.7%。
2 公路货运通道路侧事故概率预测 2.1 Logistic回归分析Logistic回归属于广义线性回归模型(generalized linear model),常用于数据挖掘,疾病诊断,事件预测等领域。考虑到本文研究数据中因变量(路侧事故发生和路侧事故不发生)为二分类,故选取二元Logistic回归模型进行路侧事故概率预测。假设n个自变量与因变量相关,记X=(x1, x2, …, xn),模型方程式[14]为
| $P(Y = 1\mid X) = \frac{{\exp \left( {{\alpha _0} + \sum\limits_{i = 1}^n {{\alpha _i}} {x_i}} \right)}}{{1 + \exp \left( {{\alpha _0} + \sum\limits_{i = 1}^n {{\alpha _i}} {x_i}} \right)}}$ | (1) |
式中:P为事件发生概率,α0为常数项,αi为偏回归系数。
将研究数据纳入二元Logistic回归模型中,初步分析结果见表 1。从表 1可以看出,圆曲线加宽对应的p值大于0.05(显著性水平),无统计学意义,即该变量对公路货运通道路侧事故发生影响不显著,在模型中应予以剔除。
| 表 1 初步分析结果 Tab. 1 Preliminary analysis result |
重新对研究数据进行回归分析,分析结果见表 2。表 2中各个变量的p值均小于0.05,说明这些变量是影响公路货运通道路侧事故发生的显著性风险因素。
| 表 2 最终分析结果 Tab. 2 Final analysis result |
根据表 2中各个变量的偏回归系数估计值,构建了货运通道路侧事故发生概率预测模型为
| $P(Y\leqslant 1) = \frac{{\exp \left( { - 5.748 + 0.224v - 0.00038R - 7.896\mu - 2.207w + 0.553{i_1} - 0.307{i_2} - 1.015\eta } \right)}}{{1 + \exp \left( { - 5.748 + 0.224v - 0.00038R - 7.896\mu - 2.207w + 0.553{i_1} - 0.307{i_2} - 1.015\eta } \right)}}$ | (2) |
式中:v为车速,km/h;R为圆曲线半径,m;μ为路面附着系数;w为硬路肩宽度,m;i1为纵坡坡度(下坡为正);i2为超高横坡度(上坡为正);η为车型,载重货车取1,铰接列车取0。
2.2 模型检验本文利用ROC(receiver operating characteristic)曲线进行模型检验,该曲线是根据一系列不同的二分类方式,以敏感性为纵坐标、特异性为横坐标绘制的。通常依据ROC曲线下的区域面积AUC(area under ROC curve)来衡量模型拟合的好坏。一般AUC的值介于0.5~1.0之间,在置信度为95%的情况下,AUC值越大,说明模型的准确性越高。根据概率模型预测结果,利用SPSS软件绘制了ROC曲线如图 2所示。从图 2可以看出,ROC曲线非常靠近左上角,且曲线下方的面积值AUC为0.975, 大于0.9,说明该路侧事故概率预测模型的拟合效果较好。

|
图 2 ROC曲线 Fig. 2 ROC curve |
利用《公路项目安全性评价规范》[15]中公路运行速度计算模型,可以测算出公路货运通道每个路段单元的运行速度,运用上述预测模型,综合考虑圆曲线半径、纵坡坡度、超高横坡度、硬路肩宽度、路面附着系数等影响因素,能够确定每个路段单元可能造成的货车路侧事故概率。
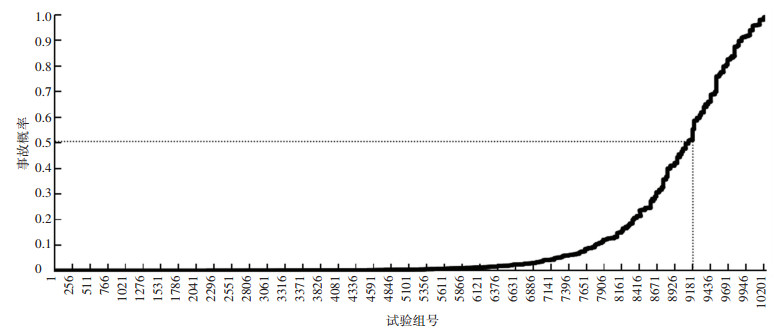
3 公路货运通道路侧事故多发路段判别根据公路货运通道路侧事故概率预测结果,图 3给出了10 240组仿真试验条件下的路侧事故概率分布特征。由图 3可得,约9 181组仿真试验为路侧事故低概率(<50%)事件,剩余1 059组为路侧事故高概率(>50%)事件,分别占总试验组数的89.7%和10.3%。由此可以看出,当路侧事故发生属于低概率事件时,该事件往往所占比例较大,当路侧事故发生属于高概率事件时,该事件往往所占比例较小。
|
图 3 路侧事故概率分布 Fig. 3 Distribution of roadside accident probability |
依据上述分析,为了识别公路货运通道路侧事故多发路段,本文借助传统交通事故多发路段判别方法——“累计频率曲线法”的思想,认为:发生路侧事故为低概率或不发生路侧事故的路段占大部分,发生路侧事故为高概率的路段占少部分,并且路侧事故发生概率越高的路段占得比例越小。结合本文试验数据,将10 240个预测的事故概率值由小到大进行排序,通过统计每个概率值对应的试验组数,进而求算各个概率值出现的频率和累计频率,由此可分离出累计频率很小,但事故风险很高的概率阈值。因此,本文以路侧事故概率作为横坐标,相应概率的累计频率为纵坐标,绘制了累计频率随路侧事故概率的变化曲线,如图 4所示。由图 4可得,随着路侧事故概率增大,累计频率的增长趋势越来越缓。根据曲线变化特点,利用SPSS软件拟合的曲线方程为
| $y = 1.158\;09{x^3} - 3.2{x^2} + 3.059x + 0.029\;4$ | (3) |

|
图 4 累计频率曲线 Fig. 4 Cumulative frequency curve |
式中:y为累计频率,x为路侧事故概率。
曲线方程决定系数R2=0.983。依据“累计频率曲线法”鉴别规则[16],通过对方程求导,得到曲线拐点处的概率值为74.2%。此外,在累计频率0.95的水平下,求得事故潜在多发点的鉴别标准为57.4%。即当货运通道路侧事故概率∈[74.2%, 100%]时,判定路段为路侧事故多发点;当货运通道路侧事故概率∈[57.4%, 74.2%)时,判定路段为路侧事故潜在多发点。由此提出了公路货运通道路侧事故多发路段判别方法。
本文选取S327线K1357+680至K2721+130段用于验证上述判别方法的有效性。S327线属于一级公路,设计速度为80 km/h,主要承担沿线地区货物周转和运输,属于典型公路货运通道。通过收集公路设计文件和运行速度观测资料,首先进行路段单元划分,随后利用路侧事故概率预测模型计算各路段单元事故概率值,最后依据上述判别方法判定K2063+178处为路侧事故多发路段。该路段载重货车85%运行速度为72 km/h,铰接列车85%运行速度为70 km/h,圆曲线半径为700 m,路面为干燥沥青材质,路面附着系数取0.7,硬路肩宽度为1.5 m,纵坡坡度为2%,横坡坡度为2%,由此求得载重货车和铰接列车行驶至上述路段发生路侧事故的概率分别为68%和79%,位于事故潜在多发点和事故多发点概率阈值范围内。根据交警部门统计资料显示,上述路段在2017—2019年共发生80余起货车路侧事故,已经被列为路侧事故高发区域。综上分析可得,通过本文提出的公路货运通道路侧事故多发路段判别方法得到的结论与事实相符,由此验证了该方法的可靠性。
4 公路货运通道线形设计 4.1 分类树CART算法针对公路货运通道路侧事故多发路段,本文采用分类树CART算法开展货运通道线形优化设计研究。CART算法属于决策树模型中典型算法之一,与ID3、C4.5等其他算法相比,该算法能够同时处理离散和连续数据,因此属于一种高效、准确的数据分类方法[17]。CART算法采用“基尼系数”(Gini index)[18]最小化准则实现树模型的简化和数据最优属性划分,基尼系数反映了数据集划分后的纯度,系数越小,说明数据集纯度越高。对于给定的数据集M,其基尼值的表达式为
| ${\mathop{\rm Gini}\nolimits} (M) = 1 - \sum\limits_{i = 1}^i {{{\left( {\frac{{{{\left| {{C_i}} \right|}^2}}}{{|M|}}} \right)}^2}} $ | (4) |
式中:i为数据集M的类别数,|Ci|为第i类别的样本量,|M|为数据集M的样本总量。
假设给定属性N,其某个取值将数据集M划分为M1和M2,此时属性N的基尼值的表达式为
| ${\mathop{\rm Gini}\nolimits} (M, N) = \frac{{\left| {{M_1}} \right|}}{M}{\mathop{\rm Gini}\nolimits} \left( {{M_1}} \right) + \frac{{\left| {{M_2}} \right|}}{M}{\mathop{\rm Gini}\nolimits} \left( {{M_2}} \right)$ | (5) |
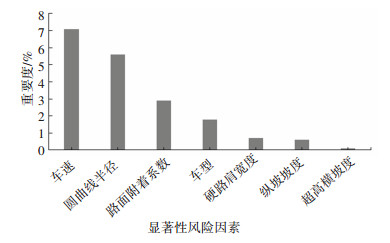
本文将10 240组试验数据按照7∶3的比例划分为训练数据和测试数据[19],首先通过训练数据产生原始决策树,为了避免对训练数据的过拟合,需要对原始决策树进行剪枝操作。本文采取后剪枝的方式,并采用网格搜索法生成所有可能的剪枝后树模型,通过交叉验证法计算测试集上各子树的基尼系数[20],从中选取基尼系数最小的子树作为最优子树,最终生成最优分类树。树模型结果显示,训练数据和测试数据的分类准确率分别为95.5%和95.8%。由于受到文章篇幅限制,本文筛选了部分最优分类树用于讨论分析,如图 5(a)、图 5(b)所示。图 5中节点0处为未分类的原始数据,依据CART算法,数据会被划分为尽可能多的子组,每个子组对应一个节点。此外,树模型同时给出了各个显著性风险因素影响路侧事故发生的重要度大小,如图 6所示。由图 6可得,车速影响路侧事故最为显著,往后依次为圆曲线半径、路面附着系数、车型、硬路肩宽度、纵坡坡度和超高横坡度。

|
图 5 分类树模型 Fig. 5 Classification tree models |
|
图 6 风险因素重要度 Fig. 6 Importance of risk factors |
由图 5可得,树模型为每个节点提供了路侧事故发生比例,即发生概率,由此可根据公路货运通道路侧事故多发路段概率阈值研究提出能够降低路侧事故风险的货运通道线形优化设计方法。通过对生成的树模型整理和分析,得到如下主要结论:
1) 由图 5(a)中节点3和节点4可得,当R≤400 m时,在v≤60 km/h条件下,路侧事故概率为7.1%;在60 km/h<v≤80 km/h条件下,路侧事故概率高达78.2%,判定为事故多发;此外,由节点7和节点8可得,在v≤60 km/h条件下,无论路面附着系数取何值,路侧事故概率均较低,说明当圆曲线半径≤400 m时,60 km/h是保证货运通道路侧事故不发生的相对安全车速。
2) 由图 5(a)中节点15和节点16可得,当R≤400 m,60 km/h<v≤80 km/h时,在i1<4%条件下,路侧事故概率为35.7%;在4%≤i1≤6%条件下,路侧事故概率为82.7%,判定为事故多发。故对于符合上述运行速度和圆曲线半径的货运通道路段,设计纵坡坡度应<4%。
3) 随着树模型继续分类,由图 5(a)中节点25和节点26可得,当4%≤i1≤6%时,在4%≤i2≤6%条件下,路侧事故概率为5.9%;在i2<4%条件下,路侧事故概率为63.9%,判定为事故潜在多发。因此,对于R≤400 m,以及60 km/h<v≤80 km/h的货运通道路段,当无法满足纵坡坡度<4%的设计要求时,设计超高横坡度应≥4%。
4) 由图 5(b)中节点19和节点20可得,当80 km/h<v≤100 km/h,400 m<R≤800 m时,在w≥2.25 m条件下,路侧事故概率为36.4%;在w≤1.5 m条件下,路侧事故概率为100%,判定为事故多发。因此,对于符合上述运行速度和圆曲线半径的货运通道路段,应设置硬路肩宽度≥2.25 m。
5) 随着树模型继续分类,由图 5(b)中节点27和节点28可得,当w≥2.25 m时,载重货车发生路侧事故的概率为5.6%,铰接列车发生路侧事故的概率高达72.1%,判定为事故潜在多发。说明在相同线形指标情况下,铰接列车比载重货车更容易发生路侧事故;此外,与铰接列车相比,增加硬路肩宽度对减少载重货车路侧事故风险影响较为显著。
5 结论通过PC-crash软件开展路侧事故仿真试验,利用二元Logistic回归分析构建公路货运通道路侧事故概率预测模型,借助“累计频率曲线法”思想,分别给出路侧事故潜在多发点和多发点概率阈值,由此提出货运通道路侧事故多发路段判别方法,并予以案例验证。针对货运通道路侧事故多发路段,采用CART算法提出货运通道线形优化设计方法。研究得到如下主要结论:
1) 显著性风险因素对公路货运通道路侧事故重要度由大到小依次为车速、圆曲线半径、路面附着系数、车型、硬路肩宽度、纵坡坡度和超高横坡度。
2) 当公路货运通道圆曲线半径≤400 m时,60 km/h是保证货运通道路侧事故不发生的相对安全车速;与载重货车相比,铰接列车更容易发生路侧事故,且增加硬路肩宽度对减少载重货车路侧事故风险影响较为显著。
3) 为了减少公路货运通道路侧事故风险,在《公路路线设计规范》(JTG D20—2017)规定的基础上,对货运通道路线设计指标进一步优化,提出以下几点建议:对于圆曲线半径R≤400 m,运行速度60 km/h<v≤80 km/h的货运通道路段,设计纵坡坡度应<4%,若无法满足纵坡坡度设计要求,设计超高横坡度应≥4%;对于运行速度80 km/h<v≤100 km/h,圆曲线半径400 m<R≤800 m的货运通道路段,应设置硬路肩宽度≥2.25 m。
| [1] |
中华人民共和国交通运输部. 2018年度道路交通事故统计年报[R]. 北京: 人民交通出版社, 2018 Ministry of Transport of the People's Republic of China. Annualroad traffic accident statistics report in 2018[R]. Beijing: China Communications Press, 2018 |
| [2] |
ELIOU N, KALIABETSOS G. A new, simple and accurate transition curve type, for use in road and railway alignment design[J]. European Transport Research Review, 2013, 6(1): 171. |
| [3] |
CASTRO M, PARDILLOMAYORA J M, SANCHEZ J F. Alignment indices as a tool to evaluate safety and design consistency in two lane rural roads[C]//International Symposium on Highway Geometric Design. Chicago: Transportation Research Board, 2005: 18
|
| [4] |
EASA S, MEHMOOD A. Establishing highway horizontal alignment to maximize design consistency[J]. Canadian Journal of Civil Engineering, 2007, 34(3): 1159. |
| [5] |
TANG Z, CHEN S, CHENG J, et al. Highway design and safety consequences: a case study of interstate highway vertical grades[J]. Journal of Advanced Transportation, 2018, 2018(1): 1. DOI:10.1155/2018/1492614 |
| [6] |
IKEDA T, MORI N. Analysis of correlation between roadway alignment and traffic accidents[J]. Regenerative Medicine, 2005, 7(2): 46. |
| [7] |
ELVIK R. The more (sharp) curves, the lower the risk[J]. Accident Analysis & Prevention, 2019, 133(10): 22. |
| [8] |
杨宏志, 胡庆谊, 许金良. 高速公路长大下坡路段安全设计与评价方法[J]. 交通运输工程学报, 2010, 10(3): 10. YANG Hongzhi, HU Qingyi, XU Jinliang. Safety design and evaluation method of long-steep downgrade sections for expressway[J]. Journal of Traffic and Transportation Engineering, 2010, 10(3): 10. DOI:10.3969/j.issn.1671-1637.2010.03.002 |
| [9] |
郭应时, 付锐, 袁伟, 等. 山区公路事故率与平面线形的关系[J]. 交通运输工程学报, 2012, 12(1): 63. GUO Yingshi, FU Rui, YUAN Wei, et al. Relation between accident rate and horizontal alignment for mountain highway[J]. Journal of Traffic and Transportation Engineering, 2012, 12(1): 63. DOI:10.3969/j.issn.1671-1637.2012.01.011 |
| [10] |
王华荣, 孙小端, 贺玉龙, 等. 山区双车道公路尾随相撞事故与道路线形的关系[J]. 北京工业大学学报, 2010, 36(9): 1236. WANG Huarong, SUN Xiaoduan, HE Yulong, et al. Effects of geometric features of rear-end crash accidents on mountainous two-lane highways[J]. Journal of Beijing University of Technology, 2010, 36(9): 1236. |
| [11] |
符锌砂, 葛婷, 李海峰, 等. 基于公路三维线形几何特性的行车安全分析[J]. 中国公路学报, 2015, 28(9): 24. FU Xinsha, GE Ting, LI Haifeng, et al. Traffic safety analysis based on geometric properties of highway three-dimensional alignment[J]. China Journal of Highway and Transport, 2015, 28(9): 24. DOI:10.3969/j.issn.1001-7372.2015.09.004 |
| [12] |
符锌砂, 何石坚, 杜锦涛, 等. 线形空间几何突变对曲线路段车道偏移的影响[J]. 中国公路学报, 2019, 32(12): 106. FU Xinsha, HE Shijian, DU Jintao, et al. Effects of spatial geometric mutation of highway alignments on lane departure at curved sections[J]. China Journal of Highway and Transport, 2019, 32(12): 106. |
| [13] |
中华人民共和国交通运输部. 公路路线设计规范: JTG D20—2017[S]. 北京: 人民交通出版社, 2017 Ministry of Transport of the People's Republic of China. Design specification for highway alignment: JTG D20—2017[S]. Beijing: China Communications Press, 2017 |
| [14] |
LÓPEZ A S V, RODRIGUEZ C A M. Flash flood forecasting in são paulo using a binary logistic regression model[J]. Atmosphere, 2020, 11(5): 473. DOI:10.3390/atmos11050473 |
| [15] |
中华人民共和国交通运输部. 公路项目安全性评价规范: JTG B05—2015[S]. 北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. Specification for highway safety audit: JTG B05—2015[S]. Beijing: China Communications Press, 2015 |
| [16] |
方守恩, 郭忠印, 杨轸. 公路交通事故多发位置鉴别新方法[J]. 交通运输工程学报, 2001, 1(1): 90. FANG Shouen, GUO Zhongyin, YANG Zhen. A new identification method for accident prone location on highway[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 90. |
| [17] |
KONAR D, PRADHAN R, DEY T, et al. Predicting students' grades using CART, ID3, and multiclass svm optimized by the genetic algorithm (GA): a case study[M]. Sikkim: John Wiley & Sons, 2020: 85.
|
| [18] |
LERMAN R I, YITZHAKI S. A note on the calculation and interpretation of the Gini index[J]. Economics Letters, 1984, 15(3): 363. |
| [19] |
程国柱, 程瑞, 徐亮. 公路小半径曲线段外侧车道路侧事故概率预测[J]. 哈尔滨工业大学学报, 2021, 53(3): 179. CHENG Guozhu, CHENG Rui, XU Liang. Probability of roadside accidents in the outer lane of small curve section highways[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 179. |
| [20] |
孙梦婷, 魏海平, 李星滢, 等. 利用CART分类树分类检测交通拥堵点[J/OL]. 武汉大学学报(信息科学版). (2019-10-14)[2020-11-16]. https://doi.org/10.13203/j.whugis20190288 SUN Mengting, WEI Haiping, LI Xingying, et al. Detection and classification of traffic congestion points using CART classification tree[J/OL]. Geomatics and Information Science of Wuhan University. (2019-10-14)[2020-11-16]. https://doi.org/10.13203/j.whugis20190288 |
 2022, Vol. 54
2022, Vol. 54


