沥青混合料是一种典型的多相复合材料,由集料、沥青和填料等不同性质的材料组成。其中,粗集料形成骨架结构,承担车辆荷载;细集料、填料和沥青填充粗集料形成的空隙,提高路面结构的整体稳定性。矿料间隙率是沥青混合料级配设计的重要体积参数,对沥青混合料性能有显著影响[1]。相比密级配或骨架密实型沥青混合料,多孔沥青混合料(PAC)作为环境友好型路面材料,为了实现在大雨期间加快路面排水、减少路面水膜、提高路面抗滑以及有效降低交通噪音等功能[2-4],需要较大空隙率,通常控制在20%左右[4-5]。空隙率通常是由矿料间隙率推求而来,因此开展PAC混合料主骨架结构和矿料间隙率物理模型的研究具有重要的工程意义。
沥青混合料的强度来源于集料的嵌挤和沥青砂浆的黏结,对抗车辙、抗裂和抗水损害等有重大意义[6]。根据尺寸大小,集料可分为粗集料和细集料[7],合理的粗细集料比例可以确保沥青混合料形成稳定的主骨架结构。沥青混合料的力学性能和体积指标高度依赖于集料的级配曲线类型[8]。文献[9]提出了接近于抛物线形状的密实型级配设计方法,但密实结构并不意味着混合料中存在主骨架结构。文献[10]引入粗细集料比作为评价指标,可粗略表征沥青混合料的骨架性能,但该比值具有经验性质,并不能反映细集料对粗集料的影响。文献[11-12]基于颗粒堆积和粒径分布理论提出了评估沥青混合料粗集料骨架结构的的分析模型,确定了形成骨架结构的主集料粒径范围(DASR),并分析了DASR与沥青混合料抗车辙[13-15]和抗裂[12]的相关性。文献[16]利用DASR的概念,将粒径小于DASR的集料称为间隙组分,将沥青与空隙的体积之和作为间隙体积,并引入干涉系数(DF)来评估间隙组分对主骨架结构的影响,最后研究了沥青砂浆、粒径小于DASR的集料含量以及空隙率对沥青混合料抗车辙和抗裂性能的影响。综上可知,DASR与沥青混合料路用性能有很好的相关性,形成的主骨架结构决定了混合料的矿料间隙率,进而影响混合料的空隙率,但并没有提出矿料间隙率的计算方法。
现有级配设计方法主要有泰勒曲线法、体积填充法和贝雷法等[17],这些方法主要针对是密级配沥青混合料。目前,常采用试错法或基于经验模型选择满足空隙率目标要求的最佳级配,其弊端就是需要开展大量的试验测试。本文将在DASR的基础上进行拓展,构建适于计算PAC混合料矿料间隙率的物理模型,方便选定满足目标空隙率要求的混合料最佳级配,可节约大量的时间和精力,能够有效控制混合料性能差的风险。
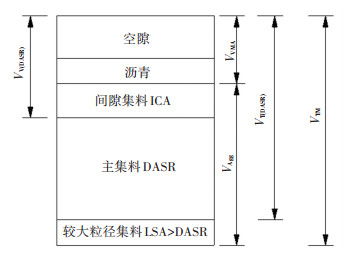
1 DASR法及其改进 1.1 原始DASR法文献[12]基于颗粒堆积理论和粒径分布构建了一种评估粗集料骨架结构的理论方法,提出了描述沥青混合料组成的物理模型。该模型认为沥青混合料由主集料(DASR)形成空间骨架结构,其间隙部分是由粒径小于DASR的集料(称为间隙集料ICA,可完全融入到DASR的内部空隙中)、沥青和空隙组成,如图 1所示。
沥青混合料经压实后矿物集料之间的有效空间体积(矿料间隙体积)所占总体积的百分比,即为矿料间隙率,类似于土体中的孔隙率。则有
| $ V_{\mathrm{VMA}}=V_{\mathrm{TM}}-V_{\mathrm{Agg}} $ | (1) |
式中:VVMA为矿料间隙体积,VTM为压实后混合料的总体积,VAgg为混合料中集料所占的体积。
如果沥青混合料在给定的集料级配下具有一定的有效沥青含量和空隙率,则可计算DASR形成主骨架的空隙率。将粒径大于DASR的集料称为较大粒径集料(LSA),其占比较少;利用混合料的总体积减去LSA的颗粒体积来计算DASR的总体积,即
| $ V_{\mathrm{T}(\text { DASR })}=V_{\mathrm{TM}}-V_{\mathrm{LSA}} $ | (2) |
式中:VT(DASR)表示DASR形成的主骨架总体积,包括DASR本身及其形成的主骨架空隙部分;VLSA表示LAS的颗粒体积。
DASR形成的主骨架空隙体积包括间隙集料(ICA)体积、有效沥青体积和空隙体积(后两者之和即为矿料间隙体积VVMA),则有
| $ V_{\mathrm{V}(\mathrm{DASR})}=V_{\mathrm{ICA}}+V_{\mathrm{VMA}} $ | (3) |
式中:VV(DASR)为DASR形成的骨架空隙体积,VICA为ICA的颗粒体积。
DASR骨架空隙率的计算表达式为
| $ \eta_{\mathrm{DASR}}=\frac{V_{\mathrm{V}(\mathrm{DASR})}}{V_{\mathrm{T}(\mathrm{DASR})}}=\frac{V_{\mathrm{ICA}}+V_{\mathrm{VMA}}}{V_{\mathrm{TM}}-V_{\mathrm{LSA}}} $ | (4) |
由式(4)可知,ICA的体积是影响主骨架空隙率的主要因素,LSA在混合料中只是取代少部分DASR,并不会影响混合料的矿料间隙率。而实际情况是,混合料中LSA比同等含量的DASR形成空隙体积要大,因而LSA不仅取代了少部分DASR,还会影响混合料的矿料间隙。另外,混合料中还包括颗粒粒径介于DASR与ICA之间的集料,这部分集料并不能完全融入到DASR形成的骨架空隙中,在占据DASR内部空隙的同时还会干涉DASR的骨架结构,进而影响混合料的矿料间隙率,将这部集料称为干涉集料PDA。针对上述不足,本文将通过考虑LSA和PDA的影响,对原始的DASR法进行改进和完善。
1.2 改进的DASR法 1.2.1 骨架空隙结构PAC混合料属于典型的骨架大空隙结构,DASR主骨架结构的稳定性取决于较小粒径集料如何融入到DASR内部的骨架空隙。通常将集料颗粒假定为球体形状在混合料中呈随机堆积排列,利用颗粒堆积理论可近似确定主骨架空隙结构(空隙类型、数量和大小)。对于规则的球体系统,可利用基于填充的数学方程对其空隙结构进行评估。若采用试验测定(如CT扫描)可获得准确的混合料空隙结构,但费用昂贵,应用受到极大限制。较小粒径集料与单个DASR骨架空隙之间的关系如图 2所示。

|
图 2 DASR形成的主骨架结构的局部稳定性 Fig. 2 Local stability of main skeleton structure formed by DASR |
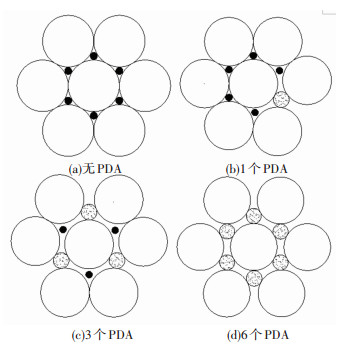
由图 2可以看出,若集料的粒径小于主骨架空隙,主骨架结构是稳定的;若集料粒径等于主骨架空隙,主骨架结构的稳定性处于临界状态;若集料粒径大于主骨架空隙,主骨架结构会遭到破坏,也就是对主骨架形成了干涉,将其称为干涉集料PDA。如图 3所示,当所有集料粒径均小于主骨架空隙尺寸时,则主骨架结构处于稳定状态,见图 3(a);PDA数量越多,主骨架结构受到的干涉影响越明显;随着PAD数量的增多,主骨架结构的接触点会显著减少,使得骨架结构的空隙率也会有所增大。
|
图 3 PDA的干涉对DASR主骨架结构稳定性的影响 Fig. 3 Influence of PDA interference on the global stability of main skeleton structure formed by DASR |
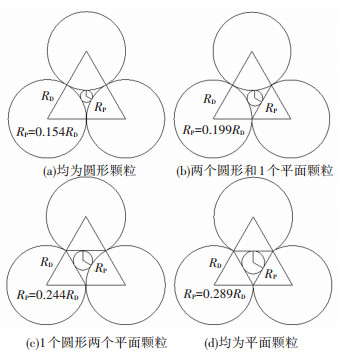
假定集料为球体形状,DASR和PDA的半径分别为RD和RP。根据堆积理论,二维平面内RD和RP之间的关系,如图 4所示。考虑集料颗粒形状的影响,取图 4中4种情况的平均值RP=0.22RD作为PDA粒径的最小值。若DASR颗粒的平均半径为RD,则PDA颗粒平均半径RP介于0.22RD~RD之间。对于粒径小于PDA的集料即为间隙集料(ICA),能够完全融入主骨架空隙中,且由于多孔沥青混合料中的细集料占比较少,不会出现主骨架空隙完全被填满的情况,也就是说所有的ICA均可完全融入到主骨架空隙中。
|
图 4 不同面主集料颗粒组合的二维分析 Fig. 4 Two-dimensional analysis of DASR particle combinations with different particle surfaces |
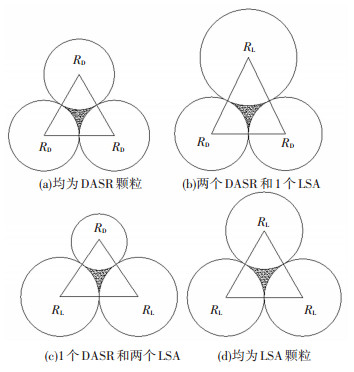
由于LSA的粒径大于DASR,且在混合料中所占比例较少,不会对主骨架结构稳定性产生较大影响[11],但会形成较大空隙,一定程度上会增大混合料的矿料间隙率。图 5给出了LSA和DASR不同组合形成的局部结构,阴影部分即为空隙,LSA和DASR的颗粒半径分别为RL和RD,其中RL>RD。3个DASR、两个DASR和1个LSA、1个DASR和两个LSA以及3个LSA颗粒等组合的中间空隙面积依次增大。3个DASR颗粒的内部空隙为
| $ A_{0}=(\sqrt{3}-0.5 {\rm{ \mathsf{ π} }}) R_{\mathrm{D}}^{2} $ | (5) |
|
图 5 不同LSA和DASR组合的二维分析 Fig. 5 Two-dimensional analysis of different combinations of LSA and DASR |
两个DASR和1个LSA颗粒的内部空隙为
| $ \begin{aligned} A_{1}=& R_{\mathrm{D}} \sqrt{R_{\mathrm{L}}^{2}+2 R_{\mathrm{L}} R_{\mathrm{D}}}-0.5 {\rm{ \mathsf{ π} }} R_{\mathrm{D}}^{2}-\\ & \frac{1}{2} \arccos \sqrt{1-\left(\frac{R_{\mathrm{D}}}{R_{\mathrm{L}}+R_{\mathrm{D}}}\right)^{2}} \end{aligned} $ | (6) |
1个DASR和两个LSA颗粒的内部空隙为
| $ \begin{aligned} A_{2}=&R_{\mathrm{L}} \sqrt{R_{\mathrm{D}}^{2}+2 R_{\mathrm{L}} R_{\mathrm{D}}}-0.5 {\rm{ \mathsf{ π} }} R_{\mathrm{L}}^{2}-\\ &\frac{1}{2} \arccos \sqrt{1-\left(\frac{R_{\mathrm{L}}}{R_{\mathrm{L}}+R_{\mathrm{D}}}\right)^{2}} \end{aligned} $ | (7) |
3个LSA颗粒的内部空隙为
| $ A_{0}=(\sqrt{3}-0.5 {\rm{ \mathsf{ π} }}) R_{\mathrm{L}}^{2} $ | (8) |
文献[11-14]基于大量测试结果,提出了一种用于计算压实后混合料中特定粒径颗粒之间中心距的理论分析程序。该程序计算表明,两个相邻粒径颗粒含量(质量)的相对比例接近70/30,如(68~70)/(32~30)时,颗粒间距开始迅速增大;如果这一相对比例超过70/30的阈值,一种粒径颗粒将会严重破坏其他粒径颗粒的相互作用能力。举例说明如下:4.75~9.5 mm和2.36~4.75 mm即为两相邻粒径,4.75~9.5 mm和9.5~13.2 mm也是两相邻粒径,根据筛孔尺寸类推;混合料中两相邻粒径颗粒含量的比值即为相对比例。
为了确保颗粒间良好的相互作用,两个相邻粒径A和B,若粒径A颗粒含量的比例不大于70%,则粒径B颗粒含量的比例不应小于30%。因此,70/30的相对比例可以作为标准用于判定相邻筛孔上的集料颗粒能否形成连续接触相互作用的颗粒骨架结构,DASR也可基于70/30的相对比例限定其粒径范围。DASR可以由1个或多个尺寸粒径的集料组成。
综上所述,由两个相邻粒径颗粒含量(质量)的相对比例为70/30,可以方便确定LSA和DASR、DASR和PDA的分界尺寸;由PDA最小粒径等于DASR粒径的0.22倍,可以确定PDA和ICA的分界尺寸。
1.2.2 主骨架空隙率根据前述分析,较大粒径集料LSA、干涉集料PDA和间隙集料ICA均会对沥青混合料的矿料间隙率产生影响。图 6为PAC混合料组成的示意图,DASR形成的主骨架结构总体积可由式(2)改写为
| $ V_{\mathrm{T}(\text { DASR })}=V_{\mathrm{TM}}-\left(V_{\mathrm{LSA}}+V_{\mathrm{PDA}}\right) $ | (9) |

|
图 6 多孔沥青混合料组成的示意图 Fig. 6 Schematic diagram of PAC compositions |
DASR形成的骨架空隙体积包括ICA颗粒体积、LSA取代作用增大的空隙体积ΔVLSA、PDA干涉作用增加的空隙体积ΔVPDA、有效沥青体积以及矿料间隙体积等。DASR的骨架空隙体积由式(3)可改写为
| $ V_{\mathrm{V}(\mathrm{DASR})}=V_{\mathrm{ICA}}+V_{\mathrm{VMA}}+\Delta V_{\mathrm{LSA}}+\Delta V_{\mathrm{PDA}} $ | (10) |
DASR骨架结构的空隙率ηDASR可由式(4)可改写为
| $ \eta_{\mathrm{DASR}}=\frac{V_{\mathrm{V}(\mathrm{DASR})}}{V_{\mathrm{T}(\mathrm{DASR})}}=\frac{V_{\mathrm{ICA}}+V_{\mathrm{VMA}}+\Delta V_{\mathrm{LSA}}+\Delta V_{\mathrm{PDA}}}{V_{\mathrm{TM}}-V_{\mathrm{LSA}}-V_{\mathrm{PDA}}} $ | (11) |
根据图 5种的4种情况,LSA作用增加的空隙率ΔηLSA为
| $ \begin{aligned} &\Delta \eta_{\mathrm{LSA}}=\frac{\Delta V_{\mathrm{LSA}}}{V_{\mathrm{TM}}-V_{\mathrm{LSA}}-V_{\mathrm{PDA}}}= \\ &\left(\frac{A_{1}+A_{2}+A_{3}-3 A_{0}}{3 A_{0}+3 {\rm{ \mathsf{ π} }} R_{\mathrm{D}}^{2}}\right) P_{\mathrm{LSA}}=\left(\eta_{\mathrm{LSA}}-\eta_{\mathrm{DASR}}\right) P_{\mathrm{LSA}} \end{aligned} $ | (12) |
虽然PDA颗粒粒径较小,但无法完全融入到混合料的主骨架空隙中,因而PDA会对主骨架起到干涉作用使空隙含量增加,同时也会占据主骨架中的部分空隙使空隙含量减小。这样,PDA在混合料中就起到两种作用效果。若混合料中只含有PDA,也会形成内部空隙。假定PDA使空隙增加的部分等于PDA经捣实后的空隙率ηPDA与其在混合料中所占比例的乘积,还需要减去PDA自身的颗粒体积,由此构建考虑PDA作用的矿料间隙率的数学表达式为
| $ \begin{aligned} \Delta \eta_{\mathrm{PDA}}=&\frac{\Delta V_{\mathrm{PDA}}}{V_{\mathrm{TM}}-V_{\mathrm{LSA}}-V_{\mathrm{PDA}}}=\\ &\frac{\frac{P_{\mathrm{PDA}}\left(V_{\mathrm{T}(\mathrm{PDA})}-V_{\mathrm{PDA}}\right)}{V_{\mathrm{T}(\mathrm{PDA})}}-V_{\mathrm{PDA}}}{V_{\mathrm{TM}}-V_{\mathrm{LSA}}-V_{\mathrm{PDA}}}=\\ &\frac{\rho_{\mathrm{DSAR}}}{P_{\mathrm{DSAR}}}\left(\eta_{\mathrm{PDA}}-\frac{1}{\gamma_{\mathrm{PDA}}}\right) P_{\mathrm{PDA}} \end{aligned} $ | (13) |
式中:PLSA、PPDA分别表示混合料中LSA和PDA所占的比例;VT(PDA)表示PDA经捣实后的总体积;VPDA表示PDA颗粒的体积;ηLSA、ηDASR、ηPDA分别表示LSA、DASR和PDA经捣实后的空隙率。
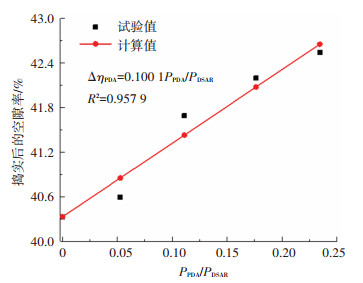
为了验证式(13)的合理性,根据《排水沥青路面设计与施工技术规范》(JTG/T 3350-03—2020)[18]和后续表 3,并由1.2.1节可知,PAC-13的主集料粒径DASR为4.75~13.2 mm,干涉集料粒径PDA为1.18~4.75 mm,PDA含量大致相当于DASR含量的5%~25%。设定集料的颗粒粒径为1.18~13.2 mm(不含有LSA和ICA),1.18~2.36 mm和2.36~4.75 mm两相邻粒径集料的相对比例为50/50,4.75~9.5 mm和9.5~13.2 mm两相邻粒径颗粒的相对比例也为50/50。根据《公路工程集料试验规程》(JTG E42—2005)[19],测得了集料捣实后空隙率随PPDA/PDASR的增加近似线性增大的变化关系,如图 7所示。将后续表 1和表 2的相关参数代入式(13)中,计算结果与实测值具有较高的吻合程度,如图 7所示,说明构建的式(13)是合理的。
|
图 7 集料捣实空隙率随PPDA/PDASR的变化关系 Fig. 7 Voids of compacted aggregate changing with the value of PPDA/PDASR |
| 表 1 集料主要技术指标 Tab. 1 Main technical indexes of aggregate |
| 表 2 经捣实后集料的空隙率和密度 Tab. 2 Aggregate void ratio and density after compaction |
| 表 3 多孔沥青混合料的级配组成 Tab. 3 Gradation of PAC for test |
由式(10)~(13)可以看出,改进后的DASR法根据沥青混合料实际情况,同时考虑了ICA、LSA和PDA对主骨架空隙率的影响。因此,在构建PAC混合料矿料间隙率的物理模型时,不仅要考虑ICA的填充作用,同时还需要进一步考虑LSA的取代作用和PDA的干涉作用对矿料间隙率的影响。
2 矿料间隙率物理模型的构建 2.1 颗粒堆积原理目前,有关固体颗粒堆积理论的研究可分为两类:一是研究评估颗粒特性、容器和堆积方法等变量如何控制颗粒的堆积;二是研究堆积体的颗粒排列和孔隙结构以解释颗粒的堆积行为[20-21]。大量研究表明,堆积体的空隙结构与颗粒形状、尺寸、粒径分布等特性存在高度相关性。
文献[22]提出了一种基于二元混合物的多组分球形颗粒堆积体空隙率的数学方法。其他学者[16-17]均将集料简化为球体形状,在此基础上开展了较为深入的研究,表明固体颗粒的堆积主要包括填充和占据两种机制。对于填充机制,新颗粒只是简单填充到已有大颗粒形成的骨架空隙中,而对骨架结构不会产生影响;若新的细小颗粒占比不多,该机制则是有效的,占据机制则不同,由于新加入的颗粒尺寸较大以至于不能完全填充到现有系统的骨架空隙中,因而新颗粒的加入会改变原有系统的骨架结构,如图 3所示。基于该机制,线性堆积模型得到了较快的发展[23],但该类模型涉及的未知变量较多(如颗粒间相互作用系数和协调数),且很难通过试验进行确定,应用受到很大限制。本文将在上述机制的基础上进行扩展,提出方便使用的矿料间隙率物理模型。
2.2 物理模型构建基于填充机制,如图 6所示,若混合料中只包含主集料DASR和间隙集料ICA,由体积设计法[24],可得
| $ \frac{P_{\mathrm{DASR}}}{\rho_{\mathrm{DASR}}}\left(\frac{V_{\mathrm{V}(\mathrm{DASR})}-V_{\mathrm{VMA}}}{V_{\mathrm{T}(\mathrm{DASR})}}\right)=\frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}} $ | (14) |
式中:PDASR和PICA分别表示DASR和ICA所占的百分比,有PDASR+PICA=100%;ρDASR表示DASR捣实后的密度;γICA表示ICA的合成毛体积相对密度;VT(DASR)和VV(DASR)分别表示DASR捣实后的总体积和空隙体积;VVMA表示矿料间隙体积。
当取VT(DASR)= 1.0,则式(14)可改写为
| $ \frac{P_{\mathrm{DASR}}}{\rho_{\mathrm{DASR}}}\left(\eta_{\mathrm{DASR}}-\eta_{1(\mathrm{VMA})}\right)=\frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}} $ | (15) |
式中:ηDASR表示DASR形成的主骨架结构的空隙率,η1(VMA)表示混合料中只包含DASR和ICA时的矿料间隙率。
由式(15),可得
| $ \eta_{1(\text {VMA})}=\eta_{\mathrm{DASR}}-\frac{\rho_{\mathrm{DASR}}}{P_{\mathrm{DASR}}} \frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}} $ | (16) |
当混合料中含有PDA时,DASR就会受到干涉发生移位,不仅会影响主骨架结构,也会影响主骨架结构的空隙率,如图 3所示。也就是说,主骨架空隙的变化与PDA所占的比例有关。对于混合料中只包括DASR、PDA和ICA的情况,考虑到PDA干涉后不仅会占据部分主骨架空隙,同时还会使得主骨架的空隙率有所增大,依据式(13)和式(15)构建相应干涉模型的表达式为
| $ \frac{P_{\mathrm{DASR}}}{\rho_{\mathrm{DASR}}}\left(\eta_{\mathrm{DASR}}-\eta_{2(\mathrm{VMA})}\right)=\frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}}+\frac{P_{\mathrm{PDA}}}{\gamma_{\mathrm{PDA}}}-\eta_{\mathrm{PDA}} P_{\mathrm{PDA}} $ | (17) |
式中:ρPDA、ηPDA分别为PDA捣实后的密度和空隙率;η2(VMA)表示混合料中只包含DASR、PDA和ICA的矿料间隙率,PDASR+PPDA+PICA=100%。
由式(17),可得
| $ \eta_{2(\mathrm{VMA})}=\eta_{\mathrm{DASR}}-\frac{\rho_{\mathrm{DASR}}}{P_{\mathrm{DASR}}}\left(\frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}}+\frac{P_{\mathrm{PDA}}}{\gamma_{\mathrm{PDA}}}-\eta_{\mathrm{PDA}} P_{\mathrm{PDA}}\right) $ | (18) |
联立式(16)和式(18),可得由于PDA作用造成骨架空隙率增加部分Δη2的表达式为
| $ \begin{aligned} \Delta \eta_{2}=&\left(\eta_{2(\mathrm{VMA})}-\eta_{1(\mathrm{VMA})}\right)=\\ & \frac{\rho_{\mathrm{DASR}}}{P_{\mathrm{DASR}}}\left(\eta_{\mathrm{PDA}} P_{\mathrm{PDA}}-\frac{P_{\mathrm{PDA}}}{\gamma_{\mathrm{PDA}}}\right) \end{aligned} $ | (19) |
如果混合料中只有DASR,则矿料间隙率即为DASR经捣实后的空隙率ηDASR。当混合料中只包含DASR和LSA时,LSA的存在将一定程度上占据部分DASR的位置并形成的空隙。由于LSA颗粒较大,可形成较大的空隙结构,也就是说LSA取代部分DASR后一定程度上也会增加主骨架结构的空隙率,依据式(12),构建相应取代模型的表达式为
| $ \frac{P_{\mathrm{DASR}}}{\rho_{\mathrm{DASR}}} \eta_{3(\mathrm{VMA})}=\frac{P_{\mathrm{DASR}}+P_{\mathrm{LSA}}}{\rho_{\mathrm{DASR}}} \eta_{\mathrm{DASR}}+\left(\eta_{\mathrm{LSA}}-\eta_{\mathrm{DASR}}\right) P_{\mathrm{LSA}} $ | (20) |
式中:η3(VMA)表示混合料中只包含LSA和DASR时的矿料间隙率,PLSA+PDASR=100%;ηLSA表示LSA捣实后的空隙率。
由式(20),可得
| $ \eta_{3(\mathrm{VMA})}=\eta_{\mathrm{DASR}}+\frac{P_{\mathrm{LSA}}}{P_{\mathrm{DASR}}}\left[\eta_{\mathrm{DASR}}+\rho_{\mathrm{DASR}}\left(\eta_{\mathrm{LSA}}-\eta_{\mathrm{DASR}}\right)\right] $ | (21) |
由LSA所致主骨架空隙率增加部分Δη3的表达式为
| $ \begin{aligned} \Delta \eta_{3} =&\eta_{3(\mathrm{VMA})}-\eta_{\mathrm{DASR}}=\\ & \frac{P_{\mathrm{LSA}}}{P_{\mathrm{DASR}}}\left[\eta_{\mathrm{DASR}}+\rho_{\mathrm{DASR}}\left(\eta_{\mathrm{LSA}}-\eta_{\mathrm{DASR}}\right)\right] \end{aligned} $ | (22) |
对于PAC混合料整体而言,结合式(16)、(19)、(22),可得到新的矿料间隙率ηVMA的表达式为
| $ \begin{aligned} \eta_{\mathrm{VMA}}=&\left(P_{\mathrm{DASR}}+P_{\mathrm{ICA}}\right) \eta_{1(\mathrm{VMA})}+P_{\mathrm{PDA}} \Delta \eta_{2}+P_{\mathrm{LSA}} \Delta \eta_{3}=\\ &\left(P_{\mathrm{DASR}}+P_{\mathrm{ICA}}\right)\left(\eta_{\mathrm{DASR}}-\frac{\rho_{\mathrm{DASR}}}{P_{\mathrm{DASR}}} \frac{P_{\mathrm{ICA}}}{\gamma_{\mathrm{ICA}}}\right)+\\ & P_{\mathrm{PDA}} \frac{\rho_{\mathrm{PDA}}}{P_{\mathrm{DASR}}}\left(P_{\mathrm{PDA}} \eta_{\mathrm{PDA}}-\frac{P_{\mathrm{PDA}}}{\gamma_{\mathrm{PDA}}}\right)+\\ & \frac{P_{\mathrm{LSA}}}{P_{\mathrm{DASR}}}\left[\eta_{\mathrm{DASR}}+\rho_{\mathrm{DASR}}\left(\eta_{\mathrm{LSA}}-\eta_{\mathrm{DASR}}\right)\right] P_{\mathrm{LSA}} \end{aligned} $ | (23) |
式中:右边第1项表示基于ICA的填充作用确定的矿料间隙率,第2项和第3项分别表示PDA的的干涉作用和LSA的取代作用造成主骨架空隙率增加的部分,PLSA+PDASR+PPDA+PICA=100%。
当沥青混合料中DASR包括多个尺寸粒径的集料时,其捣实后的毛体积密度ρDASR和空隙率ηDASR可采用加权平均的方法进行计算:
| $ \rho_{\mathrm{DASR}} =\sum\limits_{i=1}^{n} P_{\mathrm{D} i} \rho_{\mathrm{D} i} / \sum\limits_{i=1}^{n} P_{\mathrm{D} i} $ | (24) |
| $ \eta_{\mathrm{DASR}} =\sum\limits_{i=1}^{n} P_{\mathrm{D} i} \eta_{\mathrm{D} i} / \sum\limits_{i=1}^{n} P_{\mathrm{D} i} $ | (25) |
式中:PDi表示DASR中某一尺寸粒径集料所占百分比;ρDi、ηDi分别表示DASR中某一尺寸粒径集料捣实后的毛体积密度和空隙率。
3 模型验证及讨论 3.1 室内测试与验证本文试验中粗、细集料均采用玄武岩,填料为普通石灰岩矿粉,矿粉的表观相对密度为2.753。根据《公路工程集料试验规程》(JTG E42—2005)[19],测得集料的主要技术指标,见表 1。将目标集料烘干后放入的钢壁筒内,经捣实后测的目标集料的密度和空隙率,见表 2。为避免PAC混合料黏结性不足,采用高黏度改性沥青来提高混合料的抗变形和抗裂性能,即由SBS改性沥青中加入8.7%的高黏剂制备而成(60 ℃动力黏度为725 kPa·s),拌和时并掺入混合料总质量0.1%的聚酯纤维。
集料的密度ρTA和空隙率ηTA表达式分别为
| $ \rho_{\mathrm{TA}}=m_{\mathrm{TA}} / V_{\mathrm{TA}} $ | (26) |
| $ \eta_{\mathrm{TA}}=\left(1-\rho_{\mathrm{TA}} / \gamma_{\mathrm{TA}}\right) \times 100 $ | (27) |
式中:γTA为粗集料的毛体积相对密度或细集料的表观密度,mTA为粗集料或细集料的质量。
按表 3中的矿料级配和沥青用量,采用标准马歇尔击实试验制备PAC混合料试件,采用体积法测得了混合料空隙率和毛体积相对密度。由1.2.1节可知,PAC-13和PAC-10的主集料粒径DASR分别为4.75~13.2 mm和2.36~9.5 mm,PDA的粒径分别为1.18~4.75 mm和0.6~2.36 mm。由于PAC-13和PAC-10的DASR和PDA均含有两种粒径的集料,可根据所占比例采用加权平均的方法分别求得相应的密度和空隙率,见式(24)、(25)。
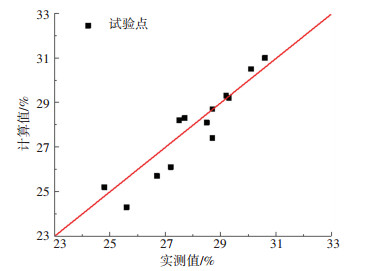
将集料物理参数(如:各档集料的所占比例、毛体积密度、捣实密度和捣实后空隙率等)代入到模型(23)中,即可计算得到不同级配沥青混合料的矿料间隙率,见表 3。将所建PAC混合料矿料间隙率模型的计算值与试验结果进行对比,如图 8所示。可以看出,图中所有的数据点都以1∶1的梯度紧密分布,相关性系数R2为0.904 6,平均绝对误差只有2.20%,说明本文所建的矿料间隙率物理模型能够较准确地反映多孔沥青混合料的空隙率大小。
|
图 8 矿料间隙率计算值与实测结果的对比 Fig. 8 Comparison between predicted and test results for VMA |
在沥青的种类及压实工艺等因素相同的情况下,PAC混合料矿料间隙率主要取决于集料的级配、棱角特征和矿料密度等因素,以下主要从集料级配组成的角度分析矿料间隙率的变化规律。
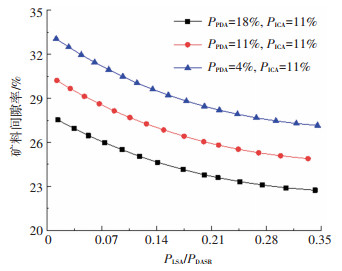
以PAC-13为研究对象,保持PDA与ICA含量不变的情况下(即PPDA+ PICA为定值),图 9给出了LSA与DASR所占比例的比值变化对矿料间隙率ηVMA影响的关系曲线。由图 9可以看出,ηVMA随着PLSA /PDASR的增加逐渐衰减,且衰减的幅度逐渐减小。虽然LSA含量的增加一定程度上会使得混合料的骨架空隙增加,但空隙尺寸的增加会导致部分PDA可完全融入到骨架空隙中无法起到干涉作用,从而导致了矿料间隙率的减小。当ICA含量一定且PLAS /PDASR相等时,矿料间隙率随着PDA含量的增加而减小;当PLSA /PDASR =0.2时,PDA含量增加7.0%,意味着LSA和PAD的含量分别减小了1.17%和5.83%,由于LSA含量减小和PDA含量减小导致矿料间隙率分别减小了0.52%和2.49%,PDA含量增加导致矿料间隙率增加了0.64%,造成矿料间隙率减小了2.38%。由此可知,LSA与DASR含量增加使得骨架空隙增加的部分远大于PDA减少导致空隙减少的部分。
|
图 9 LSA含量对矿料间隙率的影响 Fig. 9 Effects of LSA content for VMA |
保持LSA和ICA含量不变的情况下,ηVMA随着PPDA/PDASR变化的关系曲线,如图 10所示。可以看出,ηVMA随着PPDA /PDASR的增加逐渐减小,主要是因为DASR含量减小使骨架空隙减小的部分远大于PDA含量增加导致空隙增加的部分。当LSA含量一定且PPDA /PDASR相等的情况下,ηVMA随着ICA含量的减小而增加,原因在于ICA主要是填充主骨架空隙,所以ICA含量越高,矿料间隙率越小。

|
图 10 PDA含量对矿料间隙率的影响 Fig. 10 Effects of PDA content for VMA |
保持LSA和DASR含量不变的情况下,ηVMA随着PPDA/PICA变化的关系曲线,如图 11所示。由图 11可知,ηVMA随着PPDA/PICA的增加而增大且增加的幅度逐渐减缓,主要是因为PPDA/PICA的增加意味着PDA含量的增加和ICA含量的减小,由于PDA的干涉作用和ICA的充填作用,从而造成了矿料间隙率的增加。LSA含量一定且PPDA/PICA相等的情况下,矿量间隙率随着DASR含量的增加而增大;当PPDA/PICA=0.5时,DASR含量增加4.0%,意味着PDA和ICA含量的分别减小了1.33%和2.67%,由于DASR含量增加、PDA含量减小和ICA含量减小导致矿量间隙率分别增加了1.67%、0.12%和1.32%,使得矿料间隙率共增加了3.1%。由此可以看出,主集料DASR形成的骨架空隙和间隙集料ICA的填充作用是影响矿料间隙率的主要因素。

|
图 11 ICA含量对矿料间隙率的影响 Fig. 11 Effects of ICA content for VMA |
1) 针对多孔沥青混合料的多孔性特点,将矿料划分为较大粒径集料LSA、主集料DASR、干涉集料PDA和间隙集料ICA四部分,分析了DASR形成的主骨架空隙结构,确定了LSA、DASR、PDA和ICA的界限尺寸,提出了确定主骨架空隙率的方法。
2) ICA主要是填充DASR形成的主骨架空隙,PDA的干涉作用会导致主骨架结构空隙率有所增加;由于LSA可以形成较大空隙,一定程度上也会增加骨架结构的空隙体积。通过考虑ICA、PDA和LSA对DASR主骨架结构不同的作用机制,构建了沥青混合料矿料间隙率的物理模型,并通过多种级配多孔沥青混合料的试验结果验证了所建模型的合理性和有效性。
3) 在PDA和ICA含量不变的情况下,矿料间隙率随着PLSA /PDASR的增加而减小,且幅度逐渐减缓;LSA和ICA含量不变的情况下,矿料间隙率随着PPDA /PDASR含量增加而减小;在LSA和DASR含量不变的情况下,矿料间隙率随着PPDA /PICA含量的增加而增大。
4) 对于DASR形成的主骨架结构,LSA、PDA和ICA对PAC混合料矿料间隙率的影响具有不同的方向性。根据级配曲线可确定上述4种集料的分界尺寸,将集料的相关物理参数代入所提出的矿料间隙率物理模型,便可判断所选级配是否满足混合料目标空隙率的要求,很大程度上减少了PAC混合料目标配合比设计的试验量。
| [1] |
公路沥青路面施工技术规范: JTG F40—2004[S]. 北京: 人民交通出版社, 2004 Technical specifications for construction of highway asphalt pavement: JTG F40—2004[S]. Beijing: China Communications Press, 2004 |
| [2] |
陈俊, 姚成, 周若愚, 等. 多孔沥青混合料渗水性能的方向差异性及其受空隙结构的影响[J]. 东南大学学报(自然科学版), 2018, 48(5): 920. CHEN Jun, YAO Cheng, ZHOU Ruoyu, et al. Directional differentce of water permeability of porous asphalt mixture and influence of pore structure[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(5): 920. |
| [3] |
CHU L, FWA T F, TAN K H. Eveluation of wearing course mix designs on sound absorption improvement of porous asphalt pavement[J]. Construction and Building Materials, 2017, 141: 402. DOI:10.1016/j.conbuildmat.2017.03.027 |
| [4] |
王宏畅, 周明刚. 多空沥青混合料排水及抗堵塞性能研究[J]. 建筑材料学报, 2016, 19(2): 413. WANG Hongchang, ZHOU Minggang. Drain ability and anti-clogging of porous asphalt mixture[J]. Journal of Building Materials, 2016, 19(2): 413. DOI:10.3969/j.issn.1007-9629.2016.02.035 |
| [5] |
PARTL M N, PASQUINI E, CANESTRARI F, et al. Water and thermal sensitivity of open graded asphalt rubber mixtures[J]. Construction and Building Materials, 2010, 24(3): 283. DOI:10.1016/j.conbuildmat.2009.08.041 |
| [6] |
ZAUMANIS M, POULIKAKOS L D, PARTL M N. Performance-based design of asphalt mixtures and review of key parameters[J]. Materials and Design, 2018, 141: 185. DOI:10.1016/j.matdes.2017.12.035 |
| [7] |
KANDHAL P S, COOLEY L A. Coarse-versus fine-graded superpave mixtures: comparative evaluation of resistance to rutting[J]. Transportation Research Record: Journal of the Transportation Research Board, 2002, 1789: 216. DOI:10.3141/1789-24 |
| [8] |
ELLIOTT R P, FORDJR M C, GHANIM M, et al. Effect of aggregate gradation variation on asphalt concrete mix properties[J]. Transportation Research Record, 1991, 1317: 52. |
| [9] |
FULLER W B, THOMPSON S E. The laws of proportioning concrete[J]. Thansactions of the American Society of Civil Engineers, 1907, 2: 67. |
| [10] |
VAVRIK W R, PINE W J, CARPENTER S H. Aggregate blending for asphalt mix design: Bailey method[J]. Transportation Research Record: Journal of the Transportation Research Board, 2002, 1789: 146. DOI:10.3141/1789-16 |
| [11] |
KIM S, GRARIN A, ROQUE R, et al. Identification and assessment of the dominant aggregate size range (DASR) of asphalt mixture[J]. Journal of Asphalt Paving Technologies, 2006, 75: 789. |
| [12] |
ROQUE R, BIRGISSON B, KIM S, et al. Development of mix design guidelines for improved performance of asphalt mixtures[R]. Tallahassee: Florida Department of Transportation, 2006.
|
| [13] |
KIM S, ROQUE R, GRARIN A, et al. Laboratory evaluation for rutting performance based on the DASR prosity of asphalt mixture[J]. Road Materials and Pavement Design, 2008, 9(3): 421. DOI:10.1080/14680629.2008.9690126 |
| [14] |
KIM S, ROQUE R, BIRGISSON B, et al. Porosity of the dominant aggregate size range to evaluate coarse aggregate structure of asphalt mixtures[J]. Journal of Materials in Civil Engineering, 2009, 21(1): 32. DOI:10.1061/(ASCE)0899-1561(2009)21:1(32) |
| [15] |
CHUN S, KIM K, PARK B, et al. Evaluation of the effect of segregation on coarse aggregate structure and rutting potential of asphalt mixtures using dominant aggregate size range (DASR) approach[J]. KSCE Journal of Civil Engineering, 2018, 22(1): 125. DOI:10.1007/s12205-017-1372-5 |
| [16] |
GRARIN A, ROQUE R, KIM S, et al. Disruption factor of asphalt mixtures[J]. International Journal of Pavement Engineering, 2013, 14(5): 472. DOI:10.1080/10298436.2012.727992 |
| [17] |
CAI X, WU K H, HUANG W K, et al. Study on the correlation between aggregate skeleton characteristics and rutting performance of asphalt mixture[J]. Materials and Structures, 2018, 46(8): 294. |
| [18] |
排水沥青路面设计与施工技术规范: JTG/T 3350-03—2020[S]. 北京: 人民交通出版社, 2020 Technical specifications for design and construction of porous asphalt pavement: JTG/T 3350-03—2020[S]. Beijing: China Communications Press, 2020 |
| [19] |
公路工程集料试验规程: JTG E42—2005[S]. 北京: 人民交通出版社, 2005 Specifications for design of highway asphalt pavement: JTG E42—2005[S]. Beijing: China Communications Press, 2005 |
| [20] |
FURNAS C C. Grading aggregates Ⅰ—mathematical relations for beds of broken solids of maximum density[J]. Industrial and Engineering Chemistry, 1931, 23(9): 1052. DOI:10.1021/ie50261a017 |
| [21] |
ZHAO Y, XU T, HUANG X, et al. Gradation design of the aggregate skeleton in asphalt mixture[J]. Journal of Testing and Evaluation, 2012, 40(7): 1. |
| [22] |
WESTMAN A E R. The packing of particles: empirical equations for intermediate diameter ratios[J]. Journal of the American Ceramic Society, 1936, 19: 127. DOI:10.1111/j.1151-2916.1936.tb19809.x |
| [23] |
POURANIAN M R, HADDOCK J E. Determination of voids in the mineral aggregate and aggregate skeleton characteristics of asphalt mixtures using a linear-mixture packing model[J]. Construction and Building Materials, 2018, 188: 292. DOI:10.1016/j.conbuildmat.2018.08.101 |
| [24] |
张肖宁, 郭祖辛, 吴旷怀. 按体积法设计沥青混合料[J]. 哈尔滨建筑大学学报, 1995, 28(2): 28. ZHANG Xiaoning, GUO Zuxin, WU Kuanghuai. Volume method of bituminous mixture design[J]. Journal of Harbin University of Architecture and Engineering, 1995, 28(2): 28. |
 2022, Vol. 54
2022, Vol. 54