2. 重庆交通大学 机电与车辆工程学院,重庆 400074
2. School of Mechatronics and Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China
风能作为可再生能源,越来越受到人们的重视,近年来,中国风电行业发展迅速,风力发电机装机容量逐年攀升,目前已处于世界第一[1-3]。然而,中国近年来极端气象灾害频发,在重庆、云南、湖南等华中和西南地区内陆风电场,冬季低温且潮湿,风力发电机易遭到覆冰灾害的影响[4-5]。结冰的风力机叶片不仅会使得输出功率降低,严重的会导致停机[6-7]。文献[8]显示1996年至2002年期间因为叶片覆冰导致芬兰某风电场风力发电机出现问题的时长达到8 000小时以上,约占低温故障总时长的70%。研究发现,风力发电机结冰导致年发电量(AEP)降低17%,空气动力学特性降低20%~50%[9]。
由于对风力发电机叶片进行人工覆冰试验耗费大量物力及财力,近年来,利用计算机技术对风力发电机覆冰进行预测研究成为了研究热点。利用计算机信息技术对叶片覆冰进行模拟计算,不仅可以为风力发电机翼型的防冰设计提供技术参考,对后续防冰除冰工作及设备维护也有重要的指导意义。早期芬兰技术研究中心Makkonen等[10-11]借鉴飞机覆冰数值模型开发了一套风力机覆冰代码TURBICE,该模型可计算得到不同温度下风力机的覆冰形状及质量。文献[12]对大型水平轴“NREL 5MW”风力发电机叶片的覆冰增长进行了数值计算发现,随着叶片几何参数的变化,覆冰的增长速率及冰形都有一定的改变。文献[13]对大型风力发电机叶片覆冰进行预测,并分析了覆冰后转矩及功率的损失,但其预测仍为二维模型,无法获得叶片整体覆冰增长趋势。文献[14]运用商用软件Fluent对水平轴风力发电机三维雨凇覆冰进行了数值计算及人工覆冰试验,然而该项研究仅针对小型风力发电机。文献[15]对常用于大型风力发电机的翼型覆冰进行了试验及仿真计算,但计算仍然停留在单翼型,无法了解整体叶片覆冰趋势。
风力发电机叶片的覆冰预测模型不仅要考虑其准确性,同时也应考虑时间和开销,目前研究其气流场的方法有:有限元法、有限体积法、有限差分法及边界元法。本文采用的边界元法计算风力发电机叶片覆冰流场,通过降维的方法,可将三/二维问题化为二/一维问题进行分析,具有计算量小,计算时间短的优点[16]。由于风力发电机叶片外部气流场可以近似看作二维流动,而大型风力发电机叶片的尺寸较大,进行三维叶片空气流场计算不仅耗费时间长,且需要较大的计算机存储空间,导致其三维覆冰模拟较难实现[17]。本文提出了一种切片-重构的方法,对风力发电机叶片进行切片得到数个二维截面,基于边界元法对叶片外部气流场进行计算,使用拉格朗日法跟踪水滴轨迹,通过优化选择时间步长,仿真模拟各二维风力发电机叶片切片的覆冰增长,最终通过截面覆冰重构,得到三维叶片雾凇覆冰图像。
1 风力发电机叶片气液两相流数值模型当风力发电机叶片在运转时,其外部气流场合速度为风速与该截面所拥有的线速度的相反值之和,称之为相对风速,也即来流合速度。同时,风力发电机在运行的过程中,其外部空间存在气液(空气-水滴)两相流,随着温度的降低,空气中的过冷却水滴撞击到风力机叶片表面冻结形成覆冰。研究叶片外部空气流场是研究过冷却水滴运动轨迹的基础,因此,首先要对外部流场的速度分布进行计算,再将水滴视为离散相,根据空气外流场速度分布进一步计算每个水滴的运动轨迹,得到水滴在叶片表面的局部碰撞率。
边界层理论表明,结构物大气绕流场可分为边界层内的层流或湍流区域,以及边界层以外的非黏性势流区域[18-19]。
1.1 外部空气流场求解如图 1所示,假设P为外部流场中的任一点(a、b、c、d、e、f),Q为边界上的点,在边界层以外的势流区,流体可以看作是理想流体,根据拉普拉斯方程:
| $ \left\{\begin{array}{l} \frac{\partial^{2} \phi}{\partial x^{2}}+\frac{\partial^{2} \phi}{\partial y^{2}}=0 \\ v_{x}=\frac{\partial \phi}{\partial x}, v_{y}=\frac{\partial \phi}{\partial y} \end{array}\right. $ | (1) |

|
图 1 风力发电机叶片截面边界元划分 Fig. 1 Boundary element division of wind turbine blade section |
式中:ϕ为速度势;vx,vy分别为沿x轴方向,y轴方向的来流速度。
边界条件:风力发电机叶片边界为壁面,流体不可穿透,因此流体在边界的法向速度为0,即
| $ \left\{\begin{array}{l} \frac{\partial \phi}{\partial n_{Q}}=0 \\ \phi=\varphi+\varPhi \end{array}\right. $ | (2) |
| $ q=\frac{\partial \varphi(Q)}{\partial n_{Q}}=-\frac{\partial \varPhi}{\partial n_{Q}}=-\vec{v}_{\infty} \cdot \vec{n}_{Q} $ | (3) |
式中:φ为扰动速度势,Ф为定常速度势,φ(Q)为边界上源点Q的扰动速度势函数,q为风力发电机叶片边界速度势函数的法向导数,
根据格林公式得到如下边界积分方程,即流场势函数求解控制方程:
| $ \begin{aligned} \varphi(P)=& \int_{\varGamma}\left[\varphi^{*}(P, Q) \frac{\partial \varphi}{\partial n}(Q)-\right.\\ &\left.\varphi(Q) \frac{\partial \varphi^{*}}{\partial n}(P, Q)\right] \mathrm{d} \varGamma(Q) \end{aligned} $ | (4) |
| $ \varphi^{*}(P, Q)=\frac{1}{2 {\rm{ \mathsf{ π} }}} \ln \frac{1}{r(P, Q)} $ | (5) |
式中:φ*(P, Q)为拉普拉斯算子基本解,r(P, Q)为P点与Q点之间的距离。
需要确定边界上的势函数值,对于边界点P,为避免出现P与Q重合而产生奇异性,式(5)化为
| $ \begin{aligned} C(P) \varphi(P)=& \int_{\varGamma}\left[\varphi^{*}(P, Q) \frac{\partial \varphi}{\partial n}(Q)-\right.\\ &\left.\varphi(Q) \frac{\partial \varphi^{*}}{\partial n}(P, Q)\right] \mathrm{d} \varGamma(Q) \end{aligned} $ | (6) |
式中C(P)是与P点处的边界几何形状有关的常数,对于光滑边界,C(P)=1/2。
本文采用的边界元法,将风力发电机叶片的边界分割成n个边界单元,整个边界上的积分以n个边界单元上的积分的和来表示,且将节点取为微元中点。通过常量单元离散,假定每个边界单元上的势函数值与其法向导数值在边界单元上为常数,且等于节点的值。式(6)可离散为
| $ \sum\limits_{j=1}^{n} \varphi_{i j} H_{i j}=\sum\limits_{j=1}^{n} \frac{\partial \varphi}{\partial n}(Q) G_{i j} $ | (7) |
其中:
| $ H_{i j}=\hat{H}_{i j}+\frac{1}{2} \delta_{i j} $ | (8) |
| $ \hat{H}_{i j}=\int_{\varGamma_{j}} \frac{\partial \varphi^{*}}{\partial n}(P, Q) \mathrm{d} \varGamma(Q) $ | (9) |
| $ G_{i j}=\int_{\varGamma_{j}} \varphi^{*}(P, Q) \mathrm{d} \varGamma(Q) $ | (10) |
式中:i为P点所在微元序号,j为Q点所在微元序号,δij为克罗内克δ。
对于n个节点,得到联立的一次方程组,用矩阵形式可表示为
| $ \mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{\varphi }} = \mathit{\boldsymbol{G}} \cdot \mathit{\boldsymbol{Q}} $ | (11) |
式中:H和G是n×n阶的系数矩阵,φ和Q分别是边界单元节点的扰动势函数值和扰动势函数的法向导数值的列向量。
对于非边界单元,式(6)可离散为
| $ \varphi_{i}=\sum\limits_{j=1}^{n}\left(q_{j} G_{i j}-\varphi_{j} H_{i j}\right) $ | (12) |
通过式(2)~(12),采用高斯积分公式求解边界积分方程,即可求出流域内任意位置的气流速度。
1.2 边界层内流场求解临界边界层动量厚度雷诺数可作为判断流体从层流发展为湍流的准则数[17]:
| $ \left\{\begin{array}{l} R_{\Theta}=\frac{U_{\mathrm{e}} \theta}{\upsilon} \\ R_{\Theta_{\mathrm{tr}}}=\frac{U_{\mathrm{e}} \theta_{\mathrm{tr}}}{\upsilon}=430 \\ \upsilon=\frac{\mu}{\rho_{\mathrm{a}}} \end{array}\right. $ | (13) |
式中:θ为风力发电机叶片表面边界层动量厚度;θtr为层流发展为湍流的分界点的边界层动量厚度;μ为空气黏度系数;ρa为空气的密度;Ue为边界层速度,此处定义为99%来流速度。
卡门边界层动量积分关系式[20]为
| $ \frac{\mathrm{d}}{\mathrm{d} x} \int_{0}^{\delta} v^{2} \mathrm{~d} y-U_{\mathrm{e}} \frac{\mathrm{d}}{\mathrm{d} x}\left(\int_{0}^{\delta} v \mathrm{~d} y\right)=-\left(\frac{\tau_{0}}{\rho_{\mathrm{a}}}+\frac{\delta}{\rho_{\mathrm{a}}} \frac{\partial p}{\partial x}\right) $ | (14) |
式中:p为压强,δ为边界层厚度。
边界层厚度δ可由边界层动量厚度θl估算[21]:
| $ \delta=8.5 \theta_{1} $ | (15) |
边界层动量厚度θl[22]的表达式为
| $ \left\{\begin{array}{l} \theta_{\text {1_laminar }}=\left(\frac{0.45 \upsilon}{U_{\mathrm{e}}{}^{6}} \int_{0}^{s} U_{\mathrm{e}}{}^{5} \mathrm{~d} s\right)^{0.5} \\ \theta_{\text {1_turbulent }}=\left(\frac{0.015\ 6 \upsilon^{0.5}}{U_{\mathrm{e}}{}^{4.11}} \int_{s t r}^{s} U_{\mathrm{e}}{}^{3.86} \mathrm{~d} s\right)^{0.8}+\theta_{1}(s t r) \end{array}\right. $ | (16) |
式中:str表示层流与湍流分界点位置,θi(str)为分界点处的边界层动量厚度。
| $ \left\{\begin{array}{l} \tau_{\text {0_laminar }}=\frac{\mu(B+0.09)^{0.62} U_{\mathrm{e}}}{\theta_{1}} \\ \tau_{{\text {0_turbulent }}}=\frac{\rho U_{\mathrm{e}}{}^{2}}{2 C_{f}} \end{array}\right. $ | (17) |
| $ \left\{\begin{aligned} &v_{\text {laminar }}= U_{\mathrm{e}}\left[\frac{2 h}{\delta}-2\left(\frac{h}{\delta}\right)^{3}+\left(\frac{h}{\delta}\right)^{4}+\right.\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\frac{1}{6} \frac{\delta^{2}}{\upsilon} \cdot \frac{\mathrm{d} U_{\mathrm{e}}}{\mathrm{d} s} \cdot \frac{h}{\delta} \cdot\left(1-\frac{h}{\delta}\right)^{3}\right] \\ &v_{\text {turbulent }}= U_{\mathrm{e}}\left(\frac{h}{\delta}\right)^{\frac{1}{7}} \end{aligned}\right. $ | (18) |
式中:h为距离风力发电机叶片边界的垂直距离,ds为边界微元单位长度。
求解式(13)~(18),即可求出边界层内气流速度。
1.3 过冷却水滴轨迹求解本文计算水滴轨迹时利用拉格朗日法,为了得到过冷却水滴在风力发电机叶片表面的局部碰撞率,需要对过冷却水滴运动轨迹进行计算。假设水滴在距离障碍物较远时(设水滴从距离叶片前缘10倍弦长处发射)与空气拥有相同的速度,靠近障碍物时,气流沿障碍物表面绕流,过冷却水滴轨迹由于惯性的作用,与气流轨迹产生偏差,此时对过冷却水滴进行受力分析后可知,过冷却水滴在运动过程中主要受到重力FG、气流浮力Fb、水滴前后的压差阻力Fg、表观质量力FM、空气黏性阻力Fd的作用,其中占主要作用的是空气黏性阻力Fd,此处仅考虑空气黏性阻力的作用[25],根据牛顿第二定律,得
| $ F=m_{\mathrm{d}} a_{\mathrm{d}}=\frac{1}{2} \rho_{\mathrm{a}} S_{\mathrm{d}} C_{\mathrm{D}}\left|\vec{v}_{\mathrm{a}}-\vec{v}_{\mathrm{d}}\right|\left(\vec{v}_{\mathrm{a}}-\vec{v}_{\mathrm{d}}\right) $ | (19) |
其中:Sd为水滴投影面积,CD为空气阻力系数,
相对雷诺数表示为
| $ R e=\frac{2 R_{\mathrm{d}} \rho_{\mathrm{a}}\left|\vec{v}_{\mathrm{a}}-\vec{v}_{\mathrm{d}}\right|}{\mu} $ | (20) |
将式(20)代入式(19),得
| $ \frac{\mathrm{d}\overrightarrow{v}_{\mathrm{d}}}{\mathrm{d} t}=\frac{1}{k} \frac{C_{\mathrm{D}} R e}{24}\left(\vec{v}_{\mathrm{a}}-\vec{v}_{\mathrm{d}}\right) $ | (21) |
| $ \frac{C_{\mathrm{D}} R e}{24}=\left\{\begin{array}{l} 1+0.176 R e^{0.992\ 5}, 0 \leqslant {Re} \leqslant 1 \\ 1+0.166\ 7 R e^{0.671\ 2}, 1<{Re} \leqslant 800 \\ 1+0.028\ 13 R e^{0.932\ 3}, {Re}>800 \end{array}\right. $ | (22) |
k为运动水滴惯性的斯托克斯数,计算公式为
| $ k=\frac{2 R_{\mathrm{d}} \rho_{\mathrm{d}}}{9 \mu} $ | (23) |
使用差分法对式(19)求解,根据速度和加速度的一阶和二阶差分格式可得到水滴在tn时刻沿x轴方向的速度及加速度的表达式为
| $ \left\{\begin{array}{l} v_{\mathrm{d}\_x, n}=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{x_{n+1}-x_{n}}{\Delta t} \\ a_{\mathrm{d}\_x, n}=\frac{\mathrm{d}^{2} x}{\mathrm{~d} t^{2}}=\frac{x_{n+1}-2 x_{n}+x_{n-1}}{(\Delta t)^{2}} \end{array}\right. $ | (24) |
式中:Δt为时间步长,xn+1、xn和xn-1分别为水滴在tn+1时刻、tn时刻和tn-1时刻的位置的横坐标。同理可得水滴沿y轴方向的速度及加速度。
水滴轨迹追踪方程:
| $ \left\{\begin{array}{l} x_{n+1}=\frac{C_{\mathrm{D}, n} R e_{n}}{24 k}\left(v_{\mathrm{a}_{-} x, n}-v_{\mathrm{d}_{-} x, n}\right)+\left(2 x_{n}-x_{n-1}\right) \\ y_{n+1}=\frac{C_{\mathrm{D}, n} R e_{n}}{24 k}\left(v_{\mathrm{a}_{-} y, n}-v_{\mathrm{d}_{-}y, n}\right)+\left(2 y_{n}-y_{n-1}\right) \end{array}\right. $ | (25) |
式中:va_x, n和va_y, n分别为水滴在tn时刻所在位置的气流沿x、y轴方向的速度,vd_x, n和vd_y, n分别为水滴在tn时刻沿x、y轴方向的速度,yn+1、yn和yn-1分别为水滴在tn+1时刻、tn时刻和tn-1时刻的位置的纵坐标。
通过式(25)可根据水滴初始位置和初始速度求出水滴轨迹。
1.4 过冷却水滴碰撞率求解风力发电机叶片水滴局部碰撞率α1计算公式:
| $ \alpha_{1}=\frac{\mathrm{d} Y}{\mathrm{~d} L} $ | (26) |
式中:dL为两相邻水滴在叶片上碰撞位置在叶片表面的距离,dY为相邻水滴纵坐标之差。
基于以上算法计算得出的叶片表面气流场和水滴运动轨迹如图 2所示。

|
图 2 风力发电机叶片外部气液两相流 Fig. 2 Two-phase flow outside wind turbine blade |
在过冷却水滴碰撞到风力机叶片表面的过程中,忽略水滴飞溅的影响,因此捕获率α2≈1。覆冰是一种热交换的过程,在叶片表面水滴冻结过程中,可以通过传质传热平衡方程计算叶片表面的冻结率,传质传热方程表示为
| $ \left\{\begin{array}{l} m_{\mathrm{im}}+m_{\mathrm{in}}=m_{\mathrm{eva}}+m_{\mathrm{out}}+m_{\mathrm{ice}} \\ Q_{\mathrm{f}}+Q_{\mathrm{im}}+Q_{\mathrm{i}}+Q_{\mathrm{in}}=Q_{\mathrm{eva}}+Q_{\text {out }}+Q_{\mathrm{w}}+Q_{\mathrm{r}}+Q_{\mathrm{c}}+Q_{\mathrm{k}} \end{array}\right. $ | (27) |
其中:mim为撞击到叶片表面水滴的质量;min和mout为流入和流出的水质量;meva为蒸发水质量,mice为冻结水质量;Qf为空气摩擦叶片表面产生的热量;Qim为碰撞到叶片的过冷却水滴带来的动能转化的热量;Qi为水滴冻结成冰后释放的热量;Qin和Qout为流入水带来的能量和流出水带走的能量,设风力发电机叶片表面水膜温度Tw =0 ℃,则水膜的流动在微元之间不会产生能量交换,Qin、Qout均为0;Qeva为蒸发升华热损失;Qc为空气对流换热损失的热量;Qw为将叶片表面捕获的过冷却水滴加热到水膜温度所需要的热量;Qk为冰面传导热损失;Qr为长波辐射热损失。
忽略式(27)中的较小的热量项摩擦热Qf和传导热损失Qk,将各热量控制项表达式代入式(27)后可得到冻结率的计算方法:
| $ \begin{aligned} &\alpha_{3}=\frac{h_{\mathrm{c}}\left(T_{\mathrm{w}}-T\right)+\chi\left[e\left(T_{\mathrm{w}}\right)-e(T)\right]}{\alpha_{1} \cdot w \cdot V \cdot L_{\mathrm{f}}}+ \\ &\frac{-\frac{1}{2} \alpha_{1} \cdot w \cdot V^{3}+\alpha_{1} \cdot w \cdot V \cdot C_{\mathrm{w}}\left(T_{\mathrm{w}}-T\right)}{\alpha_{1} \cdot w \cdot V \cdot L_{\mathrm{f}}}+ \\ &\frac{4 \varepsilon \sigma_{\mathrm{r}} T^{3}\left(T_{\mathrm{w}}-T\right)}{\alpha_{1} \cdot w \cdot V \cdot L_{\mathrm{f}}} \end{aligned} $ | (28) |
风力发电机叶片表面微元控制体在覆冰速率dm/dt计算方法如下:
| $ \mathrm{d} m / \mathrm{d} t=V \cdot \alpha_{1} \cdot \alpha_{2} \cdot \alpha_{3} \cdot w \cdot \mathrm{d} s $ | (29) |
式中:V为水滴碰撞在叶片上的速度;w为空气液态水含量,kg/m3;ds为控制体微元的长度。
在覆冰不脱落的情况下,覆冰沿叶片法向生长,每个控制体微元的覆冰厚度增长速率为
| $ d=\frac{\mathrm{d} m}{\mathrm{~d} t} \cdot \frac{1}{\rho_{\text {ice }} \mathrm{d} s} $ | (30) |
式中:dt为覆冰时间步长;ρice为冰密度,其经验公式[26]为
| $ \rho_{\mathrm{ice}}=\left\{\begin{array}{l} 0.11 R^{0.76}, R \leqslant 10 \\ R(R+5.61)^{-1}, 10<R \leqslant 60 \\ 840, R>60 \end{array}\right. $ | (31) |
其中R为Macklin冰密度参数,R=-URd/TS,TS为叶片表面温度。
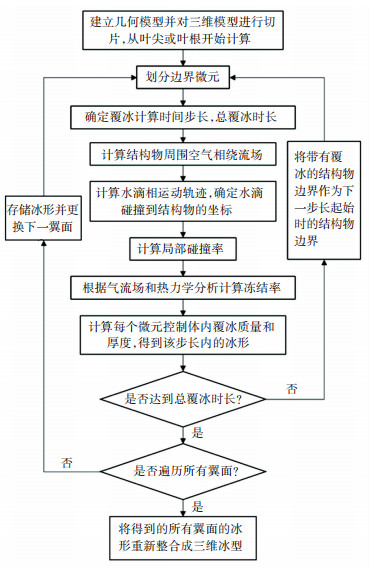
本文基于某型300 kW风力发电机叶片(叶片全长14.5 m,额定风速13 m/s)进行建模,将叶片等分为数个翼型截面进行分析,分别计算获得气-液两相流轨迹,并根据不同的截面选取合适的覆冰时间步长dt,计算覆冰厚度d,进而得出覆冰冰形,迭代直至达到总覆冰时长Tice=30 min,计算流程见图 3。
|
图 3 三维翼型覆冰仿真流程图 Fig. 3 Flow chart of 3D airfoil icing simulation |
水滴局部碰撞系数是覆冰计算中较为关键的参数,为了验证本文提出的计算空气流场和水滴轨迹最终获得碰撞率的方法的有效性,采用文献[27]中的相关参数对二维NACA0012翼型进行仿真。其中,来流合速度为44.39 m/s,液态水含量为0.78 g/m3,温度为-7.65 ℃,水滴中值直径为20 μm。并将试验结果及本文计算出的碰撞率计算结果进行比较。
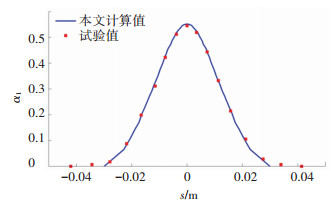
试验结果及计算结果如图 4所示,s表示碰撞点距离驻点的位置,翼型的水滴局部碰撞率呈现中间大两头小的现象。试验中s>0即叶片下表面碰撞范围略大于上表面而碰撞率略小于上表面,这是因为水滴在运动的过程中受重力的作用会稍向下偏移,但计算时由于忽略了重力的影响导致碰撞范围和碰撞率是上下对称的。通过对比可知,本文使用边界元法数值计算出的碰撞率与实验结果吻合良好。计算值的最大局部碰撞率略大于试验值,其他部分基本吻合。但计算的碰撞范围小于试验值,产生误差的可能原因有二:一是因为本文采用的离散方法求解流场积分的方程和求解水滴轨迹所取的时间步长导致的计算误差;二是因为文献中的覆冰试验不易控制,测量精度有一定的分散性,此外,在实际的覆冰试验中,水滴直径的取值分布在一定范围内,其中大尺寸水滴会导致试验中水滴碰撞范围增大,而本文采用单一水滴直径进行计算,水滴碰撞范围偏小,但从整体上看,本文数值计算的水滴局部碰撞率与试验值非常接近,表明使用该方法计算风力发电机叶片外部空气流场、水滴运动轨迹和水滴碰撞是合理的。
|
图 4 NACA0012翼型水滴局部碰撞率对比 Fig. 4 Comparison of local collision efficiency of water droplets for NACA0012 airfoil |
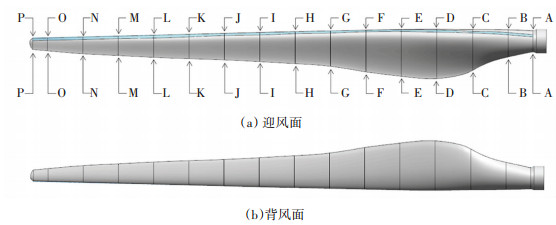
为了分析沿叶展方向的整体叶片覆冰增长特性和风速变化对覆冰形态及覆冰量的影响,本文选取了3个风速进行了冰形计算,其中,风速U分别为3、6、9 m/s,对应的风轮转速分别为27、32、38 r/min,液态水含量为0.3 g/m3,温度为-15 ℃,水滴中值直径为20 μm。图 5~7为计算得到的三维覆冰叶片。图 5显示,覆冰区域基本主要集中在迎风面,P—P截面(叶尖部)处背风面尚存在一定的覆冰,而J—J截面(叶中部)和E—E截面(叶根部)处,冰基本只存在于叶片的迎风面,在图 5(b)中几乎看不到冰的存在,这是因为沿着叶展方向翼型的不断变化和攻角的逐渐减小。同时,仿真结果显示,覆冰厚度沿着叶展的方向逐渐增大,距离叶根4 m处(E—E截面)的覆冰冰厚仅为0.15 mm,而距离叶根14.44 m处(P—P截面)的叶尖部位,冰厚达到22 mm。过冷却水滴在空气中受到惯性和阻力的影响向前运动,如果气流阻力占主要作用,则过冷却水滴将沿着气流的方向运动而绕过叶片,沿着叶展方向的翼型弦长和厚度逐渐减小,使阻力的作用逐渐减小而惯性的影响逐渐增大,同时由于沿着叶展方相对速度的增加,更加大了惯性对水滴运动的影响,最终导致了越靠近于叶尖部位截面的覆冰越厚。
|
图 5 覆冰后三维叶片成像(U=9 m/s) Fig. 5 3D images of blade icing (U=9 m/s) |

|
图 6 不同截面冰形(U=9 m/s) Fig. 6 Ice shapes with different sections (U=9 m/s) |
|
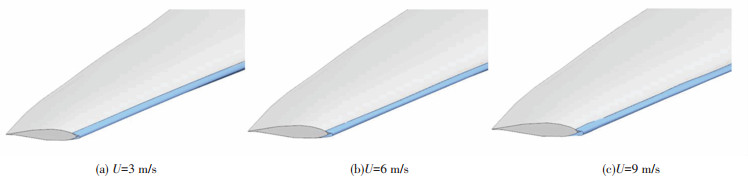
图 7 不同风速下叶尖成像 Fig. 7 Images of blade tip icing under different wind speeds |
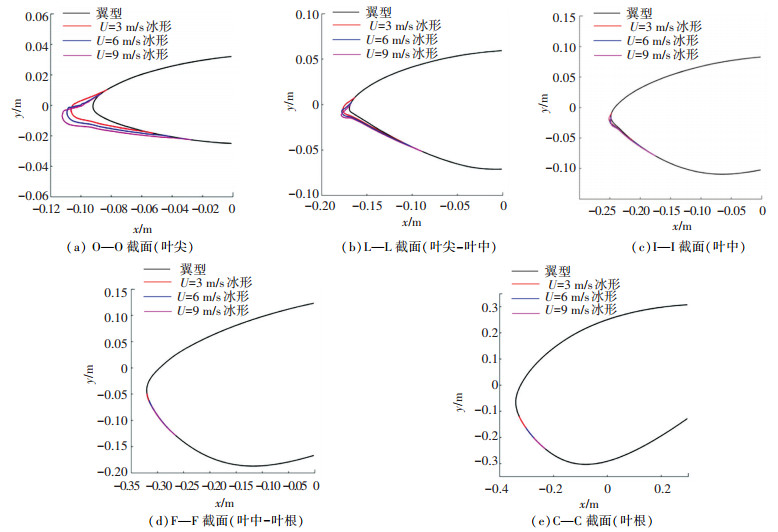
图 8显示了在不同风速下沿叶展方向不同部位的覆冰情况。图 8表明,风速的增大会使得水滴局部碰撞率增加,且单位时间内将有更多的水滴碰撞在截面上,导致覆冰厚度的增加,同时也会改变覆冰的面积和区域,在风速为3 m/s时,叶尖部位的覆冰区域明显整体小于风速为6 m/s和9 m/s时,这是由于随着风速的增大,叶片转速也将逐渐增大,气流合速度随之增大,过冷却水滴的惯性对水滴运动的影响逐渐增大,在风速较小时本会绕过叶片运动的水滴在风速增大后可能会碰撞在叶片上,导致碰撞面积的增大。但随着风速的增加,背风面覆冰区域逐渐减小,而迎风面覆冰区域逐渐增加,这是由风力发电机叶片的空气动力学特性决定的,随着风速和转速的增加,气流的攻角也会逐渐增加,使水滴碰撞区域从背风面向迎风面移动。同时,在叶中部和叶根部也出现了这种趋势,随着覆冰面积增大的同时,覆冰区域从背风面向迎风面移动,且随着截面位置向轮毂靠近,覆冰区域将只存在于叶片的迎风面,但与叶尖相比,叶根附近受风速的影响明显降低,在距离轮毂8 m(I—I截面)处,尚能看到明显的厚冰,而更靠近叶根的两个截面(F—F、C—C截面)几乎已经看不到冰。另外,风速的变化对冰形几乎没有影响,同一截面下,3种风速形成的覆冰冰形基本相同。为了分析风速对冰厚及覆冰增长速率的影响,设置沿截面法向的最大冰厚度为该处截面的冰厚。
|
图 8 风速对风力发电机叶片覆冰的影响 Fig. 8 Effect of wind speed on icing of wind turbine blades |
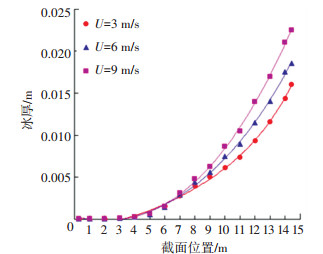
图 9显示了沿叶展方向的不同风速的冰厚变化,在3种风速下,覆冰厚度沿着叶展方向逐渐增大,在叶尖处达到最大厚度,从叶根部到叶片中部(距离轮毂0~6 m),3种风速下的冰厚度相差不大,即冰厚受风速的影响较小,且冰厚增长较缓,此时的过冷却水滴运动主要受阻力作用的影响,同时相对气流合速度差别不大,且该部分并没有明显的覆冰现象,从叶片中部到叶尖部分(距离轮毂6~14.6 m),水滴惯性逐渐占据主要作用,冰厚逐渐增大。随着风速的增大,冰厚沿叶展的增长也随之加快,冰厚差增大,一直到叶尖位置,当风速从3 m/s增加到9 m/s时,冰厚从16 mm增长到22 mm,冰厚增长速率从0.53 mm/min增长到0.73 mm/min。
|
图 9 不同风速下冰厚随叶展的变化 Fig. 9 Variation of icing thickness along the blade under different wind speeds |
综合图 8、9,受覆冰影响最大的区域是从叶片中部到叶片尖部,此趋势与文献[12]对兆瓦级大型风机的覆冰仿真中计算出的冰厚增长趋势基本一致。
4 结论基于切片-重构的思想,将风力发电机叶片沿叶展切为数个截面,对于每个截面,采用边界元法对风力发电机叶片周围大气流场进行计算,并用拉格朗日法对过冷却水滴的轨迹进行追踪。仿真得到每个截面的冰形,再将所有截面及冰形进行复原重构,最终建立了风力发电机叶片三维雾凇计算模型,同时对边界元算法用于计算大气流场的有效性进行了检验,分析了风速对叶片雾凇覆冰的影响规律。通过对比和分析可得出如下结论:
1) 在风力发电机叶片雾凇覆冰模拟中,碰撞率的计算至关重要,本文方法所得计算值和试验值十分接近,证明所提出的计算方法是合理且有效的。
2) 对某型300 kW风电设备叶片雾凇覆冰进行了仿真模拟,结果表明,雾凇覆冰冰形呈现流线型。覆冰主要聚积在叶片的前缘和迎风面靠近前缘位置,沿着叶展的方向,覆冰逐渐增厚,覆冰区域占比增大。
3) 风速对雾凇覆冰的影响主要在冰厚和覆冰区域,对冰形的变化无明显影响,且风速的变化对覆冰的影响在叶尖部位更加显著,在靠近叶根的位置,不同风速产生的冰厚都较薄,从叶中部到叶根,3种风速下冰厚的差别越来越大,直到叶尖冰厚度相差6 mm,且随着风速的增加,覆冰区域变大的同时,覆冰区域从背风面向迎风面移动。
4) 叶片的几何参数(弦长,厚度和扭转角)的变化,都会对覆冰的增长有一定的影响,这意味着通过优化叶片的几何参数,可以一定程度上降低其覆冰速率,从而减少寒冷潮湿地区安装在风电设备上的防冰和除冰装置的数量。
| [1] |
张毅. 小型风力发电机叶片覆冰的数值仿真及试验研究[D]. 重庆: 重庆大学, 2018 ZHANG Yi. Numerical study and test of icing on small wind turbine blades[D]. Chongqing: Chongqing University, 2018 |
| [2] |
蔡国伟, 雷宇航, 葛维春, 等. 高寒地区风电机组雷电防护研究综述[J]. 电工技术学报, 2019, 34(22): 4804. CAI Guowei, LEI Yuhang, GE Weichun, et al. Review of research on lightning protection for wind turbines in alpine areas[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4804. |
| [3] |
王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455. WANG Tao, ZHU Ziqiang, NIAN Heng. Review of operation technology of doubly-fed induction generator-based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455. |
| [4] |
SHU L, LIANG J, HU Q, et al. Study on small wind turbine icing and its performance[J]. Cold Regions Science & Technology, 2017, 134(2): 11. |
| [5] |
李瀚涛, 舒立春, 胡琴, 等. 考虑覆冰粗糙度影响的风力发电机叶片气动性能数值仿真[J]. 电工技术学报, 2018, 33(10): 91. LI Hantao, SHU Lichun, HU Qin, et al. Numerical simulation of wind turbine blades aerodynamic performance based on ice roughness effect[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 91. |
| [6] |
LAMRAOUI F, FORTIN G, BENOIT R, et al. Atmospheric icing impact on wind turbine production[J]. Cold Regions Science and Technology, 2014, 100: 36. DOI:10.1016/j.coldregions.2013.12.008 |
| [7] |
PARENT O, ILINCA A. Anti-icing and de-icing techniques for wind turbines: critical review[J]. Cold Regions Science and Technology, 2011, 65(1): 88. DOI:10.1016/j.coldregions.2010.01.005 |
| [8] |
LAAKSO T, HOLTTINEN H, RONSTEN G, et al. State-of-the-art of wind energy in cold climates[R]. Paris: International Energy Agency, 2003: 24
|
| [9] |
YIRTICI O, TUNCER I H, OZGEN S. Ice accretion prediction on wind turbines and consequent power losses[J]. Journal of Physics Conference, 2016, 753: 022022. DOI:10.1088/1742-6596/753/2/022022 |
| [10] |
MAKKONEN L, LAAKSO T, MARJANIEMI M, et al. Modelling and prevention of ice accretion on wind turbines[J]. Wind Engineering, 2001, 25(1): 3. DOI:10.1260/0309524011495791 |
| [11] |
MARJANIEMI M, MAKKONEN L, LAAKSO T. Turbice-the wind turbine blade icing model[C]// International Conference BOREAS V: Wind Power Production in Cold Climates. Helsinki: Finnish Meteorological Institute, 2000
|
| [12] |
VIRK M S, HOMOLA M C, NICKLASSON P J. Atmospheric icing on large wind turbine blades[J]. International Journal of Energy & Environment, 2012, 3(1): 1. |
| [13] |
郝艳捧, 刘国特, 阳林, 等. 风力机组叶片覆冰数值模拟及其气动载荷特性研究[J]. 电工技术学报, 2015, 30(10): 292. HAO Yanpeng, LIU Guote, YANG Lin, et al. Study on ice numerical simulation and its power loss characteristics for the blades of wind turbine[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 292. DOI:10.3969/j.issn.1000-6753.2015.10.039 |
| [14] |
梁健, 舒立春, 胡琴, 等. 风力机叶片雨淞覆冰的三维数值模拟及试验研究[J]. 中国电机工程学报, 2017, 37(15): 160. LIANG Jian, SHU Lichun, HU Qin, et al. 3-D numerical simulations and experiments on glaze ice accretion of wind turbine blades[J]. Proceedings of the CSEE, 2017, 37(15): 160. DOI:10.13334/j.0258-8013.pcsee.161239 |
| [15] |
JIN J Y, VIRK M S. Study of ice accretion and icing effects on aerodynamic characteristics of DU96 wind turbine blade profile[J]. Cold Regions Science and Technology, 2019, 160: 119. DOI:10.1016/j.coldregions.2019.01.011 |
| [16] |
汪泉霖. 输电线路导线无扭转覆冰过程的仿真实验方法研究[D]. 重庆: 重庆大学, 2018 WANG Quanlin. Study on the simulation experiment method of ice accretion on transmission line without torsion[D]. Chongqing: Chongqing University, 2018 |
| [17] |
刘国特. 风力发电机叶片覆冰预测与覆冰对机组出力影响研究[D]. 广州: 华南理工大学, 2014 LIU Guote. Study on the icing forecast of wind turbine blade and the influence of icing on the output of power generation[D]. Guangzhou: South China University of Technology, 2014 |
| [18] |
Jr ANDERSON J D. Fundamentals of aerodynamics[M]. 5th ed. New York: McGraw-Hill, 1984.
|
| [19] |
CHUNG T J. Computational fluid dynamics[M]. Cambridge: Cambridge University Press, 2002.
|
| [20] |
陈卓如. 工程流体力学[M]. 3版. 北京: 高等教育出版社, 2013. CHEN Zhuoru. Engineering fluid mechanics[M]. 3rd ed. Beijing: Higher Education Press, 2013. |
| [21] |
梁健. 风力机叶片覆冰预测模型研究[D]. 重庆: 重庆大学, 2017 LIANG Jian. Research on ice prediction model of wind turbine blade[D]. Chongqing: Chongqing University, 2017 |
| [22] |
THWAITES B. Approximate calculation of the laminar boundary layer[J]. Aeronautical Quarterly, 2016, 1(1): 245. |
| [23] |
WHITE F M. Viscous fluid flow[M]. 3rd ed. New York: McGraw-Hill, 2006.
|
| [24] |
MASSEY B S. Mechanics of fluids[M]. London: Van Nostrand Reinhold, 1979.
|
| [25] |
韩兴波, 蒋兴良, 毕聪来, 等. 基于分散型旋转圆导体的覆冰参数预测[J]. 电工技术学报, 2019, 34(5): 210. HAN Xingbo, JIANG Xingliang, BI Conglai, et al. Prediction of icing environment parameters based on decentralized rotating conductors[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 210. |
| [26] |
FU P. Modelling and simulation of the ice accretion process on fixed or rotating cylindrical objects by the boundary element method[D]. Chicoutimi: Universite du Quebec, 2004
|
| [27] |
SILVEIRA R A, MALISKA C R, ESTIVAM D A, et al. Evaluation of collection efficiency methods for icing analysis[C]//17th International Congress of Mechanical Engineering. Sao Paulo: Springer-Verlag, 2003: 10
|
 2022, Vol. 54
2022, Vol. 54


