2. 省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130
2. State Key Laboratory of Reliability and Intelligence of Electrical Equipment (Hebei University of Technology), Tianjin 300130, China
忆阻器作为一个新型纳米级二端口非线性电路元件[1],其在混沌电路构造[2-3]、人工神经网络[4-5]、逻辑运算[6]等工程领域均展现出了巨大的研究价值和应用前景。由于其具有可调的非线性以及特殊的记忆功能等特性,使得忆阻混沌系统通常可表现出更复杂的动力学特性以及更强的伪随机性,并且更容易产生依赖于忆阻器初始状态的多稳态[7-10]或超级多稳态特性[11-15]。因此,与普通混沌系统相比,基于忆阻器的混沌电路构造具有非常重要的研究意义。
近年来,多稳态和超级多稳态在忆阻系统中的研究已经成为了非线性动力学的一个重要的研究方向。多个吸引子的共存意味着系统可以提供多个正常的运行模式,即当系统遭到噪声或外部环境的干扰时,它可以切换到不同的稳定状态来保持系统的正常运行。同时,忆阻系统中的多稳定性也可以被用于信息工程领域中的加密信号或者伪随机数发生器。因此,具有多稳态或超级多稳态的忆阻系统的构建和研究具有理论意义与实际工程价值。2017年,Bao等[11]提出了一个基于忆阻器的退化的Jerk系统,该系统可以表现出4个线平衡和无限多吸引子共存的超级多稳态现象。同年,Bao等[12]利用忆阻器替换Yang系统中一个耦合电阻,提出了一个具有隐藏超级多稳态的四维超混沌系统。2019年,Mezatio等[13]提出了一个6D忆阻超混沌系统,该系统表现出了丰富的动力学特性,如隐藏超级多稳态、瞬态混沌以及偏移控制等行为。目前,虽然已有部分文献报道了具有超级多稳态的混沌或超混沌系统并探讨了其相关的动力学特性。然而,关于5D或更高维忆阻超混沌系统的构建及其复杂动力学特性的研究相对较少,尤其是在已有的文献中鲜有可同时表现出超级多稳态、首次在本文研究的共存超级多稳态现象、持续的混沌或超混沌行为以及偏移增量控制等丰富动力学特性的5D忆阻超混沌系统。因此,此类高维忆阻超混沌系统的构建对于非线性理论的研究和实际应用的探索具有非常重要的意义。
此外,从工程应用角度看,系统有时需要具有相同吸引子尺寸但极性相反的超混沌信号。通常,具有对称极性的系统可以产生对称的共存吸引子,而这些对称的共存吸引子往往是由单个双翼混沌吸引子破裂而产生的。因此,它们通常会伴随着系统混沌动力学的退化而不能更好地满足工程应用的需要。为了避免这一问题,Li等[16]提出了极性调整与偏置控制的方法来构建条件对称的混沌系统。此类系统可以确保系统在基本动力学特性不变的情况下为工程应用提供一对极性相反且吸引子结构相似的超混沌或混沌信号[17-18]。然而,在已报道的条件对称系统中,能表现出无限多对条件对称的共存吸引子还非常少见,尤其是在忆阻超混沌系统中。
基于以上研究,本文提出了一个新的5D忆阻超混沌系统。通过理论分析和数值仿真分别探讨了系统参数和初始值对于系统动力学行为的影响。新系统最显著的特性是可以表现出无限多吸引子共存的超级多稳态现象以及独特的共存超级多稳态现象。同时,持续的混沌动力学以及变量偏移增量控制行为也被发现并研究。此外,在新系统的基础上构建了一个条件对称的忆阻超混沌系统,当选择适当的初始条件时,该系统可以产生无限多对极性相反且吸引子结构近似一致的条件对称的共存吸引子。最后,利用Multisim电路仿真软件设计并实现了新系统的电路模型,验证了新系统的可实现性。
1 系统模型改进的四维超混沌Lü系统[19]模型为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = a(y - x + yz)}\\ {\dot y = - xz + by + w}\\ {\dot z = xy - cz}\\ {\dot w = - dx} \end{array}} \right.$ | (1) |
式中:x, y, z, w为系统(1)的4个状态变量;a, b, c, d为系统参数。
在系统(1)的基础上,利用一个磁控忆阻器W(v)=(α + βv2)替换第1个等式中状态变量y的耦合系数,并添加第五维方程作为忆阻器的内部状态变量;同时,使用状态变量x替换第2个等式右边的状态变量y,一个新的五维忆阻超混沌系统被构建, 并且其无量纲状态方程为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = - ax + dW(v)y + ayz}\\ {\dot y = - fxz + bx + w}\\ {\dot z = xy - cz}\\ {\dot w = - ex}\\ {\dot v = y} \end{array}} \right.$ | (2) |
式中:x, y, z, w, v为系统(2)的5个状态变量;a, b, c, e, d, f, α, β均为正实数。
本文选用文献[20]中提出的光滑三次非线性磁控忆阻器,其数学模型为
| $\left\{ {\begin{array}{*{20}{l}} {i = W(\varphi )u}\\ {W(\varphi ) = \alpha + \beta {\varphi ^2}}\\ {\dot \varphi = u} \end{array}} \right.$ | (3) |
式中:i和u分别为忆阻器的端电流和端电压;W(φ) 为关于φ(t)的非线性函数,具有和电导一样的量纲,称为忆导,表示依赖于忆阻器内部状态变量φ(t)的控制;φ为磁通,表示忆阻器的内部磁通变化量;α,β均为正参数。
2 系统的动力学特性 2.1 基本动力学分析系统(2)所描述的新五维忆阻超混沌系统是关于z坐标轴对称的,其对称性可在(x, y, z, w, v)→ (-x, -y, z, -w, -v)变换后由系统的不变性得到。平衡点分析是判断系统稳定的重要方式,令系统(2)的右边等于0,可以得到系统的平衡点状态方程:
| $\left\{ {\begin{array}{*{20}{l}} {0 = - ax + dW(v)y + ayz}\\ {0 = - fxz + bx + w}\\ {0 = xy - cz}\\ {0 = - ex}\\ {0 = y} \end{array}} \right.$ | (4) |
通过简单的数值求解得,新系统具有一个线平衡点集E=(0, 0, 0, 0, μ),其中μ为实数。由于系统的所有参数均为正值,根据经典的Routh-Hurwitz判据可得,系统(2)具有一个不稳定的线平衡点集。
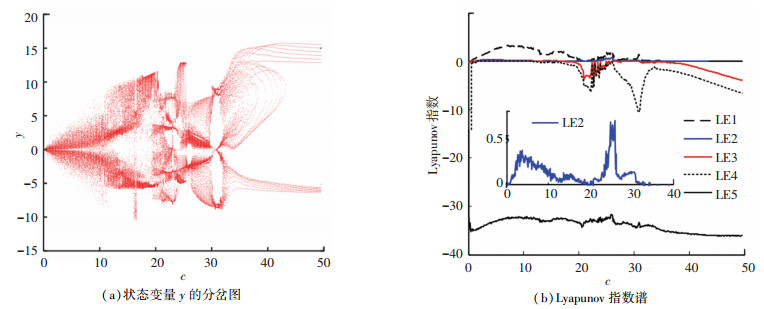
2.2 参数c对系统动力学的影响选取系统参数a=40, b=20, d=30, e=4, f=5, α=1, β=0.02且初始状态为(0, 0.1, 0, 0, 1),令参数c为控制变量,当c∈[0, 50]时,状态变量y的分岔图和Lyapunov指数谱如图 1所示。需要指出的是,本文的Lyapunov指数是基于经典的Wolf算法[21]计算得到的,步长时间和总时长分别设置为0.01 s和104 s。通过对比可知状态变量y的分岔图和Lyapunov指数谱动力学行为一致。从Lyapunov指数谱可知,当参数c∈[0.3, 18.6]和c∈[20, 30.5]时,系统(2)处于超混沌状态;当参数c∈(18.6, 20)和c∈(30.5, 33]时,系统(2)处于混沌状态;当参数c∈[0, 0.3)和c∈(33, 50)时,系统(2)处于周期状态。
|
图 1 系统(2)随参数c变化的动力学分析 Fig. 1 Dynamic analysis of system (2) with changes in parameter c |
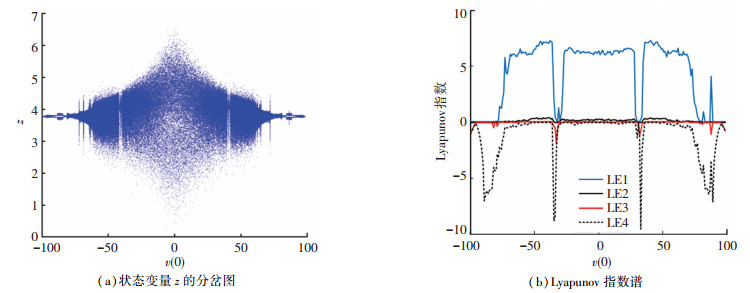
选取系统参数a=40, b=20, c=5, d=30, e=4, f=5, α=1, β=0.02和初始状态为(0, 0.1, 0, 0, v(0)),令忆阻器的初始状态v(0)为控制变量。当v(0)在[-100, 100]中变化时,状态变量z的分岔图和相应的Lyapunov指数谱如图 2所示。由分岔图可知,系统(2)随着初始条件的变化可以表现出无限多吸引子共存的超级多稳态现象。由Lyapunov指数谱可知,当v(0)∈(-74, -35)、v(0)∈(-28, 28)以及v(0)∈(35, 74)时,系统(2)处于超混沌状态;当v(0)∈(-78, -74)、v(0)∈ (74, 79)以及v(0)∈(87, 89)时,系统(2)处于混沌状态。同时,可以观察到v(0)在[-100, 0]和[0, 100]中的分岔特性以及相应的Lyapunov指数谱均近似关于v(0)=0对称,表明系统在两个对称的忆阻器初始状态范围内可表现出相似的动力学行为。
|
图 2 系统(2)随忆阻器初始状态变化的动力学分析 Fig. 2 Dynamic analysis of system (2) with changes in initial states of memristor |
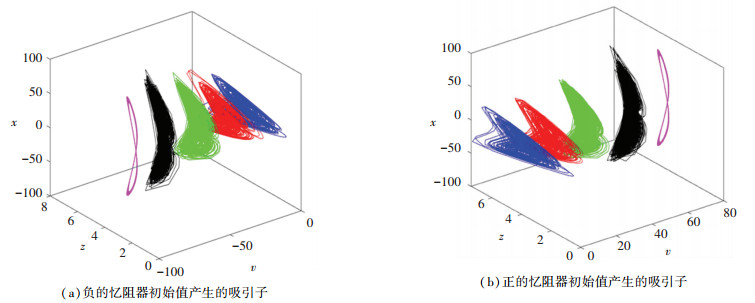
为了进一步探讨新系统的超级多稳态特性,选择不同的忆阻器初始状态来绘制不同的吸引子轨道。当取负的忆阻器初始状态时,不同初始条件产生的共存吸引子在vzx空间的投影如图 3(a)所示,图中从左向右的吸引子对应的忆阻器初始值v(0)和相应的吸引子状态分别为-80(周期)、-60(超混沌)、-35(混沌)、-15(超混沌)、-1(超混沌);当取正的忆阻器初始状态时,不同初始条件产生的共存吸引子在vzx空间的投影如图 3(b)所示,图中从左向右的吸引子对应的忆阻器初始状态v(0)和相应的吸引子状态分别为1(超混沌)、15(超混沌)、35(混沌)、60(超混沌)、80(周期)。因此,通过共存吸引子相图进一步验证了系统(2)依赖于忆阻器初始状态的超级多稳定性以及近似对称的动力学特性。此外,由图(2)的分岔图和Lyapunov指数谱可知,当仅改变忆阻器初始条件时,系统可以表现出持续的混沌或超混沌特性。因此,与其他忆阻混沌系统相比,系统(2)不仅具有依赖于初值的极端敏感性,而且可以表现出更加复杂的动力学特性、更强的鲁棒性和更大的密钥空间。因此,新系统可以被更好地应用于保密通信或图像加密等工程领域。
|
图 3 无限多共存吸引子在vzx空间的投影 Fig. 3 Projection of infinite numbers of coexisting attractors in vzx space |
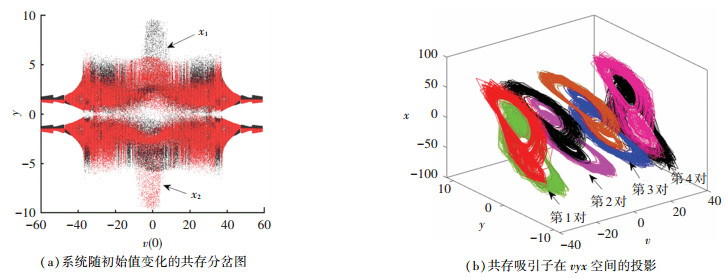
特别地,改变系统参数c=13并保持系统其他参数值不变,并且令系统初始条件分别为X1= (0, 0.1, 0, 0, v(0))和X2=(0, -0.1, 0, 0, v(0)),其中忆阻器初始条件v(0)为分岔参数。当v(0)在[-60, 60]中变化时,产生于初始条件X1和初始条件X2的共存分岔图如图 4(a)所示。由共存分岔图可知,系统在两个初始条件下均可表现出无限多吸引子共存的超级多稳态特性。因此,这个忆阻超混度系统可以表现出一个新的基于两个相反y初始值的共存超级多稳态现象。为了进一步探索系统丰富的超级多稳态特性,图 4(b)展示了4对共存吸引子在vyx空间的投影,其中,处于较上位置的4个吸引子对应于初始条件X1,相反,处于较下位置的4个吸引子对应于初始条件X2。并且表 1对图 4(b)所描述的4对共存奇异吸引子进行了总结。此外,需要说明的是,当选取更多的初始状态时,系统可以表现出无限多对奇异吸引子共存的超级多稳态现象。此现象是由于系统(2)随着参数c的增大使得系统的混沌动力学退化而导致无限多个双翼混沌或超混沌吸引子破裂而产生的。据了解,此前几乎没有文献探讨过这种独特的基于忆阻器初始值的共存超级多稳态现象。
|
图 4 系统(2)随忆阻器初始状态变化的动力学行为 Fig. 4 Dynamic behaviors of system (2) with changes in initial states of memristor |
| 表 1 共存吸引子的动力学特性 Tab. 1 Dynamic characteristics of coexisting attractors |
在一个确定的非线性系统中,当某一状态变量在该系统的右侧仅出现一次时,向该状态变量添加一个常数项将会产生一个可控的偏移量,从而使混沌信号从单极改变为双极,反之亦然。由于常数的导数为0,所以如果当一个常数引入到变量中时,微分方程不改变其形式。因此,偏移增量控制[22-25]可以在不改变系统基本动力学特性的情况下,仅通过改变一个额外的控制常数即可实现混沌信号在双极性和单极性之间相互转换。根据系统(2)可知,状态变量w仅出现在系统(2)的第2个等式右边一次且为线性变量,因此它是很容易实现系统(2)的超混沌吸引子的偏移控制。使用状态变量w + m代替w,其中m为偏移增量控制器,则系统(2)可以重写为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = - ax + dW(v)y + ayz}\\ {\dot y = - fxz + bx + (w + m)}\\ {\dot z = xy - cz}\\ {\dot w = - ex}\\ {\dot v = y} \end{array}} \right.$ | (5) |
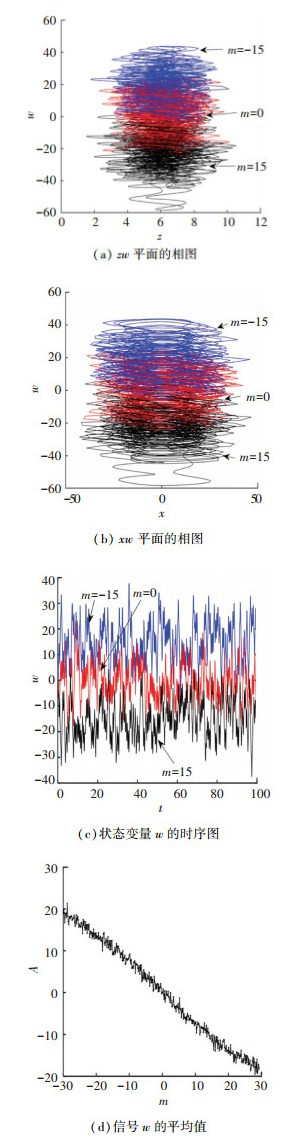
因此,通过在一定范围内改变m的大小,可以实现混沌吸引子在w轴的偏移控制。当选择参数a=40, b=20, c=5, d=30, e=4, f=5, α=1, β=0.02以及初始值为(0, 0.1, 0, 0, 1)时,图 5(a)和5(b)分别绘制了当m为-15、0、15时在zw和xw平面的不同位置产生的3个超混沌吸引子相图,图 5(c)绘制了相应的时序图,图 5(d)展示了混沌信号w的平均值(用A表示),随偏移增量控制器m变化的偏移趋势。
|
图 5 偏移增量控制器m的不同值对应的混沌吸引子相图、状态变量w的时序图及平均值曲线 Fig. 5 Phase diagram of chaotic attractors, time series diagram and average value curve of state variable w corresponding to different values of offset-boosting controller m |
由图 5(a)~5(c)可知,当m=0时,混沌信号处于w轴的正负半轴;当m=15时,混沌信号处于w轴的负半轴;当m=-15时,混沌信号处于w轴的正半轴。从图 5(d)可知,当偏移增量控制器m从-30逐渐增加到30时,混沌信号的平均值逐渐下降,即当偏移增量控制器m取正值时,吸引子向w轴的负方向偏移;当偏移增量控制器m取负值时,吸引子向w轴的正方向偏移。
3 忆阻超混沌系统的条件对称化设计前文已证系统(2)是关于z轴旋转对称的。因此,系统(2)可以通过状态变量z的一维偏置在对称系统的基础上来构造新的条件旋转对称的忆阻超混沌系统。首先对系统(2)中的z状态变量取绝对值,为构建条件对称系统做好准备工作。然后假设z → F(z),因为F(z)是非单调的,如果z → z + k使F(z+k)=-F(z),那么变量替换(x → -x, y →-y, z → z + k, w → -w, v→ -v)将使系统极性达到新的平衡,新的方程为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = - ax + dW(\varphi )y + ay|F(z)|}\\ {\dot y = - fx|F(z)| + bx + w}\\ {\dot z = xy - c|F(z)|}\\ {\dot w = - ex}\\ {\dot v = y} \end{array}} \right.$ | (6) |
式中F(z)=|z| - k。
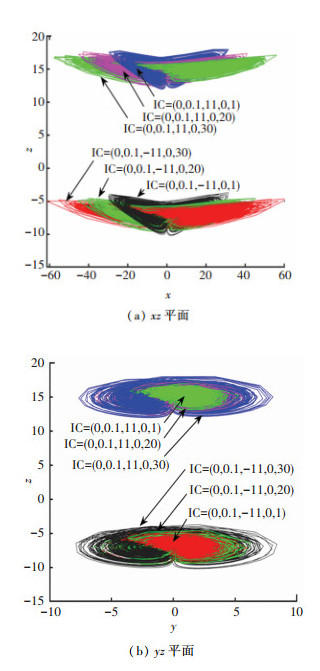
为了更直观地展示具有相反极性以及相似吸引子结构的无限多对对称的共存吸引子现象,这里选取参数a=40, b=20, c=5, d=30, e=4, f=5, α=1, β= 0.02, k=11。图 6分别展示了条件对称共存吸引子在xz和yz平面的相图。
|
图 6 系统(6)的共存吸引子相图 Fig. 6 Phase diagram of coexisting attractors of system (6) |
由图 6可知,z轴正方向的共存吸引子产生于初始状态(IC)= (0, 0.1, 11, 0, v(0));z轴负方向的共存吸引子产生于初始状态(IC)= (0, 0.1, -11, 0, v(0)),其中忆阻器初始值v(0)分别为1、20、30。同时,可以观察到在z轴正方向和负方向产生的每对条件对称的共存吸引子的大小几乎一致。更进一步,由于系统(2)具有无限多吸引子共存现象,因此,在适当的初始条件下,系统(6)可提供大量的具有相反极性且吸引子结构一致的条件对称共存吸引子。
4 忆阻超混沌系统的电路实现混沌系统的电路实现对于工程应用是非常重要的,因此,本文设计了一个简单的模拟电路来验证新的忆阻超混沌系统的动力学行为。电路中包括线性电容、线性电阻、运算放大器以及模拟乘法器等电路元器件。其中,运算放大器选择工作电压为±12 V的LM741,模拟乘法器为AD633。为了避免运算放大器输出信号饱和,将混沌信号的输出电平调小至原来的1/10,并进行时间尺度变换,令τ=τ0t,其中t0 =100。选择参数a=40, b=20, c=5, d=30, e=4, f=5, α=1, β=0.02,则系统(2)可以表示为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = - 4000x + 3000\left( {1 + 2{v^2}} \right)y + 40000yz}\\ {\dot y = - 5000xz + 2000x + 100w}\\ {\dot z = 1000xy - 500z}\\ {\dot w = - 400x}\\ {\dot v = 100y} \end{array}} \right.$ | (7) |
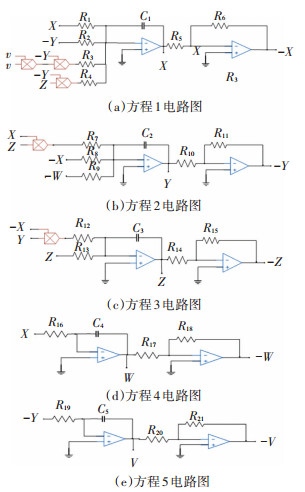
通过相应推导得到系统(2)的电路原理图,如图 7所示。根据电路原理图以及电路理论,得到以下状态方程:
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = - \frac{1}{{{R_1}{C_1}}}x + \frac{1}{{{R_2}{C_1}}}y + \frac{1}{{{R_3}{C_1}}}{v^2}y + \frac{1}{{{R_4}{C_1}}}yz}\\ {\dot y = - \frac{1}{{{R_7}{C_2}}}xz + \frac{1}{{{R_8}{C_2}}}x + \frac{1}{{{R_9}{C_2}}}w}\\ {\dot z = - \frac{1}{{{R_{12}}{C_3}}}xy + \frac{1}{{{R_{13}}{C_3}}}z}\\ {\dot w = - \frac{1}{{{R_{16}}{C_4}}}x}\\ {\dot v = - \frac{1}{{{R_{19}}{C_5}}}y} \end{array}} \right.$ | (8) |
|
图 7 系统(2)的电路原理图 Fig. 7 Circuit schematic diagram of system (2) |
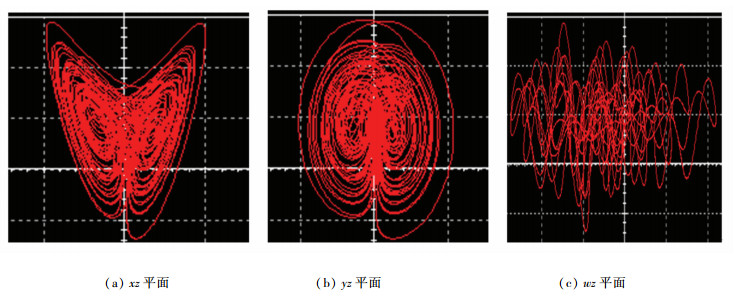
对比方程(7)和方程(8)可得图 7中的电路元件参数为:C1=C2=C3=C4=C5=100 nF,R1=2.5 kΩ,R2=3.33 kΩ,R3=1.67 kΩ,R4=0.25 kΩ,R7=2 kΩ,R8=5 kΩ,R9=100 kΩ,R12=10 kΩ,R13=20 kΩ,R16=25 kΩ,R19=100 kΩ,R5=R6=R10=R11=R14=R15=R17=R18=R20=R21=1 kΩ。采用Multisim软件对电路进行仿真实验,仿真结果如图 8所示,验证了该忆阻超混沌系统的可实现性。
|
图 8 超混沌吸引子在不同平面的相图 Fig. 8 Phase diagram of hyperchaotic attractors in different planes |
在改进Lü超混沌系统的基础上构建了一个新的五维忆阻超混沌系统。通过理论分析和数值仿真,研究了系统基于忆阻器初始状态的极端敏感性和持续的混沌或超混沌特性,表明系统具有极其复杂的动力学行为。同时,利用相图和时序图探讨了有趣的偏移控制行为。特别地,当调节单个系统参数并取适当的初始值,通过基于忆阻器初始状态变化的共存分岔图和相轨图首次研究了共存超级多稳态现象,并观察到了无限多对共存单翼混沌吸引子。此外,在所构建系统的基础上,通过引入绝对值函数构造了一个新的条件对称的忆阻超混沌系统。当取适当的初始条件,该系统可以提供无限多对具有相似结构但相反极性的条件对称吸引子。最后,电路实验与数值仿真结果一致,验证了新系统的可实现性。因此,新的忆阻超混沌系统表现出了极其丰富的动力学特性,可以为基于混沌理论的工程应用提供更好的选择。
| [1] |
CHUA L. Memristor-The missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507. DOI:10.1109/TCT.1971.1083337 |
| [2] |
包伯成, 史国栋, 许建平, 等. 含两个忆阻器混沌电路的动力学分析[J]. 中国科学: 技术科学, 2011, 41(8): 1135. BAO Bocheng, SHI Guodong, XU Jianping, et al. Dynamics analysis of chaotic circuit with two memristors[J]. SCIENTIA SINICA Technologica, 2011, 41(8): 1135. DOI:10.1007/s11431-011-4400-6 |
| [3] |
洪庆辉, 曾以成, 李志军. 含磁控和荷控两种忆阻器的混沌电路设计与仿真[J]. 物理学报, 2013, 62(23): 49. HONG Qinghui, ZENG Yicheng, LI Zhijun. Design and simulation of chaotic circuit for flux-controlled memristor and charge-controlled memristor[J]. Acta Physica Sinica, 2013, 62(23): 49. DOI:10.7498/aps.62.230502 |
| [4] |
ZHAO Liang, HONG Qinghui, WANG Xiaoping. Novel designs of spiking neuron circuit and STDP learning circuit based on memristor[J]. Neurocomputing, 2018, 314: 207. DOI:10.1016/j.neucom.2018.06.062 |
| [5] |
HONG Qinghui, ZHAO Liang, WANG Xiaoping. Novel circuit designs of memristor synapse and neuron[J]. Neurocomputing, 2018, 330(22): 11. DOI:10.1016/j.neucom.2018.11.043 |
| [6] |
VOURKAS I, SIRAKOULIS G C. Emerging memristor-based logic circuit design approaches: a review[J]. IEEE Circuits and Systems Magazine, 2016, 16(3): 15. DOI:10.1109/MCAS.2016.2583673 |
| [7] |
YU Fei, QIAN Shuai, CHEN Xi, et al. A new 4D four-wing memristive hyperchaotic system: dynamical analysis, electronic circuit design, shape synchronization and secure communication[J]. International Journal of Bifurcation and Chaos, 2020, 30(10): 2050147. DOI:10.1142/S0218127420501473 |
| [8] |
YU Fei, LIU Li, HE Binyong, et al. Analysis and FPGA realization of a novel 5D hyperchaotic four-wing memristive system, active control synchronization, and secure communication application[J]. Complexity, 2019, 2019: 1. DOI:10.1155/2019/4047957 |
| [9] |
曾以成, 成德武, 谭其威. 简洁无电感忆阻混沌电路及其特性[J]. 电子与信息学报, 2020, 42(4): 862. ZENG Yicheng, CHENG Dewu, TAN Qiwei. A simple inductor-free memristive chaotic circuit and its characteristics[J]. Journal of Electronics & Information Technology, 2020, 42(4): 862. DOI:10.11999/JEIT190859 |
| [10] |
吕晏旻, 闵富红. 基于现场可编程逻辑门阵列的磁控忆阻电路对称动力学行为分析[J]. 物理学报, 2019, 68(13): 49. LV Yanmin, MIN Fuhong. Dynamic analysis of symmetric behavior in flux-controlled memristor circuit based on field programmable gate array[J]. Acta Physica Sinica, 2019, 68(13): 49. DOI:10.7498/aps.68.20190453 |
| [11] |
BAO Bocheng, BAO Han, WANG Ning, et al. Hidden extreme multistability in memristive hyperchaotic system[J]. Chaos, Solitons and Fractals, 2017, 94: 102. DOI:10.1016/j.chaos.2016.11.016 |
| [12] |
BAO Han, WANG Ning, BAO Bocheng, et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 57: 264. DOI:10.1016/j.cnsns.2017.10.001 |
| [13] |
MEZATIO B A, MOTCHONGOM M T, WAFO TEKAM B R, et al. A novel memristive 6D hyperchaotic autonomous system with hidden extreme multistability[J]. Chaos, Solitons and Fractals, 2019, 120: 100. DOI:10.1016/j.chaos.2019.01.015 |
| [14] |
WANG Guangyi, SHI Chuanbao, WANG Xiaowei, et al. Coexisting oscillation and extreme multistability for a memcapacitor-based circuit[J]. Mathematical Problems in Engineering, 2017, 2017: 1. DOI:10.1155/2017/6504969 |
| [15] |
LAI Qiang, KUATE P, LIU Feng, et al. An extremely simple chaotic system with infinitely many coexisting attractors[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2019, 67(6): 1129. DOI:10.1109/TCSⅡ.2019.2927371 |
| [16] |
LI Chunbiao, SPROTT J C, LIU Yongjian, et al. Offset boosting for breeding conditional symmetry[J]. International Journal of Bifurcation and Chaos, 2018, 28(14): 1850163. DOI:10.1142/S0218127418501638 |
| [17] |
GU Zhenyu, LI Chunbiao, IU H H C, et al. Constructing hyperchaotic attractors of conditional symmetry[J]. The European Physical Journal B, 2019, 92(10): 221. DOI:10.1140/epjb/e2019-100165-9 |
| [18] |
LU Tianai, LI Chunbiao, JAFARI S, et al. Controlling coexisting attractors of conditional symmetry[J]. International Journal of Bifurcation and Chaos, 2019, 29(14): 1950207. DOI:10.1142/S0218127419502079 |
| [19] |
WANG Guangyi, ZHANG Xun, ZHENG Yan, et al. A new modified hyperchaotic Lü system[J]. Physica A: Statistical Mechanics and its Applications, 2006, 371(2): 260. DOI:10.1016/j.physa.2006.03.048 |
| [20] |
包伯成, 胡文, 许建平, 等. 忆阻混沌电路的分析与实现[J]. 物理学报, 2011, 60(12): 58. BAO Bocheng, HU Wen, XU Jianping, et al. Analysis and implementation of memristor chaotic circuit[J]. Acta Physica Sinica, 2011, 60(12): 58. DOI:10.7498/aps.60.120502 |
| [21] |
WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285. DOI:10.1016/0167-2789(85)90011-9 |
| [22] |
LI Chunbiao, SPROTT J C. Variable-boostable chaotic flows[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(22): 10389. DOI:10.1016/j.ijleo.2016.08.046 |
| [23] |
LI Chunbiao, WANG Xiong, CHEN Guanrong. Diagnosing multistability by offset boosting[J]. Nonlinear Dynamics, 2017, 90(2): 1335. DOI:10.1007/s11071-017-3729-1 |
| [24] |
PHAM V T, AKGUL A, VOLOS C, et al. Dynamics and circuit realization of a no-equilibrium chaotic system with a boostable variable[J]. AEU-International Journal of Electronics and Communications, 2017, 78: 134. DOI:10.1016/j.aeue.2017.05.034 |
| [25] |
ZHANG Sen, ZENG Yicheng, LI Zhijun, et al. Hidden extreme multistability, antimonotonicity and offset boosting control in a novel fractional-order hyperchaotic system without equilibrium[J]. International Journal of Bifurcation and Chaos, 2018, 28(13): 1850167. DOI:10.1142/S0218127418501675 |
 2022, Vol. 54
2022, Vol. 54


