2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
钢筋混凝土构件受剪性能的研究一直是一个难点,各国学者对剪切破坏的机理和计算方法的认识还很不一致,至今尚未建立一种普遍认可的受剪承载力计算方法。目前的受剪承载力计算公式大多是在考虑主要影响因素的基础上,采用统计分析的方法给出的[1-8]。例如:Zsutty[1]搜集分析已有剪切试验数据,建立了考虑混凝土强度、剪跨比和受拉纵筋配筋率等因素影响的混凝土板受剪承载力计算公式;Rebeiz[2]利用已有试验数据,考虑剪跨比的影响后进行了受剪承载力公式的拟合。但已有的钢筋混凝土构件剪切试验中,为使试件不发生弯曲破坏,常常布置较多的受拉纵筋,这使得试件在发生剪切破坏时受拉纵筋拉应力水平较低,纵筋销栓作用较大。例如Tureyen等[3]给出了考虑混凝土强度的经验性公式,但由于其采用简支梁进行试验,纵筋销栓作用较强。而在实际工程中,由于“强剪弱弯”的设计要求,在受弯构件靠近内支座的斜截面处构件发生剪切破坏前受拉纵筋已屈服,纵筋销栓作用很小,受剪承载力将小于试验值。
受弯构件内支座附近受剪达到极限荷载时,斜截面上同时作用弯矩和剪力。由压-剪相关关系可知,破坏时控制截面混凝土剪压区压应力和剪应力的大小相互影响,混凝土抗剪强度受截面压应力的影响,且当极限弯矩和剪力不同时,由截面平衡条件可知,剪压区高度也会随之改变[9]。而规范中并未具体考虑这些。
本文设计了一种剔除混凝土板中纵筋销栓作用的试验方案,即使板受剪破坏发生在受拉纵筋屈服的情况下。利用该方案完成了4个只在板顶配纵筋的混凝土板的受剪试验。基于平衡理论及压-剪相关关系对板的斜截面受剪承载力进行了推导。基于试验结果,拟合了考虑剪跨比和由纵向受拉钢筋引起相对剪压区高度影响的板内支座附近斜截面受剪承载力计算公式。
1 试验概况 1.1 试验方案本试验采用在混凝土板端作用力偶,斜裂缝预估起始位置以外作用竖向荷载的试验方法。加载时先在板自由端施加力偶,使板顶受拉纵筋保持在较高的应变水平,再在预估斜裂缝起始位置的外侧施加竖向荷载,逐步增大竖向荷载并调整板端力偶,保持支座附近截面弯矩缓慢增大,受拉纵筋逐渐屈服,最终使板受剪破坏。
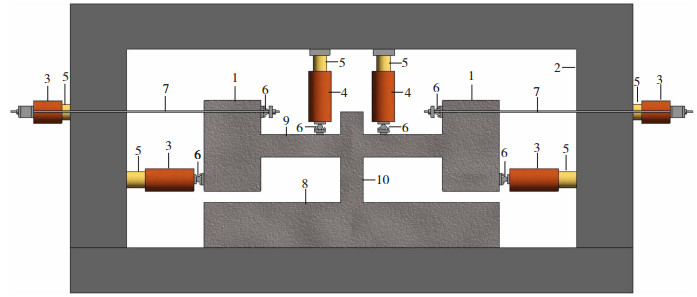
依据加载方案设计了加载装置,见图 1。试件由板、板自由端的伸臂构件、板下的扁柱和底梁组成。加载框由顶梁、立柱和底梁组成。
|
注:1.板端伸臂构件;2.加载框;3.水平千斤顶;4.竖向千斤顶;5.力传感器;6.铰支座;7.PC钢棒;8.底梁;9.试验板;10.板下扁柱。 图 1 试验加载装置 Fig. 1 Test loading device |
借助板自由端的伸臂构件,按图 1设置千斤顶,通过水平方向的千斤顶在悬臂构件上产生力偶,从而对板施加自由端力偶。通过板的预估斜裂缝起始位置外侧的竖向千斤顶来施加竖向荷载,最终使混凝土板在弯剪共同作用下发生斜截面受剪破坏。
1.2 试件设计4个试件编号为S-1~S-4,仅板顶受拉纵筋不同,其余参数均相同。板截面b×h=400 mm×200 mm,两边悬臂板净伸臂长度为700 mm。柱截面为400 mm×200 mm,柱高400 mm。仅在板顶配置受拉纵筋和分布钢筋,受拉纵筋配筋率及具体配置见表 1,分布钢筋为10@200,受拉纵筋的保护层20 mm。柱纵筋为820,箍筋为四肢箍10@100。以试件S-1为例,其尺寸及配筋见图 2,4个试件的伸臂构件、柱和底梁的尺寸与配筋以及板中分布钢筋的配置均相同,箍筋均为四肢箍。
| 表 1 试件主要参数 Tab. 1 Details of specimens |

|
图 2 试件S-1配筋(mm) Fig. 2 Reinforcement drawing of specimen S-1 (mm) |
表 2为试件混凝土的基本力学性能指标, 试件受力纵筋基本力学性能指标见表 3。
| 表 2 混凝土力学性能 Tab. 2 Mechanical properties of concrete |
| 表 3 钢筋力学性能 Tab. 3 Mechanical properties of steel bars |
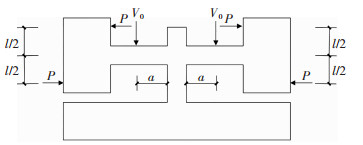
加载点位置:在预估斜裂缝起始位置的外侧施加竖向荷载,竖向荷载加载点至柱边的距离a为315 mm,见图 3。
|
注:P是水平千斤顶施加的水平荷载,V0是竖向千斤顶施加的竖向荷载。 图 3 加载点位置示意 Fig. 3 Locations of loading points |
通过在板端伸臂构件上下端分别施加等大反向的水平力,可在板自由端产生力偶。水平拉力和水平压力作用点关于板对称布置,两作用点间距l取为600 mm。水平加载点位置见图 3。
采用千斤顶进行水平和竖向荷载的施加。为了保持各千斤顶施加的力的方向固定,在每个千斤顶的作用点位置均设置铰支座,见图 1。
加载制度:正式加载过程中,先通过伸臂构件上的千斤顶施加水平力,使自由端力偶达到M01,然后保持力偶不变,施加竖向力并逐步增大竖向力至V01。当板顶受拉纵筋应变接近屈服值的80%时,防止试件受弯破坏,减小端部力偶至M02,然后继续增加竖向力。当竖向力达到V02时,板纵筋应变接近屈服值的85%。重复这一加载过程,逐步减小自由端力偶和增大竖向力,使控制截面弯矩缓慢增大,最终混凝土板的剪切破坏发生在板顶受拉纵筋屈服或接近屈服时。其中,M01~M06和V01~V06分别表示试件加载过程中各加载阶段末板自由端力偶和板上施加的竖向荷载。
加载过程中采用分级加载的方法,水平力与竖向力每级均为10 kN,加载后持荷1 min,然后施加下一级荷载。
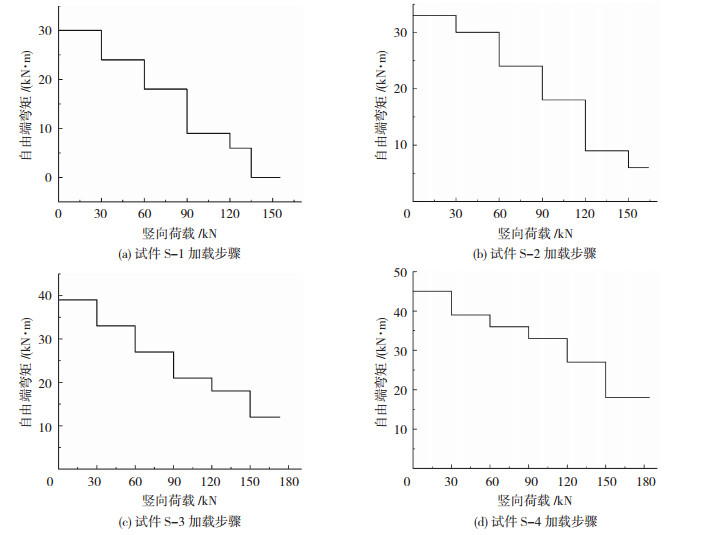
4个试件加载过程中各加载阶段末板自由端力偶M01~M06和竖向荷载V01~V06见表 4,变化趋势见图 4。
| 表 4 试件各加载阶段荷载 Tab. 4 Loads at each loading stage of the specimens |
|
图 4 试件加载步骤 Fig. 4 Loading steps |
本试验的观测内容:
1) 裂缝观测:观察垂直裂缝、斜裂缝出现时荷载,并记录裂缝发展过程以及分布形态。在板面绘制网格便于观察和记录裂缝。
2) 受拉纵筋应变:在所有板顶受力纵筋上均粘贴应变片,应变片粘贴位置为预估斜裂缝与受拉纵筋相交处。
3) 变形观测:测量混凝土板在荷载作用下的竖向变形。在混凝土板每个竖向荷载加载点下方布置位移计以观测加载点处板的竖向变形。
2 结果与分析 2.1 破坏过程和形态4个混凝土板试件的破坏过程大致相同,可将混凝土板受力至破坏的过程分为三阶段:
第一阶段:垂直裂缝出现
试件开始加载阶段未施加竖向荷载,主要受自由端力偶作用。试件上表面受拉,逐渐出现垂直裂缝。板顶受拉纵筋应变逐渐增大,并接近屈服应变。
第二阶段:斜裂缝形成
施加竖向荷载后,不断增大竖向荷载和调整板端力偶,垂直裂缝逐渐向下倾斜延伸,形成斜裂缝。
第三阶段:破坏阶段
继续增大竖向荷载,斜裂缝逐渐变宽,并逐渐向柱边延伸,最终板在弯剪耦合作用下,剪压区发生压剪复合破坏。
4个试件出现垂直裂缝、斜裂缝形成和达到极限荷载时柱边混凝土板截面的弯矩和剪力见表 5。
| 表 5 试验结果 Tab. 5 Test results |
破坏后的试件形态见图 5。4个试件破坏后特征类似,均存在一条较宽的斜裂缝,斜裂缝外侧试件有较大的竖向变形,斜裂缝下端剪压区发生剪压破坏。

|
图 5 试件破坏形态和特征 Fig. 5 Failure modes and characteristics of specimens |
广义剪跨比计算公式为
| $ \lambda=\frac{M}{V h_{0}}=\frac{P l+G l^{\prime}+V_{0} a}{\left(V_{0}+G\right) h_{0}} $ | (1) |
式中:λ为广义剪跨比,M、V分别为控制截面弯矩和剪力,P为伸臂构件上的水平力,l为伸臂构件水平力作用点间距,G为伸臂构件的自重,l′为伸臂构件重心至同侧柱边的距离,a为竖向荷载作用点至同侧柱边的距离,V0为竖向荷载,h0为混凝土板截面有效高度。
4个试件S-1~S-4的受拉纵筋配筋率依次增大,试件破坏时控制截面的极限弯矩和极限剪力均增加,广义剪跨比也增大。达到极限荷载时,4个试件的广义剪跨比分别为1.75、1.95、2.13和2.28。
2.3 受拉纵筋应变4个试件的受拉纵筋应变试验结果见表 6。从表 6可发现,在仅施加自由端力偶阶段,4个试件的受拉纵筋应变约为屈服应变的60%;当自由端力偶不断减小,竖向荷载不断增加时,受拉纵筋应变逐渐增加,在混凝土板发生破坏前,受拉纵筋均已屈服。
| 表 6 受拉纵筋应变 Tab. 6 Strain of longitudinal bars in tension |
采用上述的加载方案后,当混凝土板破坏时,纵向钢筋将屈服,斜裂缝较宽。李烨[10]、Zararis等[11-12]、Bazant[13]以及Jelic等[14]的研究表明,此时可忽略销栓作用和骨料咬合作用的贡献,剪压区混凝土承受所有剪力。同时为便于计算,将剪压区混凝土的压应力分布形状等效为矩形,假定截面内所有拉力由受拉纵筋承担。
3.1 混凝土压-剪相关曲线当弯矩和剪力作用于混凝土板时,混凝土同时受到压应力和剪应力作用。压-剪相关作用计算公式选用Bresler等[15]的公式基础上的公式:
| $ \tau_{\mathrm{u}} / f_{\mathrm{c}}=\sqrt{0.01109+0.09976\left(f_{\mathrm{cv}} / f_{\mathrm{c}}\right)-0.10907\left(f_{\mathrm{cv}} / f_{\mathrm{c}}\right)^{2}} $ | (2) |
式中:τu为压-剪共同作用下的混凝土抗剪强度,fc为混凝土轴心抗压强度,fcv为压-剪共同作用下的混凝土抗压强度。
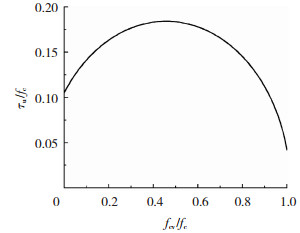
式(2)表示的混凝土压-剪相关曲线见图 6。当fcv/fc取0.46时,曲线位于极值点;当fcv/fc < 0.46时,τu随fcv的增大而增大;当fcv/fc>0.46时,τu随fcv的增大逐渐减小;当fcv/fc>0.915时,τu将比单独受剪时低。压-剪相互关联的性质将对混凝土板受剪承载力产生影响。
|
图 6 压-剪相关曲线 Fig. 6 Pressure-shear correlation curve |
混凝土板内支座附近斜截面受剪承载力计算采用图 7所示的模型。极限荷载下,截面剪力Vd可由剪压区混凝土在压-剪共同作用下的受剪承载力Vc抵抗,纵向受拉钢筋承担的拉力Nsl和剪压区混凝土承担的压力Dc可组成力偶,抵抗控制截面弯矩。

|
注:Mn为极限荷载下板自由端的弯矩;Vd为极限荷载下斜截面脱离体所受到的剪力;Ns1为极限荷载下混凝土板受拉纵筋拉力;Vc为极限荷载下脱离体剪压区高度内混凝土承担的剪力;Dc为极限荷载下脱离体剪压区高度内混凝土承担的压力。 图 7 斜截面受剪承载力计算模型 Fig. 7 Calculation model of shear capacity of inclined section |
假设控制截面剪压区的压应力和剪应力均匀分布,受压承载力Dc、受剪承载力Vc分别为:
| $ \begin{aligned} D_{\mathrm{c}} &=f_{\mathrm{cv}} b x_{\mathrm{v}} \end{aligned} $ | (3) |
| $ \begin{aligned} V_{\mathrm{c}} &=\tau_{\mathrm{u}} b x_{\mathrm{v}} \end{aligned} $ | (4) |
式中xv为等效矩形压应力图形的换算剪压区高度。
纵向受拉钢筋拉力为
| $ N_{\mathrm{s} 1}=f_{\mathrm{y}} A_{\mathrm{s}} $ | (5) |
根据控制截面平衡条件可得:
| $ \begin{gathered} V_{\mathrm{d}}=\tau_{\mathrm{u}} b x_{\mathrm{v}} \end{gathered} $ | (6) |
| $ f_{\mathrm{cv}} b x_{\mathrm{v}}=f_{\mathrm{y}} A_{\mathrm{s}} $ | (7) |
| $ M_{\mathrm{d}}=f_{\mathrm{y}} A_{\mathrm{s}}\left(h_{0}-x_{\mathrm{v}} / 2\right) $ | (8) |
式中Md为破坏时控制截面弯矩,Md=Mn+Gl′+Vna。
根据压-剪相关曲线,τu与fcv满足式(2),Md与Vd满足式(1),在已知λ的条件下,可联立式(1)、(2)、(6)、(7)和(8)求解,得到混凝土板受剪承载力Vd。由于式(2)形式复杂,直接代入求解困难,可通过迭代方法获得结果。迭代过程如下:
1) 给定剪压区高度xv,代入式(7)水平方向的力平衡条件,解出抗压强度fcv;
2) 将剪压区高度xv对应的抗压强度fcv代入压-剪相关关系,即式(2),解出抗剪强度τu;
3) 将剪压区高度xv和抗剪强度τu代入式(6),求得该剪压区高度xv对应的受剪承载力Vd;
4) 调整剪压区高度xv,重复步骤1) ~3),利用计算结果绘制Vd随xv的变化曲线,定义为受剪承载力曲线;
5) 利用式(1),将弯矩Md用剪力Vd表示,并代入式(8)得到Vd与xv的关系,绘制曲线,定义为剪力需求曲线;
6) 将受剪承载力曲线和剪力需求曲线绘于同一图中,混凝土板的受剪承载力由两曲线的交点来确定。
3.3 试件的受剪承载力计算结果对于本试验的4个混凝土板试件,利用迭代方法计算得到的结果见表 7。
| 表 7 试件计算结果 Tab. 7 Calculation results of specimens |
由计算结果可知,当板顶受拉纵筋配筋率增大时,极限荷载下控制截面的弯矩增大,受压-剪相关作用的影响,剪压区的平均压应力增大,平均剪应力减小,同时剪压区的高度增大,受剪承载力增大。
从对比可以看到,计算结果略小于试验结果,两者偏差随配筋率的增加逐渐增大。分析原因是由于配筋率增大时,极限荷载下的剪压区高度也增大,实际剪压区压应力按三角形分布的区域增加,该区域压应力较小,处于压-剪相关曲线上升段。而假设压应力和剪应力均匀分布计算得到的混凝土压应力处于压-剪相关曲线的下降段,剪应力随着压应力的增加而减小,忽略了压应力较小区域混凝土抗剪强度的增加,故结果偏小。
4 混凝土板受剪承载力计算公式的拟合与分析 4.1 计算公式拟合本文3节中的计算方法需迭代求解,不适用于实际应用。本节基于试验结果,拟合了考虑剪跨比和由纵向受拉钢筋引起相对剪压区高度影响的板内支座附近斜截面受剪承载力公式。
弯剪作用下板的受剪承载力受混凝土抗剪强度和剪压区高度的影响。弯矩和剪力共同作用下,由压-剪相关曲线可知,当压应力小于0.46fc时,随压应力的增大,混凝土抗剪强度逐渐增大;当压应力超过0.46fc时,随压应力的增大,抗剪强度逐渐减小。抗剪强度一定时,剪压区高度越大,板受剪承载力也越大。
剪压区高度对板受剪承载力的影响通过kρfyh0/fc来考虑,其中系数k通过试验数据拟合确定。压-剪相关作用对混凝土板受剪承载力的影响通过广义剪跨比来考虑。依据《混凝土结构设计规范》[16](后简称《规范》)中的计算公式,采用的计算混凝土板受剪承载力的拟合函数形式为
| $ V_{\mathrm{e}}=\frac{1.75}{\lambda+1} k \rho \frac{f_{\mathrm{y}}}{f_{\mathrm{c}}} f_{\mathrm{t}} b h_{0} $ | (9) |
利用本文试验数据通过最小二乘法拟合,可得k=6.2,则式(9)变为
| $ V_{\mathrm{e}}=\frac{10.85}{\lambda+1} \rho \frac{f_{\mathrm{y}}}{f_{\mathrm{c}}} f_{\mathrm{t}} b h_{0} $ | (10) |
将公式计算结果和试验结果进行对比,见表 8,可以看出两者吻合较好。
| 表 8 混凝土板受剪承载力拟合公式计算值和实测值 Tab. 8 Calculated values of fitted formula and measured values of shear capacity of concrete slabs |
定义相对剪压区高度为
| $ \xi=\frac{\rho \frac{f_{\mathrm{y}} h_{0}}{f_{\mathrm{c}}}}{h_{0}}=\rho \frac{f_{\mathrm{y}}}{f_{\mathrm{c}}} $ |
则式(10)变为
| $ V_{\mathrm{e}}=\frac{10.85}{\lambda+1} \xi f_{\mathrm{t}} b h_{0} $ | (11) |
式中ξ为不考虑压-剪相关作用由内力平衡计算得到的相对剪压区高度。
由式(11)可看出,受剪承载力Ve随着相对剪压区高度的增加而增大,随着广义剪跨比的增加而减小。《规范》6.3.3条中不配置箍筋和弯起钢筋的一般板类受弯构件斜截面受剪承载力应满足:
| $ V \leqslant 0.7 \beta_{\mathrm{h}} f_{\mathrm{t}} b h_{0} $ | (12) |
式中: βh为截面高度影响系数,βh=(800/h0)1/4,当h0<800 mm时取为800 mm。
对于一般h0<800 mm的板,当
《规范》中无腹筋构件的斜截面受剪承载力是以收集到的大量无腹筋梁的受剪试验数据为依据,分析得到的偏下值的计算公式,但其中仍包含了纵筋的销栓作用。因为以往进行钢筋混凝土构件剪切试验时,为避免试件弯曲破坏,常常布置较多的受拉纵筋,这使得试件在剪切破坏时受拉纵筋没有屈服,多余的强度将提供销栓作用。本试验通过使受拉纵筋在板破坏时屈服,剔除了销栓作用,所以在某一广义剪跨比下,相对剪压区高度较小时试验结果与《规范》公式结果相比更低。但由于《规范》公式是偏下值,未考虑相对剪压区高度对受剪承载力的影响,故随着相对剪压区高度的增加,拟合公式计算结果逐渐大于《规范》公式结果。
5 结论1) 设计了在自由端作用力偶,再在预估斜裂缝起始位置的外侧作用竖向荷载以使混凝土板在弯剪耦合作用下破坏的试验方案。先作用板端力偶使板顶受拉纵筋保持较大应变值,再在斜裂缝预估起始位置的外侧作用竖向荷载,然后调整力偶避免试件受弯破坏,持续增大竖向荷载以使混凝土板受剪破坏并使纵筋屈服,从而剔除了销栓作用的贡献。采用该方案,对4个纵向受拉钢筋配筋率不同的混凝土板试件进行了受剪试验。
2) 考虑混凝土压-剪相关关系并利用极限荷载下控制截面平衡条件进行了板受剪承载力的推导,介绍了迭代求解的过程。
3) 基于试验结果,建立了考虑剪跨比和由纵向受拉钢筋引起相对剪压区高度影响的板内支座附近斜截面受剪承载力计算公式。将该公式与中国《规范》公式对比分析后发现:对不配置箍筋和弯起钢筋的一般板类受弯构件,当
| [1] |
ZSUTTY T C. Beam shear strength prediction by analysis of existing data[J]. ACI Journal Proceedings, 1968, 65(11): 943. DOI:10.14359/7526 |
| [2] |
REBEIZ K S. Shear strength prediction for concrete members[J]. Journal of Structural Engineering, 1999, 125(3): 301. DOI:10.1061/(ASCE)0733-9445(1999)125:3(301) |
| [3] |
TUREYEN A K, FROSCH R J. Concrete shear strength: another perspective[J]. ACI Structural Journal, 2002, 100(5): 609. DOI:10.14359/12802 |
| [4] |
PARK H, CHOI K, WIGHT J K. Strain-based shear strength model for slender beams without web reinforcement[J]. ACI Structural Journal, 2006, 103(6): 783. DOI:10.14359/18228 |
| [5] |
梁兴文, 李晓文. 钢筋混凝土梁剪压破坏时剪压区混凝土的复合受力强度[J]. 工业建筑, 1996, 26(3): 3. LIANG Xingwen, LI Xiaowen. The strength of concrete in shear-compression zone of reinforced concrete beams under combined stresses[J]. Industrial Construction, 1996, 26(3): 3. DOI:10.13204/j.gyjz1996.03.001 |
| [6] |
吕艳梅. 高强箍筋高强混凝土梁抗剪性能试验研究与理论分析[D]. 长沙: 湖南大学, 2008 LÜ Yanmei. Theoretical and experimental research on shear capacity of high strength concrete beams with high strength stirrups[D]. Changsha: Hunan University, 2008 |
| [7] |
王景全, 戚家南. 有腹筋与无腹筋钢筋混凝土梁抗剪承载力统一计算方法[J]. 土木工程学报, 2013(7): 47. WANG Jingquan, QI Jianan. Unified strength computation model for reinforced concrete beams with and without stirrups[J]. China Civil Engineering Journal, 2013(7): 47. DOI:10.15951/j.tmgcxb.2013.07.016 |
| [8] |
李立峰, 徐开铎, 胡思聪, 等. 考虑多参数耦合的无腹筋梁抗剪承载力分析[J]. 建筑结构, 2019(6): 86. LI Lifeng, XU Kaiduo, HU Sicong, et al. Analysis of shear capacity of beams without web reinforcement considering multiple factors coupling[J]. Building Structure, 2019(6): 86. DOI:10.19701/j.jzjg.2019.06.016 |
| [9] |
李健. 考虑剪压区高度和剪跨比影响的混凝土板受剪承载力计算[D]. 哈尔滨: 哈尔滨工业大学, 2020 LI Jian. Calculation of shear capacity of concrete slabs considering depth of shear compression zone and shear span ratio[D]. Harbin: Harbin Institute of Technology, 2020 |
| [10] |
李烨. 无腹筋混凝土深梁受剪承载力尺寸效应试验研究[D]. 长沙: 湖南大学, 2016 LI Ye. Experiment study on size effect on shear strength of reinforced concrete deep beams without stirrups[D]. Changsha: Hunan University, 2016 |
| [11] |
ZARARIS P D, PAPADAKIS G C. Diagonal shear failure and size effect in RC beams without web reinforcement[J]. Journal of Structural Engineering, 2001, 127(7): 733. DOI:10.1061/(ASCE)0733-9445(2001)127:7(733) |
| [12] |
ZARARIS P D. Shear compression failure in reinforced concrete deep beams[J]. Journal of Structural Engineering, 2003, 129(4): 544. DOI:10.1061/(ASCE)0733-9445(2003)129:4(544) |
| [13] |
BAZANT Z P. Fracturing truss model: size effect in shear failure of reinforced concrete[J]. Journal of Engineering Mechanics, 1997, 123(12): 1276. DOI:10.1061/(ASCE)0733-9399(1997)123:12(1276) |
| [14] |
JELIC I, PAVLOVIC M N, KOTSOVOS M D. A study of dowel action in reinforced concrete beams[J]. Magazine of Concrete Research, 1999, 51(2): 131. DOI:10.1680/macr.1999.51.2.131 |
| [15] |
BRESLER B, PISTER K S. Strength of concrete under combined stresses[J]. ACI Structural Journal, 1958, 55(9): 321. DOI:10.14359/11358 |
| [16] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010 [S]. Beijing: China Architecture & Building Press, 2010 |
 2022, Vol. 54
2022, Vol. 54



 14
14