2. 福建工程学院 土木工程学院,福州 350118
2. School of Civil Engineering, Fujian University of Technology, Fuzhou 350118, China
预制装配式混凝土结构不仅可以实现建筑结构的快速施工,还可以优化现场施工环境、节省建筑模板,是实现建筑工业化和绿色建筑的重要技术[1]。目前,现有的装配式剪力墙多采用灌浆套筒连接,且已有较多研究成果对其抗震性能进行了研究。然而,在应用过程中发现,灌浆套筒连接的剪力墙存在竖向钢筋数量多、对位困难且套筒密实度不易保证等问题,在实际工程应用上仍存在一定的局限性且事后难以补救[2]。
基于此,部分学者[3-7]转向了施工更为便捷的螺栓连接式装配剪力墙(BASW),通过试验和理论研究,对不同构造形式的BASW的抗震性能有了更深一步的了解。研究表明,该种结构具有很好的抗震性能,是一种兼具施工效率和结构安全性的很有发展潜力的装配形式。然而,目前的BASW多是采用外部独立的连接钢件与预制墙体连接的形式,虽然其整体性和抗震性能较好,但因涉及上下预制件分别与连接钢框螺栓连接,所以存在螺栓数量多、对孔难度大等缺点。并且由于其上下预制件与连接钢框是分别连接的,在承受地震作用时与连接钢框均会产生相对滑移,从而增大整体结构的滑移量。因此,为进一步提高施工效率和结构的整体性,亟需对BASW的构造形式进行集成和优化。
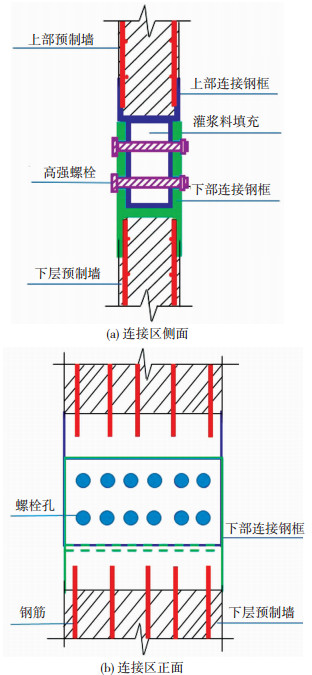
本文提出一种将连接钢框进一步集成到装配剪力墙构件中的采用螺栓连接的全装配剪力墙和边缘构件现浇的半装配剪力墙[8],连接示意见图 1。连接设计遵循“强连接、弱构件”的设计理念,根据现浇剪力墙的抗弯承载力及水平抗剪承载力计算螺栓尺寸、数量和分布。对于边缘构件现浇的半装配剪力墙,其现浇宽度应不小于JGJ 3—2010《高层建筑混凝土结构技术规程》[9]表7.2.15中对于剪力墙约束边缘构件沿墙肢长度的要求。
|
图 1 集成钢连接件的螺栓连接预制装配剪力墙接头示意 Fig. 1 Schematic of the connection frame of the proposed bolted-connection assembled shear wall |
新型装配剪力墙的整体性和抗震性是人们关注点,而结构恢复力模型是从大量试验中获取的结构的恢复力与变形的相关关系曲线,它是结构的抗震性能在结构弹塑性地震反应分析中的具体体现[10]。当前已有的关于钢筋混凝土结构恢复力模型中,较为典型的有Penzien[11]及Clough[12]的双折线模型、Takeda等[13]的三折线模型和Ramberg等[14]的曲线型模型等。然而,由于结构形式和恢复力模型中的关键参数、滞回规则的不同,无法直接适用于BASW结构中。因此,在试验研究和有限元数值分析的基础上,提出一种适用于BASW的简化恢复力模型是很有必要的,并且可以为该种结构的推广应用和弹塑性时程分析提供理论基础。
本文通过对不同剪跨比和不同装配率的6个BASW和1个现浇式结构的低周往复加载试验,并结合有限元数值分析,提出了包含结构抗震骨架曲线中屈服点、峰值点和极限点的三折线模型。随后,通过对滞回曲线的刚度退化规律和滞回规则的分析,提出了适用于BASW结构的滞回曲线恢复力模型。
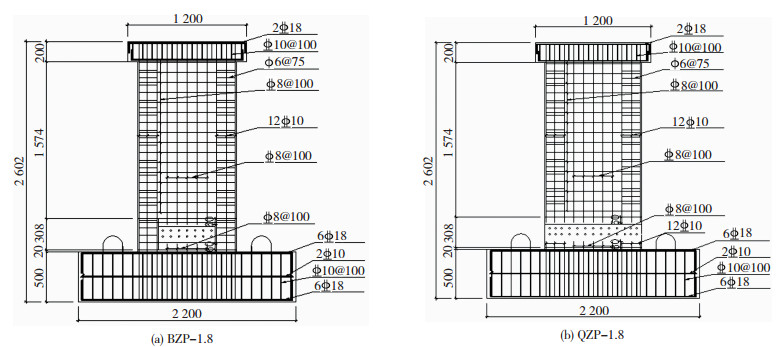
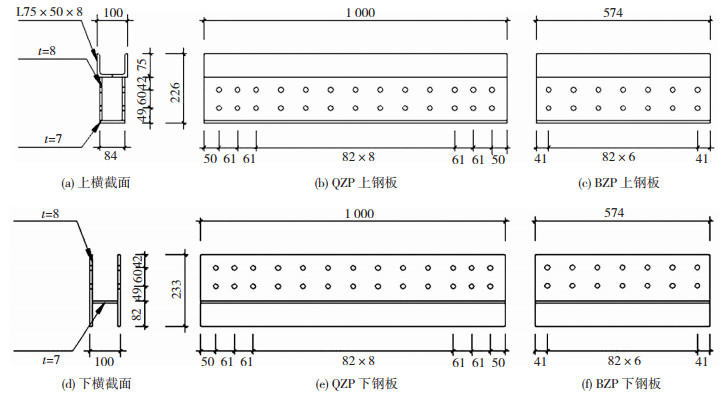
1 试验研究 1.1 试件设计与制作试验共设计7片剪力墙,均采用一字型剪力墙设计,上部墙体预制,下部墙体用基座代替,仅预留预埋钢件作为连接。编号XJ的构件为剪跨比1.8的现浇剪力墙,BZP-1.8、BZP-1.4、BZP-1.0、QZP-1.8、QZP-1.4、QZP-1.0分别为剪跨比为1.8、1.4和1.0的半装配及全装配剪力墙。试件采用相同的配筋方案,剪跨比通过墙身高度参数进行调整。以BZP-1.8和QZP-1.8为例,具体的尺寸及配筋见图 2,连接件尺寸见图 3。对于试件中的墙体部分,混凝土强度设计等级为C40,除箍筋为HPB300外,其他钢筋均采用HRB400。对于试件中的连接件部分,通过将墙体内的竖向钢筋与预埋连接钢件焊接,并通过M18螺栓将上下部墙体连接起来,栓孔对应开孔20 mm。试件采用钢材材性见表 2。
|
图 2 试件尺寸及配筋(mm) Fig. 2 Dimensions and reinforcement of specimens (mm) |
|
图 3 连接件尺寸(mm) Fig. 3 Dimensions of connection frame (mm) |
| 表 1 试件参数 Tab. 1 Parameters of specimens |
| 表 2 钢材材性 Tab. 2 Material properties of reinforcements and steel plate |
本次试验加载装置示意见图 4,加载历程见图 5。首先,通过柱顶的竖向千斤顶施加恒定轴压力318 kN(轴压比0.2),并使其保持全过程恒定。再由水平向的MTS作动器施加水平荷载,在加载前期以较小的位移增量施加并观察外侧纵筋的应变值用以确定构件的屈服荷载及屈服位移,分别施加1、2、3、3.5、4、4.5、5 mm的墙顶位移,每级往复循环一次。然后以屈服位移的整数倍加载,每级循环3次,当试件的承载力降低至极限承载力的85%时,或试件破坏(例如墙肢底部的边缘纵筋拉断)时,停止加载。

|
图 4 试验加载装置 Fig. 4 Test loading device |

|
图 5 加载历程示意 Fig. 5 Loading path |
7个试件的最终破坏模式见图 6。可看出,裂缝发展受剪力墙剪跨比影响而有所差异。总体上看剪跨比1.8的全装配、半装配以及现浇剪力墙的主裂缝均为水平向的受弯裂缝,水平裂缝发展高度基本在2/3墙高以下,而剪跨比1.4的构件墙身受剪斜裂缝明显增加,且墙身上部也出现了斜裂缝,剪跨比1.0的构件墙身中部交叉斜裂缝覆盖范围更大更广。各个试件的最终破坏形态均为受弯为主的弯剪破坏,最终破坏均为受拉侧钢筋拉断以及受压侧墙肢混凝土压溃,见图 6(h)。6个装配剪力墙试件的连接区均完好,未出现螺栓松动、变形等连接区破坏,说明连接区很好地实现了竖向内力以及水平剪力传递,满足强连接弱构件的设计要求。

|
图 6 试件最终破坏形态 Fig. 6 Final failure form of each specimen |
对比图 6(a)、(b)、(e)及对应3个构件的试验现象发现,对于1.8剪跨比的构件,其装配方式对构件的破坏模式影响不大,半装配构件两侧现浇边缘构件与预制墙身的交界面未出现明显裂缝。而对比剪跨比1.4的全装配和半装配试件,如图 6(c)及图 6(f)所示,交界面出现了竖向长裂缝,而当剪跨比1.0时,如图 6(g)所示,交界面裂缝从上至下出现贯穿。说明随着剪跨比的减小,半装配剪力墙的竖向交界面受力增大,在结构设计中应进行交界面抗剪承载力验算。
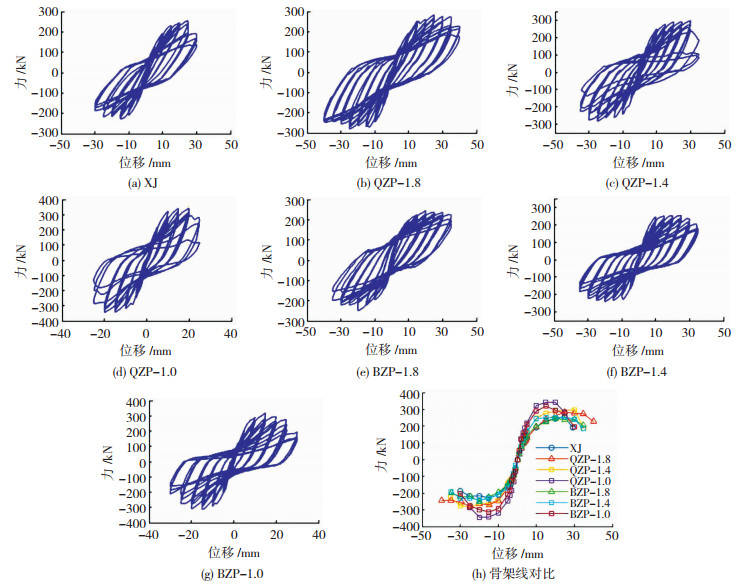
1.3.2 滞回曲线和骨架线7个试件的滞回曲线均呈比较饱满的梭形(图 7),说明该类全装配和半装配剪力墙抗震耗能能力良好。滞回曲线有一定的“捏缩”现象,与墙身混凝土开裂并与内部钢筋发生一定的滑移,以及底部连接钢框间滑移有关,尤其是在加载后期,滑移增大,“捏缩”现象更明显。
|
图 7 试件力-位移曲线及骨架线 Fig. 7 P-Δ hysteresis curves and skeleton lines |
从图 7(h)的骨架线对比可看到:1)7个试件的骨架线变化规律大致相同,都经历了未开裂前的弹性阶段、开裂但未屈服阶段、屈服后的弹塑性阶段、极限破坏阶段这4个典型阶段;2)节点初始刚度受剪跨比影响较大,剪跨比小的同类剪力墙其初始刚度更大;3)同剪跨比的全装配剪力墙及半装配剪力墙与对应现浇剪力墙初始刚度基本一致,说明本文提出的全装配连接及半装配连接不会引起结构初始刚度变化;4)剪跨比是影响试件峰值承载力的主要因素,随着剪跨比的减小,试件峰值承载力增大,以剪跨比1.8和1.0的全装配剪力墙为例,峰值承载力分别为283.7和341.8 kN;5)全装配剪力墙的峰值承载力相比于同剪跨比的现浇及半装配剪力墙要高,以剪跨比1.8为例,三者峰值承载力分别为283.7、254.4和244.6 kN,原因是全装配剪力墙的连接钢框为全长布置,使墙肢底部最终的破坏面有了一定程度的上移。而半装配剪力墙比同剪跨比的现浇剪力墙的峰值承载力低3.85%,差异较小,基本达到了等同现浇的峰值承载力。
2 数值仿真与参数分析 2.1 模型建立采用精细化实体建模方案,对混凝土、连接钢板、螺栓采用C3D8R单元,对钢筋采用T3D2单元。对于本构模型,混凝土选取ABAQUS有限元软件提供的CDP模型,其单轴拉、压应力-应变曲线参照GB 50010—2010《混凝土结构设计规范》[15],损伤因子在此基础上基于能量等价原理[16]计算。在ABAQUS的CDP模型定义中,混凝土由拉转压的受压刚度恢复系数取为0.5,由压转拉的受拉刚度恢复系数取为0。钢筋、连接钢板、螺栓则选取双线性随动强化模型,屈服后切线模量为初始模量的0.01倍。
接触面设置采用通用接触,包括上侧钢板与下侧钢板接触面、钢板与螺栓接触面、孔壁与螺栓接触面,法向定义为硬接触,切向接触定义为库伦摩擦接触,摩擦系数取0.3。钢筋与混凝土采用嵌入方式。钢筋、混凝土均采用绑定(Tie)方式与钢框约束。
对于螺栓预紧力的施加,设置多个分析步,逐步进行。即先定义第一个分析步,在该分析步中给螺栓定义临时边界条件,将螺栓荷载定义为10 N的预紧力(Apply Force);定义第二个分析步,在该分析步中移除临时边界条件,将预紧力大小改为最终的预紧力值;定义第三个分析步,在该分析步中将螺栓荷载定义为“保持当前螺栓长度(Fix at Current Length)”。
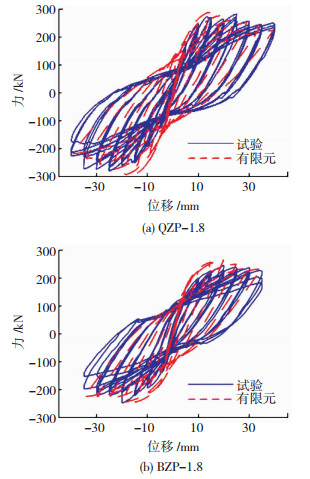
2.2 模型验证以QZP-1.8和BZP-1.8为例,有限元的分析结果与试验结果对比见图 8。可以看出总体上有限元模型与试验模型的力-位移曲线吻合良好,也体现了钢筋混凝土结构滞回曲线“捏缩”特点。由于构件制作误差以及加载设备调整误差,有限元模拟的构件正向屈服后直到峰值段的刚度相较于试验值有较明显的偏大。除此之外,构件峰值承载力与初始刚度偏差均在10%以内,具有较好的计算精度,可以应用于螺栓连接装配式剪力墙结构的有限元参数分析。
|
图 8 仿真与试验的力-位移曲线对比 Fig. 8 Comparison of P-Δ hysteresis curves between simulation and experiment |
由于试验成本和试验条件的限制,无法对更多的参数展开试验研究。基于BZP-1.8试件的剪力墙设计,墙身尺寸均为1 800×1 000×100,在满足单一变量原则的前提下,分别改变了轴压比、边缘构件配箍率、边缘构件尺寸3个参数,见表 3,并进行了参数分析,以期明晰这些参数对该类装配剪力墙抗震性能的影响,并为后续的恢复力模型研究提供更多的基础数据支持。
| 表 3 模型参数 Tab. 3 Model parameters |
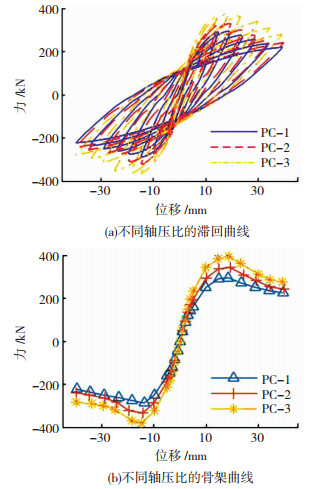
如图 9所示,轴压比对构件抗震性能影响较大。具体表现为在前期的弹性阶段,力-位移曲线基本重合,说明初始刚度受轴压比影响较小。但随着加载级的增大,轴压比越大,其峰值承载力越大(PC-1、PC-2、PC-3的峰值荷载分别为295.3、342.5、395.5 kN)。这是因为轴压力产生的截面整体压应力抵消了一部分弯矩产生的拉应力,抑制了混凝土由于受拉产生的裂缝的发展,从而推迟了模型的破坏。达到峰值承载力之后,轴压比越大,承载力下降越快,说明延性越差。
|
图 9 轴压比参数对抗震性能影响 Fig. 9 Influence of axial compression ratio on seismic performance |
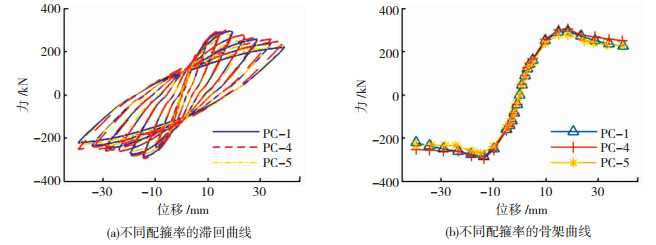
如图 10所示,在前期的弹性阶段,配箍率不同的模型其力-位移曲线基本重合,说明配箍率对初始刚度影响不大。但随着加载级增大,配箍率越大,其峰值承载力越大(PC-4、PC-1、PC-5的峰值荷载分别为303.7、295.3、279.7 kN),这是因为配箍率越大,箍筋对边缘构件混凝土的侧向约束越大,混凝土强度提高的也就越多。达到峰值后,虽然各个模型的承载力均下降,但是配箍率大的模型由于箍筋的约束,延缓了混凝土压碎进程,从而延性相对更好。
|
图 10 配箍率参数对抗震性能影响 Fig. 10 Influence of hoop ratio on seismic performance |
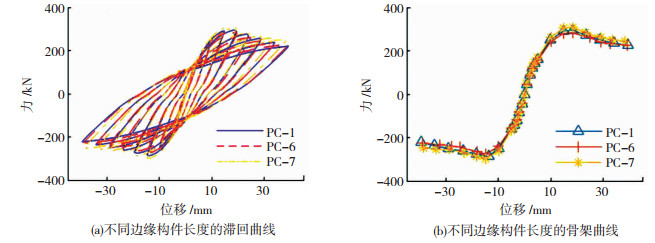
如图 11所示,前期刚度基本一致,峰值承载力PC-6、PC-1、PC-7分别为282.0、295.3、308.8 kN,各个试件承载力与均值差值均小于5%。峰值点后的下降段趋势也基本一致,PC-6、PC-1、PC-7的延性系数分别为5.5、5.6、5.4,影响较小。总体上看,边缘构件长度对构件抗震性能影响不大。
|
图 11 边缘构件长度对抗震性能影响 Fig. 11 Influence of the length of the edge member on seismic performance |
观察试验骨架曲线的形状和发展规律可知,尽管在试件屈服之前已经出现开裂现象,但是裂缝微小、总体变形较小,且试验曲线基本没有斜率变化,仍呈一条斜直线。因此,本文考虑采用由屈服点、峰值点及极限点所形成的三折线模型来研究本文的螺栓连接的装配式剪力墙的骨架曲线。
3.1.1 屈服点1) 屈服荷载Py。参考文献[17]并结合本文试验及模拟结果,拟合出Py的计算公式:
| $ \begin{gathered} \frac{P_{\mathrm{m}}}{P_{\mathrm{y}}}=1.83-0.36 n+0.96 \lambda_{\mathrm{v}}-0.13 \lambda- \\ 0.22 \alpha_{\mathrm{zp}}+0.02 \gamma_{\mathrm{a}} \end{gathered} $ | (1) |
式中:Py为屈服荷载,Pm为峰值荷载(由3.1.2节计算得到),n为轴压比,λv为配箍特征值,查JGJ 3—2010《高层建筑混凝土结构技术规程》[9]表 7.2.15得到,λ为剪跨比,αzp为装配率,取预制部分墙身长度与全墙长度hw之比,γa为边缘构件截面积与墙身截面全面积之比。
2) 屈服位移Δy。剪力墙位移主要由弯曲变形和剪切变形组成,故Δy为
| $ \varDelta_{\mathrm{y}}=\varDelta_{\mathrm{by}}+\varDelta_{\mathrm{sy}}=1.2 \frac{P_{\mathrm{y}} H}{G b_{\mathrm{w}} h_{\mathrm{w} 0}}+\frac{1}{3} \beta \frac{f_{\mathrm{y}}}{E_{\mathrm{s}} h_{\mathrm{w} 0}} H^{2} $ | (2) |
式中:H为试件高度,G为剪切模量,通常取0.4E,bw为试件宽度,hw0为试件截面有效高度,hw0=hw-a′s,(其中hw为剪力墙截面总高度,a′s为剪力墙受压区端部钢筋合力点到受压区边缘的距离),fy为钢筋抗压强度设计值,Es为钢筋弹性模量,对于参数β的计算,参考Priestley等[18]并结合本文试验及模拟结果,拟合出β的表达式:
| $ \beta=5.78+2.98 \lambda_{\mathrm{v}}-2.7 \lambda+0.48 \alpha_{\mathrm{zp}} $ | (3) |
3) 屈服刚度Ky。确定了Py及Δy后,可以得到屈服点之前的初始段刚度:
| $ K_{\mathrm{y}}=\frac{P_{\mathrm{y}}}{\varDelta_{\mathrm{y}}} $ | (4) |
1) 峰值荷载Pm。本文依据JGJ 3—2010《高层建筑混凝土结构技术规程》[9]的剪力墙受弯、受剪承载力的计算公式,并结合本文装配式剪力墙的特点,对该公式进行一定的修正,具体内容如下:
本文的钢板连接件为“强连接”设计,因此,预制部分的高度H需要扣除连接件部分的高度,即采用折减系数:
| $ \gamma=1-\frac{H_{\text {钢 }}}{H} $ | (5) |
式中H钢为连接件的高度。
由于半装配试件存在新旧混凝土结合面,从而对墙体受剪承载力具有一定削弱作用,本文假定以最不利的情况(即结合面完全脱开),并根据装配率来修正预制部分及后浇部分剪跨比,修正系数为:
| $ \omega=\frac{H}{\alpha_{\mathrm{zp}} h_{\mathrm{w}} \lambda}=\frac{1}{\alpha_{\mathrm{zp}}} $ | (6) |
| $ \omega^{\prime}=\frac{H}{0.5\left(1-\alpha_{\mathrm{zp}}\right) h_{\mathrm{w}} \lambda}=\frac{2}{1-\alpha_{\mathrm{zp}}} $ | (7) |
式中: hw为剪力墙全墙长度,包括两片边缘现浇段长度和中间预制段长度,ω为预制部分修正系数,ω′为后浇部分修正系数。
因此,修正后的剪力墙受弯、受剪承载力计算公式:
| $ \begin{gathered} \alpha_{ \mathrm{zp}} V_{1} \gamma H+\left(1-\alpha_{\mathrm{zp}}\right) V_{1} H+N\left(h_{\mathrm{w} 0}-0.5 h_{\mathrm{w}}\right)= \\ \frac{1}{\gamma_{\mathrm{RE}}}\left[A_{\mathrm{s}}^{\prime} f_{\mathrm{y}}^{\prime}\left(h_{\mathrm{w} 0}-a_{\mathrm{s}}^{\prime}\right)-0.5\left(h_{\mathrm{w} 0}-1.5 x\right)^{2} b_{\mathrm{w}} f_{\mathrm{yw}} \rho_{\mathrm{w}}+\alpha_{1} f_{\mathrm{c}} b_{\mathrm{w}} x\left(h_{\mathrm{w} 0}-0.5 x\right)\right] \end{gathered} $ | (8) |
| $ \begin{gathered} V_{2}=\frac{1}{\gamma_{\mathrm{RE}}}\left\{\left[\frac{1}{\omega \lambda-0.5}\left(0.4 f_{\mathrm{t}} b_{\mathrm{w}} h_{\mathrm{w} 0}+0.1 \alpha_{\mathrm{zp}} N\right)+\right.\right. \\ \left.0.8 f_{\mathrm{yh}} \frac{A_{\mathrm{sh}}}{s} h_{\mathrm{w} 0}\right]+2\left[\frac { 1 } { \omega ^ { \prime } \lambda - 0 . 5 } \left(0.4 f_{\mathrm{t}} b_{\mathrm{w}} h_{\mathrm{w} 0}^{\prime}+\right.\right. \\ \left.\left.\left.0.1 \frac{1-\alpha_{\mathrm{zp}}}{2} N\right)+0.8 f_{\mathrm{yh}} \frac{A_{\mathrm{sh}}}{s} h_{\mathrm{w} 0}^{\prime}\right]\right\} \end{gathered} $ | (9) |
式中:fc、ft为混凝土轴心抗压、抗拉强度设计值,x为受压区高度(式(10)),fyw、fyh、f′y为竖向、水平、边缘受压钢筋抗拉强度设计值,ρw为竖向钢筋配筋率,V1、V2为分别按受弯破坏和受剪公式计算的水平荷载,取二者较小值为峰值荷载Pm,γRE为承载力抗震调整系数,A′s为边缘构件受压钢筋面积,α′s为受压区钢筋合力点到受压区边缘的距离,Ash为所有水平分布钢筋截面积,s为水平分布钢筋间距,h′w0为边缘构件截面有效高度。
| $ N=\alpha_{1} f_{\mathrm{c}} b_{\mathrm{w}} x-\left(h_{\mathrm{w} 0}-1.5 x\right) b_{\mathrm{w}} f_{\mathrm{yw}} \rho_{\mathrm{w}} $ | (10) |
2) 峰值位移Δm。参考文献[17]并结合本文试验及模拟结果,拟合出Δm的计算式:
| $ \begin{gathered} \frac{\varDelta_{\mathrm{m}}}{\varDelta_{\mathrm{y}}}=6.51-5.1 n+4.31 \lambda_{\mathrm{v}}-0.8 \lambda- \\ 0.93 \alpha_{\text {zр }}-5.01 \gamma_{\mathrm{a}} \end{gathered} $ | (11) |
式中:Δm为峰值位移,Δy为屈服位移,γa为边缘构件面积与全截面积之比。
3) 强化段刚度Km。在确定了Pm及Δm后,可以得到Km为
| $ K_{\mathrm{m}}=\frac{P_{\mathrm{m}}-P_{\mathrm{y}}}{\varDelta_{\mathrm{m}}-\varDelta_{\mathrm{y}}} $ | (12) |
1) 极限荷载Pu计算为
| $ P_{\mathrm{u}}=0.85 P_{\mathrm{m}} $ | (13) |
2) 极限刚度Ku。Ku取为初始刚度的0.1倍。
3) 极限位移Δu。在确定了Pu及Ku后,可得到Δu计算式:
| $ \varDelta_{\mathrm{u}}=\varDelta_{\mathrm{m}}+\frac{0.15 P_{\mathrm{m}}}{K_{\mathrm{u}}} $ | (14) |
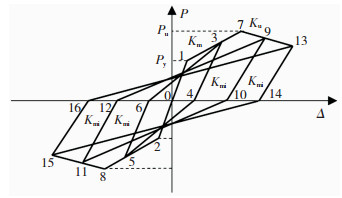
由试验的滞回曲线可知,当荷载小于屈服荷载前的滞回环基本呈斜直线,加卸载刚度未发生明显变化,因此,直至屈服点阶段,滞回曲线的加卸载刚度可取式(4)计算的屈服前刚度Ky;随着荷载进一步增大,在超过屈服荷载后的滞回环卸载曲线的刚度Kmi开始有一定程度的退化。因此,为了确定滞回曲线,需要确定卸载刚度Kmi。
如图 12所示,卸载点3、9、13、5、11、15及其对应的荷载卸载为零的点4、10、14、6、12、16所连接得到的线段即为卸载曲线,其斜率即为卸载刚度Kmi。通过对试验数据及有限元模拟结果的拟合发现,Kmi/Ky和Δi/Δy的关系以幂指数形式的相关系数最高:
| $ K_{\mathrm{mi}}=\alpha\left(\frac{\varDelta_{i}}{\varDelta_{\mathrm{y}}}\right)^{\beta} K_{\mathrm{y}} $ | (15) |
|
图 12 恢复力模型示意 Fig. 12 Schematic of restoring force model |
式中Kmi为卸载刚度,Ky为屈服前刚度,Δi为卸载点的位移,Δy为屈服点位移,α、β为系数,计算公式:
| $ \begin{gathered} \alpha=0.94-1.16 n-0.42 \lambda_{\mathrm{v}}+0.2 \lambda+ \\ 0.3 \alpha_{\text {zp }}+0.07 \gamma_{\mathrm{a}} \end{gathered} $ | (16) |
| $ \begin{gathered} \beta=0.18-0.09 n-0.01 \lambda_{\mathrm{v}}- \\ 0.29 \lambda-0.14 \alpha_{ \mathrm{zp}}-0.05 \gamma_{\mathrm{a}} \end{gathered} $ | (17) |
确定试件在往复荷载作用下的恢复力模型,需要确定其滞回规则,即正反向加卸载的路径。图 12为本文装配式剪力墙恢复力模型的滞回规则,具体描述:
1) 当荷载加载至屈服点Py(点1)之前,墙体基本处于弹性阶段,没有刚度退化及残余变形,因此这一阶段的加载刚度、卸载刚度均为屈服前的刚度Ky。路径为0-1-0-2-0。
2) 当荷载超过屈服点Py(点1)但未达到峰值点Pm(点7)时,先按骨架曲线加载到某一点(点3),该阶段卸载时发生刚度退化,按式(15)计算的卸载刚度Kmi卸载到荷载为零,再反向加载到与点3对应的负方向位置(点5),卸载时按卸载刚度Kmi卸载到荷载为零,再加载到点3。路径为0-1-3-4-5-6-3。
3) 当荷载超过峰值点Pm(点7)但未达到极限点Pu(点13),先按骨架线加载到点9,卸载刚度按式(15)计算,路径为0-1-7-9-10-11-12-9。
如此反复,便可得到滞回曲线。
3.3 恢复力模型验证根据本文提出的特征点计算公式计算得到相应计算值,并与试验值对比见表 4;图 13为螺栓连接装配式剪力墙的计算骨架曲线与试验骨架曲线的对比。由图 13可知,计算骨架曲线与试验骨架曲线的吻合度较好,各个特征点较为吻合,可以基本反映试件在水平荷载作用下的受力及变形发展情况。
| 表 4 各阶段的计算值与理论值对比 Tab. 4 Comparison of calculated and theoretical values at each stage |

|
图 13 计算骨架线与试验骨架线对比 Fig. 13 Comparison of calculated skeleton lines and test skeleton lines |
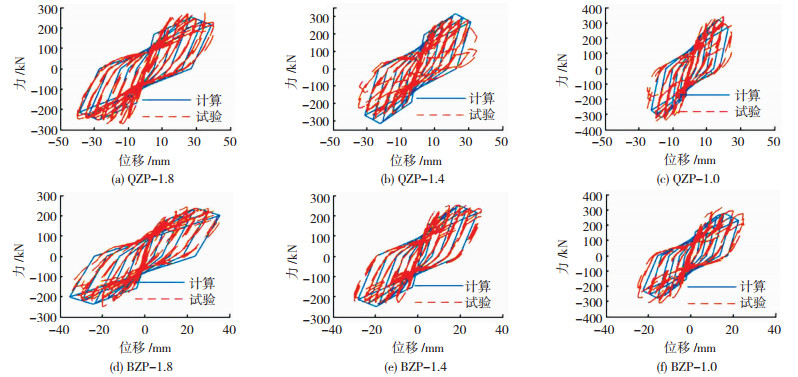
本文提出的恢复力模型与各试验滞回曲线对比见图 14。可看到,计算曲线与试验曲线总体吻合良好,说明本文提出的恢复力模型可以较好地反映这种采用螺栓水平连接的全装配和半装配剪力墙的抗震滞回性能。
|
图 14 计算滞回曲线与试验滞回曲线对比 Fig. 14 Comparison of calculated hysteresis curves and test hysteresis curves |
1) 本文提出的全装配及半装配钢筋混凝土剪力墙水平螺栓连接方式,传力可靠,采用该种连接的装配剪力墙破坏形式与对应现浇结构一致,且由于连接钢框对混凝土的约束增强作用,全装配试件的承载力要大于半装配剪力墙及现浇剪力墙。
2) 建立了三折线骨架模型,给出了屈服点、峰值点及极限点的承载力及位移计算公式。
3) 提出了在不同阶段的卸载刚度计算公式和各个阶段的滞回规则,建立了螺栓连接装配式剪力墙的恢复力模型,可以为该类结构的弹塑性时程分析提供参考。
| [1] |
刘剑, 薛彦涛, 王翠坤, 等. 钢-混凝土预制梁连接区段抗震性能试验研究[J]. 建筑结构学报, 2021, 42(3): 53. LIU Jian, XUE Yantao, WANG Cuikun, et al. Experimental study on seismic performance of connection zone of spliced precast steel-concrete beam[J]. Journal of Building Structures, 2021, 42(3): 53. DOI:10.14006/j.jzjgxb.2019.0314 |
| [2] |
潘广斌, 蔡健, 杨春, 等. 冷挤压套筒连接RC装配式剪力墙抗震性能试验研究[J]. 建筑结构学报, 2021, 42(5): 111. PAN Guangbin, CAI Jian, YANG Chun, et al. Experimental study on seismic behavior of precast RC shear walls connected by extruding steel sleeves and rebars[J]. Journal of Building Structures, 2021, 42(5): 111. DOI:10.14006/j.jzjgxb.2020.C034 |
| [3] |
SUN Jian, QIU Hongxing, LU Bo. Experimental validation of horizontal joints in an innovative totally precast shear wall system[J]. Journal of Southeast University (English Edition), 2015, 31(1): 124. DOI:10.3969/j.issn.1003-7985.2015.01.021 |
| [4] |
SUN Jian, QIU Hongxing, LU Yong. Experimental study and associated numerical simulation of horizontally connected precast shear wall assembly[J]. The Structural Design of Tall and Special Buildings, 2016, 25(13): 659. DOI:10.1002/tal.1277 |
| [5] |
赵斌, 王庆杨, 吕西林. 采用全装配水平接缝的预制混凝土剪力墙抗震性能研究[J]. 建筑结构学报, 2018, 39(12): 48. ZHAO Bin, WANG Qingyang, LV Xilin. Research on seismic behavior of precast concrete walls with fully assembled horizontal joints[J]. Journal of Building Structures, 2018, 39(12): 48. DOI:10.14006/j.jzjgxb.2018.12.006 |
| [6] |
王威, 熊峰, 徐锦祥, 等. 预制装配式混凝土墙板螺栓连接抗剪性能试验研究[J]. 四川大学学报(工程科学版), 2016, 48(6): 86. WANG Wei, XIONG Feng, XU Jinxiang, et al. Experimental study on shear behavior of the bolt connection of prefabricated concrete wallboard[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(6): 86. DOI:10.15961/j.jsuese.2016.s2.014 |
| [7] |
BORA C, OLIVA M G, NAKAKI S D, et al. Development of a precast concrete shear-wall system requiring special code acceptance[J]. PCI Journal, 2007, 52(1): 122. DOI:10.15554/pcij.01012007.122.135 |
| [8] |
姜绍飞, 赵剑, 刘展鹏, 等. 一种适用于框架剪力墙结构的装配式剪力墙及其安装方法: ZL 201710297079.2[P]. 2019-06-07 JIANG Shaofei, ZHAO Jian, LIU Zhanpeng, et al. An assembly shear wall and its installation method suitable for frame shear wall structure: ZL 201710297079.2[P]. 2019-06-07 |
| [9] |
高层建筑混凝土结构技术规程: JGJ 3—2010[S]. 北京: 中国建筑工业出版社, 2010
|
| [10] |
郭子雄, 杨勇. 恢复力模型研究现状及存在问题[J]. 世界地震工程, 2004, 20(4): 47. GUO Zixiong, YANG Yong. State-of-the-art of restoring force models for RC structures[J]. World Earthquake Engineering, 2004, 20(4): 47. |
| [11] |
PENZIEN J. Dynamic response of elasto-plastic frames[J]. American Society of Civil Engineers, 1962, 127(2): 1322. DOI:10.1061/TACEAT.0008537 |
| [12] |
CLOUGH R W. Effect of stiffness degradation on earthquake ductility requirements[C]//Proceedings of the 2nd Japan Earthquake Engineering Symposium. Tokyo: JSCE, 1966: 37
|
| [13] |
TAKEDA T, SOZEN M A, NIELSEN N N. Reinforced concrete response to simulate earthquakes[J]. Journal of the Structural Division, 1970, 96: 2557. DOI:10.1061/JSDEAG.0002765 |
| [14] |
RAMBERG W, OSGOOD W R. Description of stress-strain curves by three parameters: No. 902[R]. Washington DC: National Advisory Committee for Aeronautics, 1943
|
| [15] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010
|
| [16] |
SUPARTONO F, SIDOROFF F. Anisotropic damage modeling for brittle elastic materials[J]. Archives of Mechanics, 1985, 37(4/5): 521. |
| [17] |
张松, 吕西林, 章红梅. 钢筋混凝土剪力墙构件恢复力模型[J]. 沈阳建筑大学学报(自然科学版), 2009, 25(4): 644. |
| [18] |
PRIESTLEY M J N, KOWALSKY M J. Aspects of drift and ductility capacity of rectangular cantilever structural walls[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 1998, 31(2): 73. DOI:10.5459/bnzsee.31.2.73-85 |
 2022, Vol. 54
2022, Vol. 54



 8
8