2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
非线性时程分析是结构抗震性能评估普遍采用的方法之一,也是被认为准确性较高的方法。但是,复杂的有限元模型和较长的地震动记录使得结构的非线性时程分析十分耗时。特别是在进行增量动力分析或易损性分析时,通常需要数百甚至更多次的计算,此时提高分析效率成为一个十分重要的问题。地震动的强烈震动段决定了结构地震反应的大小,仅将强烈震动段作为输入是提高结构地震反应分析计算效率的直观方法。由于地震动强烈震动段多位于记录的初始部分,因此可以采用截断地震动尾部的方法缩短非线性时程分析的时间。
工程输入地震动持时的确定即为如何截取地震动强烈震动段的过程。虽然地震动持时的定义方法较多[1-2],但是基于Arias强度的95%持时以及75%持时的地震动记录截取方法是目前最为广泛使用的方法[3-4]。文献[5]研究表明,使用基于Arias强度的持时概念截取的地震动对规则的中低层结构的变形影响较小,但对于长周期高层结构影响较大,并不能保证对所有周期的结构表现良好。文献[6]提出了一种地震动的截取方法,该方法的思路是保证地震动截取前后结构最大位移反应不变,并且考虑结构周期延长、高阶模态、结构屈服强度估计时存在的不确定性对截取地震动的影响,因此与基于Arias强度的持时定义(与结构动力特性无关、与结构地震反应无关)相比更具有合理性。但文献[6]方法在地震动截取过程中需要进行多次数据处理工作,计算过程十分繁琐,计算相对耗时,并且对计算程序编写者的理论基础要求也较高。因此,提出保留文献[6]方法优点、同时在实现上方便且具有较高计算效率的方法十分有意义。
近年来,人工智能方法在多个领域显示出了巨大的应用潜力,也逐渐被用于解决地震工程领域的问题。文献[7]开发了基于长短期记忆递归神经网络(LSTM)的深度学习方法,用于线性和非线性结构地震反应时程的预测。文献[8]采用多输入的卷积神经网络预测了非线性单自由度体系在随机激励下的最大反应,并以地震动作为输入进行了验证。文献[9]分别采用P-DNN深度学习模型和自适应算法,对震前和震后区域范围内的损失进行了评估。利用大量数据作为驱动,深度学习端到端的学习方式直接由输入映射输出,避免了传统方法繁琐的计算过程,在简化计算的同时也可以提高计算效率。因此,本文在考虑结构动力特性影响和保证结构最大位移反应在地震动截取前后不变的基础上,尝试将人工智能方法用于地震动持时的预测,并使用2个实际的结构对提出的地震动持时预测方法进行了验证。
1 地震动持时确定方法与数据集使用地震动持时的概念是认为地震动的强烈震动段将起到决定性作用,截取掉非强烈震动段会在某些问题上获得更方便的操作或结果。在用于地震反应的时程分析时,应该保证截取掉非强烈震动段后结构的最大地震反应基本保持不变,否则截取前后的地震动可以认为不再具有等效性。因此,当作为地震动输入用于结构地震反应分析时,地震动持时的确定应该考虑待分析结构的动力特性,也应该考虑结构地震反应的等效性。另一方面,使用待分析的实际结构进行反复尝试,最终获得地震动截取时间点的方法难以实行,也违背了节省计算时间的初衷。因此,目前关于地震动持时的确定通常建立在与实际结构有关的一个单自由度体系上,然后将得到的结果直接用于实际结构。
当使用单自由度体系时,涉及如何确定单自由度体系的周期、屈服强度等参数以及明确它们与实际多自由度结构的关系。其中,单自由度体系的周期可以设置成实际结构的基本周期,并应考虑周期在强震下可能出现的延长以及实际结构中高阶模态的影响,因此应考虑比基本周期大和小的周期,这些周期可以使用多个具有不同周期的单自由度体系来考虑;对于实际结构屈服强度的估计往往存在一定的不准确性,因此可以采用一系列具有不同屈服强度系数的单自由度体系来考虑。虽然使用了一系列的单自由度体系,但是单自由度体系与实际的多自由度体系仍存在差异(对于中低层结构,多自由度结构可以等效成单自由度体系;而对于高层结构,等效成单自由度体系可能并不合适)。因此,可以认为如果对于单自由度体系持时的确定是合理的,那么对于实际的多自由度结构也可能合理;如果对于单自由度体系不合理,那么对于实际的多自由度结构合理的可能性也会较低。
文献[6]提出的地震动持时确定方法考虑了结构动力特性,同时保证了截取前后结构最大位移反应不变。针对一个基本周期为T的结构和一条输入地震动,该方法首先对周期为0.2T~2T(以0.1 s间隔取周期点)、屈服强度折减系数从1到6的一系列单自由度体系进行地震时程反应分析,并记录每个单自由度体系最大位移反应出现的时刻,将所有单自由度体系对应时刻的最大值作为本条地震动的截取时刻点。其中,0.2~2倍的系数范围参考了美国ASCE/SEI 7-16[10]规范中关于考虑周期延长和高阶模态的建议。算例表明,与使用基于Arias强度确定地震动持时的方法相比,使用该方法确定地震动持时的结构地震反应的误差较小,是一种更具合理性的地震动截取方法。但是,该方法计算具有不同屈服强度的单自由度体系最大位移反应的过程相当于计算非弹性位移反应谱,过程繁琐(以T=2.5 s的结构为例,需要进行270次时程分析并判断每一次的最大值出现时刻才能获得1条地震动的截取时间点),不利于工程师理解并在实际工程的快速运用。
采用如下方式建立深度学习模型中用于训练的样本数据集。利用文献[6]中给出的地震动持时确定方法并使用该文中使用的地震动(1 338条来自美国太平洋地震工程研究中心强震数据库[11]的地震动),本文假设了60个实际结构,对应的初始周期取0.1~6 s,周期间隔取0.1 s,计算了1 338条地震动关于每个结构的地震动持时的截取时间点,生成共计1 338×60 =80 280个数据样本。将数据样本按照约6.3∶0.7∶3的比例分为训练集、验证集和测试集,即训练集、验证集、测试集分别有50 576、5 620、24 084个样本。训练时使用训练集对深度神经网络模型中的参数权值进行更新,验证时使用验证集查看训练效果,其重点在于查看模型在训练过程中的预测精度是否有变差的趋势,测试时使用测试集评价模型的实际泛化能力。为了提高模型训练的精度和收敛速度,在训练前对输入数据样本进行了标准化预处理。
2 地震动持时预测模型深度学习方法可以实现端到端的预测,即直接输入与地震动和结构有关的特征即可预测出地震动的截取时间点,由于训练好的模型在进行预测时计算效率非常高,因此有可能弥补文献[6]方法存在的问题。文献[6]提出的方法涉及地震动非弹性位移反应谱的计算,因此如果在深度学习模型中直接将地震动时程作为输入,比较难以建立直观的输入和输出之间的联系。考虑到地震动参数是地震动的有效表征,本文以地震动参数和结构周期作为模型的输入特征,预测给定结构的地震动截取时间点。
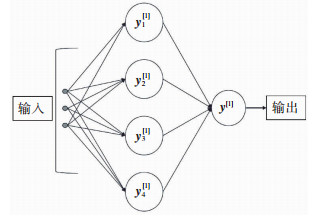
地震动持时预测是一个回归问题,其输入数据是没有时间关联性的地震动参数和结构参数。针对输入数据的特点,本文采用全连接神经网络进行训练和预测。全连接神经网络具有很好的非线性拟合能力,而且该网络的结构简单,计算效率高。全连接神经网络通常由输入层、全连接层、Dropout层和输出层组成,输入层的每个神经元对应一个输入特征,全连接指上一层神经元与其下一层神经元完全连接,Dropout层是由文献[12]提出,能在训练过程中随机将该层的一些输出特征舍弃以避免网络过拟合。对于回归问题,网络的输出层只有一个单元,是没有激活的线性层。仅包括输入层、单个全连接隐藏层及输出层组成的单层全连接神经网络见图 1,每个神经元通过上一层输出的加权运算与激活运算传递,利用反向传播算法对网络参数进行优化。该网络的神经元节点结构见图 2,节点首先执行线性运算,再通过激活函数进行非线性运算,计算公式为
| $ \boldsymbol{y}_{j}^{[i]}={\sigma}\left(\boldsymbol{w}_{j}^{[i] \mathrm{T}} \boldsymbol{x}_{j}^{[i]}+\boldsymbol{b}_{j}^{[i]}\right) $ | (1) |
|
图 1 单层全连接神经网络 Fig. 1 Single-layer of fully-connected neural network |

|
图 2 网络输入输出关系 Fig. 2 Network input and output relationship |
式中:xj[i]和yj[i]为第i层j节点的输入和输出数据,σ为激活函数,wj[i]和bj[i]为权重和偏置项。
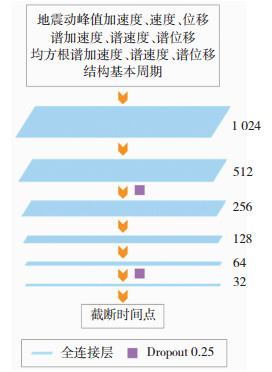
深度学习模型常通过增加隐藏层的个数、每层神经元的个数以及增加训练轮次来加强输入参数和预测结果的非线性特征,因此本文所建模型主要调节以上参数来获得最优模型。经反复调试优化,最终确定模型的框架见图 3。
该模型框架包括输入层、输出层和中间层,其中中间层由2个Dropout层和6个全连接层组成,Dropout层的舍弃率取0.25,全连接层激活函数采用Relu函数。由于数据集较大,为提高内存利用率,使模型加速收敛,采用小批量梯度下降法训练网络模型,经调试确定Batch size大小取为128。模型建立和训练的程序编制在Python语言的深度学习程序库TensorFlow[13]中完成。
该深度学习模型的整个训练过程使用基于梯度下降的Adam优化算法,Adam优化算法是一种学习率自适应算法[14],其在不断的批次训练中更新权重与偏差,使损失函数误差值最小化后得到最优模型,并在训练过程中通过评价指标评价模型在测试数据上的预测效果。由于地震动截取时间点预测问题为回归问题,因此该模型的损失函数使用了式(2)所示的均方误差损失函数,评价指标使用了式(3)所示的平均绝对误差来评估模型泛化能力。
| $ L_{\mathrm{s}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{\text {true }}^{(i)}-y_{\text {pred }}^{(i)}\right)^{2} $ | (2) |
| $ L_{\mathrm{a}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|y_{\text {true }}^{(i)}-y_{\text {pred }}^{(i)}\right| $ | (3) |
式中:ytrue为地震动截取时间点真实值,ypred为地震动截取时间点预测值。
由于无法在初始阶段判断使用哪些地震动参数作为输入特征可得到比较好的预测结果,因此该深度学习模型在初始阶段的备选输入特征变量共采用了43个(覆盖了目前关于地震动参数研究中涉及的主要参数),其中42个参数为地震动参数,剩余1个输入特征为结构基本周期,输出为地震动的截取时间点。42个地震动参数见表 1,其中31个参数从地震动中直接提取,11个参数从结构弹性反应提取,表 1参数的含义和计算方法参考文献[6]。
| 表 1 作为备选输入特征变量的42个地震动参数 Tab. 1 Forty-two ground motion parameters as alternative input parameters |
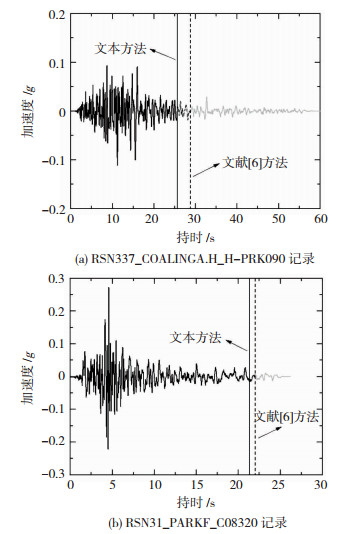
结构基本周期作为仅有的结构参数,必须作为特征变量输入。而42个地震动参数之间存在着相关性,且计算繁琐,将对使用者造成不便,不需要全部作为输入。因此,本文在基于均方误差损失函数和平均绝对误差评价指标基本不变的原则上,对地震动参数进行了多轮筛选,其筛选过程及最终训练结果见表 2。最终筛选出9个地震动参数:地震动峰值加速度、速度、位移,谱加速度、谱速度、谱位移,均方根谱加速度、谱速度、谱位移。最终9个地震动参数和结构基本周期共同作为输入特征,这些地震动参数均为常用的地震动参数且十分易于计算,其中地震动峰值加速度、速度、位移,可直接通过原始地震动记录求出,结构基本周期的谱加速度、谱速度和谱位移可通过地震动弹性反应谱直接得到,均方根谱加速度、谱速度和谱位移可经由地震动弹性反应谱计算得到。模型结构见图 3,最终模型预测结果的均方误差和平均绝对误差分别为4.18和1.22,说明该模型具有良好的泛化能力。图 4给出了深度学习模型训练过程中训练集和验证集的平均绝对误差,随着训练轮次的增加,平均绝对误差先呈下降趋势最后趋于平稳,说明模型参数已达到最佳状态。截取后的记录舍弃了强烈震动段后无影响的弱震动部分,从而减少了计算时间,节省了计算量。图 5给出了结构基本周期为1 s时,在1 338条地震动中随机选择的2条地震动记录截取前后的对比情况,图 5中竖实线为本文方法预测的持时,竖虚线为文献[6]方法预测的持时。
| 表 2 输入地震动参数筛选 Tab. 2 Selection of input ground motion parameters |

|
图 4 误差随训练轮次变化情况 Fig. 4 Variation of error with epoch |
|
图 5 截取前后的地震动记录 Fig. 5 Ground motion before and after truncation |
为了验证本文提出的方法在实际多自由度结构上的适用性,选取了两个分别为4层和16层的钢筋混凝土框架结构,两个框架结构的平面图和立面图见图 6,纵向跨度和横向跨度分别为36 m和15 m。4层框架结构总高13.2 m,采用C30混凝土。16层框架结构总高52.8 m,采用C45混凝土。两个框架结构的钢筋采用HRB335热轧钢筋,弹性模量取为2×105 MPa,结构的详细构件截面尺寸信息和配筋信息可参考文献[6]。4层框架结构和16层框架结构的基本周期分别为0.9 s和2.6 s,计算时取横向的一榀框架作为计算模型。将地震动按深度学习模型预测的截取时间点进行截断,计算结构的最大层间位移角,并且和原始地震动、文献[6]方法、基于Arias强度的95%持时及75%持时方法得到的结构最大层间位移角进行对比,验证基于人工智能方法得到的地震动持时预测方法在实际多自由度结构上的适用性。

|
图 6 算例框架结构(mm) Fig. 6 Frames used in calculation (mm) |
在1 338条地震动的测试集数据内选取400条地震动记录作为验证,利用本文建立的深度学习模型,预测结构基本周期分别为0.9 s和2.6 s时400条地震动的截取时间点,按预测值对地震动进行处理并将截取前后的记录输入到4层和16层框架结构中进行时程分析,计算截取前后的相对误差γ:
| $ \gamma=\frac{\left|D_{\text {true }}-D_{\text {pred }}\right|}{D_{\text {true }}} \times 100 \% $ | (4) |
式中:γ为截取前后最大层间位移角的相对误差,Dtrue为使用原始地震动得到的最大层间位移角,Dpred为按预测值截取地震动后结构的最大层间位移角。
统计地震动截取前后框架结构每层最大层间位移角的相对误差在5%以内、5%~20%以及20%以上范围内的地震动数量所占的比例,将本文方法、文献[6]方法、基于Arias强度的95%持时及75%持时方法进行对比。采用IDARC-2D软件[15]进行计算,各方法所得误差见表 3和表 4,表中相对误差在0.01%以下的被认为可以忽略不计而没有被记入,即表中5%以内对应的为0.01%~5%误差范围的地震动数量占比。图 7为4种方法下4层和16层结构最大层间位移角误差。
| 表 3 4层结构最大层间位移角误差 Tab. 3 Errors of maximum story drift ratios of 4-story frame |
| 表 4 16层结构最大层间位移角误差 Tab. 4 Errors of maximum story drift ratios of 16-story frame |
|
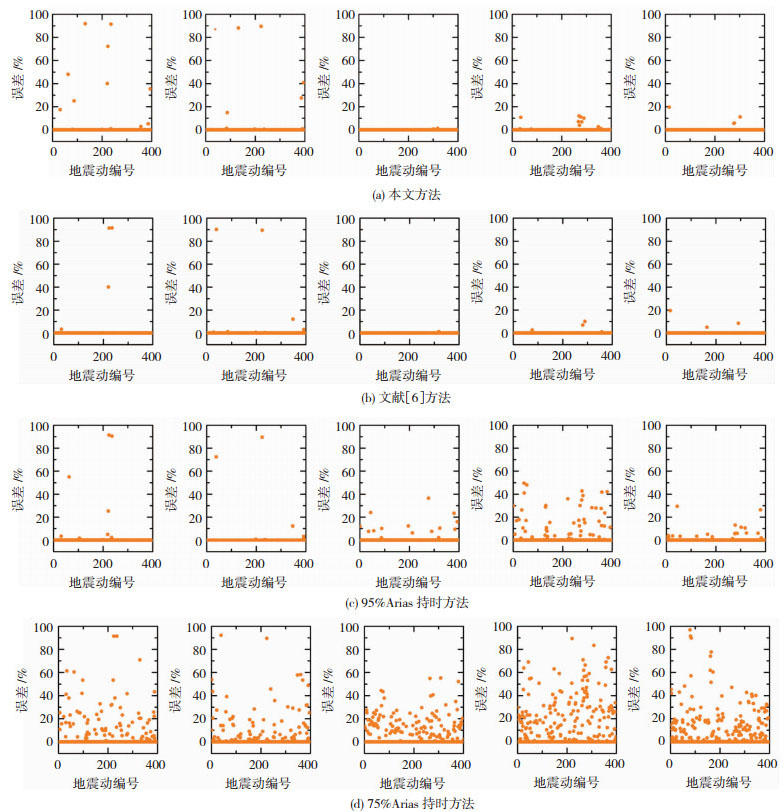
图 7 4种方法下截取前后4层和16层框架结构最大层间位移角误差(每行从左至右分别是4层框架第1、4层,16层框架第1、8、16层) Fig. 7 Errors of maximum story drift ratios of 4-story and 16-story frames under four methods before and after truncation (the five figures in each line are the 1st and 4th stories in 4-story frame, and 1st, 8th, and 16th stories in 16-story frame, respectively) |
由4种方法的计算结果对比可知,4种方法截取地震动均会带来一定误差。4种方法对应结构最大层间位移角平均误差见表 5,对于4层结构,文献[6]方法所得出的各层相对误差在0.01%以上的地震动记录所占比例最低,本文方法和95%Arias持时方法次之,但3种方法得出的各层相对误差在0.01%以上的地震动数量所占比例均在3.5%以内。75%Arias持时方法得出的各层相对误差在0.01%以上的地震动记录所占比例高达23.37%,误差较大。对于16层框架结构,文献[6]方法所得出的各层相对误差在0.01%以上的地震动数量所占比例最低,本文方法次之,但2种方法得出的各层相对误差在0.01%以上的地震动数量所占比例均在1.5%以内。基于Arias强度确定持时方法的各层相对误差在5%以上的地震动记录所占比例较高,95%Arias持时方法最高可达8.03%,75%Arias持时方法最高可达40.1%。
| 表 5 4种方法对应的结构最大层间位移角平均误差 Tab. 5 Average errors of maximum story drift ratios of 4-story and 16-story frames under four methods |
综上比较,75%Arias持时方法计算误差较大,甚至并不适用于时程反应分析中地震动的截取。95%Arias持时方法虽然在4层框架结构上表现良好,但在16层框架结构上的误差较大,这可能是由于该方法没有考虑结构周期对地震动截取的影响,造成对任何周期的结构截取后的地震动没有区别。本文方法的计算误差与文献[6]方法相当但计算效率更高,且本文方法比95%Arias持时方法和75%Arias持时方法精度好、适用性强。
4 结论提出了一种基于人工智能方法预测工程输入地震动持时的方法,与目前广泛使用的基于Arias强度的95%持时方法和75%持时方法进行了对比,得到如下结论:
1) 本文提出的基于人工智能方法的地震动持时确定方法可以保证在截取前和截取后地震动作用下结构的最大位移反应不变,同时本文方法与文献[6]方法相比,精度相当,但计算更简便、效率更高。对于现有广泛使用的地震动持时确定方法,由于没有考虑结构反应的等效,可能引起非常可观的误差。针对文中的算例,基于Arias强度的75%持时截取前和截取后的结构反应相差巨大,远低于本文提出的方法。
2) 本文提出的工程输入地震动持时确定方法考虑了结构周期的影响。若不考虑结构周期的影响,则针对任何结构截取后的地震动均相同,既可能造成保守的结果,亦可能造成不安全的结果。针对文中算例,对于4层结构,本文提出的方法与基于Arias强度的95%持时所得误差相近,且误差都较小;但对于16层结构,95%持时的误差明显过高。本文提出的方法在计算精度和适用性方面优于95%持时方法。
3) 本文未对地震动的前端进行截取,严格来说不是持时的完整内涵,而是属于地震动末端的截取方面的研究,前端截取需要进一步的研究工作。另外,本文方法的出发点是最大位移反应等效,因此对于发生在最大位移反应之后的滞回耗能引起的结构累计损伤是无法考虑的。
| [1] |
谢礼立, 张晓志. 地震动记录持时与工程持时[J]. 地震工程与工程振动, 1988, 8(1): 31. XIE Lili, ZHANG Xiaozhi. Accelerogram-based duration and engineering duration of ground motion[J]. Earthquake Engineering and Engineering Vibration, 1988, 8(1): 31. |
| [2] |
BOMMER J J, MARTINEZ-PEREIRA A. The effective duration of earthquake strong motion[J]. Journal of Earthquake Engineering, 1999, 3(2): 127. DOI:10.1080/13632469909350343 |
| [3] |
BRADLEY B A. Correlation of significant duration with amplitude and cumulative intensity measures and its use in ground motion selection[J]. Journal of Earthquake Engineering, 2011, 15(6): 809. DOI:10.1080/13632469.2011.557140 |
| [4] |
郎需军, 王文明, 马瑞升, 等. 强震持时效应对输电塔-线体系倒塌影响分析[J]. 世界地震工程, 2016, 32(4): 188. LANG Xujun, WANG Wenming, MA Ruisheng, et al. Effect analysis of strong ground motions duration on the collapse of transmission tower-line system[J]. World Earthquake Engineering, 2016, 32(4): 188. |
| [5] |
KHALOO A, NOZHATI S, MASOOMI H, et al. Influence of earthquake record truncation on fragility curves of RC frames with different damage indices[J]. Journal of Building Engineering, 2016, 7: 23. DOI:10.1016/j.jobe.2016.05.003 |
| [6] |
LI Shuang, HE Yiting, WEI Yuliang. Truncation method of ground motion records based on the equivalence of structural maximum displacement responses[J]. Journal of Earthquake Engineering, 2021. DOI:10.1080/13632469.2020.1868364 |
| [7] |
ZHANG Ruiyang, CHEN Zhao, CHEN Su, et al. Deep long short-term memory networks for nonlinear structural seismic response prediction[J]. Computers and Structures, 2019, 220: 55. DOI:10.1016/j.compstruc.2019.05.006 |
| [8] |
KIM T, KWON O S, SONG J. Response prediction of nonlinear hysteretic systems by deep neural networks[J]. Neural Networks, 2019, 111: 1. DOI:10.1016/j.neunet.2018.12.005 |
| [9] |
KIM T, SONG J, KWON O S. Pre- and post-earthquake regional loss assessment using deep learning[J]. Earthquake Engineering and Structural Dynamics, 2020, 49(7): 657. DOI:10.1002/eqe.3258 |
| [10] |
Minimum design loads for buildings and other structures: ASCE/SEI 7-16[S]. Reston: American Society of Civil Engineers, 2016
|
| [11] |
PEER ground motion database[DB/OL]. [2021-08-01]. https://ngawest2.berkeley.edu
|
| [12] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[Z/OL]. arXiv: 1207.0580. (2012-07-03). https://arxiv.org/abs/1207.0580v1
|
| [13] |
ABADI M, BARHAM P, CHEN Jianmin, et al. TensorFlow: a system for large-scale machine learning[C]//Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation. Savannah: [s. n. ], 2016: 265
|
| [14] |
KINGMA D P, BA J L. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference for Learning Representations. San Diego: [s. n. ], 2015
|
| [15] |
REINHORN A M, ROH H, SIVASELVAN M, et al. IDARC-2D Version 7.0: inelastic damage analysis of reinforced concrete structures: MCEER-09-0006[R]. Buffalo: University at Buffalo, 2010
|
 2022, Vol. 54
2022, Vol. 54