调谐液体阻尼器(TLD)是一种简单有效的被动控制装置,以容器中的液体随着结构晃动时产生的对容器壁的反力进行减震。TLD在实际工程中已有大量应用,多被运用于控制高层结构的风致振动[1-2],故对TLD的研究更多针对控制高层结构风振响应[3]。用于控制风振响应的TLD不可避免地对结构地震响应产生影响。同时,由于TLD在价格、安装等方面的优势,也有学者研究如何将其用于降低结构地震响应[4-5],结果表明利用TLD进行结构减震设计可行有效,故应进一步完善TLD在地震荷载作用下对结构影响的研究,以指导实际工程。
既有对TLD的减震效果研究主要在时域内展开,且由于水箱自身非线性较强,数值模拟难以准确反应其性能,试验则为对其更有效的研究手段。在对TLD减震性能进行研究时采用的试验方法多为传统的振动台试验[6-8]和实时混合试验[9],但受限于振动台的承载能力,通常需要对结构和TLD进行大比例缩尺。Zhu等[10]采用实时子结构试验研究了TLD的尺寸效应,结果表明对TLD进行缩尺会高估原型TLD对结构的减震性能,而实时混合试验将被控结构作为数值子结构进行数值计算,TLD作为物理子结构进行物理测试,运用该试验技术只需将水箱安装在振动台上,可极大的增加TLD试验试件尺寸,更真实的反应TLD的动力特性。Wang等[11]进行了TLD的实时子结构试验,研究了质量比及结构阻尼比对TLD减震效果的影响,研究表明质量比的增加可以提高TLD的减震效率,且TLD更适用于阻尼比低的结构。运用实时子结构试验对TLD的减震性能进行研究有效可行,故作为本研究的试验方法。
李忠献等[12]在频域内对具有相同频带间隔的多重TLD对一阶振型的控制效果进行了仿真分析,结果表明多重TLD的减震设计比单个TLD减震系统具有更好的稳定性和适用性。而从频域角度就TLD对高层结构减震效果进行的试验研究鲜有报道。本文选取一个20层钢框架结构,设计一系列正弦激励下的振动台实时子结构试验,对地震动频率与结构一阶频率比、TLD频率与结构一阶频率比、TLD质量比、结构阻尼比及正弦波输入幅值等对TLD频域减震性能的影响进行研究。
1 TLD实时混合试验系统 1.1 试验系统组成本研究中使用的实时子结构试验系统由计算系统、振动台加载系统以及数据采集传输系统组成,见图 1。实时计算系统由搭建在Simulink中的数值求解模块实现,能够实时求解结构的运动方程,生成位移信号。振动台加载系统由用以驱动振动台的控制器、振动台和油泵组成。数据传输系统中的数据采集平台由采集卡和Simulink实时模块组成,利用导线分别连接采集卡与控制器、采集卡与传感器,以实现数据的实时传输。其中,振动台的台面尺寸为3 m×3 m,最大承载质量为10 t,最大位移125 mm。

|
图 1 高层结构TLD减震实时子结构试验系统 Fig. 1 Configuration of real-time substructure testing system for TLD controlled high-rise building |
本试验选用Ohtori等[13]建议的用于结构减震性能评价的标准结构模型,它可以代表典型的高层钢结构建筑。20层Benchmark模型的计算标高为80.77 m,第1层的地震质量为5.63×105 kg,第2~19层的地震质量为5.52×105 kg,第20层的地震质量为5.84×105 kg。为了便于在频域内就关键参数对TLD减震性能的影响以及振动台实时子结构试验中实时数值仿真的实现,将原模型在Sap2000中进行建模将原模型简化为层剪切模型,简化后的层剪切模型与Sap2000直接建模得到的结构前三阶频率误差不超过1%,说明层剪切模型较好的保持了原结构的动力特性。20层层剪切模型的参数见表 1,阻尼采用Rayleigh阻尼,结构阻尼比设置为5%,识别得到结构基频为0.262 4 Hz。
| 表 1 20层Benchmark结构层剪切模型参数 Tab. 1 Shear model parameters of 20-story Benchmark structure |
TLD频率fTLD的计算公式为
| $ f_{\mathrm{TLD}}=\frac{1}{2 {\rm{\pi }}} \sqrt{\frac{{\rm{\pi }} g}{L} \tanh \left(\frac{{\rm{\pi }} h}{L}\right)} $ | (1) |
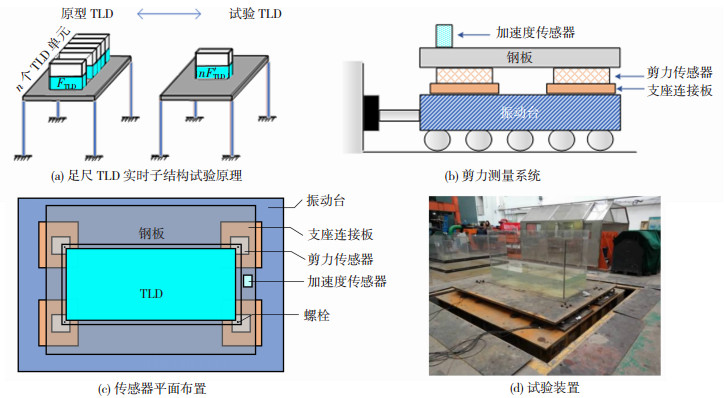
式中:L为振荡方向的长度,h为水深。为更易实现设计所需的TLD的动力特性,实际工程中所采用的TLD常由多个规格相同的TLD单元组成,且Wang等[11]证明了原型TLD的反力FTLD可由每个TLD单元实测的反力F′TLD乘以TLD单元数n后得到,故本试验采用Zhu等[14]给出的全尺寸TLD试验方法,将作为物理子结构的TLD划分为n个具有相同几何尺寸的TLD单元,仅制作其中一个TLD单元在振动台上进行测试,将实测的反力fTLD乘以TLD单元数n后得到TLD系统的总力FTLD并反馈给数值子结构,以进行下一步计算,实现足尺TLD试验的原理见图 2(a)。
|
图 2 足尺TLD试验原理、剪力测量系统、传感器平面布置与试验装置 Fig. 2 Schematic of full-scale TLD test, shear force measurement system, sensor layout, and testing setup |
选用易于观察液体运动状态且轻质高强的亚克力有机玻璃制作矩形TLD水箱模型,本试验TLD设计为控制结构一阶振型,故在保证调谐频率满足的情况下,应尽可能使水箱尺寸最大[9]。设计水箱的长度、宽度分别为2、0.8 m,考虑晃动波高后设计水箱的高度为1.2 m(此处的长宽高均为内部尺寸),以保证试验过程中液体不至于洒出。经强度验算后,水箱壁厚度与水箱底板厚度分别选取为15、10 mm。
1.4 剪力测量系统本试验的剪力测量系统由4个2×2布置的三分力传感器和一个加速度传感器组成,见图 2(b)。由第3节可知,本试验采用的物理子结构仅为一个TLD单元,所产生的反力较小,而剪力传感器量程较大,为提高剪力测量精度,在水箱与剪力传感器之间增设一块钢板。钢板与剪力传感器采用螺栓连接,三分力传感器与振动台之间用一块过渡连接板连接,传感器平面布置见图 2(c)。故三分力传感器测量的剪力包含了两部分:由水的晃动产生的反力fTLD以及钢板和水箱壁产生的惯性力。因此,作为物理子结构的一个TLD单元产生的反力fTLD应由三分力传感器测得的剪力减去钢板和水箱壁产生的惯性力。将剪力测量系统与TLD连接好后的试验装置见图 2(d)。
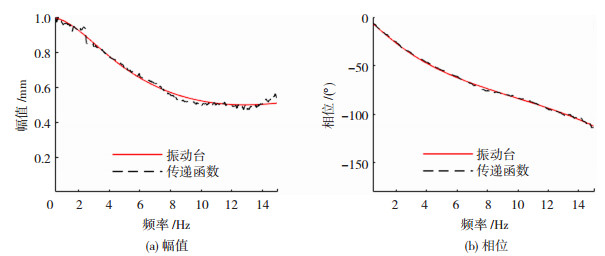
1.5 加载系统动力补偿加载系统的动力性能补偿是保证成功实现实时子结构试验的关键环节。对于以作动器为加载系统的实时子结构试验,通常将其动力特性简化为只有相位滞后没有幅值误差的纯时滞系统,通过时滞补偿提高其控制精度。振动台作为加载系统时,动力性能更复杂,同时存在相位滞后和幅值误差,需要对其采取特殊的补充措施。在振动台台面布置传感器后,将白噪声输入振动台,对振动台系统识别,使用传递函数辨识振动台特性,振动台特性与传递函数辨识得到的幅值与相位对比见图 3。振动台加载时幅值误差和相位滞后并存。为了准确补偿该动力特性,对其进行了四阶传递函数建模。图 3所示虚线与实线重合,说明该理论模型很好的描述了相位和幅值特性。
|
图 3 振动台特性与传递函数辨识对比 Fig. 3 Comparison of shaking table characteristics and transfer function identification results |
基于该理论模型,采用本文作者提出的基于模型的逆动力补偿控制器[15]对振动台动力特性进行在线实时补偿。
1.6 试验系统性能验证对剪力测量系统精度进行验证。将作为物理子结构的水箱在不装水的情况下进行振动台试验,采用幅值为25 mm的El Centro波作为激励,钢板和水箱总质量为2 127 kg。将钢板和水箱产生的惯性力作为理论值,与三分力传感器测得的力比较,结果见图 4。理论值与三分力传感器测值几乎重合,说明本试验的剪力测量系统有较高的精度。

|
图 4 反力测量系统精度验证 Fig. 4 Accuracy verification of measurement system for reaction force |
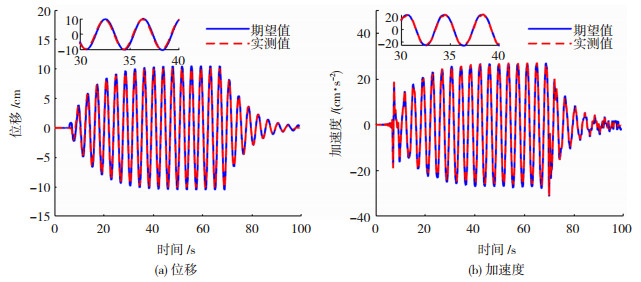
对本文搭建的如图 2(d)所示的试验系统精度进行验证。数值子结构选用建立的二十自由度Benchmark模型,在Simulink中进行求解,向制作的TLD水箱中注水至水深为114 mm,放在振动台上进行测试。输入幅值为10 mm,频率为0.262 4 Hz,持时为60 s的正弦激励,得到数值子结构输入振动台的位移及加速度的仿真响应以及振动台实现的位移及加速度的实际响应,实测结果见图 5。
|
图 5 振动台预期与实现的响应 Fig. 5 Expected and achieved responses of shaking table |
位移时程曲线与加速度时程曲线均吻合较好,可以说明,本文搭建的实时子结构试验系统具有较高的精度,能满足TLD减震下高层结构抗震性能试验研究需求。
2 试验结果从频域角度评价TLD的减震性能可更好理解时域响应机理。TLD减震试验大多采用地震动激励,只能在时域中评价其减震性能。从傅里叶分解角度来看,地震动由一系列简谐波组成,每一个简谐激励即代表了频域中的一个频响成分。因此,采用简谐激励即可通过时域试验研究TLD在频域中的减震性能。本文通过设置一系列正弦激励试验,分别研究了地震动与结构一阶频率比βin、TLD与结构一阶频率比β0、TLD质量比γm、结构阻尼比ξ以及输入幅值Ain对TLD减震规律的影响。其中,荷载频率比βin定义为正弦波输入频率与结构基频的比值,频率比β0定义为TLD频率与结构基频的比值。同时,根据结构高阶频率设置了正弦波输入工况,研究了TLD对非主控模态的影响。
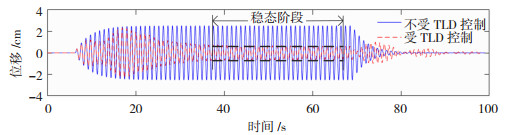
试验的结构模型采用1.2节中给出的二十层Benchmark模型,所采用的水箱参数同1.3节。减震指标选为结构顶层的减震率,分别从位移与加速度两方面进行评价。由结构动力学基本原理[16]可知,动荷载激励下线性结构动力响应的频域放大系数等同于不同频率正弦激励下结构时程响应幅值放大倍数。基于此原理,通过正弦激励获得TLD减震前后结构响应的动力放大系数,而后根据减震前后的放大系数即可求得TLD的减震率。图 6给出了TLD减震前后的结构顶层位移响应。本文试验研究中为了保证振动台的安全,在正弦输入开始阶段输入进行了削峰,从而使得开始阶段TLD的响应不够稳定。选择图中黑色虚线范围内的时程为TLD-结构在正弦激励下的稳态响应,取该范围响应峰值的均值对TLD的减震性能进行评价。由该范围的稳态响应可知,TLD减震前后结构响应规律稳定,采用上述线性结构动力响应假设进行频域减震评价是合理的。因此,位移减震率Rd及加速度减震率Ra的计算式:
| $ R_{\mathrm{d}}=1-\frac{\left|H_{\mathrm{d}}\right|}{\left|G_{\mathrm{ld}}\right|} \\ $ | (2) |
| $ R_{\mathrm{a}}=1-\frac{\left|H_{\mathrm{a}}\right|}{\left|G_{\mathrm{la}}\right|} $ | (3) |
|
图 6 结构顶层稳态响应 Fig. 6 Steady-state response of top story of structure |
式中:下标d和a分别代表相对位移与绝对加速度,H表示正弦激励下结构附加TLD时结构顶层响应稳态阶段的幅值,G表示正弦激励下结构未附加TLD时结构顶层在正弦激励下结构顶层响应与TLD减震时程中对应阶段的幅值。
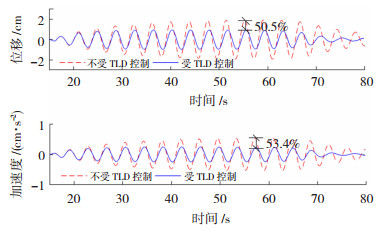
2.1 输入荷载与结构一阶频率比减震频带是评价减震装置性能的重要指标。本试验所采用的结构质量及刚度保持不变,则改变输入的正弦激励的频率,即可实现对荷载频率比的改变。为研究主控结构一阶模态条件下TLD的减震频带,据式(1)计算得当水箱中水深为114 mm时,TLD主频和结构一阶频率一致,TLD单元数为548个,对应质量比为2%,结构阻尼比设置为5%。采用不同频率正弦波输入模拟不同输入荷载与结构一阶频率比,根据结构基频0.262 4 Hz选择正弦输入频率,分别为0.209 9、0.249 3、0.262 4、0.275 5、0.446 1、0.524 8 Hz,对应的荷载频率比分别为0.8、0.95、1、1.05、1.7、2,输入幅值为15 mm,持时60 s。当输入荷载为结构基频时结构顶层的位移与加速度时程曲线见图 7,可见结构在TLD控制下位移与加速度的稳态阶段响应较不受控时均降低了约50%。荷载频率比不同时的结构顶层位移与加速度的减震率结果见图 8。
|
图 7 位移与加速度时程响应曲线 Fig. 7 Time history response curves of displacement and acceleration |
|
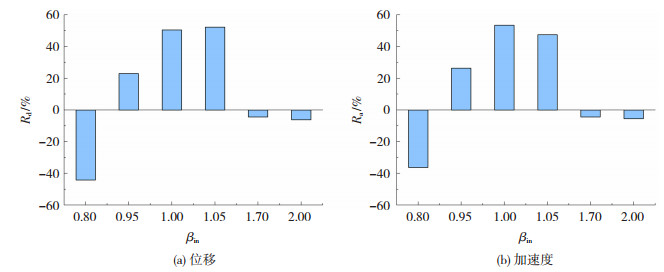
图 8 输入荷载频率对TLD减震率的影响 Fig. 8 Effect of input excitation frequency on seismic reduction rate of TLD |
当TLD与结构主控频率一致时,TLD对主控频率的地震动成分有最优的控制效果,即当输入荷载与结构一阶频率比=1时,加速度和位移减震综合效果最好。当该频率比>1时,减震效果随该频率比的增加逐渐减低,最终会产生少量的负作用;可当该频率比 < 1时,随该频率比的降低减震效果急剧下降,且很快出现较大的负作用。这说明,TLD对高于主控频率的成分有较好的控制效果,且不利作用很小,而对低于主控频率的成分减震效果较差,且极易出现不利作用。
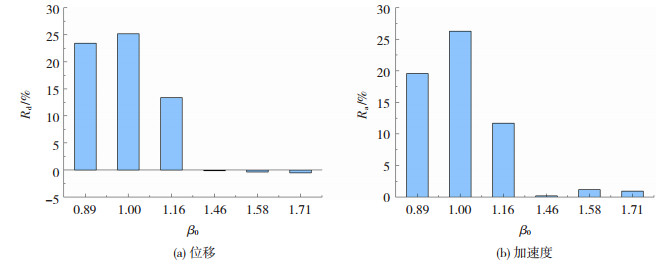
2.2 TLD与结构一阶频率比TLD的参数优化设计是保证其减震效果的前提,其中最重要的参数为TLD的自振频率。由Housner理论可知,TLD的自振频率由水箱长度和水深确定,本试验水箱长度保持不变,通过改变向同一水箱中加入的水的深度来改变频率。已有研究表明TLD频率与结构基频接近时减震效果较好[11],故以结构一阶模态自振频率为基准开展研究,水深分别设为90、114、155、253、300、362 mm,对应的TLD频率与结构一阶频率比分别为0.89、1、1.16、1.46、1.58、1.71,TLD单元数分别取为385、274、223、137、115、96个,则质量比保持为0.5%,结构阻尼比设为5%,输入的正弦波的频率为结构基频0.262 4 Hz,幅值为6 mm,持时60 s。试验得到的频率比不同时的减震率见图 9。当输入荷载频率为结构主控频率时,TLD与结构自振频率比在0.89~1.16范围内结构位移和加速度减震率均明显,且在频率比为1时减震效果较好。当TLD频率远离结构主控频率时,减震效果变弱。与图 8所示输入频域影响不同,远离主控频率后TLD产生的负作用很小。这说明,TLD更适于控制因结构共振产生的动力响应,对结构自振频率范围以外的强迫振动控制效果不明显。
|
图 9 TLD频率对减震率的影响 Fig. 9 Effect of TLD frequency on seismic reduction rate of TLD |
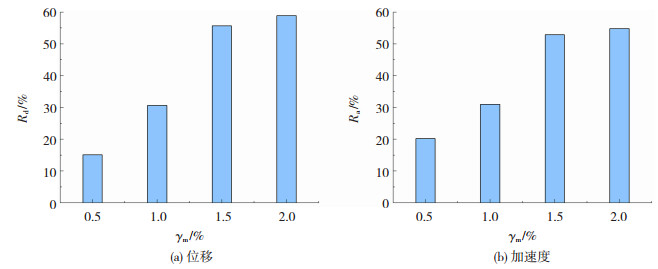
TLD安装在结构内部,质量过大会增加结构竖向荷载,太小减震效果不明显。为了进一步证实TLD质量比对减震效果的影响,采用表 1所示数值子结构的参数,通过改变TLD单元数n即可研究不同TLD质量比对TLD减震效果的影响。为研究质量比对TLD的减震效果影响,试验设计如下:水箱中水深为114 mm,以保证TLD自振频率与结构一阶频率一致,TLD单元数分别设为137、274、411、548个,对应的质量比分别为0.5%、1%、1.5%、2%,结构阻尼比设置为5%,正弦波输入频率为结构一阶频率0.262 4 Hz,输入幅值为3 mm,持时60 s。试验得到的质量比不同时的减震率见图 10。在输入荷载频率和TLD自振频率均与结构主控频率一致时,在质量比为0.5%~1.5%的范围内,随质量比的增加,减震率增幅明显,当质量比达到1.5%时,TLD对结构共振频率处响应控制效果超过50%。这说明增加TLD质量对结构的减震效果起到明显的改善作用,与Wang等[11]得到的结果一致,在2%范围内应尽可能地增加TLD质量比以保证其减震效果。
|
图 10 TLD质量比对TLD减震率的影响 Fig. 10 Effect of TLD mass ratio on seismic reduction rate of TLD |
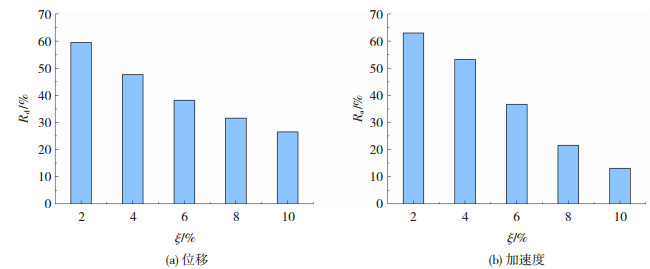
结构阻尼比是影响结构动力响应的主要因素,而以往在对TLD的减震性能进行研究时,常选用频率成分丰富的地震波进行激励,鲜有规律性结论。为研究结构阻尼比对TLD的减震效果影响,试验设计如下:水箱中水深为114 mm,TLD自振频率与结构一阶频率一致,TLD单元取274个,对应质量比1%,结构阻尼比分别设为2%、4%、6%、8%、10%,正弦波输入频率为结构一阶频率,输入幅值为6 mm,持时60 s。试验得到的减震率与不同结构阻尼比之间的关系见图 11。在输入荷载频率和TLD自振频率均与结构主控频率一致时,在结构阻尼比为2%~10%范围内,减震率随结构阻尼比增加而明显减小,TLD对结构的减震效果变差。这说明TLD对大阻尼比结构减震效果不明显,例如,TLD控制与配置阻尼器的减震体系配合就无法发挥各自的减震效果。
|
图 11 结构阻尼比对TLD减震率影响 Fig. 11 Effect of structural damping ratio on seismic reduction rate of TLD |
TLD靠水的运动减震,输入荷载幅值将影响其运动行为。为研究输入幅值对TLD的减震效果影响,设计试验如下:水箱中水深为114 mm,TLD自振频率与结构一阶频率一致,TLD单元取137个,对应质量比0.5%,结构阻尼比设置为5%,正弦波输入频率为结构一阶频率,输入幅值分别为3、4、6、8、10 mm,持时60 s。试验得到的输入幅值不同时的减震率见图 12。在输入荷载频率和TLD自振频率均与结构主控频率一致时,随输入幅值的增加,位移减震率逐渐减小,减小幅度在10%以内,加速度减震率几乎不受影响。这说明TLD在控制因结构共振产生的动力响应成分时,受输入幅值影响较小,鲁棒性较好。

|
图 12 输入幅值对TLD减震率的影响 Fig. 12 Effect of input amplitude on seismic reduction rate of TLD |
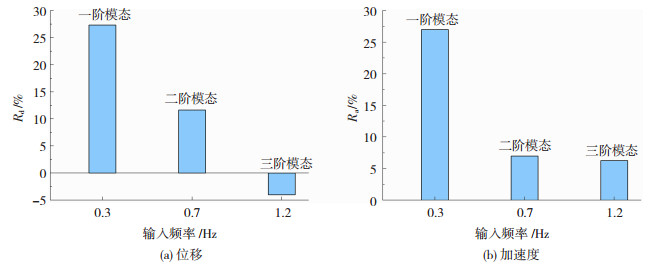
实际应用中设置TLD的核心目的为控制结构风振,同时为减小TLD竖向荷载的影响,实际工程中大多采用小质量TLD,集中在一阶模态比分散给多阶模态效果更好。本文主要讨论因风振而设置的TLD对高层结构地震响应规律的影响。相比于风振作用,地震激励包含的频域成分更丰富,为讨论根据一阶模态设计的TLD对高阶模态地震响应的控制效果,设计了如下试验:结构模型为如表 1所示的Benchmark模型,TLD水深为114 mm,TLD单元数为548个,对应质量比2%,结构阻尼比设置为5%,输入正弦激励的频率分别取为结构一阶频率0.262 4 Hz、结构二阶频率0.713 7 Hz、结构三阶频率1.165 Hz,以代表地震波中的高阶成分,输入幅值为15 mm,持时60 s。得到TLD对不同模态的减震率结果见图 13。在TLD自振频率与结构一阶频率一致时,TLD对一阶模态的控制效果最好,对二、三阶模态也有一定减震效果,对高阶振型的位移响应会产生较小的不利影响。这说明,TLD对高层结构临近主控振型的非主控振型共振产生的动力响应成分也能起到一定的减震效果,而由于TLD减震频带较窄[12],由2.1节可知,针对控制一阶振型而设计的TLD的减震频带仅为结构基频附近,对处于减震频带外的频率对应的模态仍可能产生不利影响,但产生的不利影响较小。
|
图 13 TLD对非主控模态的减震性能 Fig. 13 Seismic reduction performance of TLD for non-controlled modes |
针对TLD对高层结构减震效果频域试验研究结果不足的问题,使用实时子结构试验,通过一系列正弦激励下的TLD-结构足尺试验,研究了TLD减震性能受输入荷载与结构一阶振型频率比、TLD与结构一阶频率比、TLD质量比、结构阻尼比及输入幅值的影响,并探讨了TLD对结构非主控振型的减震能力,主要结论如下:
1) 建立了适用于大尺寸TLD减震试验的实时子结构试验系统,提高了TLD减震试验精度,极大的降低了振动台缩尺试验对TLD减震性能测试造成的误差。
2) 当TLD频率与其主控频率一致时,TLD对结构主控振型对应频率产生的共振响应有很好的减震效果,对其余频率成分控制效果较差,对小于TLD自振频率的地震动成分可能产生较大的不利影响。
3) 当TLD质量比 < 2%时,增加质量比能较大的提高减震效果,但增加结构阻尼比会较大地降低减震效果。
4) 在降低TLD主控振型产生的共振响应成分方面:TLD频率在0.89~1.16倍结构频率范围内时,均有较好减震效果,但远离结构自振频率会较大的弱化减震效果;对于共振响应成分的控制效果,对输入幅值不敏感;TLD对临近主控振型的非主控振型成分仍有一定减震作用,也可能对结构产生较小的负作用。
5) 本研究由于振动台性能限制,只针对小质量比TLD在较小输入幅值下的减震效果进行了研究,对大质量TLD及输入幅值较大时TLD进入强非线性后对结构的减震性能研究有待进一步开展。
| [1] |
WAKAHARA T, OHYAMA T, FUJI K. Suppression of wind-induced vibration of a tall building using Tuned Liquid Damper[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1992, 43(1/2/3): 1895. DOI:10.1016/0167-6105(92)90610-M |
| [2] |
瞿伟廉, 陈妍桂. TLD对珠海金山大厦主楼风振控制的设计[J]. 建筑结构学报, 1995(3): 21. QU Weilian, CHEN Yangui. Design of controlled wind vibration response of the main building of Jinshan mansion in Zhuhai with TLD[J]. Journal of Building Structures, 1995(3): 21. DOI:10.14006/j.jzjgxb.1995.03.004 |
| [3] |
李暾, 李创第, 章本照. 带TLD结构随机风振响应的解析解[J]. 哈尔滨工业大学学报, 2003, 35(4): 437. LI Tun, LI Chuangdi, ZHANG Benzhao. Analytic solution to random wind-induced response of structures with TLD[J]. Journal of Harbin Institute of Technology, 2003, 35(4): 437. DOI:10.3321/j.issn:0367-6234.2003.04.014 |
| [4] |
BANERJI P, MURUDI M, SHAH A H, et al. Tuned liquid dampers for controlling earthquake response of structures[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(5): 587. DOI:10.1002/(SICI)1096-9845(200005)29:5<587:AID-EQE926>3.0.CO;2-I |
| [5] |
张敏政, 丁世文. 利用水箱减振的结构控制研究[J]. 地震工程与工程振动, 1993(1): 40. ZHANG Minzheng, DING Shiwen. Study on structure control using tuned sloshing damper[J]. Earthquake Engineering and Engineering Dynamics, 1993(1): 40. DOI:10.13197/j.eeev.1993.01.006 |
| [6] |
FUJINO Y, PACHECO B M, CHAISERI P, et al. Parametric studies on tuned liquid damper (TLD) using circular containers by free-oscillation experiments[J]. Structural Engineering, 1988, 5(2): 381. |
| [7] |
钱稼茹, 丁雄. 用TLD减小电视塔动力反应的振动台试验研究[J]. 建筑结构学报, 1995(5): 32. QIAN Jiaru, DING Xiong. Shaking table experiment study on the suppression dynamic response of a TV tower with TLD[J]. Journal of Building Structures, 1995(5): 32. DOI:10.14006/j.jzjgxb.1995.05.004 |
| [8] |
楼梦麟, 牛伟星, 宗刚, 等. TLD控制的钢结构振动台模型试验研究[J]. 地震工程与工程振动, 2006, 26(1): 145. LOU Menglin, NIU Weixing, ZONG Gang, et al. Shaking table model test for a steel structure under control of tuned liquid damper[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(1): 145. DOI:10.3969/j.issn.1000-1301.2006.01.024 |
| [9] |
LEE S K, PARK E C, MIN K W, et al. Real-time hybrid shaking table method for the performance evaluation of a tuned liquid damper controlling seismic response of building structures[J]. Journal of Sound & Vibration, 2007, 302(3): 596. |
| [10] |
ZHU Fei, WANG Jinting, JIN Feng, et al. Real-time hybrid simulation of the size effect of tuned liquid dampers[J]. Structural Control and Health Monitoring, 2017, 24(9): e1962. DOI:10.1002/stc.1962 |
| [11] |
WANG Jinting, GUI Yao, ZHU Fei, et al. Real-time hybrid simulation of multi-story structures installed with tuned liquid damper[J]. Structural Control and Health Monitoring, 2016, 23(7): 1015. DOI:10.1002/stc.1822 |
| [12] |
李忠献, 王森林, 姜忻良. 高层建筑地震反应最优多重TLD控制[J]. 地震工程与工程振动, 1996, 16(4): 69. LI Zhongxian, WANG Senlin, JIANG Xinliang. Optimal multiple TLD control for seismic responses of tall buildings[J]. Earthquake Engineering and Engineering Vibration, 1996, 16(4): 69. |
| [13] |
OHTORI Y, CHIRSTENSON R E, SPENCER B F. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004, 130(4): 366. DOI:10.1061/(ASCE)0733-9399(2004)130:4(366) |
| [14] |
ZHU Fei, WANG Jinting, JIN Feng, et al. Real-time hybrid simulation of full-scale tuned liquid column dampers to control multi-order modal responses of structures[J]. Engineering Structures, 2017, 138: 74. DOI:10.1016/j.engstruct.2017.02.004 |
| [15] |
TANG Zhenyun, DIETZ M, HONG Yue, et al. Performance extension of shaking table based real time dynamic hybrid testing through full state control via simulation[J]. Structural Control and Health Monitoring, 2020, 27(10): e2611. DOI:10.1002/stc.2611 |
| [16] |
刘晶波, 杜修力, 李宏男, 等. 结构动力学[M]. 北京: 机械工业出版社, 2005: 55. LIU Jingbo, DU Xiuli, LI Hongnan, et al. Structural dynamics[M]. Beijing: China Machine Press, 2005: 55. |
 2022, Vol. 54
2022, Vol. 54


