隔震技术作为结构被动控制的有效方法,目前已广泛应用于工程实践,其性能与效果已在多次地震灾害中得到检验[1]。在上部结构与下部基础结构之间设置由叠层橡胶支座和黏滞阻尼器组成的基础隔震层是结构的一种有效隔震方式。能量设计原理[2]指出,由于基础隔震层抗侧刚度明显小于上部结构,地震能量一旦输入,就立即以弹性应变能的形式储存在具有侧向柔性变形能力的叠层橡胶支座中,并在往复振动下由黏滞阻尼器吸收耗散,隔震层的最大变形由此得到控制,同时避免了上部结构中支承结构重量的梁柱等主要构件的损伤。
国内外学者针对基础隔震结构响应特性与阻尼器参数优化设计进行了一定的研究。文献[1]指出设置阻尼器能够降低隔震层的剪力与位移响应,但同时也会在不同程度上激发结构的高阶振型。文献[3-4]通过对两基础隔震框架结构模型的分析,指出近震下阻尼器附加阻尼比的增加将减小上部结构响应,但远震下则会增大上部结构响应。文献[5]提出了隔震层设置黏滞阻尼器基础隔震结构基于最大响应发生时刻能量平衡方程的响应预测方法,并进一步研究了隔震层同时设置黏滞阻尼器与滞回型阻尼器时的响应预测法,给出了相应计算简图。文献[6]同样针对同时设置这2类阻尼器的隔震层进行了研究,并建议为较好地控制隔震层位移,黏滞阻尼器的附加阻尼比应在0.3与0.4之间。文献[7]针对设置阻尼器的基础隔震结构提出了最优剪力设计法,通过计算总剪力系数预测式极小值,能够确定令隔震层总剪力为最小时所需的阻尼置放量,并能够优化上部结构层间剪力。文献[8]针对隔震层设置黏滞阻尼器结构提出基于非支配排序遗传算法的阻尼器参数多目标优化方法,可获得每条地震波的Pareto前沿,并建议在优化目标阈值的基础上获得用于实际的阻尼器参数。文献[9]针对阻尼器位置与参数优化提出分布优化设计法,该法根据能量最小优化准则得到结构相应位置上的阻尼器优化参数。文献[10]根据隔离非线性方法并结合改进的基于种群可行性的约束优化遗传算法提出一种减震结构阻尼器优化方法,具有较高的设计与计算效率。文献[11]针对框架-摇摆墙结构附加阻尼器的研究中,利用层间位移角、加速度和楼层位移与相应无控结构响应之比构建设计目标函数,利用非线性动力时程分析确定了不同设计目标下的阻尼器优化布置方式。文献[12]对附加调谐黏性质量阻尼器结构的研究则提出利用主结构剪力降低率和层间位移降低率构建目标函数,同样利用时程分析得到了阻尼器优化置放量。可见,上述优化设计方法或仅关注位移等单一响应,或需借助动力时程分析,尚缺少一种针对隔震层设置阻尼器的基础隔震结构易于设计人员计算使用的优化设计方法。本文提出的直接求解隔震层位移响应比和总剪力响应比线性组合函数极小值的设计法,则能够根据位移与剪力加权系数的不同组合方式经计算确定相应附加阻尼系数。
本文将基于地震结束时刻能量平衡方程给出设置黏滞阻尼器的基础隔震层最大位移与总剪力响应的简易预测方法,并在该预测法的基础上提出根据隔震层位移和剪力设计侧重确定黏滞阻尼器附加阻尼系数的优化设计方法,并给出详细设计流程。最后通过对某6层基础隔震结构进行黏滞阻尼器优化设计和时程分析验算,验证了该设计方法的可行性。
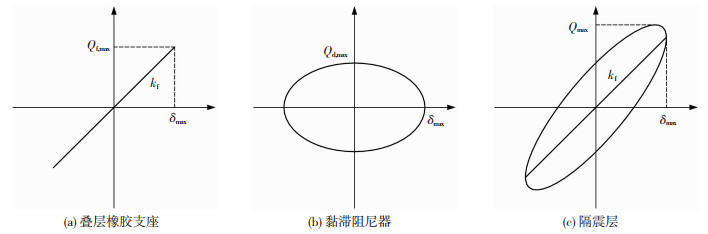
1 设计原理 1.1 基于地震结束时刻能量平衡方程的响应预测方法本文讨论剪切型模型[13]。附加黏滞阻尼器隔震层各单元的恢复力特性见图 1。下标f表示作为柔性支承单元的叠层橡胶支座;下标d表示黏滞阻尼器。橡胶支座侧向刚度记为kf,地震下剪力记为Qf,最大剪力记为Qf, max。黏滞阻尼器的恢复力特性为线性速度相关型,阻尼系数为c,地震下阻尼器剪力记为Qd,最大剪力为Qd, max。隔震层总剪力记为Q,最大总剪力为Qmax;隔震层位移记为δ,最大位移为δmax。结构基本周期为Tf,基本频率为ωf,上部结构总质量为M。为使推导公式形式简便同时令设计偏于安全,设地震输入能量全部由隔震层耗散,并忽略橡胶支座的黏性阻尼耗能。
|
图 1 恢复力特性 Fig. 1 Restoring force characteristics |
由图 1(c)可以看出,由于黏滞阻尼器与叠层橡胶支座的最大剪力存在相位差,隔震层最大总剪力并非二者之和。简谐振动下阻尼器剪力Qd与位移δ关系曲线可表示为椭圆方程:
| $ \frac{\delta^{2}}{\delta_{\max }^{2}}+\frac{Q_{\mathrm{d}}^{2}}{Q_{\mathrm{d}, \max }^{2}}=1 $ | (1) |
故任意时刻的隔震层总剪力Q可表示为
| $ Q=Q_{\mathrm{f}}+Q_{\mathrm{d}}=k_{\mathrm{f}} \delta \pm \frac{Q_{\mathrm{d}, \max }}{\delta_{\max }} $ | (2) |
对式(2)求极值可得到隔震层最大剪力Qmax与支座最大剪力Qf, max以及黏滞阻尼器最大剪力Qd, max之间的关系:
| $ Q_{\max }=\sqrt{Q_{\mathrm{f}, \max }^{2}+Q_{\mathrm{d}, \max }^{2}} $ | (3) |
定义叠层橡胶支座剪力系数αf、黏滞阻尼器剪力系数αd(以下称阻尼量)、隔震层总剪力系数α1:
| $ \alpha_{\mathrm{f}}=\frac{Q_{\mathrm{f}, \max }}{M g}, \alpha_{\mathrm{d}}=\frac{Q_{\mathrm{d}, \max }}{M g}, \alpha_{1}=\frac{Q_{\max }}{M g} $ | (4) |
由式(3)可知各系数之间有如下关系:
| $ \alpha_{1}=\sqrt{\alpha_{\mathrm{f}}^{2}+\alpha_{\mathrm{d}}^{2}} $ | (5) |
由于地震动结束结构停止振动时其弹性应变能已完全消散,隔震层设置黏滞阻尼器的基础隔震结构在结构停止振动t0的时刻能量平衡方程为
| $ W_{\mathrm{d}, \mathrm{h}}\left(t_{0}\right)=E\left(t_{0}\right) $ | (6) |
式中Wd, h表示黏滞阻尼器的黏性阻尼耗能,E表示地震输入能量。引入基准响应量,定义仅设置叠层橡胶支座时的隔震层基准位移δ0和基准剪力系数α0[7]:
| $ \delta_{0} =\frac{T_{\mathrm{f}} V_{\mathrm{E}}}{2 {\rm{ \mathsf{ π} }}} $ | (7) |
| $ \alpha_{0} =\frac{2 {\rm{ \mathsf{ π} }} V_{\mathrm{E}}}{T_{\mathrm{f}} g} $ | (8) |
式中VE为地震输入能量速度换算值,有
| $ E\left(t_{0}\right)=\frac{M V_{\mathrm{E}}^{2}}{2} $ | (9) |
由此定义RD=δmax/δ0为设置黏滞阻尼器相对于不设阻尼器的隔震层位移响应比。同理,定义RA=α1/α0为隔震层总剪力响应比。黏滞阻尼器总耗能Wd, h(t0)可表示为
| $ W_{\mathrm{d}, \mathrm{h}}\left(t_{0}\right)=n {\rm{ \mathsf{ π} }} Q_{\mathrm{d}, \max } \delta_{\max }=2 {\rm{ \mathsf{ π} }} n \frac{\alpha_{\mathrm{d}}}{\alpha_{0}} \frac{\alpha_{\mathrm{f}}}{\alpha_{0}} \frac{M V_{\mathrm{E}}^{2}}{2} $ | (10) |
式中n为黏滞阻尼器的等价往复次数,表示黏滞阻尼器耗散的能量相当于位移幅值滞回环曲线循环的次数,由以下经验公式[5]取值:
| $ n= \begin{cases}2.0, & T_{\mathrm{f}} \leqslant 5 \\ -0.33 T_{\mathrm{f}}+3.67, & 5<T_{\mathrm{f}}<8 \\ 1.0, & T_{\mathrm{f}} \geqslant 8\end{cases} $ | (11) |
将式(9)和式(10)代入式(6)可得:
| $ 2 {\rm{ \mathsf{ π} }} n \frac{\alpha_{\mathrm{d}}}{\alpha_{0}} \frac{\alpha_{\mathrm{f}}}{\alpha_{0}}=1 $ | (12) |
因此叠层橡胶支座剪力系数αf与基准剪力系数α0之比αf/α0可利用阻尼量αd表示为
| $ \frac{\alpha_{\mathrm{f}}}{\alpha_{0}}=\frac{1}{2 {\rm{ \mathsf{ π} }} n} \frac{\alpha_{0}}{\alpha_{\mathrm{d}}} $ | (13) |
又因最大位移δmax与αf之间有如下关系:
| $ \frac{\delta_{\max }}{\delta_{0}}=\frac{\alpha_{\mathrm{f}} M g / k_{\mathrm{f}}}{\alpha_{0} M g / k_{\mathrm{f}}}=\frac{\alpha_{\mathrm{f}}}{\alpha_{0}} $ | (14) |
故位移响应比RD可表示为
| $ R_{\mathrm{D}}=\frac{\delta_{\max }}{\delta_{0}}=\frac{1}{2 {\rm{ \mathsf{ π} }} n} \frac{\alpha_{0}}{\alpha_{\mathrm{d}}} $ | (15) |
总剪力响应比RA由式(5)可表示为
| $ R_{\mathrm{A}}=\frac{\alpha_{1}}{\alpha_{0}}=\sqrt{\frac{1}{4 {\rm{ \mathsf{ π} }}^{2} n^{2}}\left(\frac{\alpha_{0}}{\alpha_{\mathrm{d}}}\right)^{2}+\left(\frac{\alpha_{\mathrm{d}}}{\alpha_{0}}\right)^{2}} $ | (16) |
因此,如果已知阻尼量αd的大小,利用式(15)即可得到隔震层最大位移预测值;利用式(16)即可得到隔震层最大总剪力预测值。
地震下黏滞阻尼器最大剪力Qd, max可利用以δmax为最大振幅,以ωeq为等效激振频率的简谐振动y=δmaxsin(ωeqt)下阻尼器提供给结构体系的附加阻尼比ζd表示为
| $ Q_{\mathrm{d}, \max }=c \omega_{\mathrm{eq}} \delta_{\max }=2 \zeta_{\mathrm{d}} \frac{\omega_{\mathrm{eq}}}{\omega_{\mathrm{f}}} Q_{\mathrm{f}, \max } $ | (17) |
由式(4)、式(13)及式(17)可得阻尼量αd关于附加阻尼比ζd的表达式:
| $ \frac{\alpha_{\mathrm{d}}}{\alpha_{0}}=\sqrt{\frac{\zeta_{\mathrm{d}} \omega_{\mathrm{eq}}}{{\rm{ \mathsf{ π} }} n \omega_{\mathrm{f}}}} $ | (18) |
可见,由附加阻尼比ζd计算阻尼量αd需首先确定等效激振频率ωeq的大小与分布。
1.2 算例模型建立第1层为隔震层的5层钢框架剪切型模型(图 2)。结构层高为3 m,侧向刚度为梯形分布,最上层刚度为底层原刚度的1/2。各层质量均匀分布。结构各层具体参数见表 1。叠层橡胶支座侧向刚度分别取21 500 kN/m和12 000 kN/m,相应的结构基本周期为3.0 s和4.0 s。黏滞阻尼器的附加阻尼比作为主要分析变量分别取0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。时程分析中设定橡胶支座阻尼系数为0,同时不考虑上部结构耗能。

|
图 2 算例模型 Fig. 2 Analysis model |
| 表 1 上部结构参数 Tab. 1 Parameters of superstructure |
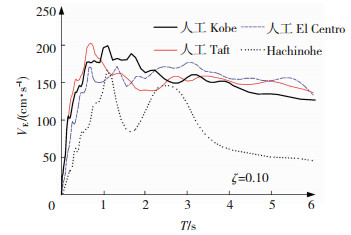
采用天然地震动记录JMA Kobe 1995 NS、Taft 1952 NS、El Centro 1940 NS的相位特性,以能量速度换算值VE=150 cm/s(二类场地,罕遇地震波)为目标拟合制成人工波[14-15],以下分别称人工Kobe、人工Taft、人工El Centro。另选取天然地震动记录Hachinohe 1968 EW,以下称Hachinohe,使用Hachinohe波进行时程分析计算时适当增大地震动加速度峰值,使能量速度换算值VE=150 cm/s。4条地震波的能量谱见图 3,可以看出3条拟合人工波的能量谱在长周期范围均接近150 cm/s,能够较好地保证地震输入能量的稳定性。
|
图 3 能量谱 Fig. 3 Energy spectrum |
根据式(18)可将结构基本频率与等效激振频率之比ωf/ωeq表示为
| $ \frac{\omega_{\mathrm{f}}}{\omega_{\mathrm{eq}}}=\frac{\zeta_{\mathrm{d}}}{{\rm{ \mathsf{ π} }} n}\left(\frac{\alpha_{0}}{\alpha_{\mathrm{d}}}\right)^{2} $ | (19) |
将时程分析结果代入式(19)右侧即得到不同地震动下的ωf/ωeq分布(见图 4)。由图 4可知,随着附加阻尼比ζd的增大,ωf/ωeq具有线性减小的趋势,并可利用以下经验公式在低阻尼(ζd<1.0)范围内基本描述并包络其大小分布:
| $ \frac{\omega_{\mathrm{f}}}{\omega_{\mathrm{eq}}}=1-0.6 \zeta_{\mathrm{d}} $ | (20) |

|
图 4 频率比与阻尼比的关系 Fig. 4 Relation between frequency ratio and damping ratio |
将式(20)代入式(18)得到由附加阻尼比ζd预测相应阻尼量αd的表达式:
| $ \frac{\alpha_{\mathrm{d}}}{\alpha_{0}}=\sqrt{\frac{\zeta_{\mathrm{d}}}{{\rm{ \mathsf{ π} }} n\left(1-0.6 \zeta_{\mathrm{d}}\right)}} $ | (21) |
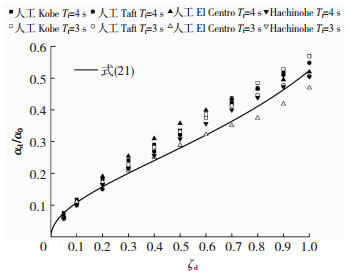
时程分析得到的阻尼量分布与式(21)的对比见图 5,其中等价往复次数n的大小取各算例平均值2.9。由图 5可知,式(21)在低阻尼(ζd<1.0)范围能够基本描述不同地震波下阻尼量与附加阻尼比的对应关系,可用于隔震层响应预测与设计中阻尼量的确定。相反地,可利用式(22)由目标阻尼量确定所需附加阻尼比ζd。
| $ \zeta_{\mathrm{d}}=\frac{{\rm{ \mathsf{ π} }} n\left(\alpha_{\mathrm{d}} / \alpha_{0}\right)^{2}}{1+0.6 {\rm{ \mathsf{ π} }} n\left(\alpha_{\mathrm{d}} / \alpha_{0}\right)^{2}} $ | (22) |
|
图 5 阻尼量与阻尼比的关系 Fig. 5 Relation between damping amount and damping ratio |
将式(21)代入式(15)即得到位移响应比RD及隔震层最大位移δmax关于附加阻尼比ζd的预测式:
| $ R_{\mathrm{D}}=\frac{\delta_{\max }}{\delta_{0}}=\frac{1}{2} \sqrt{\frac{1-0.6 \zeta_{\mathrm{d}}}{{\rm{ \mathsf{ π} }} n \zeta_{\mathrm{d}}}} $ | (23) |
将式(21)代入式(16)得到总剪力响应比RA及隔震层总剪力系数α1关于附加阻尼比ζd的预测式:
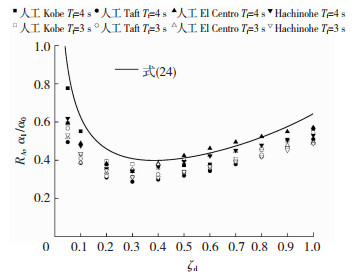
| $ R_{\mathrm{A}}=\frac{\alpha_{1}}{\alpha_{0}}=\sqrt{\frac{1-0.6 \zeta_{\mathrm{d}}}{4 {\rm{ \mathsf{ π} }} n \zeta_{\mathrm{d}}}+\frac{\zeta_{\mathrm{d}}}{{\rm{ \mathsf{ π} }} n\left(1-0.6 \zeta_{\mathrm{d}}\right)}} $ | (24) |
表 2对比了附加阻尼比为0.1、0.4、0.7时隔震层位移的时程分析值与式(23)得到的预测值的大小,从中可以看出,不同地震波下的响应预测值均不同程度地大于时程分析值,具有较好的包络性及较大的安全冗余。另外,附加阻尼比为0.1、0.4、0.7时预测法在不同地震波和不同基本周期下的预测平均精度分别为142%、134%、124%,即表现出附加阻尼比越大则预测精度越好的特点,因此该法适合于具有一定附加阻尼比(ζd≥0.1)的隔震层响应预测。
| 表 2 隔震层位移 Tab. 2 Displacement of isolation layer |
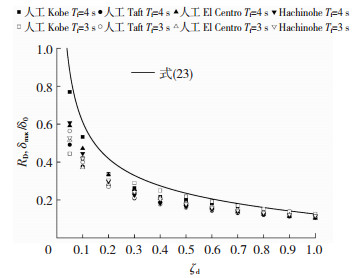
图 6为地震波作用下隔震层位移幅值与式(23)曲线的对比,可以看出,式(23)能够在广范围基本包络时程分析结果,且随着阻尼量的增大时程分析响应趋于集中,预测精度随之上升。图 7为隔震层总剪力系数分布与式(24)曲线的对比,由图 7可知式(24)能够近似预测到不同地震作用下隔震层总剪力系数响应的上限值。另外,总剪力系数分布具有明显的极小值点,而式(24)曲线同样具有极值且能够较好地描述不同地震动下总剪力系数极小值的分布特点。
|
图 6 最大位移响应 Fig. 6 Response of maximum displacement |
|
图 7 总剪力系数响应 Fig. 7 Response of total shear coefficient |
若已知不同阻尼比下隔震层总剪力系数响应的极小值,就能够确定令隔震层最大总剪力为最小时所需的阻尼比,这可以期望带来最小的加速度响应,同时降低上部结构的层间剪力[7]。对式(16)求导并求极值点得到总剪力系数α1取极小值α1min时所需阻尼量αd, α1min与基准剪力系数α0之比:
| $ \frac{\alpha_{\mathrm{d}, \alpha_{1 \min }}}{\alpha_{0}}=\sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}} $ | (25) |
将式(25)代入式(16)得到总剪力响应比极小值RA, min:
| $ R_{\mathrm{A}, \min }=\frac{\alpha_{1 \min }}{\alpha_{0}}=\sqrt{\frac{1}{{\rm{ \mathsf{ π} }} n}} $ | (26) |
将式(25)代入式(15)得到与总剪力系数极小值α1min对应的位移响应比RD, α1min:
| $ R_{\mathrm{D}, \alpha_{1 \min }}=\frac{\delta_{\max , \alpha_{1 \min }}}{\delta_{0}}=\sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}} $ | (27) |
式中δmax, α1min为与α1min所对应的隔震层最大位移。因此,如果已知能量谱VE和结构基本周期Tf,则能够大致确定通过设置黏滞阻尼器所能达到的剪力最大降低效果,并可通过式(26)、(27)确定此时隔震层最大剪力和最大位移预测值。若隔震结构基本周期设计为Tf≤5 s(由式(11)取n=2.0),则由式(26)可得总剪力响应比极小值RA, min=α1min/α0=0.40,即在该基本周期下所能得到的总剪力最大降低率约为60%。
2.2 基于位移与剪力设计侧重的优化设计最优剪力设计以隔震层总剪力系数最小化作为优化设计目标,未充分考虑隔震层位移的优化设计需求。本节延续求解响应比函数极值点确定设计阻尼量的思路,提出能够基于位移和剪力的不同设计侧重需求确定相应黏滞阻尼器阻尼系数的优化设计方法。利用隔震层位移响应比RD与总剪力响应比RA的线性组合构建优化设计目标函数Δ:
| $ \varDelta=\min R=\min \left(a R_{\mathrm{D}}+b R_{\mathrm{A}}\right) $ | (28) |
式中R为线性组合函数,a、b分别为位移加权系数和剪力加权系数,满足a+b=1。将位移响应比RD作为中间变量,由式(15)变形可将阻尼量αd与基准剪力系数α0之比利用位移响应比RD表示为
| $ \frac{\alpha_{\mathrm{d}}}{\alpha_{0}}=\frac{1}{2 {\rm{ \mathsf{ π} }} n R_{\mathrm{D}}} $ | (29) |
将式(29)代入式(16)得到总剪力响应比RA关于位移响应比RD的表达式:
| $ R_{\mathrm{A}}=\frac{\alpha_{1}}{\alpha_{0}}=\sqrt{R_{\mathrm{D}}^{2}+\frac{1}{4 {\rm{ \mathsf{ π} }}^{2} n^{2} R_{\mathrm{D}}^{2}}} $ | (30) |
故由式(28),线性组合函数R可利用位移响应比RD表示为
| $ R=a R_{\mathrm{D}}+b R_{\mathrm{A}}=a R_{\mathrm{D}}+b \sqrt{R_{\mathrm{D}}^{2}+\frac{1}{4 {\rm{ \mathsf{ π} }}^{2} n^{2} R_{\mathrm{D}}^{2}}} $ | (31) |
式(31)存在极小值的必要条件是b≠0,此时对式(31)求导并求极值点得到函数R取极小值Δ时的位移响应比RD, Δ:
| $ R_{\mathrm{D}, \varDelta}=\frac{\delta_{\max , \varDelta}}{\delta_{0}}=\frac{1}{B} \sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}} $ | (32) |
将式中的B称为优化系数,当b=0.5时:
| $ B=\left(3-\frac{2}{b}+\frac{1}{b^{2}}\right)^{\frac{1}{4}}=1.316 $ | (33) |
b≠0.5时:
| $ \begin{gathered} B= \\ {\left[\frac{2(1-2 b)}{-\left(3 b^{2}-2 b+1\right)+\sqrt{\left(3 b^{2}-2 b+1\right)^{2}+4 b^{2}(1-2 b)}}\right]^{\frac{1}{4}}} \end{gathered} $ | (34) |
由式(34)可知,当b=1时,B=1。将式(32)代入式(29)得到函数R取极小值Δ所需的优化阻尼量αd, Δ与基准剪力系数α0之比:
| $ \frac{\alpha_{\mathrm{d}, \varDelta}}{\alpha_{0}}=B \sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}} $ | (35) |
将式(35)代入式(16)得到函数R取极小值Δ时的总剪力响应比RA, Δ:
| $ R_{\mathrm{A}, \varDelta}=\frac{\alpha_{1, \varDelta}}{\alpha_{0}}=\sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}\left(\frac{1}{B^{2}}+B^{2}\right)} $ | (36) |
根据上述关系,如果已知能量谱VE和结构基本周期Tf,则因设置某加权系数组合相应优化阻尼系数所得到的隔震层位移与总剪力降低效果可以大致确定,并可通过式(32)、(36)计算相应的隔震层最大位移和总剪力系数预测值。观察式(32)、(35)、(36)可知,剪力加权系数取为b的优化设计中,优化阻尼量αd, Δ为最优剪力设计阻尼量的B倍,相应位移及位移响应比为1/B倍,总剪力系数及总剪力响应比为
将式(35)代入式(22)可得优化阻尼比ζd, Δ关于优化系数B的表达式:
| $ \zeta_{\mathrm{d}, \varDelta}=\frac{B^{2}}{2+0.6 B^{2}} $ | (37) |
可见,优化阻尼比ζd, Δ的大小仅与加权系数a、b的选取有关,而与等价往复次数n等无关。因此,当加权系数a、b确定后,利用式(37)即可快速确定优化阻尼比ζd, Δ的大小,再由cΔ=4πMζd, Δ/Tf即可得到所需优化阻尼系数。
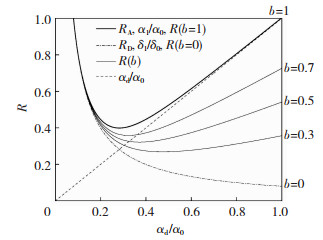
实际设计中,加权系数a、b应根据隔震层位移与剪力的优化设计侧重取值。当剪力加权系数b=0、0.3、0.5、0.7、1.0时,这5种典型组合分别代表的优化目标如表 3所示。等价往复次数n取2.0时表 3中5种组合下的线性组合函数R曲线如图 8所示,可见当b=1时,线性组合函数R=RA=α1/α0,此时优化阻尼量αd, Δ即为最优剪力设计所需阻尼量αd, α1min。随着加权系数b的减小线性组合函数R曲线趋于平缓,并逐渐靠近δmax/δ0,函数R极值点逐渐向右移动,即优化阻尼量αd, Δ逐渐增大。当b=0时,线性组合函数R=RD=δmax/δ0,函数曲线单调下降,已不存在极值,这表示将以隔震层位移作为唯一设计标准,此时应根据隔震层设计容许位移大小,利用式(29)确定设计阻尼量,再由式(22)确定黏滞阻尼器附加阻尼比。
| 表 3 加权系数组合与优化目标 Tab. 3 Weighting coefficient combinations and optimization objectives |
|
图 8 不同加权系数下的函数R Fig. 8 Function R under different weighting coefficients |
优化设计下的隔震层总剪力系数α1, Δ与最大位移δmax, Δ之间的关系可利用基本周期Tf表示:
| $ \begin{gathered} \alpha_{1, \varDelta}=\alpha_{0} \sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}\left(\frac{1}{B^{2}}+B^{2}\right)}=\frac{4 {\rm{ \mathsf{ π} }}^{2} \delta_{0}}{g T_{\mathrm{f}}^{2}} \sqrt{\frac{1}{2 {\rm{ \mathsf{ π} }} n}\left(\frac{1}{B^{2}}+B^{2}\right)}= \\ \frac{4 {\rm{ \mathsf{ π} }}^{2} \delta_{\max , \varDelta}}{g T_{\mathrm{f}}^{2}} \sqrt{1+B^{4}} \end{gathered} $ | (38) |
类似地,α1, Δ与δmax, Δ的关系也可用能量谱VE表示:
| $ \alpha_{1, \varDelta}=\frac{V_{\mathrm{E}}^{2}}{2 {\rm{ \mathsf{ π} }} n g \delta_{\max , \varDelta}} \sqrt{1+\frac{1}{B^{4}}} $ | (39) |
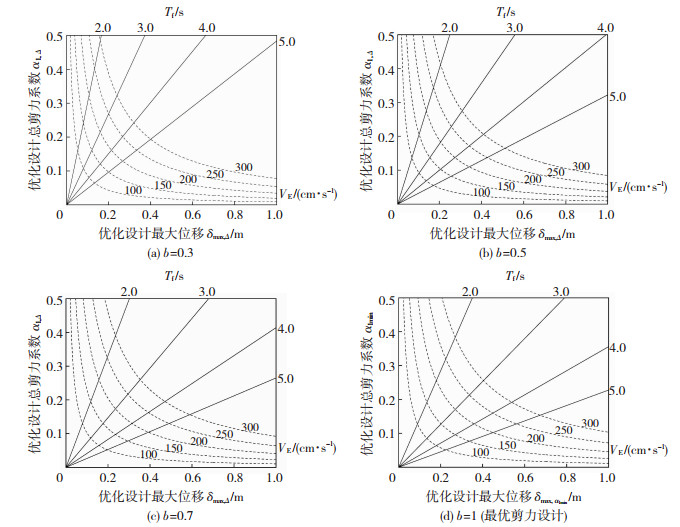
若隔震结构基本周期设计为Tf≤5 s(由式(11)取n=2.0),根据式(38)、(39)画出表 3中组合2至组合5的4种典型组合下以基本周期Tf和能量谱VE为设计参数的α1, Δ与δmax, Δ关系见图 9,可见此时利用图 9即可快速确定这4种优化设计下隔震层的大致响应。
|
图 9 优化设计下的隔震层总剪力系数与最大位移关系 Fig. 9 Relation between optimal total shear coefficient and maximum displacement |
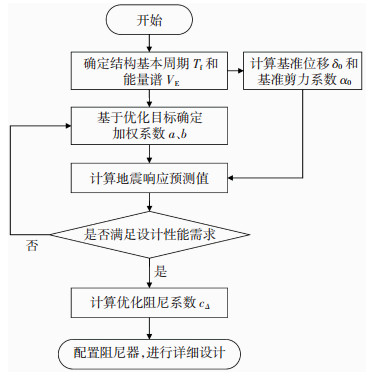
根据上述设计原则,给出基础隔震结构隔震层附加黏滞阻尼器优化设计流程见图 10。若已确定上部结构设计参数,则优化设计的具体步骤为:
|
图 10 优化设计流程 Fig. 10 Flow chart of optimal design |
1) 计算基准响应量。确定隔震结构设计基本周期Tf和能量谱VE,由式(7)计算隔震层基准位移δ0;由式(8)计算基准剪力系数α0。
2) 确定加权系数与优化系数。根据优化目标确定加权系数a、b,由式(33)或式(34)计算优化系数B。
3) 计算地震响应预测值。由式(32)计算位移响应比RD, Δ,由式(36)计算总剪力响应比RA, Δ。再由δmax, Δ=δ0RD, Δ计算隔震层位移预测值δmax, Δ,由α1, Δ=α0RA, Δ计算隔震层总剪力系数预测值α1, Δ。当设计隔震结构基本周期Tf≤5 s时,可直接利用图 9大致确定隔震层的剪力及位移响应。
4) 判断是否满足设计性能需求。比较所得响应预测值与性能需求值,若剪力及位移均能满足性能需求则由式(37)计算优化阻尼比ζd, Δ,再由cΔ=4πMζd, Δ/Tf计算优化阻尼系数。若位移不满足需求则返回步骤3)并适当减小剪力加权系数b;若总剪力系数不满足需求则返回步骤3)并适当增大剪力加权系数b。
若对隔震层响应无明确的设计性能需求,则应根据标准[16]对罕遇地震作用下支座最大水平位移的规定,将下式作为最低设计要求:
| $ \delta_{\max } \leqslant\left[u_{\mathrm{h} i}\right] $ | (40) |
式中[uhi]为隔震支座水平位移限值,其取值不应大于支座直径的0.55倍和各层橡胶总厚度的3.0倍二者中的较小值。另外,对于上部结构用途需重点考虑加速度影响的隔震层设计(如医院需考虑医疗器械防倾倒),应使加权系数的大小向剪力加权系数b倾斜。当优化设计响应预测值能够满足设计性能需求时,即说明在设计性能安全范围内优化了隔震层响应。
3 设计实例根据图 10设计流程对某6层钢框架基础隔震结构进行罕遇地震波下的隔震层附加黏滞阻尼器优化设计。结构处于二类场地,黏性阻尼比为4%,层高3 m,各层质量及侧向刚度见表 4。隔震支座采用LNR600天然叠层橡胶支座,侧向刚度为909 kN/m,橡胶层总厚度122 mm。设计中调整支座个数以使结构达到相应基本周期。以表 3中组合4的优化目标为例,则具体设计步骤:
| 表 4 上部结构设计参数 Tab. 4 Design parameters of superstructure |
1) 隔震结构基本周期设计为Tf=4.0 s,所需隔震层侧向刚度为kf=4π2M/Tf2=10 881 kN/m。二类场地罕遇地震波能量谱VE=150 cm/s。由式(7)计算隔震层基准位移δ0=95.5 cm;由式(8)计算基准剪力系数α0=0.240。
2) 由于优化目标设定为同时考虑位移和剪力,以剪力为主,故加权系数设定为a=0.3,b=0.7。由式(34)计算优化系数B=1.143。
3) 由式(32)计算隔震层位移响应比RA, Δ=0.247,由此计算最大位移预测值δmax, Δ=δ0RD, Δ=23.6 cm;由式(36)计算隔震层总剪力响应比RA, Δ=0.406,由此计算隔震层总剪力系数预测值α1, Δ=α0RA, Δ=0.098。
4) 由LNR600支座的几何力学信息计算水平位移限值[uhi]=min[33, 36.6]=33 cm > δmax, Δ=23.6 cm,满足最低设计要求,因此由式(37)初步确定黏滞阻尼器附加阻尼比为ζd, Δ=0.46,再利用cΔ=4πMζd, Δ/Tf计算阻尼系数cΔ=6 499 (kN·s)/m,之后转入阻尼器配置与详细设计阶段。
附加优化阻尼器前后基础隔震结构在人工Kobe波作用下的各项时程分析响应值见表 5,可见未设阻尼器时隔震层最大位移不满足最低设计要求,且首层与顶层加速度均较大。而当隔震层附加黏滞阻尼器后,地震作用下的各项位移及加速度幅值均大幅降低。图 11为人工Kobe波作用下隔震层位移响应时程曲线,可以看出,设置阻尼器使隔震层位移峰值明显降低,在全时程起到了良好的控制作用。
| 表 5 优化设计下的结构响应 Tab. 5 Structural response under optimal design |

|
图 11 隔震层位移响应对比 Fig. 11 Comparison of displacement responses of isolation layer |
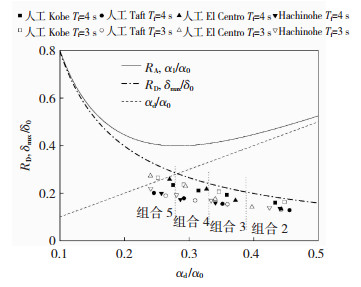
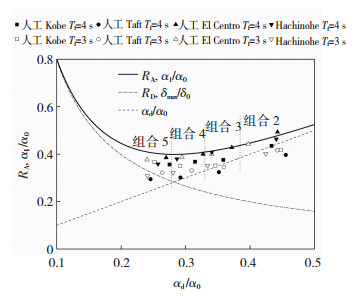
基于表 3所示组合2至组合5的4种优化目标,分别对该6层结构进行隔震层附加黏滞阻尼器优化设计。基本周期分别设计为3.0 s和4.0 s,经图 10设计流程得到的相应优化阻尼系数见表 6。利用1.2节的4条地震波对隔震层分别附加4种优化阻尼系数的6层钢框架基础隔震结构进行动力时程分析得到的隔震层位移响应比见图 12,总剪力响应比见图 13。由图 12、13可以看出4种组合的隔震层最大位移和最大总剪力与基准响应量相比均大幅降低,其中组合5即最优剪力设计,其总剪力系数的时程分析值接近于总剪力系数预测式曲线的极小值。组合2至组合4则因优化阻尼量的减小而使隔震层总剪力系数相应减小、位移幅值增大,与表 3中的优化目标基本对应。由图 12、13中时程分析值和预测式曲线的对比可知,本文预测法能够较准确地预测附加优化阻尼系数后的隔震层最大位移和最大总剪力的上限值,可用于优化设计响应安全性评价。
| 表 6 不同组合下的优化阻尼系数 Tab. 6 Optimal damping coefficient under different combinations |
|
图 12 优化设计位移响应比 Fig. 12 Displacement response ratio in optimal design |
|
图 13 优化设计总剪力响应比 Fig. 13 Total shear response ratio in optimal design |
提出了基础隔震层附加黏滞阻尼器结构基于地震结束时刻能量平衡方程的地震响应预测法,并提出根据隔震层位移与剪力设计侧重需求确定黏滞阻尼器阻尼系数的优化设计方法,通过动力时程分析和设计实例对所提方法有效性进行验证,结论如下:
1) 基于地震结束时刻能量平衡方程的响应预测方法能够快速准确地预测隔震层附加黏滞阻尼器基础隔震结构隔震层响应的上限值,具有较好的包络性,且附加阻尼越大预测精度越好。
2) 提出的阻尼量与附加阻尼比的换算关系式能够基本描述地震下二者之间的关系,可用于地震响应预测与设计中阻尼量和附加阻尼比的确定。
3) 所提设计法经两步计算即可确定所需优化阻尼系数。优化阻尼系数和地震响应预测式均适合手算,可满足中低层基础隔震结构前期设计需求。
4) 本文旨在研究并发展隔震结构基于能量平衡的设计方法,主要以规则对称的中低层剪切型基础隔震结构为分析模型进行了研究,并以附加黏滞阻尼器后的隔震层响应作为主要设计研究对象。对于上部结构为平面不对称等不规则形式以及高阶振型响应特性对响应预测与设计的影响等问题仍需进一步研究。
| [1] |
日本建筑学会. 隔震结构设计[M]. 北京: 地震出版社, 2006: 3. Architectural Institute of Japan. Recommendation for the design of base isolated buildings[M]. Beijing: Seismological Press, 2006: 3. |
| [2] |
秋山宏. 基于能量平衡的建筑结构抗震设计[M]. 北京: 清华大学出版社, 2010: 105. AKIYAMA H. Earthquake-resistant design method for buildings based on energy balance[M]. Beijing: Tsinghua University Press, 2010: 105. |
| [3] |
PROVIDAKIS C P. Effect of LRB isolators and supplemented viscous dampers on seismic isolated buildings under near fault excitations[J]. Engineering Structures, 2008, 30(5): 1187. DOI:10.1016/j.engstruct.2007.07.020 |
| [4] |
PROVIDAKIS C P. Effect of supplemental damping on LRB and FPS seismic isolators under near-fault ground motions[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(1): 80. DOI:10.1016/j.soildyn.2008.01.012 |
| [5] |
東野さやか, 北村春幸. 粘性ダンパーを付与した免震構造のエネルギーの釣合に基づく応答評価法[J]. 日本建築学会構造系論文集, 2005, 70(588): 79. HIGASHINO S, KITAMURA H. Energy-balance based seismic response prediction methods for seismic isolated buildings with rubber bearings and viscous dampers[J]. Journal of Structural and Construction Engineering, 2005, 70(588): 79. DOI:10.3130/aijs.70.79_1 |
| [6] |
王维, 裴星洙, 王星星. 基于能量原理的阻尼器隔震结构地震响应预测[J]. 世界地震工程, 2011, 27(4): 114. WANG Wei, PEI Xingzhu, WANG Xingxing. Earthquake response prediction of a base-isolated structure with dampers based on energy concept[J]. World Earthquake Engineering, 2011, 27(4): 114. |
| [7] |
北村春幸. 基于性能设计的建筑振动解析[M]. 西安: 西安交通大学出版社, 2004: 126. KITAMURA H. Seismic response analysis methods for performance based design[M]. Xi'an: Xi'an Jiaotong University Press, 2004: 126. |
| [8] |
陈瑞生, 吴进标, 刘彦辉, 等. 黏滞阻尼器-基础隔震混合体系优化研究[J]. 振动与冲击, 2020, 39(11): 93. CHEN Ruisheng, WU Jinbiao, LIU Yanhui, et al. Optimization research for base-isolated structures with fluid viscous dampers[J]. Journal of Vibration and Shock, 2020, 39(11): 93. DOI:10.13465/j.cnki.jvs.2020.11.012 |
| [9] |
王明旭, 陈国平. 基于结构能量准则的阻尼器位置及参数优化[J]. 振动、测试与诊断, 2011, 31(6): 754. WANG Mingxu, CHEN Guoping. Optimization on placement and parameters of damping design using energy criterion[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(6): 754. DOI:10.16450/j.cnki.issn.1004-6801.2011.06.001 |
| [10] |
李钢, 翟子杰, 余丁浩. 一种高效的阻尼器优化设计方法[J]. 建筑科学与工程学报, 2020, 37(5): 51. LI Gang, ZHAI Zijie, YU Dinghao. An efficient optimal design method for dampers[J]. Journal of Architecture and Civil Engineering, 2020, 37(5): 51. DOI:10.19815/j.jace.2019.05106 |
| [11] |
裴星洙, 王佩. 框架-摇摆墙结构阻尼优化设计方法研究[J]. 振动与冲击, 2014, 33(24): 112. PEI Xingzhu, WANG Pei. Damping optimization design method of a frame-rocking wall structure[J]. Journal of Vibration and Shock, 2014, 33(24): 112. DOI:10.13465/j.cnki.jvs.2014.24.019 |
| [12] |
裴星洙, 邱吉祥, 伏恬甜. 基于能量法的调谐黏性质量阻尼器地震响应预测式研究[J]. 振动与冲击, 2017, 36(19): 29. PEI Xingzhu, QIU Jixiang, FU Tiantian. Optimization design method for tuned viscous mass dampers based on the energy balance principle[J]. Journal of Vibration and Shock, 2017, 36(19): 29. DOI:10.13465/j.cnki.jvs.2017.19.005 |
| [13] |
裴星洙, 王维, 王星星. 基于能量原理的隔震结构地震响应预测法研究[J]. 工程力学, 2011, 28(7): 66. PEI Xingzhu, WANG Wei, WANG Xingxing. Earthquake response prediction of isolated structures based on energy principle[J]. Engineering Mechanics, 2011, 28(7): 66. |
| [14] |
PAN Chao, ZHANG Ruifu, LUO Hao, et al. Target-based algorithm for baseline correction of inconsistent vibration signals[J]. Journal of Vibration and Control, 2018, 24(12): 2562. DOI:10.1177/1077546316689014 |
| [15] |
PAN Chao, ZHANG Ruifu, LUO Hao, et al. Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement[J]. Advances in Mechanical Engineering, 2016, 8(10): 1. DOI:10.1177/1687814016675534 |
| [16] |
建筑隔震设计标准: GB/T 51408—2021[S]. 北京: 中国计划出版社, 2021
|
| [28] |
Standard for seismic isolation design of building: GB/T 51408—2021[S]. Beijing: China Planning Press, 2021
|
 2022, Vol. 54
2022, Vol. 54


