2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 中南大学 土木工程学院, 长沙 410083
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Civil Engineering, Central South University, Changsha 410083, China
自由曲面结构由于其卓越的建筑表现力得到了广泛应用(图 1),成为空间结构发展的主要趋势之一。自由曲面是无法用单个或几个解析函数表达的曲面,是一种明显区别于传统建筑造型的曲面。自由曲面结构早期是通过物理实验的方法形成合理形态[1]。近年来,学者们陆续提出了Bezier曲面[2]、B样条曲面[3]和非均匀有理B样条曲面(NURBS)[4]等以计算图形学为基础的形态创建方法。目前,NURBS曲线与曲面已成为结构设计领域的核心技术[5]。

|
图 1 阿布扎比Yas酒店 Fig. 1 Yas Island Marina Hotel in Abu Dhabi |
结构优化是使结构具有良好受力性能的有效方式,包括形态优化、拓扑优化等。因此,学者们基于自由曲面数学建构的方法,通过优化来得到合理的自由曲面形态。Tomas等[6]以曲面控制点高度为优化变量,分别以结构的最大位移、单元应力和结构整体质量为优化目标进行优化。Le等[7]提出了基于梯度法来实现自由曲面的形态优化。崔昌禹等[8]以结构应变能为优化目标,基于应变能敏感度调整曲面节点高度优化曲面,并在工程中得以应用。Ohmori等[9]以结构应变能及曲面优化前后的相似程度为优化目标,以曲面控制点坐标和壳体厚度为优化变量进行曲面形态优化,但实际得到的优化曲面与初始曲面形状的差别依然较大。
为使自由曲面结构既有较好的力学性能又满足建筑要求,Winslow等[10]基于传统遗传算法,通过调整曲面上两个主要方向网格线之间的角度进行自由曲面结构多目标优化。冯若强等[11]以结构应变能和杆长均方差为优化目标,曲面控制点高度为优化变量,采用加权法进行自由曲面索撑网壳的多目标优化。目前关于自由曲面网格结构的多目标优化均是基于加权法将多目标问题转化为单目标问题或采用传统遗传算法,且优化目标并未综合考虑自由曲面网格的相似性、流畅性以及规整性。
随着计算机技术的发展,元启发式算法被广泛应用于工程领域,苏岩等[12]在自由曲面网格结构形态创建过程中采用了群智能算法。然而在多目标优化问题中,现有多目标优化算法的效率不高,因此需要提高算法的寻优效率。
基于上述研究基础,本文分别基于NURBS曲线和曲面技术建立自由曲面索撑网壳、自由曲面空间网格结构,以自由曲面控制点高度为优化变量,以结构应变能、考虑曲面网格相似性、流畅性以及规整性的几何综合量化指标为目标函数。为提高优化效率及优化结果精确性,结合目标函数关于优化变量的敏感度对NSGA-Ⅱ算法进行改进,提出敏感度混合进化算法(SH-NSGA-Ⅱ),采用该算法对自由曲面网格结构进行多目标优化。将优化结果与基于NSGA-Ⅱ[13]、MOEA/D[14]以及SPEA2[15]算法的优化结果比较,验证敏感度混合进化算法的合理性。
1 自由曲面结构几何建模方法尽管诸多表示曲面的数学模型有各自的优缺点,但NURBS在工程应用中是最成功的。NURBS能够比传统的建模方式更好地控制物体表面的曲线度,从而能够创建出更逼真、生动的造型。因此,本文基于NURBS技术生成自由曲面。
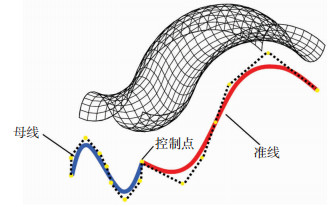
自由曲面索撑网壳的网格为平面四边形,每个单元平面内布置对角交叉索[16]。平面四边形网格由表面平移法形成[17],即首先基于NURBS曲线构造一条准线和一条母线,并将曲线按等弦长划分;将准线沿母线平行移动,再将母线和准线调换并再次平移,形成均匀的平面四边形网格(图 2)。自由曲面空间网格结构采用四边形网格,基于NURBS曲面技术构造自由曲面,采用等参线分割法[18]将曲面划分为多个四边形网格。
|
图 2 表面平移法几何原理 Fig. 2 Geometric principle of method of translation surfaces |
控制点是对曲面形状影响较大的参数,当同时调整控制点的三向坐标时,易引起结构网格畸变、曲面扭曲。因此选取控制点高度作为优化变量,自由曲面结构的优化模型表达为:
| $ \left\{\begin{array}{l} \min \boldsymbol{F}(\boldsymbol{x})=\min \left\{f_{1}(\boldsymbol{x}), f_{2}(\boldsymbol{x})\right\} \\ \text { subject to: } \boldsymbol{x}_{\min } \leqslant \boldsymbol{x} \leqslant \boldsymbol{x}_{\max } \end{array}\right. $ | (1) |
式中:F(x)为优化目标函数,f1(x)为自由曲面结构静力性能优化目标,f2(x)为几何优化目标。
2.1 静力性能优化目标常用的结构静力性能评价指标有位移、内力和应变能等。位移、内力是评价结构局部静力性能的指标,适用于内力、位移最大部位明确的结构,但自由曲面结构的形态复杂,难以确定内力、位移最大的部位。因此位移、内力不宜作为优化目标。应变能是能综合反映结构整体抵抗荷载和变形的指标,其定义为
| $ C=\frac{1}{2} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{U} $ | (2) |
式中:U为曲面结构的位移向量,P为作用在曲面结构的节点荷载向量。应变能越小,结构抵抗荷载和抗变形的能力越高,结构刚度越大,研究人员选择将应变能作为结构静力性能的评价指标[19-20]。因此,本文选取应变能作为静力性能优化目标。
2.2 几何优化目标除力学性能外,为符合建筑设计要求,自由曲面结构需要有良好的网格质量,对于网格质量的综合评价包括曲面相似性、网格流畅性、网格规整性三方面。相似性指标是用于衡量网格划分前曲面与划分后曲面的相似程度。在几何建模过程中,需要对NURBS曲线和等参线进行等弦长划分,因此曲面相似性指标D定义为
| $ D=\frac{L_{0}-L}{L_{0}} $ | (3) |
式中:L0为曲线原始长度,L为等弦长划分后曲线长度。因此,D值越小,自由曲面在网格划分前后的相似程度越好。
网格流畅性是评价自由曲面网格质量的一个重要方面。影响曲面网格流畅性的主要因素是网格节点对边的夹角以及节点的对角。若节点对边夹角β1, 3=180°,且临边夹角β1=β3,则节点具有良好的流畅性。因此,节点i的流畅性指标Fi由式(4)~(6)定义[21]:
| $ \sigma_{i}=\sqrt{\frac{\sum_{j=1}^{2}\left(\beta_{j, k}-180^{\circ}\right)^{2}}{2}}, k=j+2 $ | (4) |
| $ \tau_{i}=\sqrt{\frac{\sum_{j=1}^{2}\left(\beta_{j}-\beta_{j+2}\right)^{2}}{2}} $ | (5) |
| $ F_{i}=\sqrt{\sigma_{i}^{2}+\tau_{i}^{2}} $ | (6) |
网格规整性主要包括杆件长度和网格形状质量两方面。为保证自由曲面网格具有良好的规整性,一方面杆件长度应尽量均匀,即杆件长度标准差δL越小越好。另一方面为自由曲面各个网格形状质量,将网格形状质量系数[17]标准差δG作为网格形状规整性评价标准。因此,本文采用杆件长度标准差δL与形状质量系数标准差δG作为网格规整性指标。
| $ \delta_{\mathrm{L}}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(L_{i}-l\right)^{2}}{n-1}} $ | (7) |
式中:n为杆件总数,Li为第i根杆件的长度,l为杆件长度均值。
综合考虑曲面相似性、网格流畅性以及网格规整性,提出以综合量化指标T作为几何优化目标。其定义为
| $ T=\gamma_{1} \times D+\gamma_{2} \times F+\gamma_{3} \times \delta_{\mathrm{L}}+\gamma_{4} \times \delta_{\mathrm{G}} $ | (8) |
式中γi为各几何指标在综合量化指标中的权重,可根据实际需求设置,但需满足∑γi=1。
3 敏感度混合进化算法 3.1 目标函数敏感度优化变量的变化对目标函数的影响程度称为敏感度。敏感度是目标函数增加最快的方向,其数值为相应的变化率,将优化变量沿负敏感度方向移动可使目标函数快速减少。本文目标函数为应变能以及几何综合量化指标,优化变量为控制点的高度,目标函数与优化变量为非线性函数关系,用目标函数对控制点高度的微分形式获得目标函数的敏感度,可用下式表达:
| $ \boldsymbol{\alpha}=\left[\frac{\partial f(\boldsymbol{x})}{\partial x_{1}}, \frac{\partial f(\boldsymbol{x})}{\partial x_{2}}, \cdots, \frac{\partial f(\boldsymbol{x})}{\partial x_{n}}\right]^{\mathrm{T}} $ | (9) |
NSGA-Ⅱ算法是基于Pareto最优概念处理多目标优化问题的优化算法,是多目标优化问题中引用率最高的进化算法。该算法基于快速非支配排序和精英策略降低了算法的复杂度,保持了种群的多样性。因此基于NSGA-Ⅱ算法,结合3.1节定义的目标函数敏感度,提出了一种敏感度混合进化算法,实现了自由曲面索撑网壳以及自由曲面空间网格结构的多目标优化。基于敏感度混合进化算法的多目标优化过程如下:
1) 设置种群大小N,交叉概率c,变异因子r和迭代次数S。本文中参数设置为:N=50,c=0.95,r=1/m,m为优化变量的个数。
2) 根据实际需求,设置优化变量的变化范围。
3) 初始化种群,设置控制点坐标,以控制点高度向量x生成大小为N的初始种群P。
4) 建立自由曲面索撑网壳结构或自由曲面空间网格结构模型,生成网格节点坐标。
5) 计算目标函数关于优化变量的敏感度,确定合理步长,按式(10)更新种群,式中:x为控制点高度向量,λ为更新步长,∂fn(x)/∂x为目标函数的敏感度。
| $ \boldsymbol{x}_{\mathrm{new}}=\boldsymbol{x}-\lambda\left(\frac{\partial f_{1}(\boldsymbol{x})}{\partial \boldsymbol{x}}+\frac{\partial f_{2}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right) $ | (10) |
6) 对更新后的种群进行选择、交叉和变异,产生子代种群Q。
7) 将父代种群Pi与子代种群Q合并,得到大小为2N的种群R。
8) 对种群R进行非支配排序(F1表示Pareto序号为1的解集),将解集F1~Fk放置种群Pi+1,直至|F1∪F2∪…∪Fk+1|≥N。
9) 计算解集Fk+1的拥挤度,对解集Fk+1按拥挤度排序,按拥挤度将Fk+1存入Pi+1,直至Pi+1中解的个数为N,得到新父代种群Pi+1。
10) 若满足收敛条件则循环结束,否则返回第2步,本文以迭代次数作为收敛条件。
11) 输出解集PS,从中选取合适的解作为最终控制点高度。
4 敏感度混合进化算法本节提供了两个基于上述优化算法的自由曲面网格结构的多目标优化算例,将优化结果分别与基于NSGA-Ⅱ、MOEA/D以及SPEA2算法的优化结果比较,证明提出的算法提高了计算效率和解的精确性。算法SH-NSGA-Ⅱ中参数设置为:N=50,c=0.95,r=1/m,m为优化变量的个数。另外3种算法中的所有参数都是根据文献[13-15]中的推荐值选取的,且种群大小均为50。
4.1 自由曲面索撑网壳多目标优化现有一自由曲面索撑网壳结构,跨度和长度均为35 m。钢杆件采用100 mm×10 mm的圆钢管,钢管的弹性模量为2.06×1011 N/m2,索的弹性模量和截面面积分别为1.3×1011 N/m2、65 mm2,初始预应力为100 MPa。节点形式为刚接节点,支座处刚接,4个角点支承,自由曲面索撑网壳的初始形状见图 3。荷载形式为均布恒荷载(512 N/m2)和满跨分布活荷载(500 N/m2),控制点高度范围为[-20+x, 20+x]。

|
图 3 自由曲面索撑网壳初始形状 Fig. 3 Initial shape of free-form cable-braced grid shell |
分别采用SH-NSGA-Ⅱ、NSGA-Ⅱ、SPEA2以及MOEA/D算法对上述结构进行多目标优化,为了比较4种算法的优化效果,图 4给出了迭代步数为150时4种算法的Pareto解集,图 5给出了4种算法的Pareto最优解集。迭代步数为150时,SH-NSGA-Ⅱ的Pareto解集的范围以及均匀性明显优于其他3种算法的Pareto解集。对比分析4种算法在迭代步数为150和400时各自的Pareto解集,SH-NSGA-Ⅱ和MOEA/D算法在150步的Pareto解集与400步的Pareto解集几乎重合,说明当迭代步数为150时两种算法收敛;而算法NSGA-Ⅱ、SPEA2是在迭代步数为400时收敛。考虑计算时间,收敛时其他3种算法的计算时间分别是SH-NSGA-Ⅱ算法的2.893、2.382、2.783倍。

|
图 4 各算法的Pareto解集(步数=150) Fig. 4 Pareto solution set of each algorithm (number of iterative steps is 150) |

|
图 5 自由曲面索撑网壳的最优Pareto解集 Fig. 5 Pareto optimal solution sets of free-form cable-braced grid shell |
将SH-NSGA-Ⅱ算法得到的Pareto最优解集与其他3种算法得到的最优解集相比,最优解集的均匀性优于其他3种算法,多样性明显优于算法SPEA2、MOEA/D,精确性优于MOEA/D。综上所述,SH-NSGA-Ⅱ算法既可以获得精确性较高、多样性以及均匀性较好的Pareto最优解集,又具有较高的计算效率。
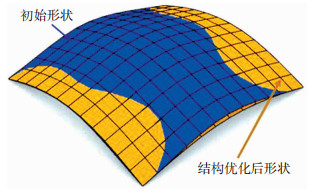
从Pareto最优解集中选取合适的解,保证应变能和几何综合量化指标均有所下降。表 1给出了优化后结构各个指标的数值,图 6为优化前后结构的形状对比。由表 1可知,优化后结构的应变能降低了21.2%,结构的最大位移下降了52.2%,即有效提高了结构的力学性能;几何综合量化指标降低了15.4%,且相似性指标、索单元长度标准差、网格质量系数标准差以及流畅性指标分别降低了24.9%、15.4%、22.2%、7.5%,从而证明了将几何综合量化指标作为目标函数可有效降低结构的各项几何指标。
| 表 1 自由曲面索撑网壳多目标优化结果 Tab. 1 Multi-objective optimization results of free-form cable-braced grid shell |
|
图 6 结构优化前后形状比较 Fig. 6 Shape comparison before and after structure optimization |
现有一自由曲面空间网格结构,跨度和长度均为25 m。钢杆件采用100 mm×10 mm的圆钢管,钢管的弹性模量为2.06×1011 N/m2。节点形式为刚接节点,支座处刚接,4个角点支承,自由曲面空间网格结构的初始形状见图 7。荷载形式为均布恒荷载(512 N/m2)和满跨分布活荷载(500 N/m2)。非边界控制点高度变化范围为[-5+x, 5+x],边界控制点高度变化范围为[-0.5+x, 0.5+x]。

|
图 7 自由曲面空间网格结构初始形状 Fig. 7 Initial shape of free-form spatial grid structure |
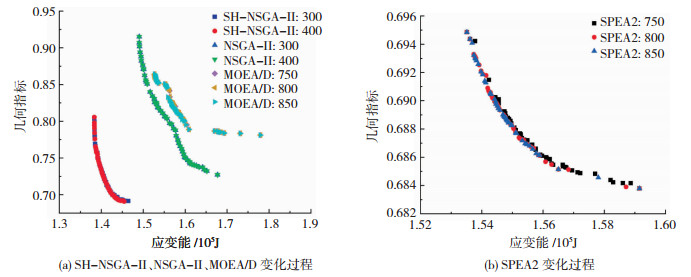
采用SH-NSGA-Ⅱ、NSGA-Ⅱ、SPEA2以及MOEA/D算法对自由曲面空间网格结构进行多目标优化,图 8给出了4种算法得到的Pareto解集随迭代步数的变化。SH-NSGA-Ⅱ和NSGA-Ⅱ算法在300步的Pareto解集与400步的Pareto解集相同,说明当迭代步数为300时算法收敛;SPEA2、MOEA/D算法在迭代步数为750、800、850时的Pareto解集几乎重合,说明在迭代步数为750时收敛。考虑计算时间(表 2),收敛时其他3种算法的计算时间分别是SH-NSGA-Ⅱ的0.953、3.066、6.091倍。
|
图 8 各算法Pareto解集随迭代步数的变化 Fig. 8 Variation of Pareto solution set obtained by each algorithm with the number of iterative steps |
| 表 2 自由曲面网格结构多目标优化结果 Tab. 2 Multi-objective optimization results of free-form grid structures |
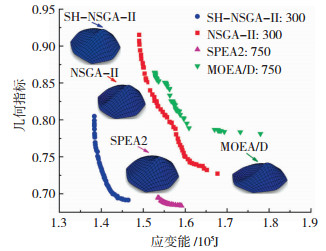
图 9为4种算法得到的Pareto最优解集,从4种算法的Pareto最优解集中选取合适的解,表 2给出了优化后结构各个指标的数值。SH-NSGA-Ⅱ算法得到Pareto最优解集的精确性优于其他3种算法,其结构应变能的下降幅度大于其他3种算法,几何指标的下降幅度明显大于NSGA-Ⅱ、MOEA/D算法,但略小于SPEA2。因此,SH-NSGA-Ⅱ算法明显提高了计算效率和解集的精确性。
|
图 9 自由曲面空间网格结构的Pareto最优解集 Fig. 9 Pareto optimal solution set of free-form spatial grid structure |
图 10为基于SH-NSGA-Ⅱ算法得到的自由曲面空间网格结构优化后的形状,且由表 2可知,基于SH-NSGA-Ⅱ算法得到的结构最大位移小于其他3种算法得到的结构最大位移。同时各项几何指标分别降低了63.5%、18.6%、19.3%、23%,验证了将几何综合量化指标作为目标函数的合理性。

|
图 10 结构优化后形状 Fig. 10 Optimized shape of free-form spatial grid structure |
为了生成既有良好的力学性能,又满足建筑要求的自由曲面网格结构,对自由曲面网格结构的多目标优化方法进行改进,提高优化方法的效率和优化后结构的性能。
基于NURBS技术、并利用表面平移法和等参线法分别建立自由曲面索撑网壳和自由曲面空间网格结构模型。选取曲面控制点的高度作为优化变量,同时为充分考虑曲面相似性、网格流畅性以及网格规整性,提出以几何综合量化指标T作为几何优化目标,选取结构应变能为静力性能优化目标,从而建立优化模型。
提出敏感度混合进化算法,基于该算法及上述优化模型进行多目标优化。通过与NSGA-Ⅱ、SPEA2以及MOEA/D算法对比验证了所提出的算法不仅可以获得精确性、均匀性更好的Pareto最优解集,而且具有较高的计算效率。
两种结构的优化结果表明:通过优化结构的形状使结构应变能下降,结构自身的力学性能有所提高。以综合量化指标为目标函数可有效提高自由曲面的相似性、流畅性以及网格规整性,具有较高的工程实用价值。
| [1] |
BLETZINGER K, RAMM E. Structural optimization and form finding of light weight structures[J]. Computers & Structures, 2001, 79(22): 2053. |
| [2] |
ESCHENAUER H A. Multicriteria structural optimization as a technique for quality improvement in the design process[J]. Computer-Aided Civil and Infrastructure Engineering, 1995, 10(4): 257. DOI:10.1111/j.1467-8667.1995.tb00288.x |
| [3] |
ANAND V. Computational methods for the representation of contour lines[J]. Computer-Aided Civil and Infrastructure Engineering, 1993, 8(2): 119. |
| [4] |
DIMITROV A, GU R, GOLPARVAR-FARD M. Nonuniform B-spline surface fitting from unordered 3D point clouds for as-built modeling[J]. Computer-Aided Civil and Infrastructure Engineering, 2016, 31(7): 483. DOI:10.1111/mice.12192 |
| [5] |
YANG Jie, ABDEL-MALEK K. Approximate swept volumes of NURBS sufaces or solids[J]. Computer Aided Geometric Design, 2005, 22(1): 1. DOI:10.1016/j.cagd.2004.08.002 |
| [6] |
TOMAS A, MARTI P. Shape and size optimisation of concrete shells[J]. Engineering Structures, 2010, 32(6): 1650. DOI:10.1016/j.engstruct.2010.02.013 |
| [7] |
LE C, BRUNS T, TORTORELLI D. A gradient-based, parameter-free approach to shape optimization[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 200(9): 985. |
| [8] |
崔昌禹, 王有宝, 姜宝石, 等. 自由曲面单层网壳结构形态创构方法研究[J]. 土木工程学报, 2013, 46(4): 57. CUI Changyu, WANG Youbao, JIANG Baoshi, et al. Study on the structural morphogenesis technique for single-layer reticulated shells of free-curved surface[J]. China Civil Engineering Journal, 2013, 46(4): 57. |
| [9] |
OHMORI H, KIMURA T, MAENE A. Computational morphogenesis of free form shells[C]//Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium. Valencia: International Association for Shell Structures, 2009: 105
|
| [10] |
WINSLOW P, PELLEGRINO S, SHARMA S B. Multi-objective optimization of free-form grid structures[J]. Structural and Multidisciplinary Optimization, 2010, 40: 257. DOI:10.1007/s00158-009-0358-4 |
| [11] |
冯若强, 葛金明, 胡理鹏, 等. 基于B样条曲线的自由曲面索支撑空间网格结构多目标形态优化[J]. 土木工程学报, 2015, 48(6): 17. FENG Ruoqiang, GE Jinming, HU Lipeng, et al. Multi-objective shape optimization of free-form cable-braced grid shells with B-spline method[J]. China Civil Engineering Journal, 2015, 48(6): 17. |
| [12] |
SU Yan, WU Yue, JI Wei, et al. Shape generation of grid structures by inverse hanging method coupled with multiobjective optimization[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33: 498. DOI:10.1111/mice.12361 |
| [13] |
DEB K, AGRAWAL S, PRATAP A, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 185. |
| [14] |
ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 715. |
| [15] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength Pareto evolutionary algorithm[C]//Proceedings of IEEE Conference on Evolutionary Methods for Design. [S. l. ]: IEEE Press, 2001: 95
|
| [16] |
GLYMPH J, SHELDEN D, CECCATO C, et al. A parametric strategy for free-form glass structures using quadrilateral planar facets[J]. Automation in Construction, 2004, 13(2): 187. DOI:10.1016/j.autcon.2003.09.008 |
| [17] |
李欣, 武岳. 索撑网壳——一种新型空间结构形式[J]. 空间结构, 2007, 13(2): 18. LI Xin, WU Yue. Grid shell—a new type of space structures[J]. Spatial Structures, 2007, 13(2): 18. |
| [18] |
丁慧, 罗尧治. 自由形态网壳结构网格生成的等参线分割法[J]. 浙江大学学报(工学版), 2014, 48(10): 1797. DING Hui, LUO Yaozhi. Isoparametric line dividing grid generation method for free-form lattice shells[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(10): 1797. |
| [19] |
崔昌禹, 姜宝石, 崔国勇. 基于敏感度的杆系结构形态创构方法[J]. 土木工程学报, 2013, 46(7): 3. CUI Changyu, JIANG Baoshi, CUI Guoyong. The sensitivity-based morphogenesis method for framed structures[J]. China Civil Engineering Journal, 2013, 46(7): 3. |
| [20] |
刘峰成, 冯若强. 考虑结构缺陷敏感性影响的单层空间网格结构形态优化研究[J]. 建筑结构学报, 2018, 39(7): 27. LIU Fengcheng, FENG Ruoqiang. Shape optimization of single-layer reticulated structure considering influence of structural imperfection sensitivity[J]. Journal of Building Structures, 2018, 39(7): 27. |
| [21] |
WANG Qisheng, YE Jun, WU Hui, et al. A triangular grid generation and optimization framework for the design of free-form gridshells[J]. Computer-Aided Design, 2019, 113: 101. |
 2022, Vol. 54
2022, Vol. 54


