2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 中南大学 土木工程学院, 长沙 410083
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Civil Engineering, Central South University, Changsha 410083, China
索撑网壳结构是在传统单层网壳的基础上,通过布置预应力拉索形成的一种刚柔混合的空间结构体系。其中柔性拉索的使用不仅能够提高整体结构的稳定性能,还能降低自重、使结构获得良好的建筑采光。由于该结构体系在受力性能和建筑美观性上的优势,在欧洲、日本等国家已经有了大型工程实例,如图 1所示德国的汉堡历史博物馆等[1]。

|
图 1 汉堡历史博物馆 Fig. 1 Museum of Hamburg History |
网壳结构的稳定性能[2]一直是结构设计中的关键。国内外学者[3-7]对双向网格型索撑网壳的稳定性能进行了系统研究,探究了不同布索方式和初始索力的影响规律。此外,由于实际工程中的索撑网壳通常采用图 2中的装配式半刚性节点,所以对节点刚度的研究同样至关重要。马会环等[8]、曹正罡等[9]通过弹簧单元模拟节点半刚性,对单层网壳的稳定性能展开了研究。López等[10]对螺栓球节点进行足尺的模型试验,并基于试验数据分析了节点刚度对网壳稳定性的影响。但是装配式节点在制作与安装过程中,还难免存在尺寸偏差与安装误差,如各零件间可能存在的间隙、螺栓孔的定位偏差以及螺帽是否拧紧等。这些几何缺陷[11]必将不同程度地影响节点的受力方式,导致节点实际刚度与理论刚度存在偏差。所以,还应将半刚性节点的刚度偏差作为一种初始缺陷,在索撑网壳的稳定性分析中予以考虑。

|
图 2 典型索撑网壳节点 Fig. 2 Typical joints in cable-stiffened latticed shells |
本文分析了节点刚度缺陷对柱面索撑网壳稳定性的影响规律,尤其考虑了所有节点的初始刚度偏差不均匀分布的情况。首先对典型的半刚性节点进行了有限元模拟,获得了无初始缺陷状态下的节点刚度; 在此基础上,对具有初始节点刚度缺陷的半刚性索撑网壳进行了非线性全过程分析,对结构的受力机理、破坏模式进行了深入研究; 最后从节点刚度不对称的角度,提出了柱面索撑网壳失稳模式的判别方法,并通过随机算例对方法进行了验证,为索撑网壳的结构设计和工程应用提供了参考。
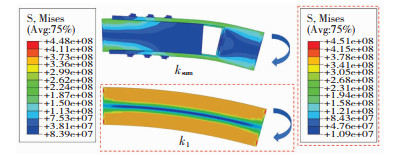
1 典型半刚性节点的有限元模拟分析图 2中的装配式节点是索撑网壳中常用的节点形式,由内钢管、开洞的外钢管和螺栓杆三部分组成。为了获得无缺陷状态下节点在平面内、平面外的转动刚度和扭转刚度,基于ABAQUS有限元软件建立了实体模型,见图 3。并且为简化计算,取1/4节点进行模拟分析。在计算中假设节点各个部件间紧密接触、互不穿透,且不考虑接触面间的摩擦。钢管采用Q345号钢材和双折线本构模型。边界条件为内钢管取半截面(截面A)处固定约束,并在外钢管最右端截面(截面B)处分别施加绕x、y、z轴的转角荷载。1/4模型的应力结果见图 4,外钢管上的弯矩经由螺栓与孔壁间的相互作用传递到内钢管上,最后通过提取左侧固定端截面上的弯矩与右侧外钢管端部的转角位移,计算出了模型的转动刚度ksum。

|
图 3 1/4实体节点模型 Fig. 3 One-fourth solid joint model |
|
图 4 节点应力云图 Fig. 4 Stress nephogram of joint model |
此外,为了剔除网壳杆件刚度kl的影响,根据钢管截面尺寸建立了有限元模型。同样地,通过在钢管末端施加转角荷载的方式得到了弯矩转角曲线,从而确定了杆件刚度kl。最后,通过式(1)计算得到半刚性节点的实际转动刚度kj,kj绕x、y、z轴的3个转动刚度见表 1。
| $ \frac{1}{{{k_{\rm{j}}}}} = \frac{1}{{{k_{{\rm{sum}}}}}} - \frac{1}{{{k_{\rm{1}}}}} $ | (1) |
| 表 1 节点刚度统计表 Tab. 1 Joint stiffness statistics (kN · m)/rad |
本节分别对刚接柱面索撑网壳、各节点具有相同刚度缺陷和随机刚度缺陷的半刚接柱面索撑网壳进行了稳定性全过程分析,对比说明刚度缺陷对结构失稳模式和极限承载力的影响。
2.1 刚接柱面索撑网壳稳定性分析算例的几何尺寸见图 5,横向和纵向均划分为20个网格。网壳杆件采用截面200 mm×150 mm×10 mm的矩形钢管,屈服强度为345 MPa,通过beam188单元模拟。交叉索采用37ϕ4的钢绞线,通过link180单元模拟,初始预应力为300 MPa。边界条件为沿两纵边的铰接约束。

|
图 5 柱面索撑网壳模型 Fig. 5 Cylindrical cable-stiffened latticed shell model |
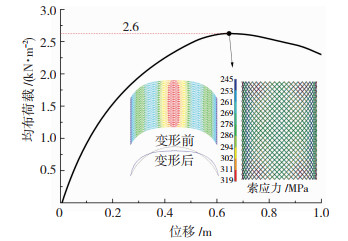
在均布荷载作用下,索撑网壳中部向下凹陷,左右两侧向上凸起。随着变形不断增加,结构最终发生正对称的极值点失稳,变形最大点的荷载位移曲线见图 6。此外,由于拉索布置于四边形网格的对角线上,导致其只能控制网格的面内剪切变形,所以仅位于柱壳非约束边附近的少量索参与抵抗了结构变形,这一过程中索力的最大增加量为初始索力的7%,最大减小量为初始的17%。
|
图 6 刚接柱面网壳的荷载-位移曲线 Fig. 6 Load - displacement curve of rigidly connected cylindrical latticed shell |
为探究节点刚度缺陷的影响,将半刚性节点的实际刚度与理论刚度间的偏差定义为节点刚度缺陷,并以刚度差值占理论刚度值的百分比来衡量缺陷的大小。由2.1节可知,索撑网壳在承受荷载并达到极限承载力的过程中,结构变形始终以竖向位移为主,未发生明显的平面内变形。所以,半刚性节点的面内转动刚度kjz和扭转刚度kjx对沿两纵边约束的柱壳影响较小,故在本节建立的具有刚度缺陷的数值模型中,均只考虑了节点平面外转动刚度kjy的缺陷。算例模型尺寸见图 5,基于ANSYS软件采用3个combin39弹簧单元模拟半刚性节点绕3个方向的转动刚度,通过改变弹簧刚度对具有刚度缺陷的节点进行模拟。对于考虑节点半刚性且无初始刚度缺陷的结构,节点的面外转动刚度kjy见表 2,面内转动刚度和扭转刚度与表 1一致。而对于所有节点具有相同刚度缺陷和随机刚度缺陷的结构,节点的kjz和kjx均与无初始刚度缺陷的结构相同,kjy则是在理论刚度(20 000 (kN · m)/rad)的基础上产生一定程度的变化。
| 表 2 稳定承载力统计表 Tab. 2 Stability bearing capacity statistics |
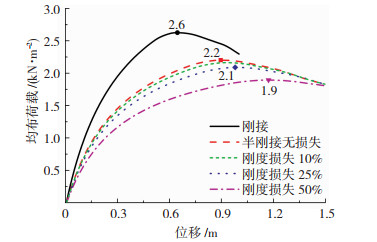
将网壳中所有节点都具有相同刚度偏差的缺陷定义为同一节点刚度缺陷,并对不同幅值下的具有同一节点刚度缺陷的索撑网壳进行稳定性分析。当节点面外转动刚度无损失、损失10%、损失25%和损失50%时,结构的荷载位移曲线见图 7,稳定承载力结果见表 2。从中可发现,考虑节点半刚性且无刚度损失时的失稳模式与节点刚接时一致,均发生正对称失稳。但是,考虑节点半刚性后,结构整体刚度和承载力显著降低,说明了节点半刚性对索撑网壳的稳定性能有较大影响。而对于具有同一节点刚度缺陷的半刚性索撑网壳,当刚度损失不超过25%时,失稳模式和极限承载力相比于理想半刚接结构均无明显改变。当同一节点刚度缺陷的幅值小于10%时,可以不考虑缺陷带来的影响。从图 7中还可发现,荷载位移曲线随着缺陷幅值的增加逐渐平缓。这主要是由于网壳是一种“形状抵抗”型结构,结构的受力更依赖于形状抗力而非材料抗力。当变形较小时,节点位置稍有变化就会对结构整体刚度产生较大影响。但随着节点刚度损失的增加,失稳时结构的变形越大,对于节点位置变化的敏感程度随之下降,“形状抵抗”的贡献逐渐降低。所以结构失稳就越不突然,曲线下降得越平缓。
|
图 7 具有相同节点刚度缺陷索撑网壳的荷载-位移曲线 Fig. 7 Load - displacement curve of cable-stiffened latticed shell with same joint stiffness defect |
装配式节点在安装过程中难免存在随机误差,如螺栓预紧力偏差,螺栓与孔壁间的间隙等。因此,结构中的各个节点将产生不同程度的刚度损失,故简单地假设每个节点均具有相同的刚度缺陷与实际情况不符。为了更好地反映工程实际,应将节点刚度缺陷考虑为一种随机分布。
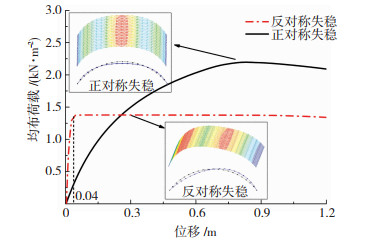
对一个具有随机节点刚度缺陷的索撑网壳进行分析,假设各节点的刚度损失在0%~2%之间均匀分布。具体刚度分布情况见图 8,以点的大小和颜色表示节点实际面外转动刚度的大小,1代表节点刚度无损失,即20 000 (kN·m)/rad;0代表节点刚度损失达到了给定最大值,即19 600 (kN·m)/rad。结构在均布荷载作用下的荷载位移曲线见图 9中的红色点划线。当最大位移达到0.04 m,荷载达到1.4 kN/m2后,结构开始向一侧偏移,最终发生反对称失稳。

|
图 8 柱面网壳随机节点刚度分布示意 Fig. 8 Distribution of random joint stiffness of cylindrical latticed shell |
|
图 9 随机算例荷载-位移曲线 Fig. 9 Load - displacement curve of random example |
为说明随机刚度缺陷的影响规律,统计了60个节点刚度缺陷幅值为2%、3%的随机算例结果,列于表 3。结果中出现了正对称失稳和反对称失稳两种模式。当发生正对称失稳时,结构的极限承载力为2.2 kN/m2左右,和考虑节点半刚性且无缺陷时一致。当结构发生反对称失稳时,极限承载力大幅降低,仅为前者的64%。出现两种不同的失稳模式说明了柱面索撑网壳存在不利的节点刚度缺陷分布,导致结构的失稳模式发生改变,承载力大幅降低。而随着最大缺陷幅值的增加,发生反对称失稳的频率也相应增加。当节点刚度缺陷的最大幅值为2%时,发生反对称失稳的频率为27%;当缺陷幅值提高到3%时,发生反对称失稳的频率增加到了50%。综上,两纵边支承的柱面索撑网壳对随机节点刚度缺陷较敏感。
| 表 3 稳定承载力统计表 Tab. 3 Stability bearing capacity statistics |
由2节分析可知,同一节点刚度缺陷的幅值达到25%时,结构发生正对称失稳,极限承载力相比于无缺陷结构下降了不到5%;而随机节点刚度缺陷的最大幅值为2%时,结构的极限承载力最多下降了36%,失稳模式转变为侧向反对称失稳。由于沿两纵边支承柱面索撑网壳的几何构型与失稳模式均沿纵向左右对称,故合理推测节点刚度缺陷的不对称分布是诱导结构发生反对称失稳、降低极限承载力的主要原因。为了验证这一结论,将位于对称轴一侧的节点设置为无刚度损失,另一侧的节点均设置为具有2%的初始刚度缺陷,对这种结构进行稳定性分析,得到的荷载位移曲线见图 10。从中可看出,即使节点刚度缺陷幅值仅为2%,结构也发生了反对称失稳。

|
图 10 刚度不对称分布的荷载-位移曲线 Fig. 10 Load - displacement curve of asymmetric stiffness distribution |
由上述分析可知,节点刚度的不对称分布是导致柱面索撑网壳承载力下降的关键因素。故为了衡量节点刚度关于纵向几何对称轴的不对称程度,本文定义了节点刚度的不对称度β,具体公式为
| $ \beta = \frac{1}{n}\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {{\alpha _j}\left( {k_{ij}^{'} - {k_{ij}}} \right)} } {d_{\max }} $ | (2) |
式中:n为节点所处的行数;m为节点所处的列数; dmax为节点刚度缺陷幅值,表示为无缺陷节点刚度的百分比; kij为第i行第j列节点刚度的相对大小; k'ij为kij对称位置处节点刚度的相对大小; kij∈[0, 1],当kij=0时,表示该节点刚度缺陷达到了dmax; 当kij=1时,表示该节点刚度没有缺陷。
此外,节点所处位置不同,其刚度缺陷对结构稳定性的影响也不同。故式(2) 中还引入了位置敏感系数αj,以此量化节点位置的重要程度,计算公式为
| $ {\alpha _j} = \frac{1}{{D_{\max }^j}} $ | (3) |
式中:αj为第j列节点的位置敏感系数,Dmaxj为仅由第j列节点刚度缺陷导致结构失稳模式转变时的临界缺陷幅值。以图 5的柱面索撑网壳为例,对位置敏感系数αj的具体计算方法进行说明:
1) 首先,生成具有节点刚度缺陷的有限元模型(缺陷仅存在于第j列节点)。模型中第j列节点的相对刚度为0,其余位置处节点的刚度均为1, 见图 11。
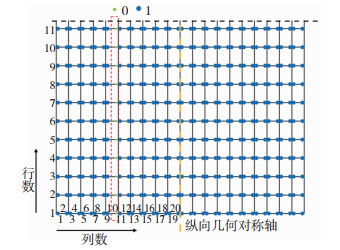
|
图 11 柱面网壳单列节点刚度缺陷示意 Fig. 11 Schematic of single-row joint stiffness defects of cylindrical latticed shell |
2) 不断改变第j列节点刚度的缺陷幅值并对结构进行稳定性计算。通过试算的方式,得到使结构从正对称失稳转变为反对称失稳的临界缺陷幅值。以图 11为例,当缺陷幅值为0.9%时,结构发生正对称失稳;当缺陷幅值增加至1.1%时,结构发生反对称失稳。则Dmax10=1%即为导致该结构失稳模式变化的临界缺陷幅值,即第10列节点的位置敏感系数α10=100。
3) 对位于不同列数的节点进行计算,并重复上述过程。见图 12,最终得到全部节点的位置敏感系数。

|
图 12 位置敏感系数 Fig. 12 Position sensitive coefficient |
由表 3的结果可知,应存在一个节点刚度不对称度的临界值β0, 当节点刚度的不对称程度超过此临界值后,结构将发生反对称失稳。为确定柱面索撑网壳节点刚度的临界不对称度,现统计最大缺陷幅值为2%、3%的各30个随机算例的计算结果,其中节点刚度不对称度与相应的失稳模态见图 13。当不对称度β≥1时,结构发生反对称失稳;而当β < 1时,结构发生正对称失稳,故取β0=1为两纵边支承柱面索撑网壳的临界不对称度。
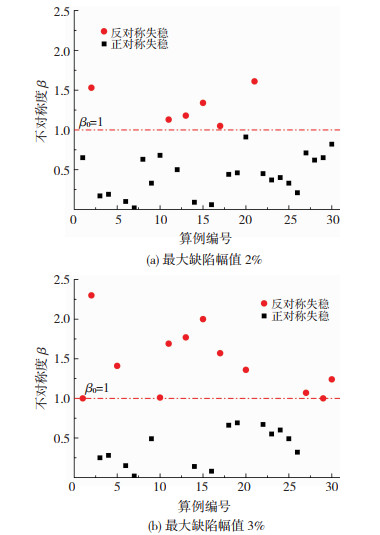
|
图 13 40 m网壳随机算例结果 Fig. 13 Results of random examples of 40 m latticed shells |
为了验证临界不对称度的可靠性,以跨度为30 m的柱面索撑网壳为例进行验算。模型的纵向长度为45 m,网格数为15×15,其余参数与图 5中一致。同样地,统计了30个随机算例的结果,节点刚度不对称度与失稳模式见图 14。当不对称度β < 1时,结构发生正对称失稳;当不对称度β≥1时,结构均发生反对称失稳,证明了判别方法的正确性。
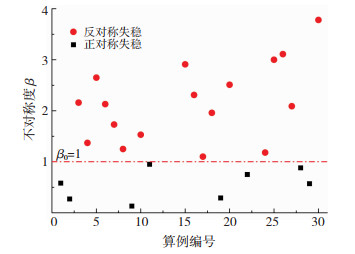
|
图 14 30 m网壳随机算例结果 Fig. 14 Results of random examples of 30 m latticed shells |
为更全面、更真实地反映工程实际,对具有节点刚度缺陷的柱面索撑网壳进行了静力稳定性分析,并通过多个随机算例研究了节点刚度缺陷不均匀分布对结构失稳模式与极限承载力的影响,得到如下结论:
1) 同一节点刚度缺陷对两纵边支承的柱面索撑网壳稳定性能影响较小。10%的刚度损失仅让结构的承载力降低不到2%。且随着缺陷幅值的增加,结构的失稳模式没有发生改变,均为正对称失稳。
2) 两纵边支承的柱面索撑网壳对随机节点刚度缺陷较为敏感。考虑随机节点刚度缺陷时,结构可能出现两种失稳模式,一种是承载力较高的正对称失稳,另一种是承载力较低的反对称失稳,其承载力仅为正对称失稳的2/3,故在工程设计中应考虑节点刚度缺陷不均匀分布的影响。
3) 可通过节点刚度不对称度β对两纵边支承柱面索撑网壳的失稳模式进行判断,并确定了结构失稳模式发生改变时的临界不对称度β0=1。当不对称度β < 1时,结构发生正对称失稳;当不对称度β≥1时,结构发生反对称失稳。通过90个随机算例,验证了该判别方法的可靠性,并为施工中的误差控制提供了一个标准。
| [1] |
曹正罡, 武岳, 范峰. 索撑网壳结构体系在自由曲面采光顶中的应用与发展[C] //第十二届全国现代结构工程学术研讨会暨第二届全国索结构技术交流会论文集. 北京: 中国钢结构协会, 2012: 86 CAO Zhenggang, WU Yue, FAN Feng. Application and development of cable-supported reticulated shell structure system in free-form surface daylighting roof[C]//Proceedings of the 12th National Symposium on Modern Structural Engineering and the 2nd National Conference on Cable Structure Technology Exchange. Beijing: China Steel Construction Society, 2012: 86 |
| [2] |
沈世钊. 网壳结构的稳定性[J]. 土木工程学报, 1999, 36(2): 11. SHEN Shizhao. Stability of reticulated shell structure[J]. China Civil Engineering Journal, 1999, 36(2): 11. |
| [3] |
LI Pengcheng, WU Minger. Parametric study of cable-stiffened single-layer cylindrical latticed shells with different supporting conditions[J]. Journal of Constructional Steel Research, 2016, 121: 457. DOI:10.1016/j.jcsr.2016.03.028 |
| [4] |
LI Pengcheng, WU Minger, WANG Hao, et al. Experimental and numerical analysis of cable-stiffened single-layer spherical latticed shells[J]. Advances in Structural Engineering, 2016, 19(3): 488. DOI:10.1177/1369433216630120 |
| [5] |
宋同, 吴明儿. 拉索配置对双向网格单层网壳结构稳定性能的影响[C]//庆祝刘锡良教授八十华诞暨第八届全国现代结构工程学术研讨会论文集. 天津: 中国钢结构协会, 2008: 891 SONG Tong, WU Minger. The influence of cable configuration on the stability of bidirectional single-layer reticulated shell[C]// Celebrating the 80th Birthday of Professor Liu Xiliang and the Proceedings of the 8th National Symposium on Modern Structural Engineering. Tianjin: China Steel Construction Society, 2008: 891 |
| [6] |
壮一郎九嶋. 対角材としてPC鋼棒部材を組み込んだ単層2方向格子ドームの座屈性状に関する実験的研究[J]. 日本建築学会構造系論文集, 2006, 71(603): 85. |
| [7] |
壮一郎九嶋. テンション材を対角材として組み込んだ単層2方向格子ドームの座屈性状に関する数値解析的研究[J]. 日本建築学会構造系論文集, 2007, 72(617): 121. |
| [8] |
马会环, 范峰, 曹正罡, 等. 半刚性螺栓球节点单层球面网壳受力性能研究[J]. 工程力学, 2009, 26(11): 73. MA Huihuan, FAN Feng, CAO Zhenggang, et al. Mechanical performance of single-layer reticulated domes with semi-rigid bolt-ball joints[J]. Engineering Mechanics, 2009, 26(11): 73. |
| [9] |
曹正罡, 范峰, 马会环, 等. 螺栓球节点试验及在单层网壳结构中的应用性[J]. 哈尔滨工业大学学报, 2010, 42(4): 525. CAO Zhenggang, FAN Feng, MA Huihuan, et al. Experiment of bolt-ball joint and its application in single-layer reticulated shells[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 525. DOI:10.11918/j.issn.0367-6234.2010.04.005 |
| [10] |
LÓPEZ A, PUENTE I, SERNA M A. Numerical model and experimental tests on single-layer latticed domes with semi-rigid joints[J]. Computers & Structures, 2007, 85(7/8): 360. DOI:10.1016/j.compstruc.2006.11.025 |
| [11] |
蔡健, 贺盛, 姜正荣, 等. 单层网壳结构稳定分析中初始几何缺陷最大值的研究[J]. 建筑结构学报, 2015, 36(6): 86. CAI Jian, HE Sheng, JIANG Zhengrong, et al. Investigation on maximum value of initial geometric imperfection in stability analysis of single layer reticulated shells[J]. Journal of Building Structures, 2015, 36(6): 86. DOI:10.11918/j.issn.0367-6234.2016.03.001 |
 2022, Vol. 54
2022, Vol. 54


