波纹钢板是指平钢板通过辊轧形成的表面起伏的板件,其面外刚度较大且抗剪切屈曲能力较强,因此常被应用于桥梁结构中[1-4]。波纹钢板还可用于剪力墙结构中,其具有较高的侧向承载力和稳定的滞回性能[5-8]。在组合结构领域,波纹钢板混凝土剪力墙的延性与耗能能力较优,这得益于混凝土既可约束波纹钢板的变形,又和波纹钢板表面的凹槽互相咬合嵌固,从而确保二者之间的有效黏结锚固与共同受力变形[9-12]。因此,波纹钢板与混凝土界面的黏结滑移性能是保证二者协同工作的必要条件,并且可对整体的组合效应产生重要影响。
目前,关于钢-混凝土界面黏结滑移的研究主要集中于型钢混凝土结构,研究结果表明界面黏结力主要包含化学胶结力、摩擦力和机械咬合力[13]。而针对钢板混凝土组合结构黏结滑移性能的研究较少,在实际工程中主要通过在平钢板上布置抗剪连接件来强化平钢板与混凝土的组合效应[14-16]。波纹钢板混凝土结构界面黏结面积较大,在保证黏结性能的同时可适当减少甚至不使用抗剪连接件,与平钢板混凝土结构相比可减少工程造价。此外,有关波纹钢板混凝土剪力墙的黏结滑移研究较少,其界面黏结机理与滑移破坏模式不同于型钢混凝土结构,且相关的理论及设计方法不够完善,亟需通过相应的研究来为实际工程提供理论基础,因此对波纹钢板-混凝土界面黏结滑移性能的研究很有必要。
为研究波纹钢板-混凝土界面黏结滑移性能,充分发挥波纹钢板混凝土组合结构的性能优势,并为波纹钢板混凝土剪力墙的设计提供理论基础,本文通过10个波纹钢板混凝土试件的推出试验,综合考虑混凝土强度、保护层厚度及埋置长度对波纹钢板-混凝土界面黏结性能的影响,研究试件破坏形态、黏结滑移受力机理、应变分布规律、特征黏结强度及黏结滑移本构关系等。
1 试验概况 1.1 试件设计试验设计了10个波纹钢板混凝土试件,试件的主要变化参数为混凝土保护层厚度、混凝土强度及波纹钢板埋置长度。试件具体参数见表 1。波纹钢板尺寸由规范[17]确定,波纹钢板厚度为8 mm,波脊、波谷长度分别为70、100 mm,波角为45°,波纹钢板长度由埋置长度决定。为了便于推出,所有试件的波纹钢板上端突出混凝土60 mm,下端突出混凝土10 mm。以试件S-1为例,其具体尺寸见图 1。
| 表 1 试件设计参数 Tab. 1 Design parameters of specimens |
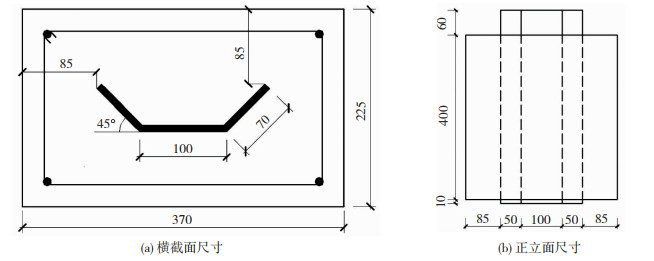
|
图 1 试件S-1尺寸(mm) Fig. 1 Dimensions of specimen S-1 (mm) |
试验采用的商品混凝土设计强度分别为C30、C40、C50和C60。在浇筑试件的当天浇筑立方体混凝土标准试块,每个标号的混凝土浇筑3个标准立方体试块,与试件在同等条件下养护28 d。波纹钢板采用8 mm厚的Q235钢板折弯加工而成,纵筋采用12 mm的HRB400带肋钢筋,箍筋采用6 mm的HPB300光圆钢筋。表 2为混凝土的材性试验结果,表 3为钢材的材性试验结果。
| 表 2 混凝土材性试验结果 Tab. 2 Mechanical properties of concrete |
| 表 3 钢材材性试验结果 Tab. 3 Mechanical properties of steel |
推出试验在西安建筑科技大学结构与抗震实验室WAW-1000液压伺服万能试验机上进行,加载装置见图 2。试件加载通过位移控制,加载速率为0.3 mm/min,正式加载前预加载5 kN以保证接触面充分接触。当试件发生明显破坏或荷载处于残余稳定阶段时停止加载。

|
图 2 试验加载装置 Fig. 2 Test setup |
为便于加载,试件上下端均布置有钢垫板,上端为普通厚钢板,下端为开波纹孔的厚钢板,开孔是为波纹钢板可自由向下推出。由于试件上端与作动头接触,下端与固定台座接触,因此确定试件上端为加载端,下端为自由端。试件上下各布置一个位移传感器,分别测量加载端和自由端在加载过程中的滑移量。为反映波纹钢板应变的连续性,应变片等间距布置在波谷和波脊内侧中间位置,用纱布加环氧树脂隔离混凝土与应变片。以试件S-1为例,位移计与应变片的测点布置见图 3。
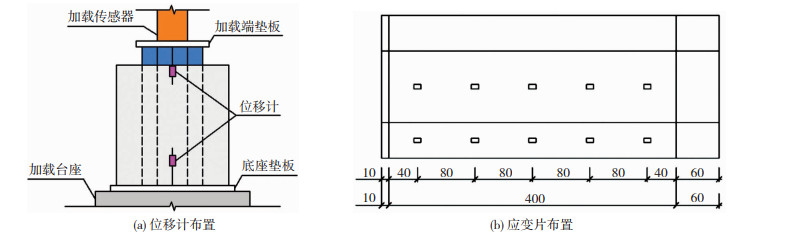
|
图 3 试验测点布置(mm) Fig. 3 Layout of test points (mm) |
为便于描述试件破坏位置,先对试件方位进行定义,见图 4。加载初期,试件S-1、S-2、S-3、S-4、S-6、S-10加载端先开始滑移,当荷载达到极限荷载的18%时,自由端开始滑移;试件S-7加载端与自由端同时产生滑移;试件S-5、S-8、S-9初期加载端与自由端均无明显滑移,加载端随荷载增大先产生滑移,自由端随后产生滑移。
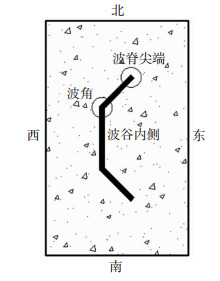
|
图 4 试件方位 Fig. 4 Orientation of specimen |
所有试件的破坏过程较为类似,可表现为:当荷载不断增加达到峰值时,试件内部发出“嘭”的声响,混凝土与钢板之间部分界面脱离,荷载随即陡降,此时试件内部化学胶着力丧失,黏结力由摩擦力与机械咬合力承担。随着滑移量增大,荷载逐渐降低,加载端北侧波纹钢板波脊尖端处出现细微裂缝,并不断向试件边缘延伸。同时,试件西侧中部出现一条上下贯通的纵向裂缝。
加载后期,钢板被缓慢推出,在荷载残余阶段,荷载稳定在极限荷载的23%左右。最终,试件表面裂缝主要集中于加载端、自由端和西侧,在北侧和南侧也存在贯通裂缝,裂缝宽约1~2 mm。
2.2 破坏类型试件破坏类型可分为黏结劈裂破坏和黏结锚固破坏。黏结劈裂破坏的典型试件为S-4,见图 5(a)。特征是波纹钢板与混凝土发生沿纵向的剪切滑移,裂缝出现在试件西侧且迅速发展至上下两端形成贯通裂缝,同时波脊尖端出现劈裂裂缝。残余荷载一般为极限荷载的20%左右。黏结劈裂破坏的延性较差,主要原因是波纹钢板与混凝土界面间黏结力不足,在实际工程设计中应当避免。

|
图 5 试件破坏形态 Fig. 5 Failure modes of specimens |
黏结锚固破坏的典型试件为S-9,见图 5(b)。特征是保护层厚度较大,埋置长度较短,箍筋及波纹钢板基本都处于弹性阶段,残余荷载一般为极限荷载的40%左右。由于钢板被推出时,向外膨胀的趋势加剧了钢板外侧混凝土的法向正应力作用,因此会有膨胀裂缝形成,此裂缝产生较晚且延伸速度较慢,在靠近波谷处裂缝较窄,远离波谷处裂缝较宽。
2.3 荷载-滑移曲线图 6为各试件加载端和自由端的荷载-滑移曲线。各曲线变化规律较为类似,都经历了荷载上升段、荷载下降段及荷载残余段。如图 6(b)所示,试件S-2加载端与自由端滑移量相差较大,这是因为混凝土浇筑不密实,加载端钢板与混凝土界面间存在微裂纹及孔洞,更容易产生滑移。如图 6(e)所示,试件S-5荷载下降后又明显上升,这是因为其在混凝土浇筑时产生了初始缺陷,荷载下降之后,黏结界面间被挤碎的混凝土碎屑填充了混凝土与钢板间的孔隙,使试件界面短期内恢复正常的黏结性能,在黏结力失效后荷载继续下降。
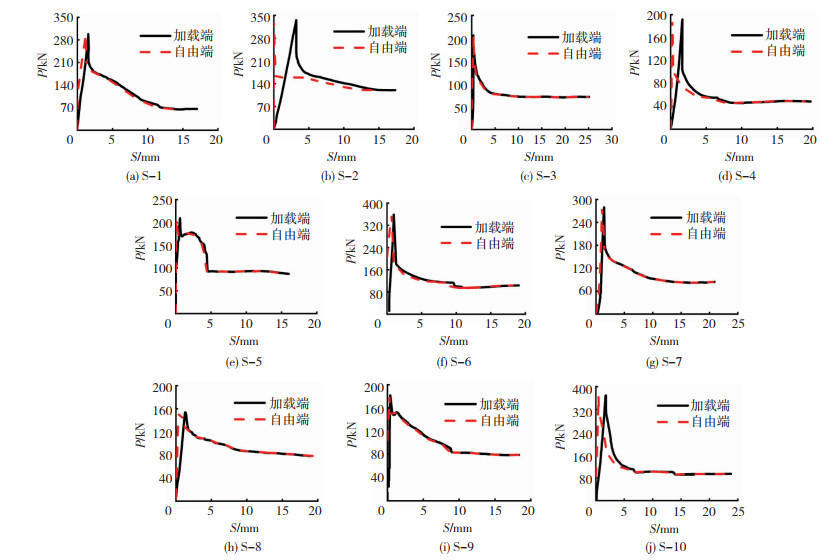
|
图 6 试件荷载-滑移曲线 Fig. 6 Load - slip curves of specimens |
由于试件自由端的荷载-滑移曲线除滑移量稍滞后之外,其余规律与加载端的基本相似,同时考虑到自由端易受试件浇筑或加载等因素的影响,因此主要对加载端的荷载-滑移曲线进行分析。
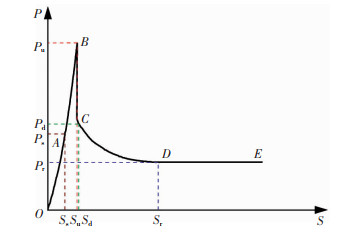
通过归纳可将试件加载端荷载-滑移曲线总结成图 7的特征荷载-滑移曲线,分为3个阶段:荷载上升段OB,荷载下降段BD与荷载残余段DE。
|
图 7 特征荷载-滑移曲线 Fig. 7 Characteristic load - slip curve |
为方便描述,定义各特征点:O为坐标原点;A为初始滑移点即荷载增速转折点,对应荷载为Ps,滑移为Ss;B为峰值点,对应荷载为Pu,滑移为Su;C为骤降点,对应荷载为Pd,滑移为Sd;D为残余点,对应荷载为Pr,滑移为Sr。
上升段OB:由OA段和AB段组成。其中OA段为微滑移段,界面发展情况见图 8(a)。该阶段界面主要由黏结扩散段和协同受力段组成,主要黏结力为化学胶着力。其中AB段为滑移段,界面发展情况见图 8(b)。该阶段裂缝迅速扩展,随着黏结扩散段的化学胶着力逐渐失效,界面黏结层混凝土产生破碎带,摩擦力和机械咬合力逐渐增加。
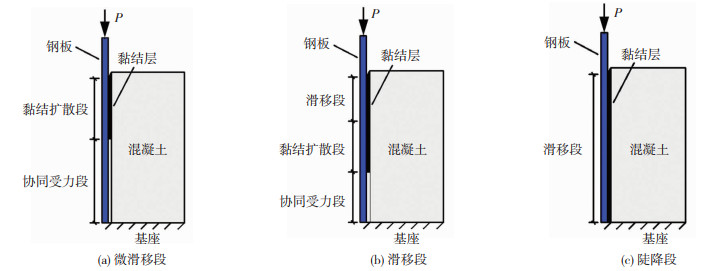
|
图 8 界面发展情况 Fig. 8 Interface development |
下降段BD:由BC段和CD段组成。其中BC段为陡降段,界面发展情况见图 8(c)。此时滑移区已扩展至自由端,全界面产生滑移,内部化学胶着力突然减小。其中CD为缓降段,黏结力主要由摩擦力和机械咬合力组成。
残余段DE:此阶段黏结力几乎完全由摩擦力组成,黏结力一般为峰值荷载的25%左右,混凝土裂缝完全停止发展。
2.4 波纹钢板应变规律 2.4.1 真实应变当加载到峰值荷载之后,大部分应变片因黏结界面的破坏而损坏,因此本文选取典型试件的荷载上升阶段的波纹钢板应变分布来分析其规律。
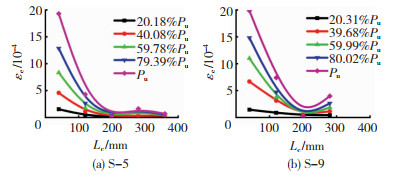
图 9为波纹钢板真实应变分布情况,由图 9可知应变大致沿埋置长度呈指数分布的形式,即随埋置长度的增加而减小,在自由端处应变最小,且波脊应变大于波谷应变。试件S-9波谷应变在靠近自由端区域内有明显的过零点现象,即应变反向增加,该现象是特例。这主要是因为在荷载上升阶段,黏结界面失效范围由加载端逐步向自由端扩展,此阶段存在滑移区与黏结区共存的区域。自由端混凝土受底部约束会产生向上的荷载,从而对底部钢板有向上的反力,此时向下的黏结力小于向上的约束反力,因此在钢板局部存在纵向受拉区,应变出现过零点现象。
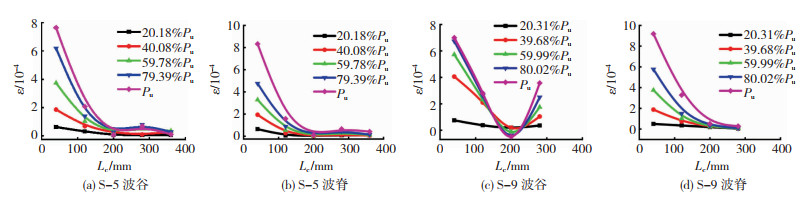
|
图 9 波纹钢板真实应变分布 Fig. 9 Actual strain distribution of corrugated steel plate |
对波纹钢板取一段微元体进行分析,见图 10。
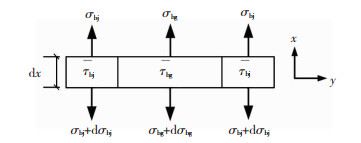
|
图 10 波纹钢板应力微元体 Fig. 10 Stress of micro-element of corrugated steel plate |
由于波纹钢板在推出过程中未发生屈服,根据试件平衡条件建立其力学平衡方程:
| $ \tau (x)D = {D_{{\rm{bg}}}}{\bar \tau _{{\rm{bg}}}}(x) + 2{D_{{\rm{bj}}}}{\bar \tau _{{\rm{bj}}}}(x) $ | (1) |
| $ 2{\bar \tau _{{\rm{bg}}}}(x) = \frac{{{\rm{d}}{\sigma _{{\rm{bg}}}}(x)}}{{{\rm{d}}x}}t $ | (2) |
| $ 2{\bar \tau _{{\rm{bj}}}}(x) = \frac{{{\rm{d}}{\sigma _{{\rm{bj}}}}(x)}}{{{\rm{d}}x}}t $ | (3) |
化简可得
| $ \tau (x)D = \frac{{Et}}{2}\frac{{\rm{d}}}{{{\rm{d}}x}}\left[ {{D_{{\rm{bg}}}}{{\bar \varepsilon }_{{\rm{bg}}}}(x) + 2{D_{{\rm{bj}}}}{{\bar \varepsilon }_{{\rm{bj}}}}(x)} \right] $ | (4) |
式中:τ(x)为平均黏结应力,D为波纹钢板截面展开长度,Dbg和Dbj分别为波谷和波脊长度,τbg(x)和τbj(x)分别为波谷和波脊的平均黏结应力,εbg(x)和εbj(x)分别为波谷和波脊的平均应变,σbg(x)和σbj(x)分别为波谷和波脊的轴向应力,E为钢材弹性模量,t为波纹钢板厚度。
由此可定义等效应变为
| $ {\varepsilon _{\rm{e}}}(x) = {\bar \varepsilon _{{\rm{bg}}}}(x) + 2\frac{{{D_{{\rm{bj}}}}}}{{{D_{{\rm{bg}}}}}}{\bar \varepsilon _{{\rm{bj}}}}(x) $ | (5) |
则试件S-5和S-9的等效应变分布见图 11。
|
图 11 波纹钢板等效应变分布 Fig. 11 Equivalent strain distribution of corrugated steel plate |
本文以平均黏结应力来表征波纹钢板与混凝土界面间的黏结强度,计算公式为
| $ \tau = \frac{P}{{D{L_{\rm{e}}}}} $ | (6) |
选取荷载上升段转折点应力τs,荷载峰值点应力τu以及荷载残余段应力τr作为判断标准,综合分析各参数变化对黏结强度的影响。
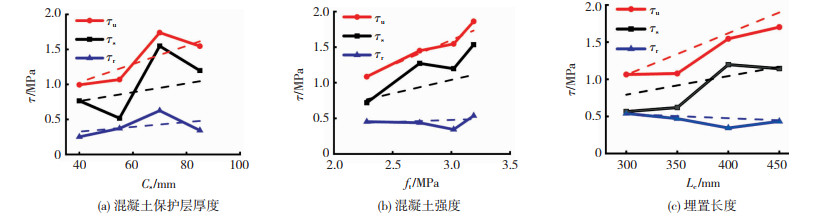
3.1.1 混凝土保护层厚度图 12(a)为试件的黏结强度与混凝土保护层厚度的关系图。总体上,试件黏结强度随保护层厚度增大而增大,但当保护层厚度由70 mm增大至85 mm时,黏结强度有所下降。这种现象产生的原因可能是当保护层厚度过大时,试件外边缘混凝土在内部黏结界面层还未破坏之前便达到抗拉强度,而试件的配箍率不足导致混凝土提前开裂,黏结强度随之下降。
|
图 12 特征黏结强度影响参数 Fig. 12 Influencing parameters of characteristic bond strength |
图 12(b)为试件黏结强度与混凝土强度的关系图。由于混凝土抗拉强度或抗压强度变化对黏结强度的影响规律一致,本文选取抗拉强度来显示其规律。初始黏结强度τs与极限黏结强度τu总体上随混凝土强度增加而增大,而残余黏结强度τr与混凝土强度无明显关系。这是因为混凝土强度的改变对化学胶着力影响很大,在未达到峰值荷载之前,混凝土与钢板界面间的化学胶着力起主要作用,而当界面层破坏之后,化学胶着力退出工作,黏结力主要由摩擦力与机械咬合力承担。
3.1.3 波纹钢板埋置长度图 12(c)为试件黏结强度与波纹钢板埋置长度关系图。初始黏结强度τs、极限黏结强度τu与埋置长度总体呈线性增长的关系,而残余黏结强度τr与埋置长度的关系不太明显。主要原因是钢板与混凝土的有效接触面积随着埋置长度的增加而增加,进而试件的黏结扩散长度有所增大,相对应的黏结强度也会因此提升。而残余段黏结力主要由摩擦力承担,界面粗糙度对其影响很大,埋置长度的改变对残余黏结强度的影响较小。
3.2 特征黏结强度计算式基于上述关于混凝土强度、保护层厚度以及波纹钢板埋置长度对黏结强度的影响关系,通过线性回归的方法拟合出了各参数与特征黏结强度的关系式,在图 12中以虚线表示,具体表达式为:
| $ {\tau _{\rm{s}}} = 0.38{f_{\rm{t}}} + 0.0063{C_{\rm{s}}} + 0.0025{L_{\rm{c}}} - 1.64 $ | (7) |
| $ {\tau _{\rm{u}}} = 0.70{f_{\rm{t}}} + 0.013{C_{\rm{s}}} + 0.0056{L_{\rm{c}}} - 3.84 $ | (8) |
| $ {\tau _{\rm{r}}} = 0.056{f_{\rm{t}}} + 0.0034{C_{\rm{s}}} - 0.00056{L_{\rm{c}}} + 0.24 $ | (9) |
由表 4可知,计算值与试验值之间的误差整体上相对较小,初始黏结强度τs、极限黏结强度τu、残余黏结强度τr计算值与试验值比值的平均值分别为1.22、1.03、1.03,变异系数分别为0.50、0.12、0.18。试件S-10初始黏结强度τs误差较大,原因是波纹钢板埋置长度增大到450 mm时黏结扩散区域变大,初始滑移点的荷载值相应减小,因此试验值偏小,导致初始黏结强度计算值与试验值的变异系数较大。除此之外,本文选取了相关文献[18-19]中与本试验相似的试件S-4和SC-12,按上述部分公式计算后发现误差较小,可证明该公式计算波纹钢板混凝土组合构件的极限黏结强度与残余黏结强度是有效的。
| 表 4 特征黏结强度试验值与计算值的对比 Tab. 4 Comparison between test and calculated values of characteristic bond strength |
混凝土本构采用塑性损伤模型,其应力-应变关系及损伤因子根据《混凝土结构设计规范》[20]来确定。钢材本构选用弹塑性强化模型,其弹性模量E=210 GPa,强化阶段模量为0.01E,屈服强度取材性试验测值,泊松比为0.3。
4.1.2 波纹钢板-混凝土界面黏结滑移本构模型根据试验所得黏结强度-滑移曲线形状并结合上述分析,将黏结强度和滑移量进行无量纲化处理,令x=S/Su,y=τ/τu,给出界面黏结滑移本构模型:
1) 上升阶段
| $ y = \left\{ {\begin{array}{*{20}{l}} {{k_1}x, }&{x \le \frac{{{S_{\rm{s}}}}}{{{S_{\rm{u}}}}}}\\ {{k_2}x + b, }&{\frac{{{S_{\rm{s}}}}}{{{S_{\rm{u}}}}} < x \le 1} \end{array}} \right. $ | (10) |
将初始滑移特征点
2) 下降及残余阶段
对于含陡降段试件:
陡降段
| $ x = 1, \frac{{{\tau _{\rm{d}}}}}{{{\tau _{\rm{u}}}}} \le y \le 1 $ | (11) |
缓降及残余段
| $ y = \frac{x}{{mx + n}}, x > 1 $ | (12) |
将荷载陡降特征点
| $ n = \frac{{{\tau _{\rm{u}}}}}{{{\tau _{\rm{d}}}}} - m $ | (13) |
对于无陡降段试件
| $ y = \frac{x}{{mx + 1 - m}}, x > 1 $ | (14) |
其中上述m均可根据试验数据点拟合得出
| $ m = - 0.024{f_{\rm{t}}} - 4.56{C_{\rm{s}}} + 1.79{L_{\rm{c}}} - 4.64 $ | (15) |
混凝土、波纹钢板和垫板均为C3D8R单元,钢筋为T3D2单元,并采用结构化网格划分方式。本文采用Connector连接器单元来模拟波纹钢板与混凝土界面间的黏结滑移,该单元的法向不考虑滑移,两个切向的荷载-滑移曲线可根据4.1.2节中的界面黏结滑移本构关系式转化得出。由于连接器单元设置在波纹钢板与混凝土的共有节点上,因此模型需确保波纹钢板与混凝土接触面的网格单元和节点位置对应准确。
模型顶部有波纹钢板上部横截面耦合点,同时也作为加载点,采用与试验相同的位移加载模式。模型底部垫块设置为刚体,约束其所有自由度,垫块上表面与混凝土下表面采用Tie约束。钢筋笼整体内嵌于混凝土中。为提高模型收敛性,约束连接器的全部转动方向。有限元模型见图 13,图中红点为连接器单元。

|
图 13 有限元模型 Fig. 13 Finite element model |
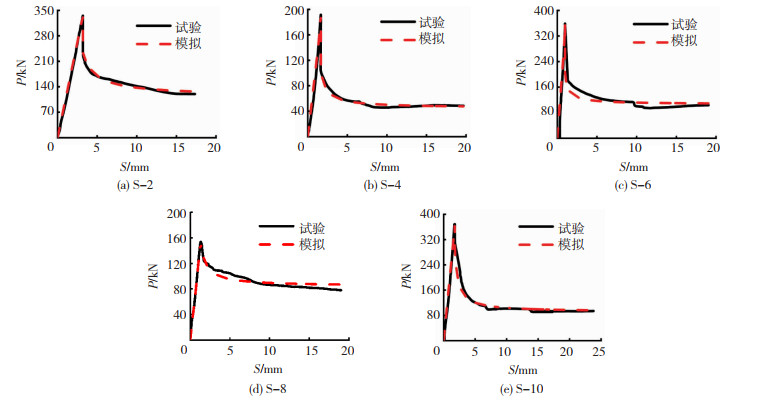
本文选取含陡降段与不含陡降段的典型试件进行了建模分析,有限元模型与试验的荷载-滑移曲线对比见图 14,可看出模拟曲线与试验曲线吻合度较高,有限元模型能较为准确地模拟真实界面的黏结滑移,说明此数值模拟方法具有一定的可行性。
|
图 14 有限元模型与试验荷载-滑移曲线对比 Fig. 14 Comparison between load - slip curves of finite element model and test |
根据10个波纹钢板混凝土推出试件的试验结果,对波纹钢板- 混凝土界面黏结滑移性能的主要影响参数及黏结强度进行了研究,得到以下结论:
1) 波纹钢板混凝土组合试件破坏形式可分为黏结劈裂破坏和黏结锚固破坏,破坏时主要产生劈裂裂缝和膨胀裂缝。黏结劈裂破坏为脆性破坏,其延性较差;黏结锚固破坏的裂缝产生较晚且延伸速度较慢。
2) 对各试件加载端荷载-滑移曲线进行了综合分析和归纳,将受力过程分为5个阶段,分别为微滑移段、滑移段、陡降段、缓降段及残余段。波纹钢板与混凝土界面可分为黏结扩散段、协同受力段和界面滑移段,其中黏结扩散段与协同受力段主要包含化学胶着力,界面滑移段主要包含摩擦力与机械咬合力。
3) 对波纹钢板荷载上升段的波谷与波脊应变进行了分析,结果表明应变大致沿埋置长度呈指数分布的形式,波脊应变一般大于波谷应变。钢板自由端范围内可能存在受拉区,从而出现过零点现象。并对波纹钢板微元体进行力学分析,理论推导出其等效应变公式,可较好预测真实应变分布。
4) 综合分析了混凝土强度、保护层厚度与埋置长度对波纹钢板混凝土界面黏结强度的影响,结果表明上述参数对初始黏结强度与极限黏结强度影响较大,对残余黏结强度影响较小。并通过线性回归的方法拟合出各参数与特征黏结强度的关系式,理论值与试验值误差较小,可为波纹钢板混凝土剪力墙的承载力设计提供理论基础。
5) 基于ABAQUS有限元软件对典型试件进行了数值分析,提出了波纹钢板-混凝土界面黏结滑移本构模型,并创新性地将其应用于连接器单元来模拟界面黏结滑移。有限元模型的荷载-滑移曲线与试验曲线吻合度较高,表明此数值模拟方法可较好预测实际工程中的界面黏结滑移性能。
| [1] |
王思豪, 刘玉擎, 庄卫林, 等. 波形钢腹板组合梁抗震性能试验[J]. 哈尔滨工业大学学报, 2018, 50(3): 61. WANG Sihao, LIU Yuqing, ZHUANG Weilin, et al. Experimental investigation on seismic behaviors of composite girder with corrugated steel web[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 61. DOI:10.11918/j.issn.0367-6234.201705067 |
| [2] |
SHAHMOHAMMADI A, MIRGHADERI R, HAJSADEGHI M, et al. Application of corrugated plates as the web of steel coupling beams[J]. Journal of Constructional Steel Research, 2013, 85: 178. DOI:10.1016/j.jcsr.2013.02.009 |
| [3] |
HE Jun, LIU Yuqing, CHEN Airong, et al. Bending behavior of concrete-encased composite I-girder with corrugated steel web[J]. Thin-Walled Structures, 2014, 74: 70. DOI:10.1016/j.tws.2013.08.003 |
| [4] |
NIKOOMANESH M R, GOUDARZI M A. Experimental and numerical evaluation of shear load capacity for sinusoidal corrugated web girders[J]. Thin-Walled Structures, 2020, 153: 106798. DOI:10.1016/j.tws.2020.106798 |
| [5] |
谭平, 魏瑶, 李洋, 等. 波纹钢板剪力墙抗震性能试验研究[J]. 土木工程学报, 2018, 51(5): 8. TAN Ping, WEI Yao, LI Yang, et al. Experimental investigation on performance of corrugated steel plate shear wall[J]. China Civil Engineering Journal, 2018, 51(5): 8. DOI:10.15951/j.tmgcxb.2018.05.002 |
| [6] |
LUO Qirui, WANG Wei, SUN Zhuangzhuang, et al. Seismic performance analysis of corrugated-steel-plate composite shear wall based on corner failure[J]. Journal of Constructional Steel Research, 2021, 180: 106606. DOI:10.1016/j.jcsr.2021.106606 |
| [7] |
CAO Qiang, HUANG Jingyu. Experimental study and numerical simulation of corrugated steel plate shear walls subjected to cyclic loads[J]. Thin-Walled Structures, 2018, 127: 306. DOI:10.1016/j.tws.2018.01.042 |
| [8] |
王威, 张龙旭, 苏三庆, 等. 波形钢板剪力墙抗震性能试验研究[J]. 建筑结构学报, 2018, 39(5): 36. WANG Wei, ZHANG Longxu, SU Sanqing, et al. Experimental research on seismic behavior of corrugated steel plate shear wall[J]. Journal of Building Structures, 2018, 39(5): 36. DOI:10.14006/j.jzjgxb.2018.05.005 |
| [9] |
WANG Wei, REN Yingzi, LU Zheng, et al. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls[J]. Journal of Constructional Steel Research, 2019, 160: 136. DOI:10.1016/j.jcsr.2019.05.019 |
| [10] |
王威, 刘格炜, 苏三庆, 等. 波形钢板剪力墙及组合墙抗剪承载力研究[J]. 工程力学, 2019, 36(7): 197. WANG Wei, LIU Gewei, SU Sanqing, et al. Research on the shear bearing capacity of corrugated steel plate shear wall and composite wall[J]. Engineering Mechanics, 2019, 36(7): 197. DOI:10.6052/j.issn.1000-4750.2018.06.0356 |
| [11] |
MOROZOV E V, LOPATIN A V, TAYGIN V B. Design, analysis, manufacture and testing of composite corrugated horn for the spacecraft antenna system[J]. Composite Structures, 2016, 136: 505. DOI:10.1016/j.compstruct.2015.11.004 |
| [12] |
JÁGER B, DUNAI L, KÖVESDI B. Girders with trapezoidally corrugated webs subjected by combination of bending, shear and path loading[J]. Thin-Walled Structures, 2015, 96: 227. DOI:10.1016/j.tws.2015.08.015 |
| [13] |
伍凯, 郑惠铭, 陈峰, 等. 型钢-钢纤维混凝土组合结构的黏结破坏及传力机理研究[J]. 建筑结构学报, 2020, 41(10): 134. WU Kai, ZHENG Huiming, CHEN Feng, et al. Bond failure and load transfer mechanism in steel and steel fiber reinforced concrete composite structures[J]. Journal of Building Structures, 2020, 41(10): 134. DOI:10.14006/j.jzjgxb.2018.0743 |
| [14] |
赵秋, 蔡文平, 陈宝春. 基于平钢板连接件的钢-RPC组合桥面板抗剪试验研究[J]. 工程力学, 2017, 34(8): 171. ZHAO Qiu, CAI Wenping, CHEN Baochun. Shear-test research on smooth-plate shear-force connector of steel and RPC composite deck[J]. Engineering Mechanics, 2017, 34(8): 171. DOI:10.6052/j.issn.1000-4750.2016.04.0326 |
| [15] |
董宏英, 赵翊舟, 曹万林, 等. 配置栓钉钢板与外包高强混凝土界面黏结-滑移性能研究[J]. 建筑结构学报, 2021, 42(2): 122. DONG Hongying, ZHAO Yizhou, CAO Wanlin, et al. Interfacial bond-slip behavior between steel plate with studs and coated high-strength concrete[J]. Journal of Building Structures, 2021, 42(2): 122. DOI:10.14006/j.jzjgxb.2020.C066 |
| [16] |
苏小卒, 黄长鑫. 受栓钉强度控制的钢板-混凝土界面黏结滑移性能试验与本构模型[J]. 建筑结构学报, 2018, 39(3): 167. SU Xiaozu, HUANG Changxin. Experiment and constitutive modeling of bond-slip behavior of steel plate-concrete interface with strength controlled by stud shear connectors[J]. Journal of Building Structures, 2018, 39(3): 167. DOI:10.14006/j.jzjgxb.2018.03.020 |
| [17] |
波纹腹板钢结构技术规程: CECS 291: 2011[S]. 北京: 中国计划出版社, 2011 Technical specification for steel structures with corrugated webs: CECS 291: 2011[S]. Beijing: China Planning Press, 2011 |
| [18] |
王威, 李元刚, 苏三庆, 等. 波形钢板混凝土黏结滑移性能试验研究与数值模拟分析[J]. 土木工程学报, 2019, 52(11): 19. WANG Wei, LI Yuangang, SU Sanqing, et al. Experimental study and numerical simulation on bond-slip behavior between corrugated steel plate and concrete[J]. China Civil Engineering Journal, 2019, 52(11): 19. DOI:10.15951/j.tmgcxb.2019.11.002 |
| [19] |
王威, 赵春雷, 苏三庆, 等. 带栓钉波形钢板混凝土组合构件粘结滑移性能与承载力分析[J]. 工程力学, 2019, 39(9): 114. WANG Wei, ZHAO Chunlei, SU Sanqing, et al. Experimental study on bond-slip behavior and bearing capacity of corrugated steel plate concrete composite member with stud[J]. Engineering Mechanics, 2019, 39(9): 114. DOI:10.6052/j.issn.1000-4750.2018.07.0411 |
| [20] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture and Building Press, 2010 |
 2022, Vol. 54
2022, Vol. 54


