钢筋锈蚀是导致RC结构耐久性降低的重要影响因素。锈蚀初期,由于混凝土的包裹作用,钢筋的锈蚀程度较轻而不易被察觉。当锈蚀程度能够被察觉时,混凝土内部已经开裂,甚至保护层脱落,这将严重影响结构的安全性和耐久性[1-2]。因此,开展RC结构中钢筋锈蚀监测,对保障结构安全尤为重要。
半电池电位法和光纤传感技术等在钢筋的锈蚀监测中应用广泛[3],然而,这些方法存在安装不便、易损坏、无法实时监测等缺点。因此,实际工程中急需一种稳定、高效的监测方法来弥补这一不足。近年来,压电陶瓷以其灵敏度高、价格低廉等优点被广泛应用于结构健康监测中,其对钢筋锈蚀监测的适用性已得到了验证。如Du等[4]发现钢筋锈蚀会严重导致应力波衰减,Liu等[5]根据监测信号的主频分量变化,定性地评价了钢筋混凝土的腐蚀程度。同时,Sriramadasu等[6]根据导波模式的变化将钢筋锈蚀过程划分为:起始、发展和直径减小3个阶段。通常,钢筋锈蚀是从表面钝化膜的破坏开始的,随后由于蚀坑位置的增多和锈蚀产物的累积,混凝土与钢筋之间的黏结性能逐步退化,最终导致结构承载力的降低。胡志坚等[7]对RC构件的锈胀力分析也验证了这一点。因此,考虑到钢筋脱钝、脱黏在整个腐蚀过程中的关键作用,确定钢筋的锈蚀全过程及通过监控指标量化其与锈蚀率的关系,对实际工程中钢筋锈蚀的预防和结构的修复意义重大。
此外,由于混凝土内部钢筋锈蚀的隐蔽性,很多学者在关注锈蚀发展过程的同时也较为关注锈蚀位置[8]。随着监测技术的发展,成像技术被逐步运用于锈蚀产物的检测中,如通过计算机断层扫描技术(XCT)可以呈现钢筋和锈蚀产物的三维可视化表征[9]及钢筋锈蚀分布[10];通过电阻层析成像技术分析钢筋锈蚀区域等[11]。然而,锈蚀最先发生于混凝土内部,在结构表面安装的传感器发射的信号需要通过混凝土保护层才能检测到钢筋,且锈蚀发生的时间、位置和程度都存在随机性。因此,如何实现准确评估RC结构中钢筋锈蚀损伤程度和位置是急需解决的问题。目前,基于嵌入式压电传感技术与成像方法相结合的损伤定位技术已经成功应用于航空航天及桥梁工程结构的健康监测中[12-13],其中概率成像方法能够实现稀疏传感器条件下的成像。如Hong等[14]采用该技术以直观的方式呈现了金属结构的损伤从开始到宏观形成的连续自适应的结果,而Liu等[15]则实现了复合材料的清晰损伤定位,这些都为混凝土结构损伤定位提供了新思路。
本文通过嵌入式压电传感器,研究了浸泡于3.5%NaCl溶液的RC梁中钢筋的腐蚀全过程。采用基4FFT对连续监测的信号进行频谱分析,从而有效地表征了钢筋的脱钝、脱黏和失效3个阶段的特征,并建立损伤因子与锈蚀率的定量关系。此外,基于修正权重函数的概率成像方法实现了混凝土内部钢筋锈蚀损伤的成像定位。
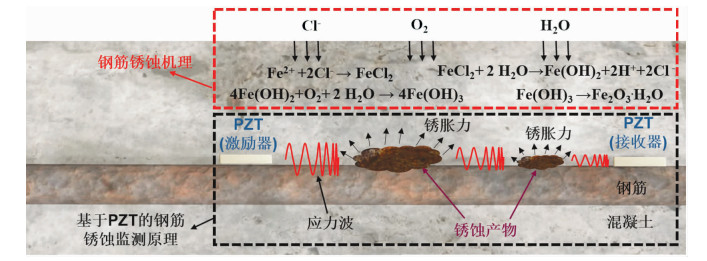
1 钢筋的锈蚀监测与成像定位 1.1 基于压电传感器的钢筋锈蚀监测机理氯离子被认为是危害RC结构安全性的侵蚀介质之一,这是因为在潮湿环境中氯离子具有较强的渗透能力,能够通过混凝土内部的孔隙到达钢筋表面,从而成为钢筋锈蚀时的催化剂。自然环境下,钢筋的锈蚀是一个电化学过程,其机理是:当钢筋表面的氯离子达到临界浓度时,钢筋表面形成的致密钝化膜开始发生局部破坏,与未破坏部位连通形成原电池。其中,锈蚀的钢筋作为原电池的阳极,未发生锈蚀的钢筋表面作为阴极,混凝土中的氧气和水分作为电解液。氯离子则作为催化剂不断加速铁离子的流失,铁离子反应后最终形成铁锈(主要成分是Fe2O3和Fe3O4)附着于钢筋表面[2]。在锈蚀过程中,随着铁锈体积的不断增大,其对混凝土的膨胀作用不断加剧,最终导致RC结构的锈胀开裂(钢筋锈蚀机理见图 1)。
|
图 1 混凝土中钢筋锈蚀机理及PZT监测方法 Fig. 1 Corrosion mechanism of steel bar in concrete structure and monitoring method based on PZT |
基于压电陶瓷(piezoelectric lead zirconate titanate, PZT)的钢筋锈蚀监测是将一对PZT片粘贴于钢筋表面,激励导波信号从其中一端传感器发出,通过锈蚀损伤的钢筋传播,由另一端传感器接收,见图 1。锈蚀过程中钢筋钝化膜破坏、钢筋与混凝土的脱黏等都会造成导波信号的波形、频率和幅值发生变化,因此,通过对比导波信号在不同锈蚀状态的变化来确定钢筋的锈蚀程度和锈蚀位置。
1.2 信号分析及锈蚀程度评估离散傅里叶变换(DFT)被广泛应用于信号分析中,然而,由于DFT的计算量较大,高效且计算量小的快速傅里叶变换(FFT)得以快速发展。其中,基4FFT的计算效率尤为显著,它是通过每次把序列信号一分为四,最后分割成4点DFT来实现信号分析的,具体计算步骤如下:
首先,将采集到的序列信号x(n)(n=0, 1, …, N-1)的DFT定义为
| $ X(k) = \sum\limits_{n = 0}^{N - 1} x (n)W_N^{nk}, k = 0, 1, \cdots , N - 1 $ | (1) |
式中
若N=4M,则将x(n)分成4个N/4点的序列x1(n)、x2(n)、x3(n)、x4(n)(n=0, 1, …, N/4-1),即
| $ x(n) = {x_1}(n) + {x_2}(n) + {x_3}(n) + {x_4}(n) $ | (2) |
式中x1(n)=x(n), x2(n)=x(n+N/4), x3(n)= x(n+N/2), x4(n)=x(n+3N/4), n=0, 1, …, N/4-1。
然后,把x(n)代入式(1),则有
| $ \begin{array}{l} X(k) = \sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n)W_N^{nk} + {x_2}(n)W_N^{(n + N/4)k} + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;{x_3}(n)W_N^{(n + N/2)k} + {x_4}(n)W_N^{(n + 3N/4)k}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n) + {x_2}(n)W_N^{N/4k} + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;{x_3}(n)W_N^{N/2k} + {x_4}(n)W_N^{3N/4k}} \right]W_N^{nk}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0, 1, \cdots , N - 1 \end{array} $ | (3) |
最后,把X(k)按频率抽取,则有
| $ \left\{ \begin{array}{l} x(4k) = \sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n) + {x_2}(n) + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;{x_3}(n) + {x_4}(n)} \right]W_{N/4}^{nk}\\ x(4k + 1) = \sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n) - {\rm{j}}{x_2}(n) - } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_3}(n) + {\rm{j}}{x_4}(n)} \right]W_N^nW_{N/4}^{nk}\\ x(4k + 2) = \sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n) - {x_2}(n) + } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_3}(n) - {x_4}(n)} \right]W_N^{2n}W_{N/4}^{nk}\\ x(4k + 3) = \sum\limits_{n = 0}^{N/4 - 1} {\left[ {{x_1}(n) + {\rm{j}}{x_2}(n) - } \right.} \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_3}(n) - {\rm{j}}{x_4}(n)} \right]W_N^{3n}W_{N/4}^{nk} \end{array} \right. $ | (4) |
以上即是按频率抽取的基4FFT。通过将一个N点DFT转化为4个N/4点DFT来计算,依此类推,直至分解到最后一级。基4FFT的乘法量约减少25%,加法量也略有减少。经过基4FFT提取的信号频域峰值随着腐蚀时间的变化而变化,其变化趋势反映了相应的钢筋锈蚀状态。其中,钢筋的脱钝、脱黏将会造成导波信号的改变,提取导波信号的频谱特征即可作为RC结构中钢筋脱钝、脱黏的判断依据。
研究发现,通过信号的频谱变化可以观察到钢筋腐蚀特征的变化,但是却难以量化腐蚀程度。因此,可通过定义损伤因子FDI来评估钢筋的锈蚀程度,计算式为
| $ {F_{{\rm{DI}}}} = \left| {1 - \frac{{{D_{i\max }}}}{{{H_{\max }}}}} \right| $ | (5) |
式中Hmax为无损伤参考信号的频域峰值,Dimax为i时刻采集信号的频域峰值。
通过建立损伤因子与锈蚀率的定量关系,即可达到对RC结构中钢筋的锈蚀程度评估的目的。但RC结构中钢筋的锈蚀位置是随机变化的,如何确定钢筋锈蚀位置,对实际结构的安全性和可靠性评估具有重大意义。
1.3 新的钢筋锈蚀概率成像定位概率成像算法是将待检测区域均匀地划分为多个分布的网格(网格节点即像素点),网格中的每对传感器均形成一条激励-接收路径,每条路径中的每个像素点都有一个值(即经过该像素点的全部路径的概率之和)来表示该处存在损伤的概率,则最大概率值即表示损伤最可能位置。待检测区域中像素点(x, y)的损伤概率值可定义为
| $ P(x, y) = \sum\limits_{i = 1}^N {{F_{{\rm{DI}}i}}} \cdot {w_i}\left[ {{R_i}(x, y)} \right] $ | (6) |
式中:FDIi为第i条路径的损伤因子,Ri(x, y)为像素点(x, y)距激励、接收传感器的相对距离,wi[Ri(x, y)]为第i条路径的损伤权重分布函数。
其中,Ri(x, y)如式(7)和图 2所示。
| $ {R_i}(x, y) = \frac{{\sqrt {{{\left( {x - {x_{\rm{s}}}} \right)}^2} + {{\left( {y - {y_{\rm{s}}}} \right)}^2}} + \sqrt {{{\left( {x - {x_{\rm{t}}}} \right)}^2} + {{\left( {y - {y_{\rm{t}}}} \right)}^2}} }}{{\sqrt {{{\left( {{x_{\rm{s}}} - {x_{\rm{t}}}} \right)}^2} + {{\left( {{y_{\rm{s}}} - {y_{\rm{t}}}} \right)}^2}} }} $ | (7) |

|
图 2 相对距离示意 Fig. 2 Schematic of relative distance |
式中:(x, y) 为任一像素点坐标,(xs, ys)为激励传感器坐标,(xt, yt)为接收传感器坐标。
其中,假定权重分布函数wi[Ri(x, y)]为一线性衰减的椭圆分布,其表达式为
| $ w[R(x, y)] = \left[ {\begin{array}{*{20}{l}} {1 - \frac{{R(x, y)}}{\beta }, }&{R(x, y) < \beta }\\ {0, }&{R(x, y) \ge \beta } \end{array}} \right. $ | (8) |
式中β是控制椭圆分布影响区域的参数。
可以看出,权重分布函数wi[Ri(x, y)]只和相对距离Ri(x, y)有关,并且会影响成像结果。随着相对距离Ri(x, y)的增加,权重分布函数的值逐步降低。由于钢筋表面的传感器采用一维布置,钢筋锈蚀在稀疏传感器条件下的成像精度很难保证,常用的监测阵列椭圆成像理论(式(8))将不再适用。因此,在使用损伤概率成像算法中的权重分布函数时,还应充分考虑各条激励-接收路径中损伤因子的影响。
为此,提出一种新的算法,即在综合考虑上述情况的前提下,对权重分布函数进行了修正。
| $ {w_i}\left[ {{R_i}(x, y)} \right] = \left\{ {\begin{array}{*{20}{l}} {1 - \left[ {\frac{{{R_i}(x, y)}}{\beta } - \left( {1 - \frac{{{F_{{\rm{DI}}i}}}}{{{F_{{\rm{DI}}\max }}}}} \right)} \right], \left( {1 - \frac{{{F_{{\rm{Dli}}}}}}{{{F_{{\rm{DImax}}}}}}} \right)\beta \le {R_i}(x, y) < \left( {2 - \frac{{{F_{{\rm{Dli}}}}}}{{{F_{{\rm{Dl}}\max }}}}} \right)\beta }\\ {1 + \left[ {\frac{{{R_i}(x, y)}}{\beta } - \left( {1 - \frac{{{F_{{\rm{Dli}}}}}}{{{F_{{\rm{DI}}\max }}}}} \right)} \right], {R_i}(x, y) < \left( {1 - \frac{{{F_{{\rm{Dli}}}}}}{{{F_{{\rm{DImax}}}}}}} \right)\beta }\\ {0, 其他 } \end{array}} \right. $ | (9) |
式中FDIi是第i条激励-接收路径的损伤因子,FDImax是所有路径中的最大损伤因子。
同时,为降低成像结果的边界效应,后续分析中将通过归一化的方式对各路径的损伤概率值进行处理,并采用映射函数形成最终的概率图像。
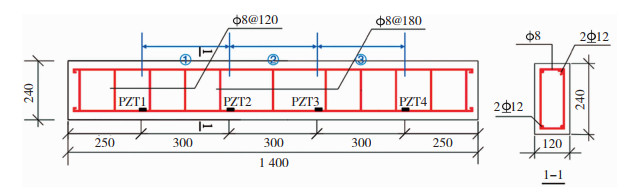
2 试验验证 2.1 试验概况 2.1.1 试件制作构件尺寸为1 400 mm×120 mm×240 mm(长×宽×高),混凝土强度设计等级为C30,配合比为水泥∶水∶砂∶石=1 ∶0.45 ∶1.35 ∶2.68,其中水泥采用强度等级为42.5的普通硅酸盐水泥,砂为中砂,石子最大粒径为20 mm。构件配筋及PZT传感器布置见图 3。纵筋等级为HRB335,架立筋直径为10 mm,受拉筋直径为12 mm,箍筋等级为HPB300,直径为8 mm,混凝土保护层为20 mm。混凝土抗压强度采用3组标准立方体试件(150 mm×150 mm×150 mm)的平均值;纵向受力钢筋等级为HRB335,纵筋的拉伸性能试验根据GB/T 228—2002《金属材料室温拉伸试验方法》的规定进行,见表 1。混凝土和钢筋的弹性模量参考GB 50010—2010《混凝土结构设计规范》,分别取值3.0×104、2.0×105 MPa。钢筋锈蚀监测主要是针对底部受拉钢筋,因此将4个PZT传感器以间隔350 mm的距离粘贴于钢筋表面,PZT的参数见表 2。在监测过程中,将监测区域划分为3个区段(图 3),并依次进行信号的采集:区段①,PZT2作为驱动器激励信号,PZT1作为接收器接收信号;区段②,PZT2激励信号,PZT3接收信号;区段③,PZT4激励信号,PZT3接收信号。
|
图 3 构件配筋及PZT传感器布置(mm) Fig. 3 Reinforcement of components and arrangement of PZT sensors (mm) |
| 表 1 混凝土与钢筋性能参数 Tab. 1 Performance parameters of concrete and steel bar |
| 表 2 PZT-5A型压电陶瓷性能参数 Tab. 2 Performance parameters of piezoelectric ceramics (PZT-5A) |
自然界中钢筋锈蚀是一个缓慢的过程,为了快速实现钢筋的不同锈蚀程度,采用施加外部电流的方式进行加速锈蚀。为了避免箍筋锈蚀带来的影响,构件浇筑时对箍筋与纵筋的交叉位置进行涂刷绝缘漆、缠绕绝缘胶带处理。在室温下养护28 d后,将RC梁浸泡在3.5%的NaCl溶液(类海水溶液)中。通电过程中,RC梁中纵筋作为阳极,浸泡于NaCl溶液中的铝板作为阴极形成通电回路。
根据文献[16],构件的腐蚀最佳电流密度为0.045~3 mA/cm2。因此,为了实现良好的锈蚀效果,试验中采用的设计电流密度为1.99 mA/cm2。由法拉第定律(Faraday's law)可知,电极上发生化学变化物质的量与通过该电极的电量成正比[17],因此,钢筋的理论锈蚀率可采用下式计算
| $ \rho = 1 - {\left( {1 - \frac{{ti}}{{13441d}}} \right)^2} $ | (10) |
式中: t为通电锈蚀时间,s;i为锈蚀电流密度,A;d为钢筋直径,m。
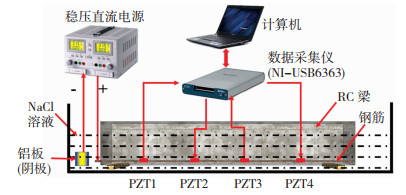
试验监测装置和加速锈蚀装置见图 4。
|
图 4 基于PZT传感器的钢筋加速锈蚀和监测系统 Fig. 4 Accelerated corrosion and monitoring system for steel bars based on PZT sensors |
其具体过程为:首先采用稳压直流电源对RC梁中的钢筋进行通电锈蚀;随后,使用NI信号采集仪(型号:USB6363)和计算机进行导波信号的激励和接收;之后,观察RC梁的外观有无产生裂缝;如此持续进行,直至RC梁产生贯通的锈胀裂缝。采用扫频正弦脉冲信号作为激励信号,其频率范围为10~250 kHz,电压为10 V,采样频率为2 MHz/s。为了减小外界因素的影响,每次采集5组信号进行处理。
2.2 监测信号分析 2.2.1 时域分析通电初期,锈蚀主要发生在钢筋表面,从RC梁外观上很难发现结构的变化。随着通电时间的增长,RC梁表面不断有铁锈溶液析出。最终,在RC梁的横截面(图 5左)、侧面(沿纵筋方向,图 5右上) 和梁底(图 5右下)处产生的锈胀裂缝均不断延长和变宽。

|
图 5 锈胀裂缝 Fig. 5 Rust expansion cracks |
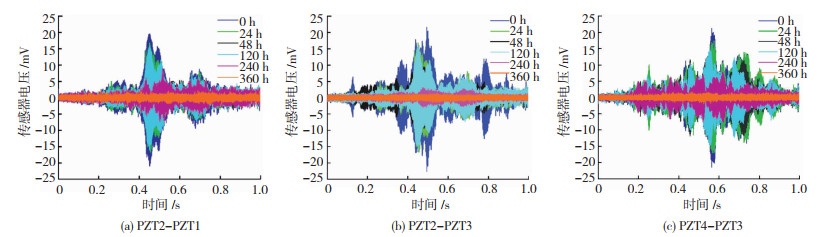
为了清晰显示出信号的变化过程,这里对具有代表性的信号进行叠加绘制。3个监测段的时域信号叠加,见图 6。可以看出,3个监测段存在相同的特征:锈蚀初期(0~120 h),信号幅值衰减较小;当锈蚀到240 h时,信号幅值已有较大幅度的减小;当达到360 h时,信号的幅值几乎为0。说明虽然监测的位置不同,但钢筋锈蚀过程中信号的衰减规律是一致的。为了量化钢筋的锈蚀程度,后续将通过基4FFT进行信号的频谱分析,并采用新的损伤概率成像方法进行锈蚀位置的定位分析。
|
图 6 时域信号 Fig. 6 Time domain signals |
虽然锈蚀导致信号幅值衰减,但其振动频率并未发生太大改变。利用钢筋的这一特性,采用基4FFT的频谱分析获取各监测区段的频域峰值(即信号在钢筋上传输的能量值)见图 7~9。

|
图 7 PZT2-PZT1组接收信号的频谱分析 Fig. 7 Frequency spectrum analysis of received signals from PZT2-PZT1 |

|
图 8 PZT2-PZT3组接收信号的频谱分析 Fig. 8 Frequency spectrum analysis of received signals from PZT2-PZT3 |
|
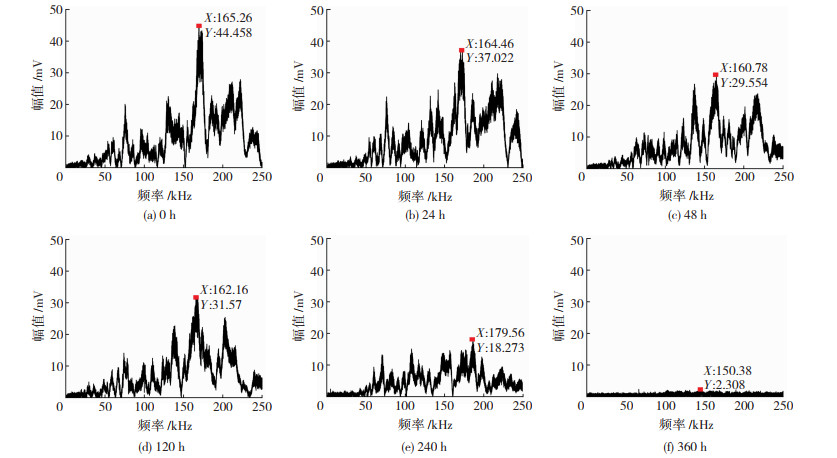
图 9 PZT4-PZT3组接收信号的频谱分析 Fig. 9 Frequency spectrum analysis of received signals from PZT4-PZT3 |
从图 7~9可看出,随着腐蚀时间的增加,各监测段的信号幅值呈现出先减小后增大再减小的趋势,这是由于钢筋锈蚀过程分别经历了表面钝化膜破坏、钢筋与混凝土脱黏及钢筋截面面积减小3个阶段,具体分析如下:
1) 对于同一监测段,3个区段的信号频谱峰值均在未锈蚀阶段达到最大值。当通电锈蚀48 h,其峰值分别降低了45.34%、54.72%和33.52%,表明此时钢筋的锈蚀速度较快;然而,锈蚀120 h,其峰值又分别提高到了未腐蚀阶段的24.29%、26.74%和28.99%,此时表明钢筋周围的密实度较高,提高了信号的传输效率;随后信号峰值持续下降到最小值。
2) 对比3个监测段的频率区间可知,RC结构内部锈蚀钢筋的共振频率在130~180 kHz之间,造成这一差别的主要原因是不同区段钢筋的蚀坑位置、锈蚀程度及与混凝土黏结程度的差异性。
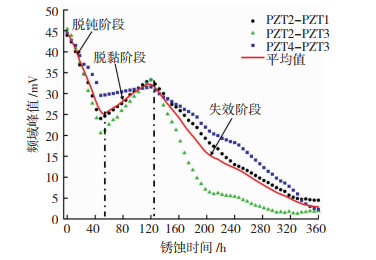
2.3 钢筋锈蚀监控分析 2.3.1 RC梁中钢筋锈蚀监控过程分析通过对前述代表点的频域分析,可得出钢筋锈蚀过程的变化特征。为详细确定钢筋的锈蚀过程,本文提取了全部监测信号的频域峰值见图 10。可看出,信号的频域峰值随腐蚀时间的增长,同样呈现出先减小后增大,再逐步减小的趋势,因此可将钢筋的锈蚀过程分为3个阶段。
|
图 10 频域峰值随腐蚀时间的变化 Fig. 10 Variation of peak value in frequency domain with corrosion time |
1) 脱钝阶段:此时钢筋表面钝化膜发生破坏。由于氯离子的催化作用,钢筋表面铁离子不断流失,形成锈蚀产物,从而导致信号在钢筋表面的传输中发生散射和反射。随着锈蚀产物的不断累积,有更多的能量通过界面传递给了混凝土,使得传感器接收信号的频域峰值不断下降。
2) 脱黏阶段:随着蚀坑面积增加,锈蚀产物在钢筋表面不断累积,其体积将会增大5~6倍,引起钢筋与混凝土的脱黏,此时,传入混凝土中的信号能量减少。因此,呈现出频域峰值小幅度上升的趋势。但是由于铁锈的增多,钢筋将逐步与混凝土脱离,失去黏结锚固力,随后进入第3个阶段。
3) 失效阶段:当混凝土内部的锈胀力达到一定程度时,由于混凝土的抗拉性能较差将会产生锈胀裂缝,随着锈胀裂缝的增多,接收信号的频域峰值则不断下降,钢筋的直径也不断减小,最终因局部钢筋锈断,导致接收信号中断。
可看出,通过压电传感监控的方法,可以判断出混凝土结构中钢筋锈蚀发展的全过程。通过对钢筋锈蚀过程的三阶段划分,有效地揭示钢筋在锈蚀过程中的状态。为此,下文将从钢筋的腐蚀机理方面展开对比研究。
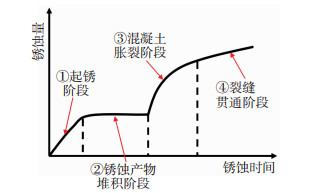
2.3.2 锈蚀过程验证分析Melchers等[18-19]提出了海洋环境下的混凝土结构锈蚀开裂的现象模型,从而将混凝土结构中钢筋的锈蚀过程划分为:①起锈,②锈蚀产物堆积,③混凝土胀裂,④裂缝贯通4个阶段,见图 11。
|
图 11 混凝土内部钢筋的锈蚀量与锈蚀时间的关系 Fig. 11 Relationship between corrosion amount and corrosion time of steel bar in concrete |
结合2.3.1节中监控信号频域峰值的变化趋势可知,当钢筋表面氯离子浓度达到一定程度时,钢筋表面在混凝土碱性环境中形成的致密钝化膜会被逐步破坏,从而失去保护作用,导致钢筋开始发生锈蚀,此时称为①起锈阶段(图 10中的脱钝阶段);随着锈蚀的持续发生,钢筋表面堆积的锈蚀产物越来越多,阻碍了氧气和水分的传输,从而降低了钢筋的锈蚀速率,此时称为②锈蚀产物堆积阶段;随后由于锈蚀产物的不断累积,混凝土内部的锈胀力不断增大,致使钢筋与混凝土发生脱离,也即进入到了图 10中的脱黏阶段;之后,随着锈胀力的进一步增大,混凝土开始沿钢筋纵向开裂,即③混凝土胀裂阶段;最后,由于裂缝的产生,钢筋锈蚀速度大大加快,最终达到了④混凝土裂缝的贯通阶段,也即结构进入到了图 10中的失效阶段。因此,对比图 10和图 11发现,通过对钢筋锈蚀的全过程监测,可以定性地判断出RC梁中钢筋所处的锈蚀状态,并可为钢筋的锈蚀损伤定位及锈蚀损伤程度的界定打下良好的基础。
3 钢筋锈蚀损伤定位与量化评估对于长期服役的RC结构,从外观上很难观测到其内部钢筋的锈蚀。并且由于构件所处环境及承受荷载的差异性,其损伤程度也会存在较大差别。因此,通过压电传感器对钢筋锈蚀过程中产生的损伤进行定位和损伤程度量化显得尤为重要。
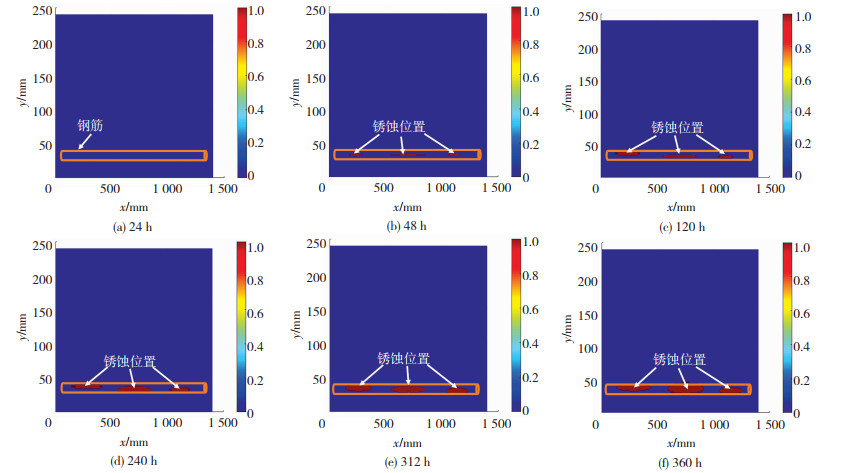
3.1 钢筋锈蚀损伤定位为了识别钢筋锈蚀位置及其变化趋势,采用新的概率成像方法对RC梁中钢筋的锈蚀位置进行成像和定位分析。为了消除边界效应,形成清晰的图像,文中采用将损伤概率值归一化的处理方法,并提取适当的图像阈值(-3 dB),成像结果见图 12。
|
图 12 钢筋腐蚀损伤概率成像 Fig. 12 Damage probability imaging of steel bar corrosion |
从图 12可看出,随着腐蚀时间的增加,钢筋锈蚀程度越来越严重。锈蚀24 h时,由于钢筋表面氯离子的浓度较低,钝化膜还未出现较大范围的破坏,此时图中未出现明显的锈蚀痕迹;48 h时,RC梁跨中率先出现了锈蚀产物,这与混凝土浇筑的均匀性有关:由于粗、细骨料分布不均匀,导致局部混凝土内孔隙的“畅通性”存在差别,从而造成跨中钢筋表面氯离子最先达到临界浓度,进而产生锈蚀反应;120 h时,RC梁的两端也出现了明显的锈蚀产物,并且随着锈蚀时间的增加,所成图像中的锈蚀区域不断增大,说明锈蚀产物在不断累积。还可以发现,基于修正权重函数的概率图像与频谱分析结果一致。说明通过该技术不但可以实现RC结构内部钢筋从初始锈蚀状态到结构表面出现锈胀裂缝的全过程定位,而且可以呈现出锈蚀损伤的累积程度,有效提高了RC结构的性能评估精度,对于结构的安全使用意义重大。
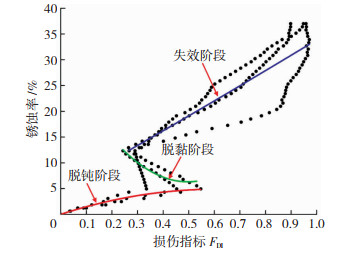
3.2 基于频域损伤因子的钢筋锈蚀程度量化分析通过频谱分析可以确定RC梁中钢筋锈蚀的脱钝、脱黏过程,但却难以量化钢筋的锈蚀程度。工程中常采用锈蚀率来量化钢筋的腐蚀程度,因此,文中通过式(10)计算不同通电时间的钢筋锈蚀率,在与式(5)得到的损伤因子FDI联立的情况下,建立了RC梁内钢筋锈蚀损伤监测信号与锈蚀率的定量关系(图 13)。可以看出,钢筋的锈蚀率与损伤因子FDI的关系呈分段式变化。为了量化钢筋的锈蚀程度,采用分段拟合的方式,对损伤因子FDI和锈蚀率的关系进行分析,结果见式(11)。
|
图 13 损伤因子FDI与理论锈蚀率关系曲线 Fig. 13 Curves of relationship between damage factor (FDI) and theoretical corrosion rate |
| $ y = \left\{ {\begin{array}{*{20}{l}} { - 13.29{x^2} + 16.09x + 0.01}&{{\rm{脱钝阶段}}}\\ {96.73{x^2} - 96.06x + 30.17, }&{\;{\rm{脱黏阶段}}}\\ {1.15{x^2} + 27.81x + 4.93, }&{{\rm{破坏阶段}}} \end{array}} \right. $ | (11) |
式中:x是不同通电腐蚀时间的损伤因子FDI;y是不同通电腐蚀时间对应的锈蚀率,%。
可以看出,初始锈蚀阶段钢筋FDI呈现出上升趋势;在锈蚀中期,随着锈蚀量的增加,大量的锈蚀产物堆积于钢筋表面,反而形成了损伤因子FDI减小的“假象”;锈蚀后期,随着混凝土的开裂,FDI再次呈现快速上升的趋势。因此,区别选用式(11)中3个公式的依据是:1)当FDI呈现减小趋势时,采用脱黏阶段对应的公式计算锈蚀率;当FDI呈现增大趋势时,考虑采用脱钝或破坏阶段对应的公式进行计算;2)结构表面无锈胀裂缝时,表明钢筋的锈蚀程度较小,采用脱钝阶段对应的公式计算锈蚀率;结构表面存在明显锈胀裂缝时,表明钢筋的锈蚀程度较为严重,采用破坏阶段对应的公式计算锈蚀率。将试验采集信号得到的损伤因子FDI代入式(11)发现,相对误差均在±15%以内,说明其精度可行,可满足工程实际需求。
4 结论通过基于PZT的RC梁中钢筋锈蚀的实时监测试验,在频谱分析和修正权重函数的概率成像方法基础上,实现了钢筋锈蚀全过程监控及钢筋锈蚀损伤定位, 主要结论如下:
1) 通过基4FFT的频谱分析,发现钢筋在锈蚀48 h后,3个区段频的谱峰值分别降低了45.34%、54.72%和33.52%;在锈蚀120 h后,峰值又分别提高了24.29%、26.74%和28.99%,随后峰值则持续减小,即分别对应于钢筋锈蚀全过程中的脱钝、脱黏和失效3个阶段。
2) 新的概率成像方法实现了精确定位钢筋表面锈蚀位置从发生到发展的目的,有效提高了精细化评估结构内部钢筋锈蚀损伤程度。
3) 结合钢筋腐蚀的3个阶段,建立损伤因子FDI与钢筋锈蚀率之间的关系模型,并给出各个阶段的使用条件,实现了评估RC结构中钢筋锈蚀程度的目的。
基于PZT监测和概率成像技术对RC结构的钢筋锈蚀预警及锈蚀位置的呈现具有良好的适用性,可以作为侵蚀环境下既有RC结构锈蚀程度和锈蚀位置的分析方法。然而,由于侵蚀环境和材料类别的差异性,在后续研究中仍需要进一步提高导波信号的准确性,并提高成像精度。
| [1] |
王丹芊. 新型耐蚀钢筋在混凝土环境中的钝化及氯盐侵蚀行为研究[D]. 南京: 东南大学, 2016: 4 WANG Danqian. Investigation of the passivity and chloride-induced behavior of new corrosion-resistant steel rebar in concrete[D]. Nanjing: Southeast University, 2016: 4 |
| [2] |
汪奔. 混凝土保护层锈胀开裂时间预测模型及细观裂纹扩展分析[D]. 成都: 西南交通大学, 2018: 8 WANG Ben. A model for prediction of time to corrosion-induced concrete cover cracking and analysis of meso-crack propagation[D]. Chengdu: Southwest Jiaotong University, 2018: 8 |
| [3] |
FAN L, TAN X, ZHANG Q H, et al. Monitoring corrosion of steel bars in reinforced concrete based on helix strains measured from a distributed fiber optic sensor[J]. Engineering Structures, 2020, 204: 110039. DOI:10.1016/j.engstruct.2019.110039 |
| [4] |
DU P, XU D, HUANG S, et al. Assessment of corrosion of reinforcing steel bars in concrete using embedded piezoelectric transducers based on ultrasonic wave[J]. Construction and Building Materials, 2017, 151: 927. DOI:10.1016/j.conbuildmat.2017.06.153 |
| [5] |
LIU P, HU Y, GENG B, et al. Corrosion monitoring of the reinforced concrete by using the embedded annular piezoelectric transducer[J]. Journal of Materials Research and Technology, 2020, 9(3): 3517. DOI:10.1016/j.jmrt.2020.01.088 |
| [6] |
SRIRAMADASU R C, BANERJEE S, LU Y. Sensitivity of longitudinal guided wave modes to pitting corrosion of rebars embedded in reinforced concrete[J]. Construction and Building Materials, 2020, 239: 7. DOI:10.1016/j.conbuildmat.2019.117855 |
| [7] |
胡志坚, 夏雷雷, 程晨, 等. 钢筋混凝土构件锈蚀开裂与锈胀力分析[J]. 哈尔滨工业大学学报, 2020, 52(3): 102. HU Zhijian, XIA Leilei, CHENG Chen, et al. Investigation on corrosion-induced cracking and corrosion expansive pressure in reinforced concrete members[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 102. DOI:10.11918/201812061 |
| [8] |
赵新, 易伟建, 徐圣. 钢筋混凝土梁锈蚀损伤定位与识别[J]. 振动与冲击, 2007, 26(8): 38. ZHAO Xin, YI Weijian, XU Sheng. Location and identification of corrosion damage of reinforced concrete beams[J]. Journal of Vibration and Shock, 2007, 26(8): 38. DOI:10.3969/j.issn.1000-3835.2007.08.009 |
| [9] |
郑帆, 史桂昀, 董必钦, 等. 钢筋混凝土通电加速锈蚀行为可视化表征[J]. 硅酸盐学报, 2018, 46(8): 1083. ZHENG Fan, SHI Guiyun, DONG Biqin, et al. Visual characterization on current accelerated corrosion profile of reinforcements[J]. Journal of the Chinese Ceramic Society, 2018, 46(8): 1083. DOI:10.14062/j.issn.0454-5648.2018.08.06 |
| [10] |
XI X, YANG S. Investigating the spatial development of corrosion of corner-located steel bar in concrete by X-ray computed tomography[J]. Construction and Building Materials, 2019, 221(10): 1183. DOI:10.1016/j.conbuildmat.2019.06.023 |
| [11] |
孙世栋, 秦磊, 任宏伟, 等. 基于电阻层析成像的混凝土钢筋锈蚀无损检测[J]. 无损检测, 2020, 42(1): 39. SUN Shidong, QIN Lei, REN Hongwei, et al. Nondestructive testing of concrete steel-bar corrosion based on ERT[J]. Nondestructive Testing, 2020, 42(1): 39. DOI:10.11973/wsjc202001009 |
| [12] |
SONG H, YANG Y. Noncontact super-resolution guided wave array imaging of subwavelength defects using a multiscale deep learning approach[J]. Structural Health Monitoring, 2020, 147592172094295. DOI:10.1177/1475921720942958 |
| [13] |
ZENG L, HUANG L, LIN J. Damage imaging of composite structures using multipath scattering Lamb waves[J]. Composite Structures, 2019, 5(216): 338. DOI:10.1016/j.compstruct.2019.03.008 |
| [14] |
HONG M, SU Z Q, LU Y, et al. Locating fatigue damage using temporal signal features of nonlinear Lamb waves[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 194. DOI:10.1016/j.ymssp.2015.01.020 |
| [15] |
LIU Y, HONG X, ZHANG B. A novel velocity anisotropy probability imaging method using ultrasonic guided waves for composite plates[J]. Measurement, 2020, 166: 10. DOI:10.1016/j.measurement.2020.108087 |
| [16] |
杨晓明, 吴天宇, 陈永林. 人工加速锈蚀钢筋混凝土构件中钢筋锈蚀率与锈蚀电流的关系研究[J]. 硅酸盐通报, 2016, 35(10): 3415. YANG Xiaoming, WU Tianyu, CHEN Yonglin. Relationship between the current and corrosion ratio in corroded reinforced concrete component obtained by artificial accelerated corrosion method[J]. Building of the Chinese Ceramic Society, 2016, 35(10): 3415. |
| [17] |
高志玉, 朱劲松. 混凝土内部钢筋锈蚀监测及黏结滑移性能研究[J]. 工业建筑, 2016, 46(2): 97. GAO Zhiyu, ZHU Jinsong. Monitoring of reinforcement corrosion within concrete and research on bond slip performance[J]. Industrial Construction, 2016, 46(2): 97. DOI:10.13204/j.gyjz201602020 |
| [18] |
MELCHERS R E. Mathematical modelling of the diffusion controlled phase in marine immersion corrosion of mild steel[J]. Corrosion Science, 2003, 45(5): 925. DOI:10.1016/S0010-938X(02)00208-1 |
| [19] |
MELCHERS R E, LI C Q. Phenomenological modeling of reinforcement corrosion in marine environments[J]. ACI Materials Journal, 2006, 103(1): 28. DOI:10.1109/VAST.2006.261436 |
 2022, Vol. 54
2022, Vol. 54


