2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 哈尔滨工业大学 土木工程学院,哈尔滨 150090;
4. 城市与工程安全减灾教育部重点实验室(北京工业大学),北京 100124
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
4. Key Laboratory of Urban Security and Disaster Engineering (Beijing University of Technology), Ministry of Education, Beijing 100124, China
高烈度震区受损的建筑,修复难度大、成本高,为减少因推倒重建产生的建筑垃圾对环境的破坏,可恢复结构和韧性城市的理念逐渐成熟。可恢复功能抗震社区这一概念是由Bruneau等[1]于2003年首次提出,可恢复功能的意义在于经地震后无需或稍加修复便能恢复其原有功能[2],在震前预防和震后重建方面都具有显著的工程价值。刚性连接是传统摇摆框架结构采用的柱脚形式,使之具有较大的竖向承载力和抗侧刚度,但据震害调查显示,破坏概率最大的部位即为底层柱脚节点,从而导致整体倒塌。
Lui等[3]利用计算机模拟了半刚性框架在自由振动、强迫振动和地震激励下的响应特性,发现连接刚性和P-delta效应的存在会降低框架刚度,也会影响半刚性框架的能量耗散量。Eatheron等[4]通过7个拟静力循环加载试验,探究了一种以“蝴蝶型”金属阻尼器连接的2片联肢钢桁架的抗震性能,验证了其保证主体框架保持弹性反应的能力,可将塑性变形限制在保险丝构件内,实现了受水平力时接近零的侧向位移。Xie等[5]建立了多层双管自复位屈曲约束支撑钢框架计算模型, 分析了双管自复位屈曲约束支撑的工作机理、滞回响应和管长公差对自复位系统初始刚度的影响机理;并研究了构件性能对结构地震反应和自复位能力的影响。何金洲等[6]基于在大震作用下的时程分析,发现摇摆界面上的屈曲约束支撑可以稳定发挥耗能能力,使整个结构体系的侧向变形和结构损伤更加均匀,且提高了整体结构抵抗地震损伤的可恢复性。Xu等[7]采用组合碟形弹簧和磁流变流体装置设计了一种自复位变阻尼耗能支撑,试验结果表明该耗能支撑具有完整的准旗形滞回响应,激活力小,刚度突变少,耗能大,性能稳定。Issa等[8]利用闭环动力测试研究了新开发的自复位支撑系统——基于活塞的自复位装置的抗震性能, 并判定能量耗散能力和初始刚度;结果表明,在各种地震作用下,自复位支撑系统表现出良好的自复位性能。
已有研究更注重结构体系自复位能力的实现方式以及增强结构耗能能力的手段。但结构体系在实现上述功能的同时,柱脚的变形能力及损伤控制存在较大问题,因为柱脚往往承受最大的水平力作用且转动需求最大,甚至容易造成柱脚先于结构体系发生破坏导致结构整体倒塌。本文从可替换的框架柱脚入手,提出一种设置屈曲约束钢板(buckling restraint steel plate,BRSP)的半刚性可抬升的可替换框架柱脚。在不影响主体结构承载力和抗侧刚度的基础上,分别从BRSP与框架柱翼缘的厚度比、宽度比和轴向刚度比3个方面分析了BRSP框架柱脚的耗能机制和尺寸参数的选取依据;通过分析BRSP与构件的接触情况,讨论了BRSP在耗能过程中的稳定性和有效性。
1 BRSP-框架柱脚的设计思想摇摆墙和摇摆桁架等摇摆结构通过放松柱脚约束,使摇摆结构在地震作用时能绕柱脚发生转动。摇摆结构刚度较大,保持整体变形的模式,可以控制与其相连的主体结构的变形模式,避免变形集中,同时又能提高主体结构的抗侧力和抗震性能。与摇摆结构相连的主体框架柱脚发生塑性损伤,所以本文设计为带有可替换耗能板的可抬起柱脚形式,提高了结构体系的可恢复性和抗震性能。采用BRSP的框架柱脚由框架柱、BRSP、内侧垫板、外侧盖板和螺栓固定板组成,见图 1。

|
图 1 BRSP-框架柱脚节点 Fig. 1 BRSP-frame column base joint |
该框架柱脚的设计特点在于:螺栓固定板下端与BRSP的焊接处设置了一个10°的斜面,可使柱翼缘与地梁发生一定范围内的相对转动。BRSP与柱翼缘之间设置单独的内垫板,保证BRSP与柱脚翼缘之间紧密连接并协同变形。BRSP外侧盖板可增大承载力和抗剪屈服力,且防止BRSP发生面外屈曲,同时可与BRSP发生摩擦以实现耗能。用螺栓通过BRSP的底部槽型孔将盖板、BRSP以及柱翼缘紧密连接,同时不影响柱脚与地梁的接触间隙活动。BRSP可通过弹塑性拉伸和压缩耗散能量,是可更换的保险丝构件。
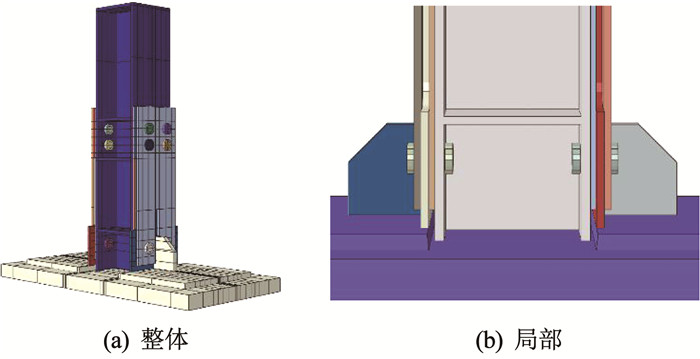
2 BRSP-框架柱脚的有限元模型通过ABAQUS/CAE建立了BRSP- 主体框架柱脚的有限元模型(图 2),进行耗能节点的有限元分析。
|
图 2 BRSP-框架柱脚节点有限元模型 Fig. 2 FE model of BRSP-frame column base joint |
根据50个Q235和Q345试件的钢材循环加载试验结果[9],采用10.9等级的M20高强螺栓,螺栓预紧力取155 kN,σy=940 MPa,εy=0.46%, σu=1 130 MPa,εu=10%,接触面摩擦系数为0.4。
钢材性能经数据拟合后的校准参数见表 1。
| 表 1 Q235B钢的校准参数 Tab. 1 Calibration parameters of Q235B steel |
表 1中
根据ABAQUS中的延性损伤准则分析钢材塑性损伤的发展过程。文献[10]确定了钢材等效塑性损伤应变
| $ \bar \varepsilon _0^{\rm{pl}}=\left\{\begin{array}{l} \infty, \eta \leqslant-1 / 3 \\ C_{1} /(1+3 \eta), -1 / 3<\eta \leqslant 0 \\ C_{1}+\left(C_{2}-C_{1}\right)\left(\eta-\eta_{0}\right)^{2}, 0<\eta \leqslant \eta_{0} \\ C_{2} \eta_{0} / \eta, \eta>\eta_{0} \end{array}\right. $ | (1) |
式中:C1为钢材平板纯剪切状态下(η=0)的等效塑性损伤应变
文献[12]将10组Q235钢板拉伸试验进行回归处理后,得到钢材损伤因子D与塑性位移比关系为
| $ D = 1.3{\left( {\frac{{{{\bar u}^{{\text{pl}}}}}}{{{{\bar u}_{\text{f}}}}}} \right)^{7.6}} $ | (2) |
式中:
| $ {{\bar u}^{{\text{pl}}}} = L{{\bar \varepsilon }^{{\text{pl}}}} $ | (3) |
| $ {{\bar u}_{\text{f}}} = L{{\bar \varepsilon }_{\text{f}}} $ | (4) |
式中:L为有限元单元的特征长度, εpl为钢材等效塑性应变, εf为钢材完全断裂时的等效塑性破坏应变。可由有限元单元特征长度L通过进一步计算得到损伤因子D,即确定损伤演化准则。
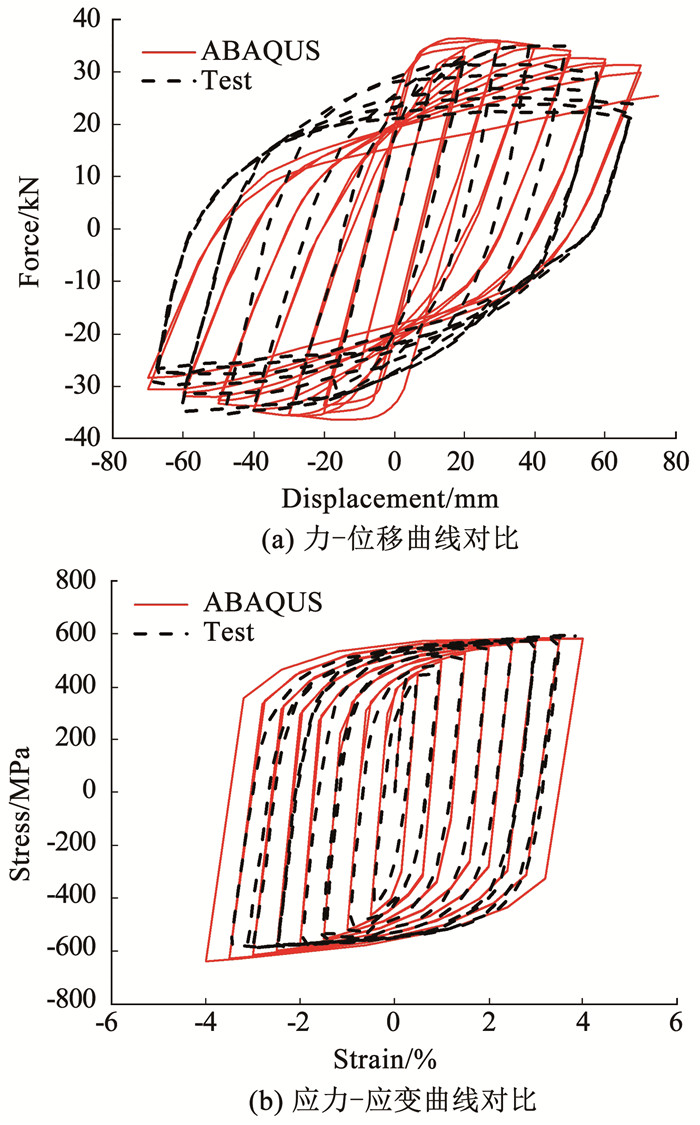
根据文献[13]和文献[9]验证试件截面尺寸,钢材选用Q235B,根据应力三轴度的起始损伤和损伤演化准则,分析钢材在低周大应变下的损伤发展。ABAQUS有限元分析结果见图 3,根据参数SDEG和DUCTCRT对损伤状态进行评价。
|
图 3 考虑强度退化、损伤起始和演化准则的模型的验证 Fig. 3 Verification of models considering strength degradation, damage initiation, and evolution criteria |
试验梁经循环加载后,出现了承载力和刚度的显著退化现象,考虑基于应力三轴度损伤准则后的滞回曲线与原试验曲线吻合一致,表明该损伤准则在型钢梁循环加载应用中的正确性。
2.2 螺栓建模与验证为保证螺栓连接建模的正确性,选取文献[14]的高强螺栓拼接节点试验进行验证。该试验研究了6组共12个试件,对梁拼接节点处的高强螺栓进行了循环加载试验,以研究节点的滞回性能。本文所验证的试件为SJS-1,试件参数见表 2。
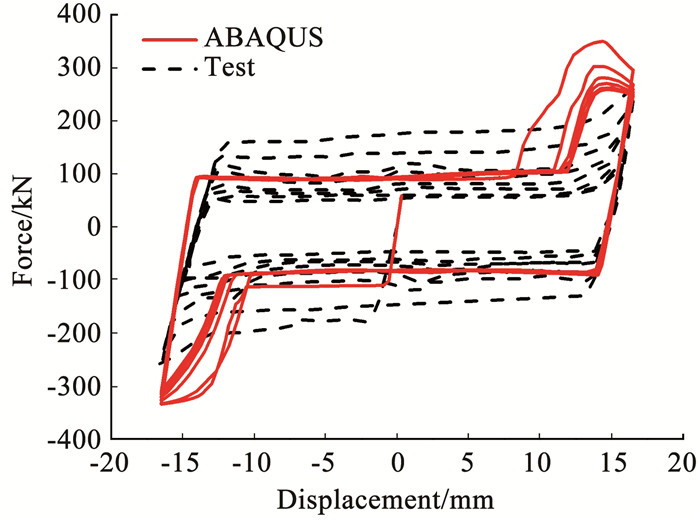
试验加载为位移加载,以螺栓与孔壁接触时的位移为控制位移,在此位移循环60周,进而分析其低周疲劳性能和耗能效果。试验滞回曲线和有限元模拟滞回曲线见图 4,二者大致吻合;其存在差别的原因在于试验时的螺栓存在预应力损失、疲劳及接触面摩擦力变化的现象,而模拟时无法纳入该因素。
|
图 4 高强螺栓节点的ABAQUS与试验滞回曲线对比 Fig. 4 Comparison of ABAQUS and test hysteretic curves of high-strength bolted splice joint |
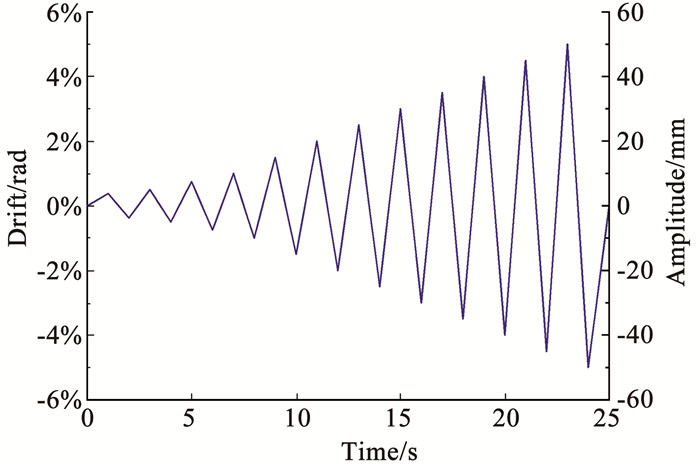
本文采用拟静力加载方式,加载制度、加载历程和加载幅值根据张艳霞等[15]对自复位结构的摩擦耗能分析得到,通过采用以水平位移为控制变量的循环加载方式,加载至层间位移角5%时释放约束,以得到结构残余变形量。本文节点模型的加载制度曲线见图 5。加载位置在选取的柱脚段的最上方,以获得最大的加载效率,同样的位移幅值下产生最大的构件内力。
|
图 5 加载制度 Fig. 5 Loading protocol |
本文研究的结构体系的各部分构件属于可拆解可替换构件,可分别进行有限元模型的验证。在进行结构组装时,考虑了各部分构件的接触和相互作用效应,同时考虑装配式构件的协调变形和协同受力。对关键局部和对结构性能有显著影响的部位建立精细化模型,对其他部分建立宏观模型,以实际情况确定模型间的连接方式,验证模型混合建模方法的可靠性以及各模型间的协调工作性[16],并能得到整体结构受力特征和微观破坏过程[17]。
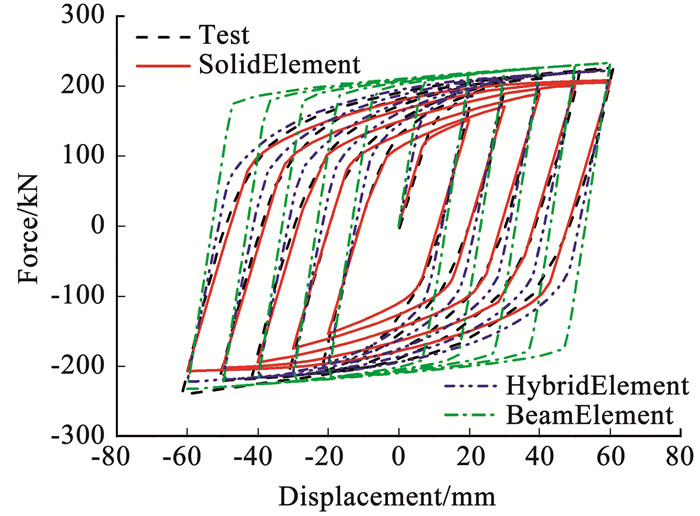
将杆系模型、实体单元模型和混合模型的多尺度有限元模型与试验结果进行梁柱节点域剪切变形验证,分析结果见图 6。
|
图 6 梁柱节点域剪切变形的有限元与试验滞回曲线对比 Fig. 6 Comparison of FE and test hysteretic curves of shear deformation in beam-column joint domain |
由图 6可以发现,梁单元宏观模型无法准确模拟局部变形和损伤情况,模拟结果明显高于试验结果,且刚度和承载力最高;实体单元模型的刚度和承载力略低于试验结果,这是因为考虑了损伤演化和刚度退化,但整体上优于宏观模型。混合模型能综合考虑宏观和微观损伤特征,整体上与试验吻合度较高。
3 BRSP-框架柱脚的耗能机制分析BRSP - 耗能框架柱脚由BRSP、外侧盖板、内侧垫板和钢柱组成。分别从BRSP板厚度、削弱段宽度、轴向刚度3个方面展开对比分析,BRSP的参数按照BRSP与柱翼缘相应参数的比例形式确定。
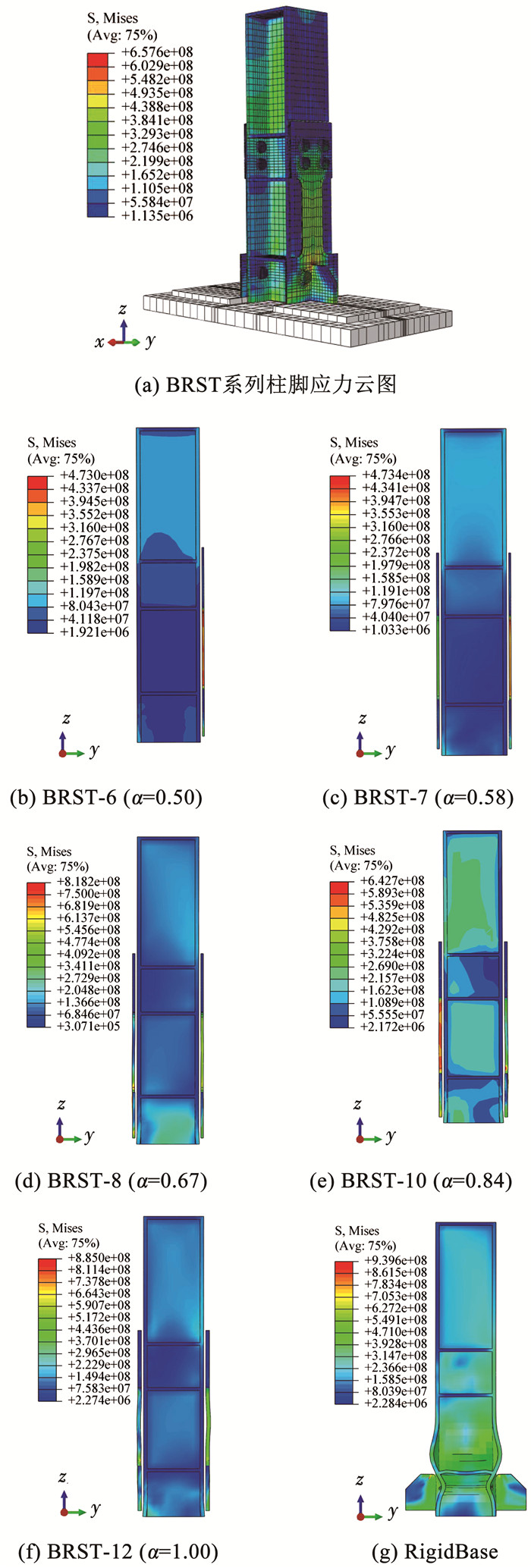
3.1 厚度比对柱脚滞回性能的影响将BRST-X系列模型的柱脚与传统刚性连接柱脚进行对比,X表示BRSP厚度值(单位:mm),BRSP板厚度与柱翼缘厚度的比值即厚度比,用α表示。为控制变量,削弱段宽度均为100 mm,5%层间位移角最终状态的柱脚有限元应力云图见图 7(a); 可以看出,塑性损伤集中在BRSP削弱段和底端加劲肋焊接处周边,因为在焊接加劲肋的部位,对BRSP端部放大截面进行开孔以保证加劲肋能够穿过,所以在该处也出现了应力集中的情况,而框架柱基本处于弹性状态。说明在较大侧向位移下,可通过BRSP削弱段的塑性变形耗散能量,从而能避免框架柱发生严重的塑性变形。不同厚度比α的BRST模型与传统刚接柱脚模型(RigidBase)的对比云图见图 7(b)~(g)。
|
图 7 不同厚度比α的BRSP与传统刚接柱脚钢板的对比 Fig. 7 Comparison between BRSP with different thickness ratios α and plates of traditional rigid column base joints |
根据变形云图可看出RigidBase模型存在明显强度退化的原因在于随着损伤的积累,柱脚翼缘发生了严重的塑性变形;但基于相同本构关系的BRST模型并未出现显著的性能退化,柱脚也未出现较大塑性变形。说明BRST系列模型的受力方式更合理,耗能作用显著,更适合作为具有可恢复性的框架柱脚。
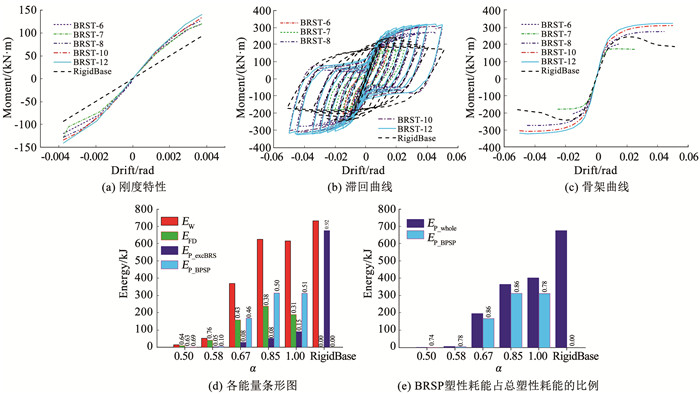
为量化分析厚度比α对柱脚钢板受力性能的影响并与刚接柱脚模型进行对比,见图 8(a); 可以看出,柱脚刚度随着α的增大而增大,其中传统柱脚(可视为厚度比α=0)的刚度仅为参考模型BRST-10的70%,可见该BRSP柱脚能够满足初始刚度需求。
|
图 8 从能量角度分析厚度比α对BRSP柱脚性能的影响 Fig. 8 Effect of thickness ratio α on the performance of BRSP column base in terms of energy |
各模型的弯矩-层间位移角关系曲线见图 8(b)。相对于刚性柱脚节点,半刚性摇摆结构体系框架柱脚具有一定的自复位能力,在滞回曲线上表现的捏拢现象是当外加作用变为零、柱脚复位到初始零位移位置的一种表现。结构自复位能力的增强能够减小其残余变形,对于提高结构的抗震能力和增强结构可修复性具有重要意义。其中BRST-6模型的BRSP轴向刚度最小,层间位移角超过2%的结构不能继续发展延性,分析发现该BRSP已有较大的塑性损伤积累,表明BRSP轴向刚度过小时不能满足结构发生较大侧移的需求。
BRST系列模型与RigidBase模型的骨架曲线见图 8(c)。对比BRST系列曲线可发现,随着厚度比α增大,结构耗能增多,抗侧移能力增大,但增幅逐渐减小,说明厚度比α存在一个合理范围。
结构的水平位移已经加载到5%位移角,远远超过中国规范1/50位移角的要求,此时传统的刚性柱脚节点已经发生了明显的刚度退化(图 8(b)滞回曲线和图 8(c)骨架曲线都有明显的表征); 但对于本文提出的新型半刚性柱脚节点,由于其构造合理,变形能力强,即使在很大加载位移下也未出现性能退化,曲线未出现下降段。
ABAQUS中关于能量平衡的表达式为
| $ {E_{\rm{I}}} + {E_{\rm{V}}} + {E_{{\rm{FD}}}} + {E_{{\rm{KE}}}} = {E_{\rm{W}}} $ | (5) |
式中:EI为内能;EV为黏性耗散能;EFD为摩擦耗能;EKE为动能;EW为外荷载做功。
内能的表达式为
| $ {E_{\rm{I}}} + {E_{\rm{E}}} + {E_{\rm{P}}} + {E_{{\rm{CD}}}} = {E_{\rm{A}}} $ | (6) |
式中:EE为可恢复的弹性应变能;EP为非弹性过程的能量耗散(如塑性耗能等);ECD为黏弹性或者蠕变过程的能量耗散;EA为伪应变能。
就本文研究的模型,关心的能量形式有摩擦耗能EFD、塑性耗能EP以及外荷载做功EW,能量平衡的表达式改写为
| $ {E_{{\rm{FD}}}} + {E_{\rm{P}}} = {E_{\rm{W}}} $ | (7) |
通过积分处理得到不同厚度比α的BRST系列模型和RigidBase的模型各能量大小见图 8(d)。可以发现:1)α值越大,达到相同侧移外荷载所需做的功EW越多,即结构的抗侧刚度越大;2)体系的摩擦耗能EFD占比随着α值的增大而降低;3)BRSP塑性耗能EP_BRSP占整体塑性耗能EP_whole的比例随着α值的增大而先增大后降低;4)RigidBase模型没有通过摩擦耗散能量,而是通过柱子的塑性变形耗散绝大部分能量。
为确定合理的厚度比α,EP_BRSP与EP_whole的比例可作为重要参考,见图 8(e)。可以看出,BRSP耗能占比有先增大后减小的趋势,从BRST-6的74%到BRST-8和BRST-10的86%,随后降低至BRST-12的78%。
所以要通过BRSP的塑性变形耗散更多的能量,就需要合理控制厚度比α。经数据拟合后得到表达式:
| $ \frac{{{E_{{\rm{P\_BRSP}}}}}}{{{E_{{\rm{P\_whole}}}}}} = - 1.788{\alpha ^2} + 2.781\alpha - 0.212 $ | (8) |
BRSP的耗能占比最高可达到86%,综合考虑耗能性能和施工便捷,可取BRSP的合理厚度比α为0.85。
3.2 宽度比对柱脚滞回性能的影响以BRSD-β系列模型与传统刚接柱脚进行对比,β表示BRSP宽度与柱翼缘宽度的比值, 即宽度比。为控制变量,根据前文分析得BRSP合理厚度比为0.85。不同宽度比β的BRSD模型与RigidBase模型在5%层间位移角最终状态的柱脚有限元应力云图对比见图 9。

|
图 9 不同宽度比β的BRSP与传统刚接柱脚钢板的对比 Fig. 9 Comparison between BRSP with different width ratios β and plates of traditional rigid column base joints |
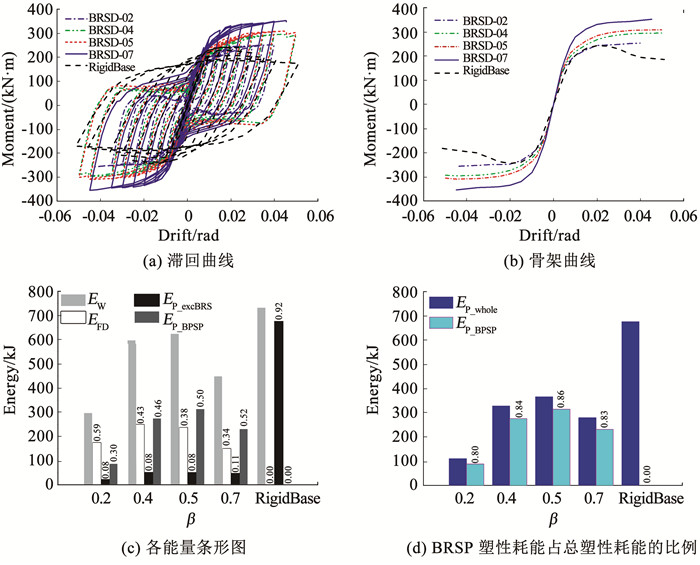
各模型的滞回曲线见图 10(a),随着宽度比β的增大,曲线越饱满,抗侧移能力越好,耗能能力越强。宽度比β的变化能明显影响结构性能,设计BRSP宽度时应对比分析宽度比β的最优取值以获得最佳的结构性能。
|
图 10 从能量角度分析宽度比β对BRSP柱脚性能的影响 Fig. 10 Effect of width ratio β on the performance of BRSP column base in terms of energy |
BRSD系列模型与RigidBase模型的骨架曲线,见图 10(b)。当层间位移角 < 2%时,BRSD模型的刚度随着层间位移角的增大而增大,并且BRSD系列模型与RigidBase模型骨架曲线近似重合,说明其抗侧能力相近。就骨架曲线而言,当层间位移角超过2%时,前者逐渐平缓,后者显著下降,表明RigidBase模型发生了塑性损伤,致使其承载能力退化。而BRSD系列模型在5%层间位移角时,仍可保持刚度和承载能力维持稳定。所以BRSD模型具备的耗能特性相较于传统刚接柱脚,更适合作为具有可恢复性的框架柱脚。
厚度比对柱脚滞回性能的影响从能量的角度出发,定量分析不同宽度比β的BRSD系列模型各能量大小, 见图 10(c)。可以发现:1)β值越大,相同层间位移角下的外力做功EW越大,即达到相同位移所需的外力更大,柱脚抗侧移能力更强;2)β值越大,摩擦耗能EFD总量先增加后减小,但EFD的占比却在一直降低;3)β值越大,整体塑性耗能EP_whole越大。
为确定合理的宽度比β,以塑性耗能利用率(即BRSP的塑性耗能能量EP_BRSP占整体塑性耗能能量EP_whole的比例)作为重要参考,见图 10(d); 可以看出,随着β增大,BRSP耗能占比先增后减,从β=0.2的80%到β=0.4的84%,随后增到β=0.5的86%,再降到β=0.7的83%。因此,为实现BRSP的耗能利用率最大化的目标,β的取值范围为0.4~0.7,经数据拟合后得到下式:
| $ \frac{{{E_{{\rm{P\_BRSP}}}}}}{{{E_{{\rm{P\_whole}}}}}} = - 0.583{\beta ^2} + 0.590\beta - 0.704 $ | (9) |
考虑到制作工艺和构造便利,合理的宽度比β可取为0.50。
3.3 轴向刚度比对柱脚耗能能力的影响针对BRSP的轴向刚度与一侧柱翼缘的轴向刚度之比,即轴向刚度比ω对结构性能的影响进行分析,见表 3。
| 表 3 柱脚模型的轴向刚度比 Tab. 3 Axial stiffness ratios of different column base models |
根据前文的计算结果,以轴向刚度比ω分析各模型中BRSP的塑性耗能能力和利用率,见表 4和图 11。
| 表 4 不同轴向刚度比ω的BRSP模型耗能占比 Tab. 4 Energy dissipation ratio of BRSP models with different axial stiffness ratios ω |
|
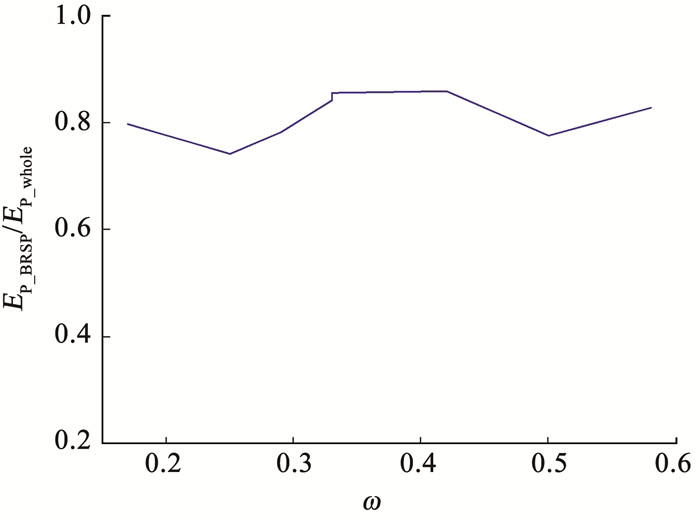
图 11 不同轴向刚度比ω的BRSP模型的耗能占比曲线 Fig. 11 Energy dissipation ratio curve of BRSP models with different axial stiffness ratios ω |
可以看出,随着轴向刚度比ω增加,BRSP的塑性耗能占比上下波动,变化范围较为固定。当ω在[0.17,0.58]范围内时,BRSP塑性耗能占比处在0.74~0.86范围内,塑性耗能占比均较大; 但当ω低于0.2或大于0.5时柱脚的整体耗能能力较弱,因此综合考虑柱脚的耗能总量和BRSP耗能占比,同时考虑到制作工艺和构造安全,ω不宜取得过大或过小。因此,将轴向刚度比ω控制在[0.3,0.5]范围内时,BRSP的塑性耗能占总体塑性耗能的比值在80%左右,从而可将大部分塑性损伤控制在BRSP上,基本能够实现损伤可控、结构可恢复。
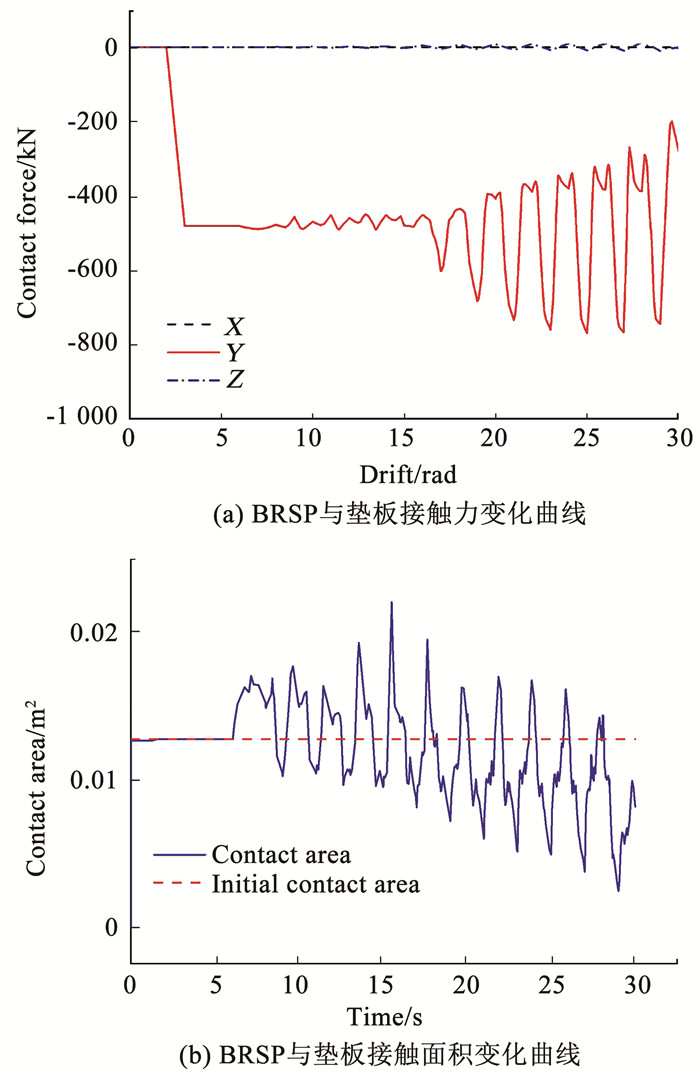
4 BRSP-框架柱脚的构件接触分析 4.1 BRSP与内侧垫板的接触分析BRSP与内侧垫板的接触力和接触面积的变化见图 12。X向、Y向和Z向接触力分别记为CFN1、CFN2和CFN3。接触力值一直维持在较高的水平,甚至超过了800 kN;垫板可较好地分散BRSP的接触力,随后传递至柱翼缘,从而避免柱翼缘处的应力集中现象。加载过程中的接触面积基本保持在初始接触状态,未出现较大分离,说明内侧垫板从加载开始到结束都起到了分散接触力的作用。
|
图 12 BRSP与垫板接触力和接触面积的变化过程 Fig. 12 Contact force and contact area variation between BRSP and backing plate |
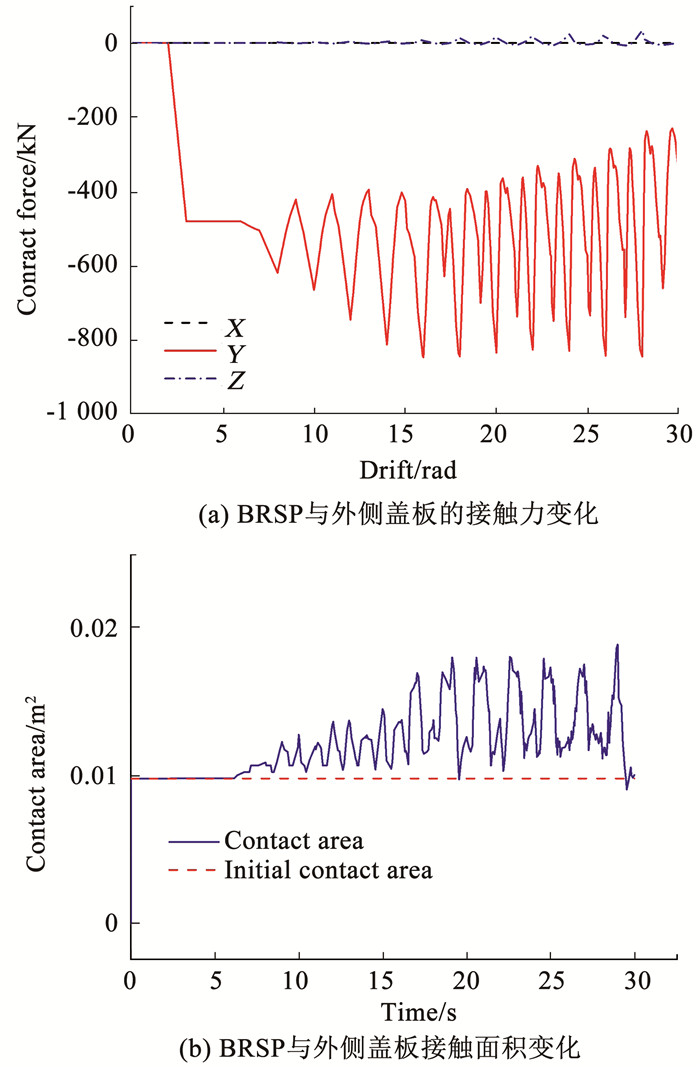
BRSP与外侧盖板的接触力和接触面积的变化见图 13。接触力值一直处于较高的水平,接近800 kN,而侧向力的最大值约为400 kN,说明盖板能为BRSP提供侧向约束,使之不发生面外屈曲变形,避免引起刚度下降,从而继续发挥其耗能作用。盖板与BRSP未出现较大分离,接触良好。
|
图 13 BRSP与盖板接触力和接触面积变化 Fig. 13 Contact force and contact area variation between BRSP and cover plate |
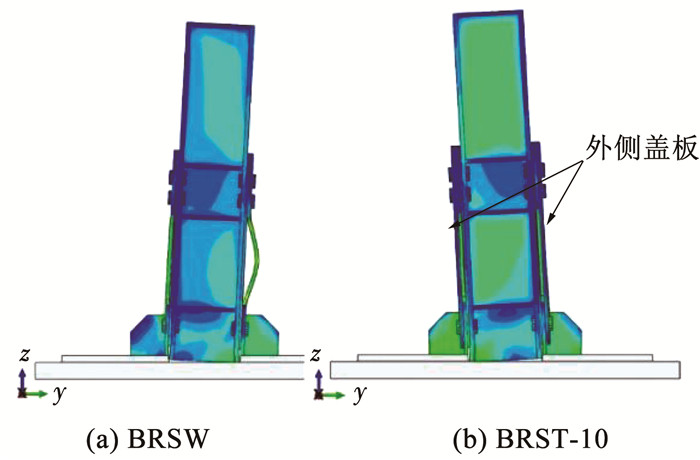
为探究外侧盖板对BRSP整体性能的影响,就BRSP外侧没有布置盖板的模型BRSW(without cover plate)及BRST-10模型进行耗能对比分析,5%层间位移角最终状态的柱脚有限元应力云图见图 14。
|
图 14 BRSW与BRST-10模型对比 Fig. 14 Comparison between BRSW and BRST-10 model |
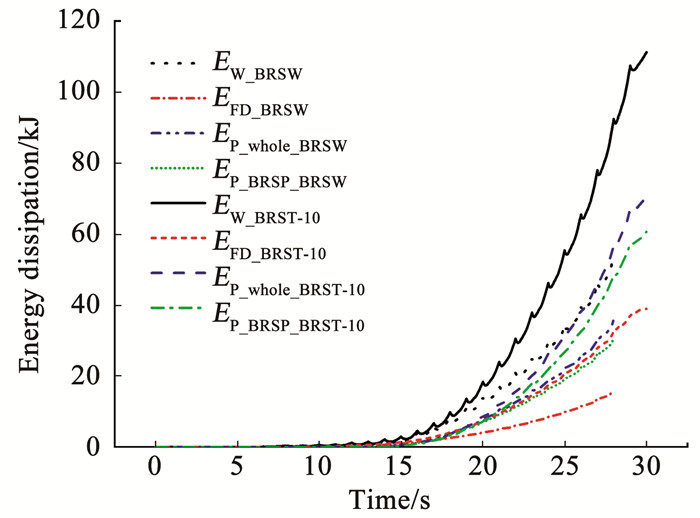
可以看出,BRSW模型在较大层间位移角下,BRSP削弱段中部发生了显著的面外侧移,这是由于缺少外侧盖板的侧向约束而导致的。从耗能角度来看,两种模型的耗能对比及具体耗能数据见图 15和表 5。
|
图 15 BRSW和BRST-10模型耗能曲线对比 Fig. 15 Comparison of energy dissipation curves between BRSW and BRST-10 model |
| 表 5 BRSW和BRST-10模型的各耗能项数据 Tab. 5 Energy dissipation data of BRSW and BRST-10 model |
从表 5中可以看出,在外荷载作用下,BRST-10和BRSW模型通过摩擦耗散的能量占比分别为38% 和31%,这是由于BRSW缺少外侧盖板与BRSP进行摩擦耗能,外侧盖板通过摩擦提供了7%的附加总耗能。此外,在相同层间位移角下,BRSW模型的外力做功更少,表明结构承载能力较差。尽管BRSW中的BRSP塑性耗能占比为87%,与BRST-10的86%相当,但结构总体耗能能力差和位移响应大同样证明了外侧盖板在耗能和提高结构承载能力上的重要作用。
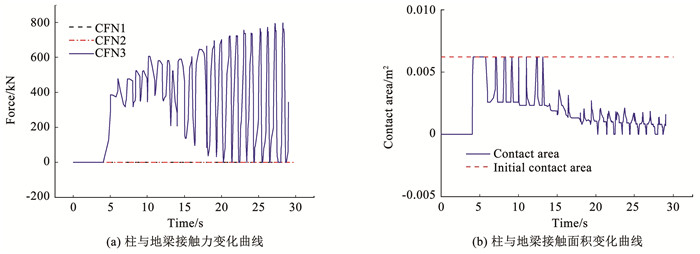
4.3 桁架柱脚与地梁的接触分析由于该框架柱可实现半抬升,柱发生上下抬起时,与地梁的接触较为频繁。为避免竖向承载力降低和发生侧向变形,需固定柱脚的位置并分析摇摆桁架柱脚与地梁的接触情况。柱脚底部与地梁的接触力和接触面积变化曲线见图 16。由于柱脚可抬升,X向和Y向接触力(CFN1和CFN2)基本为0;当层间位移角大于3%时,Z向的接触力(CFN3)和接触面积均有变为零的时刻,说明柱脚发生的抬升行为过大。即在层间位移角3%以内,竖向承载力传递稳定,而层间位移角大于3%时,整体结构的倒塌风险有所增大。所以可通过附加摇摆桁架等抗侧力体系防止结构在较大的水平作用下,因抗力不足而发生倒塌。
|
图 16 柱与地梁的接触变化 Fig. 16 Contact variation between columns and ground beams |
本文提出一种可抬升的半刚性框架柱脚形式,并安装可更换的BRSP耗散能量,减少框架柱脚的损伤,同时能够保证框架结构的竖向承载力和抗侧刚度,从而提高结构的抗震性能和可恢复性。根据已有的材料本构关系和高强螺栓连接节点试验, 验证了本文BRSP-框架柱脚模型的可靠性。通过精细化分析得到以下主要结论:
1) 对比分析了BRSP与框架柱翼缘取不同厚度比α和宽度比β时的滞回曲线和骨架曲线,分析了BRSP与框架柱翼缘取不同轴向刚度比ω时的BRSP塑性耗能占比,探究了BRSP的柱脚耗能机制。建议在框架柱脚布置可替换的BRSP时,其尺寸参数选取可参考:厚度比α为0.85、宽度比β为0.50且ω在[0.3,0.5]范围内,以达到最优的结构性能,使BRSP的塑性耗能能力被充分利用。
2) 通过分析BRSP与垫板和盖板的接触力、接触面积随时间的变化规律探究了垫板和盖板对柱脚耗能能力的影响,结果表明:内侧垫板和外侧盖板不仅能够有效防止BRSP发生面外屈曲,同时盖板通过摩擦产生的耗能占总耗能的7%。
3) 本文选取的是结构关键部位即柱脚节点作为研究对象,并非针对某一类特定的结构体系,且所有结论都是通过几何尺寸或构造特征的相对比值给出,不是针对某一个特定的柱脚节点给出绝对的具体取值。因此本文结论对于同类柱脚节点及采用此类柱脚节点的结构体系的分析设计具有很好的借鉴价值。
| [1] |
BRUNEAU M, CHANG S E, EGUCHI R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19(4): 733. DOI:10.1193/1.1623497 |
| [2] |
吕西林, 陈云, 毛苑君. 结构抗震设计的新概念——可恢复功能结构[J]. 同济大学学报(自然科学版), 2011, 39(7): 941. LV Xilin, CHEN Yun, MAO Yuanjun. New concept of structural seismic design: Earthquake resilient structures[J]. Journal of Tongji University (Natural Science), 2011, 39(7): 941. DOI:10.3969/j.issn.0253-374x2011.07.001 |
| [3] |
LUI E M, LOPES A. Dynamic analysis and response of semirigid frames[J]. Engineering Structures, 1997, 19(8): 644. DOI:10.1016/S0141-0296(96)00143-5 |
| [4] |
EATHERTON M R, MA Xiang, KRAWINKLER H, et al. Quasi-static cyclic behavior of controlled rocking steel frames[J]. Journal of Structural Engineering, 2014, 140(11): 04014082. DOI:10.1061/(ASCE)ST.1943-541X.0001005 |
| [5] |
XIE Qin, ZHOU Zhen, HUANG Jiahao, et al. Influence of tube length tolerance on seismic responses of multi-storey buildings with dual-tube self-centering buckling-restrained braces[J]. Engineering Structures, 2016, 116: 26. DOI:10.1016/j.engstruct.2016.02.023 |
| [6] |
何金洲, 贾明明, 吕大刚, 等. 摇摆桁架-BRB-钢框架体系耗能减震效果研究[J]. 建筑结构学报, 2017, 38(增刊1): 34. HE Jinzhou, JIA Mingming, LV Dagang, et al. Energy dissipation and damping effect analysis of rocking truss-BRB-steel frame system[J]. Journal of Building Structures, 2017, 38(S1): 34. DOI:10.14006/j.jzjgxb.2017.S1.005 |
| [7] |
XU Longhe, XIE Xingsi, LI Zhongxian. Development and experimental study of a self-centering variable damping energy dissipation brace[J]. Engineering Structures, 2018, 160: 270. DOI:10.1016/j.engstruct.2018.01.051 |
| [8] |
ISSA A S, ALAM M S. Experimental and numerical study on the seismic performance of a self-centering bracing system using closed-loop dynamic (CLD) testing[J]. Engineering Structures, 2019, 195: 144. DOI:10.1016/j.engstruct.2019.05.103 |
| [9] |
王萌. 强烈地震作用下钢框架的损伤退化行为[D]. 北京: 清华大学, 2013 WANG Meng. Damage and degradation behaviors of steel frames under severe earthquake[D]. Beijing: Tsinghua University, 2013 |
| [10] |
YU Hailing, JEONG D Y. Application of a stress triaxiality dependent fracture criterion in the finite element analysis of unnotched Charpy specimens[J]. Theoretical and Applied Fracture Mechanics, 2010, 54(1): 54. DOI:10.1016/j.tafmec.2010.06.015 |
| [11] |
BAO Yingbin, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81. DOI:10.1016/j.ijmecsci.2004.02.006 |
| [12] |
周天华, 李文超, 管宇, 等. 基于应力三轴度的钢框架循环加载损伤分析[J]. 工程力学, 2014, 31(7): 146. ZHOU Tianhua, LI Wenchao, GUAN Yu, et al. Damage analysis of steel frames under cyclic load based on stress triaxiality[J]. Engineering Mechanics, 2014, 31(7): 146. DOI:10.6052/j.issn.1000-4750.2013.01.0090 |
| [13] |
郝际平, 陈绍蕃. 钢结构在循环荷载作用下的局部屈曲和低周疲劳的试验研究[J]. 土木工程学报, 1996, 29(6): 40. HAO Jiping, CHEN Shaofan. Experimental study on local buckling and low cycle fatigue of steel structures under cyclic loading[J]. China Civil Engineering Journal, 1996, 29(6): 40. |
| [14] |
胡安吉. 高强螺栓拼接节点的耗能机理研究[D]. 苏州: 苏州科技学院, 2009 HU Anji. Study on energy dissipation of splice joints in steel structures[D]. Suzhou: Suzhou University of Science and Technology, 2009 |
| [15] |
张艳霞, 叶吉健, 赵微, 等. 自复位平面钢框架推覆分析[J]. 地震研究, 2014, 37(3): 476. ZHANG Yanxia, YE Jijian, ZHAO Wei, et al. Pushover analysis of self-centering steel moment-resisting plane frame[J]. Journal of Seismological Research, 2014, 37(3): 476. DOI:10.3969/j.issn.1000-0666.2014.03.023 |
| [16] |
石永久, 王萌, 王元清. 基于多尺度模型的钢框架抗震性能分析[J]. 工程力学, 2011, 28(12): 20. SHI Yongjiu, WANG Meng, WANG Yuanqing. Seismic behavior analysis of steel frame by multi-scale calculation method[J]. Engineering Mechanics, 2011, 28(12): 20. |
| [17] |
陆新征, 林旭川, 叶列平. 多尺度有限元建模方法及其应用[J]. 华中科技大学学报(城市科学版), 2008, 25(4): 76. LU Xinzheng, LIN Xuchuan, YE Lieping, et al. Multiscale finite element modeling and its application in structural analysis[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2008, 25(4): 76. |
 2022, Vol. 54
2022, Vol. 54


