2. 通信网信息传输与分发技术重点实验室,石家庄 050081
2. Science and Technology on Communication Networks Laboratory, Shijiazhuang 050081, China
加权分数傅里叶变换(weighted fractional Fourier transform, WFRFT)作为一种广义的傅里叶变换近来受到学者的关注,其变换本身具有完备的数学理论支撑,信号调制方式在通信系统下具有明确的物理含义,可以实现单载波体制与多载波体制的无缝切换[1];在同时具有大多普勒和多径的双选信道下具备出色的抗衰落性能[2]。此外由于WFRFT内部4个分量可互相形成自干扰信号,且其中多载波分量具备高斯化特征,作为一种独特的信号隐藏技术被应用于物理层安全领域中[3]。文献表明WFRFT安全应用可从利用WFRFT自身特性[4]、WFRFT与扩频等传统加密技术结合[5]、WFRFT信息论理论安全[6]三个角度出发。然而,在目前检索的WFRFT安全算法文献当中,无论是多参数加权分数傅里叶变换[7](multiple parameter weighted fractional Fourier transform, MP-WFRFT)还是广义多项分数傅里叶变换[8](general multi-fractional Fourier transform, GMFRFT), 其数学机理均来源于Shih[9]于1995年提出的多系列态函数加权叠加的分数傅里叶变换。该变换中各项加权系数仅由一个阶数因子决定,故在实际安全领域中存在单参数抗扫描性差以及具有周期性等弊端。
最初的WFRFT通信系统应用由光学上的傅里叶变换得来,受此启发,本文利用二维分数傅里叶变换在图像加密上的特殊性质将一维WFRFT扩展至二维以进一步增强安全性能。
1 二维离散分数傅里叶变换的定义与性质从变换的定义形式上看,分数傅里叶变换可以分为两大类。一类是以Chirp信号为基底的Chirp类分数傅里叶变换,另一类则为多态函数组合的加权类分数傅里叶变换。Chirp类分数傅里叶变换因其以连续信号为“基”而广泛应用于雷达、测距系统;而加权类分数傅里叶变换虽然与Chirp类分数傅立叶变换相比出现较晚,但其离散算法和实现方式都更为简单,因而在信息光学、图像加密等领域得到了广泛应用。
二维加权分数傅里叶变换(two-dimensional weighted fractional Fourier transform, 2DWFRFT)可看作一维加权分数傅里叶的扩展变换,首先给出一维单参数4-WFRFT的定义。
任意复数向量x=[x(0), x(1), …, x(N-1)]T的N点α阶WFRFT变换可表示为
| $ \mathscr{F}_{\omega}^{\alpha}[\boldsymbol{x}]=\boldsymbol{F}^{\alpha} \boldsymbol{x}=\left(\omega_{0}^{\alpha} \boldsymbol{I}+\omega_{1}^{\alpha} \boldsymbol{F}+\omega_{2}^{\alpha} \boldsymbol{P}+\omega_{3}^{\alpha} \boldsymbol{P} \boldsymbol{F}\right) \boldsymbol{x} $ | (1) |
式中Fα为N×N阶WFRFT矩阵,[F]k, n=(1/
ωαl加权系数的具体形式为
| $ \omega_{\alpha}^{l}=\frac{1}{4} \sum\limits_{k=0}^{3} \exp \left[\frac{2 {\rm{ \mathsf{ π} }} \mathrm{j}}{4}(\alpha-l) k\right] $ | (2) |
式中l=0, 1, 2, 3;j、π分别为虚数单位与圆周率。
下面介绍二维离散分数傅里叶的定义及性质。
根据文献[10]的描述,可以扩展出大小为N×N的多参数离散分数傅里叶矩阵:
| $ \boldsymbol{F}^{\overline{\boldsymbol{\alpha}}}=\sum\limits_{k=0}^{N-1} \lambda_{k}^{\alpha_{k}} \boldsymbol{e}_{k} \boldsymbol{e}_{k}^{\mathrm{T}}, 0 \leqslant m, n \leqslant N-1 $ | (3) |
式中:
| $ \mathscr{F}_{2 \mathrm{D}}^{\overline{\boldsymbol{\alpha}}, \overline{\boldsymbol{\beta}}}(\boldsymbol{M})=\boldsymbol{F}^{\overline{\boldsymbol{\alpha}}} \cdot \boldsymbol{M} \cdot \boldsymbol{F}^{\overline{\boldsymbol{\beta}}} $ | (4) |
式中β=[β1, β2, …, βN]为长度1×N的参数向量。
二维离散分数傅里叶变换具有幺正性、边界性、可加性、周期性。
1) 幺正性:
| $ \begin{aligned} \left(\boldsymbol{F}^{\overline{\boldsymbol{\alpha}}}\right)^{\mathrm{H}}\left(\boldsymbol{F}^{\overline{\boldsymbol{\alpha}}}\right)=&\left(\boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}}} \boldsymbol{V}^{\mathrm{T}}\right)^{\mathrm{H}}\left(\boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}}} \boldsymbol{V}^{\mathrm{T}}\right)=\\ &\left(\boldsymbol{V} \boldsymbol{\varLambda}^{-\overline{\boldsymbol{\alpha}}} \boldsymbol{V}^{\mathrm{T}}\right)\left(\boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}}} \boldsymbol{V}^{\mathrm{T}}\right)=\boldsymbol{V} \boldsymbol{V}^{\mathrm{T}}=\boldsymbol{I} \end{aligned} $ | (5) |
2) 边界性:
当α为零向量,即α=0=[0, 0, …, 0]时,存在性质Fα=VΛ0VT=VVT=I;当α=1=[1, 1, …, 1]时,存在性质Fα=VΛ1VT=VΛVT=F。
3) 可加性:
| $ \begin{aligned} \boldsymbol{F}^{\overline{\boldsymbol{\alpha}_{1}}} \cdot \boldsymbol{F}^{\overline{\boldsymbol{\alpha}_{2}}}=&\left(\boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}_{1}}} \boldsymbol{V}^{\mathrm{T}}\right)\left(\boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}_{2}}} \boldsymbol{V}^{\mathrm{T}}\right)=\\ & \boldsymbol{V} \boldsymbol{\varLambda}^{\overline{\boldsymbol{\alpha}_{1}}+\overline{\boldsymbol{\alpha}_{2}}} \boldsymbol{V}^{\mathrm{T}}=\boldsymbol{F}^{\overline{\boldsymbol{\alpha}_{1}}+\overline{\boldsymbol{\alpha}_{2}}} \end{aligned} $ | (6) |
4) 周期性:对所有整数k来说,Fα以4为周期,即
| $ \left\{\begin{array}{l} \mathrm{e}^{-\mathrm{j} \frac{{\rm{ \mathsf{ π} }}}{2} k\left(\alpha_{k}+\frac{4}{k}\right)}=\mathrm{e}^{-\mathrm{j} \frac{{\rm{ \mathsf{ π} }}}{2} k \alpha_{k}}, k \neq 0 \\ \mathrm{e}^{-\mathrm{j} \frac{{\rm{ \mathsf{ π} }}}{2} k}=1, k=0 \end{array}\right. $ | (7) |
可以看出,性质1)代表多参数变换具有酉变换特性;而根据边界性可推导出当α=1, β=1时,二维离散分数傅里叶变换退化为二维傅里叶变换。
需要说明的是,虽然多参数变换的周期性使得二维离散分数傅里叶变换仍具有以4为周期的重复特性,但横纵多个参数的引入确实增加了抗参数扫描的难度,为应用于物理层安全奠定了理论基础。
2 基于2DWFRFT的安全信号设计方案 2.1 可行性分析与系统模型现有文献中已有一些将WFRFT用于抗截获手段的方法,但无论是单参数加权变换还是多参数加权变换、多项加权变换,其数学机理均为一维WFRFT,而2DWFRFT将原有的一维WFRFT信号扩展至二维,采用信号矩阵横、纵两个维度的不同参数四项加权变换对信号进行加密重组,对于非合作接收机而言,需要在M×N维数轴上同时搜索截获多个参数才能正确恢复出数据;直观地讲,相较于原先的单参数破解参数搜索次数提升至M×N倍。结合前文公式阐述2DWFRFT的信号构建可行性, 并将算法应用于实际通信系统中。
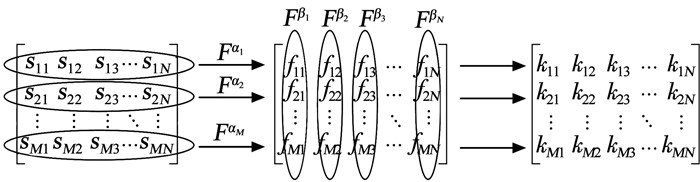
考虑一列数字基带映射调制后的向量信号x=[x(0), x(1), …, x(N-1)]T,将其重组为M路N点的矩阵信号S。之后以S的每行数据为原始序列进行N点4-WFRFT,且每行变化的参数分别设置为α1, α2, …, αM,见图 1,每个行向量的变换过程可表示为
|
图 1 2DWFRFT正变换原理示意 Fig. 1 Schematic of 2DWFRFT |
| $ \begin{aligned} \mathscr{F}^{\alpha_{i}}\left(F_{i}\right)=& \omega_{0}^{\alpha_{i}} F_{i}+\omega_{1}^{\alpha_{i}} F_{i}^{\prime}+\omega_{2}^{\alpha_{i}} F_{i}^{\prime \prime}+\omega_{3}^{\alpha_{i}} F_{i}^{\prime \prime \prime}, \\ & i=1,2,3, \cdots, M \end{aligned} $ | (8) |
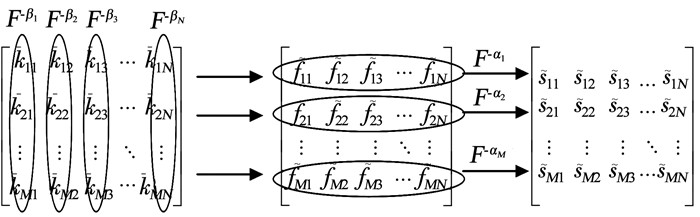
同理,如图 2所示对每个列向量按参数β进行M点WFRFT,变换过程表示为
|
图 2 2DWFRFT反变换原理示意 Fig. 2 Schematic of two-dimensional inverse weighted fractional Fourier transform |
| $ \begin{aligned} \mathscr{F}^{\beta_{i}}\left(F_{i}\right)=& \omega_{0}^{\beta_{i}} F_{i}+\omega_{1}^{\beta_{i}} F^{\prime}{ }_{i}+\omega_{2}^{\beta_{i}} F^{\prime \prime}{ }_{i}+\omega_{3}^{\beta_{i}} F^{\prime \prime \prime}{ }_{i}, \\ & i=1,2,3, \cdots, N \end{aligned} $ | (9) |
上述2项中等式右边首项为原始向量,第2项为原始向量经过傅里叶变换后的向量,第3项为原始向量的反转向量,尾项为第2项的反转向量。
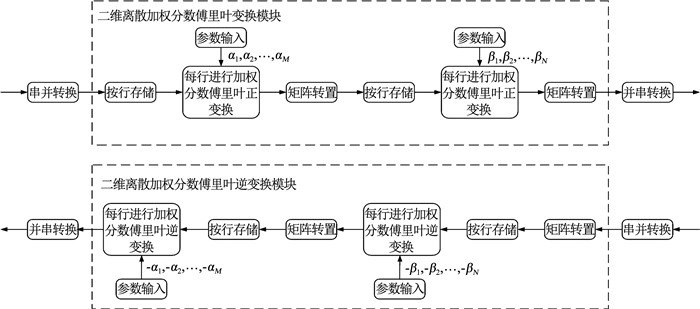
由于收发两端皆为合作方,共享变换参数,合法接收端可通过二维离散分数傅里叶逆变换进行解调恢复原始数据,流程见图 3,其中列与行的参数(β′与α′)分别为: β′=(-β1, -β2, -β3, …, -βN), α′=(-α1, -α2, -α3, …, -αM)。
|
图 3 2DWFRFT模块流程示意 Fig. 3 Schematic of 2DWFRFT modules |
需要注意的是,以任意向量参数(α与β)进行的2DWFRFT无矩阵表达式,只能以式(8)、(9)进行信号处理过程描述。但若每行与每列加权变换参数取值分别相同,即α1=…=αM=α,β1=…=βN=β时,2DWFRFT具有类似式(6)的简洁表达式,形如:
| $ \boldsymbol{k}=\left(\boldsymbol{F}^{\beta} \otimes \boldsymbol{F}^{\alpha}\right) \boldsymbol{x} $ | (10) |
式中
| $ \boldsymbol{x}=\left(\boldsymbol{F}_{N}^{-\beta} \otimes \boldsymbol{F}_{M}^{-\alpha}\right) \boldsymbol{k} $ | (11) |
在实际通信系统中,考虑硬件的时间资源消耗,通常采用浮点数乘法次数来衡量某种算法的实现复杂度。由文献[1]得知,一维4-WFRFT在系统实现时主要由FFT模块、反转模块及加权系数合并模块构成,其中FFT模块所需实现复杂度为O(N log N),四项加权系数合并模块所需实现复杂度为O(4N)。在忽略加法运算的前提下,对于具有维度M×N的矩阵信号,其进行一维WFRFT的计算复杂度为O(MN log MN+4MN),算法相应的计算自由度为Θ1D=M×N。二维分数傅里叶变换可表示成两次一维WFRFT的级联形式,其计算复杂度为O(MN log MN+8MN),计算自由度Θ2D=2MN,计算自由度带来2倍的提升,而计算自由度是衡量变换安全水平的标准之一[11];从安全性角度来说,当变换的计算自由度越大时,可为所在的信息系统提供越高的安全保障。以现在5G常规波形,调制子载波数目2 048为例,O(MN log MN+4MN)=30 720,O(MN log MN+8MN)=38 912,计算复杂度增加26%,计算自由度增加100%。而本文所提算法复杂度的提升不高,在现有系统中完全可以接受。
表 1为各主要模块所需复杂度对比,由表 1可见,本文算法相较于原一维加权算法以牺牲少量复杂度的代价换取安全性能的提升,后续将对其安全性能方面的收益进行定量分析。
| 表 1 信号实现复杂度对比 Tab. 1 Implementation complexity comparison of signals |
物理层安全作为目前一个基于香农理论扩展出的保密领域受到了越来越广泛的关注,其核心参数指标安全容量由香农定义。本节基于MISO窃听信道模型分析所提安全传输方案的安全容量。
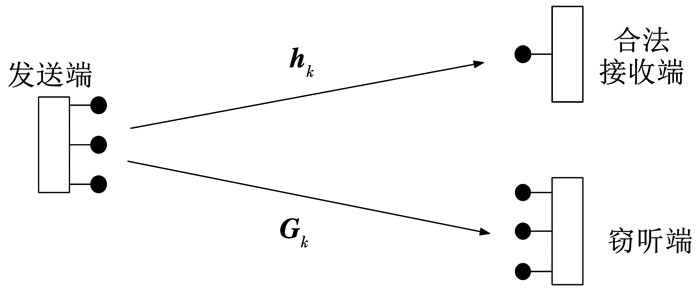
考虑如图 4所示的常规物理层MISO窃听信道模型,其中发送端(配置多天线)与合法接收端(配置单天线)通过合法信道hk进行通信,并且在发送端的广播范围内存在某个多天线窃听端对信号进行侦听,窃听信道表述为Gk;假设两信道均满足平坦瑞利衰落信道分布,且相互独立。令x表示合法端发送信息的基带符号映射,则合法接收端与窃听端接收信号模型可分别表示为:
|
图 4 基于2DWFRFT的MISO窃听信道模型 Fig. 4 2DWFRFT-based MISO wiretap channel model |
| $ y_{k}=\boldsymbol{h}_{k} \mathscr{\mathscr { F }}_{2 \mathrm{DWFRFT}}^{-\overline{\boldsymbol{\alpha}}, \overline{\boldsymbol{\beta}}}\left[x_{k}\right]+\boldsymbol{v}_{k} $ | (12) |
| $ \boldsymbol{z}_{k}=\boldsymbol{G}_{k} \mathscr{F}_{2 \text { DWFRFT }}^{-\overline{\boldsymbol{\alpha}}, \overline{\boldsymbol{\beta}}}\left[x_{k}\right]+\boldsymbol{e}_{k} $ | (13) |
其中υk~CN(0, σb2)及ek~CN(0, σe2INe)为方差σb2与σe2的零均值循环复高斯随机噪声。
这里直接考虑最坏的情况,即假设窃听端已知本文采用了2DWFRFT对信号进行加密,但具体变换参数未知,同时窃听端已知全局信道信息(即hk、Gk),则合法接收端与窃听端对源数据符号序列的解调信号分别为
| $ \begin{aligned} r_{\mathrm{B} k}=& \mathscr{F}_{2 \mathrm{DWFRFT}}^{-\overline{\boldsymbol{\alpha}},-\overline{\boldsymbol{\beta}}}\left[\boldsymbol{h}_{k}^{*} y_{k}\right]=\\ & \mathscr{F}_{2 \mathrm{DWFRFT}}^{-\overline{\boldsymbol{\alpha}},-\overline{\boldsymbol{\beta}}}\left[\left|\boldsymbol{h}_{k}\right|^{2} \mathscr{F}_{2 \mathrm{DWFRFT}}^{\overline{\boldsymbol{\alpha}}, \overline{\boldsymbol{\beta}}}\left[x_{k}\right]\right]+\boldsymbol{h}_{k}^{*} v_{k}=\\ &\left|\boldsymbol{h}_{k}\right|^{2} x_{k}+\boldsymbol{h}_{k}^{*} v_{k} \end{aligned} $ | (14) |
| $ \begin{aligned} r_{\mathrm{E} k}=& \mathscr{F}_{2 \mathrm{DWFRFT}}^{-\overline{\boldsymbol{\alpha}^{\prime}},-\overline{\boldsymbol{\beta}^{\prime}}}\left[\boldsymbol{G}_{k}^{*} z_{k}\right]=\\ & \mathscr{F}_{2 \mathrm{DWFRFT}}^{-\overline{\boldsymbol{\alpha}^{\prime}},-\overline{\boldsymbol{\beta}^{\prime}}}\left[\left\|\boldsymbol{G}_{k}\right\|_{\mathrm{F}}^{2} \mathscr{F}_{2 \mathrm{DWFRFT}}^{\overline{\alpha}, \overline{\boldsymbol{\beta}}}\left[x_{k}\right]\right]+\boldsymbol{G}_{k}^{*} e_{k}=\\ &\left\|\boldsymbol{G}_{k}\right\|_{\mathrm{F}}^{2} \mathscr{F}_{2 \mathrm{DWFRFT}}^{\Delta \overline{\boldsymbol{\alpha}}, \Delta \overline{\boldsymbol{\beta}}}\left[x_{k}\right]+\boldsymbol{G}_{k}^{*} e_{k} \end{aligned} $ | (15) |
根据文献[12],3点窃听模型下安全容量定义为主信道(合法收发两端)及窃听信道(发送与窃听两端)所能承载的最大互信息量之差:
| $ C_{\text {sec }}=\underset{{\boldsymbol h}_{k}, {\boldsymbol G}_{k}}{E}\left[\log _{2}\left(1+\gamma_{\mathrm{B}}\right)-\log _{2}\left(1+\gamma_{\mathrm{E}}\right)\right]^{+} $ | (16) |
式中:E[·]用于求取输入信号的均值期望,[·]+=max(·, 0),符号γB与γE分别为接收端以及窃听端处的信干噪比。在推导这两处的信干噪比时,为了方便书写参数差异,假设所有二维信号进行变换时行数与列数的加权阶数取值相同。
根据一维WFRFT的定义,参数匹配差异下的加权变换
| $ \begin{aligned} \mathscr{F}^{\Delta \alpha}\left[x_{k}\right]=& \omega_{0}^{\Delta \alpha} x_{k}+\omega_{1}^{\Delta \alpha} F\left[x_{k}\right]+\\ & \omega_{2}^{\Delta \alpha} F^{\prime}\left[x_{k}\right]+\omega_{3}^{\Delta \alpha} F^{\prime \prime}\left[x_{k}\right] \end{aligned} $ | (17) |
式中: F、F′、F″分别表示对原序列进行1~3次傅里叶变换; Δα=α-α′, Δβ=β-β′表示因加权参数保密性造成的窃听端与发送端参数匹配差异; ωpΔα满足如下等式:
| $ \begin{aligned} \omega_{p}^{\Delta \alpha}=& \omega_{0}(\alpha) \omega_{p}(\beta)+\omega_{1}(\alpha) \omega_{p+3}(\beta)+\\ & \omega_{2}(\alpha) \omega_{p+2}(\beta)+\omega_{3}(\alpha) \omega_{p+1}(\beta) \\ & p=0,1,2,3 \end{aligned} $ | (18) |
由式(18)可进一步推导
| $ \begin{aligned} \mathscr{F}_{2 \mathrm{DWFRFT}}^{\Delta \alpha, \Delta \beta}\left[x_{k}\right]=& \mathscr{F}_{\text {column }}^{\Delta \beta}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]=\\ & \omega_{0}^{\Delta \beta} \mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]+\omega_{1}^{\Delta \beta} F_{\text {column }}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]+\\ & \omega_{2}^{\Delta \beta} F^{\prime}{ }_{\text {column }}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]+\\ & \omega_{3}^{\Delta \beta} F_{\text {column }}^{\prime \prime}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right] \end{aligned} $ | (19) |
由式(17)可知,在一维加权分数傅里叶框架下,窃听端对原始数据的估算解调由4个子信号加权构成。当Δα≠0时,各信号分量之间相互干扰。因此,只有部分原始信号的能量被窃听端收集用于信息内容截获,而其余部分信号能量则以干扰形式存在。式(19)中的
而对于合法接收端而言,
| $ \gamma_{\text {Bob }}=\left\|h_{k}\right\|^{2} P_{0} / \sigma_{b}^{2} $ | (20) |
| $ \begin{aligned} \gamma_{\text {Eve }}=& \frac{E\left[\left\|\boldsymbol{G}_{k}\right\|_{\mathrm{F}}^{2} \cdot\left|\omega_{0}^{\Delta \alpha} \omega_{0}^{\Delta \beta} x_{k}\right|^{2}\right]}{E\left[\left|\left(\omega_{1}^{\Delta \beta} F_{\text {column }}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]+\omega_{2}^{\Delta \beta} F^{\prime}{}_{\text {column }}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]+\omega_{3}^{\Delta \beta} F^{\prime \prime}{}_{\text {column }}\left[\mathscr{F}_{\text {row }}^{\Delta \alpha}\left[x_{k}\right]\right]\right) \cdot\left\|\boldsymbol{G}_{k}\right\|_{\mathrm{F}}^{2}+\boldsymbol{G}_{k}^{*} \boldsymbol{e}_{k}\right|^{2}\right]}=\\ & \frac{\left\|\boldsymbol{G}_{k} \omega_{0}^{\Delta \alpha} \omega_{0}^{\Delta \beta}\right\|^{2} P_{0}}{\sigma_{e}^{2}+\left\|\boldsymbol{G}_{k}\right\|_{\mathrm{F}}^{2}\left(1-\left|\omega_{0}^{\Delta \alpha} \omega_{0}^{\Delta \beta}\right|^{2}\right) P_{0}} \end{aligned} $ | (21) |
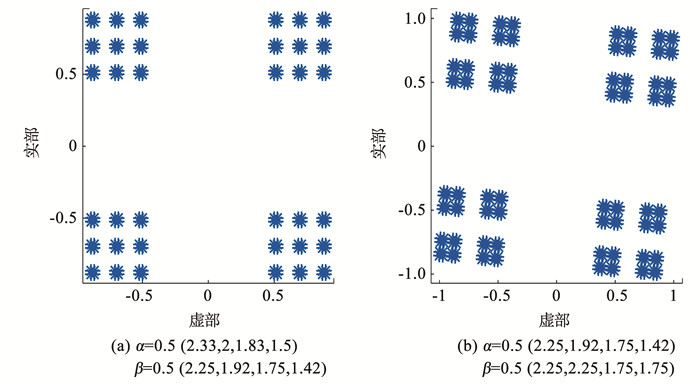
图 5是正交相移键控(quadrature phase shift keying, QPSK)调制信号经过一维多参数4-WFRFT变换后在分数域的星座图,可以看出一维变换具有将原星座点进行旋转、扩散的作用。仿真参数设置见表 2,其中vk为多参数加权变换系数因子;图 5(a)中星座分裂为9个星座团,而图 5(b)中可分裂为16个星座团。图 6则展示相同的QPSK信号在经过2DWFRFT后可进一步对星座进行旋转、分裂,在不同参数下星座团个数可分别扩展至36、64,突破原一维变换的星座点特征限制,这表明2DWFRFT方案在干扰非合作接收机检测星座方面可提供更丰富的星座特征。
| 表 2 各星座图变换参数 Tab. 2 Parameters selection under different constellations |

|
图 5 QPSK不同参数下WFRFT星座 Fig. 5 Constellation of WFRFT-QPSK signals under different parameter conditions |
|
图 6 QPSK不同参数下2DWFRFT星座 Fig. 6 Constellation of 2DWFRFT-QPSK signals under different parameter conditions |
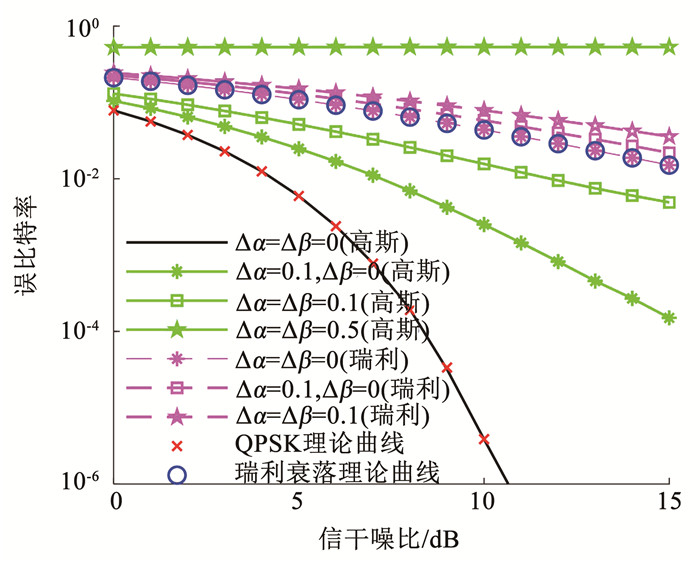
图 7是考虑在不同信道条件(高斯信道、平坦瑞利衰落信道)下,窃听端已知所采用的传输模式但解调参数有误差情况下的误码率(bit error rate, BER)性能曲线。其中信号采用QPSK调制,子载波个数为1 024,行向量与列向量的加权参数分别统一,并分别为0.1、0.5。当窃听端未知所采用的传输模式时,对接收信号直接解调的误比特率为0.5,即窃听端只能对数据序列进行随机猜测。合作接收端采用相应的参数能够进行正确解调并且误码率与理论曲线相重合。当假设窃听端已知所采用的传输模式并尝试进行搜索时,相比于单参数的WFRFT在15 dB下的安全性能表现,行向量与列向量参数只相差Δα=Δβ=0.1时,误码率就会由10-4恶化至10-2,足以证明其对参数的敏感性。
|
图 7 窃听端随Δα、Δβ变化误码率性能曲线 Fig. 7 BER performance of the eavesdropper with varying Δα, Δβ |
图 8以通信系统的安全容量作为评价指标对2DWFRFT物理层安全通信系统的安全性能进行分析。仿真中信道服从独立同分布瑞利衰落,且其信道增益满足hk~CN(0, 1),Gk~CN(0, INe),并假设合法接收端与窃听端处的噪声功率相同,即σe2=σb2。当窃听端天线数目为1时,2DWFRFT物理层安全通信系统由信噪比、Δα及Δβ决定。系统可达安全容量随信噪比的增加而单调上升,与此同时,相比于一维WFRFT单参数Δα的安全性能,引入Δβ后安全容量进一步提升,且提升部分的容量随Δβ增大而增加。

|
图 8 不同参数下2DWFRFT安全容量 Fig. 8 Secrecy capacity of 2DWFRFT under different parameter conditions |
图 9是2DWFRFT与文献[13]中人工噪声方法在安全性能上的对比,仿真中发射天线数固定为8,接收天线数设置为1、2、4、6且此时假设最坏情况,即窃听端噪声干扰为0 dB,人工噪声功率分配系数(即人工噪声功率与发射总功率占比)为0.5。由于受限于空间自由度,人工噪声方法的安全容量会随着窃听天线数增加而减小,这源于窃听信道容量随窃听端天线数目增加而增大;而此时本文所提方法由于不依赖信道零空间的提取,其安全容量在阶数差值较大时对窃听端天线数目具有鲁棒性,在不需要额外消耗干扰功率的条件下可以有效抑制窃听端对信息的获取,达到较高的安全可达速率。同时值得注意的是,2DWFRFT作为一种通用的基带数字信号处理方法,理论上可以与人工噪声方法结合使用。

|
图 9 2DWFRFT安全容量随窃听天线数Ne变化趋势 Fig. 9 Secrecy capacity of 2DWFRFT with varying Ne |
本文开展了2DWFRFT的研究,对一维单参数4-WFRFT进行了二维扩展,并将其应用于通信系统当中, 最后针对抗截获性能,在MISO窃听信道下对安全容量进行了定量分析。主要结论如下:
1) 2DWFRFT阶数由多个参数向量决定,相比一维WFRFT的单参数,在抗参数扫描方面具备机理优势。
2) 2DWFRFT可表示成两次一维WFRFT的级联形式,仅以部分计算复杂度的代价换来计算自由度的2倍提升。
3) 在变换后的星座图混淆方面,2DWFRFT可突破一维变换的分裂点数限制,提供更加丰富的星座变换特征。
4) 在安全性能方面, 与传统人工噪声方法相比,2DWFRFT方案不仅继承了一维变换不依赖信道特性、无需消耗额外干扰功率的优点,同时由于多参量的引入其安全容量可进一步提升。
| [1] |
MEI Lin, SHA Xuejun, RAN Qinwen, et al. Research on the application of 4-weighted fractional Fourier transform in communication system[J]. Science China Information Sciences, 2010, 53(6): 1251. DOI:10.1007/s11432-010-0073-1 |
| [2] |
LIN Xu, MEI Lin, FANG Xiaojie, et al. HCM successive transmission scheme with banded MMSE equalization based on fast convolution over doubly-selective fading channels[J]. IEEE Communications Letters, 2020, 24(2): 451. DOI:10.1109/LCOMM.2019.2954309 |
| [3] |
CHENG Qian, FUSCO V, ZHU Jiang, et al. WFRFT-aided power-efficient multi-beam directional modulation schemes based on frequency diverse array[J]. IEEE Transactions on Wireless Communications, 2019, 18(11): 5211. DOI:10.1109/TWC.2019.2934462 |
| [4] |
梁源, 达新宇. 基于多参数加权分数阶傅里叶变换的星座预编码系统研究与实现[J]. 电子与信息学报, 2018, 40(4): 825. LIANG Yuan, DA Xinyu. Analysis and implementation of constellation precoding system based on multiple parameters weighted type fractional Fourier transform[J]. Journal of Electronics & Information Technology, 2018, 40(4): 825. |
| [5] |
FANG Xiaojie, SHA Xuejun, LI Yong. Secret communication using parallel combinatory spreading WFRFT[J]. IEEE Communications Letters, 2015, 19(1): 62. DOI:10.1109/LCOMM.2014.2359200 |
| [6] |
FANG Xiaojie, ZHANG Ning, ZHANG Shan, et al. On physical layer security: Weighted fractional Fourier transform based user cooperation[J]. IEEE Transactions on Wireless Communications, 2017, 16(8): 5498. DOI:10.1109/TWC.2017.2712158 |
| [7] |
RAN Qiwen, ZHAO Tieyu, YUAN Lin, et al. Vector power multiple-parameter fractional Fourier transform of image encryption algorithm[J]. Optics & Lasers in Engineering, 2014, 62: 80. DOI:10.1016/j.optlaseng.2014.05.008 |
| [8] |
RAN Qiwen, YEUNG D S, TSANG E C C, et al. General multifractional Fourier transform method based on the generalized permutation matrix group[J]. IEEE Transactions on Signal Processing, 2005, 53(1): 83. DOI:10.1109/TSP.2004.837397 |
| [9] |
SHIH C C. Fractionalization of Fourier transform[J]. Optics Communications, 1995, 118(5/6): 495. DOI:10.1016/0030-4018(95)00268-D |
| [10] |
HSUE Wenliang. Enhancing security of double random phase encryption schemes based on discrete fractional Fourier transforms[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 66(9): 1602. DOI:10.1109/TCSⅡ.2018.2889968 |
| [11] |
YOUSSEF A M. On the security of a cryptosystem based on multiple-parameters discrete fractional Fourier transform[J]. IEEE Signal Processing Letters, 2008, 15(1): 77. DOI:10.1109/LSP.2007.910299 |
| [12] |
SHANNON C E. Communication theory of secrecy systems[J]. The Bell System Technical Journal, 1949, 28(4): 656. DOI:10.1002/j.1538-7305.1949.tb00928.x |
| [13] |
ZHOU Xiangyun, MCKAY M R. Secure transmission with artificial noise over fading channels: Achievable rate and optimal power allocation[J]. IEEE Transactions on Vehicular Technology, 2010, 59(8): 3831. DOI:10.1109/TVT.2010.2059057 |
 2022, Vol. 54
2022, Vol. 54


