2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
光学遥感目标检测是光学遥感图像处理领域中的一项基础性研究工作[1-2]。在光学遥感目标检测中,目标尺度的巨大差异一直是阻碍模型精度提升的一大因素。例如大片的操场和道路旁的小汽车,操场的尺度是汽车的几十倍甚至几百倍,同时兼顾二者的特征提取较为困难。随着多层神经网络提取的特征不断丰富,多尺度目标的检测精度已经获得了大幅提升。而这些精度的提升依赖于以浮点型运算为主的高计算量卷积神经网络。为了实现将检测模型部署于边缘端(如搭载图像处理功能的卫星终端)的任务,研究人员需提前量化浮点型算法以适应可编程门阵列(field programmable gate array, FPGA)、专用集成电路(application specific integrated circuit, ASIC)等平台。量化是将参数值(Weight)和激活值(Activation)从浮点型数据转化为定点型的过程。Krishnamoorthi[3]给出了关于量化及反量化的具体方式和步骤。
现阶段,算法在FPGA端的推断部署过程为:首先,在CPU/GPU端训练算法并量化;之后,导出必要的参数值;然后,在FPGA端设计模型的IP核并搭建系统框架;随后,在CPU端设计交互窗口,控制调用FPGA端程序;最后,输入图片并输出结果。对于量化的研究多集中于在CPU/GPU端的量化算法的研究。然而,由于CPU/GPU和FPGA平台资源情况不同,在FPGA端实际部署时会存在精度下降的现象,主要有以下3点原因:
首先,在大量量化算法的文献中,模型量化时的缩放系数常保持浮点类型[4],而FPGA属于全定点计算。因而对缩放系数的量化时,若将超过规定量化范围的数据直接截断[5]会造成大量精度损失。
其次,不同平台适用的数据类型及精度不同。现阶段算法训练及推断中常用PyTorch框架。由于该框架没有低比特定点数据类型,须用浮点数进行伪量化,会造成CPU模拟量化结果与FPGA不同。
最后,网络架构设计的差异。在训练时,卷积层和激活层是无关联的两个独立层。但FPGA要求卷积运算输出定点值结果,即激活值需要量化为下层卷积层可直接参与卷积运算的定点数。
以上3点原因为平台转换过程中的主要不匹配因素。基于此,本文提出在硬件层面实现每层可控的系数调节卷积层的方法,即分段量化整体缩放系数,以充分利用定点数的表达范围,实现在FPGA端高精度地部署检测网络。
由于待检测图像的尺寸偏大,检测模型的计算量庞大,而边缘端设备资源稀少,整幅图像难以完整进行一次卷积运算,因而在边缘端需要切割图片并分块进行卷积计算。而这些步骤无疑造成了检测速度减慢。再加上检测模型存在图像预处理和后处理步骤,这些步骤在硬件部署中常被分配在CPU端完成。CPU端主要负责计算量少的部分,而对于基于候选框的算法[6]来说,其后处理含有复杂的非极大值抑制(non-maximum suppression,NMS)操作,会导致检测时间拉长。因此,本文使用无预选框模型CenterNet[7]的检测流程来设计部署算法。这种无预选框模型的后处理过程摒弃了NMS操作,更适合于实际部署。而为了提高检测速度,本文考虑将检测流程中的图片预处理及后处理等耗时计算过程从串行的CPU端(本文采用ARM处理器)移入并行的FPGA中,从而缩减了总处理时长。为快速便捷地实现异构系统搭建,本文采用了Python productivity for ZYNQ (PYNQ)框架,即为ZYNQ系列硬件平台提供Python接口的一种软件开发框架。ZYNQ的硬件本质为ARM与FPGA的异构系统。基于该框架,研究人员可通过Python轻松访问FPGA,利于算法的快速开发应用。
综上所述,为在边缘端快速高精度地部署检测模型,本文提出了在卷积核中分段量化整体缩放系数的方法,并充分考虑了检测模型中预处理和后处理的并行化因素,缩短了检测时间。实验证明本文所提方法具备检测精度高、部署简单、推断时间快等特点。
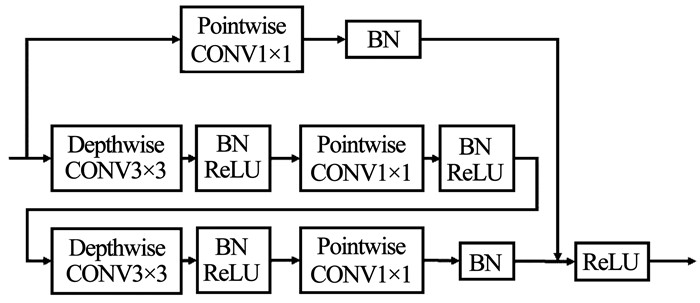
1 CTiny网络结构及PYNQ设计概述 1.1 CTiny模型结构介绍本文的检测模型基于CenterNet检测框架而得, 该检测模型将目标视作点,适合于多尺度目标检测。本文采用的CTiny模型的主干网络为ResNet_9[8],其中的卷积运算和反卷积运算均采用分离卷积,ResNet中的Residual模块的详细流程见图 1。
|
图 1 Residual模块的详细流程 Fig. 1 Detailed process of Residual module |
为实现卷积层的高复用性,将卷积核大小统一为3×3、1×1和4×4。网络中的卷积模块按照功能分为普通分离卷积(Depthwise Convolution3×3, DW)、分离反卷积(Depthwise Deconvolution4×4, DDW)以及点卷积(Pointwise Convolution1×1, PW)。
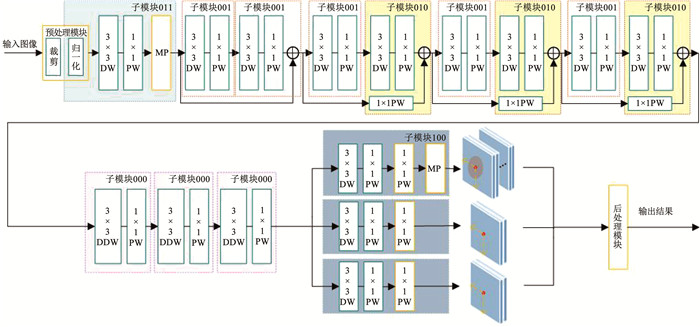
1.2 基于PYNQ的子模块设计由于CTiny网络结构较复杂,以及输入图片的分辨率较大,将网络所有层放在FPGA上处理并不现实。因此,本文需根据资源使用情况及模块复用性,对网络进行模块划分。这里共划分为5个模块见表 1,其中ADD代表ResNet网络中的直连层相加操作,MP指最大池化操作。本网络的整体架构见图 2。
| 表 1 子模块划分 Tab. 1 Submodule division |
|
图 2 CTiny整体网络架构 Fig. 2 Overall network architecture of CTiny |
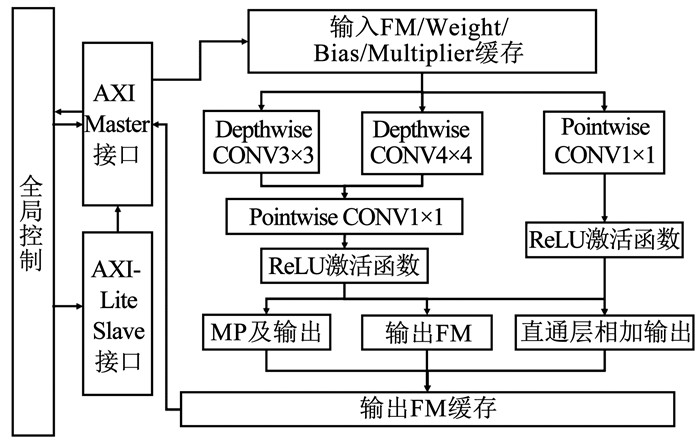
鉴于板上资源的限制,每个子模块的处理流程为:首先,从AXI总线读取特征图和参数值并传入处理寄存器,由于图片尺寸较大,读取待处理数据的过程需重复多次; 然后,进行DW或DDW操作,循环处理每个通道的特征图,并通过AXI总线传入总缓存; 待到所有通道处理完毕,再从总缓存中传回特征图缓存值,并将所有通道的值累加以完成一次PW运算; 最后,将处理完毕的数据通过AXI总线传回ARM端。至此完成了一次完整的子模块处理流程。本文的CTiny模型在FPGA上的总体网络模型设计见图 3,其中FM代表特征图。
|
图 3 基于FPGA的总体网络模型设计 Fig. 3 Overall network model design based on FPGA |
本文所提的分段量化整体缩放系数的方法主要应用于卷积层内。Weight量化中每个卷积核独享一个量化缩放系数,Activation量化则是每层中所有卷积核共享一个量化缩放系数。
设第i层激活值浮点数为Ai,第i+1层的激活值为Ai+1。相对应地,参与FPGA中MAC运算的量化激活值为Ai及Ai+1,这里采用对称量化,激活值的量化比特数为NA,该过程如下:
| $ A_{i}=\overline{A}_{i} \times S_{i}^{A} $ | (1) |
式中
设参数值的量化比特数为Nw,量化系数为Si, jW, 其中下标i指第i层卷积,下标j代表卷积的第j个通道。则该层中的不同通道的卷积量化过程如式(2)所示,其中H和W为卷积核的高和宽。
| $ \begin{aligned} \overline{A}_{i+1, j} \times S_{i+1}^{A}=& \sum\limits_{H} \sum\limits_{W}\left(\overline{A}_{i, j, h, w} \times S_{i}^{A}\right) \times \\ &\left(\overline{W}_{i, j, h, w} \times S_{i, j}^{W}\right)+b_{i} \end{aligned} $ | (2) |
再将式(2)传入批量归一化层(batch normalization,BN),γ为BN层的缩放系数,β为偏移,μ为批量数据的均值,σ为标准差。将BN层融入卷积层的过程见式(3),可保证一次卷积运算直接得到下一层的量化输入值。
| $ \overline{A}_{i+1, j}=M \times\left(\sum\limits_{H} \sum\limits_{W} \overline{W}_{i, j, h, w} \overline{A}_{i, j, h, w}+B\right) $ | (3) |
式中:
这里先叠加B的原因是可以提前一步确定计算结果是否比零小,比零小的数据不再进行乘M的计算,更节约计算成本。本文以有符号的16 bit的定点数表示两种系数,其中M为远小于1的小数,因此需要将其量化为[-215, 215-1]。而为了不消耗MAC资源,采用左/右移操作来实现两种缩放系数的反量化。
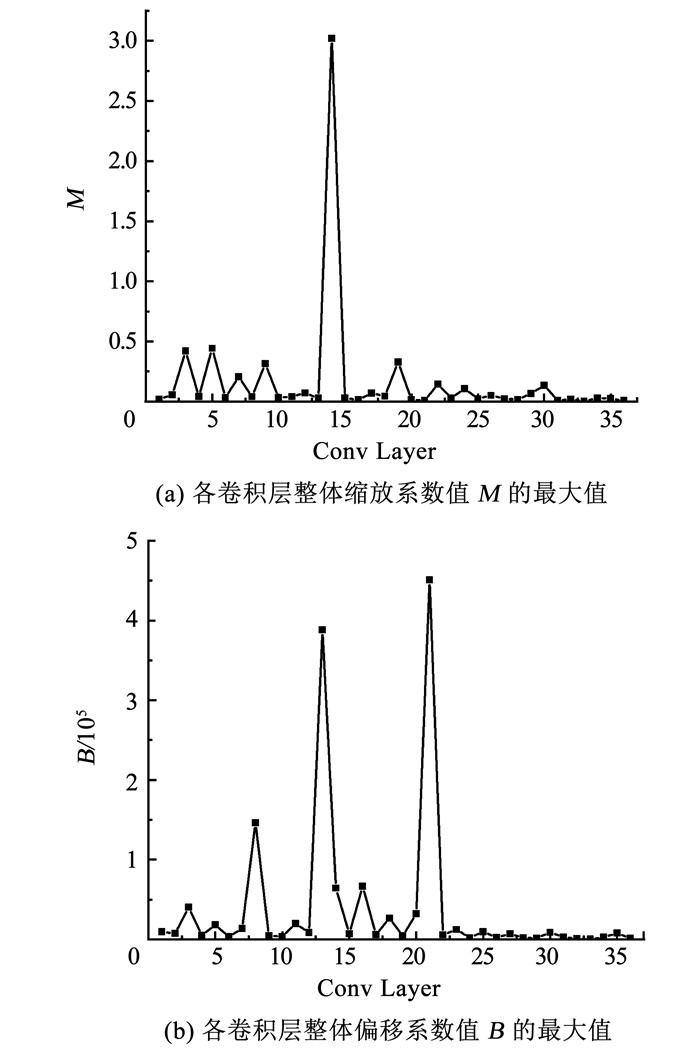
本文所用检测网络的卷积层包含卷积运算和反卷积运算,其中卷积层进行图片尺度的缩小,而反卷积层实现图片尺度的扩大,最终输出高分辨率热点图,输出尺寸为原始图片的1/4。图 4(a)和(b)分别为各层卷积激活值的整体缩放系数及整体偏移系数的最大值统计图。横坐标为各卷积层的索引值,纵坐标分别为整体缩放系数值和整体偏移系数值。不同层的整体缩放系数最大相差1 000倍,而整体偏移系数相差4 000倍。Zhang等[5]将二者每层缩放固定值但不影响最终效果,原因是该工作的检测目标呈现尺度相似的特点,且检测网络的卷积层较为规整,不包含ResNet的直连层。但面对本文这种背景复杂、目标尺度差异大的检测图像,包含直连层的检测网络才能得到较好的检测精度。为了使本设计具有更强的易迁移性和通用性,提出分段量化整体缩放系数。
|
图 4 各卷积层的M和B的统计图 Fig. 4 Statistical graphs of M and B of each convolutional layer |
由上述可知,M的值极小而B的值极大。部署时需要将其通过线性运算分布于[-215, 215-1]。为了使缩放系数有较大的表达范围,本文将分段量化方式细分为分块量化和逐层量化。分块量化需要设置块数为R,而逐层量化则为每一层卷积设置不同量化系数,R为层数。设某一段每个卷积层整体缩放系数为M,其定点数为M,M的右移位数为KM,偏移系数B的左移位数为KB,这样B可获得较大分布范围,对于检测大尺度目标效果显著。为了经过四舍五入后与浮点数更接近,需叠加一个常量G,且G=Sleft(1, KM-1)。这里算法的参数值存储需要配合该硬件的改进。则该段的计算过程为
| $ \begin{aligned} &Y=S_{\text {right }}\left(\overline{M} \times\left[X+S_{\text {left }}\left(B, K_{B}\right)\right]+G, K_{M}\right) \\ &\text {s. t. } \min \sum\limits_{R}\left(\left|\operatorname{round}\left(S_{\text {left }}\left(M, K_{M}\right)\right)-\overline{M}\right|\right) \end{aligned} $ | (4) |
其中Sleft(·)为左移运算,Sright(·)为右移运算。
2.2 CTiny检测模型的系统搭建 2.2.1 卷积层设计PYNQ-Z2开发板的资源无法处理整幅图片,因此需将图像分割为片上能处理的最小处理单元[9-10]。因FPGA中计算资源的限制,需在输出通道数、特征图长度及宽度3个维度进行循环展开,分块进行卷积运算[11-12]。本文主要设计方式与Zhang等[5]保持一致,将特征图在宽高维度作为循环展开的外层循环,通道维度作为内层循环,由此可实现特征图在通道维度的并行计算。
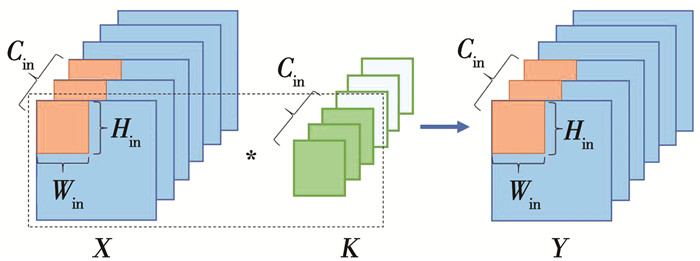
这里主要介绍DW及PW的分块处理流程。DW的处理流程见图 5。本文将Weight通过AXI总线传入片上缓存区域,并转换为所需的三维结构。设所需处理的特征图为
|
图 5 DW卷积分块处理流程 Fig. 5 Block processing flow of DW convolution |
PW模块的设计与DW类似。由于PW负责各通道的加权操作,不涉及宽高维度,因此对于步长为2的情况,本文只存储真正参与卷积运算的数值,实现提前间隔采样,避免了存储资源的浪费。
2.2.2 非对称填充及下采样拼接在进行卷积操作之前,需要从总线中读取所需要的数据,并组合成为片上能处理的最小单元,将该过程定为Load_IMG。为了提高资源利用率,Load_IMG需令特征图的缓存满足所有子模块的需求,即包含两次下采样卷积(步长为2以及最大池化操作)、一次下采样卷积、无下采样卷积和反卷积。
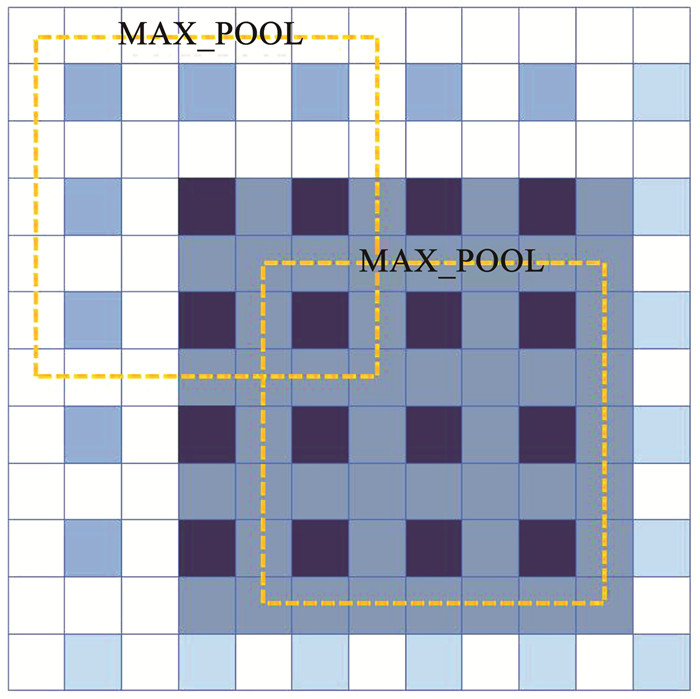
这里主要考虑两次下采样卷积的情况。本文提出一种左右非对称填充方法,即在图像左上侧补充3个像素点,右下侧补充1个像素点。该过程的详细介绍见图 6。设图中输入图片大小为8×8,如阴影所示,左边填充3,右边填充1后,得到12×12的图片。进行第一次卷积操作后,得到6×6的图片大小(浅蓝色像素点)。之后进行最大池化操作(图中的MAX_POOL),便可得到预期的2×2的图片。而对比于通常意义上的左右对称填充(需要左右各填充3个像素点),可以减小缓存的图片尺寸,从而降低计算资源。
|
图 6 非对称填充方法 Fig. 6 Asymmetric padding method |
为方便操作,本文采用下采样拼接的方法解决DW中卷积步长为2的情况。该步骤将4个片上处理单元视为一组,设置输出坐标点的分块位置,每输入完一组图片(4张)便可得到原始图片大小,便于后续的存储和读取。
2.3 图片预处理及后处理的FPGA设计 2.3.1 图片预处理的FPGA设计本文采用的输入图像为8 bit存储的RGB三通道数据。常见的检测算法需要先对图片进行数值归一化,得到正负皆有的正态分布数据。而在部署过程中,该步骤存在一定的困难: 其一,FPGA中的特征图为无符号的8 bit定点数,若将归一化后的原始图像通过均匀量化转为[0, 255]之间,会产生放缩和偏移量,在硬件设计中无多余模块进行输入数据的反量化处理,而开辟新的模块会造成资源浪费; 其二,两次转换会造成较大的精度损失。因此,本文考虑在Load_IMG步骤中融入归一化操作。
设原始输入图像为X0,数据集均值为
| $ X=\left(\frac{X_{0}}{255}-\mu_{\text {data }}\right) \times \frac{1}{\sigma_{\text {data }}}=\frac{X_{0}}{255 \times \sigma_{\text {data }}}-\frac{\mu_{\text {data }}}{\sigma_{\text {data }}} $ | (5) |
数据归一化后经过卷积层和BN层后的结果如式(6)所示:
| $ \begin{aligned} A_{i+1, j}=& \frac{\gamma}{\sqrt{\sigma^{2}+\varepsilon}} \times\left[S_{i, j}^{W} \sum\limits_{H} \sum\limits_{W} \overline{W}_{i, j, h, w}\left(\frac{{\bar x}_{i, j, h, w}}{255 \cdot \sigma_{\text {data }}}-\frac{\mu_{\text {data }}}{\sigma_{\text {data }}}\right)\right]+\\ & \frac{\gamma}{\sqrt{\sigma^{2}+\varepsilon}} \times S_{i}^{A} S_{i, j}^{W}\left(\beta \frac{\sqrt{\sigma^{2}+\varepsilon}}{\gamma}-\mu+b_{i}\right) \end{aligned} $ | (6) |
与式(3)对照可得
| $ \begin{aligned} A_{i+1, j}=& \frac{\gamma S_{i, j}^{W} S_{i}^{A}}{\sqrt{\sigma^{2}+\varepsilon}} \times \sum\limits_{H} \sum\limits_{W} \overline{W}_{i, j, h, w} \overline{x}_{i, j, h, w}-\\ & \frac{\gamma S_{i, j}^{W} S_{i}^{A}}{\sqrt{\sigma^{2}+\varepsilon}} \times 255 \times \mu_{\text {data }} \times \sum\limits_{H} \sum\limits_{W} \overline{W}_{i, j, h, w}+\\ & \frac{\gamma S_{i, j}^{W} S_{i}^{A}}{\sqrt{\sigma^{2}+\varepsilon}} \times S_{i}^{A} S_{i, j}^{W}\left(\beta \frac{\sqrt{\sigma^{2}+\varepsilon}}{\gamma}-\mu+b_{i}\right) \end{aligned} $ | (7) |
| $ I=-255 \cdot \mu_{\mathrm{data}} \cdot \sum\limits_{H} \sum\limits_{W} \overline{W}_{i, j, h, w} $ | (8) |
其中I是与输入数据无关的常数,其只与通道有关,因此可以提前计算出输入3个通道的数值,并将其视为整体偏移系数的一部分。
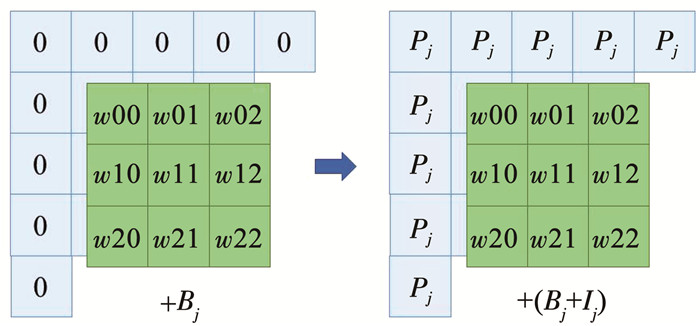
归一化处理时,载入图像Load_IMG过程中需要对原始图像进行补零操作。因为算法层面是在归一化之后补零,而本文所提硬件方法是在归一化之前补零。当按照上述的输入层归一化融合操作后,硬件层面补充的零值相当于实际运算中多余偏移值P。因此本设计将补充值按照不同通道分别补充P=255×μdata,代替以往的零值。该过程见图 7,其中j代表第j通道,Bj为原始的整体偏移系数。
|
图 7 输入层融合归一化操作 Fig. 7 Input layer integrating normalization operations |
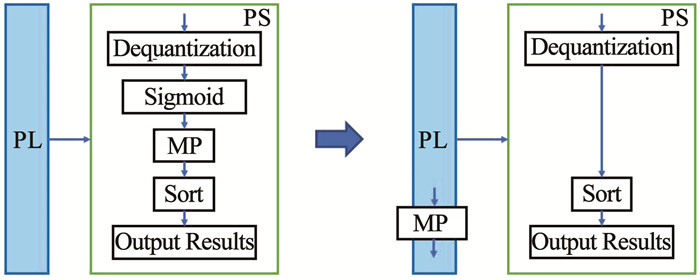
CTiny网络输出结果为高分辨率的热点图,并通过最大池化的方法找到一定区域内的最大值,以此确定目标的位置。最大池化操作在串行的ARM端运行极为缓慢,因此本文考虑将算法中的最大池化操作和Sigmoid操作调换顺序,在FPGA端处理MP,以此可大大降低预测时间。因图像处理结果输出值大于0等同于Sigmoid操作输出值大于0.5,所以FPGA端的MP操作可提前筛选掉分类概率小于0.5的目标。如图 8所示,PS指ARM端,PL指FPGA端。将MP操作提前后,Sigmoid操作可在后续处理过程中省去。因后续已经确定目标出现位置,只需将宽、高和偏移量提取出即可,此举可极大地节约检测时间。
|
图 8 最大池化的PL融合过程 Fig. 8 Process of integrating the Max Pooling into PL |
本文所用开发平台为PYNQ-Z2开发板。该开发板采用PYNQ框架,基于Xilinx ZYNQ-7000的FPGA平台,支持用户在ARM端(PS端)进行Python编程及调试。用户设计的电路模块运行于FPGA端(PL端),可作为IP核供PS端调用。PS端采用ARM Cortex-A9,运行频率为650 MHz,PL端工作频率为100 MHz,FPGA型号为xc7z020clg400。设置AXI传输带宽为128位,片上处理中的Hin和Win均为36,并行通道处理数Cin为16。参数值为8位传入,实际计算时只考虑6位。鉴于硬件部署时间周期过长,本文首先采用高层次综合(high level synthesis,HLS)的方式快速构建设计架构[13],并由软件端将C语言直接转换成适合的硬件描述语言,以构建无预选框检测模型的IP核;其次,在Vivado软件搭建异构系统整体框架;最后,在ARM端通过Python调用numpy、time、PIL等软件库,通过编程控制检测系统的输入输出及内存分配。
CTiny输出的检测结果为定位热点图、回归热点图和中心偏移热点图。定位热点图的处理较为复杂,需要首先在ARM端进行各像素点的Sigmoid函数处理,之后对各点排序,在前K个目标点(文中K取64)中挑出预测值大于0.5的点,获得其二维坐标索引; 之后,根据索引值在回归热点图和偏移热点图中分别得到坐标索引对应的宽高值和偏移值; 最后,经过目标中心点叠加偏移和宽高值后,可输出最终预测目标框的数值。
按照前文的模块划分,简化后的CTiny网络的详细结构见表 2。最后三层均为检测分支,特征图大小不发生改变。检测分支网络的中间输出通道数为64。
| 表 2 CTiny网络结构 Tab. 2 Structure of CTiny network |
本实验中数据集采用公开的光学遥感数据集NWPU VHR-10[14]。NWPU VHR-10有标注信息的图像650张,共包含10类目标,分别为:飞机、舰船、油罐、棒球场、网球场、篮球场、田径场、港口、桥梁和车辆。本文只采用包含目标的图像进行训练。对数据集进行裁剪处理,裁剪后图像尺寸为640×640,两张相邻图像的重叠像素点为140。经线性变换后,输入网络的图像尺寸为512×512。将裁剪后数据集的20%作为测试集。从各类中随机挑出两张作为可视化测试图片,用以检测输出检测标记框是否准确。
本文采用的检测指标为所有类别的平均检测精度的均值(mean average precision,mAP)。首先,本文中检测算法设置一张图中检出目标数最多为64;其次,在64个候选目标框中挑选其中与真实目标框的交并比大于0.5的框,并认为这些预测框检测到了目标。交并比(intersection over union,IoU)是两个候选框之间的交集与并集的比值,其公式如式(9)所示:
| $ I_{\mathrm{ou}}=\frac{P_{\mathrm{R}} \cap G_{\mathrm{T}}}{P_{\mathrm{R}} \cup G_{\mathrm{T}}} $ | (9) |
式中PR为预测目标框,GT为真实目标框。然后,计算预测目标中每类的平均精度(AP),即Precision-Recall曲线下的面积。其中准确率(Precision)是指被预测为正样本中的真实正样本的比例,而召回率(Recall)指被预测为正样本占所有真实正样本的比例。最后,通过求取AP的平均值得到本算法的mAP值,mAP值越高,检测性能越好。
3.3 实验结果 3.3.1 检测精度为验证本文所提方法的有效性,本文评估了全浮点数检测网络RICAOD[15]和Yolo-v2[16],以及定点数检测网络CTiny、CTiny_cut、CTiny_block和CTiny_piece基于NWPU VHR-10数据集的平均检测精度,并详细对比了各类别的平均精度。表 3为各模型参数对比,表 4为精度对比结果。表 3中的32 bit指浮点数,其余为量化的定点数位宽。其中的RICAOD基于平台NVIDIA TITAN X GPU,Yolo-v2和CTiny基于NVIDIA GTX 1080 GPU,而FPGA平台均为Xilinx ZYNQ。表中RICAOD和Yolo-v2网络作为对比模型,二者均为基于预选框的检测模型,生成不同尺度、不同长宽比的候选框以匹配目标,反映了现阶段基于NWPU VHR-10数据集的基本检测水平。RICAOD的主干网络为AlexNet的改进版,由于采用了全连接层而导致参数量较大。Yolo-v2的主干网络为DarkNet-19。从表 4可以看出,与两个浮点型检测模型的效果对比,无预选框检测模型CTiny基本可以满足检测精度需求,虽然主干网络只有9层完整卷积(共18层分离卷积),参数值和激活值也分别量化为了6 bit和8 bit,但其平均检测精度达到了89.08%。
| 表 3 不同模型的参数对比 Tab. 3 Parameter comparison of different models |
| 表 4 VHR-10数据集的平不同模型在NWPU均检测精度对比 Tab. 4 Comparison of mean average precisions of different models on NWPU VHR-10 dataset |
在FPGA端实现时,需将卷积层、归一化层、激活层合并为一层,参数的表征形式从浮点数变为全定点数,这会导致模型的检测精度大幅降低,如表 4中CTiny和CTiny_cut两列数据所示,侧面反映出同一模型在两个平台转换的不匹配。经前文分析,可通过M和B的量化方式提升模型性能。因此,采用直接截断、分块量化和逐层量化的方式处理M和B,结果如表 4中CTiny_cut、CTiny_block和CTiny_ piece所示,其中截断操作采取整体缩放系数值扩大214的结果。通过结果可以看出,直接截断的方法CTiny_cut效果最差,分析是因为大量削减了数值中的大数,而这些大数往往是决定检测效果的关键数据。CTiny_block取折中的方法,分析每层量化系数和偏置的数值,统计它们的分布范围,最终将其划分在4个区域块中。CTiny_block综合考虑了所有层的量化系数和偏置的影响,有效提高了检测效果。而针对每层系数均做处理的CTiny_piece则进一步提高了该小型定点网络的检测性能,其平均检测精度相比CTiny_cut和CTiny_block分别提高了14.27%和2.63%,证明了本文所提高放缩的分段量化整体缩放系数的有效性。
3.3.2 前向推断时间考虑到不同型号的FPGA开发板对同一个检测模型的执行性能相差很大,尤其是在部署较深网络时,硬件的时钟频率、资源大小等均会影响硬件的布局布线和运行时间。因此,本文采取在同一块开发板上运行Yolo-v2和CTiny。二者实验的操作流程基本一致,均采用在PL端进行一次完整的卷积运算(一次普通卷积或两次分离卷积)之后将数据传回PS端,然后进行下一次卷积运算。结果显示,本设计在较低的时钟频率上,依旧可达到较快的检测速率。
从表 4的实验结果可以看出在FPGA端提前进行MP处理对时间提升的有效性。其中,图像预处理时间指图片从SD卡中读取并载入内存中的总时长。后处理时间是指FPGA输出的结果经PS端计算得出目标框位置的总时长。图像处理时间指图片从输入PL端到输出的总用时,而FPGA时间指FPGA中的所有层的总时间,二者相减即可得到PS端的寄存器赋值寻址等操作所用时长。CTiny_piece和CTiny_block均为在PL端实现MP操作,而CTiny_ piece(woMP)的Sigmoid函数和MP操作均在PS端实现。由表 5可以看出CTiny_piece(woMP)的后处理时间长达9.228 s,远远不能达到实际需求; 而将Sigmoid操作省去,在FPGA端提前处理MP则将后处理时间控制在0.24 s,极大地减少了后处理时间,而FPGA端时间仅增加了0.008 s,证明了本设计的有效性。
| 表 5 基于PYNQ-Z2开发板的前向推断时间 Tab. 5 Inference time based on PYNQ-Z2 development board |
由于Yolo模型是基于预选框的检测模型,其后处理中的NMS操作涉及到大量数据的循环比较操作,从表 5中可看出FPGA的耗费时间较长。而本文的无预选框模型不需NMS操作,耗费时间的操作为MP及索引操作,只需一次排序,因此采用本文的MP提前实现的操作后,可显著缩减后处理时间。
同时表 5比较了Yolo-v2的处理时间,可以看出片上资源过少对检测时间的限制较大。Yolo-v2的FPGA端处理时间已经达到了1.13 s。因为FPGA板资源过少,不得不进行模块划分。频繁与ARM端通信以及数据的复制、组合、移动、读取、写入等操作会大量增加处理时间。
3.3.3 FPGA资源占用率CTiny网络在FPGA部署的资源占用情况见表 6。为了充分利用计算资源,本文设计的复合卷积IP核对DSP的利用率达到了100%。因本文设计中大量采用了HLS中的循环展开操作,因此对查找表(LUT)的使用率较高,达到了86%左右。因为分层量化更为复杂,故CTiny_piece的资源占用率相较CTiny_block有大幅增多,运行功率也增加了0.016 W。
| 表 6 FPGA资源耗费 Tab. 6 FPGA resource consumption |
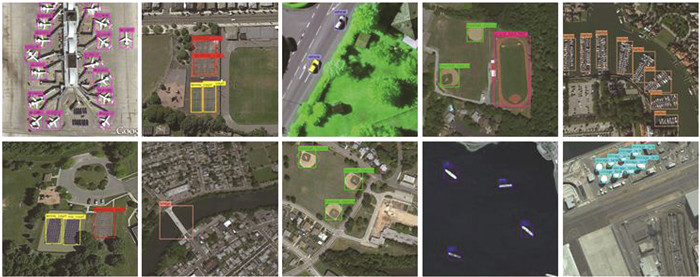
为更直观地验证检测效果,图 9是每个类别的可视化检测结果。结果显示,本设计完成了基于PYNQ框架的CTiny网络实现,并达到了较高的检测精度。
|
图 9 基于PYNQ的CTiny的可视化检测效果图 Fig. 9 Visual detection results of CTiny based on PYNQ |
本文基于PYNQ框架实现了无预选框检测模型CTiny的IP核设计及异构系统架构部署,主要结论如下:
1) 本文提供了可分离卷积层的FPGA实现,并提出了分段量化整体缩放系数的方式,可供CPU/GPU端训练的算法高效低损地部署于FPGA上,提高了部署后的检测精度。
2) 设计了一套基于PYNQ框架的无预选框检测网络CTiny的异构系统架构,可实现卷积运算、反卷积运算、批量归一化处理、激活函数、ResNet直连层等功能。
3) 本文充分考虑图片预处理及后处理的并行性,将两个过程中的耗时计算从串行的ARM端移入并行的FPGA中,有效缩短了图像的总检测时长。
实验结果反映出本文所提设计的有效性,为预训练的检测算法在FPGA上部署提供了实验基础,具备较为广泛的应用前景。
未来将结合现阶段的模型部署方式,兼从内存访问、带宽等多方面对系统做整体优化和改进,并使用资源更为丰富的FPGA开发板,以提高模型的总体检测速率。
| [1] |
LU Xiaoyan, ZHONG Yanfei, ZHENG Zhuo. A novel global-aware deep network for road detection of very high resolution remote sensing imagery[C]//2020 IEEE International Geoscience and Remote Sensing Symposium. Waikoloa: IEEE, 2020: 2579. DOI: 10.1109/IGARSS39084.2020.9323155
|
| [2] |
DONG Zhipeng, WANG Mi, WANG Yanli, et al. Object detection in high resolution remote sensing imagery based on convolutional neural networks with suitable object scale features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 2104. DOI:10.1109/TGRS.2019.2953119 |
| [3] |
KRISHNAMOORTHI R. Quantizing deep convolutional networks for efficient inference: A whitepaper[Z]. arXiv: 1806.08342. 2018[2021-07-06]. https://arxiv.org/pdf/1806.08342
|
| [4] |
JACOB B, KLIGYS S, CHEN Bo, et al. Quantization and training of neural networks for efficient integer-arithmetic-only inference[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 2704. DOI: 10.1109/CVPR.2018.00286
|
| [5] |
ZHANG Xiaofan, HAO Cong, LU Haoming, et al. SkyNet: A champion model for DAC-SDC on low power object detection[Z]. arXiv: 1906.10327. 2019[2021-07-06]. https://arxiv.org/abs/1906.10327
|
| [6] |
REDMON J, FARHADI A. YOLO9000: Better, faster, stronger[C]// Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Honolulu: IEEE, 2017: 6517. DOI: 10.1109/CVPR.2017.690
|
| [7] |
ZHOU Xingyi, WANG Dequan, KRÄHENBVHL P. Objects as points[Z]. arXiv: 1904.07850, 2019[2021-07-06]. https://arxiv.org/abs/1904.07850
|
| [8] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770. DOI: 10.1109/CVPR.2016.90
|
| [9] |
MELONI P, DERIU G, CONTI F, et al. A high-efficiency runtime reconfigurable IP for CNN acceleration on a mid-range all-programmable SoC[C]//Proceedings of 2016 International Conference on ReConFigurable Computing and FPGAs (ReConFig). Cancun: IEEE, 2016: 1. DOI: 10.1109/ReConFig.2016.7857144
|
| [10] |
LIU Ye, WANG Yin, CHANG Liang, et al. A fast and efficient FPGA-based level set hardware accelerator for image segmentation[C]//Proceedings of 2020 IEEE International Conference on Integrated Circuits, Technologies and Applications(ICTA). Nanjing: IEEE, 2020: 61. DOI: 10.1109/ICTA50426.2020.9331957
|
| [11] |
MA Yufei, CAO Yu, VRUDHULA S, et al. Optimizing the convolution operation to accelerate deep neural networks on FPGA[J]. IEEE Transactions on Very Large Scale Integration Systems, 2018, 26(7): 1354. DOI:10.1109/TVLSI.2018.2815603 |
| [12] |
LI Huimin, FAN Xitian, JIAO Li, et al. A high performance FPGA based accelerator for large-scale convolutional neural networks[C]//Proceedings of the 26th International Conference on Field Programmable Logic and Applications. Lausanne: IEEE, 2016: 1. DOI: 10.1109/FPL.2016.7577308
|
| [13] |
魏楚亮, 陈儒林, 高谦, 等. 基于高层次融合的卷积神经网络FPGA硬件加速[J]. 光学精密工程, 2020, 28(5): 1212. WEI Chuliang, CHEN Rulin, GAO Qian, et al. FPGA-based hardware acceleration for CNNs developed using high-level synthesis[J]. Optics and Precision Engineering, 2020, 28(5): 1212. |
| [14] |
CHENG Gong, ZHOU Peicheng, HAN Junwei. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7405. DOI:10.1109/TGRS.2016.2601622 |
| [15] |
LI Ke, CHENG Gong, BU Shuhui, et al. Rotation-insensitive and context-augmented object detection in remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 2337. DOI:10.1109/TGRS.2017.2778300 |
| [16] |
陈辰, 柴志雷, 夏珺. 基于Zynq7000 FPGA异构平台的YOLOv2加速器设计与实现[J]. 计算机科学与探索, 2019, 13(10): 1677. CHEN Chen, CHAI Zhilei, XIA Jun. Design and implementation of YOLOv2 accelerator based on Zynq7000 FPGA heterogeneous platform[J]. Journal of Frontiers of Computer Science and Technology, 2019, 13(10): 1677. DOI:10.3778/j.issn.1673-9418.1903027 |
 2022, Vol. 54
2022, Vol. 54


