线性调频(linear frequency modulation,LFM)信号因其时宽带宽积较大与低截获等优点,在雷达、声呐和通信等领域广泛应用[1-3],对LFM信号的参数估计一直是研究的重点。LFM信号作为一种非平稳信号,基于其时-频特性的估计算法受到了广泛关注[4-6],然而受限于时-频分辨率和交叉项之间的矛盾,该类算法的应用存在局限性。中心频率-调频率(centroid frequency-chirp rate,CFCR)域[7-9]分析作为一种新兴的LFM信号分析方式,通过将LFM信号变换为CFCR域的尖峰,提升了估计性能,然而该类算法需要引入时间延迟,若信号积累时间较短,则难以满足算法的延迟要求。齐林等[10]提出了一种基于分数阶傅里叶变换(fractional Fourier transform,FrFT)的估计算法,该算法利用LFM信号在分数域的分布特性,对旋转角度和分数域频率进行二维峰值搜索进而估计出信号参数。基于FrFT的估计算法相较于传统时频分析方法而言无交叉项且能量聚敛性更好;而与基于CFCR的估计算法相比,FrFT对信号的持续时间并无限制。
在工程应用中,需要对FrFT进行离散化处理。离散分数阶傅里叶变换(discrete fractional Fourier transform,DFrFT)中运用较为广泛的主要是Ozaktas算法[11]与Pei算法[12]。相较于Ozaktas算法,Pei算法通过在时域与分数域选取适当的采样间隔,使得DFrFT具有正交性和可逆性;且在所有近似FrFT的离散算法中,Pei算法具有最低的计算复杂度[13-14]。但是Pei算法对LFM信号调频率进行估计的原理是通过余切函数逼近信号调频率,若待估计信号调频率较高,参数估计误差很大,很难实现有效估计。
为了解决Pei算法在高调频率段参数估计误差较大的问题,本文在Pei算法的基础上,结合量纲归一化方法[15],提出了新的调频率估计方法,在旋转角度搜索步长有限的条件下,有效提升高调频率段的参数估计性能。
1 LFM信号估计原理作为经典傅里叶变换的一种广义形式,FrFT可视作将信号的坐标轴在时-频平面上绕原点逆时针旋转。连续信号s(t)的p阶FrFT定义[16-17]为
| $ S_{\alpha}(u)=F_{p}[s(t)]=\int_{-\infty}^{+\infty} K_{\alpha}(u, t) s(t) \mathrm{d} t $ | (1) |
式中:α为旋转角度,p为变换阶次,满足p=2α/π; Fp[·]为p阶FrFT运算的算子符号,Kα(u, t)为FrFT核函数,定义为
| $ K_{\alpha}(u, t)=\left\{\begin{array}{l} A_{\alpha} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }}\left(t^{2}+u^{2}\right) \cot \alpha-\mathrm{j} 2 {\rm{ \mathsf{ π} }} t u \mathrm{csc}\ \alpha}, \alpha \neq k {\rm{ \mathsf{ π} }} \\ \delta(t-u), \alpha=2 k {\rm{ \mathsf{ π} }} \\ \delta(t+u), \alpha=(2 k \pm 1) {\rm{ \mathsf{ π} }} \end{array}\right. $ | (2) |
式中:
假设连续LFM信号s(t)为
| $ s(t)=A \exp \left(\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{0} t+\mathrm{j} {\rm{ \mathsf{ π} }} \mu_{0} t^{2}\right) $ | (3) |
式中:A为信号幅值,f0为初始频率,μ0为调频率。
联立式(1)与式(3)可得
| $ \begin{aligned} S_{\alpha}(u)=& A A_{\alpha} \int_{-\infty}^{+\infty} \exp \left[\mathrm{j} {\rm{ \mathsf{ π} }} t^{2}\left(\cot \alpha+\mu_{0}\right)+\right.\\ &\left.\mathrm{j} 2 {\rm{ \mathsf{ π} }} t\left(f_{0}-u \mathrm{csc}\ \alpha\right)+\mathrm{j} {\rm{ \mathsf{ π} }} u^{2} \cot \alpha\right] \mathrm{d} t \end{aligned} $ | (4) |
式中Sα(u)为时域信号s(t)的分数域表示。由式(4)可知,若核函数与LFM信号的调频率相匹配,即α=arccot(-μ0),信号在分数域有最佳的能量聚集性,分布形式为冲激函数,在u=f0sin α处取得能量峰值。利用此特性,首先在不同旋转角度下分别计算LFM信号的FrFT结果,然后通过旋转角度与分数域的二维峰值搜索寻得峰值点坐标(α0, u0),进而估计信号的参数,可得待估计LFM信号的调频率与中心频率表达式:
| $ \left\{\begin{array}{l} \mu_{0}=-\cot \alpha_{0} \\ f_{0}=u_{0} \csc \alpha_{0} \end{array}\right. $ | (5) |
Pei算法表达式见式(6),为满足离散变换的可逆性,两域采样间隔需满足限制条件式(7)。
| $ S_{\alpha}(m)=\left\{\begin{array}{l} \sqrt{\frac{\sin \alpha-\mathrm{j} \cos \alpha}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha m^{2} \Delta u^{2}} \\ \ \ \sum\limits_{n=-N}^{N} \mathrm{e}^{-\mathrm{j}\frac{2 {\rm{ \mathsf{ π} }} n m}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha n^{2} \Delta t^{2}} s(n), \sin \alpha>0\\ \sqrt{\frac{-\sin \alpha+\mathrm{j} \cos \alpha}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha m^{2} \Delta u^{2}} \\ \ \ \sum\limits_{n=-N}^{N} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{ \mathsf{ π} }} n m}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha n^{2} \Delta t^{2}} s(n), \sin \alpha<0 \end{array}\right. $ | (6) |
| $ \Delta u \Delta t=\frac{\sin \alpha}{2 N+1} $ | (7) |
式中:Δt为时域采样间隔,Δt=1/fs; fs为采样频率; Δu为分数域采样间隔; s(n)为信号s(t)以Δt为采样间隔等间隔采样所得; n=-N, …, N-1, N; m=-N, …, N-1, N。
以Δα为旋转角度搜索步长,对信号进行步进DFrFT变换,则s(n)的pαl阶DFrFT变换为
| $ \begin{gathered} S_{\alpha_{l}}(m)=\sqrt{\frac{\sin \alpha_{l}-\mathrm{j} \cos \alpha_{l}}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha_l m^{2} \Delta u^{2}} \\ \sum\limits_{n=-N}^{N} \mathrm{e}^{-\mathrm{i} \frac{2 {\rm{ \mathsf{ π} }} n m}{2 N+1}} \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \cot \alpha_{l} n^{2}\Delta t^{2} s(n)} \end{gathered} $ | (8) |
式中αl为离散搜索中可取的旋转角度αl=lΔα,l为整数。
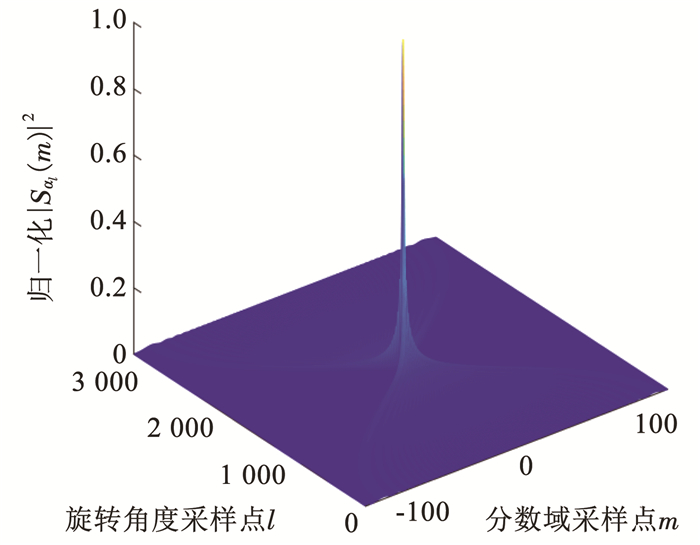
图 1为离散LFM信号在匹配与非匹配旋转角度下的DFrFT表示,可以观察出信号的分数域分布的聚敛性差异。图 2为信号能量的二维分布。由图 2可知,离散LFM信号在二维平面上会出现明显的能量尖峰,假设峰值点坐标为
| $ \left\{\begin{array}{l} \hat{\mu}_{0}=-\cot \left(\hat{l}_{0} \Delta \alpha\right) \\ \hat{f}_{0}=\frac{\hat{m}_{0}}{(2 N+1) \Delta t} \end{array}\right. $ | (9) |

|
图 1 LFM信号的离散分数域分布 Fig. 1 Distribution of LFM signal in the domain of DFrFT |
|
图 2 LFM信号能量二维分布 Fig. 2 Two-dimensional distribution of LFM signal power |
由式(9)可知,传统离散估计算法对调频率的估计表达式为余切函数,若信号调频率较大,
对信号量纲归一化预处理时,首先应确定原始信号的时域与分数域范围。假设待估计信号为式(2)所示,观测时间为T,则观测时间即为信号时宽;信号在旋转角度为α的分数域的带宽Bα=|Tμ0sin α|。因为待估计信号的调频率信息在实际估计过程中未知,所以需要通过已知信息确定近似的分数域范围。依据分数域采样定理[18-19],为了能精确重建原信号,采样频率应满足
| $ f_{\mathrm{s}} \geqslant\left|B_{\alpha} \csc \alpha\right| $ | (10) |
在估计过程中采样频率为已知信息,可将信号的分数域带宽设定为|fssin α|,则近似分数域范围可包括原始信号的所有频率分量。确定两域宽度后,为将不同量纲的两域变换到相同的无量纲域内,定义量纲归一化因子Cα,归一化过程可描述为
| $ \left\{\begin{array}{l} x=t / C_{\alpha} \\ y=u \cdot C_{\alpha} \end{array}\right. $ | (11) |
为使无量纲域的宽度相等,归一化因子应满足
| $ C_{\alpha}=\sqrt{T /\left(f_{\mathrm{s}}|\sin \alpha|\right)} $ | (12) |
联立式(11)和式(12)可得无量纲域宽度
| $ \left\{\begin{array}{l} \hat{\mu}_{0}=-\frac{T}{f_{\mathrm{s}}} \cos \left(l_{\mathrm{Est}} \Delta \alpha\right) \operatorname{sgn}\left[\sin \left(l_{\mathrm{Est}} \Delta \alpha\right)\right] \\ \hat{f}_{0}=\frac{m_{\mathrm{Est}}}{(2 N+1) \Delta x_{\alpha_{l}}} \sqrt{\frac{T}{f_{\mathrm{s}}\left|\sin \left(l_{\mathrm{Est}} \Delta \alpha\right)\right|}} \end{array}\right. $ | (13) |
式中sgn[·]为符号函数。由式(13)可知,本文算法对中心频率的方式与Pei算法并无区别,而对调频率的估计表达式由余切函数转化为余弦函数,因此后文主要针对本文算法对调频率的参数估计性能展开讨论。
3 算法性能分析 3.1 离散估计精度在离散参数估计过程中,受旋转角度搜索步长的限制,估计值与实际值之间的最大估计误差可能达到半个搜索步长,为了衡量各算法的离散估计精度,本文以无噪环境中所产生的最大调频率估计误差作为度量标准,则Δμ可定义为
| $ \Delta \mu=\mu\left(\alpha_{0}\right)-\mu\left(\alpha_{0}+\Delta \alpha / 2\right) $ | (14) |
式中μ(α)为估计旋转角度为α时的调频率估计结果。
联立式(13)与式(14), 可得本文算法的最大调频率估计误差为
| $ \begin{gathered} \Delta \mu_{\mathrm{Imp}}=\frac{f_{\mathrm{s}}}{T}\left|\cos \alpha_{0}-\cos \left(\alpha_{0}+\Delta \alpha / 2\right)\right| \approx \\ \frac{\Delta \alpha f_{\mathrm{s}}}{2 T} \sqrt{1-\left(\frac{T \mu_{0}}{f_{\mathrm{s}}}\right)^{2}} \end{gathered} $ | (15) |
由式(15)可知,待估计信号调频率应满足1-(Tμ0/fs)2≥0,即本文算法可估计的最高调频率为±fs/T。在可估计范围内,离散估计精度与Δα和fs/T相关,旋转角度的搜索步长越小,离散估计精度越高,理论上当Δα→0时,可完全消除离散估计误差,但是计算量也会随之显著提升;另一方面,ΔμImp随fs/T的增大而增大,因此缩小采样频率或延长观测时间也是提升精度的有效手段。本文算法、Pei算法和Ozaktas算法的最大调频率估计误差对比,见表 1。
| 表 1 最大调频率估计误差表达式 Tab. 1 Expressions for the maximum estimation errors of chirp-rate |
在旋转角度搜索步长、采样频率和观测时间均相同的条件下,两种传统算法与本文算法的最大估计误差比分别为
| $ \frac{\Delta \mu_{\text {Pei }}}{\Delta \mu_{\text {Imp }}}=\frac{\left(\mu_{0}^{2}+1\right)}{\sqrt{\left(f_{\mathrm{s}} / T\right)^{2}-\mu_{0}^{2}}} $ | (16) |
| $ \frac{\Delta \mu_{0 \mathrm{z}}}{\Delta \mu_{\mathrm{Imp}}}=\frac{f_{\mathrm{s}}\left[\mu_{0}^{2}+\left(f_{\mathrm{s}} / T\right)^{2}\right]}{T \sqrt{\left(f_{\mathrm{s}} / T\right)^{2}-\mu_{0}^{2}}} $ | (17) |
由式(16)与式(17)可得,相较于Pei算法,调频率在
上述针对离散估计精度的分析是在无噪声环境中进行的,而现实估计场景中往往夹杂着噪声,当环境中存在高斯白噪声时,考虑附加噪声的LFM信号为
| $ x(t)=s(t)+w(t),-T / 2 \leqslant t \leqslant T / 2 $ | (18) |
式中w(t)为零均值高斯白噪声。在高斯白噪声环境中,可通过估计量的统计特性来度量算法的抗噪性能,因为由搜索步长引发的估计误差已分析,在模型中设定搜索步长趋近于0,对采样点数(l, m)的搜索转化为对于信号参数(μ, f)的直接搜索,设定含噪信号的检验统计量Mx(μ, f)如下:
| $ M_{\mathrm{x}}(\mu, f)=M_{\mathrm{s}}(\mu, f)+M_{\mathrm{sw}}(\mu, f)+M_{\mathrm{w}}(\mu, f) $ | (19) |
| $ \begin{aligned} M_{\mathrm{s}}(\mu, f)=& \frac{1}{2 N+1} \sum\limits_{n=-N}^{N} \sum\limits_{k=-N}^{N} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }}(n-k) f \Delta x_{\alpha}} \\ & \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \mu\left(n^{2}-k^{2}\right) \Delta x_{\alpha}^{2}} s(n) s^{*}(k) \end{aligned} $ | (20) |
| $ \begin{aligned} M_{\mathrm{sw}}(\mu, f)=& \frac{2}{2 N+1} \sum\limits_{n=-N}^{N} \sum\limits_{k=-N}^{N} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }}(n-k) f \Delta x_{\alpha}} \\ & \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \mu\left(n^{2}-k^{2}\right) \Delta x_{\alpha}^{2}} s(n) w^{*}(k) \end{aligned} $ | (21) |
| $ \begin{aligned} M_{\mathrm{w}}(\mu, f)=& \frac{1}{2 N+1} \sum\limits_{n=-N}^{N} \sum\limits_{k=-N}^{N} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }}(n-k) f \Delta x_{\alpha}} \\ & \mathrm{e}^{\mathrm{j} {\rm{ \mathsf{ π} }} \mu\left(n^{2}-k^{2}\right) \Delta x_{\alpha}^{2}} w(n) w^{*}(k) \end{aligned} $ | (22) |
式中:Ms(μ, f)为信号项的检验统计量,Mw(μ, f)为噪声项检验统计量,Msw(μ, f)为交叉项的检验统计量。
在无噪声条件下,单分量LFM信号的检验统计量Mx(μ, f)在(μEst, fEst)处取得峰值,Mx(μ, f)对μ和f的偏导数在峰值点处为0;而在有噪环境中,假设峰值点受噪声影响偏移至(μEst+δμEst, fEst+δfEst),则Mx(μ, f)在峰值点处关于μ与f的偏导数应满足
| $ \left\{\begin{array}{l} \left.\frac{\partial M_{\mathrm{x}}(\mu, f)}{\partial \mu}\right|_{_{f=f_{\mathrm{Est}}+\mathtt{δ} f_{\mathrm{Est}}}^{\mu=\mu_{\mathrm{Est}}+\mathtt{δ} \mu_{\mathrm{Est}}}}=0 \\ \left.\frac{\partial M_{\mathrm{x}}(\mu, f)}{\partial f}\right|_{^{\mu=\mu_{\mathrm{Est}}+\mathtt{δ} \mu_{\mathrm{Est}}+\mathtt{δ} f_{\mathrm{Est}}}_{f=f_{\mathrm{Est}}+\mathtt{δ} f_{\mathrm{Est}}}}=0 \end{array}\right. $ | (23) |
因为分析的信道环境通常为高信噪比环境,噪声项Mw(μ, f)相对较小,在此忽略其影响,对式(23)进行泰勒展开得
| $ \left\{\begin{array}{l} \left.\frac{\partial M_{\mathrm{s}}(\mu, f)}{\partial \mu}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}}+\left.\frac{\partial M_{\mathrm{sw}}(\mu, f)}{\partial \mu}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}}+ \\ \ \ \left.\left(\mathtt{δ} \mu_{\mathrm{Est}} \frac{\partial^{2}}{\partial \mu^{2}}+\mathtt{δ} f_{\mathrm{Est}} \frac{\partial^{2}}{\partial \mu \partial f}\right) M_{\mathrm{s}}(\mu, f)\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}} \approx 0 \\ \left.\frac{\partial M_{\mathrm{s}}(\mu, f)}{\partial f}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}}+\left.\frac{\partial M_{\mathrm{sw}}(\mu, f)}{\partial f}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}}+ \\ \ \ \left.\left(\mathtt{δ} f_{\mathrm{Est}} \frac{\partial^{2}}{\partial f^{2}}+\mathtt{δ} \mu_{\mathrm{Est}} \frac{\partial^{2}}{\partial \mu \partial f}\right) M_{\mathrm{s}}(\mu, f)\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}} \approx 0 \end{array}\right. $ | (24) |
由式(24)计算可得
| $ \begin{aligned} \mathtt{δ} \mu_{\mathrm{Est}}=& \frac{1}{N(N+1)(2 N+1)\left(4 N^{2}+4 N-3\right)} \cdot \\ &\left.\frac{45}{2 A^{2} {\rm{ \mathsf{ π} }}^{2} \Delta x_{\alpha}^{4}} \cdot \frac{\partial M_{\mathrm{sw}}(\mu, f)}{\partial \mu}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}} \end{aligned} $ | (25) |
联立式(13)和式(25)可得参数修正后的调频率估计偏移δμ为
| $ \begin{aligned} \mathtt{δ} \mu=& \frac{1}{N(N+1)(2 N+1)\left(4 N^{2}+4 N-3\right)}\cdot \\ &\left.\frac{45 C_{\alpha}^{2}}{2 A^{2} {\rm{ \mathsf{ π} }}^{2} \Delta x_{\alpha}^{4}} \cdot \frac{\partial M_{\mathrm{sw}}(\mu, f)}{\partial \mu}\right|_{\mu=\mu_{\mathrm{Est}} \atop f=f_{\mathrm{Est}}} \end{aligned} $ | (26) |
由式(26)可得δμ的统计特性:
| $ E(\mathtt{δ} \mu)=0 $ | (27) |
| $ \begin{aligned} \operatorname{Var}(\delta \mu)=& \frac{1}{N(N+1)(2 N+1)\left(4 N^{2}+4 N-3\right)}\cdot \\ & \frac{45 C_{\alpha}^{4}}{2 {\rm{ \mathsf{ π} }}^{2} \Delta x_{\alpha}^{4} R_{\mathrm{SN}}} \end{aligned} $ | (28) |
式中:RSN为信噪比,RSN=A2/σ2,σ2为高斯白噪声的均方值,式(28)可视为调频率估计的渐进克拉美罗界[20-21]。
依据上述分析,本文算法的参数估计过程是渐进无偏与渐进有效的,与Ozaktas算法的克拉美罗界相比较[10],当采样频率与观测时间相同时,两种算法的抗噪性能相同。
4 仿真结果与分析为了验证本文所提出的新型算法对调频率估计性能的改进效果,需要对其进行仿真验证。在仿真过程中,采用归一化均方误差ENMS(normalized mean square error,NMSE)作为各算法估计性能的度量标准,设置采样点数为511个,采样频率为10 MHz,观测时间为0.511 ms。
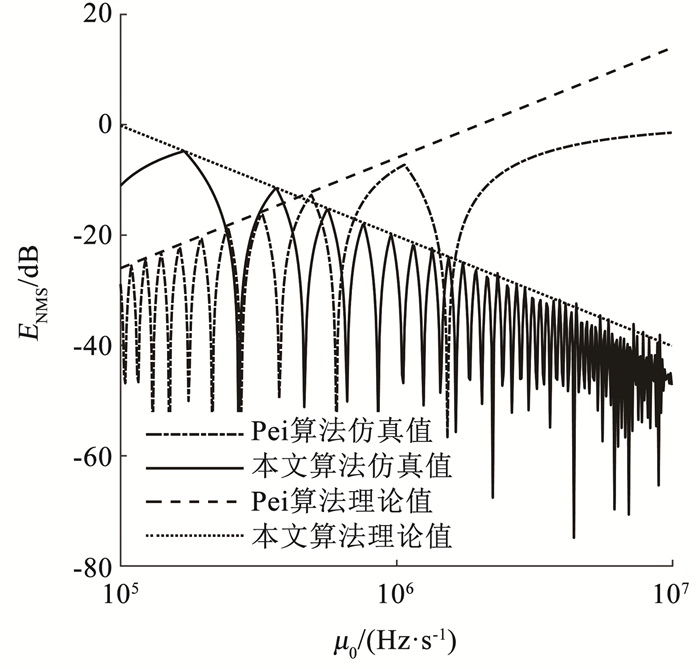
实验1 为验证本文算法的调频率离散估计精度相较于Pei算法的改进效果,本实验在105 Hz·s-1≤μ0≤107 Hz·s-1范围内进行仿真分析,设定旋转角度搜索步长为10-6,本文算法和Pei算法的理论最大误差ENMS曲线和实际仿真ENMS曲线见图 3。由图 3可知,两种算法的离散估计性能随信号调频率的增大变换趋势相反,本文算法的ENMS总体上与调频率的变化呈负相关,Pei算法则相反;当105 Hz·s-1≤μ0≤4.4×105 Hz·s-1,Pei算法估计精度更高;而当4.4×105 Hz·s-1 < μ0≤107 Hz·s-1,Pei算法的ENMS较大,无法实现对参数的有效估计,本文算法的估计性能逐渐优于Pei算法。实验仿真所得两种算法的优劣势区间与前文理论分析结果相符。
|
图 3 不同调频率下的归一化均方误差 Fig. 3 ENMS under different chirp-rates |
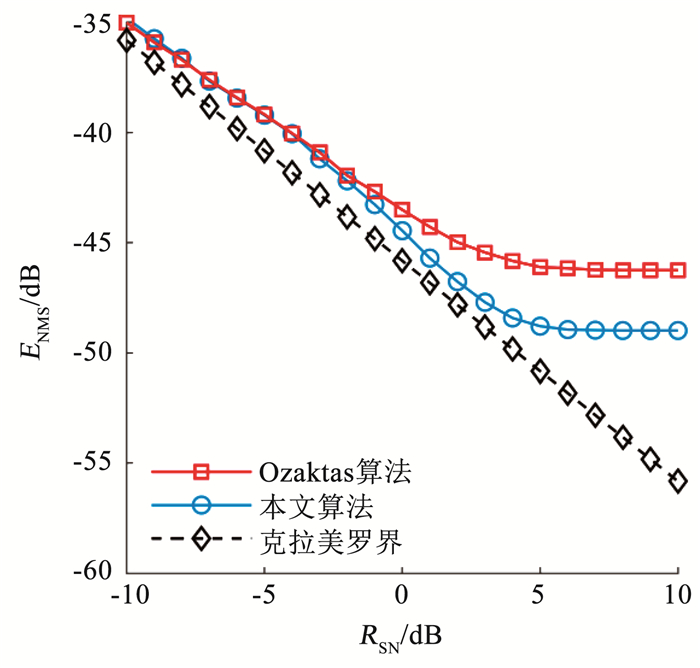
实验2 为了进一步验证本文算法在旋转角度搜索步长有限的有噪环境下的估计性能,本实验设定RSN=-10∶1∶10 dB,旋转角度搜索步长为10-3,待估计信号的调频率为1010 Hz·s-1,由于Pei算法在高调频率区段的估计误差过大,无法有效估计信号参数,没有仿真意义,所以本实验仅对本文算法和Ozaktas算法的ENMS进行仿真比较。在不同信噪比下,分别进行5 000次蒙特卡洛仿真,两种算法的仿真曲线见图 4。由图 4可知,当-10 dB≤RSN≤-2 dB时,噪声是参数估计误差的主要影响因素,而两种算法的抗噪性能相近,因此在该信噪比区间内二者的ENMS相近;当-2 dB < RSN≤6 dB时,随着噪声强度的减弱,噪声产生的估计误差逐渐减小,而基于前文分析,本文算法的离散估计误差小于Ozaktas算法,所以本文算法的ENMS曲线低于Ozaktas算法且随调频率增大差距逐渐扩大;当-6 dB < RSN≤10 dB,受离散估计精度的限制,两种算法的ENMS均呈现明显的地板效应,此时本文算法相较于Ozaktas算法的ENMS值下降约3 dB。
|
图 4 不同信噪比下的归一化均方误差 Fig. 4 ENMS under different signal-to-noise ratios |
本文提出一种基于新型DFrFT的LFM信号参数估计算法,并对该算法的参数估计性能进行了理论分析,提出了本文算法相较于传统算法的优势区间表达式。与传统算法相比,在旋转角度搜索步长相等的条件下,本文算法既有效提升了高调频率段的调频率分辨率,又保留了Pei离散算法结构简洁与运算可逆的优良特性。仿真结果验证了本文提出的优势区间的合理性,本文算法在优势区间的离散估计精度明显优于Pei算法;同时,在相同仿真条件下,所提算法在含噪环境中的估计精度对比Ozaktas算法也有一定程度的提升。
| [1] |
YOUSSEF A, DRIESSEN P F, GEBALI F, et al. A novel smeared synthesized LFM TC-OLA radar system: Design and performance evaluation[J]. IEEE Access, 2019, 7: 18574. DOI:10.1109/ACCESS.2019.2892113 |
| [2] |
YAO Shuai, YU Wenhui, FANG Shiliang, et al. Robust active sonar detection in frequency and time dispersive channels using matching envelope spectrum of multi-pulse LFM signals[J]. IEEE Access, 2020, 8: 159990. DOI:10.1109/ACCESS.2020.3020624 |
| [3] |
刘冰凡, 陈伯孝. 基于OFDM-LFM信号的MIMO雷达通信一体化信号共享设计研究[J]. 电子与信息学报, 2019, 41(4): 801. LIU Bingfan, CHEN Baixiao. Integration of MIMO radar and communication with OFDM-LFM signals[J]. Journal of Electronics and Information Technology, 2019, 41(4): 801. DOI:10.11999/JEIT180547 |
| [4] |
HAIMOVICH A M, PECKHAM C D, TETI J G. SAR imagery of moving targets: application of time-frequency distributions for estimating motion parameters[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1994, 2238: 238. DOI:10.1117/12.177719 |
| [5] |
李家强, 金荣洪, 耿军平, 等. 基于高斯短时分数阶傅里叶变换的多分量LFM信号检测与参数估计[J]. 电子与信息学报, 2007, 29(3): 570. LI Jiaqiang, JIN Ronghong, GENG Junping, et al. Detection and estimation of multi-component LFM signals based on gauss short-time fractional Fourier transform[J]. Journal of Electronics and Information Technology, 2007, 29(3): 570. |
| [6] |
YIN Qingbo, SHEN Liran, LU Mingyu, et al. Selection of optimal window length using STFT for quantitative SNR analysis of LFM signal[J]. Journal of Systems Engineering & Electronics, 2013, 24(1): 26. DOI:10.1109/JSEE.2013.00004 |
| [7] |
LI Dong, ZHAN Muyang, SU Jia, et al. Performance analysis of coherently integrated CPF for LFM signal under low SNR and its application to ground moving target imaging[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 55(11): 6402. DOI:10.1109/TGRS.2017.2727508 |
| [8] |
LÜ Xiaolei, BI Guoan, WAN Chunru, et al. Lv's distribution: Principle, implementation, properties and performance[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3576. DOI:10.1109/TSP.2011.2155651 |
| [9] |
ZHENG Jibin, LIU Hongwei, LIU Qinghuo. Parameterized centroid frequency-chirp rate distribution for LFM signal analysis and mechanisms of constant delay introduction[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6435. DOI:10.1109/TSP.2017.2755604 |
| [10] |
齐林, 陶然, 周思永, 等. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学E辑: 技术科学, 2003, 33(8): 749. QI Lin, TAO Ran, ZHOU Siyong, et al. Detection and parameter estimation of multicomponent LFM signals based on fractional Fourier transform[J]. Chinese Science E: Technical Science, 2003, 33(8): 749. DOI:10.3321/j.issn:1006-9275.2003.08.008 |
| [11] |
OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions Signal Process, 1996, 44(9): 2141. DOI:10.1109/78.536672 |
| [12] |
PEI S C, DING J J. Closed-form discrete fractional and affine Fourier transforms[J]. IEEE Transactions on Signal Processing, 2000, 48(5): 1338. DOI:10.1109/78.839981 |
| [13] |
陶然, 邓兵, 王越. 分数阶Fourier变换在信号处理领域的研究进展[J]. 中国科学E辑: 信息科学, 2006, 36(2): 113. TAO Ran, DENG Bing, WANG Yue. Research progress of fractional Fourier transform in signal processing[J]. Chinese Science E: Information Science, 2006, 36(2): 113. DOI:10.3321/j.issn:1006-9275.2006.02.001 |
| [14] |
陶然, 张峰, 王越. 分数阶Fourier变换离散化的研究进展[J]. 中国科学E辑: 信息科学, 2008, 38(4): 481. TAO Ran, ZHANG Feng, WANG Yue. Research progress on discretization of fractional Fourier transform[J]. Chinese Science E: Information Science, 2008, 38(4): 481. DOI:10.3321/j.issn:1006-9275.2008.04.001 |
| [15] |
赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360. ZHAO Xinghao, DENG Bing, TAO Ran. Dimensional normalization in the digital computation of the fractional Fourier transform[J]. Journal of Beijing University of Technology, 2005, 25(4): 360. DOI:10.3969/j.issn.1001-0645.2005.04.019 |
| [16] |
NAMIAS V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3): 241. DOI:10.1093/imamate/25.3.241 |
| [17] |
ALMEIDA L B. The fractional Fourier transform and time-frequency representations[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3084. DOI:10.1109/78.330368 |
| [18] |
邓兵, 陶然, 杨曦. 分数阶Fourier域的采样及分辨率分析[J]. 自然科学进展, 2007, 17(5): 655. DENG Bing, TAO Ran, YANG Xi. Sampling and resolution analysis in fractional Fourier domain[J]. Progress in Natural Science, 2007, 17(5): 655. DOI:10.3321/j.issn:1002-008X.2007.05.014 |
| [19] |
张卫强, 陶然. 分数阶傅里叶变换域上带通信号的采样定理[J]. 电子学报, 2005, 33(7): 1196. ZHANG Weiqiang, TAO Ran. Sampling theorem of band-pass signal in fractional Fourier transform domain[J]. Acta Electronica Sinica, 2005, 33(7): 1196. DOI:10.3321/j.issn:0372-2112.2005.07.010 |
| [20] |
PELEG S, PORAT B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase[J]. IEEE Transactions on Signal Processing, 1991, 39(3): 749. DOI:10.1109/78.80864 |
| [21] |
RISTIC B, BOASHASH B. Comments on "The Cramer-Rao lower bounds for signals with constant amplitude and polynomial phase"[J]. IEEE Transactions on Signal Processing, 1998, 46(6): 1708. DOI:10.1109/78.678501 |
 2022, Vol. 54
2022, Vol. 54


