纤维金属层板具有出色的力学性能,是未来能够替代金属的最具有竞争力的材料之一[1-5]。特别是使用交替铝合金薄层和玻璃纤维增强的热塑性层制备的层板在航空航天工业、汽车工业和轨道交通工业中体现出巨大的潜力[6-7]。与传统的热固性纤维金属层板相比,基于热塑性的层板具有优良的成形性性能优势[8-9]。采用纤维增强热塑性树脂替代热固性预浸料制备热塑性纤维金属层板,使得高效的一体成形方式成为可能。此外,热塑性纤维金属层板相比于热固性层板还具有以下特点:在制造过程中具有再成形或者再加工的可能性[10];维修过程相对于热固性纤维金属层板简单高效;也具有其他纤维金属层板耐疲劳的特性[11];同时具有良好的耐冲击能力[12]。
板材成形是机械制造业的基础行业,其发展程度反映了一个国家的制造工艺和技术水平。在板材成形领域,包括成形极限曲线在内的成形极限图(forming limit diagram,FLD)是一种根据主应变和次应变分布来表征板材成形性能的有效工具[13-14]。相比于金属板材成形性能的表征,纤维金属层板由于复合材料层内纤维的存在,其平行或垂直纤维方向的成形极限受路径依赖性的影响比较明显,由此表征的层板成形性能误差较大[15]。研究表明,基于纤维应变-应变比建立的成形极限曲线可以有效地消除路径依赖性的影响[16]。然而,如果沿用传统的金属成形条状试样,试样中的大量纤维会被切割掉,因此在成形极限测试中,纤维的滑动很容易发生,干扰纤维应变的计算。
因此,为了解决上述问题,设计了适合纤维金属层板成形极限性能评价的切槽试样,并对切槽试样进行凸模试验以研究玻璃纤维增强铝合金层板在室温下的可成形性。此外,比较了两种类型试样的破坏模式和成形极限图的差异,并且构造了更合适的成形极限图来表征纤维金属层板的纤维拉伸断裂和界面分层失效。
1 试验材料与方法 1.1 试样制备及实验方法试验材料: 铝合金,2024-T3,厚度为0.6 mm,江苏利昌金属制品有限公司;Gf/PA预浸料固化后单层厚度为0.125 mm,上海吉尼斯先进材料有限公司。
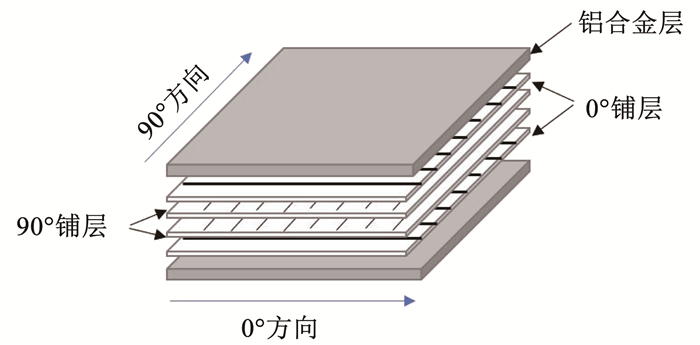
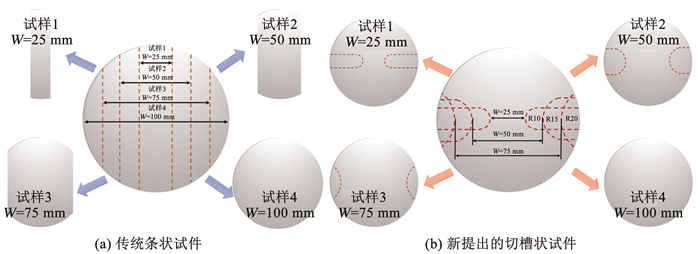
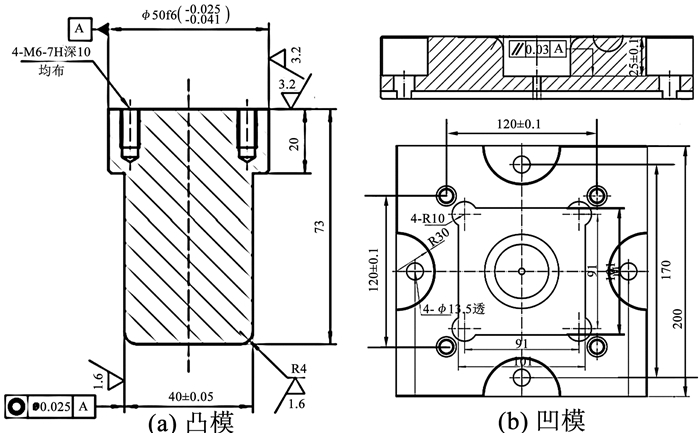
为了提高铝合金与Gf/PA复合材料的界面结合性能,在喷丸机上用碳化硅(SiC)砂粒对铝板单面进行喷砂处理,喷砂工艺参数见表 1。喷砂后,用表面粗糙度测试仪检测铝板表面粗糙度为1.5 μm。铺放Gf/PA预浸料和金属层板, 见图 1, 然后热压成型,铺层方式为[Al/0°/90°/90°/0°/Al]。采用水切割的方式将制备好的层板切割成如图 2所示的试样形状。之后在YF28-100/180型双动液压机上开展成形试验,拉深模具见图 3。
| 表 1 喷砂工艺参数 Tab. 1 Process parameters of sandblasting |
|
图 1 Gf/PA预浸料-铝合金层板铺层结构 Fig. 1 Laminated structure of Gf/PA prepreg-aluminum alloy laminate |
|
图 2 试件形状 Fig. 2 Shape of specimens |
|
图 3 拉深模具形状及尺寸(mm) Fig. 3 Shape and dimension of drawing die(mm) |
在成形试验前,首先采用奥斯汀电解液打标机对试样表面进行电化学腐蚀打标处理。其次,为了获取试样的应变分布情况,采用ARGUS光学应变测量仪(图 4)对成形后的试样按照单相机分步测量的方法进行了拍摄及后续表面应变的计算处理。

|
图 4 光学应变测量仪 Fig. 4 Optical strain measuring device |
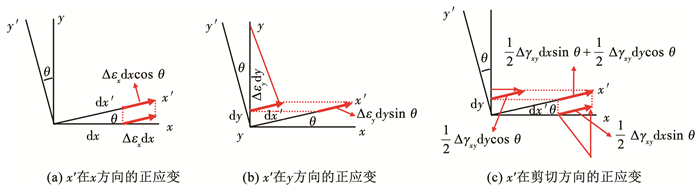
由于纤维和基体的应变极限差别很大,因此在成形过程中纤维的断裂可能要发生在基体断裂和金属层断裂之前。当纤维断裂和界面分层为主要失效模式时,可以将纤维应变引入到成形极限图中,但是由于纤维金属层板又包含金属层,因此在引入纤维应变来评判复合材料成形性的同时也采用应变比来评判金属层的成形性能, 并将两者结合以绘制纤维金属层板的成形极限曲线。纤维应变代表作用在玻璃纤维上的应变量。在ARGUS光学应变测量系统中通过应变变换获得纤维应变,纤维应变计算原理见图 5。通过对成形后的上下金属层的标点进行相减计算得到的纤维应变瞬时增量进行累加,得到最终的纤维应变,然后用瞬时旋转增量、瞬时全局法向应变和瞬时剪切应变增量对纤维应变的瞬时增量进行更新,纤维应变是由表面应变通过坐标变换技术计算出来的[16]。在ARGUS光学应变测量系统中创建用于计算纤维应变的Python脚本,其计算流程见图 6,各方向增量计算式如下:
| $\left\{\begin{array}{l}\Delta \varepsilon_{x}^{i}=\varepsilon_{x}^{i}-\varepsilon_{x}^{i-1} \\ \Delta \varepsilon_{y}^{i}=\varepsilon_{y}^{i}-\varepsilon_{y}^{i-1} \\ \Delta \gamma_{x y}^{i}=\gamma_{x y}^{i}-\gamma_{x y}^{i-1}\end{array}\right.$ | (1) |
|
图 5 纤维应变计算原理 Fig. 5 Schematic diagram of fibre strain calculation |
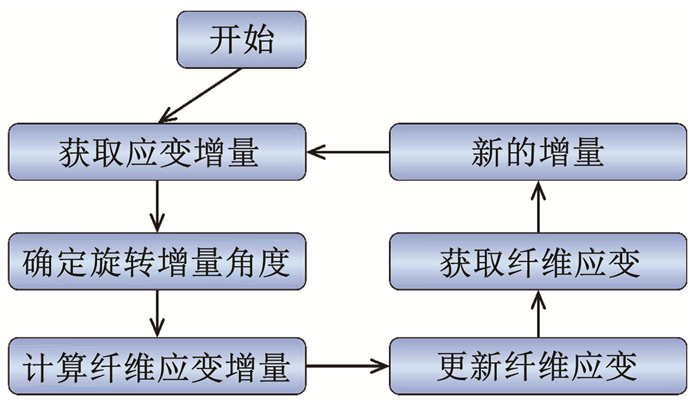
|
图 6 纤维应变计算流程图 Fig. 6 Flow chart of fibre strain calculation |
式中: i为计算的第i个时间增量; εx,εy,γxy为全局坐标X,Y和剪切方向上的应变; 而Δεx,Δεy,Δγxy为全局坐标X,Y和剪切方向上的应变增量。
首先根据式(2)计算沿X′方向的伸长率,并计算沿X和Y方向的分量
| $d_{x^{\prime}}^{i}=\frac{d_{x}}{\cos \theta^{i}}, d_{x^{\prime}}^{i}=\frac{d_{y}}{\sin \theta^{i}} $ | (2) |
式中θi为旋转角度; dx,dy,dx′i分别对应于沿X,Y和X′方向的伸长率。
沿X′方向的最终伸长增量是X方向上的正应变,Y方向上的正应变以及剪切应变中所有分量的总和,见式(3)~(6)。
| $\delta_{x^{\prime}}^{i}=\Delta \varepsilon_{x}^{i} d_{x} \cos \theta^{i}+\Delta \varepsilon_{y}^{i} d_{y} \sin \theta^{i}+ \\ \qquad\frac{1}{2} \Delta \gamma_{x y}^{i} d_{x} \sin \theta^{i}+\frac{1}{2} \Delta \gamma_{x y}^{i} d_{y} \cos \theta^{i} $ | (3) |
| $\Delta \varepsilon_{x^{\prime}}^{i}=\frac{\delta_{x^{\prime}}^{i}}{d_{x^{\prime}}^{i}}=\Delta \varepsilon_{x}^{i} \cos ^{2} \theta^{i}+\Delta \varepsilon_{y}^{i} \sin ^{2} \theta^{i}+ \\ \qquad \Delta \gamma_{x y}^{i} \sin \theta^{i} \cos \theta^{i} $ | (4) |
其中δx′i是沿X′方向的合成增量伸长率,Δεx′i是沿X′方向的应变增量。
通过应用三角恒等式(5),可以将式(4)中沿X′方向的增量应变简化为式(6):
| $\cos ^{2} \theta^{i}=\frac{1+\cos 2 \theta^{i}}{2}, \sin ^{2} \theta^{i}=\frac{1-\cos 2 \theta^{i}}{2} $ | (5) |
| $\begin{array}{l} \Delta \varepsilon_{x^{\prime}}^{i}=\frac{\Delta \varepsilon_{x}^{i}+\Delta \varepsilon_{y}^{i}}{2}+\frac{\Delta \varepsilon_{x}^{i}-\Delta \varepsilon_{y}^{i}}{2} \cos 2 \theta^{i}+ \\ \qquad\frac{1}{2} \Delta \gamma_{x y}^{i} \sin 2 \theta^{i}\end{array} $ | (6) |
由于x′⊥y′,通过用(90°+θi)代替式(3)和式(6)中的θi,可以获得沿Y′方向的增量伸长率和增量应变,见式(7)~(9)。
| $\delta_{y^{\prime}}^{i}=-\Delta \varepsilon_{x}^{i} d_{x} \sin \theta^{i}+\Delta \varepsilon_{y}^{i} d_{y} \cos \theta^{i}+\\ \qquad \frac{1}{2} \Delta \gamma_{x y}^{i} d_{x} \cos \theta^{i}-\frac{1}{2} \Delta \gamma_{x y}^{i} d_{y} \sin \theta^{i} $ | (7) |
| $d_{y^{\prime}}^{i}=\frac{d_{x}^{i}}{\sin \theta^{i}}, d_{x^{\prime}}^{i}=\frac{d_{y}^{i}}{\cos \theta^{i}} $ | (8) |
| $\Delta \varepsilon_{y^{\prime}}^{i}= \frac{\Delta \varepsilon_{x}^{i}+\Delta \varepsilon_{y}^{i}}{2}-\frac{\Delta \varepsilon_{x}^{i}-\Delta \varepsilon_{y}^{i}}{2} \cos 2 \theta^{i}-\\ \qquad \frac{1}{2} \Delta \gamma_{x y}^{i} \sin 2 \theta^{i} $ | (9) |
其中δy′i和Δεy′i分别为沿Y′方向的合成增量伸长率和沿Y′方向的合成应变。
然后根据式(10)计算旋转增量角为
| $\begin{aligned} \Delta \gamma_{x^{\prime} y^{\prime}}^{i}=& \frac{\delta_{x^{\prime}}^{i}}{d_{y^{\prime}}^{i}}+\frac{\delta_{y^{\prime}}^{i}}{d_{x^{\prime}}^{i}}=\left(\Delta \varepsilon_{y}^{i}-\Delta \varepsilon_{y}^{i}\right) \sin 2 \theta^{i}+\\ & \gamma_{x y}^{i} \cos 2 \theta^{i} \end{aligned} $ | (10) |
式中Δγx′y′i为旋转增量角。
沿着两个方向的纤维应变可以在每个时间步长上进行相应更新。如式(11)所示,在建立纤维金属层板成形极限曲线时,这两个应变的最大值用于表示此时的纤维应变。另外,在每次增量结束时,旋转角也应该更新。因此
| $\left\{\begin{array}{l}\varepsilon_{X}^{i}=\varepsilon_{X}^{i-1}+\Delta \varepsilon_{X^{\prime}}^{i} \\ \varepsilon_{Y}^{i}=\varepsilon_{Y}^{i-1}+\Delta \varepsilon_{Y^{\prime}}^{i} \\ \theta^{I}=\theta^{I-1}+\Delta \gamma_{x^{\prime} y^{\prime}}^{I} \\ \varepsilon_{\text {fibre }}=\max \left\{\varepsilon_{X}^{i}, \varepsilon_{Y}^{i}\right\}\end{array}\right.$ | (11) |
其中εXi和εYi为沿纤维方向的应变,εfibre为纤维金属层板成形极限曲线中使用的纤维应变值。
除纤维应变外,应变比是纤维金属层板成形极限曲线中使用的另一个参数,可以根据式(12)进行计算:
| $R_{\mathrm{s}}=\frac{\varepsilon_{\text {minor }}}{\varepsilon_{\text {major }}} $ | (12) |
式中: Rs为应变比(strain ratio,SR), εminor为次应变,εmajor为主应变。
2 结果与分析 2.1 路径依赖性分析路径依赖性是指复合材料的极限主应变会受其历史应变路径的影响,当将传统的成形极限曲线应用于纤维金属层板时,这种影响就会显现出来。为了研究纤维金属层板的路径依赖效应,在单向拉伸试样和W75mm(W指宽度)试样中选取了两个点,并比较了它们的主应变演化。单向拉伸试样的测试点位于断裂线上,而W75mm试样的测试点位于凸模圆角区域。比较这两个点的原因是:在变形过程中两者具有相似的变形模式,但经历了完全不同的历史路径,这在考察路径依赖对传统成形极限曲线的影响时具有重要意义。
图 7(a)是W75mm试样与单向拉伸试样在传统成形极限图上的主应变演变对比。单向拉伸试样的应变变形是在破坏时获得的,而W75mm试样的应变变形是在成形深度为10 mm时获得的,其破坏时深度为11 mm。成形模式可以用成形极限中不同的应变比表示,从双向拉伸(Rs=1)到纯剪切(Rs=-1)不等。尽管两个试样在关注点经历了相同的单向拉伸加载方式,但值得注意的是,与单向拉伸试样相比,W75mm试样可以承受明显更高的极限主应变。与经历单一成形模式(恒定应变路径)的单向拉伸试样不同,W75mm试样由于成形过程中承受复杂应力的性质而经历应变路径的变化。这暗示了一种路径依赖现象,使得极限主应变受到路径的影响。这种效应会显著影响传统成形极限曲线的有效性。因此,传统的成形极限曲线不适用于纤维金属层板的成形极限判断。
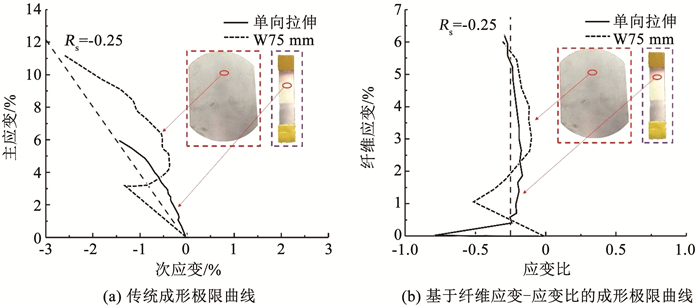
|
图 7 路径依赖性分析 Fig. 7 Analysis of path dependence |
然后在基于纤维应变-应变比的成形极限图(图 7(b))上比较两个测试点的纤维应变路径演化。显然,W75mm试样的最大纤维应变并未超过单向拉伸试样所定义的极限纤维应变。这清楚地表明,使用纤维应变-应变比衡量测试点纤维路径变化可以帮助消除路径依赖效应。同时提出了利用纤维应变和应变比建立适用于层板的成形极限曲线的可能性,基于纤维应变-应变比的成形极限曲线可以成功地消除路径依赖效应,因此有望比传统的成形极限曲线更有效。
图 8显示了在与图 7相同的表面点上的主应变及其分量的演化。在单向拉伸试验中,主应变由沿拉伸方向的应变主导,垂直方向由于泊松效应而经历负应变变形。单向拉伸试样中剪切分量不明显,而W75mm试样中剪切应变分量占主导地位,且大于纵向和横向应变。纤维金属层板的破坏以凸模圆角区域的破坏为主。因此,玻璃纤维应该是层板伸长率的限制因素,因为与PA基体相比,玻璃纤维的伸长率要低得多。因此,作用在玻璃纤维上的拉伸应变量对层板的破坏有影响,而剪切应变的影响不大。此外,大的剪切应变被认为是在传统成形极限曲线中观察到的路径依赖现象的原因。这是因为剪切应变可能会导致更高的主应变,但不一定会导致这类材料系统的失效。因此,基于纤维应变-应变比的成形极限曲线能够成功地消除路径依赖效应,因为它只考虑了作用在玻璃纤维上的拉伸应变量,而剪切应变通过坐标变换使其仅起到变换旋转角的作用。
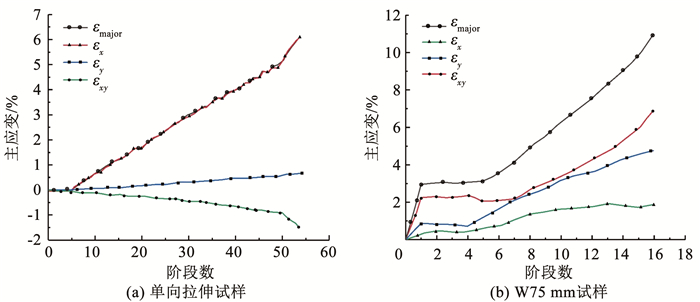
|
图 8 测试点应变演化 Fig. 8 Strain evolution at test point |
因此,当层板以纤维拉伸断裂和界面分层失效模式为主时,基于纤维应变-应变比的计算得到的成形极限图可以对两者进行识别区分。
2.2 条状试件基于纤维应变-应变比的成形极限分析图 9是条状试样不同宽度下即将断裂前的成形情况,试样的极限成形深度控制在10 mm。另外,根据文献[17-20]和本研究得到的实验结果,确定了条状纤维金属层板试样成形后的两种典型破坏模式,即I型-纤维拉伸断裂模式、II型-剪切和纤维拔出模式,且断裂均发生在凸模圆角区域。宽度为75 mm和100 mm的试样在玻璃纤维断口表面呈现出明显的I型-纤维拉伸断裂破坏模式,反映了纤维在拉伸状态下的损伤特征。模式II的失效破坏模式以基体破坏为主,伴随有纤维拔出破坏。由于试样成形和制件和工艺固有问题,25 mm和50 mm宽试样首先经历了拉伸和剪切的耦合变形,然后由于边界条件的约束较弱,其纤维被整体拔出。

|
图 9 条状成形试样及失效模式 Fig. 9 Strip forming specimens and their failure modes |
图 10是条状试样上下层在失效前的主应变轮廓。在图中可以观察到主应变较大的区域,即凸模圆角区域,这也是成形试验中最容易损坏的区域; 不同的条状试样在这两个主要破坏区域表现出不同的主应变分布; 不同破坏模式的试样其极限应变值存在较大差异。这些证据表明条状试样的破坏模式不同。对于宽度为75 mm和100 mm的试样,极限主应变都集中在凸模圆角区域,试样沿横向纤维方向断裂,破坏模式为I型,这是因为横向纤维在试样腰部游离,降低了试样的承载能力。换言之,纵向的固定纤维必须承担冲头的大部分载荷; 当纵向纤维在应变集中区断裂时,断裂会沿横向纤维方向扩展。
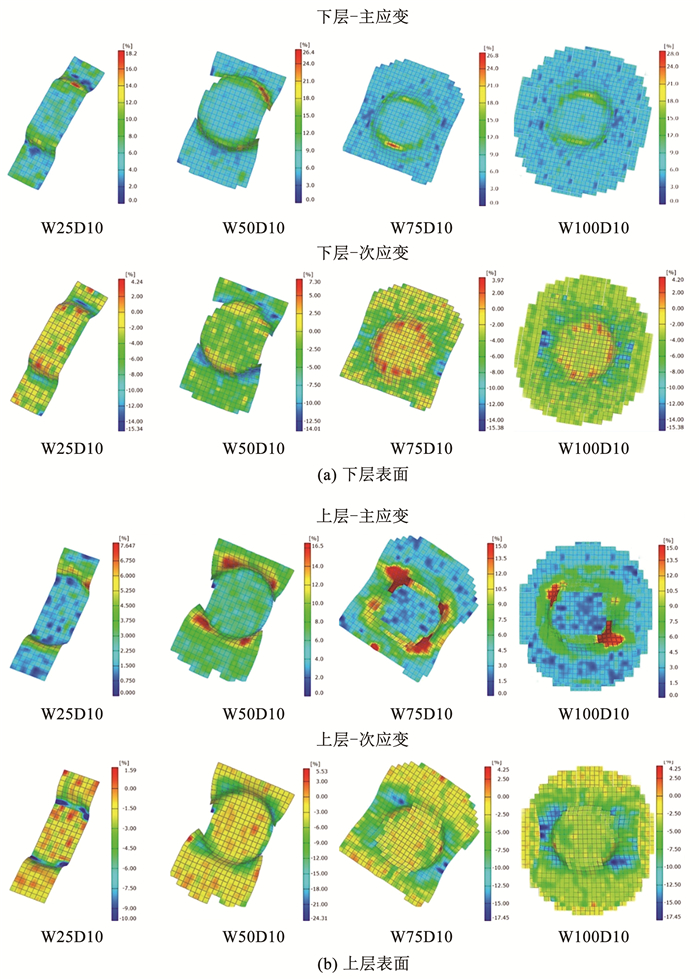
|
图 10 条状试样即将失效前的光学应变测量主应变及次应变分布 Fig. 10 Major and minor strain distributions of strip forming specimens before failure |
宽度为25 mm和50 mm的试样在成形试验中被大量拉伸,并以Ⅱ型失效模式断裂。这意味着在成形试验期间存在剪切变形,这可能导致纤维失效的高伸长率。由于W25mm试样宽度较窄,腰部的纤维仅受基体的约束; 因此,纤维可以在断裂之前在最大变形区从基体中拉出。因此,25 mm和50 mm宽度的试样的极限强度是由剪切行为和纤维与基体的黏结强度共同决定的。
图 11为条状试样基于纤维应变-应变比的成形极限图。根据极限纤维应变的分布,将它们连接成适当的曲线即可形成新型成形极限曲线。
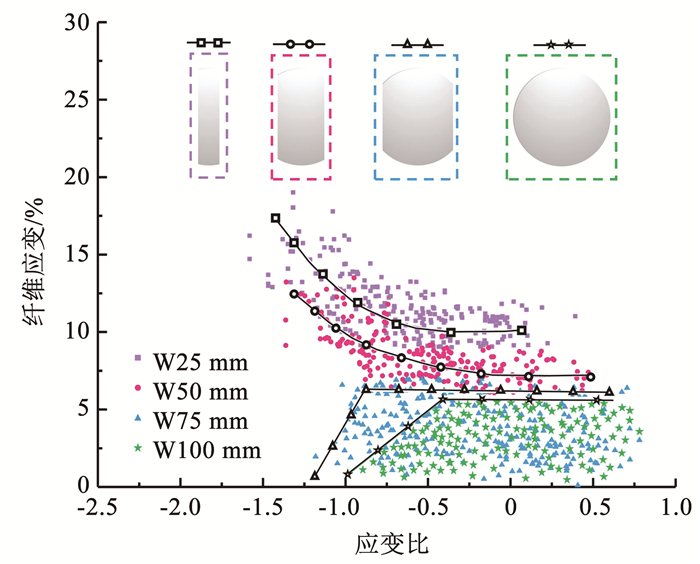
|
图 11 条状成形试件纤维应变-应变比成形极限图 Fig. 11 Forming limit diagram of fibre strain-strain ratio of strip forming specimen |
极限应变的大幅度增加表明试样可能经历了异常的变形模式。对于W25mm和W50mm试样而言,较窄的宽度使得两者以II型基体破坏为主要的失效模式,这导致了成形极限图中的纤维应变虚高。从图 9所示的试样断裂处的SEM图像可以看出,断裂处纤维之间存在一定的剪切角度。此外,由于试样截断纤维的不连续性,导致基体对纤维的限制不够充分。在试验过程中,这些因素导致纤维拔出而不是断裂,造成纤维应变增量增加。另外,界面分层失效现象同样会导致纤维应变量的增加,但是由于界面分层失效现象大多在局部发生,对纤维应变增量的影响与整体的纤维剪切拔出失效模式相比并不显著,这也表明腰部宽度较窄的条状试样采用基于纤维应变-应变比的成形极限曲线区分不出纤维拉伸断裂与界面分层失效。但是,对于W75mm试样,其试样计算所得的应变均控制在6%以下。纤维应变先有一个上升的过程,然后稳定在6%以下,当超过这一区间层板就失效。W100mm试样纤维计算应变上升得较W75mm更缓慢,应变控制得更低。另外,图 11曲线的走势实际上就是层板成形过程中变形模式的演化,这是传统成形极限曲线所不能直观表示的。
通过上述的研究证明了基于纤维应变-应变比的成形极限曲线能够消除路径依赖性,纤维应变的计算方式适用于以纤维拉伸断裂和界面分层为主要失效模式的纤维金属层板的成形极限分析。然而,如果沿用传统金属成形的条状试样,仅当腰部较宽的试样才能适用,而腰部较宽试样的特点就是边界条件较高以及破坏模式为Ⅰ型。因此,为了更好的匹配基于纤维应变-应变比的成形极限曲线,需要设计新的符合以纤维拉伸断裂和界面分层失效为主要失效模式的成形极限测试试样。
2.3 切槽试件基于纤维应变-应变比的成形极限分析常规条状试样是为金属成形实验设计的,但金属试样没有基体和增强体;在金属成形过程中,纤维与基体之间不会发生纤维拔出或剪切;而在成形试验过程中,可以在纤维金属层板条状试样中观察到这种行为,显著影响了纤维金属层板的成形极限表征。这意味着传统金属成形实验中使用的条状试样不能保持纤维的连续性。为此,设计了切槽试样,通过考虑纤维的连续性和断裂位置来解决这些问题,见图 2(b)。切槽试样采用两条长切口,两侧长宽比分别为两条切口,以保持试样的纤维连续性;两切槽之间的距离决定试样的宽度。在试验过程中,采用压边圈实现了更好的固定,从而强化了边界条件,消除了纤维弯曲剪切断裂或拉出。
图 12为纤维金属层板在失效前对应的主应变。所有试样均可明显观察到在凸模圆角区域的较高主应变值。上下层的极限误差在3%~6%附近相当接近。此外,压边圈附近的主应变相对较小,表现出较强的抗弯性能。这是由于压边圈和切槽为在不改变试样宽度的情况下能够固定更多材料而使得边界条件增强。因此,所提出的切槽设计能够将失效模式直接指向纤维拉伸断裂和界面分层。
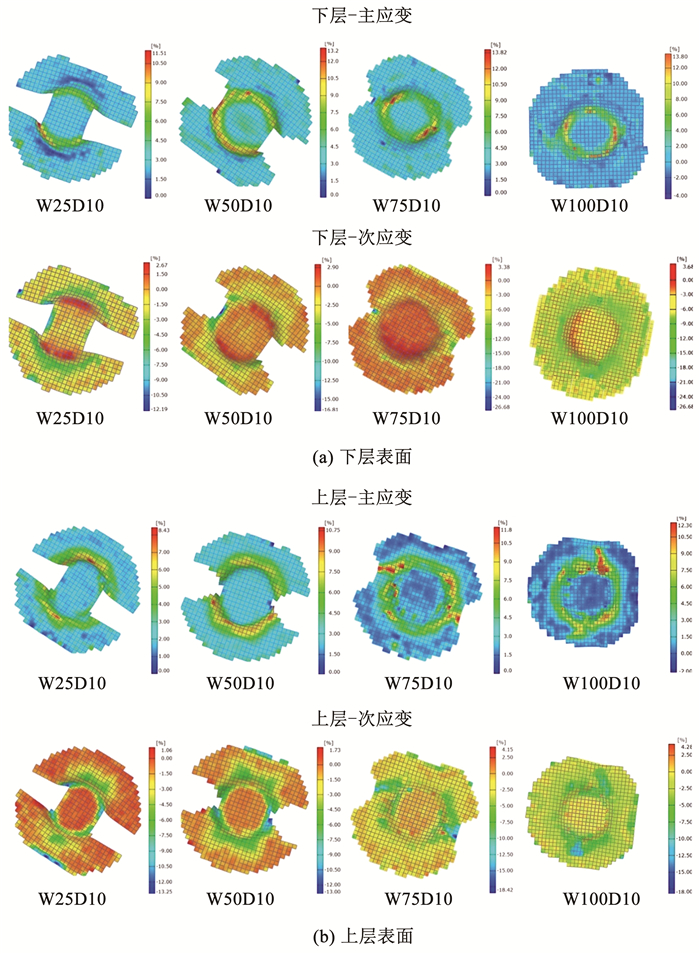
|
图 12 切槽试样即将失效前的光学应变测量主应变及次应变分布 Fig. 12 Major and minor strain distributions of notched forming specimens before failure |
图 13为切槽状试样在不同宽度下即将断裂前的成形情况,极限成形深度控制在10 mm。可以看出,所有试样的潜在破坏模式均表现为典型的I型破坏。

|
图 13 切槽状成形试件及潜在失效模式 Fig. 13 Notched forming specimens and their potential failure modes |
图 14为切槽状试样基于纤维应变-应变比的成形极限图。根据极限纤维应变的分布,将它们连接成适当的曲线即可形成成形极限曲线,其破坏准则如下:
| $\varepsilon_{\text {fibre }}=\left\{\begin{array}{l}11+10 x, -1 \leqslant x<-0.5 \\ 6 \%, -0.5 \leqslant x \leqslant 1\end{array}\right. $ | (13) |

|
图 14 切槽状成形件纤维应变-应变比成形极限 Fig. 14 Forming limit diagram of fibre strain-strain ratio of notched forming specimen |
与图 11相比,切槽试样在相同变形模式下的纤维应变要比条状试样低得多。由于切槽试样腰部的纤维连接在一起,边界条件增强,纤维断裂成为主要的破坏模式,因此,切槽试样的极限应变水平为6%。基于纤维应变-应变比的切槽试样的成形极限曲线在一定程度上克服了条状试样的缺点。因此,成形安全区域为纤维计算应变低于6%的区域。成形极限曲线由两部分组成,即相对于Rs在-1~-0.5范围内的斜线,表示剪切变形和拉伸变形的模式;以及相对于Rs在-0.5~1的水平线,表示试样从单向拉伸变形到双向拉伸变形。因此,基于纤维应变-应变比的成形极限曲线反映了纤维金属层板在各种变形状态下的变形能力,包括纯剪切、单向拉伸、平面应变和双向拉伸变形模式。因此,切槽试样能够适应不同的变形模式。
但是,从图 14可以发现,在变形演化的最后阶段,一些纤维应变值偏离了成形极限区间。上述的分析可知,基于纤维应变-应变比的测试方法可以规避路径依赖性对成形极限测试的影响。因此,可能是除纤维拉伸断裂以外的其他失效模式出现,导致纤维应变出现异常值。通过提取这些点找到对应的区域,发现其均出现在弯曲变形较大的凹模圆角区域的部分位置。图 14是对该区域的扫描电镜观察,可以发现出现了界面分层失效。由于纤维应变的获取是通过计算上下层金属的应变差值,再通过坐标变换得到。这要求良好的界面结合性能以保证层板整体的协同变形能力。因此,随着变形量的加深,界面分层失效会导致纤维应变出现异常值。另外,由于界面分层失效会提前于纤维拉伸断裂失效发生,因此,界面分层失效区域都在纤维拉伸断裂失效区域的上方。切槽试样的基于纤维应变-应变比的成形极限图包含3个区域:成形安全区-纤维拉伸断裂区-界面分层区。所以,该成形极限测试方法既可以判断层板的可成形性,还可以判断层板出现界面分层的位置。
作为评估纤维金属层板成形性的有效工具,成形极限曲线可用于预测冲压过程中的样品破坏。成形极限曲线位置越高,材料的可成形性越好。此外,由切槽试样建立的成形极限曲线涉及不同的变形模式,并表现出相同的破坏机理,并且也考虑了纤维金属层板中不同成分的影响。因此,通过使用提出的这种新颖设计,也可以对具有其他连续纤维和热塑性预浸料组成的纤维金属层板的成形极限曲线进行表征。
3 结论1) 在所有条状试样中,确定了两种主要的破坏模式,即模式I-纤维拉伸断裂,模式II-纤维拔出和剪切。失效模式II仅出现在条状试样宽度较窄的试样中,这是基体失效模式占主导的结果。设计的切槽试样通过更好地保持纤维连续性成功地克服了这些问题,使纤维拉伸断裂和界面分层成为主要的破坏模式。
2) 对于常规的条状试样,将腰部的纤维切掉,仅用PA基体约束。但是,切槽试样可以更好地确保纤维的连续性,因此可以通过使用压边圈更好地限制纤维并提供牢固的边界条件。试样在成形过程中表现出不同的变形阶段; 不同的阶段显示出不同的变形演化模式,几乎涵盖了所有可能的变形模式。
3) 切槽试样可以将纤维应变控制在6%以内,可以明显区分出纤维拉伸断裂和界面分层失效。因此,基于纤维应变-应变比的切槽试样成形极限图包含3个区域:成形安全区-纤维拉伸断裂区-界面分层区。所以,该成形极限测试方法既可以判断层板的可成形性,还可以判断层板出现界面分层的位置。设计的切槽试样获得的成形极限曲线可以将变形演化与破坏机理结合起来,从而更有效地表征纤维金属层板的可成形性。
4) 金属的界面处理及与复合材料的结合强度对成形极限影响很重要,所得结论应该只限于在铝合金与Gf/PA预浸料的界面处理条件下得到的成形极限图,其他界面处理后的成形极限结果不适用本文的结论。
| [1] |
SINMAZGELIK T, AVCU E, BORA M O, et al. A review: Fibre metal laminates, background, bonding types and applied test methods[J]. Materials & Design, 2011, 32(7): 3671. DOI:10.1016/j.matdes.2011.03.011 |
| [2] |
STOLL M M, SESSNER V, KRAMAR M, et al. The effect of an elastomer interlayer thickness variation on the mechanical properties of fibre-metal-laminates[J]. Composite Structures, 2019, 219: 90. DOI:10.1016/j.compstruct.2019.03.042 |
| [3] |
VOGELESANG L B, VLOT A. Development offibre metal laminates for advanced aerospace structures[J]. Journal of Materials Processing Technology, 2000, 103(1): 1. DOI:10.1016/S0924-0136(00)00411-8 |
| [4] |
YING Linwei, YANG Fengpeng, WANG Xi. Analytical method for the axial crushing force of fibre-reinforced tapered square metal tubes[J]. Composite Structures, 2016, 153: 222. DOI:10.1016/j.compstruct.2016.05.108 |
| [5] |
吴素君, 解晓伟, 晋会锦, 等. 纤维金属层板力学性能的研究现状[J]. 复合材料学报, 2018, 35(4): 733. WU Sujun, XIE Xiaowei, JIN Huijin, et al. Mechanical properties of fibre metal laminates: A review[J]. Acta Materiae Compositae Sinica, 2018, 35(4): 733. DOI:10.13801/j.cnki.fhclxb.20171208.005 |
| [6] |
MAMALIS D, OBANDE W, KOUTSOS V, et al. Novel thermoplastic fibre-metal laminates manufactured by vacuum resin infusion: The effect of surface treatments on interfacial bonding[J]. Materials & Design, 2019, 162: 331. DOI:10.1016/j.matdes.2018.11.048 |
| [7] |
SANTIAGO R, CANTWELL W, ALVES M. Impact on thermoplastic fibre-metal laminates: experimental observations[J]. Composite Structures, 2017, 159: 800. DOI:10.1016/j.compstruct.2016.10.011 |
| [8] |
LANGDON G S, CANTWELL W J, NURICK G N. The blast response of novel thermoplastic-based fibre-metal laminates-some preliminary results and observations[J]. Composites Science & Technology, 2005, 65(6): 861. DOI:10.1016/j.compscitech.2004.09.025 |
| [9] |
ABDULLAH M R, PRAWOTO Y, CANTWELL W J. Interfacial fracture of the fibre-metal laminates based on fibre reinforced thermoplastics[J]. Materials & Design, 2015, 66: 446. DOI:10.1016/j.matdes.2014.03.058 |
| [10] |
WOLLMANN T, HAHN M, WIEDEMANN S, et al. Thermoplastic fibre metal laminates: Stiffness properties and forming behaviour by means of deep drawing[J]. Archives of Civil and Mechanical Engineering, 2018, 18(2): 442. DOI:10.1016/j.acme.2017.09.001 |
| [11] |
RAJABI A, KADKHODAYAN M, MANOOCHEHRI M, et al. Deep-drawing of thermoplastic metal-composite structures: Experimental investigations, statistical analyses and finite element modeling[J]. Journal of Materials Processing Technology, 2015, 215: 159. DOI:10.1016/j.jmatprotec.2014.08.012 |
| [12] |
RAJABI A, KADKHODAYAN M. An investigation into the deep drawing of fibre-metal laminates based on glass fibre reinforced polypropylene[J]. International Journal of Engineering, 2014, 27(3): 349. DOI:10.5829/idosi.ije.2014.27.03c.01 |
| [13] |
DWIVEDI R, AGNIHOTRI G. Study of deep drawing process parameters[J]. Materials Today: Proceedings, 2017, 4(2): 820. DOI:10.1016/j.matpr.2017.01.091 |
| [14] |
SOKOLOVA O A, CARRADO A, PALKOWSKI H. Metal-polymer-metal sandwiches with local metal reinforcements: A study on formability by deep drawing and bending[J]. Composite Structures, 2011, 94(1): 1. DOI:10.1016/j.compstruct.2011.08.013 |
| [15] |
ZEIN H, EI-SHERBINY M, ABD-RABOU M, et al. Effect of die design parameters on thinning of sheet metal in the deep drawing process[J]. American Journal of Mechanical Engineering, 2013, 1(2): 20. DOI:10.12691/ajme-1-2-1 |
| [16] |
WANG Wentian, LOWE A, DAVEY S, et al. Establishing a new forming limit curve for a flax fibre reinforced polypropylene composite through stretch forming experiments[J]. Composites Part A: Applied Science and Manufacturing, 2015, 77: 114. DOI:10.1016/j.compositesa.2015.06.021 |
| [17] |
ZANJANI N A, SEXTON A, KALYANASUNDARAM S. Induced forming modes in a pre-consolidated woven polypropylene composite during stretch forming process at room temperature: I. Experimental studies[J]. Composites Part A: Applied Science and Manufacturing, 2015, 68: 251. DOI:10.1016/j.compositesa.2014.09.023 |
| [18] |
ZANJANI N A, WANG Wentian, KALYANASUNDARAM S. The effect of fibre orientation on the formability and failure behavior of a woven self-reinforced composite[J]. Journal of Manufacturing Science and Engineering, 2015, 137(5): 051012. DOI:10.1115/1.4030894 |
| [19] |
SUN Guangyong, ZHANG Wenxu, WANG Zhen, et al. A novel specimen design to establish the forming limit diagram for GFRP through stamping test[J]. Composites Part A: Applied Science and Manufacturing, 2020, 130: 105737. DOI:10.1016/j.compositesa.2019.105737 |
| [20] |
WANG Wentian, LOWE A, KALYANASUNDARAM S. Investigating the forming limits of a flax fibre-reinforced polypropylene composite in different water treatment conditions[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87: 103. DOI:10.1007/s00170-016-8492-9 |
 2022, Vol. 54
2022, Vol. 54


