2. 西安市智慧高速公路信息融合与控制重点实验室(长安大学),西安 710064
2. Xi'an Key Laboratory of Intelligent Expressway Information Fusion and Control (Chang'an University), Xi'an 710064, China
随着无人机的迅速发展,基于相关滤波器的航拍跟踪方法成为目前的研究热点[1]。文献[2]首次在目标跟踪中应用相关滤波,并结合灰度特征提出了MOSSE滤波器; 文献[3]通过引入循环矩阵,提出了CSK算法,解决了样本冗余问题; 在此基础上,文献[4]结合多通道方向梯度直方图(histogram of oriented gradient,HOG)特征[5]提出了KCF算法; 文献[6]利用颜色名(color name,CN)属性提出了一种自适应颜色属性相关滤波器ACNCF。上述MOSSE、CSK、KCF和ACNCF算法都采用固定的跟踪窗口,无法适应目标尺度的变化。为了解决该问题,文献[7]提出了DSST算法,添加了尺度估计的相关滤波器,但额外训练增加了计算量; 文献[8]引入空间正则化提出了SRDCF算法,但采用的迭代方式求解速度很慢; 文献[9]结合HOG与颜色直方图两种特征,提出了Staple互补分类器,但其跟踪结果易受复杂环境影响; 文献[10]提出了BACF算法,对背景辨识能力较强,但目标严重遮挡时其跟踪精度低; 文献[11]提出了ECO算法,跟踪耗时较多; 为缓解滤波器退化的问题,文献[12]提出了STRCF算法,在目标状态突变时限制滤波器的更新速度,但目标遮挡时其跟踪表现不好; 文献[13]提出了LCT跟踪算法,将在线随机蕨分类器用于目标重检测,但其寻优精度和收敛速度仍需进一步提升。因此,本文提出了一种航拍目标的长期跟踪算法,从建立鲁棒性外观模型、缓解边界效应、防止滤波器退化、目标重检测4个角度改进传统算法,提升了计算精度和速度,解决了目标遮挡、移出视野等问题。
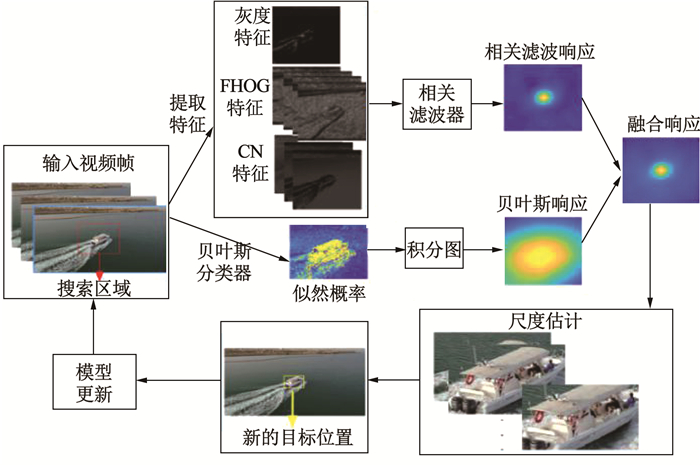
1 改进算法 1.1 多特征互补分类器自适应融合设计在相关滤波器中,将FHOG特征、CN特征和灰度特征进行特征融合,在贝叶斯分类器中则使用颜色直方图特征。二者组成互补分类器,利用多特征的优势构建鲁棒性的外观模型。改进算法流程见图 1。
|
图 1 互补分类器多特征融合算法框图 Fig. 1 Block diagram of multi-feature fusion algorithm of complementary classifier |
统计目标前景和背景颜色直方图,分别记为HO和HB,根据贝叶斯后验概率预测图像块中每个像素点x的目标概率,计算方式如式(1)所示:
| $ \begin{gathered} P\left(x \in \boldsymbol{O} \mid \boldsymbol{O}, \boldsymbol{B}, b_{x}\right) \approx \\ P\left(b_{x} \mid x \in \boldsymbol{O}\right) P(x \in \boldsymbol{O}) \\ \sum\nolimits_{\boldsymbol{\varOmega} \in\{\boldsymbol{O}, \boldsymbol{B}\}} P\left(b_{x} \mid x \in \boldsymbol{\varOmega}\right) P(x \in \boldsymbol{\varOmega}) \end{gathered} $ | (1) |
式中:O和B分别表示目标前景和背景区域,bx代表某个像素点x的值位于直方图第b个区间中。
式(1)化简为
| $ P\left(x \in \boldsymbol{O} \mid \boldsymbol{O}, \boldsymbol{B}, b_{x}\right) \approx \frac{\boldsymbol{H}_{\rm O}\left(b_{x}\right)}{\boldsymbol{H}_{\rm O}\left(b_{x}\right)+\boldsymbol{H}_{\mathrm{B}}\left(b_{x}\right)} $ | (2) |
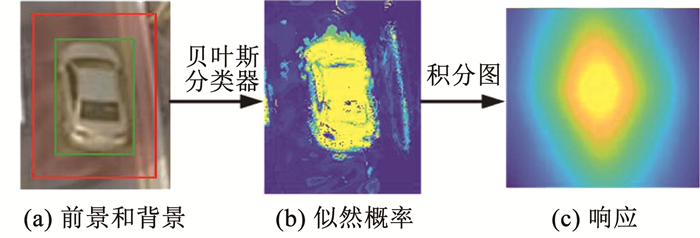
根据式(2)得到似然概率图,利用积分图计算似然概率图中与目标尺寸大小相关的矩形区域内所有像素之和,获得贝叶斯分类器的响应见图 2。
|
图 2 目标前景和背景、似然概率以及贝叶斯分类器响应 Fig. 2 Diagram of target foreground and background, likelihood probability, and Bayesian classifier response |
积分图上(x, y)处的值S(x, y)为
| $ \boldsymbol{S}(x, y)=\sum\limits_{x_{1} \leqslant x, y_{1} \leqslant y} \boldsymbol{L}\left(x_{1}, x_{2}\right) $ | (3) |
式中: L(x1, x2)为似然概率图位置(x1, x2)的概率值,S(x, y)为(x, y)左上角区域中概率值之和。通过式(4),可以快速计算任意矩形区域中所有概率值的和,也即响应图。
| $ \boldsymbol{R}_{\text {hist }}(m, n)=\boldsymbol{S}(x, y)+\boldsymbol{S}(u, v)-\boldsymbol{S}(x, v)-\boldsymbol{S}(u, y) $ | (4) |
式中:Rhist为贝叶斯分类器响应,(x, y)为矩形右下角坐标,(u, v)为矩形左上角坐标,m和n分别为矩形长和宽。
颜色直方图在线更新为
| $ \left\{\begin{array}{l} \boldsymbol{H}_{\rm O}^{t}=\left(1-\eta_{\text {hist }}\right) \boldsymbol{H}_{\rm O}^{t-1}+\eta_{\text {hist }} \widetilde{\boldsymbol{H}}_{\rm O}^{t} \\ \boldsymbol{H}_{\mathrm{B}}^{t}=\left(1-\eta_{\text {hist }}\right) \boldsymbol{H}_{\mathrm{B}}^{t-1}+\eta_{\text {hist }} \widetilde{\boldsymbol{H}}_{\mathrm{B}}^{t} \end{array}\right. $ | (5) |
式中:ηhist为学习率,HOt、HBt和
将一幅RGB彩色图像变换为单通道的灰度图像有多种形式,本文使用的形式为
| $ G=R \times 0.299+G \times 0.587+B \times 0.114 $ | (6) |
FHOG特征提取的过程为:1)建立像素级特征映射;2)空间聚合, 将梯度方向划分为18个方向敏感通道和9个方向不敏感通道;3)归一化和截断。
根据4个相对邻域定义归一化因子:
| $ \begin{aligned} F_{\delta, \gamma}(i, j)=&\left(\|\boldsymbol{C}(i, j)\|^{2}+\|\boldsymbol{C}(i+\delta, j+\gamma)\|^{2}+\right.\\ &\left.\|\boldsymbol{C}(i, j+\gamma)\|^{2}+\|\boldsymbol{C}(i+\delta, j)\|^{2}\right)^{1 / 2} \end{aligned} $ | (7) |
式中:δ,γ∈{i, j}; C(i, j)为单元特征向量; Eβ(v)表示向量v用β截断,将向量v中大于β的值设为β。对cell特征归一化和截断后,串联起来得到新的特征:
| $ \boldsymbol{H}(i, j)=\left(\begin{array}{l} E_{\beta}\left(\boldsymbol{C}(i, j) / F_{-1,-1}(i, j)\right) \\ E_{\beta}\left(\boldsymbol{C}(i, j) / F_{+1,-1}(i, j)\right) \\ E_{\beta}\left(\boldsymbol{C}(i, j) / F_{+1,+1}(i, j)\right) \\ E_{\beta}\left(\boldsymbol{C}(i, j) / F_{-1,+1}(i, j)\right) \end{array}\right) $ | (8) |
根据方向敏感和不敏通道,最终得到31维FHOG特征[19]。利用RGB值和颜色名之间建立的字典映射表(32 768×10),可以快速提取10维CN特征[20]。将FHOG、CN和1维灰度特征融合,得到一个42维的新特征,构建更加鲁棒的外观模型。在相关滤波框架下目标位置周围提取图像块,并融合3种特征,维数记为k∈{1,…,K}。岭回归训练得到滤波器h如下:
| $ \underset{\boldsymbol{h}}{\operatorname{argmin}}\left\{\left\|\sum\limits_{k=1}^{K} \boldsymbol{h}^{k} \otimes \boldsymbol{\phi}^{k}-y\right\|+\lambda \sum\limits_{k=1}^{K} \boldsymbol{h}^{k}\right\} $ | (9) |
式中:hk和ϕk为k通道的滤波器和特征,⊗为循环相关操作,y为高斯期望输出,参数λ为正则化项。对式(9)求解可得到滤波器h。直接求解无法解决边界效应和滤波器退化问题,故后续还需加入自适应时空正则化设计。
1.1.3 互补分类器自适应融合设计贝叶斯分类器可以较好区分目标和背景,但对光照变化、目标相似物比较敏感。而多特征相关滤波对目标形状变化比较敏感。如果某个分类器受复杂环境影响导致跟踪结果较差,直接将响应图融合会影响最终跟踪效果,故互补分类器采用自适应融合。在输入视频序列中提取图像块作为搜索区域,对贝叶斯和相关滤波分类器独立训练;利用前者得到每个像素的得分,同时结合积分图计算贝叶斯分类器的响应;然后将后者作用于提取的42维特征,得到相关滤波响应;将两种响应按照图 1融合。定义两种响应中心偏离距离Md,表示如下:
| $ M_{\mathrm{d}}=\sqrt{\left(u_{\mathrm{cf}}-u_{\mathrm{hist}}\right)^{2}+\left(v_{\mathrm{cf}}-v_{\mathrm{hist}}\right)^{2}} $ | (10) |
式中(ucf, vcf)和(uhist, vhist)分别为相关滤波器和贝叶斯分类器的响应图峰值位置。根据Md可得到响应偏移,但无法估计跟踪可靠性。另外,贝叶斯鲁棒性不如相关滤波器,故根据贝叶斯响应去判断跟踪可靠性Mh,定义为
| $ M_{\mathrm{h}}=\frac{N\left(\boldsymbol{R}_{\text {hist }}>\eta_{\mathrm{h}} \max \left(\boldsymbol{R}_{\text {hist }}\right)\right)}{S_{\mathrm{m}} \times S_{\mathrm{n}}} $ | (11) |
式中:N(Rhist>ηhmax(Rhist))表示区域响应图中响应值大于ηhmax(Rhist)的像素数;Sm×Sn为响应图尺寸;参数ηh用于控制响应值的变化范围。定义第t帧的自适应融合状态SA(t)如下所示(τd和τh为阈值参数):
| $ S_{\mathrm{A}}(t)=\left\{\begin{array}{l} 1, \text { if } M_{\mathrm{d}}>\tau_{\mathrm{d}} \text { and } M_{\mathrm{h}}>\tau_{\mathrm{h}} \\ 0, \text { otherwise } \end{array}\right. $ | (12) |
1) SA(t)为1时,表示贝叶斯响应是可靠的,将其与相关滤波的响应图线性融合,得到融合响应图:
| $ \boldsymbol{R}=(1-\alpha) \boldsymbol{R}_{\mathrm{cf}}+\alpha \boldsymbol{R}_{\text {hist }} $ | (13) |
式中:Rcf为相关滤波分类器响应,Rhist为贝叶斯分类器响应,α为常数融合系数。
2) 当SA(t)为0时,表示响应不确定,采用自适应融合策略,调整式(8)为
| $ \boldsymbol{R}=\left(1-\alpha^{\prime}\right) \boldsymbol{R}_{\mathrm{cf}}+\alpha^{\prime} \boldsymbol{R}_{\mathrm{hist}} $ | (14) |
式中α′表示贝叶斯分类器响应图在融合响应中的占比。
1.2 自适应时空正则化 1.2.1 拟解决的两个问题1) 边界效应问题。边界效应严重限制了跟踪性能,讨论如下:a)训练阶段:循环位移产生大量样本,但只有一个是真实的,滤波器训练前样本集需要叠加余弦窗,消除样本边界的不连续性,减少不合理样本。但余弦窗将边缘区域像素全变成零,会滤掉需要学习的有限背景信息。b)检测阶段:余弦窗限制了检测区域,简单扩充检测图像块会降低算法速度。如果目标移动到检测区域边缘,部分目标像素会被余弦窗过滤掉,造成跟踪结果变差;一旦部分目标移出检测区域,此时余弦窗会过滤掉仅存的目标像素,造成跟踪失败。
2) 滤波器退化问题。相关滤波跟踪器通常在每一帧中更新模型,当遇到目标遮挡、移出视野等复杂场景时,会造成滤波器的污染和退化,导致跟踪失败。为解决边界效应问题,当前多采用扩大搜索区域的方式,会引入大量背景信息供滤波器学习,遮挡、光照变化等也会加重滤波器的退化。
1.2.2 响应变化定义局部响应变化向量Π=[|Π1|, |Π2|, …, |ΠT|],在目标边界框中的二维可视化,为空间正则化做准备,它的第i个元素|Πi|定义为
| $ \boldsymbol{\varPi}{}^{i}=\frac{\boldsymbol{R}_{t}\left[\boldsymbol{\psi}_{\Delta}\right]^{i}-\boldsymbol{R}_{t-1}{}^{i}}{\boldsymbol{R}_{t-1}{}^{i}} $ | (15) |
式中:Rt[ψΔ]为平移算子,可以使两个响应图Rt和Rt-1中的两个峰重合,消除运动影响; Ri为响应图R中第i个元素。定义全局响应变化变量Π2,表示两个响应图的变化,这里使用欧几里得范数定义,公式如下:
| $ {\varPi}_{2}=\left\|\boldsymbol{R}_{t}\left[\psi_{\Delta}\right]-\boldsymbol{R}_{t-1}\right\|_{2}^{2} $ | (16) |
Π还表示跟踪框的局部可信度,光照变化或者部分遮挡的情况下都能使外观的可信度降低,滤波器在学习这些外观时应受到惩罚,避免受到干扰。过大的Π2可能表示跟踪结果错误,应停止滤波器学习。相对较大的值则加速滤波器学习,提高目标对环境变化的适应性。
1.2.3 模型自适应时空正则化1) 自适应空间正则化
像素可信度较低的滤波器在学习时应加以限制,这里通过空间正则化参数
| $ \tilde{\boldsymbol{u}}=\boldsymbol{P}^{\mathrm{T}} \delta \log (\boldsymbol{\varPi}+1)+\boldsymbol{u} $ | (17) |
式中:
2) 自适应时间正则化
引入时间正则化,滤波器的变化率在损失函数中由固定参数θ惩罚,但这并不通用。故尝试通过联合优化惩罚项和滤波器确定超参数值。因此,定义了一个参考值
| $ \tilde{\theta}=\frac{\zeta}{1+\log \left(\nu \varPi_{2}+1\right)}, \varPi_{2} \leqslant \phi $ | (18) |
式中ζ和ν表示超参数。当Π2高于阈值ϕ时,即响应图中存在畸变,滤波器停止学习; 如果低于ϕ,响应图变化越剧烈,
根据全局响应自适应调整滤波器的学习,可以减缓滤波器退化,但随着模型更新中的累积误差,还可能产生跟踪漂移。更新过程中唯一确认没有受污染的是初始滤波器。如果滤波器与初始滤波器变化过大,模型很可能完全退化了,需要改进。在学习过程中,应该考虑用初始滤波器去约束更新范围。根据最近Nr帧滤波器的平均值与初始滤波器的差值变化来惩罚滤波器的学习,为了优化求解方便,前Nr帧不根据初始滤波器对滤波器的学习进行惩罚, 公式如下:
| $ \overline{\boldsymbol{h}}{}_{N_{\mathrm{r}}}^{k}=\left\{\begin{array}{l} \boldsymbol{h}_{1}^{k}, t<N_{\mathrm{r}} \\ \frac{1}{N_{\mathrm{r}}} \sum\limits_{t=t-N_{\mathrm{r}}-1}^{t} \boldsymbol{h}{}_{t}^{k}, t \geqslant N_{\mathrm{r}} \end{array}\right. $ | (19) |
式中:
| $ \begin{gathered} \varepsilon\left(\boldsymbol{H}_{t}, \theta_{t}\right)=\frac{1}{2}\left\|y-\sum\limits_{k=1}^{K} \boldsymbol{h}{}_{t}^{k} \otimes \boldsymbol{\phi}{}_{t}^{k}\right\|_{2}^{2}+ \\ \frac{1}{2} \sum\limits_{k=1}^{K}\left\|\tilde{\boldsymbol{u}} \odot \boldsymbol{h}{}_{t}^{\boldsymbol k}\right\|+\frac{\theta_{t}}{2} \sum\limits_{k=1}^{K}\left\|\boldsymbol{h}{}_{t}^{k}-\boldsymbol{h}_{t-1}^{k}\right\|+ \\ \frac{1}{2}\left\|\theta_{t}-\tilde{\theta}\right\|_{2}^{2}+\frac{\theta_{1}}{2} \sum\limits_{k=1}^{K}\left\|\overline{\boldsymbol{h}}{}_{N_{\mathrm{r}}}^{k}-\boldsymbol{h}_{1}^{k}\right\| \end{gathered} $ | (20) |
式中:
采用ADMM优化求解式(20),构建辅助变量
| $ \begin{gathered} L_{t}\left(\boldsymbol{H}_{t}, \theta_{t}, \hat{\boldsymbol{G}}_{t}, \hat{\boldsymbol{M}}_{t}\right)=\varepsilon\left(\boldsymbol{H}_{t}, \theta_{t}, \hat{\boldsymbol{G}}_{t}\right)+ \\ \frac{\gamma}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\sqrt{T} \boldsymbol{F} \boldsymbol{h}{}_{t}^{k}\right\|_{2}^{2}+ \\ \sum\limits_{k=1}^{K}\left(\hat{\boldsymbol{g}}{}_{t}^{k}-\sqrt{T} \boldsymbol{F} \boldsymbol{h}{}_{t}^{k}\right)^{\mathrm{T}} \hat{\boldsymbol{m}}{}_{t}^{k} \end{gathered} $ | (21) |
式中:
| $ \boldsymbol{V}{}_{t}^{k}=\frac{\boldsymbol{m}{}_{t}^{k}}{\gamma}\left(\boldsymbol{V}{}_{t}^{k}=\left[V_{t}^{1}, V_{t}^{2}, \cdots, V_{t}^{K}\right]\right) $ | (22) |
式(21)可以变换为
| $ \begin{gathered} L_{t}\left(\boldsymbol{H}_{t}, \theta_{t}, \hat{\boldsymbol{G}}_{t}, \hat{\boldsymbol{V}}_{t}\right)=\varepsilon\left(\boldsymbol{H}_{t}, \theta_{t}, \hat{\boldsymbol{G}}_{t}\right)+ \\ \frac{\gamma}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\sqrt{\boldsymbol{T}} \boldsymbol{F} \boldsymbol{h}{}_{t}^{k}+\hat{\boldsymbol{v}} k_{t}\right\|_{2}^{2} \end{gathered} $ | (23) |
利用ADMM求解以下子问题:
1) 子问题
| $ \begin{gathered} \hat{\boldsymbol{G}}^{*}=\underset{\hat{\boldsymbol{G}}}{\operatorname{argmin}}\left\{\frac{1}{2}\left\|\hat{y}-\sum\limits_{k=1}^{K} \hat{\boldsymbol{g}}{}_{t}^{k} \otimes \hat{\boldsymbol{\phi}}{}_{t}^{k}\right\|_{2}^{2}+\right. \\ \frac{\theta_{t}}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\hat{\boldsymbol{g}}_{t-1}^{k}\right\|_{2}^{2}+ \\ \left.\frac{\gamma}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\sqrt{{T}} \boldsymbol{F} \boldsymbol{h}{}_{t}^{k}+\hat{\boldsymbol{v}}{}_{t}^{k}\right\|_{2}^{2}\right\} \end{gathered} $ | (24) |
式中*为子问题的最优解。式(24)直接求解非常困难,因此,在每个像素的K个通道对
| $ \boldsymbol{\varGamma}_{j}^{*}\left(\hat{\boldsymbol{G}}_{t}\right)=\frac{1}{\gamma+\theta_{t}}\left(\mathrm{I}-\frac{\boldsymbol{\varGamma}_{j}\left(\hat{\boldsymbol{\varPhi}}_{t}\right) \boldsymbol{\varGamma}_{j}\left(\hat{\boldsymbol{\varPhi}}_{t}\right)^{T}}{\theta_{t}+\gamma+\boldsymbol{\varGamma}_{j}\left(\hat{\boldsymbol{\varPhi}}_{t}\right)^{T} \boldsymbol{v}_{j}\left(\hat{\boldsymbol{\varPhi}}_{t}\right)}\right) \boldsymbol{\rho} $ | (25) |
式中
向量ρ采用式(26)表示如下:
| $ \boldsymbol{\rho}=\boldsymbol{\varGamma}_{j}(\hat{\boldsymbol{\varPhi}}) \hat{\boldsymbol{y}}_{j}+\theta_{t} \boldsymbol{\varGamma}_{j}\left(\hat{\boldsymbol{G}}_{t-1}\right)-\gamma \boldsymbol{\varGamma}_{j}\left(\hat{\boldsymbol{V}}_{t}\right)+\gamma \boldsymbol{\varGamma}_{j}\left(\sqrt{T} \boldsymbol{F} \boldsymbol{H}_{t}\right) $ | (26) |
2) 子问题h:
| $ \begin{aligned} \boldsymbol{h}^{k *}=\underset{\boldsymbol{h}^{k}}{\operatorname{argmin}} &\left\{\frac{1}{2}\left\|\tilde{\boldsymbol{u}} \odot \boldsymbol{h}{}_{t}^{k}\right\|_{2}^{2}+\frac{\theta_{1}}{2} \sum\limits_{k=1}^{K}\left\|\overline{\boldsymbol{h}}_{N_{\mathrm{r}}}^{k}-\boldsymbol{h}_{1}^{k}\right\|_{2}^{2}+\right.\\ &\left.\frac{\gamma}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\sqrt{T} \boldsymbol{F} \boldsymbol{h}{}_{t}^{k}+\hat{\boldsymbol{v}}{}_{t}^{k}\right\|_{2}^{2}\right\} \end{aligned} $ | (27) |
得到hk的解为
| $ \boldsymbol{h}^{k *}=\left\{\begin{array}{l} {\left[\tilde{\boldsymbol{U}}^{\mathrm{T}} \tilde{\boldsymbol{U}}+\gamma T \mathrm{I}\right]^{-1} \gamma T\left(\boldsymbol{v}{}_{t}^{k}+\boldsymbol{g}{}_{t}^{k}\right)=\frac{\gamma T\left(\boldsymbol{v}{}_{t}^{k}+\boldsymbol{g}{}_{t}^{k}\right)}{(\tilde{\boldsymbol{u}} \odot \tilde{\boldsymbol{u}})+\gamma T}, t \leqslant N_{\mathrm{r}}} \\ \frac{\gamma T\left(\boldsymbol{v}{}_{t}^{k}+\boldsymbol{g}{}_{t}^{k}\right)-\theta_{1} \boldsymbol{h}_{1}^{k} / N_{\mathrm{r}}+1 / N_{\mathrm{r}}^{2}\left(\sum\nolimits_{t=t-N_{\mathrm{r}}}^{t-1} \boldsymbol{h}{}_{t}^{k}\right)}{(\tilde{\boldsymbol{u}} \odot \tilde{\boldsymbol{u}})+\gamma T+\theta_{1} / N_{\mathrm{r}}^{2}}, t>N_{\mathrm{r}} \end{array}\right. $ | (28) |
式中
3) 子问题θt:
| $ \begin{aligned} \theta_{t}^{*}=\underset{\theta_{t}}{\operatorname{argmin}} &\left\{\frac{\theta}{2} \sum\limits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\hat{\boldsymbol{g}}_{t-1}^{k}\right\|_{2}^{2}+\frac{1}{2}\left\|\theta_{t}-\tilde{\theta}\right\|_{2}^{2}\right\}=\\ & \tilde{\theta}-\frac{\sum\nolimits_{k=1}^{K}\left\|\hat{\boldsymbol{g}}{}_{t}^{k}-\hat{\boldsymbol{g}}_{t-1}^{k}\right\|_{2}^{2}}{2} \end{aligned} $ | (29) |
4) 拉格朗日乘子更新:在解决了上述3个子问题后,可以将拉格朗日乘子更新为
| $ \hat{\boldsymbol{V}}{}^{i+1}=\hat{\boldsymbol{V}}{}^{i}+\gamma^{i}\left(\hat{\boldsymbol{G}}{}^{i+1}-\hat{\boldsymbol{H}}{}^{i+1}\right) $ | (30) |
式中i和i+1为迭代索引。步长正则化常数γ(初始等于1)的形式为
| $ \gamma^{(i+1)}=\min \left(\gamma_{\max }, \beta \gamma^{i}\right), \beta=10, \gamma_{\max }=10\ 000 $ | (31) |
通过迭代求解上述4个子问题,可以有效优化目标函数,在t帧中得到最优滤波器
| $ \boldsymbol{R}_{t}=I_{\mathrm{FT}}\left[\sum\limits_{k=1}^{K}\left(\hat{\boldsymbol{z}}{}_{t}^{k} \odot \hat{\boldsymbol{g}}_{t-1}^{k}\right)\right] $ | (32) |
式中:Rt为第t帧响应图,IFT为傅里叶逆变换操作,
为解决目标尺寸变化问题[14],引入尺度相关滤波器。提取多个不同尺度样本,建立尺度金字塔。设目标为P×R,提取s个大小为anP×anR的训练样本,a为尺度系数,n∈{[(-s-1)/2], …, [(s-1)/2]},所有样本调整到相同的一维尺寸。通过计算最大响应获得目标尺度。
1.4 模型自适应更新传统相关滤波跟踪算法每一帧更新模型比较耗时,需要采用稀疏更新来优化,即目标变化足够大时再更新滤波器,这样会带来不必要的计算。因此,本文每Ns帧更新一次滤波器,尺度模型仍每帧更新一次,不受Ns影响。大量实验表明,因为稀疏更新减少了对最近训练样本的过拟合,模型适度不频繁更新反而会提升跟踪效果。此外,还有利于样本受到遮挡影响时,模型学习到较少的干扰噪声。贝叶斯分类器中颜色直方图模型每帧都更新,但缺少评估当前跟踪状态,易学习到较多噪声。故引入一种自适应方式进行更新。当Π2>ϕ时,说明出现了光照变化、遮挡及移除视野等情况,自适应融合状态SA(t)认为颜色响应可能不可靠。此时仍快速更新,会造成模型漂移,因此需对学习率ηhist进行调整,公式为
| $ \eta_{\text {hist }}=\left\{\begin{array}{l} \varepsilon \times \eta^{\prime}{ }_{\text {hist }}, \text { if } S_{\mathrm{A}}(t)=1 \text { or } \varPi_{2}>\phi \\ \eta^{\prime}{}_{\text {hist }}, \text { otherwise } \end{array}\right. $ | (33) |
式中η′hist为颜色直方图模型的初始学习率,跟踪可靠时用来更新;不可靠时,用参数ε(0 < ε < 1)修正学习率。
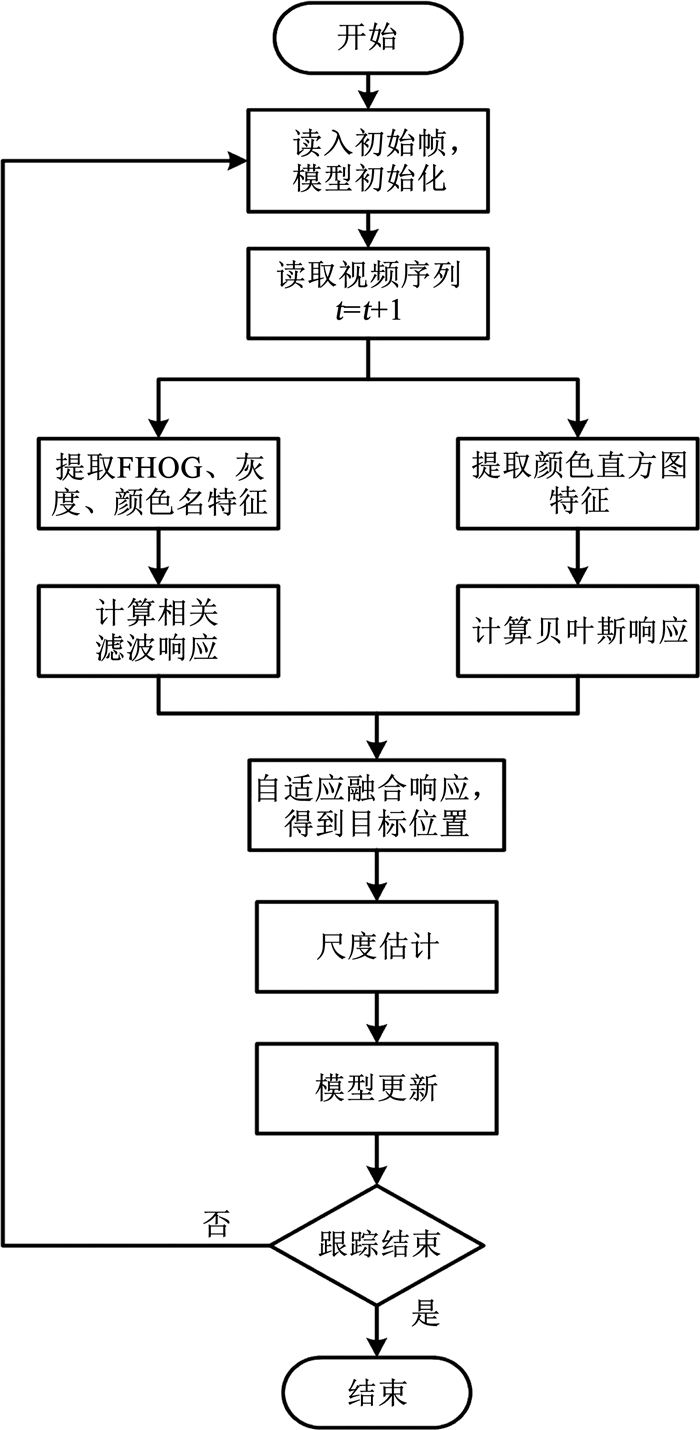
1.5 算法流程自适应时空正则化跟踪算法流程见图 3。
|
图 3 本文算法流程图 Fig. 3 Flow chart of proposed algorithm |
加入重检测模块可以检测目标跟踪质量。当检测到跟踪不可靠时,恢复丢失目标,从而提高处理异常情况的鲁棒性。但频繁调用检测器,会影响算法的速度。
2.1 跟踪不确定性检测相关滤波器根据相关响应进行目标定位,为了防止滤波器退化,设计一种新的不确定性检测机制qt,通过峰值旁瓣比PSR和峰值绝对值定义,如式(34)所示:
| $ q_{t}=P_{\mathrm{SR}}\left(\boldsymbol{R}_{t}\right) \cdot \max \left(\boldsymbol{R}_{t}\right) $ | (34) |
式中Rt为第t帧的相关响应图。在跟踪不确定性检测中,qt的相对值取决于目标外观的变化,是正常跟踪过程中不确定度的一个微弱指标。当在相对较短的时间尺度上出现遮挡时,定位质量将会显著降低。设qt为最近Nq连续帧上计算得到的平均定位质量,如果qt和qt之间的比值超过预定阈值τq,则认为跟踪不确定,即
| $ \bar{q}_{t} / q_{t}>\tau_{\mathrm{q}} $ | (35) |
出现遮挡时,比值显著提高,表明遮挡过程中跟踪高度不确定,见图 4。

|
图 4 平均跟踪质量与当前跟踪质量的比值变化 Fig. 4 Variation of ratio of average tracking quality to current tracking quality |
另外,结合全局响应变量Π2,设计一种新的目标当前跟踪状态判断Ct,如式(36)所示:
| $ C_{t}=\left\{\begin{array}{l} 1, \text { otherwise } \\ 0, \text { if } \bar{q}_{t} / q_{t}>\tau_{\mathrm{q}} \text { or } \varPi_{2}>\phi \end{array}\right. $ | (36) |
式中:τq为比值阈值,ϕ为全局响应阈值。Ct为1表示跟踪状态是可信的,将短期跟踪结果直接输出;Ct为0表示跟踪不确定,需进行目标恢复。
2.2 目标恢复为实现目标恢复,需使用不被错误训练样本污染的视觉模型,即初始化时学习的滤波器。对于短期遮挡而言,可能产生更好检测效果。虽然长期跟踪可以减少短期模型污染,但却无法终止污染。因此,需要维护多个重检测滤波器HDE={hiDE}i∈1, …, NDE,利用更新频率处理污染。上标DE表示变量属于本节的重检测滤波器。滤波器频繁更新可以学习最近的外观变化,能适应目标变化,但也增加了学习噪声的概率。而更新频率较低,遇到干扰较多时,可以增加鲁棒性学习,但也可能因为更新过慢,不能适应目标的快速变化,导致跟踪失败。因此,需维护多个重检测滤波器,其中一个从不更新(初始滤波器),保证出现类似于初始训练视图时,模型可以从污染中恢复。第i个滤波器每niDE帧更新一次,类似于短期滤波器:
| $ \boldsymbol{h}_{i}^{\mathrm{DE}}=(1-\eta) \boldsymbol{h}_{i-1}^{\mathrm{DE}}+\eta \boldsymbol{h}_{t}^{\mathrm{ST}} $ | (37) |
式中:hiDE为保存的第i个检测滤波器,hiST为在第t帧求出的短期跟踪滤波器,ST表示变量属于短期跟踪,即1.2节算法,η为学习率。
目标遮挡消失后重新出现的位置,较大可能就在消失点附近,因此添加了一个随机行走运动模型作为目标搜索区域大小增长方法,也即目标的运动先验,表示为
| $ \begin{gathered} \boldsymbol{\pi}\left(\boldsymbol{X}_{t}\right)=\boldsymbol{N}\left(\boldsymbol{X}_{t} ; \boldsymbol{X}_{\mathrm{c}}, \Sigma_{t}\right)= \\ \exp \left[-\left(\boldsymbol{X}_{t}-\boldsymbol{X}_{\mathrm{c}}\right)^{\mathrm{T}} \Sigma_{t}^{-1}\left(\boldsymbol{X}_{t}-\boldsymbol{X}_{\mathrm{c}}\right) / 2\right] \end{gathered} $ | (38) |
式中:π(Xt)是一个高斯函数,对角协方差Σt=diag(σxt2, σyt2),Xc为最后一个可靠估计的位置中心。Δt为上次确认的跟踪评估与当前帧的差值绝对值。模型方差随Δt增加而逐渐增大,在遮挡时间内逐渐增加尺度搜索,例如[σxt2, σyt2]=[xw, xh]asΔt,其中,as为尺度增长参数,xw和xh分别为目标的长和宽。目标重检测时,从HDE中挑选一个滤波器,对周围零填充,然后与整张图片提取的特征进行相关操作得到响应RDE,与运动先验π(Xt)相乘得到最大响应位置作为待检测的估计位置XtDE,即
| $ \boldsymbol{X}_{t}^{\mathrm{DE}}=\max \left(\boldsymbol{\pi}\left(\boldsymbol{X}_{t}\right) \odot \boldsymbol{R}^{\mathrm{DE}}\right) $ | (39) |
在XtDE周围提取特征后与之前存储的所有滤波器分别进行相关操作。为提升效率,每幅图像只评估单个滤波器,循环使用HDE中所有滤波器和目标大小尺度SDE在随后的图像序列中检测,直到找回目标。通过RDE计算得到跟踪质量qtDE,与短期组件的跟踪质量qtST比较,质量分数较高的位置为最终目标位置估计,公式如下:
| $ \left(\boldsymbol{X}_{t}, q_{t}\right)=\left\{\begin{array}{l} \left(\boldsymbol{X}_{t}^{\mathrm{ST}}, q_{t}^{\mathrm{ST}}\right), q_{t}^{\mathrm{ST}} \geqslant q_{t}^{\mathrm{DE}} \\ \left(\boldsymbol{X}_{t}^{\mathrm{DE}}, q_{t}^{\mathrm{DE}}\right), \text { otherwise } \end{array}\right. $ | (40) |
如果估计的位置是可靠的,短期组件和检测器更新,否则模型不更新。
2.3 算法流程基于重检测的长期跟踪算法,具体流程如下。
步骤1:初始化
长期跟踪器在第1帧时初始化,训练得到初始模型h1ST并保存。在剩余帧中,在不同的时间尺度上保存NDE个视觉模型,用于目标定位和检测HDE={hiDE}i∈1, …, NDE,没有更新的模型等于初始化模型,如h1DE=h1ST。
步骤2:计算相关滤波响应
在第t帧提取前一帧目标定位周围的一个区域,使用短期跟踪滤波器ht-1ST计算相关响应RtST。
步骤3:跟踪可靠性判断
根据相关响应RtST得到目标位置XtST,并计算定位质量qtST和全局响应变量,然后得到目标当前状态判断Ct。当Ct为1时,表示跟踪状态是可信的,将短期跟踪结果直接输出; 当Ct为0时,表示跟踪状态不可信,检测器也会被激活以处理潜在的目标丢失,执行以下步骤。
步骤4:得到相关响应
检测滤波器hiDE从存储的检测器序列HDE选择出来与从整个图像中提取的特征做相关操作。
步骤5:目标定位
将相关响应RDE与运动先验π(Xt)相乘,得到最大响应的位置作为待检测的估计位置XtDE,在XtDE周围提取特征后与之前存储的所有滤波器分别进行相关操作,跟踪质量qtDE相关响应计算得到,然后根据由短期分量估计的位置和由检测器估计的位置。最终目标位置估计为质量分数较高的位置。
步骤6:判断终止条件
判断是否跟踪结束,跟踪未结束则返回步骤1,跟踪结束则完成所有视频序列的目标跟踪。
1) 实验环境为:MATLAB 2018a,CPU:I7-8700HQ,RAM:16 GB,tracker_benchmark_v1.1测评工具。
2) 实验采用UAV123数据集[18],包含无人机在低空拍摄获取的123个视频序列,用于跟踪测试,其中包括20个长期跟踪序列,称为UAV20L,用于测试长期跟踪性能。在所有序列中都使用矩形框对目标进行了标注。包括12种视觉属性标注,用于在不同场景下跟踪器的评估:相似目标(similar object,SOB)、相机运动(camera motion,CM)、快速运动(fast motion,FM)、光照变化(illumination variation,IV)、背景干扰(background clutter,BC)、长宽比变化(aspect ratio change,ARC)、部分遮挡(partial occlusion,POC)、完全遮挡(full occlusion,FOC)、移出视野(out-of-view,OV)、低分辨率(low resolution,LR)、尺度变换(scale variation,SV)和视点变化(viewpoint change,VC)。
3) 评价参数
a) 精确度指中心位置误差(center location error,CLE)小于某一阈值的帧数与总帧数的比值,表达式为
| $ C_{\mathrm{LE}}=\sqrt{\left(x_{t}-x_{t}^{\text {truth }}\right)^{2}+\left(y_{t}-y_{t}^{\text {truth }}\right)^{2}} $ | (41) |
式中: (xt, yt)为跟踪得到的目标中心,(xttruth, yttruth)为人工标注目标中心。精确度图可以反映目标跟踪算法的定位目标中心的性能。本文设定阈值为20像素。
b) 成功率指重叠率(overlap rate,OR)大于某阈值的帧数与总帧数的比值。OR计算式为
| $ O_{\mathrm{R}}=\frac{\left|\boldsymbol{r}_{t} \cap \boldsymbol{r}_{t}^{\text {truth }}\right|}{\left|\boldsymbol{r}_{t} \cup \boldsymbol{r}_{t}^{\text {truth }}\right|} $ | (42) |
式中: rt为跟踪框,rttruth为人工标注框。成功率图显示的数字代表曲线下面积(area under the curve,AUC)。
3.2 自适应时空正则化实验本文算法用Our表示,对比算法为ECO_HC[11]、STRCF[12]、BACF[10]、AutoTrack[15]、DSST[7]、fDSST[16]、Staple[9]、Staple_CA[17]、LCT[13]、KCF[4]。
3.2.1 实验参数相关滤波分类器中,自适应时空正则化参数δ=0.2,ζ=13,θ1=0.1,ν=2*10-5,Nr=100,全局响应阈值ϕ=3 000,ADMM迭代次数设为4,滤波器更新频率Ns=3。贝叶斯分类器中,颜色直方图划分为32个区间,学习率ηhist=0.04,参数ε=0.01。阈值τd=0.6,τh=25,ηh=0.8,融合系数a=0.3,自适应融合系数α′=0.1,目标区域的尺寸被统一缩放到150*150。尺度估计中a=1.02,尺度s=33。
3.2.2 定量分析1) 总体性能评估
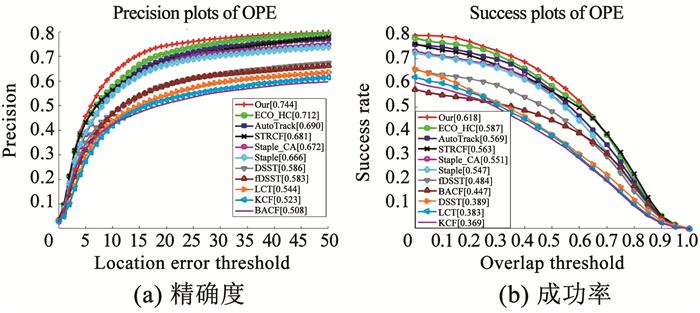
本文算法的精确度和成功率分别为0.744和0.511,在比较的跟踪器中排名第一,见图 1。实验表明本文算法精确度比ECO_HC、AutoTrack、Staple和STRCF分别提升了2.8%、7.8%、11.7%和9.3%,成功率分别提升了4.5%、7.4%、13.6%和6.2%。
|
图 5 11种算法在UAV123数据集上的结果 Fig. 5 Results of 11 algorithms on UAV123 dataset |
本文算法运行速度为64.2帧/s,与其他几种算法相比,本文算法在成功率和精确度得到提升的同时,速度上仍满足实时性。算法速度对比结果见表 1。
| 表 1 11种算法速度对比 Tab. 1 Comparison of calculation speed of 11 algorithms |
2) 属性性能分析
图 6和表 2为11种算法在UAV123数据集12种属性下的成功率。表 2中加粗代表成功率排名第一,可知本文算法的成功率在SOB、CM、FM、IV、BC、ARC、POC、LR、SV和VC 10种属性下排名第一;OV情况下与STRCF并列第一;在FOC情况下排名第二,但与排名第一的ECO_HC相差较小,属于误差允许范围内。因为视频属性标注是直接对一整段视频标注,而有的视频帧与标注属性并不符合,因此只需在整体数据集和大部分属性上性能优异即可。
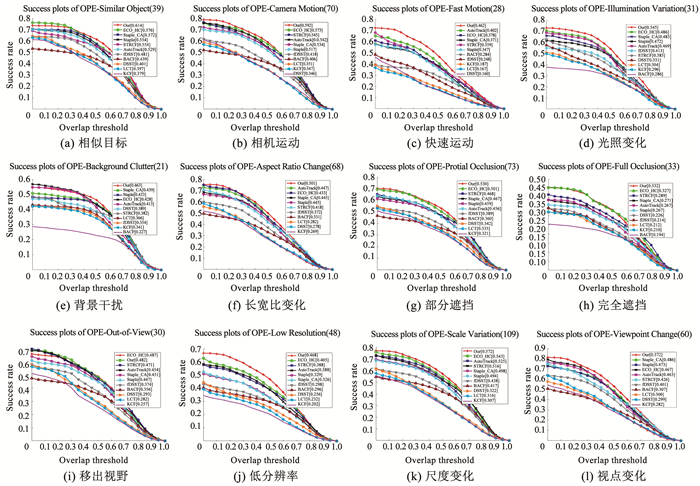
|
图 6 11种算法在UAV123数据集12种属性下成功率的定性分析 Fig. 6 Qualitative analysis of success rate of 11 algorithms on UAV123 dataset under 12 attributes |
| 表 2 11种算法在UAV123数据集12种属性下成功率的定量分析 Tab. 2 Quantitative analysis of success rate of 11 algorithms on UAV123 dataset under 12 attributes |
由表 2可以看出,在完全遮挡情况下,所有跟踪算法成功率都较低,还需要重检测设计。
3.2.3 定性分析为直观分析跟踪性能,选取UAV123数据集中有代表性的视频序对本文与其他10种算法进行比较。完全遮挡情况下所有算法跟踪成功率都较低,故将遮挡属性单独定性分析(图 7),而将其他属性一起定性分析(图 8)。
1) 遮挡属性分析
a) 在序列car9_1的285帧,目标受相似目标干扰,LCT算法直接跟踪失败,在853帧目标受到部分遮挡后,只有BACF和本文算法能跟踪上目标。
b) 在序列car14_1的828帧,目标到达图像边缘,经历了POC、FOC和OV,在930帧进入视野。随着尺度变化,在1 248帧时,此时只有本文算法能够成功跟踪,其他所有算法,随着跟踪过程累积误差造成跟踪失败,并再也无法找回目标。
c) 在序列group2_2_1的1 284帧受背景干扰,BACF跟踪失败;在1 476帧时,目标经历POC和FOC,KCF、AutoTrack、LCT、Staple跟踪失败;在1 620帧时,fDSST跟踪失败,此时本文算法仍然能正常跟踪。
d) 在序列person10_1的191帧目标经历了POC、FOC和OV,在280帧时重新回到视野,此时所有算法全部跟踪失败。
e) 在序列person14_1_1的151帧目标经历了POC和FOC,204帧重新回到视野,此时所有算法跟踪失败。
f) 在序列person19_3_1的3 072帧,目标出现POC和FOC,在3 246帧时重新回到视野,此时所有算法全部跟踪失败,并且都不能找回丢失的目标。
本文算法能在car9_1、car14_1,group2_2_1序列跟踪上目标。在person10_1、person14_1_1、person19_3_1序列中,所有算法都跟踪失败,说明防止退化的方法有一定作用,但针对遮挡和离开视野问题仍需进一步改进。
2) 其他属性分析
a) 序列boat9中目标经历了SV、ARC和LR。在835帧,KCF和LCT随着模型累计误差,跟踪器完全退化;在1 309帧,目标尺度和长宽比变化较大,大多数跟踪器跟踪框与目标相差较多,说明已累积了较多误差。
b) 在序列car16_1_1的246帧中存在FM和SV,大多跟踪器累积了较多误差,与真实目标框相差较多,在385帧6个跟踪器跟踪失败。
c) 序列wakeboard5_1中目标经历了POC、SV和FM。在463帧,Staple、BACF、fDSST、LCT、KCF跟踪失败; 在792帧STRCF跟踪失败; 在1062帧Staple_CA跟踪失败。只有本文算法、ECO_HC、AutoTrack和DSST跟踪成功,但前两种算法跟踪框更接近目标框。
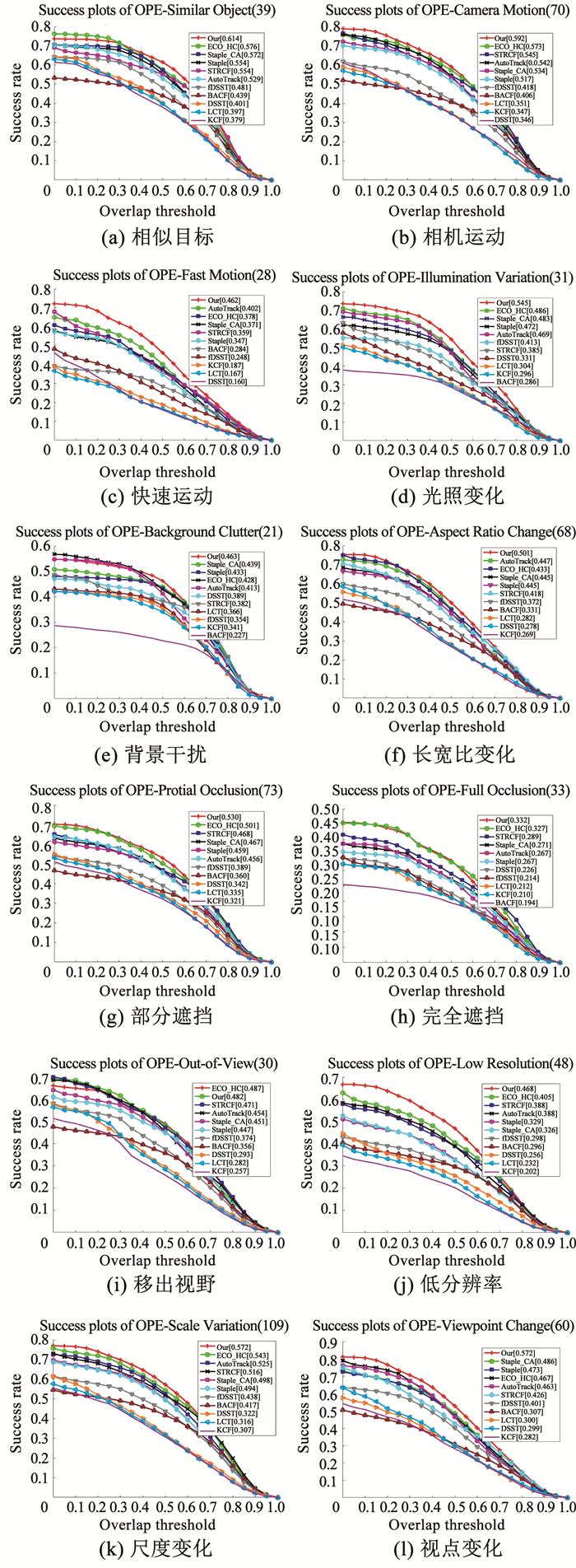
|
图 7 11种算法在6组序列跟踪结果(遮挡属性) Fig. 7 Tracking results of 11 algorithms on six sets of sequences (occlusion attribute) |

|
图 8 11种算法在6组序列跟踪结果(其他属性) Fig. 8 Tracking results of 11 algorithms on six sets of sequences (other attributes) |
d) 序列wakeboard6_1中目标经历了POC、SV和FM。在102帧,DSST、LCT、KCF跟踪失败;在485帧,除了本文算法, 其他算法都跟踪失败,并从690帧和1 104帧可以看出,后续只有本文算法能正确跟踪目标。
e) 在序列person12_2_1的102帧,目标受到IV影响,BACF、fDSST、KCF、LCT、DSST跟踪失败,在1 057帧目标由阴影进入阳光下,此时AutoTrack也跟踪失败;1 319帧目标被遮挡,Staple_CA与Staple跟踪失败,只有本文算法和ECO_HC能成功跟踪目标。
f) 序列car10_1中目标经历了SV和SOB。从199帧、426帧、700帧可以看出,环境变化相对简单时所有算法都能较好地跟踪目标。
3.3 重检测实验1) 实验参数
a) 参数设置:短期跟踪器的参数与前文相同。重检测滤波器数量NDE=5,其中每个重检测滤波器更新频率niDE={0,1/180,1/90,1/15,1/3},尺度因子为{0.5,0.7,1,1.2,1.5,2},学习率η=0.02,随机运动模型尺度增长参数设置为as=1.05,不确定性阈值τq=2.7,全局响应阈值ϕ=3 000,最近帧Nq=90。
b) 对比算法为:ECO_HC、STRCF、BACF、AutoTrack、DSST、fDSST、Staple、Staple_CA、LCT、KCF,短时跟踪算法用Our表示,本节算法用Our_LT表示。
2) 定量分析
a) 总体性能评估。本文方法的精确度和成功率分别为0.725和0.507,在比较的跟踪器中排名第一,见图 9。实验结果表明,加入重检测模块后比Our的精确度和成功率分别提升了18.5%和12.4%;与ECO_HC、AutoTrack、Staple和STRCF相比,Our_LT算法准确度分别提升了29.5%、45.3%、53.3%和26.1%,成功率分别提升了20.7%、46.5%、46.5%和23.7%。同时,Our_LT速度达到46.9帧/s,满足实时性。

|
图 9 12种算法在UAV20L数据集上的结果 Fig. 9 Results of 12 algorithms on UAV20L dataset |
b) 属性性能分析。图 10对比了12种算法的成功率。由图 10可以看出,Our_LT在部分遮挡、完全遮挡和离开视野3个属性上,比Our算法分别提升了15.5%、75.6%、8.9%,比ECO_HC算法分别提升了25.9%、87.8%、15.0%,比ECO_HC算法分别提升了24.7%、99.1%、20.8%。这说明加入重检测后,跟踪成功率得到了很大提升。部分遮挡和离开视野时,目标仍有一部分在图像中,故部分鲁棒性较强的短期算法还可以找到目标。在目标完全遮挡时,几乎所有的短期跟踪算法都失效。因此,在完全遮挡属性下,Our_LT得到了显著提升。实验表明重检测能够有效解决目标完全遮挡的问题。
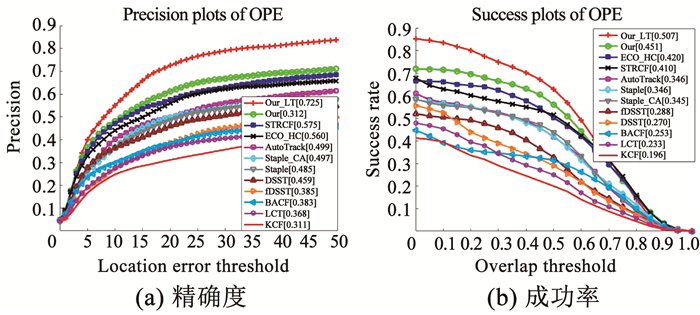
|
图 10 12种算法在3种属性下成功率 Fig. 10 Success rate of 12 algorithms under three attributes |
3) 定性分析
为了进一步验证跟踪性能,在UAV20L数据集中选取4组具有代表性的视频序列(car1、group3、person14、person19),包含部分遮挡、全部遮挡、离开视野、相似目标等各种复杂变化,来定性验证改进算法的跟踪性能,见图 11。Our_LT与其他11种跟踪算法相比,取得了更好的跟踪效果。
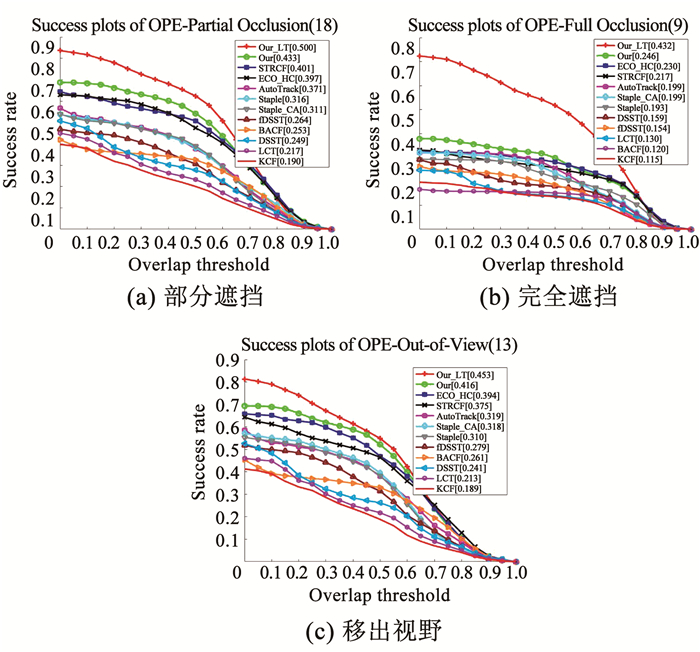
|
图 11 11种算法在4组序列上的跟踪结果 Fig. 11 Tracking results of 11 algorithms on four sets of sequences |
a) 在序列car1的828帧,受相似物体干扰,KCF跟踪失败,随着模型更新,跟踪器完全退化。LCT和BACF模型在跟踪过程中不断的累积误差,在1 542帧跟踪器也完全退化。目标在1 542帧完全遮挡后,在1 608帧时目标回到视野,只有Our_LT算法能成功跟踪,其他算法都跟踪失败。目标在1 932帧到达图像边缘,并在后续帧离开视野,在2 010帧进入视野,此时仍然只有Our_LT算法能够成功跟踪,其他算法随着累积误差造成跟踪失败,再也无法找回目标。可以看出,Our_LT算法能够在部分遮挡、完全遮挡、离开视野情况下稳定跟踪,并在目标丢失后重新找回目标。
b) 在序列group3的1 967帧,目标受到背景干扰和部分遮挡,只有Our_LT算法能正确跟踪目标,其他算法都跟踪失败;在2 250帧时,目标受到完全遮挡,在2 346帧再次出现,在3 978、4 825帧目标受到部分遮挡,Our_LT算法均能够跟踪目标。可以看出,Our_LT算法能够在部分遮挡、完全遮挡时稳定跟踪目标。
c) 序列person14中的目标经历了相似物体干扰、部分遮挡、完全遮挡和离开视野。目标在133帧受到完全遮挡,在199帧再次出现,只有Our_LT能够正确跟踪目标,其他算法都失败。目标在2 040帧离开视野,在2 221帧重新进入视野,Our_LT仍可以找回目标并跟踪。目标在2 833帧部分遮挡,但Our_LT仍能正确跟踪目标。可以看出,Our_LT算法可以在部分遮挡、完全遮挡、离开视野时稳定跟踪,并在目标丢失后重新找回。
d) 序列person19中的目标经历了部分遮挡、完全遮挡和离开视野。在1 002帧时,目标离开视野,在1 180帧重新进入视野,此时只有Our_LT、Our和LCT能跟踪上目标。Our和LCT算法跟踪准确的原因是目标从离开视野到重新进入,两个滤波器还未完全退化。之后目标离开视野,1 988帧再次进入视野时,可以看到Our_LT开始并没有找到目标,在2 041帧重新找回目标,此时只有Our_LT和Our算法可以跟踪目标,说明防止滤波器退化在一定情况下还可以处理移除视野的问题。但在3 078帧目标完全遮挡,Our算法跟踪失败。在3 400帧时目标又被部分遮挡,此时只有Our_LT算法能正确跟踪目标。可以看出,Our_LT算法能在部分遮挡、完全遮挡、离开视野时稳定跟踪,且目标丢失后能重新找回。
4 结论本文提出了一种无人机航拍目标的长期跟踪算法,并从4个方面进行改进。实验结果表明,本文算法在目标出现严重遮挡、移出视野等情况时,获得了较好的跟踪效果,且仍满足实时性。但在实际应用中,长期跟踪面临的复杂情况还有很多,因此,下一步还需对重检测模块进行更深入的研究。
| [1] |
HUANG He, SONG Jing, GUO Lu, et al. Haze removal method based on a variation function and colour attenuation prior for UAV remote-sensing images[J]. Journal of Modern Optics, 2019, 66(12): 1282. DOI:10.1080/09500340.2019.1615141 |
| [2] |
BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]// IEEE Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2544. DOI: 10.1109/CVPR.2010.5539960
|
| [3] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]//European Conference on Computer Vision. Berlin: Springer, 2012: 702. DOI: 10.1007/978-3-642-33765-9_50
|
| [4] |
HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 37(3): 583. DOI:10.1109/TPAMI.2014.2345390 |
| [5] |
DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005: 886. DOI: 10.1109/CVPR.2005.177
|
| [6] |
DANELLJAN M, KHAN F S, FELSBERG M, et al. Adaptive color attributes for real-time visual tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1090. DOI: 10.1109/CVPR.2014.143
|
| [7] |
DANELLJAN M, HAGER G, KHAN F S, et al. Accurate scale estimation for robust visual tracking[C]//British Machine Vision Conference. Nottingham: BMVA Press, 2014: 1. DOI: 10.5244/C.28.65
|
| [8] |
DANELLJAN M, HAGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Santiago: IEEE, 2015: 4310. DOI: 10.1109/ICCV.2015.490
|
| [9] |
BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: Complementary learners for real-time tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1401. DOI: 10.1109/CVPR.2016.156
|
| [10] |
GALOOGAHI H K, FAGG A, LUCEY S. Learning background-aware correlation filters for visual tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Venice: IEEE, 2017: 1135. DOI: 10.1109/ICCV.2017.129
|
| [11] |
DANELLJAN M, BHAT G, KHAN F S, et al. ECO: Efficient convolution operators for tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 6638. DOI: 10.1109/CVPR.2017.733
|
| [12] |
LI Feng, TIAN Cheng, ZUO Wangmeng, et al. Learning spatial-temporal regularized correlation filters for visual tracking[C]//IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 4904. DOI: 10.1109/CVPR.2018.00515
|
| [13] |
MA Chao, YANG Xiaokang, ZHANG Chongyang, et al. Long-term correlation tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 5388. DOI: 10.1109/CVPR.2015.7299177
|
| [14] |
DANELLJAN M, HAGER G, KHAN F S, et al. Accurate scale estimation for robust visual tracking[C]//British Machine Vision Conference. Nottingham: BMVA Press, 2014: 1. DOI: 10.5244/C.28.65
|
| [15] |
LI Yiming, FU Changhong, DING Fangqiang, et al. AutoTrack: Towards high-performance visual tracking for UAV with automatic spatio-temporal regularization[C]//IEEE Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 11920. DOI: 10.1109/CVPR42600.2020.01194
|
| [16] |
DANELLJAN M, HAGER G, KHAN F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 39(8): 1561. DOI:10.1109/TPAMI.2014.2345390 |
| [17] |
MUELLER M, SMITH N, GHANEM B. Context-aware correlation filter tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 1396. DOI: 10.1109/CVPR.2017.152
|
| [18] |
MUELLER M, SMITH N, GHANEM B. A benchmark and simulator for UAV tracking[C]//European Conference on Computer Vision. Cham: Springer, 2016: 445. DOI: 10.1007/978-3-319-46448-0_27
|
| [19] |
FELZENSZWALB P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part-based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 32(9): 1627. DOI:10.1109/TPAMI.2009.167 |
| [20] |
POSSEGGER H, MAUTHNER T, BISCHOF H. In defense of color-based model-free tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 2113. DOI: 10.1109/CVPR.2015.7298823
|
 2022, Vol. 54
2022, Vol. 54


