2. 贵州省结构工程重点实验室(贵州大学),贵阳 550025
2. Guizhou Key Laboratory for Structure Engineering (Guizhou University), Guiyang 550025, China
拱是一种古老的结构形式,通过特殊的曲线构造将截面上的弯矩转化为沿着拱轴线的轴力,并将承载的荷载转化成为支座上的反力。它被广泛应用于大型屋盖、桥梁等大跨度空间结构之中。本文研究的双箱型空腹圆弧钢拱是一种较为新颖的结构,在结构和理论上具有一定的创新性。因为它具有良好的通风及透光性能且节约材料、加工方便,所以在很多情况下有较好的工程应用价值。拱按其截面类型的不同可分为实腹式、平面及空间桁架拱等。在钢拱平面内的稳定性及强度方面,国内外学者进行了大量的研究工作。文献[1-8]通过理论推导、试验及数值分析的方法,对各种拱平面内的弹性、弹塑性稳定进行了详细分析,并提出相应的强度设计理论公式; 文献[9]运用理论推导与数值模拟相结合的方法, 分析了倒三角形截面板管连接式钢圆弧拱在平面内的稳定承载力及失稳破坏机理,得出其承载力和强度设计的理论公式。桁架拱可分为平面拱、空间拱和空腹拱等。在双肢的格构式拱与空腹桁架拱平面内的稳定性分析方面,文献[10]推导了两铰双肢缀板格构式圆弧拱考虑截面剪切变形影响的弹性屈曲荷载公式; 文献[11]对钢管桁架拱的整体稳定实用设计方法进行了研究; 文献[12]对平面板管连接式钢圆弧拱在平面内的失稳与破坏的机理进行深入的分析,得出了其相应的强度设计理论公式。但目前未见有文献对新型钢拱——双箱型空腹圆弧钢拱在平面内的稳定性进行过相关研究,本文就此问题进行分析。
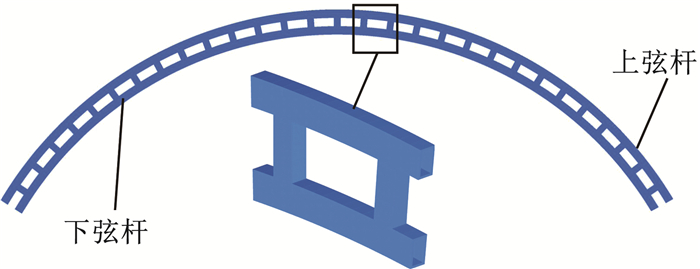
1 拱结构形式及有限元模型 1.1 拱的结构形式双箱型空腹圆弧钢拱是采用矩形腹杆连接上下矩形弦杆而构成的拱结构,弦杆及腹杆均由相应规格的钢板焊接而成,腹杆轴线与弦杆轴线始终保持两两互相垂直。弦杆和腹杆采用焊接的方式连接,其结构三维模型见图 1。
|
图 1 双箱型空腹圆弧钢拱三维图 Fig. 1 Three-dimensional view of double-box open-spandrel circular steel arch |
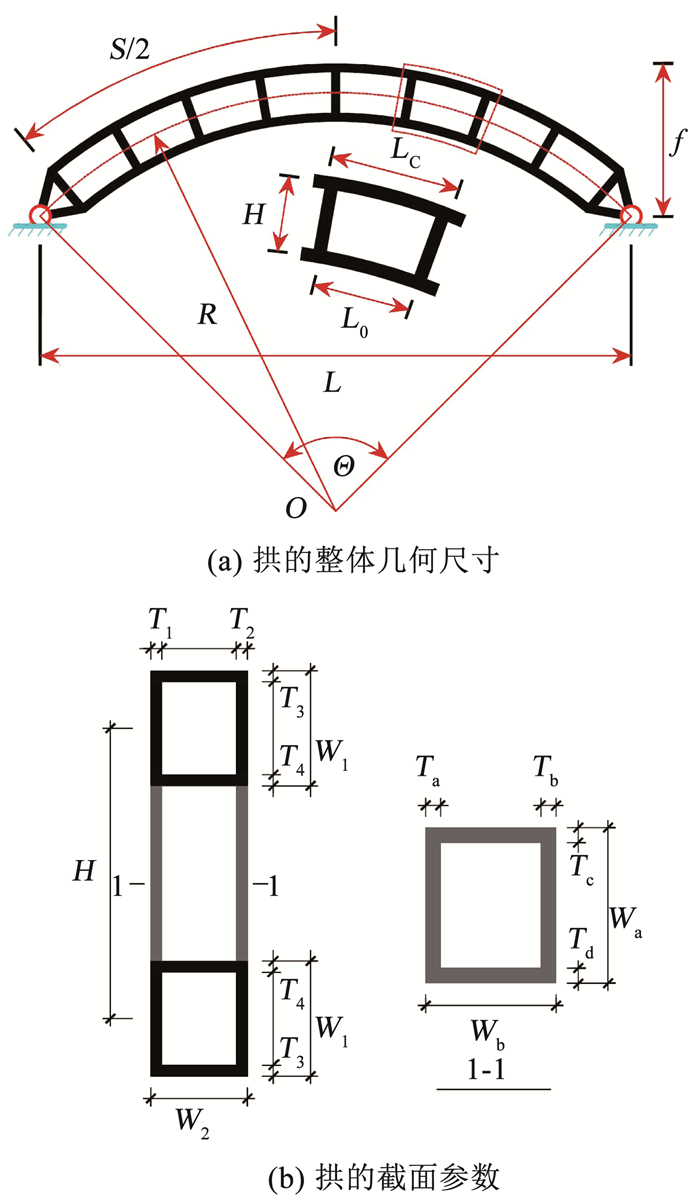
本文有限元模型的整体尺寸及截面参数见图 2。其中:L为钢拱跨度;f为钢拱矢高;R为钢拱轴线半径;S为钢拱轴线弧长;Θ为拱轴线所对圆心角;H为截面高度;LC为节段长度;L0为腹杆之间的净距;W1、W2分别为焊接成弦杆钢板的高度和宽度;T1、T2、T3、T4分别为焊接成箱型弦杆钢板的厚度;Wa、Wb分别为焊接成腹杆钢板的长度和宽度; Ta、Tb、Tc、Td分别为焊接成腹杆钢板的厚度。
|
图 2 拱的相关参数 Fig. 2 Relevant parameters of arch |
文中使用有限元软件ANSYS建立模型并进行数值分析。钢材取理想本构关系,弹性模量E=2.06×105 MPa,泊松比υ=0.3,腹杆屈服强度fy1=235 MPa,弦杆屈服强度fy2=235 MPa,拱脚设为固定铰支座。在大挠度弹塑性计算分析中,初始几何缺陷取一阶反对称屈曲模态。根据文献[13],δ幅值取为S/1 000(S为拱弧长)。本文不考虑残余应力,主要研究拱在3种均布荷载作用下的弹性、弹塑性稳定性。
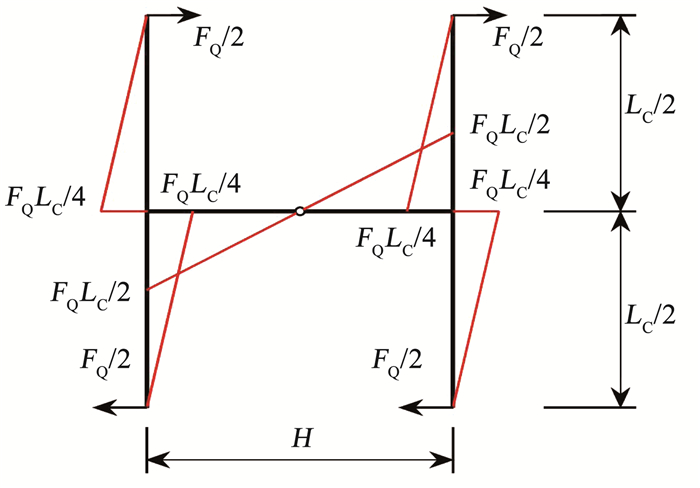
2 拱平面内的整体弹性屈曲 2.1 双箱型空腹圆弧钢拱截面剪切刚度双箱型空腹圆弧钢拱在外部荷载作用下,拱平面内的弹性屈曲荷载不能忽略拱截面整体剪切变形的影响。已有文献推导了平面内带有斜腹杆的钢管桁架拱的剪切刚度。因为双箱型空腹圆弧钢拱仅由上下弦杆抵抗截面的剪力,所以在纯剪力FQ作用下,其受剪机理可参考双肢缀板式格构柱进行分析。钢拱在纯剪力作用下拱微段的受力分析见图 3。
|
图 3 纯剪力FQ下拱微段的弯矩 Fig. 3 Bending moment distribution of arch segment under pure shear force FQ |
如图 3所示用图乘法计算得到拱微段在纯剪力FQ作用下总变形值δ的表达式为
| $ \delta=\frac{F_{\mathrm{Q}} L_{\mathrm{C}}^{3}}{48 E I_{0}}+\frac{F_{\mathrm{Q}} L^{2} H}{24 E I_{\mathrm{t}}} $ | (1) |
若考虑腹杆在剪力作用下的剪切应变,则拱截面的剪切刚度可表示为
| $ K_{\mathrm{V}, \mathrm{P}}=\frac{1}{\frac{L_{\mathrm{C}}^{2}}{24 E I_{0}}+\frac{L_{\mathrm{C}} H}{12 E I_{\mathrm{t}}}+\frac{\mu L_{\mathrm{C}}}{H A_{\mathrm{t}} G}} $ | (2) |
式中:E为材料弹性模量,I0为单根弦杆截面惯性矩,It为单根腹杆截面惯性矩,μ为腹杆截面剪应力不均匀分布系数且取μ=1.3,At为腹杆截面面积,G为剪切模量且取E=2.6G。
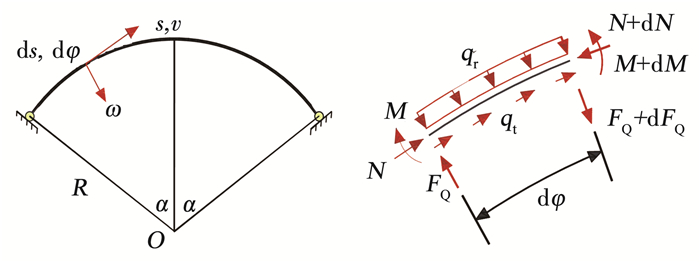
2.2 钢拱平面内弹性屈曲理论公式推导 2.2.1 拱的经典弹性屈曲理论公式推导圆弧拱坐标和微元的平衡见图 4,基于Kirchhoff方程[10]推导出在全跨径向均布荷载作用下, 不考虑剪切变形影响时两端铰接的双箱型空腹圆弧钢拱平面内的弹性屈曲荷载为
| $ q_{\mathrm{cr}, 0}=\frac{E I_{x}}{R^{3}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{\varTheta^{2}}-1\right) $ | (3) |
|
图 4 圆弧拱坐标和微元的平衡 Fig. 4 Balance of circular arc arch coordinates and elements |
其中
| $ E I_{x}=2 E I_{0}+\frac{E A_{0} H^{2}}{2} $ | (4) |
式中:I0为单根箱型弦杆截面惯性矩,A0为单根箱型弦杆的截面面积。
2.2.2 考虑拱截面整体及腹杆剪切变形影响的弹性屈曲理论公式双箱型空腹圆弧钢拱与实腹式拱相比,其平面内的弹性屈曲荷载不能忽略拱截面的剪切变形的影响。在式(3)的基础上考虑剪切变形的影响,推导思路主要是将圆弧拱的径向位移ω分解为:1)截面剪切变形引起的径向位移ω1;2)弯曲变形引起的径向位移ω2。则
| $ \omega=\omega_{1}+\omega_{2} $ | (5) |
由定义,截面γ满足:
| $ \gamma=\frac{Q}{K_{\mathrm{V}, \mathrm{P}}}=\frac{\mathrm{d} \omega_{2}}{\mathrm{~d} S}=\frac{\mathrm{d} M}{K_{\mathrm{V}, \mathrm{P}} \mathrm{d} S} $ | (6) |
对式(6)变形整理得
| $ \omega_{2}=\frac{M(S)}{K_{\mathrm{V}, \mathrm{P}}} $ | (7) |
由式(7)整理得式(8):
| $ \begin{aligned} \omega+\frac{\mathrm{d}^{2} \omega}{\mathrm{d} \varphi^{2}}=&\left(\omega_{1}+\frac{\mathrm{d}^{2} \omega_{1}}{\mathrm{~d} \varphi^{2}}\right)+\left(\omega_{2}+\frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} \varphi^{2}}\right)=\\ &-\frac{M R^{2}}{E I_{x}}+\frac{M}{K_{\mathrm{V}, \mathrm{P}}}+\frac{\mathrm{d}^{2} M}{\mathrm{~d} S^{2}} \end{aligned} $ | (8) |
又由弯矩的表达式:
| $ M=q R \omega $ | (9) |
则在全跨径向均布荷载的作用下双箱型空腹圆弧钢拱在平面内的弹性屈曲荷载可写为
| $ q_{\mathrm{cr}}=\frac{q_{\mathrm{cr}, 0}}{1+\frac{q_{\mathrm{cr}, 0} R}{K_{\mathrm{V}, \mathrm{P}}}} $ | (10) |
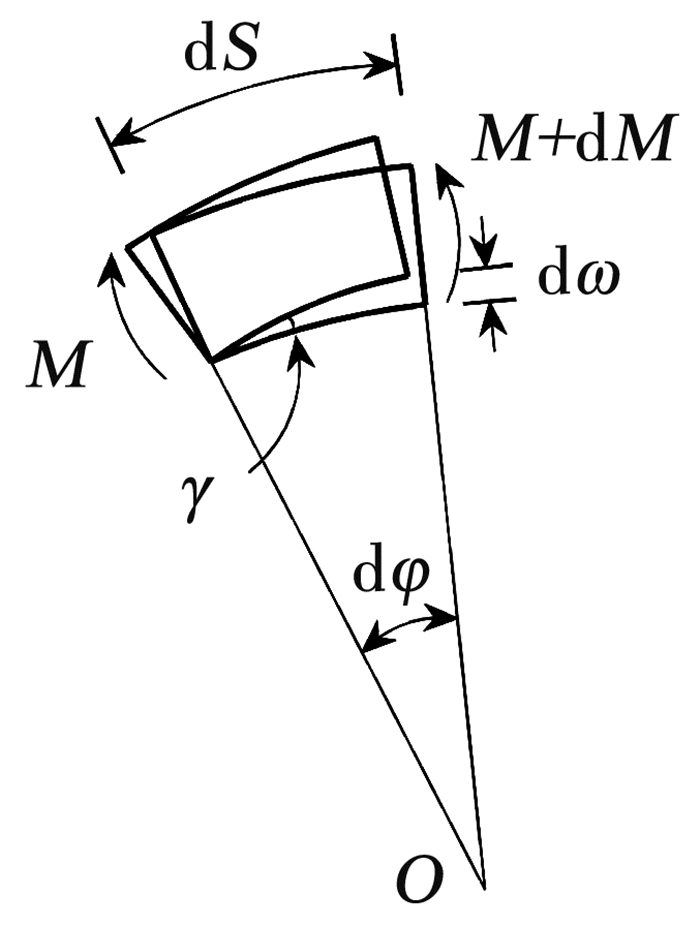
式(10)可用于分析双箱型空腹圆弧钢拱在全跨径向均布荷载作用下, 忽略上下弦杆局部剪切变形影响在平面内的弹性屈曲荷载。在式(10)的基础上考虑钢拱上下弦杆剪切变形对弹性屈曲荷载的影响(受力见图 5),进而推导出双箱型空腹圆弧钢拱在平面内考虑双剪切变形影响的弹性屈曲荷载公式。
|
图 5 弦杆剪切变形 Fig. 5 Shear deformation of chord |
由图 5可得拱微段截面的剪力为
| $ Q=\frac{\mathrm{d} M}{\mathrm{~d} S} $ | (11) |
式中: dM为拱微段的截面弯矩,dS为拱微段的弧长。
因为弯曲剪应力不是沿截面均匀分布的,所以相应的剪应变采用平均剪应力表示, 则有:
| $ \gamma=\frac{\mathrm{d} \omega}{\mathrm{d} S}=\frac{Q}{G A_{\mathrm{S}}} $ | (12) |
式中: AS为有效抗剪截面面积,G为剪切模量。由式(11)、(12)得:
| $ \frac{\mathrm{d} \omega}{\mathrm{d} \varphi}=\frac{1}{G A_{S}} \times \frac{\mathrm{d} M}{\mathrm{~d} \varphi} $ | (13) |
整理式(13)得:
| $ \frac{\mathrm{d}^{2} \omega}{\mathrm{d} \varphi^{2}}+\omega=-\frac{M R^{2}}{E I_{x}}+\frac{1}{G A_{\mathrm{S}}} \times \frac{\mathrm{d}^{2} M}{\mathrm{~d} \varphi^{2}} $ | (14) |
又由M=qRω,则推导出考虑双剪切变形影响的双箱型空腹圆弧钢拱在平面内的弹性屈曲荷载表达式:
| $ q=\frac{q_{\mathrm{cr}, 0}}{1+\frac{q_{\mathrm{cr}, 0} R}{K_{\mathrm{V}, \mathrm{P}}}}\left[\frac{1}{1+\left({\rm{ \mathsf{ π} }}^{2} E I_{x}\right) /\left(2 \varTheta^{2} G A_{\mathrm{S}} R^{2}\right)}\right] $ | (15) |
式中:AS=A0/μ,A0为弦杆截面面积,μ为弦杆截面的剪应力分布不均匀系数且取μ=1.3。
2.3 避免拱局部弹性失稳的限制条件双箱型空腹圆弧钢拱的节段弦杆发生局部失稳与整体几何长细比和节段弦杆几何长细比间的比值有关,则可将节段弦杆局部失稳的问题转换为拱的整体几何长细比与节段弦杆几何长细比间的关系进行研究,从而分析出避免弦杆发生局部失稳的限制条件。拱的整体几何长细比λG、节段弦杆几何长细比λC分别定义为
| $ \lambda_{\mathrm{G}}=\frac{S}{\sqrt{I_{\mathrm{G}} / A}} $ | (16) |
| $ \lambda_{\mathrm{C}}=\frac{S}{\sqrt{I_{0} / A_{0}}} $ | (17) |
式中:A=2A0,S为拱弧长,IG为拱的整体截面惯性矩,I0为单根弦杆截面惯性矩,A0为单根弦杆截面面积。
当双箱型空腹圆弧钢拱的节间距离LC较大时,不能忽略拱轴线的曲率所带来的影响,节间的上下弦杆可看作是单独的一个箱形截面钢拱,其可能发生分肢失稳且变形,见图 6。则可采用钢拱的弹性屈曲荷载公式进行分析,考虑到双箱型空腹圆弧钢拱的腹杆对弦杆有约束作用,此种约束等效为转动弹簧的作用。将一个圆弧线弦杆取出,可得到简化计算模型见图 7,转动弹簧刚度设为k1。

|
图 6 分肢失稳变形 Fig. 6 Componeat instability and deformation |

|
图 7 节间弧形弦杆简化计算模型 Fig. 7 Simplified calculation model of arc chord |
根据推导圆弧钢拱弹性屈曲荷载的方法,推导得到平衡微分方程:
| $ \left\{\begin{array}{l} u=C_{2} /(q R) \sin (k \varphi)+C_{4} \sin \varphi \\ \omega=C_{6}-\left[C_{2} /(k q R) \cos (k \varphi)+C_{4} \cos \varphi\right] \\ M=C_{2} \sin (k \varphi) \end{array}\right. $ | (18) |
其中
| $ k=\sqrt{1+\frac{q R^{3}}{E I}} $ | (19) |
拱两端有转动弹簧约束的边界条件:
| $ \left\{\begin{array}{l} u\left(-\frac{\varTheta}{2}\right)=\left(\frac{\varTheta}{2}\right)=0 \\ \omega\left(-\frac{\varTheta}{2}\right)=\omega\left(\frac{\varTheta}{2}\right) \\ M\left(\frac{\varTheta}{2}\right)=\left(k_{1} \frac{\mathrm{d} u}{\mathrm{~d} \varphi}\right)_{\varphi=\frac{\varTheta}{2}} \end{array}\right. $ | (20) |
将式(20)代入到式(18)中,若要求未知向量[C2,C4,C6]T有非零解,则有方程(21):
| $ \left|\begin{array}{cc} \sin \left(\frac{k \varTheta}{2}\right) & q R \sin \left(\frac{\varTheta}{2}\right) \\ k k_{1} \cos \left(\frac{k \varTheta}{2}\right) & q R k_{1} \cos \left(\frac{\Theta}{2}\right) \end{array}\right|=0 $ | (21) |
求解式(21)得超越方程(22):
| $ k_{1}=\frac{\tan \left(\frac{\varTheta}{2}\right)\left[k k_{1}-\tan \left(\frac{k \varTheta}{2}\right)\right]}{\tan \left(\frac{k \varTheta}{2}\right)} $ | (22) |
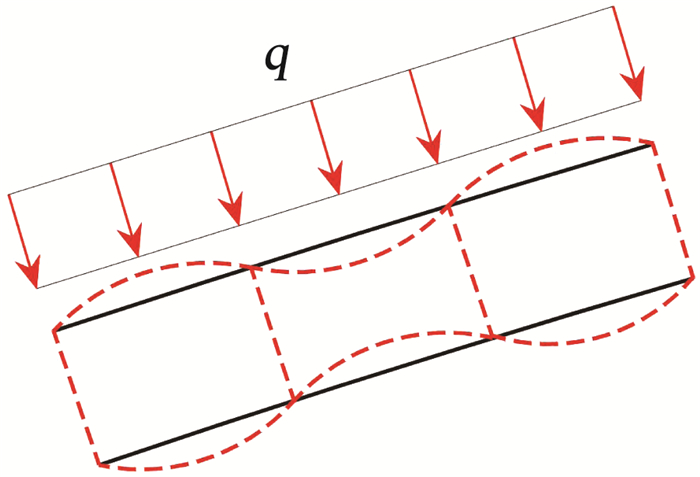
式(22)较为特殊,分3种情况:1)当k1=0时,对应两端铰接的拱;2)当k1=∞时,对应两端刚接的无铰拱;3)当k1∈(0,∞)时,弹簧刚度k1为有限值,此时式(22)没有显式解。若采用数值解法,每当腹杆刚度或弦杆刚度改变时都会改变k1的值,使得计算量巨大。文中将双箱型空腹圆弧钢拱的节段圆弧弦杆简化为两端铰接的圆弧拱。当节间弦杆两端铰接时,弦杆发生一阶反对称屈曲时所对应的荷载为最小荷载。所以,取这种情况下的荷载估算双箱型空腹圆弧钢拱弦杆发生局部屈曲的弹性屈曲荷载,失稳变形见图 8。
|
图 8 分肢失稳变形(腹杆两端铰接) Fig. 8 Componeat instability and deformation(hinged webs at both ends) |
由于箱型截面的抗剪刚度较大,因此节段弦杆可以按全跨径向均布荷载作用下两端铰接的实腹式钢拱的弹性屈曲荷载公式进行分析,则节段圆弧上弦杆的弹性屈曲荷载为
| $ q_{\mathrm{cr}, 1}=\frac{E I_{0}}{\left(R+\frac{H}{2}\right)^{3}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{\theta_{0}^{2}}-1\right) $ | (23) |
为保证双箱型空腹圆弧钢拱在整体弹性屈曲之前弦杆不发生局部屈曲,由等稳定理论,应满足条件(24),即:
| $ N_{\mathrm{cr}}=q R<N_{\mathrm{cr}, 0}<N_{\mathrm{cr}, 1}=q_{\mathrm{cr}, 1}\left(R+\frac{H}{2}\right) $ | (24) |
整理式(24)得:
| $ \frac{E I_{x}}{R^{3}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{\varTheta^{2}}-1\right)<\frac{E I_{0}}{\left(R+\frac{H}{2}\right)^{3}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{\theta_{0}^{2}}-1\right)\left(R+\frac{H}{2}\right) $ | (25) |
将式(16)、(17)及S=RΘ代入式(25),得到拱的整体几何长细比和节段弦杆的几何长细比关系式:
| $ \frac{\lambda_{\mathrm{C}}}{\lambda_{\mathrm{G}}}<\sqrt{\frac{4 {\rm{ \mathsf{ π} }}^{2}-\theta_{0}^{2}}{4 {\rm{ \mathsf{ π} }}^{2}-\varTheta^{2}}} $ | (26) |
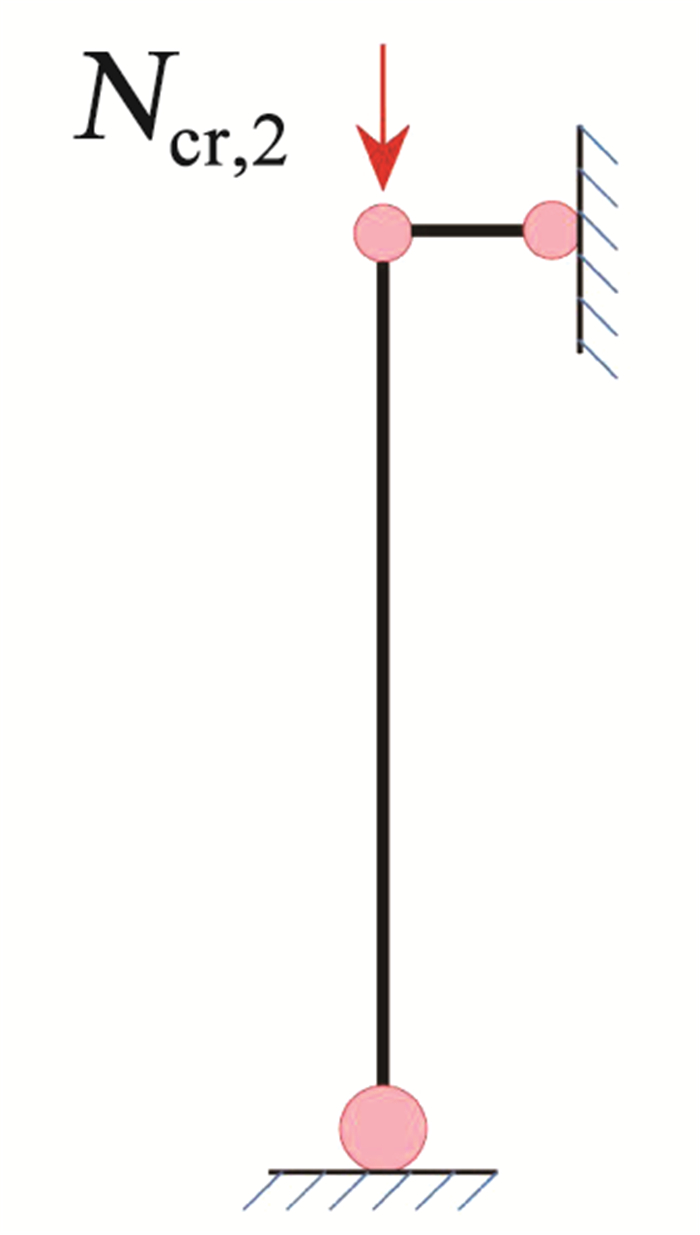
由式(26)知,当Θ=θ0时,弦杆间没有腹杆连接,此时弦杆独立作用,属于最不利情况。所以式(26)作为限制弦杆局部屈曲的发生条件时可保守写为: λC/λG < 1。若腹杆截面高度较高或尺寸较小时,则腹杆平面的外抗弯刚度较小,腹杆局部弹性失稳会在整体失稳之前发生。经分析可知,拱在发生腹杆局部失稳时,拱顶处位移最大。弦杆对腹杆具有转动约束的作用,文中采用简化的方法取拱顶的两相邻节段进行分析,将腹杆简化为两端铰接的受压杆见图 9。
|
图 9 连接腹杆的简化计算模型 Fig. 9 Simplified calculation model of connecting web |
由图 9可得腹杆的临界荷载为
| $ N_{\mathrm{cr}, 2}=\frac{{\rm{ \mathsf{ π} }}^{2} E A_{\omega}}{\left(\lambda_{\omega}\right)^{2}} $ | (27) |
| $ \lambda_{\omega}=\frac{k H}{\sqrt{I_{\omega} / A_{\omega}}} $ | (28) |
根据等稳定理论,为限制拱的腹杆局部屈曲不发生在整体屈曲之前,应满足条件:
| $ N_{\mathrm{cr}}=q R<N_{\mathrm{cr}, 0}=q_{\mathrm{cr}, 0} R<N_{\mathrm{cr}, 2} $ | (29) |
式(29)整理得:
| $ \frac{E I_{x}}{R^{3}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{\varTheta^{2}}-1\right) R<N_{\mathrm{cr}, 2}=\frac{{\rm{ \mathsf{ π} }}^{2} E A_{\omega}}{\left(\lambda_{\omega}\right)^{2}} $ | (30) |
则整体长细比与腹杆长细比间的比值为
| $ \frac{\lambda_{\omega}}{\lambda_{\mathrm{G}}}<\sqrt{\frac{A_{\mathrm{t}}}{2 A_{0}}\left(\frac{4 {\rm{ \mathsf{ π} }}^{2}}{4 {\rm{ \mathsf{ π} }}^{2}-\varTheta^{2}}\right)} $ | (31) |
式(31)可作为双箱型空腹圆弧钢拱在平面内限制腹杆局部屈曲在整体弹性屈曲之前发生的条件。
2.4 拱的整体弹性屈曲荷载公式合理性验证本文中双箱型空腹圆弧钢拱在全跨径向均布荷载的作用下的弹性屈曲荷载计算公式建议采用式(10)或式(15),并验证式(10)、(15)的正确性。取模型参数:f/L=0.3,L=60~140 m,H=2.5 m;弦杆:W1=1.0 m, W2=0.4 m,T1=T2=T3=T4=0.05 m;腹杆:Wa=0.4~1.0 m,Wb=0.4 m,Ta=Tb=Tc=Td=0.05 m建立有限元计算模型,对比分析见图 10。

|
图 10 分析结果对比 Fig. 10 Comparison of analysis results |
由图 10可得出以下几点结论:
1) 由图 10(a)可知, 随着拱跨度不断增大,双箱型空腹圆弧钢拱的弹性屈曲荷载不断减小,且随着拱跨度的增大,式(10)、(15)的理论值与有限元结果和Timoshenko解间的差值不断减小。这表明随着拱跨度增大,剪切变形的影响逐渐减小。
2) 图 10(b)、(c)表明随着腹杆高度或净距的增大,式(10)、(15)的理论值与有限元结果吻合度依然很好,但是Timoshenko解与有限元结果吻合度逐渐降低。
3) 图 10(d)表明拱在矢跨比为0.25处承载力最大;图 10(e)、(f)表明双箱型空腹圆弧钢的承载力受剪切变形影响很大,工程上不能忽视其影响。
4) 综合图 10得:式(10)、(15)的理论值与有限元结果间的误差都在10%以内。这表明对于计算空腹拱,式(10)、(15)较Timoshenko公式更为合理。
3 拱在平面内的弹塑性稳定 3.1 全跨径向均布荷载作用 3.1.1 拱的整体弹塑性失稳与破坏机理双箱型空腹圆弧钢拱在全跨径向均布荷载作用下属于纯压状态,压力由弦杆承担。当拱的节段弦杆长细比较大时,在压力作用下弦杆局部弹塑性失稳会在整体弹塑性失稳之前发生。此时,需要对节段弦杆的长细比进行限制,避免局部失稳在整体失稳之前发生。根据GB 50017—2017《钢结构设计标准》[14], 为避免上下弦杆的局部失稳在整体失稳之前发生,需要对节段弦杆的长细比λC进行限制,λC应满足:λC < min[40, 0.5λ0x]。
其中换算长细比λ0x定义为
| $ \lambda_{0 x}=\sqrt{\lambda_{\mathrm{G}}^{2}+\frac{{\rm{ \mathsf{ π} }} \lambda_{\mathrm{C}}^{2}}{12}\left(1+\frac{2}{k}\right)} $ | (32) |
式中: λG为整体长细比,λC为节段弦杆长细比,k为腹杆与弦杆线刚度比值。
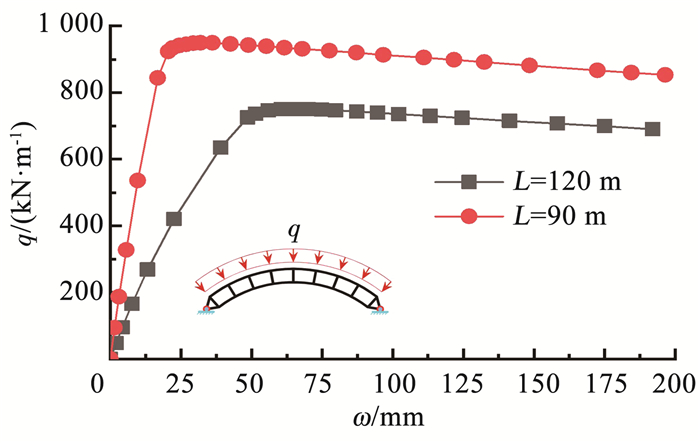
取模型参数:f/L=0.3, L0=H, H=2.5 m;弦杆:W1=1.0 m, W2=0.4 m,T1=T2=T3=T4=0.05 m;腹杆:Wa=0.8 m,Wb=0.4 m,Ta=Tb=Tc=Td=0.05 m; 跨度L=90 m和120 m。建立精准的有限元模型进行弹塑性全过程分析,得全跨径向均布荷载下荷载-拱顶竖向位移曲线见图 11。
|
图 11 荷载-拱顶竖向位移曲线 Fig. 11 Load-arch vertical displacement curve |
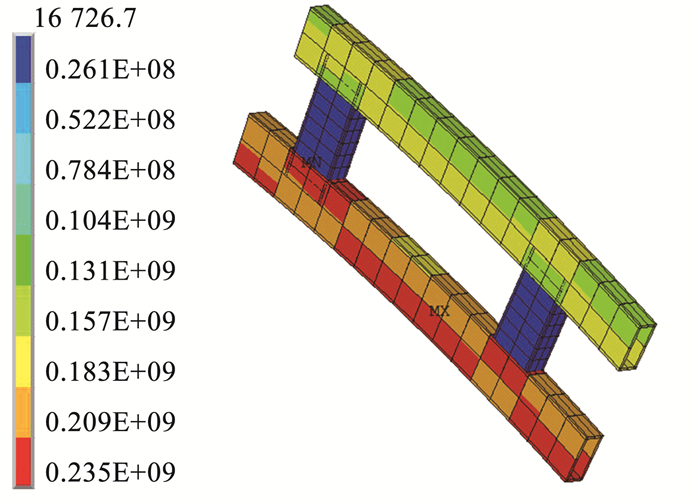
由图 11可知,在全跨径向均布荷载作用下,拱失稳属于极值点失稳。由于存在几何初始缺陷,双箱型空腹圆弧钢拱从施加荷载开始就发生反对称变形,见图 12; 此时弦杆受压,拱顶发生竖直向下的变形; 随着变形的增加,因为二阶效应而受到弯矩的作用,弯矩值在全跨1/4L和3/4L处最大,且弯矩转化为由上下弦杆承担的轴拉力及轴压力,然后又随着荷载的不断增加而达到拱的极限承载力; 紧接着随拱整体变形的增大,荷载逐渐下降,弦杆几乎出现全截面屈服,见图 13; 最终钢拱在全跨3/4L处下弦杆出现结构破坏。

|
图 12 拱反对称变形 Fig. 12 Anti-symmetric deformation of arch |
|
图 13 拱3/4L处受压弦杆破坏处应力(Pa) Fig. 13 Stress distribution of compressed chord at 3/4L of arch (Pa) |
本文研究的双箱型空腹圆弧钢拱,其拱轴线为曲线且主要承受横向压力作用,所以双肢缀板式格构柱的设计方法不能直接套用来验证其处于纯压状态下的稳定极限承载力。综合考虑相关因素,本文采用正则化长细比λn和稳定系数φ来研究纯压状态下双箱型空腹圆弧钢拱的整体稳定性。正则化长细比λn及稳定系数φ分别见式(33)、(34):
| $ \lambda_{\mathrm{n}}=\sqrt{\frac{N_{\mathrm{y}}}{N_{\mathrm{cr}}}}=\sqrt{\frac{2 f_{\mathrm{y}} A_{\mathrm{c}}}{q_{\mathrm{cr}} R}} $ | (33) |
| $ \varphi=\frac{N_{\mathrm{u}}}{N_{\mathrm{y}}}=\frac{q_{\mathrm{u}} R}{2 f_{\mathrm{y}} A_{\mathrm{c}}} $ | (34) |
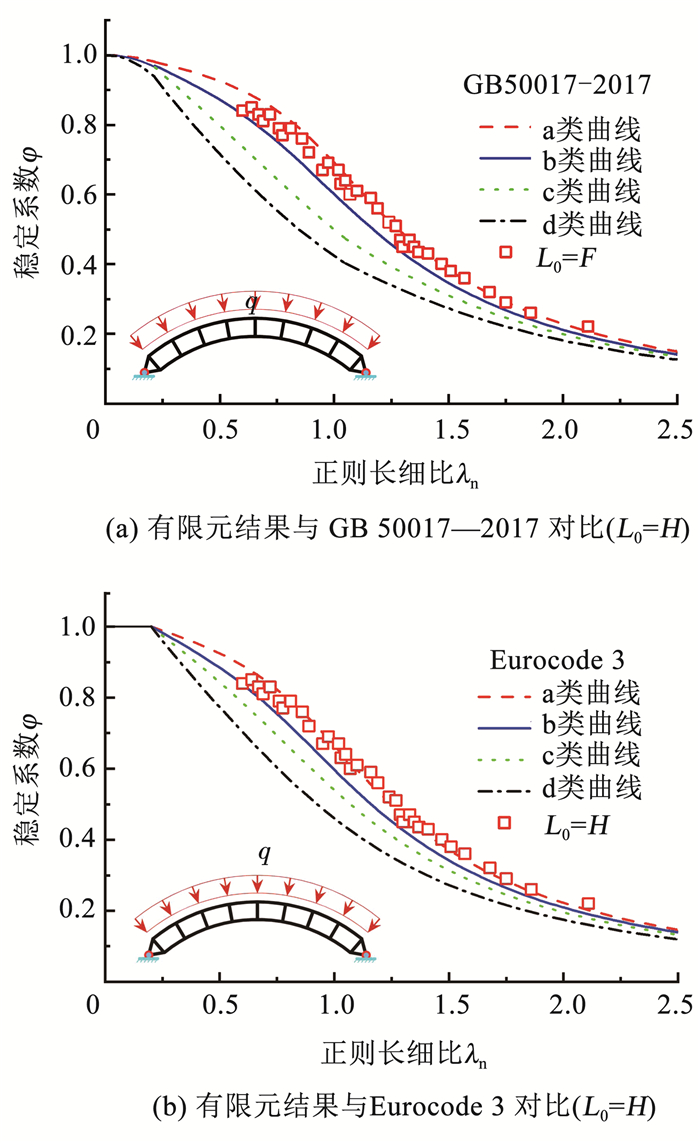
取L0=H,改变其他参数建立所有符合λc/λ0x < 0.5的计算模型。将所有符合要求的有限元模型计算结果的φ-λn曲线关系绘于图 14中,并与中国标准GB 50017—2017《钢结构设计标准》[14]及欧盟标准Eurocode 3[15]的a,b,c,d四类柱子类曲线对比。
|
图 14 拱在均布径向荷载作用下的φ-λn曲线 Fig. 14 φ-λn curve of arch under uniform radial load |
由图 14可知,数值计算点基本上位于规范GB 50017—2017和Eurocode 3柱子曲线a类与b类之间。这说明在全跨径向均布荷载作用下,双箱型空腹圆弧钢拱可参考轴心受压柱的方法进行验算。则双箱型空腹圆弧钢拱的极限承载力设计公式可写为
| $ N_{\mathrm{u}}=\varphi N_{\mathrm{y}} \leqslant N_{\mathrm{y}} $ | (35) |
上述表明:双箱型空腹圆弧钢拱稳定设计可按GB 50017—2017《钢结构设计标准》或Eurocode 3中的稳定曲线b类进行设计。
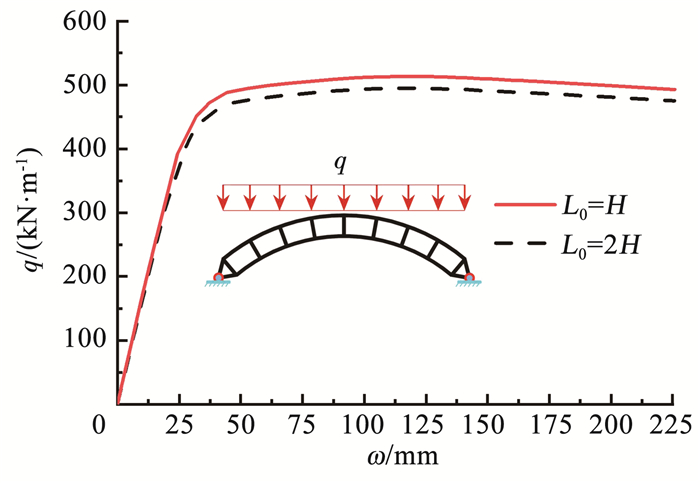
3.2 全跨竖向均布荷载作用 3.2.1 拱的整体破坏双箱型空腹圆弧钢拱在轴力和弯矩的共同作用下,拱在全跨1/4L和3/4L处弯矩值最大。当钢拱节段长度和截面高度较小时,弯矩产生的弦杆轴力较大,节段弦杆和腹杆端部弯矩较小,一般不发生局部破坏,而发生整体破坏。取拱模型参数:f/L=0.3, L0=H, H=2.50 m;弦杆:W1=1.0 m, W2=0.4 m,T1=T2=T3=T4=0.05 m;腹杆:Wa=0.8 m,Wb=0.4 m,Ta=Tb=Tc=Td=0.05 m;节间距离L0=H和2H, 建立有限元模型进行弹塑性分析,得荷载-拱顶竖向位移曲线见图 15。
|
图 15 荷载-拱顶竖向位移曲线 Fig. 15 Load-dome vertical displacement curve |
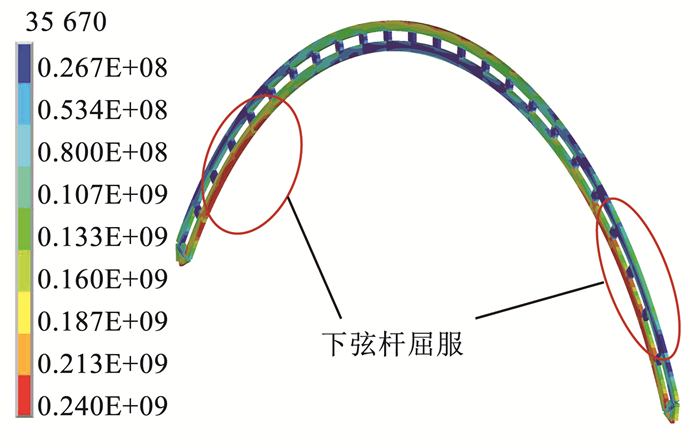
图 15可知,双箱型空腹圆弧钢拱随着腹杆间净距L0的增大,稳定极限承载力会下降且曲线直线段的斜率也会降低,这表明随L0增大,拱的整体刚度减小。当钢拱达到稳定极限承载力时,在两端拱脚附近的下弦杆会先发生屈服, 见图 16。
|
图 16 拱达到极限承载力时的整体应力分布(L0=2H)(Pa) Fig. 16 Integral stress distribution of arch at ultimate bearing capacity (L0=2H)(Pa) |
双箱型空腹圆弧钢拱的整体破坏是由弯矩及轴力的共同作用引起的。双箱型空腹圆弧钢拱的剪切变形较大,截面的抗剪刚度较小,不能忽略二阶效应的影响,本文中拱在全跨竖向均布荷载作用下的稳定极限承载力采用式(36)进行验算:
| $ \frac{N^{*}}{\varphi N_{\mathrm{y}}}+\frac{\mu M^{*}}{M_{\mathrm{y}}} \leqslant 1 $ | (36) |
式中:N*为一阶弹性屈曲分析所得的最大轴力;M*为一阶弹性屈曲分析所得的最大弯矩;Ny为全截面屈服时的截面轴力;My为全截面屈服时的截面弯矩My=fy1HA0;φ为稳定系数;μ为考虑二阶效应的弯矩放大系数;μ=1/[1/(1-N*/NcrR)], μ≤1.4, (Ncr为全跨径向均布荷载作用下的弹性屈曲荷载)。
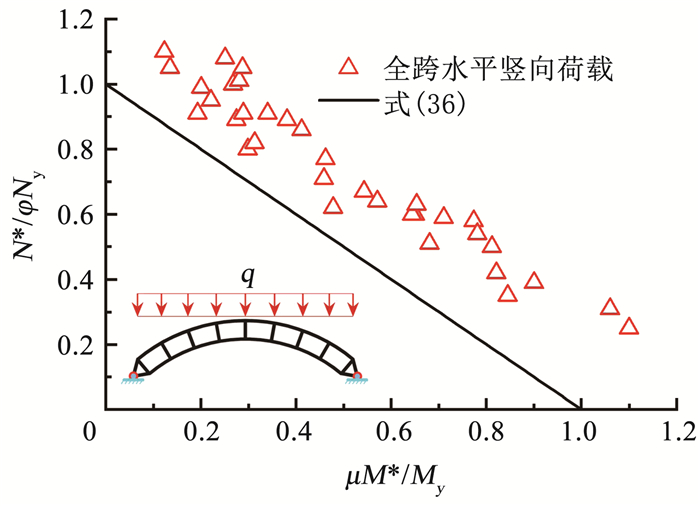
双箱型空腹圆弧钢拱采用有限元数值分析方法对设计式(36)进行验证。分析计算拱在全跨竖向均布荷载作用下的破坏模式和极限承载力,保证腹杆不发生屈服,并将所有整体破坏模式下得到的极限承载力带入到设计式(36)中,结果见图 17。
|
图 17 全跨竖向均布荷载作用下式(36)验证 Fig. 17 Verification of Eq.(36) for full span under uniform vertical load |
由图 17可知,有限元计算结果都在式(36)的右上方。这表明:1)式(36)可保守验证双箱型空腹圆弧钢拱在全跨竖向均布荷载作用下发生整体弹塑性破坏时的稳定极限承载能力;2)拱在全跨竖向均布荷载作用下发生整体弹塑性失稳时,弯矩起主要作用。
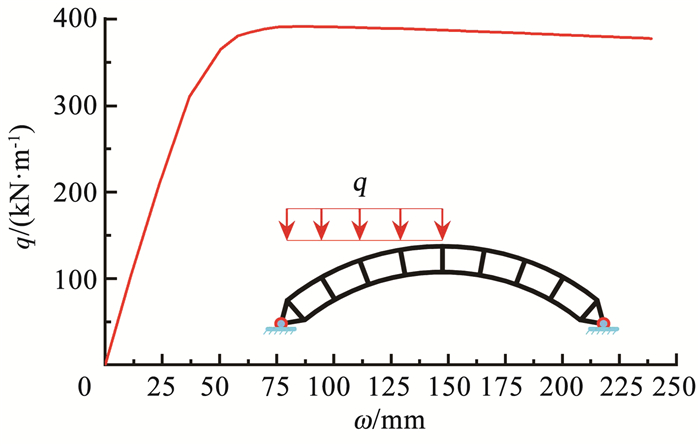
3.3 半跨均布竖向荷载作用 3.3.1 拱的整体破坏当双箱型空腹圆弧钢拱的截面高度与节段长度都较小时,截面弯矩产生的轴力较大, 所以拱在弯矩与轴力共同作用下将发生整体破坏。采用大挠度弹塑性分析方法研究双箱型空腹圆弧钢拱在半跨均布竖向荷载作用下的整体破坏。拱整体破坏时荷载-拱顶竖向位移曲线见图 18。
|
图 18 荷载-拱顶竖向位移曲线 Fig. 18 Load arch-dome vertical displacement curve |
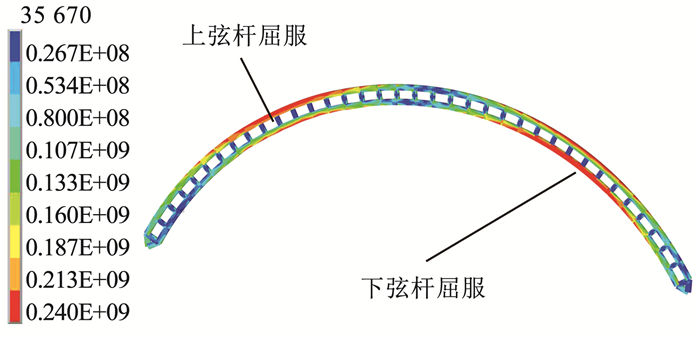
当双箱型空腹圆弧钢拱在半跨竖向均布荷载作用下时,拱上弦杆在1/4L处、下弦杆在3/4L处发生屈服,其整体应力分布见图 19。
|
图 19 半跨均布竖向荷载作用下拱的整体应力分布(Pa) Fig. 19 Integral stress distribution of arch at half span under uniform vertical load (Pa) |
在半跨竖向均布荷载作用下, 双箱型空腹圆弧钢拱的整体破坏模式和全跨径向(竖向)均布荷载作用下的整体破坏模式相似,都是受压弦杆发生塑性大变形。采用有限元数值分析方法对设计式(36)进行验证。在保证腹杆不发生屈服的条件下分析拱在半跨竖向均布荷载作用下的破坏模式及极限承载力,并将所有整体破坏模式下得到的极限承载力代入式(36)中,结果见图 20。

|
图 20 半跨均布竖向荷载作用下式(36)验证 Fig. 20 Verification of Eq.(36) for half span under uniform vertical load |
由图 20可知,有限元计算结果都分布在式(36)的右上方,这表明:1)式(36)可保守地验算双箱型空腹圆弧钢拱在半跨竖向均布荷载作用下整体弹塑性破坏时的稳定极限承载能力;2)拱在半跨竖向均布荷载作用下发生整体弹塑性失稳时,弯矩起主要作用。
4 结论本文运用理论推导结合数值分析的方法,对双箱型空腹圆弧钢拱平面内的稳定性进行了深入分析,得到以下结论:
1) 双箱型空腹圆弧钢拱最先在全跨1/4L和3/4L处发生屈曲,从而导致钢拱发生整体失稳。
2) 对于双箱型空腹圆弧钢拱,式(10)受剪机理与双肢缀板格构柱类似,可参考但不能完全套用。考虑双剪切变形影响得出的式(15)是合理的,能更精确地计算空腹拱的弹性屈曲承载力,可为科研人员对空腹拱的研究提供一些新方法,同时也可供实际工程应用作参考,具有一定的创新性和现实指导意义。
3) 双箱型空腹圆弧钢拱结构较新颖,其结构通风及透光性好,且节约材料,造型更美观,具有较大的实际应用价值。分析结果表明剪切变形对拱承载力的削弱可以达到50%甚至更大,所以工程应用中不能忽略剪切变形的影响。
4) 双箱型空腹圆弧钢拱在平面内限制弦杆发生局部失稳条件为:λC/λG < 1, 限制腹杆发生局部失稳条件为式(31)。
5) 基于大量拱承载力有限元数值分析的结果,建议在全跨径向均布荷载作用下双箱型空腹圆弧钢拱的整体稳定极限承载力可用轴心受压柱的设计方法进行设计,根据规范中的b类柱子稳定曲线进行设计。
6) 本文使用弹塑性有限元数值方法研究了双箱型空腹圆弧钢拱在全跨竖向均布荷载和半跨竖向均布荷载作用下的破坏机理、破坏模式及极限承载能力。表明双箱型空腹圆弧钢拱在平面内荷载作用下整体破坏模式表现为轴力与弯矩共同引起的整体稳定性破坏。
7) 针对钢拱的整体破坏模式,根据其破坏机理并结合有限元数值分析的极限承载能力值,提出了相应的双箱型空腹圆弧钢拱稳定性能设计的方法。使用整体轴力与弯矩的二项式验算整体稳定承载能力。
| [1] |
DIZANGIAN B, GHASEMI M R. An efficient method for reliable optimum design of trusses[J]. Steel & Composite. Structures, 2016, 21(5): 1069. DOI:10.12989/scs.2016.21.5.1069 |
| [2] |
DIMOPOUIOS C A, GANTES C J. Design of circular steel arches with hollow circular cross-sections according to EC3[J]. Journal of Constructional Steel Research, 2008, 64(10): 1077. DOI:10.1016/j.jcsr.2007.09.009 |
| [3] |
PI Yonglin, TRAHAIR N S. In-plane buckling and design of steel arches[J]. Journal of Structural Engineering, 1999, 125: 1291. DOI:10.1061/(ASCE)0733-9445(1999)125:11(1291) |
| [4] |
PI Yonglin, BRADFORD M A. In-plane strength and design of fixed steel I-section arches[J]. Engineering Structures, 2004, 26(3): 291. DOI:10.1016/j.engstruct.2003.09.011 |
| [5] |
刘璐璐, 刘爱荣, 卢汉文. T型截面拱在拱顶集中力作用下的平面外弯扭失稳[J]. 工程力学, 2020, 37(增刊1): 151. LIU Lulu, LIU Airong, LU Hanwen. Flexural-torsional buckling of pin-ended arches with T-section under a central radial concentrated load[J]. Engineering Mechanics, 2020, 37(S1): 151. DOI:10.6052/j.issn.1000-4750.2019.04.S026 |
| [6] |
杨永华, 吴杰. 单轴对称截面圆弧拱平面外稳定性研究[J]. 工程力学, 2012, 29(3): 27. YANG Yonghua, WU Jie. Out of plane stability of mono-symmetric circular arches[J]. Engineering Mechanics, 2012, 29(3): 27. |
| [7] |
韦建刚, 李晓辉, 陈礼榕, 等. 钢管混凝土哑铃形截面拱空间受力性能试验研究[J]. 工程力学, 2015, 32(11): 71. WEI Jianggang, LI Xiaohui, CHEN Lirong, et al. Experimental studies of out-of-plane mechanical behavior on CFST dumbbell section arch[J]. Engineering Mechanics, 2015, 32(11): 71. DOI:10.6052/j.issn.1000-4750.2013.07.0602 |
| [8] |
杨洋, 童根树. 水平弹性支承圆弧钢拱的弹性屈曲分析[J]. 工程力学, 2011, 28(3): 9. YANG Yang, TONG Genshu. In-plane elastic buckling of steel circular arches with horizontal spring support[J]. Engineering Mechanics, 2011, 28(3): 9. |
| [9] |
何海玉, 袁波, 马信欣, 等. 倒三角形截面板管连接式钢圆弧拱在平面内的稳定承载力研究[J]. 应用力学学报, 2021, 38(1): 216. HE Haiyu, YUAN Bo, MA Xinxin, et al. Study on the stability bearing capacity of plate-pipe connection steel circular arc arch with inverted triangular section in plane[J]. Journal of Applied Mechanics, 2021, 38(1): 216. |
| [10] |
A.H. 金尼克. 拱的稳定性[M]. 吕子华, 译. 北京: 建筑工业出版社, 1958 KNINIK A H. Arch stability[M]. LV Zihua, translate. Beijing: Architectural Engineering Press, 1958 |
| [11] |
黄逸群. 钢管桁架整体稳定实用设计方法[D]. 天津: 天津大学, 2017 HUANG Yiqun. Practical design method for integral stability of steel tube truss[D]. Tianjin: Tianjin University, 2017 |
| [12] |
HE Haiyu, YUAN Bo, CHEN Hongniao, et al. In-plane failure mechanism and stability bearing capacity design of planar plate-tube-connected circular steel arches[J]. Mechanics Based Design of Structures and Machines, 2020, 1. DOI:10.1080/15397734.2020.1713157 |
| [13] |
尹宸哲, 禹奇才, 刘爱荣, 等. 初始缺陷圆弧拱面内非线性失稳实验研究[J]. 中山大学学报(自然科学版), 2018, 57(2): 87. YIN Chenzhe, YU Qicai, LIU Airong, et al. Experimental study on non-linear destabilization in arc arch with initial defects[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2018, 57(2): 87. DOI:10.13471/j.cnki.acta.snus.2018.02.012 |
| [14] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Steel structure design specification: GB 50017—2017[S]. Beijing: China Building Industry Press, 2017 |
| [15] |
Eurocode 3. Design of steel structures, general rules and rules for buildings. EN1993-1-1[S]. Brussels: CEN European Committee for Standardization, 2004
|
 2022, Vol. 54
2022, Vol. 54


