压缩感知理论旨在以亚奈奎斯特速率采样信号，高能效地获取信号的稀疏表征。该理论表明，具有稀疏性的图像/视频信号可通过少量随机观测值进行恢复^[1]。文献[2]提出一种基于时域帧分层的视频压缩感知编码框架，该框架实质上是采用三维多尺度变换对视频信号进行表征，其测量端的实现复杂度过高。分布式压缩感知为视频压缩感知提供了部分理论基础，每帧单独测量生成的多帧观测向量通常服从某种联合稀疏模型，根据空时联合信息利用程度的不同，视频重构的性能及资源消耗也不一样^[3]。视频压缩感知需要设计一个可以高概率地满足有限等距性质(restricted isometry property, RIP)且尽可能保存足够有效信息的观测矩阵^[4-5]。文献[6]将卷积神经网络与压缩感知相结合，形成视频压缩感知网络(video compressed sensing network, VCSNet)，通过端到端的训练来提升重建视频的保真度，但忽视了设计满足RIP的观测矩阵。Gaussian随机观测矩阵是普适满足RIP的常用观测矩阵。此外，分块压缩感知(block compressive sensing, BCS)对测量端的传感或存储资源要求较低，不仅可以实现低内存的观测矩阵，并且可以逐块或并行传输^[7-8]。BCS将每帧分成同等尺寸的子块，对每个子块进行独立观测，得到相应的观测值。

视频码流通常由连续的图像组(group of pictures, GOP)构成，每一组GOP含有一个关键帧以及后续若干非关键帧。残差信号通常比原始信号具有更大的稀疏性，基于GOP-BCS典型架构的残差稀疏重构是目前最具代表性的视频压缩感知重构技术：各帧先进行独立的帧内重构，然后非关键帧利用已重构的参考帧进行片匹配重构。文献[9]提出了多假设(multi-hypothesis, MH)帧间片匹配算法，将已重构的关键帧作为当前帧的参考帧，结合Tikhonov正则化对当前帧进行残差稀疏重构。在MH算法的基础上，文献[10]在分裂布雷格曼迭代中不断更新信号残差的权重，构建重加权残差稀疏(reweighted residual sparsity, RRS)模型，实现多假设预测精度和重建帧质量的交替提升。进一步地，文献[11]提出了一种结合长短距离(long short distance, LSD)的帧间片匹配算法，通过在一个GOP内动态地确定参考帧，在一定程度上改进了重建质量。对于视频压缩感知重构，文献[12]提出了一种结合光流的结构组稀疏(structural group sparsity, SGS)算法，其中帧间片匹配交替地实现光流估计和残差稀疏重构，该最新算法适合于非关键帧采样率较低的情况。

在GOP-BCS典型架构下，测量端逐帧地采用分块随机观测进行视频信号的表征，关键帧采样率与非关键帧采样率称为联合采样率。现有的帧间片匹配算法仅关注非关键帧采样率较低的情况，此时低质量的多个非关键帧特别适合进行稀疏建模，单一的假设片选择模式有利于结合稀疏模型取得稳定的片匹配性能。对于更多联合采样率的情况，仍有待提出有效的片匹配重构机制。本文的主要创新点在于：改变了以往单一的参考帧选取方式，根据联合采样率的变化自适应地执行双向的帧间片匹配重构，以更好地应对不同联合采样率导致的码流变化，稳定地改善视频序列的重建质量。

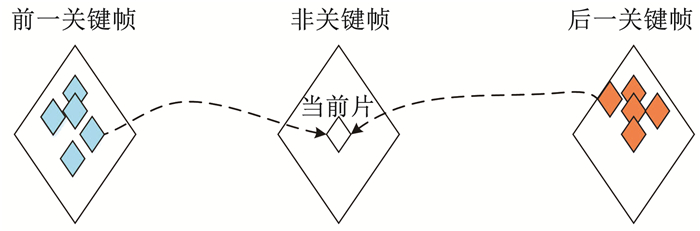
视频残差稀疏重构首先对关键帧和非关键帧分别进行帧内重构，每个GOP的关键帧通常具有较高的采样率，因此关键帧在帧内重构之后具有较好的恢复效果，可作为最终的重构结果；而非关键帧使用了较低的采样率，在完成帧内重构后，还需要进行帧间重构，使用其他帧的重构结果作为参考帧进行片匹配，非关键帧的参考帧可以是其前一关键帧或后一关键帧，图 1给出了非关键帧的当前片从前后参考帧中选取假设片的示意图。在获得最终的重构结果前，每个非关键帧均需要执行多次迭代的帧间重构。

Fig. 1

图 1 非关键帧片匹配的示意 Fig. 1 Schematic diagram of non-keyframe patch matching

在每次迭代的帧间重构中，当前帧分成重叠的若干个片，以降低块效应。当前片在以其所处位置为中心的搜索窗内，从参考帧中选取与其具有较高相似度的一组假设片，通过稀疏化当前片与其假设片之间的残差进行视频重构。在参考帧中使用均方误差(mean square error, MSE)准则搜索出与当前片近似的一组假设片，选出其中MSE较小的K个假设片，h_k表示当前片x的第k个假设片(1≤k≤K)。一般而言，第k个假设片的权重α_k与其MSE之间有着近似反比例的关系，若某假设片与当前片的相似度不高，则该假设片会被赋予一个较小的权重，即MSE大的分配较小权重，MSE小的分配较大权重，执行如下的权重度量学习：

式中s²表示片大小。当前片x的残差R(x)是当前片与其假设片线性组合之间的差值，该残差可表示为

式中第k个假设片的权重α_k会影响多假设片匹配的预测精度。当关键帧采样率与非关键帧采样率不一致时，现有的重构算法在变化的联合采样率下呈现出不稳定的恢复性能。

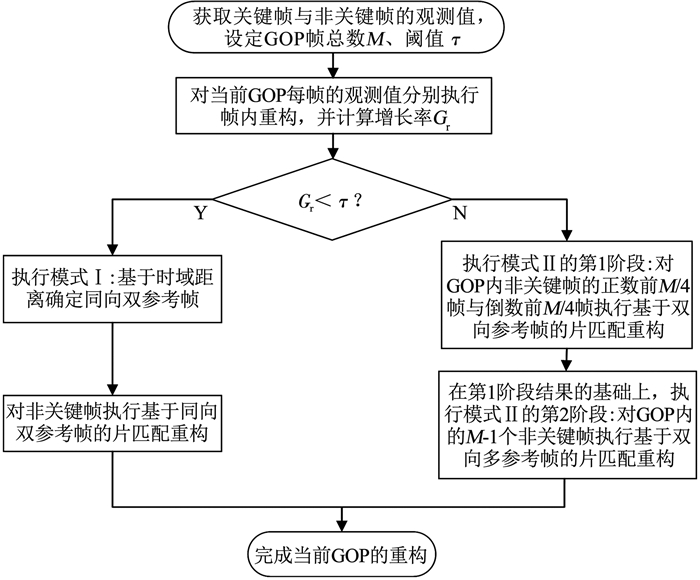
视频码流的每个GOP由一个关键帧和若干非关键帧组成。为了应对更多联合采样率的情况，本文提出了一种采样率自适应的帧间片匹配(subrate-adaptive interframe patch matching, SIPM)重构算法，所提SIPM算法根据关键帧与非关键帧采样率的变化情况自适应地挑选假设片，并加入了新的参考帧选取机制。图 2是SIPM算法的流程，主要包括以下3个步骤：

Fig. 2

图 2 采样率自适应的帧间片匹配 Fig. 2 Subrate-adaptive interframe patch matching

步骤1  视频码流由若干个GOP组成，每组GOP的帧总数为M，每一组GOP的第一帧是关键帧，后续的M-1帧是非关键帧。每帧的观测值独立地进行帧内重构，至此完成关键帧的重构，接下来准备进行非关键帧的帧间重构。

步骤2获取关键帧采样率S_k、非关键帧采样率S_n，计算关键帧采样率较非关键帧采样率的增长率G_r=(S_k-S_n)/S_n，并与阈值τ进行比较：若G_r < τ，表明各帧的重建质量差别不大，邻近非关键帧也具有较好的参考价值，因此使用步骤3中的模式Ⅰ对非关键帧进行帧间重构；否则，引入更为精细的参考帧机制，使用步骤3中的模式Ⅱ对非关键帧进行多阶段的片匹配重构。

步骤3  本步骤只对采样率较低的非关键帧进行帧间重构。根据步骤2中的模式选择，对当前GOP的非关键帧执行模式Ⅰ或模式Ⅱ。

模式Ⅰ：基于帧间的时域距离，当前帧选取最近的关键帧和同向的邻近非关键帧的重构结果作为参考帧，见图 3，图中每个GOP的帧总数M=8，帧1、帧9为关键帧，其余帧为非关键帧，箭头指向参考帧。随后，模式Ⅰ使用残差稀疏模型进行基于同向双参考帧的片匹配重构。

Fig. 3

图 3 模式Ⅰ的参考帧示意 Fig. 3 Schematic diagram of reference frames for mode Ⅰ

模式Ⅱ：为了充分利用关键帧与非关键帧的重构结果，模式Ⅱ分为第1阶段与第2阶段。如图 4所示，把各帧重构的结果(包括重构的中间结果：有些帧可能多次进行重构)按照重构的先后次序进行编号，记作R_i，其中i为某帧在模式Ⅱ中的重构序号。

Fig. 4

图 4 模式Ⅱ的参考帧示意 Fig. 4 Schematic diagram of reference frames for mode Ⅱ

第1阶段：为当前GOP内的帧M=8(最后一个非关键帧)挑选帧间片匹配的参考帧，将当前GOP关键帧与下一GOP关键帧作为两个参考帧，然后使用残差稀疏模型进行求解，得到序号1的重构结果R₁。对于当前GOP的帧2(首个非关键帧)，其参考帧是当前GOP关键帧与下一GOP关键帧，同样对其执行残差稀疏模型，得到序号2的重构结果R₂。对于当前GOP的帧3(第2个非关键帧)，其参考帧是R₁与R₂，为其运行残差稀疏模型，得到序号3的重构结果R₃。对于当前GOP的帧M-1(倒数第2个非关键帧)，其参考帧是R₃与R₂，然后进行重构得到序号4的重构结果R₄。以此类推，直到完成当前GOP非关键帧的正数前M/4帧与倒数前M/4帧的重构。

第2阶段：基于当前GOP的首个非关键帧在上述第1阶段的重构结果，进行再次重构，其参考帧是下一GOP关键帧与其相邻非关键帧在上述第1阶段的重构结果(当前GOP的第2个非关键帧在上述第1阶段的重构结果)，利用选取的2个参考帧运行残差稀疏模型，得到重构结果$ {{R}_{\frac{M}{2}+1}}$；对于倒数第1个非关键帧进行重构，其参考帧是当前GOP的关键帧与当前GOP的倒数第2个非关键帧在第1阶段的重构结果${{R}_{\frac{M}{2}+2}} $；接下来对当前GOP的正数第2个关键帧进行重构，其参考帧是${{R}_{\frac{M}{2}+1}} $与$ {{R}_{\frac{M}{2}+2}}$，得到其重构结果${{R}_{\frac{M}{2}+3}} $；接下来，依次从GOP的两端向中心交替地进行重构，每个非关键帧的参考帧是在第2阶段中先其重构的前两次重构结果，至此完成基于双向多参考帧的片匹配重构。

仿真实验在装有MATLAB R2020a的计算机上进行，其主要配置为：Intel Core i9-10900K CPU、16 GB内存和Windows 10操作系统。针对不同的视频码流，分别选取多组GOP进行测试，并为待重构的视频帧从1开始按观测顺序进行编号，每个GOP的帧总数M=8。为验证所提算法在各种联合采样率下的恢复效果，仿真实验基于GOP-BCS典型架构，在5组联合采样率(0.7, 0.1)、(0.7, 0.2)、(0.7, 0.4)、(0.7, 0.6)、(0.7, 0.7)下对视频码流进行残差稀疏重构，括号中的前一个值为关键帧采样率，括号中的后一个值为非关键帧采样率，前3组联合采样率为现有算法所采用。所有算法共有的测试参数设置如下：测量端采用Gaussian随机观测矩阵，分块尺寸为16×16；在参考帧中，片尺寸s²=8²，假设片的搜索窗尺寸L=30×30，当前片挑选的假设片个数K=10。每个视频序列选取前25帧进行测试，其中帧1、帧9、帧17、帧25为关键帧，其余帧为非关键帧。在本文所提SIPM算法中，阈值τ选取常用的分界点0.5，配合采样率自适应的帧间片匹配重构，可取得整体较优的重建质量。

为了便于叙述，文献[9]中的帧间片匹配算法简称MH，文献[10]中的帧间片匹配算法简称RRS，文献[11]中的帧间片匹配算法简称LSD，文献[12]中的帧间片匹配算法简称SGS。将本文SIPM算法与这4种代表性的帧间重构算法进行比较。当执行同样的帧内重构算法后，MH算法主要基于前一关键帧进行片匹配重构，RRS算法基于前后两个关键帧进行片匹配重构，LSD算法则在GOP内先验地挑选假设片，SGS算法对帧间残差信号进行复杂的光流估计，这些算法均忽略了联合采样率的差异化，所提SIPM算法能根据关键帧与非关键帧采样率的相对变化自适应地执行帧间片匹配。典型地，实验选择CIF格式(分辨率352×288)的Akiyo、News、Foreman、Container、Football、Calendar视频序列，在5组联合采样率下依次执行MH、RRS、LSD、SGS与SIPM算法。

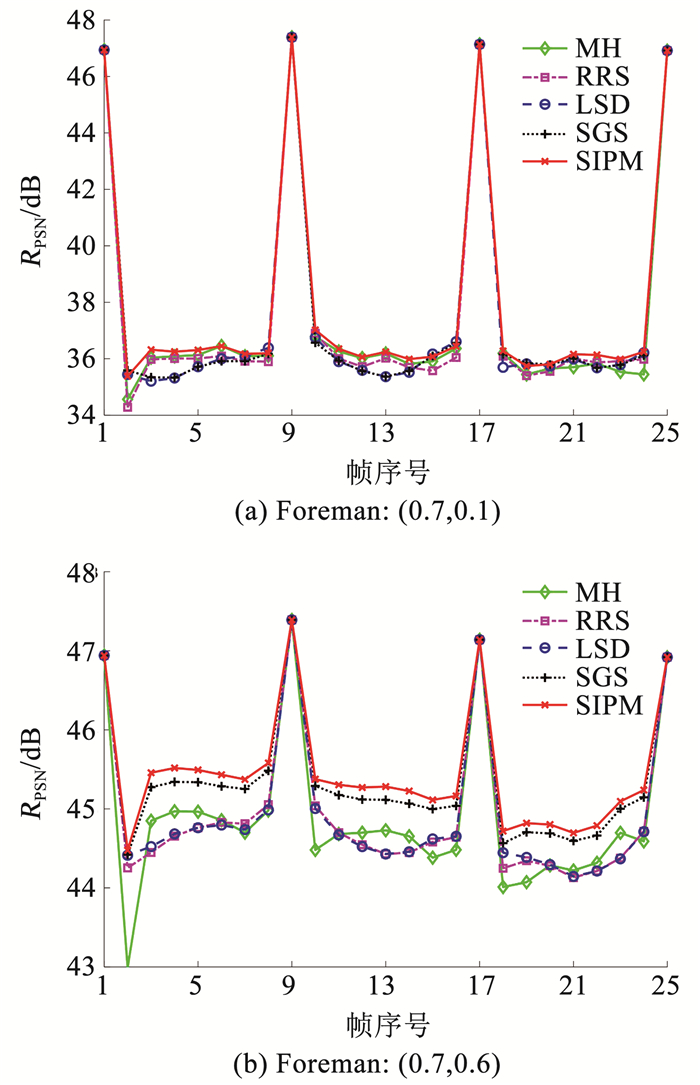
首先，在联合采样率(0.7, 0.1)和(0.7, 0.6)下，图 5给出了利用不同算法恢复Foreman序列的逐帧结果，峰值信噪比(peak signal noise ratio, PSNR)越大表示重建质量越好，本文以R_PSN表示。当非关键帧采样率不断降低，即增长率G_r越来越大时，在两个相邻的关键帧中各帧的重建质量形成一个不断加深的波谷。因此，联合采样率的差异对于恢复效果具有显著的影响，所提SIPM算法根据不同联合采样率执行差异化的帧间片匹配，得到了较好的整体性能。

Fig. 5

图 5 不同算法的逐帧RPSN比较 Fig. 5 Frame-by-frame RPSN comparison of different algorithms

为了直观地比较各种算法的重构性能，图 6给出了在不同联合采样率下各种算法对Foreman序列进行重构的平均结果。从图中可看出，SIPM算法的重建质量在测试条件下优于现有算法。由于SIPM算法学习到了质量更高的参考帧信息，其恢复效果的改善较为明显。

Fig. 6

图 6 不同联合采样率的重构结果 Fig. 6 Reconstruction results under different subrate combinations

表 1进一步地给出了各种算法在不同视频序列上重建质量的平均R_PSN值，在每组联合采样率中，关键帧采样率是逗号前的数值，非关键帧采样率是逗号后的数值。当增长率G_r较低时，帧间质量差别不大，SIPM算法的帧间重构较好地挖掘了邻近帧的参考价值；而当增长率G_r较高时，SIPM算法通过更为精细的参考帧选取，执行多次迭代的帧间重构，充分利用了质量更好的关键帧信息。

表 1

表 1 各种算法在不同视频序列上的平均RPSN Tab. 1 Average RPSN values of different algorithms on different sequences   dB 联合采样率 视频序列 MH RRS LSD SGS SIPM (0.7, 0.1) Foreman 35.31 36.06 36.09 35.98 36.25 Container 30.92 31.76 32.25 34.06 33.83 News 33.89 34.17 35.93 36.07 36.33 Akiyo 34.27 35.01 35.37 36.29 35.67 Calendar 28.76 29.36 30.02 30.48 30.35 Football 25.98 26.41 26.56 26.67 26.73 (0.7, 0.2) Foreman 38.50 39.20 39.37 39.38 39.66 Container 32.32 33.75 33.95 34.47 34.30 News 35.42 36.03 36.51 37.39 37.69 Akiyo 36.46 36.82 37.15 38.26 38.03 Calendar 31.85 32.39 33.15 34.67 34.46 Football 28.05 28.67 28.91 29.78 30.19 (0.7, 0.4) Foreman 41.22 42.10 42.1 42.42 42.67 Container 34.97 34.72 36.11 37.15 36.74 News 37.11 38.23 38.78 39.47 39.91 Akiyo 37.52 38.04 38.29 38.89 39.26 Calendar 34.36 35.27 36.01 37.32 37.63 Football 29.95 30.65 32.47 32.41 32.56 (0.7, 0.6) Foreman 44.25 44.68 44.77 45.22 45.41 Container 37.52 38.38 38.85 39.22 39.57 News 39.72 41.21 42.13 42.31 42.69 Akiyo 41.69 43.14 43.98 44.19 44.57 Calendar 36.65 37.18 37.62 38.15 38.48 Football 32.92 33.56 33.94 34.56 34.76 (0.7, 0.7) Foreman 45.58 46.37 46.52 47.05 47.33 Container 38.55 39.46 40.72 41.09 41.36 News 40.58 42.07 43.11 43.34 43.78 Akiyo 42.37 44.52 44.57 44.82 45.31 Calendar 37.78 38.31 38.75 39.28 39.61 Football 34.05 34.69 35.07 35.69 35.89

表 1 各种算法在不同视频序列上的平均RPSN Tab. 1 Average RPSN values of different algorithms on different sequences

最后，对各种算法的复杂度进行简要分析。本文SIPM算法的复杂度主要由挑选假设片的过程所决定。考虑到上述测试参数的设置，SIPM算法在极端场景下可能接近RRS算法复杂度的2倍，但大多数场景下均达不到此上限。在实际测试中，对于CIF大小的视频序列，RRS、LSD、SGS算法重构每帧图像分别平均花费大约3、4、7 min，而SIPM算法重构每帧图像平均花费约5 min。本文SIPM算法通过增加少量的复杂度，相比现有算法取得了更好的平均R_PSN值。

针对视频压缩感知的联合采样率变化，本文提出了一种采样率自适应的帧间片匹配重构算法，所提算法动态地利用了视频重构过程中的帧间相关性。当关键帧所提供的参考信息较少时，所提算法执行基于同向双参考帧的片匹配重构，反之则采用更为精细的多阶段片匹配重构。在各种联合采样率下，所提算法按照关键帧采样率较非关键帧采样率的增长率情形进行自适应的帧间片匹配重构，有效地减少了帧间变化引入的干扰，相比现有重构算法能够获得更为稳定的重建质量。