干扰决策是电子战中进行有效对抗的重要环节,而人工决策由于实时性与科学性较差,很难满足战场瞬息万变的态势要求。随着认知无线电[1]等技术的发展,干扰方要达到较好的干扰效果变得更加困难,但无线通信媒介自身的开放性给干扰攻击的实现保留了可行性。近年来,智能干扰已经成为认知电子战的一个重要研究领域,涌现出了利用遗传算法、粒子群算法等[2-3]实现干扰参数寻优的理论,但这些方法都需要通信方的先验通信参数。强化学习作为不需要先验信息的方法,能在未知环境中通过不断与环境交互来学习最优行为策略,目前在通信干扰与抗干扰领域已有初步应用,如文献[4]将干扰无线网络过程建模为增广马尔科夫决策过程,并利用Q学习算法进行干扰决策,通过实验表明干扰方可学习到干扰成本、网络吞吐量等重要信息; 文献[5]提出了基于多臂赌博机框架的干扰赌博机(jamming bandit,JB)算法,该在线学习算法通过学习最佳干扰样式对通信方进行干扰。然而,上述研究的强化学习算法学习速度较慢,这在动态变化的战场环境中十分受限。国内外学者进行了相关研究,以期提高学习算法的学习速度,文献[6]采用一种双层强化学习的干扰决策算法,以牺牲交互时间为代价来加快收敛速度; 文献[7]利用正强化思想提升最佳动作的概率,并结合对信号正交分解使得算法可以在更短的时间内学习到最佳干扰样式; 文献[8]提出在认知无线电网络节点中增加基于同策略Q学习算法的合作机制,利用宽带频谱感知和同步贪婪算法来加速学习过程并降低丢包率; 文献[9]在迁移学习框架中结合Soft-Q算法,将从当前节点获取的抗干扰信息转移到相邻节点来加快该节点的学习过程; 文献[10]在策略选择过程中通过增加一个价值附加值来平衡探索与利用,提高算法学习速度。
强化学习算法的学习速度常受探索-利用困境[11]制约,而多臂赌博机策略是平衡探索-利用的常用方法,在ε-greedy、softmax、置信上界(upper confidence bound,UCB)、UCB1-Tuned[12]等基础上,又涌现了方差置信上界(upper confidence bound variance,UCBV)及其改进算法[13-14]、有效方差置信上界(efficient upper confidence bound variance,EUCBV)[15]等。
为提高算法学习速度,本文将有效方差置信上界思想引入Q学习算法中,通过剔除次优干扰动作缩小动作空间,结合同策略方式贪婪利用当前最优干扰动作来提升稳定性。在认知干扰决策应用场景中,分别在单对单、多对多情形下对算法的干扰成功率和干扰总收益进行研究。
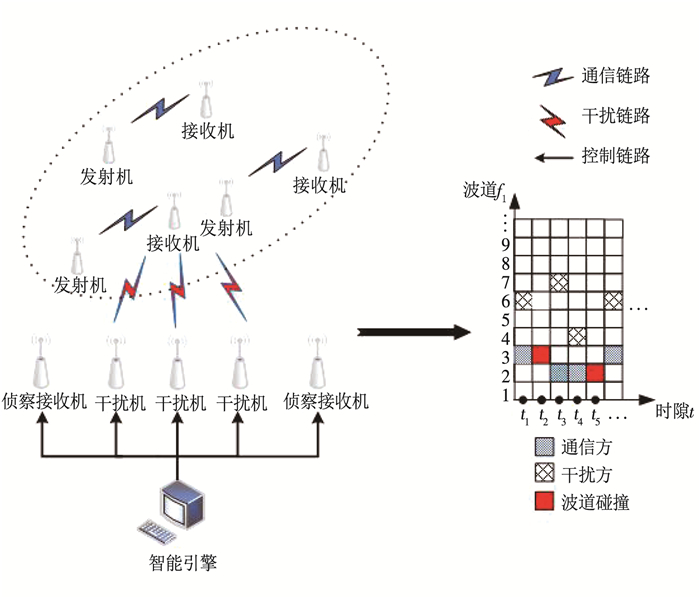
1 对抗场景与模型建立 1.1 对抗场景通信干扰需建立在频率击中、空域对准、能量压制等条件基础上,文献[5-7]主要研究当通信方使用固定通信参数时干扰方如何加快学习干扰参数,而实际场景中通信方受到干扰后通常会优先选择切换波道以躲避干扰。本文主要研究侧重频域的智能干扰决策,假设通信方使用定频通信系统,且每个通信节点重要性指数相同,见图 1。目标频谱区域内有N个可选择的波道,假设每个波道fi对应的是互不干扰、相互独立的等带宽正交信道。每对通信用户(一对通信收发机)根据作战想定制定波道切换的策略,通过切换通信波道来躲避干扰。干扰方利用智能算法来学习其通信策略变化的内在规律,实现对通信波道的跟踪和预测并加以干扰。文中将连续时间设定为离散时隙,简化对抗过程如下:在每个时隙t的起始时刻,每个通信用户可以随机选择N个波道中的任意一个波道ftc(c=1, 2, …, N)进行通信。每个干扰机根据当前的波道状态以及干扰反馈信息,利用决策算法选择一个波道ftj(j=1, 2, …, N)进行干扰。
|
图 1 对抗场景示意 Fig. 1 Schematic diagram of countermeasure environment |
图 1中,智能引擎通过智能算法指引各干扰机对通信用户进行联合干扰。考虑到干扰效果实时评估一直是电子战领域的研究难题[16],为便于分析,假设通信方使用包含确认帧/非确认帧(ACK/NACK)信息的协议机制[5],且成功干扰需同时满足:1)通信用户和干扰方在同一个时隙内选择了同一个波道(ftc=ftj);2) 干扰方侦收到的单位时间NACK数据包数量τ大于预设定门限值τ0。单位时间NACK平均数量可由误包率给出,传输出错时需回传NACK包[5]。通信接收双方亦根据ACK/NACK信息决定是否切换波道,如果通信用户在一个时隙内未受到干扰,则在下一个时隙将继续使用此波道进行通信;否则将按原策略在下一个时隙起始时刻重新选择通信波道。只有当某时隙网内所有的通信用户都受到干扰,才可认为协同干扰有效。
1.2 模型建立假设通信方传输数据采用数字调制,设通信信号低通等效表达式为
| $ x(t)=\sum\limits_{m=-\infty}^{\infty} \sqrt{P_{x}} x_{m} g(t-m T) $ | (1) |
式中:Px为通信接收机收到的平均信号功率;g(t)为实值脉冲波形;T为码元间隔;xm是随机变量,为该数字调制方式的码元符号,假设其在所有可能的星座点上均匀分布,并对能量进行归一化,即有E(|xm|2)≤1。
假设信号x(t)在高斯白噪声(AWGN)信道中进行传输,由文献[3]可知对于数字调制信号,最佳干扰为脉冲率为q∈(0, 1)的脉冲干扰。设干扰信号的低通等效表达式为
| $ j(t)=\sum\limits_{m=-\infty}^{\infty} \sqrt{P_{j}} j_{m} g(t-m T) $ | (2) |
式中: Pj为通信接收机收到的干扰信号功率;jm是随机变量,表示干扰信号的码元符号。假设通信收发双方完全同步,则经过匹配滤波和抽样判决后在接收机处收到的信号表达式为
| $ \begin{array}{r} y_{k}=y\left(f_{t}^{c}, f_{t}^{j}\right)=\left(\sqrt{P_{x}} x_{k}+n_{k}\right)+ \\ \sqrt{P_{j}} j_{k} \cdot \varphi\left(f_{t}^{c}, f_{t}^{j}\right), k=1,2, \cdots \end{array} $ | (3) |
式中: nk是方差为σ2的零均值加性高斯白噪声;φ(ftc, ftj)为波道碰撞指示函数,可由下式表示:
| $ \varphi\left(f_{t}^{c}, f_{t}^{j}\right)=\left\{\begin{array}{l} 1, f_{t}^{c}=f_{t}^{j} \\ 0, f_{t}^{c} \neq f_{t}^{j} \end{array}\right. $ | (4) |
只有当φ(ftc, ftj)=1时,表示干扰机与通信方在同一波道,接收机才会受到干扰信号的影响。接收机处的信噪比和干扰方的干噪比可分别表示为
| $ R_{\mathrm{SN}}=\frac{P_{x}}{\sigma^{2}}, R_{\mathrm{JN}}=\frac{P_{j}}{\sigma^{2}} $ | (5) |
结合上文对抗场景可知当前环境状态只取决于上一时刻的状态,与过去所经历的无关,满足马尔科夫链属性,故将通信干扰决策问题建模为马尔科夫决策过程(MDP)[17]。MDP可用元组 < S, A, P, R>表示,其中S代表环境状态空间,A代表干扰动作空间,P代表状态转移概率,R代表奖励函数。4个元素的具体定义如下:
环境状态空间S:“一对一”(单个干扰机对抗单对通信用户)场景中,在时隙t,环境的状态可表示为
| $ s_{t}=\left(f_{t}^{c}, f_{t}^{j}, \tau\right) $ | (6) |
式中:ftc为t时隙通信方所在波道且c=1, 2, …, N; ftj为t时隙干扰机所干扰的波道且ftj∈A,A为干扰机的动作空间; τ为单位时间侦收到的NACK包数量。
在“多对多”场景中,环境状态可表示为
| $ \begin{gathered} s_{t}=\left\{\left(f_{t}^{c_{1}}, f_{t}^{j_{1}}, \tau_{1}\right),\left(f_{t}^{c_{2}}, f_{t}^{j_{2}}, \tau_{2}\right), \cdots,\right. \\ \left.\left(f_{t}^{c_{i}}, f_{t}^{j_{i}}, \tau_{i}\right)\right\} \end{gathered} $ | (7) |
式中:i为网内通信用户编号, i=2, 3;ftci为t时隙第i个用户所在波道,ftji为t时隙第i个干扰机所干扰的第i个波道。
干扰动作空间A:“一对一”场景中,干扰动作为at,at∈{1, 2, …, N}。“多对多”场景中,在时隙t第i个干扰机根据智能引擎指令选择干扰动作,将联合干扰动作表示为
| $ a_{t}=\left(a_{t}^{1}, a_{t}^{2}, \cdots, a_{t}^{i}\right) $ | (8) |
式中ati为第i个干扰机的干扰动作。
状态转移概率矩阵P:在时隙t,干扰方根据当前所处的环境状态st选择动作at,环境转移到下一个时隙t+1状态st+1,则状态转移概率为
| $ p\left(s^{\prime} \mid s, a\right)=\operatorname{Pr}\left\{S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right\} $ | (9) |
且满足
| $ \sum\limits_{s^{\prime} \in S} \sum\limits_{s \in S, a \in A(s)} p\left(s^{\prime} \mid s, a\right)=1 $ | (10) |
本文在无通信方的先验信息条件下研究干扰决策,即状态转移概率对于干扰方是未知的。
干扰收益函数R:假设在时隙t环境状态为st,干扰方选择干扰动作at,环境达到状态st+1后干扰方获得收益R。由于连续的干扰会引起通信接收端接收数据包的急剧恶化,本文将收益函数定义为某时隙侦收到的单位时间内NACK包数量,同时规定干扰方某时隙干扰成功获得的收益,正相关于到当前时隙为止干扰方连续干扰成功的时隙总数与当前时隙NACK包数之积;某时隙干扰失败获得的收益与到当前时隙为止通信方连续非正常通信的时隙数成负相关,如式(11)所示:
| $ R=\left\{\begin{array}{l} k *\left(t_{2}-t_{1}\right) * \tau, \varphi\left(f_{t}^{c}, f_{t}^{j}\right)=1, \tau>\tau_{0} \\ -k *\left(t_{4}-t_{3}\right), \varphi\left(f_{t}^{c}, f_{t}^{j}\right)=0 \end{array}\right. $ | (11) |
式中:k为比例常数;τ为该时隙干扰方侦收到的NACK包数量;τ0为预设定门限值;t1、t2构成的时隙区间[t1, t2](t2>t1),表示通信方在此区间内受到干扰方连续干扰;t3、t4构成的时隙区间[t3, t4](t4>t3),表示通信方在此区间内均正常通信。
将干扰方获得的干扰总收益定义为所有时隙内各个干扰机获得干扰收益之和,即
| $ R_{\mathrm{sum}}=\sum\limits_{t=0}^{T} R_{t}^{i} $ | (12) |
式中t为通信时隙,Rti为第i个干扰机在该时隙的干扰收益, i=1, 2, 3。干扰方的最佳干扰策略π*是在一定时间内最大化干扰总收益Rsum, 表示为
| $ \pi^{*}=\operatorname{argmax}_{\pi} E_{\tau \sim \pi(\tau)}\left[R_{\operatorname{sum}(\tau)}\right] $ | (13) |
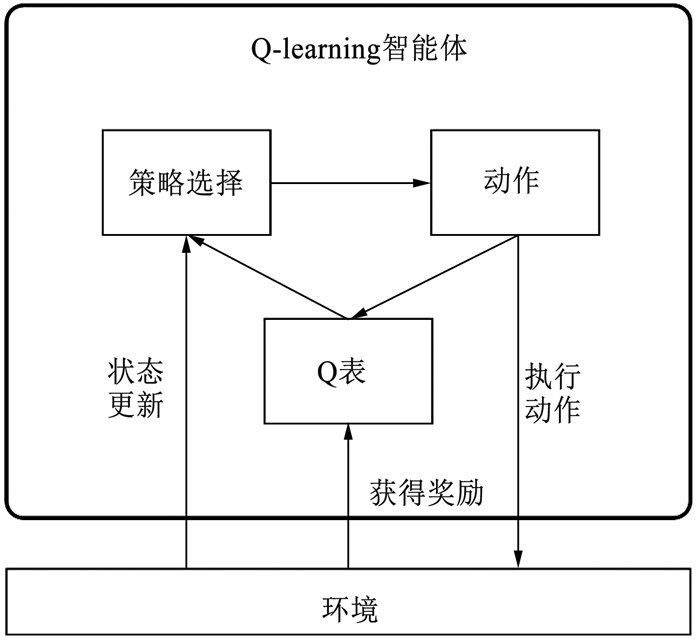
强化学习方法按是否已知环境状态的转移概率可分为基于模型和无模型两类算法[18],按学习方式可分为基于值函数和基于策略函数的强化学习算法。Q学习[19]是一种无模型且基于值函数的算法,其算法框架见图 2。
|
图 2 Q学习算法框图 Fig. 2 Block diagram of Q-learning algorithm |
智能体在当前状态St通过与环境不断交互,根据学习到的知识,选择执行动作At后获得反馈信息Rt+1并转移到下个状态St+1,按式(14)更新所采取动作的价值并存入Q表。
| $ \begin{gathered} Q\left(S_{t}, A_{t}\right)=Q\left(S_{t}, A_{t}\right)+ \\ \alpha\left[R_{t+1}+\gamma \max \limits_{a} Q\left(S_{t+1}, a\right)-Q\left(S_{t}, A_{t}\right)\right] \end{gathered} $ | (14) |
式中:α∈(0, 1)为学习步长,表征算法每次迭代的步长,α越大则每次更新的幅度就越大,提升了学习速度但会增加波动性,α越小则学习速度较慢但更稳定;γ∈(0, 1)为折扣因子,体现智能体对当前动作在将来产生影响的重视程度,γ越小表示智能体越重视眼前收益,γ越大表示智能体更注重长远收益。
在学习过程中,Q学习算法在每个状态遵循ε-greedy策略选择动作,如式(15)所示:
| $ \pi(a \mid s)=\left\{\begin{array}{l} \underset{a}{\operatorname{argmax}} Q(s, a), p=1-\varepsilon \\ \text {randomly select }, p=\varepsilon \end{array}\right. $ | (15) |
即以1-ε的概率选择当前状态下收益最高的动作,以ε的概率进行随机选择。
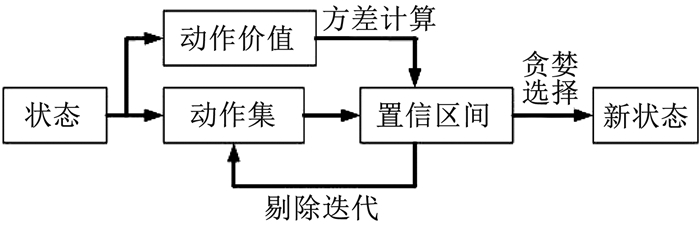
本文为实现智能体在未知环境中能较好地从探索阶段过渡到利用阶段,将有效方差置信上界思想引入到Q学习算法中。有效方差置信上界核心思想是在置信区间中加入方差值,通过剔除不在置信区间的动作减小探索成本,见图 3。
|
图 3 有效方差置信上界策略 Fig. 3 Efficient upper confidence bound variance strategy |
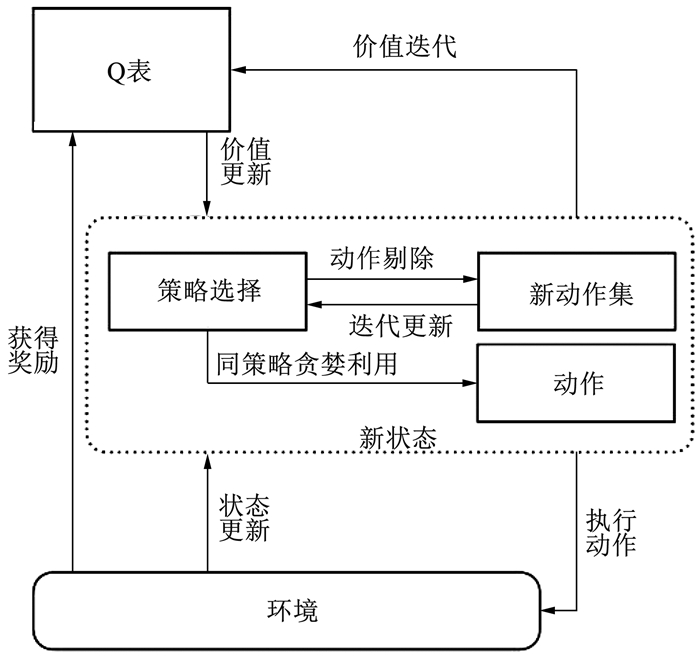
在此基础上, 借鉴文献[8]将使用异策略随机探索转为使用同策略贪婪利用,提出了融合有效方差置信上界的改进Q学习算法。在引入置信区间的同时,根据各个动作的估计价值上限,剔除不在置信区间的动作,以削减在动作空间的探索成本,使得算法能更快收敛到最佳动作,且同步更新该状态的所有动作价值来更充分地利用历史信息,使得算法在任意一个状态都能准确选择价值最高的动作。算法框架见图 4。
|
图 4 融合有效方差置信上界的Q学习算法框图 Fig. 4 Block diagram of Q-learning algorithm based on efficient upper confidence bound variance |
本文算法具体过程如下:
首先设置步长α∈(0, 1]、折扣因子γ>0、迭代次数T,初始状态集合为S+,状态s对应的动作集为A(s), s∈S+; 初始化状态动作对价值矩阵Q(s, a)=0|S|×|A|, 状态动作对平均奖励矩阵P(s, a)=0|S|×|A|, 状态动作对执行次数矩阵N(s, a)=0|S|×|A|,s∈S+,a∈A(s); 探索因子ρ∈(0, 1],常量
在当前状态s,智能体遵循策略π(a|s)即选择动作, 则
| $ \pi(a \mid s)= \begin{cases}\underset{a \in A(s)}{\operatorname{argmax}}\left\{\hat{r}_{a}+\sqrt{\frac{\rho\left(\hat{v}_{a}+2\right) \log _{\mathrm{e}}\left(\psi T \varepsilon_{m}\right)}{4 N(s, a)}}\right\} & \forall N(s, a) \neq 0 \\ a & \exists N(s, a)=0\end{cases} $ | (16) |
式中
| $ \hat{v}_{a}=\frac{1}{N(s, a)} \sum\limits_{l=1}^{N(s, a)}\left(r_{a, l}-\hat{r}_{a}\right)^{2} $ | (17) |
随后进行当前状态的动作剔除,如果动作i满足式(18),则从动作空间A(s)m剔除动作i,得到新的动作集A(s)′m:
| $ \begin{gathered} \hat{r}_{i}+\sqrt{\frac{\rho\left(\hat{v}_{i}+2\right) \log _{\mathrm{e}}\left(\psi T \varepsilon_{m}\right)}{4 z_{i}}}< \\ \max \limits_{j \in A(s)}\left\{\hat{r}_{j}-\sqrt{\frac{\rho\left(\hat{v}_{j}+2\right) \log _{\mathrm{e}}\left(\psi T \varepsilon_{m}\right)}{4 z_{j}}}\right\} \end{gathered} $ | (18) |
当时间步t≥Nm且m≤M时,更新剔除参数:
剔除因子
| $ \boldsymbol{\varepsilon}_{m+1}=\frac{\boldsymbol{\varepsilon}_{m}}{2} $ | (19) |
当前轮次所有状态对应的动作集合
| $ A(s)_{m+1}=A(s)^{\prime}{}_{m}, \forall s \in S^{+} $ | (20) |
动作探索访问上界值
| $ n_{m+1}=\left\lceil\frac{\log _{\mathrm{e}}\left(\psi T \varepsilon_{m}^{2}\right)}{2 \varepsilon_{m}}\right\rceil $ | (21) |
所有动作总访问上界值
| $ N_{m+1}=t+\left|A(s)_{m+1}\right| n_{m+1} $ | (22) |
动作剔除轮次
| $ m=m+1 $ | (23) |
执行动作a,观察反馈奖励r和下一状态s′,按式(24)同步更新与状态s关联的该动作集合中所有动作价值:
| $ \forall a Q(s, a)=Q(s, a)+\alpha\left[r+\gamma \max \limits_{a} Q\left(s^{\prime}, a\right)-Q(s, a)\right] $ | (24) |
式中α是学习步长,为确定的非负常数,且满足下式条件:
| $ \alpha \in[0,1), \sum\limits_{t=1}^{\infty} \alpha_{t}<\infty, \sum\limits_{t=1}^{\infty}\left(\alpha_{t}\right)^{2}<\infty $ | (25) |
算法1 融合有效方差置信上界的改进Q学习算法
步骤1:设置学习步长α∈(0, 1],折扣因子γ>0,迭代次数T,初始化矩阵Q(s, a)=0|S|×|A|,P(s, a)=0|S|×|A|,N=0|S|×|A|,ρ∈(0, 1],
步骤2:当t≤T时,对当前的状态s∈S+,遵循策略π(a|s)选择动作,并更新该状态的动作空间A(s)m。
步骤3:令t=t+1,按式(19)~(23)更新剔除参数。
步骤4:根据式(24)更新Q表。
步骤5:重复步骤2~4直到Q表收敛或s到达最终状态。
结合本文的对抗场景与决策模型,提出基于上文改进Q学习的智能干扰决策算法,算法将指引多个干扰机的智能引擎作为智能体,见图 5。

|
图 5 干扰决策算法框图 Fig. 5 Block diagram of jamming decision algorithm |
详细算法如下:
算法2 基于改进Q学习的干扰决策算法
步骤1:设定初始值同算法1,初始化干扰动作集A0。
步骤2:在每个状态st={(ftc1, ftj1, τ1),(fttc2, fj2, τ2), …, (ftci, ftji, τi)}, i=2, 3;干扰方依据π(a|s)即式(16)选择当前时隙要干扰的干扰动作at,并进行当前状态下的干扰动作剔除,得到新动作集At。
步骤3:干扰方执行干扰动作at,获得干扰反馈信息,若干扰成功,则通信方依据策略重新选择波道;否则,通信方不变更波道,环境进入下一个状态,st+1={(ftc1, ftj1, τ1)′,(ftc2, ftj2, τ2)′, …, (ftci, ftji, τi)′}, i=2, 3。
步骤4:当|At|>1时,重复步骤2和3。
步骤5:当|At|=1时,遍历At中所有的干扰动作直到所有时隙结束。
本文在0~5 MHz频率范围内划置了N个正交波道,设每个波道的带宽均为Bi,为了减少仿真环境存在的随机性与偶然性,每组仿真实验重复1 000次,取所有仿真实验数据的平均值作为最后的实验结果。实验1为单个干扰机对抗单对通信用户,通信方采用伪随机波道切换策略来躲避干扰;实验2为单个干扰机对抗单对通信用户,通信方初始阶段采用伪随机波道切换策略,当通信受阻率超过忍耐值P后将变更随机种子,改变通信策略;实验3为多个干扰机对抗多个通信用户(多对通信收发机),当通信网内通信总受阻率超过忍耐值P后各用户均变更各自伪随机波道切换序列的随机种子。3个实验中都将本文算法和UCBH-Q算法[10],以及经典强化学习算法Q学习、Soft-Q、动态ε-Q算法进行对比,并从干扰成功率和干扰总收益两个方面对实验结果进行分析研究。
实验及模型参数设置见表 1。
| 表 1 实验及模型参数 Tab. 1 Experiment and model parameters |
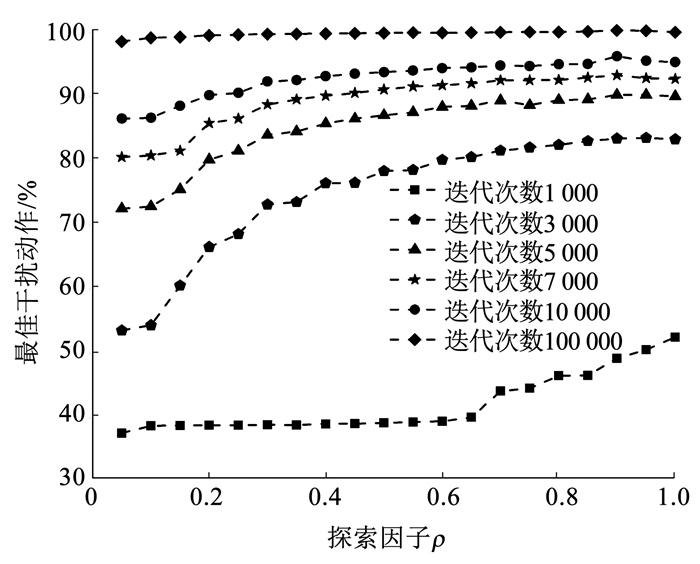
首先考察在本文算法中设置的探索因子ρ对算法寻优性能的影响。图 6给出了ρ值不同时,本文算法决策最佳干扰动作的平均概率对比。
|
图 6 探索因子对本文算法性能的影响 Fig. 6 Influence of exploring factor on the performance of proposed algorithm |
算法1中探索因子ρ不仅决定每个干扰动作的价值置信上界大小,同时也会相应改变价值置信区间,因此ρ的大小一定程度上影响剔除次优动作与寻优的速度。由图 6对比曲线可知,随着迭代次数的增加,算法寻优效果越明显,干扰成功率越接近于理想上界值。当总迭代数为设定的最大值105时,算法的干扰成功率已趋近于1,但实际对抗环境中大的交互次数条件常常伴随着巨大的成本代价(如暴露干扰机位置等)而很难具备。当探索因子ρ的值介于0.8~1.0之间时,本文算法的寻优性能趋于饱和。在后续仿真实验中,设置本文算法的探索因子ρ为0.9,各仿真实验迭代次数均为T=104。
实验1 通信方使用的固定策略为策略1,即通过设置随机种子,产生伪随机数列,数列中的元素代表波道序号,根据伪随机波道序列切换波道。
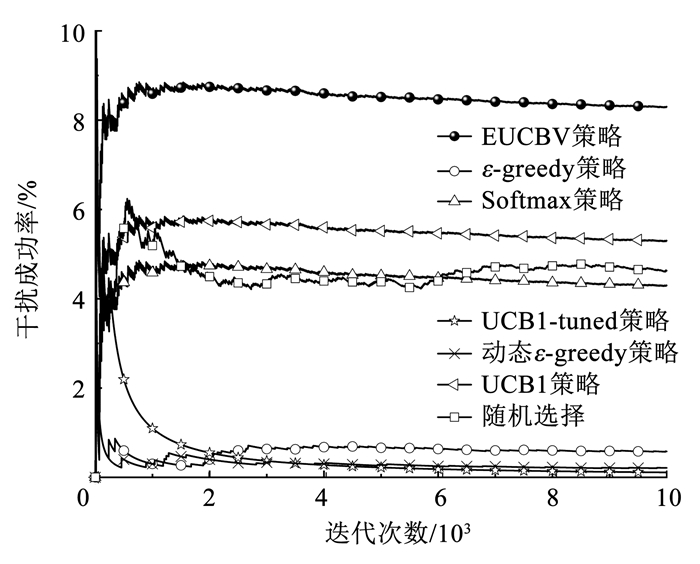
首先对比了干扰方直接使用有效方差置信上界等多臂赌博机(MAB)策略的干扰成功率,见图 7。
|
图 7 采用不同多臂赌博机策略的干扰成功率 Fig. 7 Jamming success rate of different MAB strategies |
由图 7可知,在MAB策略的干扰实验中,有效方差置信上界策略相对较优,但最高干扰成功率不超过9%。这是由于MAB策略多用于收益满足平稳分布的场景,但在对抗场景下通信方受到干扰后会改变通信策略,故对于干扰方而言收益分布是非平稳的,各MAB策略的决策性能不佳。这同时也表明基于统计概率的干扰方式不适用于变化的对抗环境。
对抗使用伪随机策略1通信的单个通信用户时,各强化学习算法的干扰成功率见图 8。

|
图 8 对抗伪随机策略1的干扰成功率 Fig. 8 Jamming success rate against the first pseudo-random strategy |
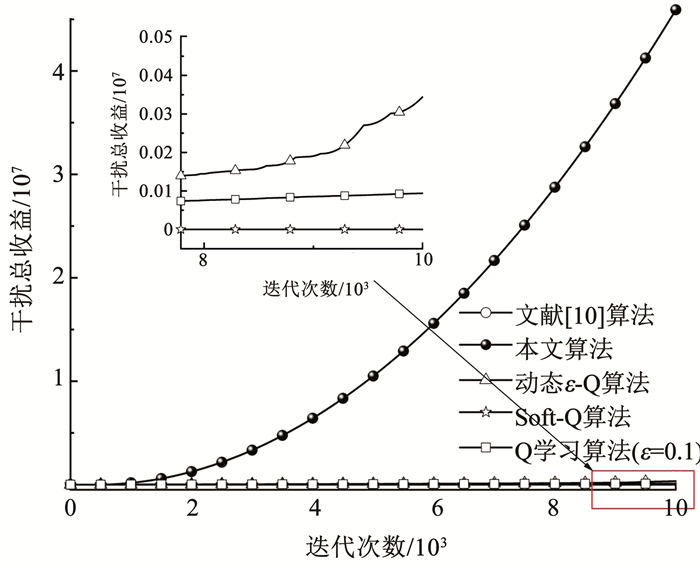
从图 8的干扰成功率曲线可以看到,随着迭代次数的增加,5种算法通过与环境不断交互并学习历史经验,可使干扰成功率逐渐增加并趋于稳定。本文算法和文献[10]算法的学习轨迹大体一致,此外本文算法初始需遍历干扰动作空间因而起始阶段学习速度相对较慢,但后期可迅速收敛,在迭代次数到3 000时算法优势开始显现(图 8),最终干扰成功率高于其他几种算法。各算法的干扰总收益对比见图 9。
|
图 9 对抗伪随机策略1的干扰总收益 Fig. 9 Total jamming rewards against the first pseudo-random strategy |
图 9中,在当前设置的奖励函数条件下,与其他算法相比,本文算法和文献[10]算法所获得的干扰总收益有明显提升。
当单个通信用户使用伪随机策略1通信时,各算法的性能对比见表 2。
| 表 2 对抗伪随机策略1各算法的性能对比 Tab. 2 Performance comparison of algorithms against the first pseudo-random strategy |
由本文设置的干扰奖励函数可知,连续成功的干扰可获得更大的收益,即使在干扰成功率差别不大的情况下,干扰总收益仍可能存在较大的差距。例如表 2中Soft-Q算法虽然干扰成功率只比前两种算法低了一个百分点,但在干扰总收益上却相差了两个数量级,原因主要在于其他算法是根据最佳干扰动作的概率分布选择干扰动作,具有一定随机性,很难实现连续稳定的成功干扰,而本文算法是依据价值高低直接选择最佳动作,消除了决策过程的偶然性。
实验2 实验2为单个干扰机对抗使用可变通信策略的单用户,进一步考察各算法在变化环境中的学习速度。通信方使用的可变通信策略为策略2,即初始阶段采用伪随机的波道切换策略,当通信受阻率超过规定忍耐值后,则变更随机种子,使用新波道序列进行通信。
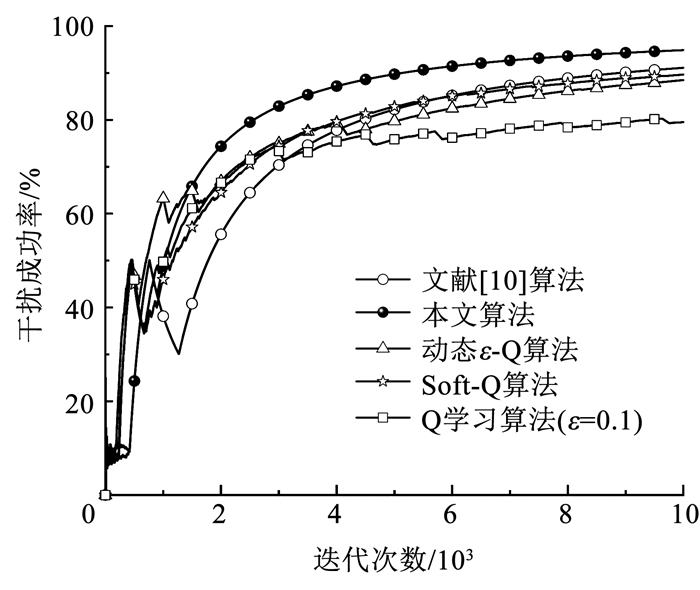
对抗使用伪随机策略2通信的单通信用户时,各算法的干扰成功率见图 10。
|
图 10 对抗伪随机策略2的干扰成功率 Fig. 10 Jamming success rate against the second pseudo-random strategy |
从图 10的干扰成功率曲线可以看出,初始阶段上述几种算法都可以实现干扰成功率的缓慢上升。当通信受阻率超过忍耐值后,由于通信方改变波道切换的策略,干扰成功率急剧下降,而后随着时间推移,干扰成功率再次上升。说明在通信方改变通信策略后,强化学习算法仍可以学习到新的干扰策略来应对通信方策略的变化。且从曲线对比可知,本文算法的学习轨迹更稳定,波动性更小。
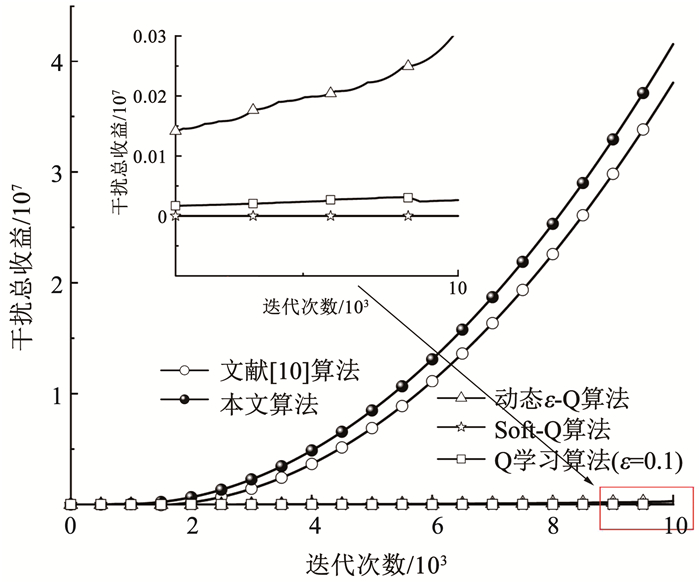
对抗伪随机策略2时,各算法获得的干扰总收益见图 11。
|
图 11 对抗伪随机策略2的干扰总收益 Fig. 11 Total jamming rewards against the second pseudo-random strategy |
图 11中,由于初始阶段各学习算法需要大量的交互经验,前期干扰获得的总收益一直处于较低水平,而后获得足够的经验样本后,干扰总收益回升。从曲线对比可看到当通信方的策略发生改变时,本文算法可以获得更高的干扰总收益,表现出比其他学习算法在变化环境中更强的学习和适应能力。表 3给出了对抗伪随机策略2时各算法的性能对比。
| 表 3 对抗伪随机策略2的各算法性能对比 Tab. 3 Performance comparison of algorithms against the second pseudo-random strategy |
实验3 构造“多对多”对抗场景,对比多个干扰机对抗使用可变通信策略的多用户时各算法性能,进一步考察算法在变化环境中的协同干扰决策能力。实验设置3个干扰机(或有3个干扰通道的单干扰机)和3个通信用户,每个通信用户均使用伪随机策略2进行通信,当某时隙所有用户都受到干扰时才视为协同干扰成功。
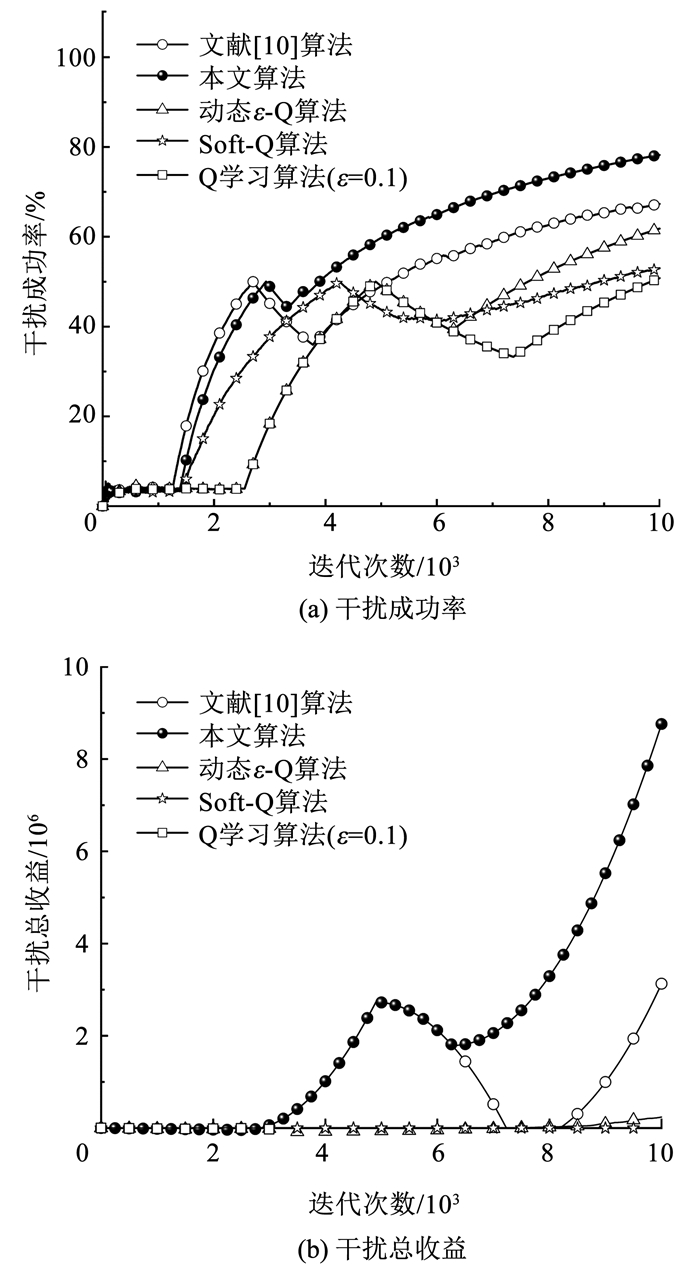
此时各算法的协同干扰效果见图 12。
|
图 12 “多对多”场景下各算法的协同对抗性能对比 Fig. 12 Performance comparison of "many-to-many" cooperative countermeasure of different algorithms |
由图 12可知,由于协同干扰条件下环境更复杂且干扰方的联合干扰动作空间变大,加之学习过程中各通信用户的策略变化,使得决策空间维度增加,决策难度增大,当通信用户改变策略后各算法的干扰成功率和干扰总收益出现了大幅度下降。本文算法最终干扰成功率接近80%,较传统Q学习算法高50%以上。
4 结论针对当前智能干扰决策算法收敛速度较慢、决策效率不高的问题,提出了一种基于改进Q学习的智能干扰决策算法。在通信干扰决策场景下,仿真验证了该算法提升决策的有效性。本文算法有较强扩展性,可将干扰动作空间延拓至多个干扰机的联合干扰动作,利用动作剔除方法降低联合干扰动作的空间维度,实现干扰资源受限情况下的协同干扰决策,实验表明该算法可实现相对较好的协同对抗效果。本文也存在一些不足,例如: 由于在初始阶段需遍历动作空间而当决策空间过大或决策空间连续时,算法学习速度较慢、效率不高。下一步考虑更充分地利用与环境交互得到的历史经验,在进一步缩减迭代次数条件下保证算法决策的可靠性。
| [1] |
SUN Hongjian, NALLANATHAN A, WANG Chengxiang, et al. Wideband spectrum sensing for cognitive radio networks: A survey[J]. IEEE Wireless Communications, 2013, 20(2): 74. DOI:10.1049/iet-net.2020.0122 |
| [2] |
BAYRAM S, VANLI N D, DULEK B, et al. Optimum power allocation for average power constrained jammers in the presence of non-Gaussian noise[J]. IEEE Communications Letters, 2012, 16(8): 1154. DOI:10.1109/LCOMM.2012.052112.120098 |
| [3] |
AMURU S, BUEHRER R M. Optimal jamming against digital modulation[J]. IEEE Transactions on Information Forensics & Security, 2015, 10(10): 2212. DOI:10.1109/TIFS.2015.2451081 |
| [4] |
AMURU S, BUEHRER R M. Optimal jamming using delayed learning[C]//Proceedings of 2014 IEEE Military Communications Conference. Baltimore: IEEE, 2014: 1530. DOI: 10.1109/MILCOM.2014.252
|
| [5] |
AMURU S, TEKIN C, van der SCHAAR M, et al. Jamming bandits—A novel learning method for optimal jamming[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2794. DOI:10.1109/TWC.2015.2510643 |
| [6] |
颛孙少帅, 杨俊安, 刘辉, 等. 采用双层强化学习的干扰决策算法[J]. 西安交通大学学报, 2018, 52(2): 65. ZHUANSUN Shaoshuai, YANG Junan, LIU Hui, et al. An algorithm for jamming decision using dual reinforcement learning[J]. Journal of Xi'an Jiaotong University, 2018, 52(2): 65. DOI:10.7652/xjtuxb201802010 |
| [7] |
颛孙少帅, 杨俊安, 刘辉, 等. 基于正强化学习和正交分解的干扰策略选择算法[J]. 系统工程与电子技术, 2018, 40(3): 37. ZHUANSUN Shaoshuai, YANG Junan, LIU Hui, et al. Jamming strategy learning based on positive reinforcement learning and orthogonal decomposition[J]. Systems Engineering and Electronics, 2018, 40(3): 37. DOI:10.3969/j.issn.1001-506X.2018.03.05 |
| [8] |
SLIMENI F, CHTOUROU Z, SCHEERS B, et al. Cooperative Q-learning based channel selection for cognitive radio networks[J]. Wireless Networks, 2019, 25(7): 4162. DOI:10.1007/s11276-018-1737-9 |
| [9] |
HAN Chen, NIU Yingtao. Multi-regional anti-jamming communication scheme based on transfer learning and Q learning[J]. KSⅡ Transactions on Internet and Information Systems, 2019, 13(7): 3340. DOI:10.3837/tiis.2019.07.001 |
| [10] |
JIN Chi, ZHU Z A, BUBECK S, et al. Is Q-learning provably efficient?[C]// Proceedings of 32nd Conference on Neural Information Processing Systems. Montréal: [s. n. ], 2018: 4867
|
| [11] |
WANG Wenbo, KWASINSKI A, NIYATO D, et al. A survey on applications of model-free strategy learning in cognitive wireless networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1740. DOI:10.1109/COMST.2016.2539923 |
| [12] |
MAILLARD O A, MUNOS R, STOLTZ G. A finite-time analysis of multi-armed bandits problems with Kullback-Leibler divergences[J]. Journal of Machine Learning Research, 2011, 19(1): 18. |
| [13] |
AUDIBERT J Y, MUNOS R, SZEPESVÁRI C. Exploration-exploitation tradeoff using variance estimates in multi-armed bandits[J]. Theoretical Computer Science, 2009, 410(19): 1885. DOI:10.1016/j.tcs.2009.01.016 |
| [14] |
AUER P, ORTNER R. UCB revisited: improved regret bounds for the stochastic multi-armed bandit problem[J]. Periodica Mathematica Hungarica, 2010, 61(1/2): 58. DOI:10.1007/s10998-010-3055-6 |
| [15] |
MUKHERJEE S, NAVEEN K P, SUDARSANAM N, et al. Efficient-UCBV: An almost optimal algorithm using variance estimates[C]//Proceedings of 32nd AAAI Conference on Artificial Intelligent. San Francisco: AAAI, 2018: 6419
|
| [16] |
张春磊, 杨小牛. 认知电子战与认知电子战系统研究[J]. 中国电子科学研究院学报, 2014, 9(6): 551. ZHANG Chunlei, YANG Xiaoniu. Research on the cognitive electronic warfare and cognitive electronic warfare system[J]. Journal of CAEIT, 2014, 9(6): 551. DOI:10.3969/j.issn.1673-5692.2014.06.001 |
| [17] |
NIE Junhong, HAYKIN S. A Q-learning-based dynamic channel assignment technique for mobile communication systems[J]. IEEE Transactions on Vehicular Technology, 1999, 48(5): 1677. DOI:10.1109/25.790549 |
| [18] |
SUTTON R S, BARTO A G. Reinforcement learning: An introduction[M]. Boston: MIT Press, 1998: 25.
|
| [19] |
WATKINS C J C H. Learning from delayed rewards[D]. Cambridge: University of Cambridge, 1989: 27
|
 2022, Vol. 54
2022, Vol. 54


