近些年来,在气候变暖、科学技术发展、经济效益驱动以及一些政治和军事领域的显著价值需求下,极地航线开发、极地资源的勘探以及极地环境利用成为一种必然且迫切的趋势[1]。这些变化极大地促进了更加频繁的极地地区海洋结构物的作业活动,除此之外,多数内陆结冰水域仍旧常年进行各种海上作业活动。然而冰的存在能够对结构物造成严重的损害,甚至造成结构物的破坏而无法正常作业。由此研究冰力学性能和破坏模式及其与结构物相互作用过程是支持极地以及冰区结构物发展的重要手段之一,而建立精确的冰本构模型是这其中的关键技术之一。
基于数值计算的冰力学特性、冰-结构物作用过程等研究近几年快速发展:最初,学者们通常采用基于试验获得的经验数据和数学物理分析的方法来计算冰的力学特性并且用于冰与结构物相互作用过程的冰载荷预报以及船舶运动性能预报[2-4]。然而上述文献中对于海冰性质研究的方法,极大地依赖于经验数据,不足以发展成完整成熟的数值模型[5]。后来,学者们纷纷采用基于传统连续介质力学方法的数值手段来研究海冰的特性,例如有限元方法FEM[6-8],改进有限元方法[9-10],以及其他考虑冰细微参数的方法等[11]。然而传统介质力学方法在处理大变形或者断裂问题具有一定的局限性,不能准确地模拟冰破坏过程的裂纹扩展路径。为了克服上述的科学问题,学者开始尝试建立基于无网格方法的冰本构模型,这些方法里发展比较成型的有:离散元方法(Discrete element method, DEM)[12-13],光滑粒子动力学(Smoothed particle hydrodynamics, SPH)[14-16]以及近场动力学方法(Peridynamics, PD)[17-19]等。其中DEM方法由于其颗粒状的模型形式具有模拟浮碎冰和结构物碰撞、浮碎冰之间碰撞的优势。而SPH和PD方法的粒子离散形式使其在海冰破碎以及裂纹扩展方面更具有更突出的优势,不管是哪种粒子数值模型,虽然能够处理断裂问题,但是并不能完整精确地模拟冰力学性能和破坏特性,由此这些方法仍然处于发展前期,还需要投入大量的研究工作来建立适用于冰的准确数值模型。
近场动力学方法(PD),是近二十年新兴的一种非局部、无网格粒子、积分形式的计算方法,在断裂问题域和非断裂问题域上都可以连续求解[20]。该方法最早由Silling等[21-22]提出并建立推导了其控制方程,给出了基本的数值实现程序案例。PD方法主要两种表现形式[21-23],经推导和比较[24]两种表达方式大同小异且具有相类似的计算精度。PD发展至今主要有键型、常规状态型和非常规状态型3种形式。且该方法已经成功应用于材料的弹性、塑性、热力学等多种物理问题计算分析领域[25-27]。然而PD应用于冰计算领域刚刚起步,多数文献采用基于键型的弹性模型来模拟冰的破坏特性,例如,冰与刚体柱的作用过程、冰桨作用过程等,忽略了泊松比的真实状态和海冰具有塑性屈服过程的力学特性。由此本文主要的目的是建立基于状态型PD方法的冰弹塑性本构模型,消除了键型对泊松比的限制,加入了冰破坏过程塑性变形过程,为后续的冰与结构物的作用过程提供支撑。
1 基于常规近场动力学的弹塑性本构模型 1.1 基于常规近场动力学的弹塑性理论 1.1.1 近场动力学理论近场动力学方法将连续介质离散为均匀的物质点。在参考坐标系下,其运动方程为
| $ \begin{aligned} \rho(\boldsymbol{x}) \ddot{\boldsymbol u}(\boldsymbol{x}, \boldsymbol{t})=& \cdots \\ & \int\limits_{H}\left(\boldsymbol{t}\left(\boldsymbol{u}^{\prime}-\boldsymbol{u}, \boldsymbol{x}-\boldsymbol{x}^{\prime}, \boldsymbol{t}\right)-\right.\\ &\left.\boldsymbol{t}^{\prime}\left(\boldsymbol{u}-\boldsymbol{u}^{\prime}, \boldsymbol{x}^{\prime}-\boldsymbol{x},\right)\right) \mathrm{d} \boldsymbol{H}+\boldsymbol{b}(\boldsymbol{x}, \boldsymbol{t}) \end{aligned} $ | (1) |
上式的离散形式为
| $ \begin{aligned} \boldsymbol{\rho}_{(k)} \ddot{\boldsymbol u}_{(k)}=& \cdots \\ & \sum\limits_{j=1}^{N}\left(\boldsymbol{t}\left(\boldsymbol{u}_{(j)}-\boldsymbol{u}_{(k)}, \boldsymbol{x}_{(j)}-\boldsymbol{x}_{(k)}, \boldsymbol{t}\right)-\right.\\ &\left.\boldsymbol{t}^{\prime}\left(\boldsymbol{u}_{(k)}-\boldsymbol{u}_{(j)}, \boldsymbol{x}_{(k)}-\boldsymbol{x}_{(j)}, \boldsymbol{t}\right)\right) \mathrm{d} V_{(j)} \cdots+b_{(k)} \end{aligned} $ | (2) |
式中,每个粒子的信息用其位置坐标表示,即x(k),该粒子占据的空间大小为V(k)且密度为ρ(k)。在笛卡尔坐标中,材料点受到外界作用的位移为u(k),此时的位置向量为y(k)。由此,材料点k在未变形状态下的位置为x(k),其位移和外力向量分别用u(k)(x(k), t)和b(k)(x(k), t)表示,对k点有作用的域(近场域)表示为Hx(k)。
1.1.2 塑性理论本文将海冰视作各向同性的均匀介质材料。下述本构模型的建立基于该假设成立。根据经典连续介质力学中的塑性定义,当材料在加载/卸载条件下的应力水平超过屈服应力时,材料在完全卸载时会发生永久(或塑性)变形。与弹性变形不同,塑性变形取决于加载历史。因此,塑性变形更加关注每一时间步力密度增量和拉伸增量的关系。用PD进行塑性分析时,需要对等效应力进行描述,这是因为在塑性分析中,弹性区域受屈服面限制。此外,屈服面在每个加载步骤中的增长和移动都需要确定,因此需要将等效塑性拉伸描述为硬化内变量。
为了用参量的增量形式表达PD中的塑性变形,将外界作用下两个材料点之间的拉伸增量Δs(k)(j)以及力密度增量Δt(k)(j)分解成弹性项和塑性项如下:
| $ \Delta s_{(k)(j)} =\Delta s_{(k)(j)}^{e}+\Delta s_{(k)(j)}^{p} $ | (3) |
| $ \Delta t_{(k)(j)} =\Delta t_{(k)(j)}^{e}+\Delta t_{(k)(j)}^{p} $ | (4) |
本文的塑性理论中假设塑性变形与体积变形无关,由此塑性拉伸的过程体积膨胀为0,即Δθp=0。PD方法中静水压力分别在力密度函数和应变能密度的弹性项中,用p=-kθ表述,其中k为冰的体积模量。本文模型中塑性变形与静水压力无关。同样地,每一步的应变能密度增量分解为弹性应变能密度增量和塑性应变能密度增量如下:
| $ \Delta W_{(k)}=\Delta W_{(k)}^{e}+\Delta W_{(k)}^{p} $ | (5) |
传统的塑性理论中,塑性变形由屈服面来判定。参照传统塑性理论屈服面定义为[28]
| $ \varPhi_{(k)}\left(\bar{\sigma}, \sigma_{y}\right)=\left|\bar{\sigma}_{(k)}\right|-\sigma_{y} \leqslant 0 $ | (6) |
式中: σ(k)为k点的等效应力,σy为屈服应力。弹塑性理论中加载/卸载条件可以表示为
| $ \left\{\begin{array}{l} \varPhi_{(k)}\left(\bar{\sigma}, \sigma_{y}\right)<0, \Delta s_{(k)(j)}^{p}=0, \text { 弹性加载 } \\ \varPhi_{(k)}\left(\bar{\sigma}, \sigma_{y}\right)=0, \Delta s_{(k)(j)}^{p}=0, \text { 弹性卸载 } \\ \varPhi_{(k)}\left(\bar{\sigma}, \sigma_{y}\right)=0, \Delta s_{(k)(j)}^{p} \neq 0, \text { 塑性加载 } \end{array}\right. $ | (7) |
依据Von-Mises塑性屈服准则,塑性屈服发生在偏斜应变部分的应变能密度达到极限值的时候,对于单轴压缩来说,这个极限值等于材料达到初始屈服应力σ0时的应变能密度,即
| $ \sigma_{y 0}=\sqrt{3 J_{2}}=\sqrt{6 \mu W_{(k)}^{\mu}} $ | (8) |
式中J2为应力偏张量的第二不变量。为了在一般荷载情况下使用该方程,需要定义等效应力。等效应力可定义为[29]
| $ \bar{\sigma}_{(k)}=\sqrt{6 \mu W_{(k)}^{\mu}\left(s_{(k)(j)}^{e}\right)} $ | (9) |
也可以表达成屈服函数增量的形式ΔΦ(k),ΔΦ(k)是一个非正的函数,当ΔΦ(k)=0时为中性加载过程,此时为不考虑硬化规律的理想塑性变形状态,即屈服函数不受到s(k)(j)p的任何影响。依据屈服函数增量-力密度增量的关系和应变能密度增量-伸长增量的关系可以推导出如下关系[29]:
| $ \Delta s_{(k)(j)}^{p} V_{(j)}=C_{(k)} \frac{\partial \Delta \varPhi_{(k)}}{\partial t_{(k)(j)}} $ | (10) |
式中,C(k)为一个正比例常数,上式作为常态条件表述了塑性伸长增量的流动法则。
在式(7)中,理想塑性(无硬化)状态下,所有加载/卸载过程中,σy是恒定的。然而,塑性变形在不同的状态下与等效塑性拉伸具有相关性,这种相关性有多种情况,例如各向同性硬化关系、运动硬化和混合硬化关系等[28]。本文采用线性各向同性硬化模型[29],即式(6)可改写为
| $ \varPhi_{(k)}=\left|\bar{\sigma}_{(k)}\right|-\sigma_{y}\left(\overline{s}{}_{(k)}^{p}\right) \leqslant 0 $ | (11) |
其中
| $ \sigma_{y}\left(\overline{s}{}_{(k)}^{p}\right)=\sigma_{y 0}+G\left(\overline{s}{}_{(k)}^{p}\right) $ |
式中,s(k)p定义为等效塑性拉伸量,即
| $ \Delta \overline{s}{}_{(k)}^{p}=A_{0} \sqrt{W_{(k)}^{\mu} \Delta s_{(k)(j)}^{p}} $ |
在简单的单轴拉伸情况下,无膨胀项,可以确定塑性增量拉伸引起的畸变应变能密度,并由此提取参数A0。参数A0已在文献[30]中针对不同的物体维度推导得出,本文未列出。
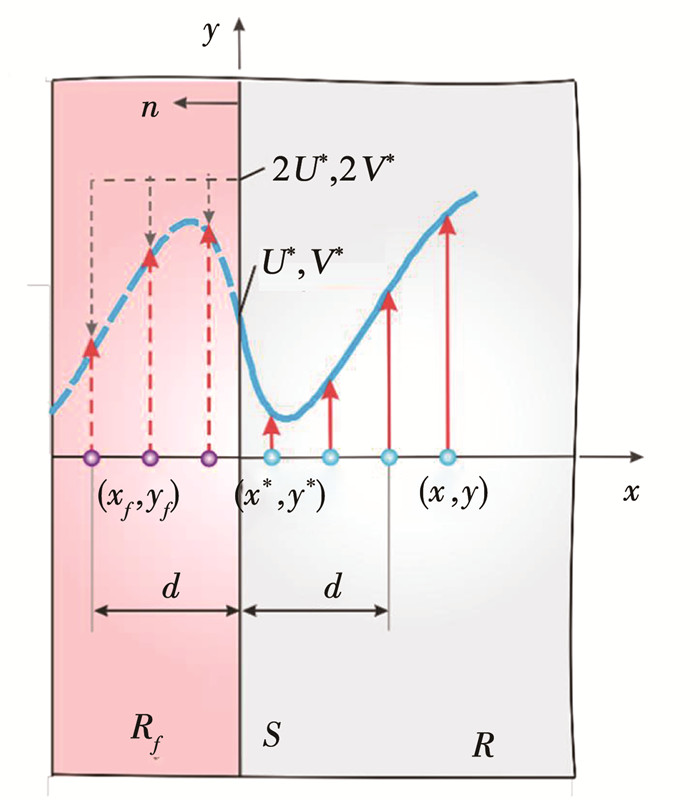
1.2 边界条件由于PD运动方程不包含任何空间导数,因此一般不需要约束条件来求解积分微分方程。与局部理论不同,边界条件是通过非零体积的虚拟边界层施加的。基于数值实验,Macek等[30]建议虚拟边界层的范围等于领域尺寸δ,以确保施加的规定约束在真实区域中得到准确反映。位移边界条件可以通过对虚拟层中的材料点进行约束来施加,使边界曲面上的条件得到明确满足。因此,虚拟层中的位移值可以基于实域值和边界条件指定值的线性外推来近似。类似地,也可以通过近似虚拟区域中的牵引力值来施加牵引力边界条件,从而使真实区域和虚拟层中的牵引力变化恢复边界表面上施加的牵引力。图 1表示了位移边界条件的施加方式,图中Rf表示虚拟粒子边界,宽度为δ,R为真实粒子区域,位移和速度边界条件为U*和V*。则边界条件可以表达为:
| $ \begin{aligned} &u_{f}\left(x_{f}, y_{f}, t+\Delta t\right)=2 U^{*}\left(x^{*}, y^{*}, t+\Delta t\right)-u(x, y, t) \\ &v_{f}\left(x_{f}, y_{f}, t+\Delta t\right)=2 V^{*}\left(x^{*}, y^{*}, t+\Delta t\right)-v(x, y, t) \end{aligned} $ | (12) |
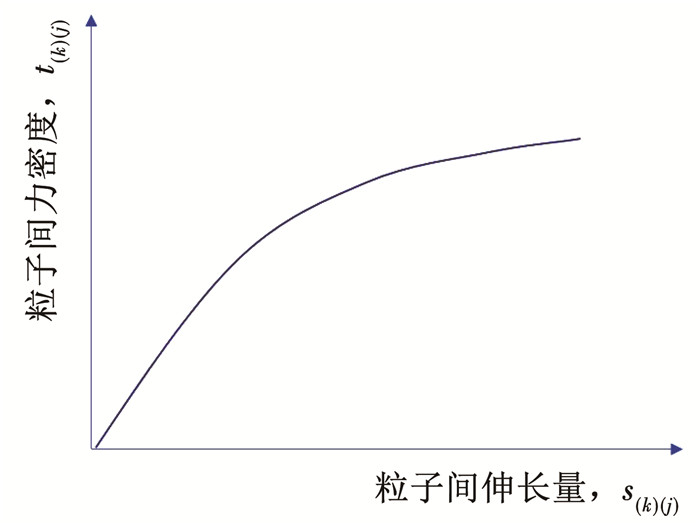
基于PD方法的弹性变形中,失效的判断标准为极限伸长量,当变形后粒子间的伸长量达到极限伸长量s0时,则判断为失效,此过程不可逆。极限伸长量可以通过材料的极限能量释放率得到,粒子间的伸长量和力密度的关系呈线性。然而在塑性变形中,粒子间力密度和伸长量的关系呈典型的非线性,如图 2所示,因此弹塑性本构模型中的失效准则不能再简单地使用最终状态的伸长量来判断,必须对整个变形过程伸长量对应的力密度积分来判断材料的失效。图 2曲线下的面积代表弹塑性变形微势w(k)(j),该函数代表变形的程度,可由下式得到:
| $ w_{(k)(j)}=\int_{0}^{s_{(k)(j)}} \boldsymbol{t}_{(k)(j)}\left|\boldsymbol{x}_{j}-\boldsymbol{x}_{k}\right| \mathrm{d} \boldsymbol{s}_{(k)(j)} $ | (13) |
|
图 2 塑性理论中的变形本构关系 Fig. 2 Constitutive relationship in plastic deformation |
如果一个新的裂纹产生,则穿越这个裂纹的所有粒子间的作用都必须消失。同理,消除两个粒子间作用所需的极限能量释放率作为判别粒子间作用是否失效的标准,则可以表达为
| $ \left\{\begin{array}{l} \bar{g}_{(k)(j)}<g_{c}, \text { 则作用仍存在 } \\ \bar{g}_{(k)(j)} \geqslant g_{c}, \text { 则作用已消失 } \end{array}\right. $ | (14) |
式中: g(k)(j)为两个粒子间的能量释放率,gc为消除这个作用所需的极限能量释放率。这个失效过程是不可逆的,即判断粒子间作用力消失后,将引入一个用来表述作用失效与否的函数ψ(k)(j)。该函数的取值为0或1,且将进一步被传递到力的计算过程。g(k)(j)和gc的计算方法已被推导如下[20]:
| $ \bar{g}_{(k)(j)}=\frac{1}{\Delta x h}\left(\frac{1}{2}\left(w_{(k)(j)}+w_{(j)(k)}\right)\right) V_{(k)} V_{(j)} $ | (15) |
| $ g_{c}=\frac{G_{c}}{N_{c}} $ | (16) |
式中:Gc为材料的极限能量释放率,Nc为PD的对应参数,在一维时取值为12,二维时取值为36,三维时取值为560。
粒子作用的失效通过上述准则判断之后,失效的粒子作用之间力将被移除。此时,通过监测粒子之间相互作用的失效与否就可以表述材料的破坏过程。因此引入局部破坏系数φ(x(k), t)来表述材料在局部位置的破坏程度,该参数的物理意义是:材料点k在其作用域内失效粒子作用与总粒子作用的比值,由下式计算:
| $ \varphi\left(x_{(k)}, t\right)=1-\frac{\int_{H} \psi_{(k)(j)} \mathrm{d} V}{\int\limits_{H} \mathrm{~d} V} $ | (17) |
PD方法的控制方程主要采取积分形式,因此在数值实现时,计算域被分解成粒子形式。计算每个粒子在每个时间步长的物理信息,作为下一时间步的基础值,每个时间步下对所有粒子的物理信息求和积分则为该步长的变形状态。
本文参考了文献[24]中给出的键型PD的程序基础框架。本文的数值执行过程在上述程序框架进行补充完善。首先,常规型PD积分过程中增加了体积膨胀项,可按下式数值执行:
| $ \theta_{(k)}=\sum\limits_{j=1}^{N_{i}} \mathrm{~d} \psi_{(k)(j)} \delta s_{(k)(j)} \Lambda V_{j} $ | (18) |
时间积分内的数值执行过程将全部替换为塑性变形的数值过程,可参考文献[28-29]中的数值实现方法。对于失效准则的积分过程,式(13)将采用如下积分过程实现:
| $ { }^{t+\Delta t} w_{(k)(j)}=t_{w_{(k)(j)}}+\Delta w_{(k)(j)} $ | (19) |
| $ \Delta w_{(k)(j)}=\frac{1}{2}\left({ }^{t+\Delta t} t_{w_{(k)(j)}}+{ }^{t} t_{w_{(k)(j)}}\right)\left({ }^{t+\Delta t} \xi-{ }^{t} \xi\right) $ | (20) |
局部破坏系数的数值执行形式为
| $ \varphi\left(x_{(k)}, t\right)=1-\frac{\sum\limits_{j=1}^{N} \psi_{(k)(j)} V_{(j)}}{\sum\limits_{j=1}^{N} V_{(j)}} $ | (21) |
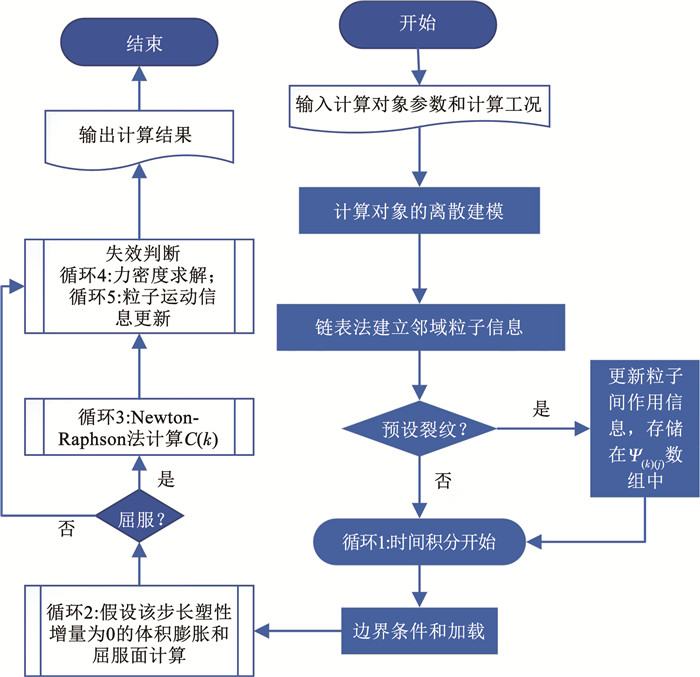
数值框架流程如图 3所示。
|
图 3 数值实现程序框图 Fig. 3 Flowchart of numerical implementation |
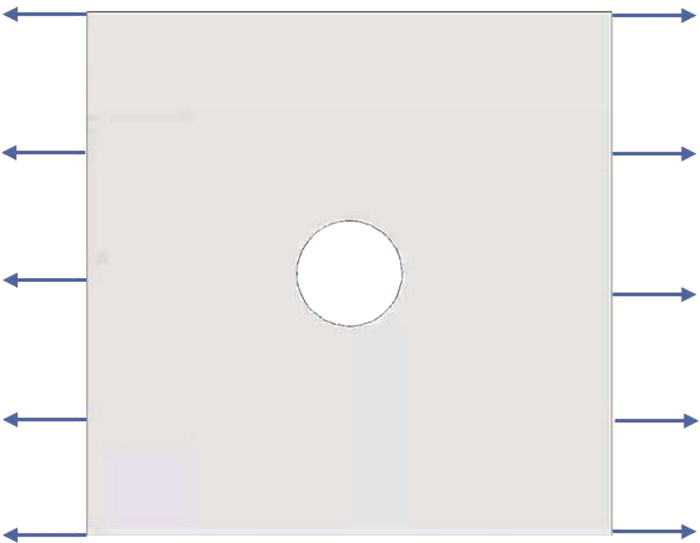
为了验证文章模型的准确性和程序的可靠性,首先计算了带孔二维板的变形问题。二维板的尺寸选取长和宽分别为L=H=1.0 m,板的厚度为h=0.01 m,孔的尺寸为D=0.3 m。弹性模量为E=200 MPa,密度为ρ=4 428 kg/m3,泊松比为ν=1/3,刚度模量为K=50 GPa。离散状态的粒子间距为dx=0.002 5 m。同时采用有限元分析软件Abaqus计算了板的有限元变形,有限元分析中,网格大小与粒子间距相同,网格数有8 910个。板的左右两侧采用位移约束,其位移变形约束表示为:ux(x=0, y, t)=-0.001 m和uy(x=L, y, t)=0.001 m。板的工况示意图如图 4所示。
|
图 4 二维板拉伸变形示意图 Fig. 4 Sketch map of 2D plate under tension |
正如预期的那样,塑性变形在高应力集中区域开始。图 5中给出了带孔板的等效应力和位移的变化,与有限元结果对比完全一致,该案例验证了本文程序的准确性。
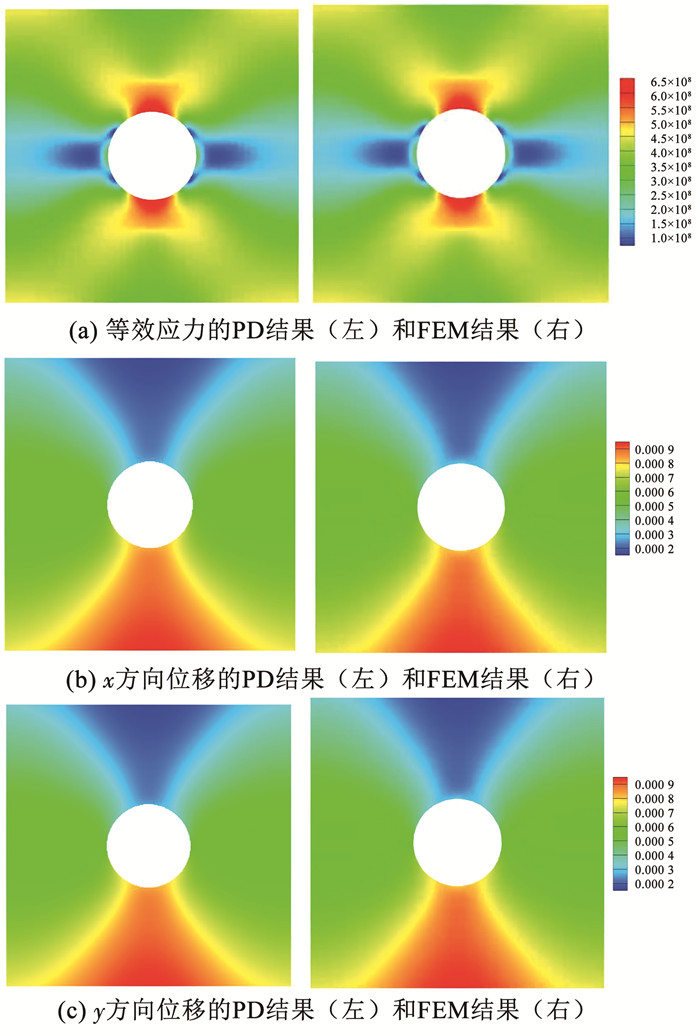
|
图 5 有孔板拉伸状态下的等效应力、x方向位移以及y方向位移 Fig. 5 Variations of effective stress, displacement in x direction, and displacement in y direction of plate with a hole under tension |
冰的弯曲强度是计算冰-船作用的关键参数之一,四点弯曲试验可以用来测量冰的弯曲强度。为了验证本文冰模型的准确性,选用Ehlers和Kujala进行的试验[32]作为对比验证,该试验模型及加载工况示意如图 6所示。
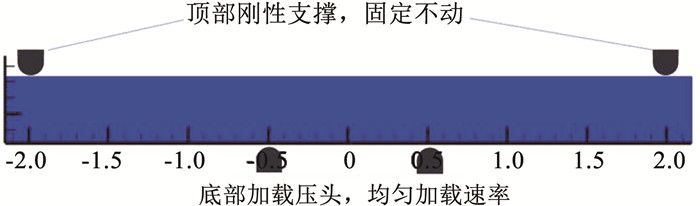
|
图 6 冰四点弯曲试验示意图 Fig. 6 Schematic diagram of four-point bending test of ice |
该试验中,冰梁的尺寸为L=4.25 m, H=0.4 m和B=0.365 m。上方的固定支撑位于中点向两边2 m处,底部位移压头位于0.5 m处。上方的支撑在空间中固定,下方的支撑以Vsupport=0.003 580 m/s匀速向上移动。海冰参数的选取参考试验和文献中对冰力学性能相关分析设定[32-34],冰材料的极限能量释放率采用了文献[35]中的参考值,见表 1。
| 表 1 试验工况设定和海冰参数 Tab. 1 Test conditions and parameters of ice |
文中采用2D进行计算,因此弹性模量转换成2D参数为E/(1-v2)[34]。结果如图 7、8所示。冰的弯曲载荷和时间的关系曲线如图 9所示。
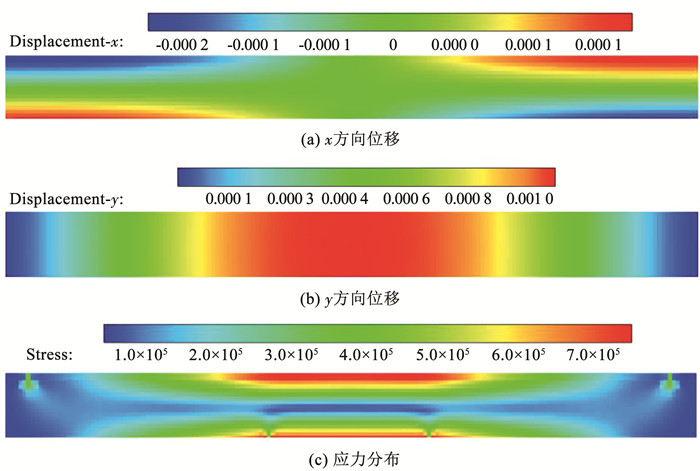
|
图 7 t=0.31 s, Vsupport=0.003 580 m/s(未发生破坏之前)冰四点弯曲试验数值计算结果 Fig. 7 Numerical results of four-point bending test of ice (before damage) (t=0.31 s, Vsupport=0.003 580 m/s) |
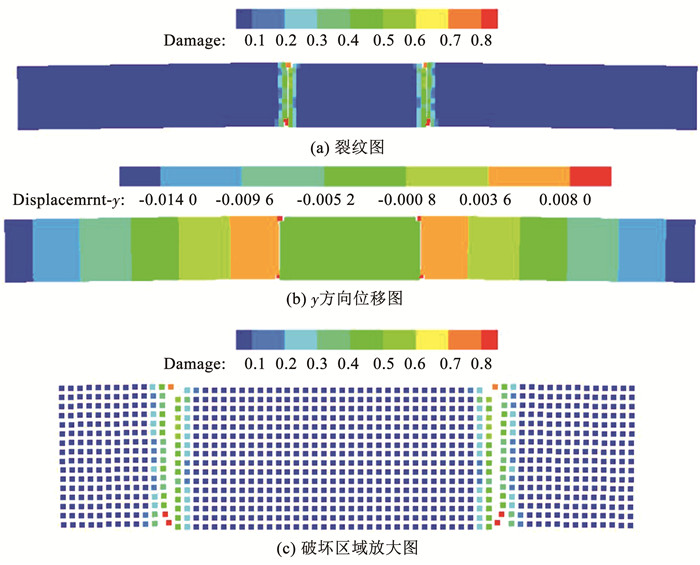
|
图 8 t=1.00 s, Vsupport=0.003 580 m/s(破坏之后)冰四点弯曲试验数值计算结果 Fig. 8 Numerical results of four-point bending test of ice (after damage) (t=1.00 s, Vsupport=0.003 580 m/s) |
|
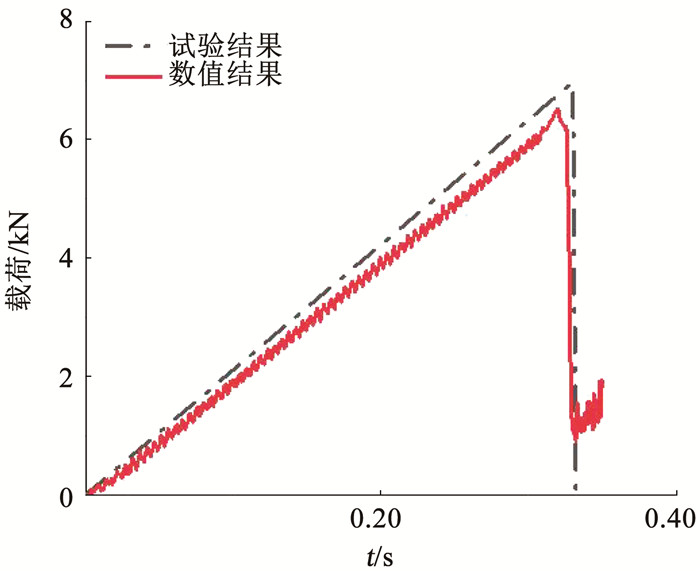
图 9 Vsupport=0.003 580 m/s冰四点弯曲载荷-时间曲线图 Fig. 9 Force-time curve of four-point bending test of ice (Vsupport=0.003 580 m/s) |
从计算结果可以发现,冰梁在下部位移支撑和上层约束支撑的共同作用,发生微小变形,如图 7(a)、(b)所示,两个移动支撑之间的冰梁位移最大,且这段部分各个位置的位移量基本相同。冰梁上越远离移动支撑部位的纵向位移变形越小,这样的变形一直持续到0.31 s之前。此时海冰未发生破坏,由于固定支撑和加载支撑的约束原因,冰x方向和y方向的位移符合物理规律。还可以通过等效应力分布图观测到:高应力分布在拉伸和压缩集中的部位,例如冰梁的上侧边缘和下侧边缘,如图 5(c)所示,这两侧的位置是冰梁挤压和拉伸最为严重的位置。该应力现象与文献[35]中通过有限元方法计算的结果具有很高的一致性。从图 8可以观测到:冰梁弯曲后分裂成3部分,断裂位置对应于底部压头加载位置。该现象和试验现象具有极高的一致性。另外为了进一步验证计算结果的准确性,对比数值计算和试验中的力-时间曲线(图 9)可知:数值计算结果和试验结果吻合度极高。
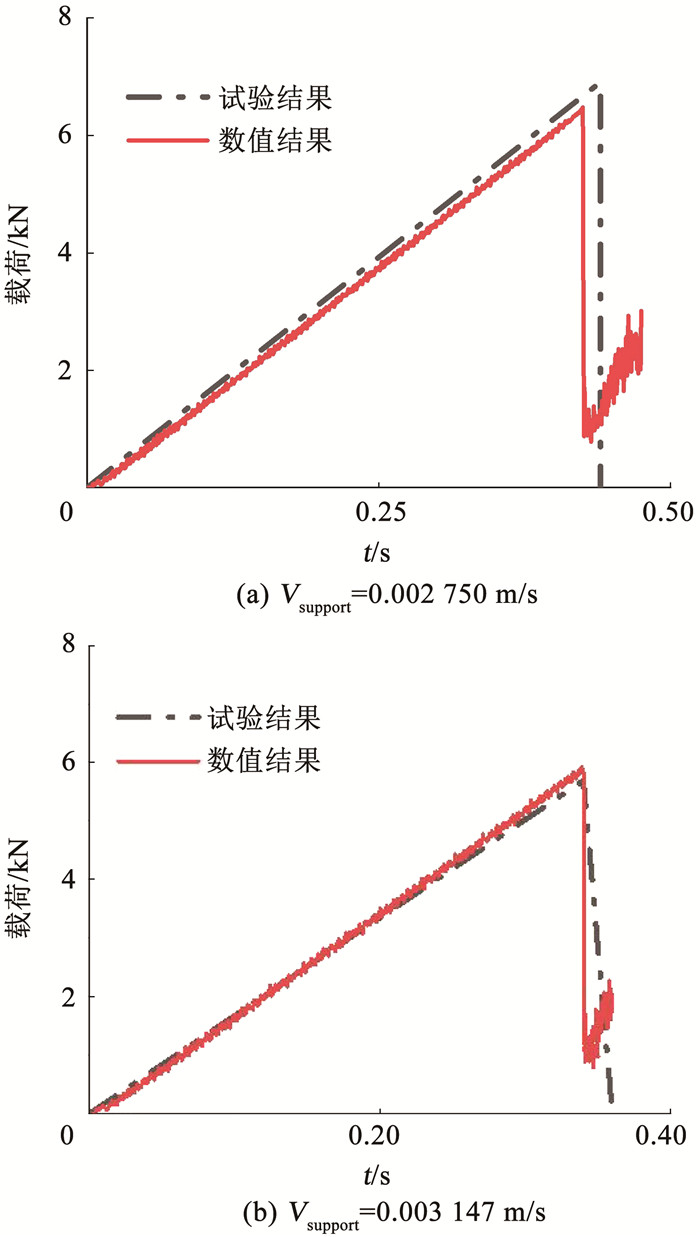
为了验证本文的数值模型能够模拟不同时间工况下冰梁的弯曲破坏,分别选取了Vsupport=0.002 750 m/s和Vsupport=0.003 147 m/s加载工况进行对比验证,载荷-时间变化关系计算结果如图 10所示,数值结果和试验结果基本保持一致。由试验结果可知:加载速度为Vsupport=0.003 580 m/s时的弯曲最大载荷最大,断裂时间最短。表 2列出了3种加载速度下数值计算和试验对应的极值载荷数值极其发生时间,从表中可以看出试验的结果和计算值的误差在10%以内,说明本文建立的无网格法冰本构模型能够模拟冰的弯曲破坏过程。
|
图 10 冰四点弯曲载荷-时间曲线图 Fig. 10 Force-time curve of four-point bending test of ice |
| 表 2 数值计算和试验中3种速度工况对应的计算结果 Tab. 2 Numerical simulation and test results under three velocity conditions |
1) 本文建立的模型能够准确模拟冰在拉伸时的断裂现象和裂纹扩展模式。
2) 冰的四点弯曲过程中,裂纹出现在固定刚性支撑的位置。
3) 冰梁弯曲后分裂成3部分,断裂位置对应于底部压头加载位置。该现象和试验现象具有极高的一致性。
4) 对于冰的四点弯曲过程,加载速度为Vsupport= 0.003 580 m/s时的弯曲最大载荷最大,断裂时间最短。
| [1] |
KHON V C, MOKHOV I I, LATIF M, et al. Perspectives of northern sea route and northwest passage in the twenty-first century[J]. Climatic Change, 2009, 100(3/4): 757. DOI:10.1007/s10584-009-9683-2 |
| [2] |
LIU Jiancheng. Mathematical modeling ice-hull interaction for real time simulations of ship manoeuvring in level ice[D]. St. John's, NL: Memorial University of Newfoundland, 2009
|
| [3] |
ERCEG S, EHLERSA S. Semi-empirical level ice resistance prediction methods[J]. Ship Technology Research, 2017, 64(1): 1. DOI:10.1080/09377255.2016.1277839 |
| [4] |
CHO S R, LEE S. A prediction method of ice breaking resistance using a multiple regression analysis[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7(4): 708. DOI:10.1515/ijnaoe-2015-0050 |
| [5] |
VON BOCK UND POLACH R, MOLYNEUX D. Model ice: A review of its capacity and identification of knowledge gaps[C]//Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering. Trondheim, Norway: American Society of Mechanical Engineers, 2017. DOI: 10.1115/OMAE2017-61808
|
| [6] |
KUUTTI J, KOLARI K, MARJAVAARA P. Simulation of ice crushing experiments with cohesive surface methodology[J]. Cold Regions Science and Technology, 2013, 92: 17. DOI:10.1016/j.coldregions.2013.03.008 |
| [7] |
LI Fang, KORGESAAR M, KUJALA P, et al. Finite element based meta-modeling of ship-ice interaction at shoulder and midship areas for ship performance simulation[J]. Marine Structures, 2020, 71: 102736. DOI:10.1016/j.marstruc.2020.102736 |
| [8] |
WANG Chenxu, FENG Feng, LIU Yu. Research on bow forms of songhua river icebreaker[J]. Procedia Engineering, 2012, 31: 228. DOI:10.1016/j.proeng.2012.01.1016 |
| [9] |
GAO Yan, HU Zhiqiang, RINGSBERG J W, et al. An elastic-plastic ice material model for ship-iceberg collision simulations[J]. Ocean Engineering, 2015, 102: 27. DOI:10.1016/j.oceaneng.2015.04.047 |
| [10] |
XU Ying, HU Zhiqiang, RINGSBERG J W, et al. Nonlinear viscoelastic-plastic material modelling for the behaviour of ice in ice-structure interactions[J]. Ocean Engineering, 2019, 173: 284. DOI:10.1016/j.oceaneng.2018.12.050 |
| [11] |
VON BOCK UND POLACH R, EHLERS S. Model scale ice—Part B: Numerical model[J]. Cold Regions Science and Technology, 2013, 94: 53. DOI:10.1016/j.coldregions.2013.06.009 |
| [12] |
LIU Lu, JI Shunying. Bond and fracture model in dilated polyhedral DEM and its application to simulate breakage of brittle materials[J]. Granular Matter, 2019, 21(3): 41. DOI:10.1007/s10035-019-0896-4 |
| [13] |
XU Zhijie, TARTAKOVSKY A M, PAN Wenxiao. Discrete-element model for the interaction between ocean waves and sea ice[J]. Physical Review E, 2012, 85(1 Pt 2): 016703. DOI:10.1103/PhysRevE.85.016703 |
| [14] |
DAS J, POLIC ' D, EHLERS S, et al. Numerical simulation of an ice beam in four-point bending using SPH[C]//Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, California: American Society of Mechanical Engineers, 2014. DOI: 10.1115/OMAE2014-23228
|
| [15] |
LIU Yang, QIAO Yue, LI Tiange. A correct smoothed particle method to model structure-ice interaction[J]. Cmes-Computer Modeling in Engineering & Sciences, 2019, 120(1): 177. DOI:10.32604/cmes.2019.06338 |
| [16] |
ZHANG Ningbo, ZHENG Xing, MA Qingwei. Updated smoothed particle hydrodynamics for simulating bending and compression failure progress of ice[J]. Water, 2017, 9(11): 882. DOI:10.3390/w9110882 |
| [17] |
LIU R W, XUE Y Z, LU X K, et al. Simulation of ship navigation in ice rubble based on peridynamics[J]. Ocean Engineering, 2018, 148: 286. DOI:10.1016/j.oceaneng.2017.11.034 |
| [18] |
WANG Qing, WANG Yi, ZAN Yingfei, et al. Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion[J]. Journal of Marine Science and Technology, 2018, 23(1): 52. DOI:10.1007/s00773-017-0454-x |
| [19] |
YE Liyu, GUO Chunyu, WANG Chao, et al. Peridynamic solution for submarine surfacing through ice[J]. Ships and Offshore Structures, 2020, 15(5): 535. DOI:10.1080/17445302.2019.1661626 |
| [20] |
NGUYEN C T, OTERKUS S. Ordinary state-based peridynamic model for geometrically nonlinear analysis[J]. Engineering Fracture Mechanics, 2020, 224: 106750. DOI:10.1016/j.engfracmech.2019.106750 |
| [21] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175. DOI:10.1016/s0022-5096(99)00029-0 |
| [22] |
SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151. DOI:10.1007/s10659-007-9125-1 |
| [23] |
MADENCI E, OTERKUS E. Peridynamic theory and its applications[M]. New York: Springer, 2014.
|
| [24] |
DIYAROGLU C. Peridynamics and its applications in marine structures[D]. Glasgow: University of Strathclyde, 2016. DOI: 10.48730/7b5t-bw98
|
| [25] |
OTERKUS S. Peridynamics for the solution of multiphysics problems[D]. Tucson, AZ: University of Arizona, 2015
|
| [26] |
FOSTER J T, SILLING S A, CHEN W W. Viscoplasticity using peridynamics[J]. International Journal for Numerical Methods in Engineering, 2010, 81(10): 1242. DOI:10.1002/nme.2725 |
| [27] |
GAO Yan, OTERKUS S. Peridynamic analysis of marine composites under shock loads by considering thermomechanical coupling effects[J]. Journal of Marine Science and Engineering, 2018, 6(2): 38. DOI:10.3390/jmse6020038 |
| [28] |
PASHAZAD H, KHARAZI M. A peridynamic plastic model based on von Mises criteria with isotropic, kinematic and mixed hardenings under cyclic loading[J]. International Journal of Mechanical Sciences, 2019, 156: 182. DOI:10.1016/j.ijmecsci.2019.03.033 |
| [29] |
MADENCI E, OTERKUS S. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening[J]. Journal of the Mechanics and Physics of Solids, 2016, 86: 192. DOI:10.1016/j.jmps.2015.09.016 |
| [30] |
MACEK R W, SILLING S A. Peridynamics via finite element analysis[J]. Finite Elements in Analysis and Design, 2007, 43(15): 1169. DOI:10.1016/j.finel.2007.08.012 |
| [31] |
OTERKUS S, MADENCI E, AGWAI A. Peridynamic thermal diffusion[J]. Journal of Computational Physics, 2014, 265: 71. DOI:10.1016/j.jcp.2014.01.027 |
| [32] |
EHLERS S, KUJALA P. Optimization-based material parameter identification for the numerical simulation of sea ice in four-point bending[J]. Proceedings of the Institution of Mechanical Engineers Part M-Journal of Engineering for the Maritime Environment, 2014, 228(1): 70. DOI:10.1177/1475090213486892 |
| [33] |
DAS J. Modeling and validation of simulation results of an ice beam in four-point bending using smoothed particle hydrodynamics[J]. International Journal of Offshore and Polar Engineering, 2017, 27(1): 82. DOI:10.17736/ijope.2017.ik01 |
| [34] |
SAZIDY M S. Development of velocity dependent ice flexural failure model and application to safe speed methodology for polar ships[D]. St. John's, NL: Memorial University of Newfoundland, 2015
|
| [35] |
TIMCO G W, WEEKS W F. A review of the engineering properties of sea ice[J]. Cold Regions Science and Technology, 2010, 60(2): 107. DOI:10.1016/j.coldregions.2009.10.003 |
 2022, Vol. 54
2022, Vol. 54