2. 寒地城乡人居环境科学与技术工业和信息化部 重点实验室(哈尔滨工业大学), 哈尔滨 150090
2. Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
常规气藏改建的地下储气库进行数值模拟时,一般不考虑储层物性参数随地层压力的变化情况[1]。低渗透气藏改建的地下储气库,储层非均质性强、物性条件复杂,在地下储气库的注气过程中,随着气体的不断注入,储层的地层压力从原始地层压力开始不断增加[2-3]。对于低渗透储层来说,地层压力的微小变化就会引起储层孔隙度和渗透率的变化,进而影响地下储层的渗流能力,最终影响地下储气库的注入量[4]。文献[5]认为渗透率越低的储层,其渗透率随地层压力变化的越剧烈。文献[6]认为气藏开采时孔隙度的变化范围较渗透率来说小得多,对气藏的开采结果没有影响。但是在储气库的注采过程中,不能照搬气藏开采的理论,在扩容建库时,强注可能引起孔隙结构的变化,进而影响岩石的压缩性,在注采过程中也需考虑其变化规律。因此,在分析低渗透气藏改建的地下储气库的注采运行过程时,需考虑渗透率和孔隙度随地层压力的变化。
为了获得低渗透气藏型储气库注气过程中储层物性参数的变化规律,本文首先基于地质统计学中的变差函数理论确定储层渗透率和孔隙度等参数的初始分布情况。然后依据反问题理论,利用已知井点处地层压力的实测值和计算值之差构建目标函数,实现了对储层渗透率和孔隙度的反演求解。本文通过案例证明了模型的正确性并利用最小二乘法拟合得到了渗透率和孔隙度与地层压力之间的函数关系式。
1 模型的建立及求解 1.1 反问题理论基础反问题从数学模型的角度来看就是模型识别问题。反问题一般通过系统辨识或模型辨识来完成,借助数学物理方法,通过对微分方程中未知参数的确定,来完成对源的辨识[7-8]。在渗流力学领域,反问题一般是指从某些模型参数或者模型动态推断或者识别整个模型。在求解正问题时,观察数据的数目一般等于或大于待求参数的数目,这时正问题的解是唯一且稳定的。而在求解反问题时,观察数据的数目则小于待求参数的数目,这时模型的解不唯一,需要附加一定的条件保证解的存在性和唯一性[9]。这往往通过构造目标函数,使目标函数最小化来实现[10]。
考虑单相渗流试井压力的数据时,待确定的模型参数是储层孔隙度和渗透率。观察的数据值为地层压力,观察的数据个数小于待测定的参数个数,为了获得与观察数据的个数相吻合的模型参数的实现,需利用地层压力的实测值和计算值构造目标函数并在目标函数中引入正则化参数和光滑泛函来保证模型解的唯一性和确定性。
1.2 反演的目标函数在低渗透气藏型储气库参数反演的问题中,已知边界条件和初始时刻部分位置的孔隙度和渗透率,可以在一些适宜的位置布置一些压力的测点,通过这些测点来估计储层孔隙度和渗透率的变化。假设布置N个压力测点,测点的压力记为Pi*(i=1, 2, …, N),则储层物性参数反演可以通过使以下函数的最小化来实现:
| $ \min J(X)=\sum\limits_{i=1}^{N}\left\|P_{i}(X)-P_{i}^{*}\right\|^{2} $ | (1) |
式中:Pi(X)为通过正问题求解得到的第i个测点的计算压力值, X为待反演的物性参数,本文中指孔隙度和渗透率,本文待求解的参数是低渗透储层的孔隙度和渗透率,已知参数是测点地层压力,待求解的参数大于已知参数,这样的反问题是不适定的。为了数值求解的稳定性,本文利用正则化方法在泛函J(X)中引入光滑泛函,用如下泛函代替J(X):
| $ \begin{aligned} \min J^{\alpha}(X)=& \sum\limits_{i=1}^{N}\left\|P_{i}(X)-P_{i}^{*}\right\|^{2}+\\ & \alpha_{1}\left(\left\|M_{1} X\right\|^{2}+\left\|M_{2} X\right\|^{2}+\left\|M_{3} X\right\|^{2}\right) \end{aligned} $ | (2) |
式中:M1、M2、M3分别为x、y和z方向的二阶光滑矩阵,α1为正则化参数。
数值模拟中利用随机误差可以得到共轭梯度法的收敛条件:
| $ \begin{aligned} \min J^{\alpha_{1}}(X)=& \sum\limits_{i=1}^{N}\left\|P_{i}(X)-P_{i}^{*}\right\|^{2}+\\ & \alpha_{1}\left(\left\|M_{1} X\right\|^{2}+\left\|M_{2} X\right\|^{2}+\right.\\ &\left.\left\|M_{3} X\right\|^{2}\right)<N \sigma^{2} \end{aligned} $ | (3) |
式中: N为测点个数,σ为测点压力的残差。
1.3 反演的方法本文采用共轭梯度法对目标函数进行求解。共轭梯度法的循环方式为
| $ X^{n+1}=X^{n}+\alpha^{n} d^{n} $ | (4) |
式中: Xn为待反演的渗透率和孔隙度的第n次的预测值, an为迭代步长, dn为共轭梯度搜索方向,表示为
| $ d^{n}=-\nabla J^{\alpha_{1}}\left(X^{n}\right)+\beta^{n-1} d^{n-1} $ | (5) |
设xi为反演的渗透率与孔隙度的向量,则目标函数的梯度向量
| $ \nabla J^{\alpha_{1}}=\left(\frac{\partial J^{\alpha_{1}}}{\partial x_{1}}, \frac{\partial J^{\alpha_{1}}}{\partial x_{2}}, \cdots, \frac{\partial J^{\alpha_{1}}}{\partial x_{M}}\right) $ | (6) |
其中
| $ \begin{aligned} \frac{\partial J^{\alpha_{1}}}{\partial x_{N}}=& 2 \sum\limits_{i=1}^{N}\left\{\left[P_{i}(X)-P_{i}^{*}\right] \frac{\partial P_{i}(X)}{\partial x_{n}}\right\}+\\ & 2 \alpha_{1}\left(M_{1}^{\mathrm{T}} M_{1}+M_{2}^{\mathrm{T}} M_{2}+M_{3}^{\mathrm{T}} M_{3}\right) X \end{aligned} $ |
因此,求解目标函数的关键是求得储层压力对渗透率和孔隙度的变化率。
1.4 地层压力对储层渗透率和孔隙度变化率的求解气体在低渗透气藏改建的地下储气库中的流动属于低速流,遵循达西渗流规律[11-12],其控制方程可以写成如下形式:
| $ \nabla(K \nabla P)+\frac{\mu}{\rho} \delta_{\mathrm{a}} q=\mu \phi c(P) \cdot \frac{\partial P}{\partial \tau} $ | (7) |
式中: μ为流体黏度, K为储层绝对渗透率, P为储层的压力, ρ为气体密度, ϕ为储层孔隙度, c为岩石的压缩系数, q为源(汇)项,表示单位时间单位地层体积注入或采出的流量,注入井取正值,采出井取负值。
边界条件:
| $ P=P_{0}, \tau=0 $ | (8) |
| $ P=\bar{P}, x, y, z \in \varGamma_{1} $ | (9) |
| $ \frac{\partial P}{\partial n} \mid \varGamma_{2}=f, x, y, z \in \varGamma_{2} $ | (10) |
记
| $ \begin{gathered} \int_{v} k \delta P \nabla^{2} P \mathrm{~d} v+\int_{v} \delta P Q \mathrm{~d} v-\int_{v} \phi C \delta P \frac{\partial P}{\partial \tau} \mathrm{d} v- \\ \int_{\varGamma_{2}} \delta P\left(\frac{\partial P}{\partial n}-f\right) \mathrm{d} \varGamma=0 \end{gathered} $ | (11) |
经分部积分可得:
| $ \begin{gathered} \Pi=\int_{v}\left\{\frac{k}{2}\left[\left(\frac{\partial P}{\partial x}\right)^{2}+\left(\frac{\partial P}{\partial y}\right)^{2}+\left(\frac{\partial P}{\partial z}\right)^{2}\right]\right\} \mathrm{d} v+ \\ \int_{v}\left(Q P-\varphi C P \frac{\partial P}{\partial \tau}\right) \mathrm{d} v+\int_{\varGamma_{2}} P f \mathrm{d} \varGamma=0 \end{gathered} $ | (12) |
根据变分原理,使泛函(12)的变分δΠ=0,即
| $ [\boldsymbol{K}]\{\boldsymbol{P}\}+[\boldsymbol{D}]\{\partial P / \partial {\tau}\}=[\boldsymbol{E}]\{\boldsymbol{Q}\}+[\boldsymbol{R}]\{\boldsymbol{f}\} $ | (13) |
式中:{P}为不包括给定值在内的节点压力向量, {f}、{Q}分别为f、Q的节点向量, [K], [D], [E], [R]是与变量相关的矩阵。
将方程中的已知量和未知量分离,有限元列式可以表示成如下形式:
| $ \begin{gathered} \left(\sum\left[\boldsymbol{K}_{j}^{u}\right] \cdot k_{j}^{u}\right)\{\boldsymbol{P}\}+\left[\boldsymbol{D}_{j}^{u}\right] \boldsymbol{\phi}_{j}^{u}\{\partial P / \partial \boldsymbol{\tau}\}= \\ {\left[\boldsymbol{K}_{P}\right]\{\overline{\boldsymbol{P}}\}+[\boldsymbol{E}]\{\boldsymbol{Q}\}+[\boldsymbol{R}]\{\boldsymbol{f}\}} \end{gathered} $ | (14) |
式中:kju为未知的储气库渗透率, ϕju为未知的储气库孔隙度, [Kju],[Dju],[KP],[E]和[R]分别为已知的矩阵。
将式(14)可进一步改写为
| $ \left[\boldsymbol{K}_{\mathrm{a}}\right]\{\boldsymbol{P}\}+\left[\boldsymbol{D}_{\mathrm{a}}\right]\{\partial P / \partial \tau\}=\{\boldsymbol{W}\} $ | (15) |
对式(15)进行时间上的Galerkin的差分离散有
| $ \begin{aligned} &\left(\left(2\left[\boldsymbol{K}_{\mathrm{a}}\right]+\frac{3}{\Delta \tau}\left[\boldsymbol{D}_{\mathrm{a}}\right]\right)\{\boldsymbol{P}\}_{\tau}=\right. \\ &3\{\boldsymbol{W}\}+\left(\frac{3}{\Delta \tau}\left[\boldsymbol{D}_{\mathrm{a}}\right]-\left[\boldsymbol{K}_{\mathrm{a}}\right]\right)\{\boldsymbol{P}\}_{\tau-\Delta \tau} \end{aligned} $ | (16) |
方程(16)两边同时对{kju}求导,整理可得:
| $ \begin{aligned} \frac{\partial\{\boldsymbol{P}\}_{\tau}}{\partial\left\{k_{j}^{u}\right\}}=&\left(2\left[\boldsymbol{K}_{\mathrm{a}}\right]+\frac{3}{\Delta \tau}\left[\boldsymbol{D}_{\mathrm{a}}\right]\right)^{-1} \cdot \\ &\left\{\left(\frac{3}{\Delta \tau}\left[\boldsymbol{D}_{\mathrm{a}}\right]-\left[\boldsymbol{K}_{\mathrm{a}}\right]\right) \cdot \frac{\partial\{\boldsymbol{P}\}_{\tau-\Delta \tau}}{\partial\left\{k_{j}^{u}\right\}}-\right.\\ &\left.2 \sum\left[\boldsymbol{K}_{j}^{u}\right] \cdot\{\boldsymbol{P}\}_{\tau}-\sum\left[\boldsymbol{K}_{j}^{u}\right] \cdot\{\boldsymbol{P}\}_{\tau-\Delta \tau}\right\} \end{aligned} $ | (17) |
| $ \begin{aligned} \frac{\partial\{\boldsymbol{P}\}_{\tau}}{\partial\left\{\boldsymbol{\phi}_{j}^{u}\right\}}=& \frac{\partial\{\boldsymbol{P}\}_{\tau-\Delta \tau}}{\partial\left\{\boldsymbol{\phi}_{j}^{u}\right\}}+\left[\boldsymbol{D}_{\mathrm{a}}\right]^{-1}\left(\left[\boldsymbol{D}_{j}^{u}\right]\{\boldsymbol{P}\}_{\tau-\Delta \tau}-\right.\\ & {\left.\left[\boldsymbol{D}_{j}^{u}\right]\{\boldsymbol{P}\}_{\tau}\right) } \end{aligned} $ | (18) |
由式(17)、(18)可知,要确定在τ时刻压力对渗透率和孔隙度的变化率,必须已知τ-1时刻的储层渗透率和孔隙度的分布,以此类推,要想求解各时刻地层压力对孔隙度和渗透率的变化率,必须知道储层渗透率和孔隙度的初始分布。
1.5 储层参数初始分布的确定考虑单相渗流试井压力的数据时,待确定的模型参数是网格的孔隙度和渗透率,流体参数已知。观察的数据值为地层压力,观察的数据个数小于待测定的参数个数,为了获得与观察数据的个数相吻合的模型参数的实现,基于地质统计学的变差函数理论确定储层渗透率和孔隙度的初始分布。
在地质统计学的差值方法中,直接由已知数据计算计算出来的实验变差函数可能导致奇异矩阵多解,因此一般用被证明了可以保证方程组有唯一解和非负均方差的理论模型来代替实验变差函数,其中比较常用的理论模型是球状模型,其表达式如下:
| $ \gamma(h)=\left\{\begin{array}{lc} C_{0}+C\left[\frac{3 h}{2 a}-\frac{1}{2}\left(\frac{h}{a}\right)^{3}\right], & 0 \leqslant h<a \\ C_{0}+C, & h \geqslant a \end{array}\right. $ | (19) |
式中: C0为块金值,表示在很短的距离内变量的空间变异性, C为拱高,表示区域化变量在空间上的变异性的程度, C与C0之和表示基台值,反映的是区域化变量在空间上的总变异性, a为变程,反映的是区域化变量的变异范围。
对式(19)进行求解,需已知C0、C和a的值。根据文献[13],C0、C和a的值可由已知数据的均值和方差进行计算得到。对于球状模型的求解,可以利用Kriging插值法实现。Kriging法通过引进以距离为自变量的变差函数来计算权值,由于变差函数既可以反映自变量的空间结构特性,又可以反映变量的随机分布特性,利用Kriging方法进行空间数据差值往往可以获得理想的效果[14]。
本文确定储层初始参数分布时,观测井点的物性参数已知,通过拟合变差函数曲线, 采用Kriging方法确定低渗透气藏改建储气库储层参数的分布。
1.6 目标函数的求解首先利用Kriging插值法确定储层渗透率和孔隙度的初始分布,然后利用参数的分布确定各时刻地层压力对渗透率和孔隙度的变化率,将求得的变化率式(17)、(18)代入式(6),然后使用Newton-Raphson法进行求解。求解的具体步骤如下:
1) 根据低渗透气藏型储气库各已知井点处的渗透率和孔隙度,确定储层参数的初始分布情况,计算待测井点处地层的压力值。
2) 测量已知井点处的压力值,将计算值和测量值代入方程(1),判断是否满足收敛条件,若满足执行步骤4),不满足则执行步骤3)。
3) 将求得新的压力对渗透率和孔隙度的变化率代入方程(1)~(5),然后重复步骤1)和2)。
4) 输出得到的渗透率和孔隙度的值,结束程序。
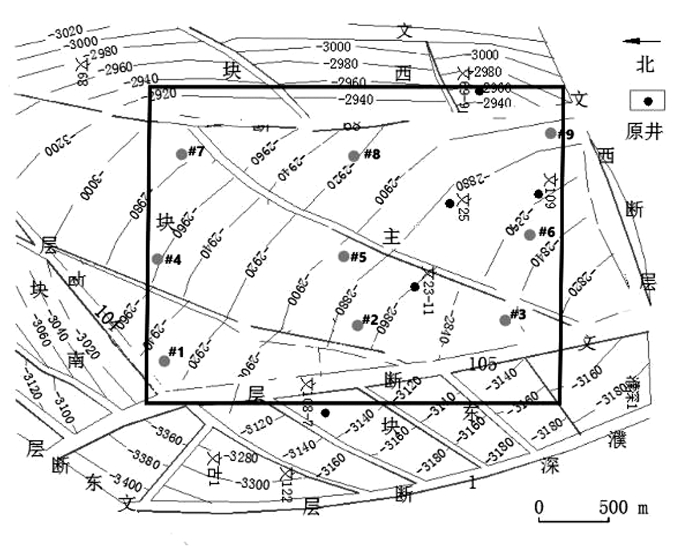
2 算例分析借鉴文献[15]储气库的注采运行数据,通过注气流量和观察井的压力,利用渗流反问题构建目标函数计算注气后储层物性参数的变化。考虑如图 1所示的储层,假定上、下、左、右均为不渗透边界,在其中选取面积为400 m×400 m的区域,该储层分布有9口井,其中1、3、5、7和9号井以定注入量q=21×104 Nm3/d注入,其他井为观测井。计算过程中地层物性参数和其他参数值见表 1。
|
图 1 储气库储层井位分布 Fig. 1 Well location distribution of underground gas storage |
| 表 1 计算模型的物性参数与其他参数 Tab. 1 Physical parameters and other parameters of calculation model |
测点压力的残差为σd=0.006 MPa,在注入井和观测井处的初始孔隙度和渗透率已知,见表 2。其中,渗透率的单位为μm2。
| 表 2 观测井点处的孔隙度和渗透率 Tab. 2 Porosity and permeability at observation wells |
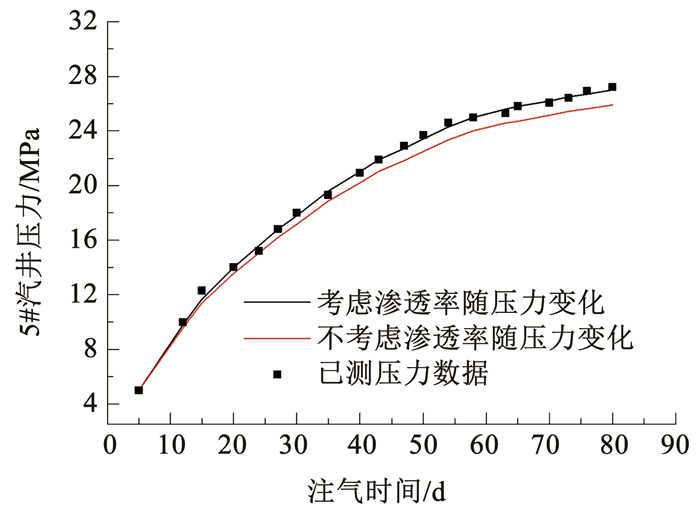
为验证模型的正确性,本文首先根据地质统计学中的变差函数理论,以已知井点处的渗透率和孔隙度为基础,确定了储层参数的初始分布。通过计算地层压力对渗透率和孔隙度的变化率,利用共轭梯度法确定了注气后储层参数的分布。利用新的储层参数重新计算了低渗透气藏型储气5#注入井的压力,将计算结果和5#注入井的已测压力进行拟合,并将其与渗透率和孔隙度当作常数的传统计算方法进行对比,结果如图 2所示。由图 2可知,重新计算的5#注入井压力和已测压力的曲线基本重合,二者误差最大为2.56%,平均值为0.99%,说明计算结果准确。而采用传统计算方法得到的5#注入井压力和已测压力二者误差最高可达7.89%。比较采用两种方法重新计算获得的5#注入井压力可知,在注气初期,二者相差不大,曲线基本重合。而在注气中后期,二者之间的差值逐渐增大,在注气结束时达到最大,二者相差1.1 MPa。
|
图 2 重新计算得到的5#注入井压力和已测压力对比曲线 Fig. 2 Comparison of recalculated and measured pressure of 5# injection well |
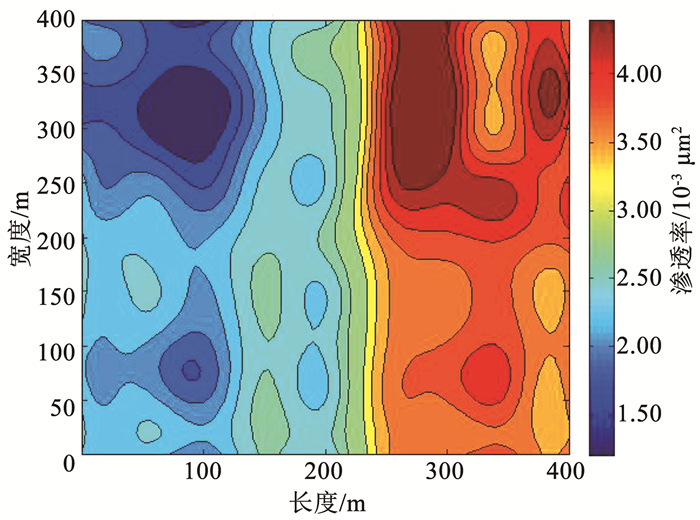
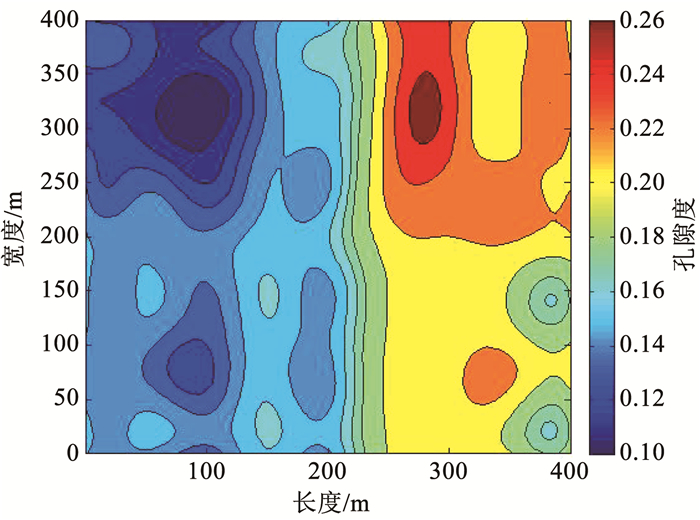
根据已知井点处渗透率和孔隙度的初始值,可以计算出渗透率和孔隙度的均值分别为2.05×10-3 μm2和0.18,方差分别为0.165和0.005,根据均值和方差可取变程a为162 m,C0和C的值分别为0和0.002 5,将a、C0和C的值代入式(19),利用Kriging插值法可以得到储气库初始渗透率和孔隙度分布等值线和云图,如图 3、4和图 5、6所示。
|
图 3 储层初始渗透率分布等值线图 Fig. 3 Contour map of initial reservoir permeability distribution |
|
图 4 储层初始孔隙度分布等值线图 Fig. 4 Contour map of initial reservoir porosity distribution |
|
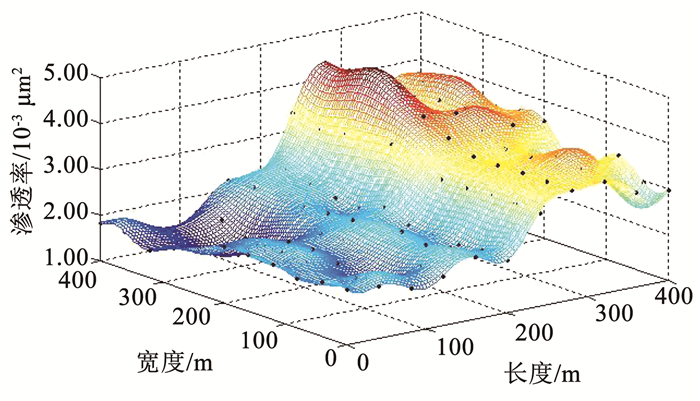
图 5 储层初始渗透率分布云图 Fig. 5 Cloud map of initial reservoir permeability distribution |
|
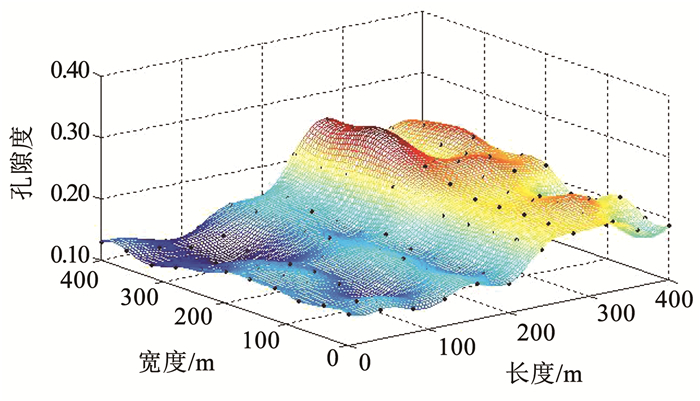
图 6 储层初始孔隙度分布云图 Fig. 6 Cloud map of initial reservoir porosity distribution |
对比图 3、图 5和图 4、图 6可以发现,低渗透气藏改建地下储气库在注气初期,渗透率和孔隙度的分布趋势基本一致,二者呈现一定的相关性。
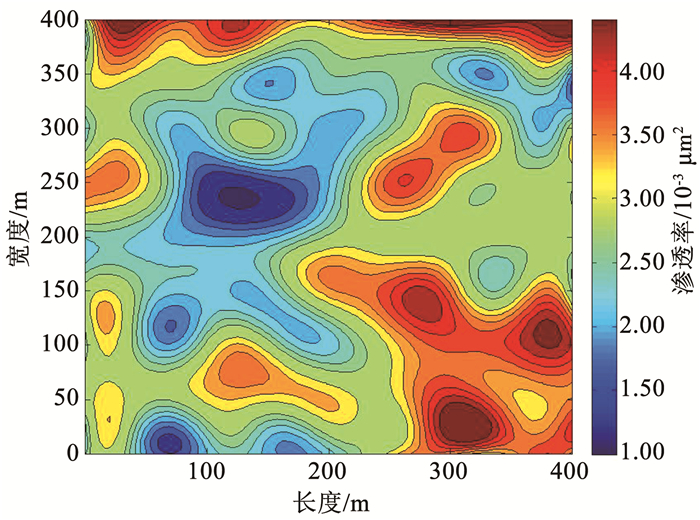
利用获得的储层渗透率和孔隙度初始分布作为已知条件,将其代入到式(14)、(15)中,计算得到各时刻地层压力对渗透率和孔隙度的变化率,将计算得到的变化率代入到最优化目标函数中,并利用1#、3#、5#、7#和9#注采井的测量压力作为拟合条件,反演得到的低渗透气藏改建储气库储层渗透率和孔隙度的分布情况如图 7、8和图 9、10所示。
|
图 7 反演储层渗透率分布等值线图 Fig. 7 Contour map of calculated permeability distribution |

|
图 8 反演储层孔隙度分布等值线图 Fig. 8 Contour map of calculated porosity distribution |
|
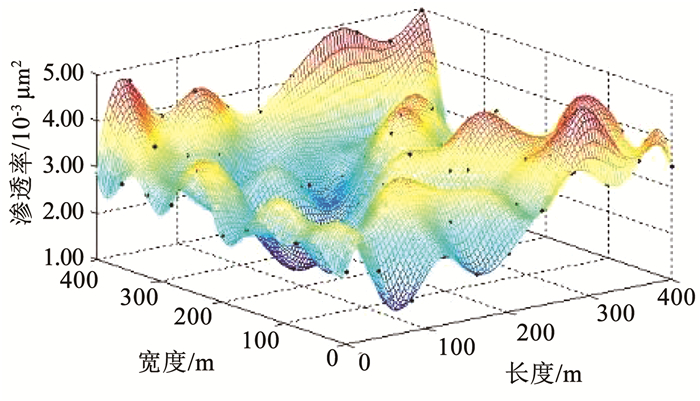
图 9 反演储层渗透率分布云图 Fig. 9 Cloud map of calculated permeability distribution |
|
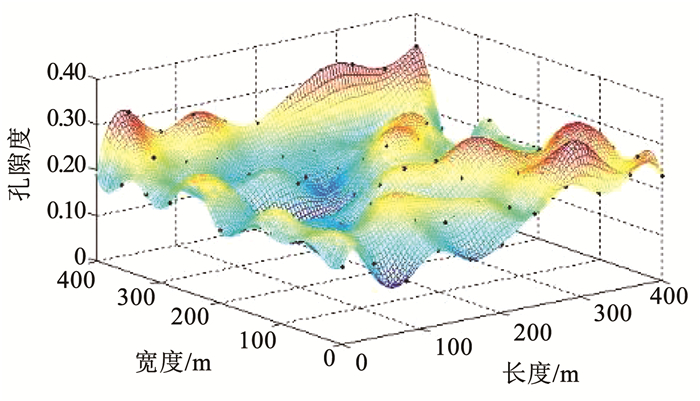
图 10 反演储层孔隙度分布云图 Fig. 10 Cloudmap of calculated porosity distribution |
对比图 3、图 7和图 4、图 8可以发现,随着气体的不断注入,在储层各个位置的渗透率和孔隙度也随之变化,并且各位置的渗透率和孔隙度变化幅度都不相同,二者之间的相关性不再一致。对比图 3、图 5和图 7、图 9可以发现,低渗透储层渗透率经过注气后其分布规律发生了较大的变化,其中变化最大的位置是在5#注采井附近,其渗透率从1.66×10-3 μm增加到2.81×10-3 μm。由此可见,对于低渗透储层改建的地下储气库来说,要分析其注采气过程,必须考虑渗透率随着孔隙流体压力的变化情况。
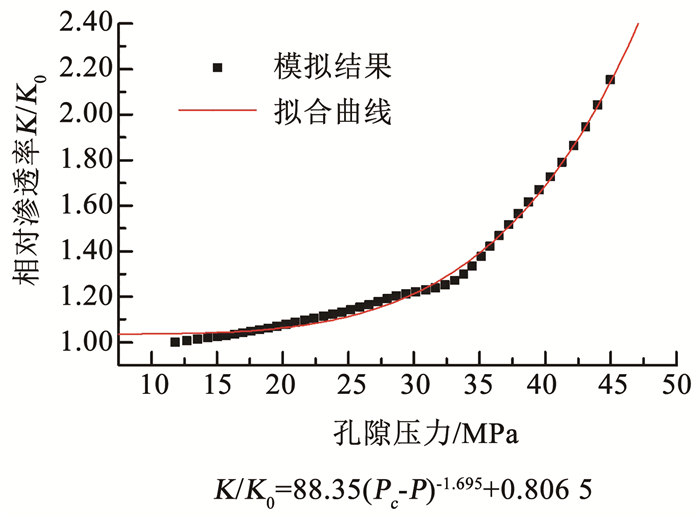
2.3 渗透率和孔隙度与地层压力的拟合为了分析低渗透储层渗透率和孔隙度随着孔隙流体压力的变化规律,本文对渗透率变化幅度最大的注入井附近的各地层压力下的渗透率和孔隙度进行了拟合,得到的渗透率和孔隙度随孔隙流体压力的变化结果如图 11、12所示。
|
图 11 渗透率随地层压力变化规律 Fig. 11 Variation of permeability with formation pressure |
|
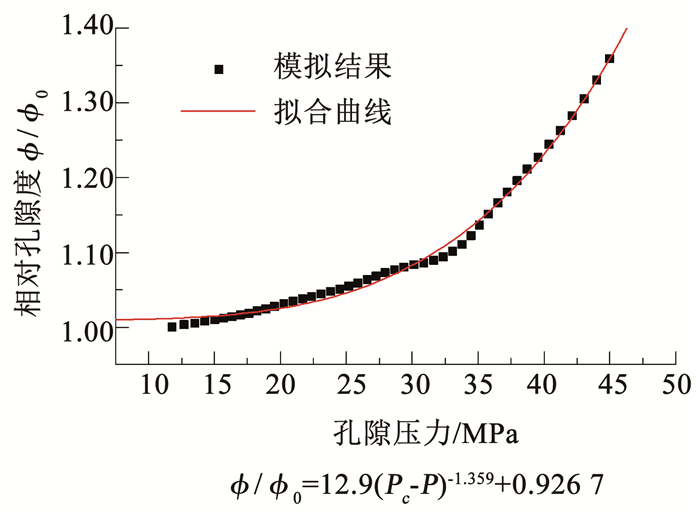
图 12 孔隙度随地层压力变化规律 Fig. 12 Variation of porosity with formation pressure |
图 11、12反映了低渗透储层型地下储气库在注气时,渗透率和孔隙度随孔隙流体压力的变化规律。从图 11、12以及拟合的表达式可以看出,低渗透气藏型储气库随着天然气的不断注入,储层地层压力不断增加,渗透率和孔隙度也随之增加。但是相比较渗透率随地层压力的变化而言,孔隙度随着储层压力的增加变化极其缓慢,在建立方程时可以忽略。但是在低渗透气藏型储气库中,渗透率随着压力变化极大,不可忽略,在建立储气库的注采方程时,不可当作常数处理,在建立渗流方程时需将其拟合成储层地层压力的表达式。
3 结论1) 本文首先利用地质统计学中的变差函数理论,依据已知观测井处的孔隙度和渗透率,确定了储层初始孔隙度和渗透率的分布,并基于反问题理论,利用储气库井点处地层压力的实测值和计算值的差值构建目标函数,反演得到了注气后储层孔隙度和渗透率的分布;
2) 利用观测井的压力实测数据,证明了构建的反问题模型的正确性,并将反演的渗透率和孔隙度与压力之间的关系进行拟合,得到了渗透率和孔隙度与地层压力之间的关联式。
| [1] |
SUN Junchang, XU Hongcheng, WANG Jieming, et al. Injection-production mechanisms and key evaluation technologies for underground gas storages rebuiltfrom gas reservoirs[J]. Natural Gas Industry B, 2018, 5(6): 616. DOI:10.1016/j.ngib.2018.11.010 |
| [2] |
SHAO Jiaxin, YOU Lijun, KANG Yili, et al. Experimental study on stress sensitivity of underground gas storage[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107577. DOI:10.1016/j.petrol.2020.107577 |
| [3] |
GAO Zhiye, YANG Xibing, HU Chenhui, et al. Characterizing the pore structure of low permeability Eocene Liushagang Formation reservoir rocks from Beibuwan Basin in northern South China Sea[J]. Marine and Petroleum Geology, 2019, 99: 107. DOI:10.1016/j.marpetgeo.2018.10.005 |
| [4] |
ZHANG Hao, ZHONG Ying, KURU E, et al. Impacts of permeability stress sensitivity and aqueous phase trapping on the tight sandstone gas well productivity-A case study of the Daniudi gas field[J]. Journal of Petroleum Science and Engineering, 2019, 177: 261. DOI:10.1016/j.petrol.2019.02.044 |
| [5] |
齐桂雪. 枯竭气藏型储气库储层应力敏感性实验研究[J]. 石油地质与工程, 2020, 34(3): 79. QI Guixue. Experimental study on reservoir stress sensitivity of underground storageof depleted gas reservoirs[J]. Petroleum Geology and Engineering, 2020, 34(3): 79. DOI:10.3969/j.issn.1673-8217.2020.03.015 |
| [6] |
CAO Nai, LEI Gang. Stress sensitivity of tight reservoirs during pressure loading and unloading process[J]. Petroleum Exploration and Development, 2019, 46(1): 138. DOI:10.1016/S1876-3804(19)30013-8 |
| [7] |
RAMM A G. Inverse problem of potential theory[J]. Applied Mathematics Letters, 2018, 77: 1. DOI:10.1016/j.aml.2017.09.012 |
| [8] |
SANDERS T, PLATTE R B, SKEEL R D. Effective new methods for automated parameter selection in regularized inverse problems[J]. Applied Numerical Mathematics, 2020, 152: 29. DOI:10.1016/j.apnum.2020.01.015 |
| [9] |
SASTRE F, VELAZQUEZ A, DE LEON L S, et al. Method to solve redundant inverse problems based on a Latent Semantic Analysis approach. Application to an aerojet engine[J]. Aerospace Science and Technology, 2020, 102: 105854. DOI:10.1016/j.ast.2020.105854 |
| [10] |
郭家桥, 张新明. 采用改进Tikhonov正则化方法优化多层平板药物控释[J]. 哈尔滨工业大学学报, 2019, 51(10): 99. GUO Jiaqiao, ZHANG Xinming. Applying the modified Tikhonov regularization method to the optimization of multi-laminated drug controlled release[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 99. DOI:10.11918/j.issn.0367-6234.201712017 |
| [11] |
YOU Lijun, WANG Zhe, KANG Yili, et al. Experimental investigation of porosity and permeability change caused by salting out in tight sandstone gas reservoirs[J]. Journal of Natural Gas Geoence, 2018, 3(6): 347. DOI:10.1016/j.jnggs.2018.12.003 |
| [12] |
ZHU Weiyao, TIAN Wei, GAO Ying, et al. Study on experiment conditions of marine shale gas seepage law[J]. Journal of Natural Gas Geoscience, 2016, 1(2): 157. DOI:10.1016/j.jnggs.2016.05.006 |
| [13] |
BEAN B, SUN Yan, MAGUIRE M. Interval-valued kriging for geostatistical mapping with imprecise inputs[J]. International Journal of Approximate Reasoning, 2021, 140: 31. DOI:10.1016/j.ijar.2021.10.003 |
| [14] |
张泽斌, 张鹏飞, 郭红, 等. Kriging序贯设计方法在滑动轴承优化中的应用[J]. 哈尔滨工业大学学报, 2019, 51(7): 179. ZHANG Zebin, ZAHNG Pengfei, GUO Hong, et al. Implementation of Kriging model based sequential design on the optimization of sliding bearing[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 179. DOI:10.11918/j.issn.0367-6234.201810147 |
| [15] |
邬法勇. Z-W23地下储气库设计与注采能力分析[D]. 青岛: 中国石油大学(华东), 2014 WU Fayong. Design and Injectivity/Productivity Analysis for Z-W23 Underground Gas Storage[D]. Qingdao: College of Petroleum Engineering China University of Petroleum (East China), 2014 |
 2022, Vol. 54
2022, Vol. 54


