2. 寒地城乡人居环境科学与技术工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090;
3. 山东建筑大学 热能工程学院, 济南 250101;
4. 中国建筑科学研究院有限公司, 北京 100101
2. Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Thermal Engineering, Shandong Jianzhu University, Jinan 250101, China;
4. China Academy of Building Research, Beijing 100101, China
地热能资源丰富,具有分布广、清洁环保、储量大、稳定可靠等特点[1]。在建筑行业地热能开发利用过程中,浅层地源热泵系统应用较为广泛[2],但其对空调全年冷热负荷要求较高,长期运行后系统性能会显著下降[3],并且浅层地埋管换热器埋管占地面积较大。近年来,中深层地源热泵系统作为新兴的地热能利用形式,通常其埋管深度在1 000~3 000 m,具有地埋管换热器占地面积小、对全年冷热负荷平衡要求低、系统取热性能稳定等优势[4],受到了广泛关注。
与传统浅层地埋管换热器相比,中深层地埋管供热技术只在近年来得以迅速发展[5],并且其发展现状是工程实践先于理论研究,有很多问题尚待于研究[6]。其中,在中深层地埋管换热器取热特性方面,Li等[7]对影响中深层地埋管换热器取热特性的因素进行分析,研究结果表明增大外管管径和流速有利于提升中深层地埋管换热器的取热量;Liu等[8]对中深层地埋管换热器管内循环工质的流速进行了优化,并提出最佳流速为0.7 m/s;Fang等[9]发现增大中深层地埋管换热器的内套管热阻能够提升其换热能力。而对中深层地埋管换热器周围的岩土热恢复特性等问题研究较少,其中,贾林瑞等[10]研究了单取热工况地下岩土温度热响应,发现1 400~1 800 m处的岩土温度变化率最快;Cai等[11]对间歇运行模式下中深层地埋管换热器取热稳定性进行了研究,发现不同运停比运行时的岩土温度热恢复效果较好;Song等[12]研究结果表明岩土经过为期8个月的热恢复期,其温度基本能恢复至初始状态。但上述研究主要是针对单个供热周期,其目的是量化设计参数对中深层套管式地埋管换热器取热性能的影响以及揭示岩土的热恢复规律。考虑到中深层地热地埋管供热系统需长期运行,因此,为明确利用该系统供热的可持续性,需要对中深层套管式地埋管换热器长期取热的稳定性进行相关研究。
此外,中深层地埋管换热器取热对周围岩土的热扰与诸多参数相关,如运行时间、管径、循环流量、回填材料导热系数及岩土热物性等。在工程实践过程中,为解决中深层地埋管换热器钻孔间距不当造成的热短路以及土地资源浪费等问题,首先要确定中深层地埋管换热器取热对周围岩土的热扰与上述哪些参数相关性较大,因此,需要对上述参数做敏感性分析。
基于此,本文建立了中深层地埋管换热器数值传热模型,基于有限差分法将控制方程离散求解,并利用项目实测数据进行验证,在此基础上研究长期运行下中深层套管式地埋管换热器的出水温度以及岩土的温度变化。此外,对影响中深层套管式地埋管换热器热扰的运行参数进行了敏感性分析,探寻中深层地埋管换热器的热影响半径与相关参数的表达式,为日后的工程实践提供理论指导。
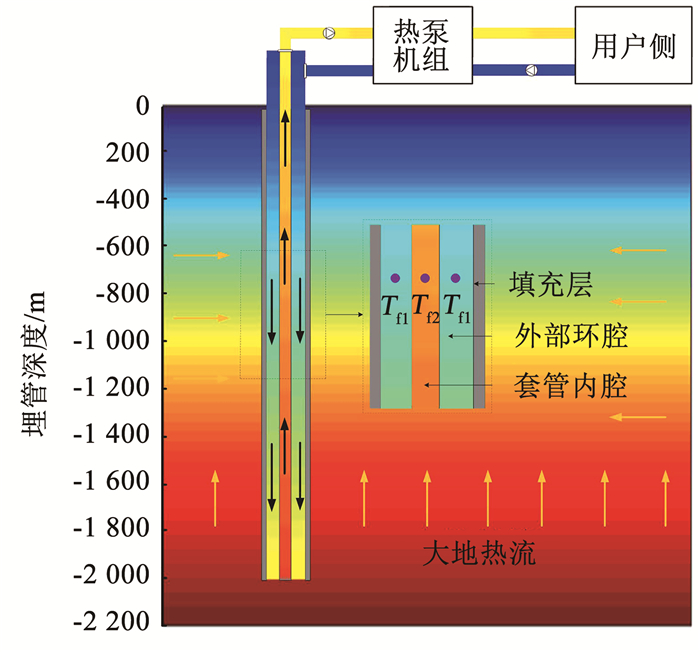
1 数值模型建立 1.1 物理模型中深层同轴套管式地埋管换热器的取热原理如图 1所示,在循环水泵的驱动下循环工质(水)由套管外部环腔注入,经地埋管换热器周围高温岩土层加热后通过内套管反向流动,流出地面后进入热泵机组。
|
图 1 中深层地埋管换热器的换热原理 Fig. 1 Heat exchange principle of MDBHE |
中深层地埋管换热器的取热过程主要包括内套管流体与外部环腔流体的对流换热、环腔流体与外管壁的对流换热以及外套管与周围岩土的导热,其换热过程较为复杂,并且地下岩土环境具有不确定性,因此做出以下假设:
1) 忽略地下渗流作用的影响,将岩土中传热视为单纯的导热问题[13];
2) 忽略地表温度波动的影响[14];
3) 假定数值模拟区域的径向边界处的温度分布不受地埋管换热器的影响;
4) 假定同轴套管式换热器内循环体主要以对流传热,忽略其轴向的热传导。
1.2 控制方程基于以上假设,每层岩土的导热方程可写为[15]
| $ \frac{1}{a_{\mathrm{k}}} \frac{\partial T}{\partial \tau}=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial T_{\mathrm{s}}}{\partial r}\right)+\frac{\partial T_{\mathrm{s}}^{2}}{\partial z^{2}} $ | (1) |
式中:ak为不同岩土层的热扩散率,m2/s;Ts为岩土层温度,℃;Δτ为时间步长,s;r、z分别为径向长度与竖直方向长度,m。
当管内流体工质以图 1所示的方式流动时,外部环腔内流体的能量方程为
| $ C_{1} \frac{\partial T_{\mathrm{f} 1}}{\partial \tau}=\frac{T_{\mathrm{f} 2}-T_{\mathrm{f} 1}}{R_{2}}+\frac{T_{\mathrm{b}}-T_{\mathrm{fl}}}{R_{1}}-C \frac{\partial T_{\mathrm{f} 1}}{\partial z} $ | (2) |
内管流体的能量方程为
| $ C_{2} \frac{\partial T_{\mathrm{f} 2}}{\partial \tau}=\frac{T_{\mathrm{f} 1}-T_{\mathrm{f} 2}}{R_{2}}+C \frac{\partial T_{\mathrm{f} 2}}{\partial z} $ | (3) |
式(2)、(3)描述的是在中深层地埋管换热器正常取热阶段下的能量方程,当系统停运时,外部环腔内流体及内管流体的流速为零,此时地埋管周围岩土处于热恢复状态。与正常取热阶段下的能量方程相比,热恢复阶段能量方程中的系数C为零。
其中:
| $ \begin{aligned} C_{1}=& \frac{{\rm{ \mathsf{ π}}}}{4}\left(d_{1 \mathrm{i}}^{2}-d_{2 \mathrm{o}}^{2}\right) \rho c+\frac{{\rm{ \mathsf{ π}}}}{4}\left(d_{1 \mathrm{o}}^{2}-d_{1 \mathrm{i}}^{2}\right) \rho_{2} c_{2}+\\ & \frac{{\rm{ \mathsf{ π}}}}{4}\left(d_{\mathrm{b}}^{2}-d_{1 \mathrm{o}}^{2}\right) \rho_{\mathrm{g}} c_{\mathrm{g}} \\ C_{2}=& \frac{{\rm{ \mathsf{ π}}}}{4} d_{2 \mathrm{i}}^{2} \rho c+\frac{{\rm{ \mathsf{ π}}}}{4}\left(d_{2 \mathrm{o}}^{2}-d_{2 \mathrm{i}}^{2}\right) \rho_{1} c_{1} \end{aligned} $ |
式中:C=MCf为循环液的热容流量, kJ/(s·K);db为钻孔半径, m;di、do分别为套管的内径和外径,m;ρc、ρ1c1、ρ2c2、ρgcg分别为循环水比定容热容,外管比定容热容、内管比定容热容、回填材料比定容热容,J/(m3·K)。此外,外管内循环水和钻孔壁之间的热阻R1以及内外管循环水之间的热阻R2由下式求得:
| $ {R_1} = \frac{1}{{{\rm{ \mathsf{ π} }}{d_{1{\rm{i}}}}{h_1}}} + \frac{1}{{2{\rm{ \mathsf{ π} }}{k_{{\rm{p}}1}}}}\ln \left( {\frac{{{d_{1{\rm{o}}}}}}{{{d_{1{\rm{i}}}}}}} \right) + \frac{1}{{2{\rm{ \mathsf{ π} }}{k_{\rm{g}}}}}\ln \left( {\frac{{{d_{\rm{b}}}}}{{{d_{1{\rm{o}}}}}}} \right) $ | (4) |
| $ {R_2} = \frac{1}{{{\rm{ \mathsf{ π} }}{d_{2{\rm{i}}}}{h_2}}} + \frac{1}{{2{\rm{ \mathsf{ π} }}{k_{{\rm{p}}2}}}}\ln \left( {\frac{{{d_{2{\rm{o}}}}}}{{{d_{2{\rm{i}}}}}}} \right) + \frac{1}{{{\rm{ \mathsf{ π} }}{d_{2{\rm{o}}}}{h_1}}} $ | (5) |
式中:kg、kp1、kp2分别为回填材料、外管和内管的导热系数,W/(m·K);h1、h2分别为套管外管和内管的对流换热系数,W/(m2·K)。
1.3 初始及边界条件在任一深度的地层的初始地温可以表达为下式[9]:
| $ \begin{aligned} T_{(z)}=& T_{\mathrm{a}}+\frac{q_{\mathrm{g}}}{h_{\mathrm{a}}}+\sum\limits_{j=1}^{m-1} \frac{q_{\mathrm{g}}}{k_{j}}\left(H_{j}-H_{j-1}\right)+\\ & \frac{q_{\mathrm{g}}}{k_{\mathrm{m}}}\left(z-H_{\mathrm{m}-1}\right) \end{aligned} $ | (6) |
式中:Hj为第j层地层底部的坐标;qg为大地热流,W/m2;ta为地表温度,℃;ha为空气与地表的对流换热系数,W/(m2·K);km为岩土的导热系数,W/(m·K)。
外部环腔流体与内管流体能量方程的边界体条件为:
| $ {T_{{\rm{f}}1}} = {T_{{\rm{f2}}}} - \frac{Q}{C}, Z = 0 $ | (7) |
| $ {T_{{\rm{f}}1}} = {T_{{\rm{f2}}}}, Z = H $ | (8) |
式中:Q为取热功率,kW;C=MCf为循环液的热容流量, kJ/(s·K);Z为埋管深度,m。
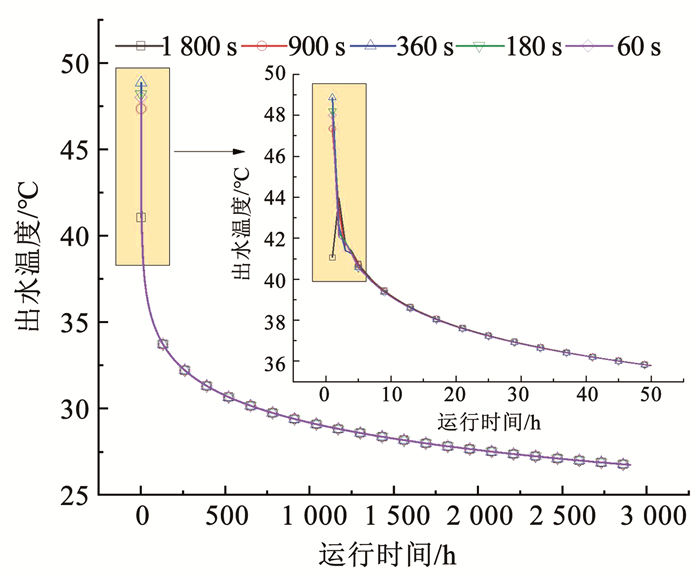
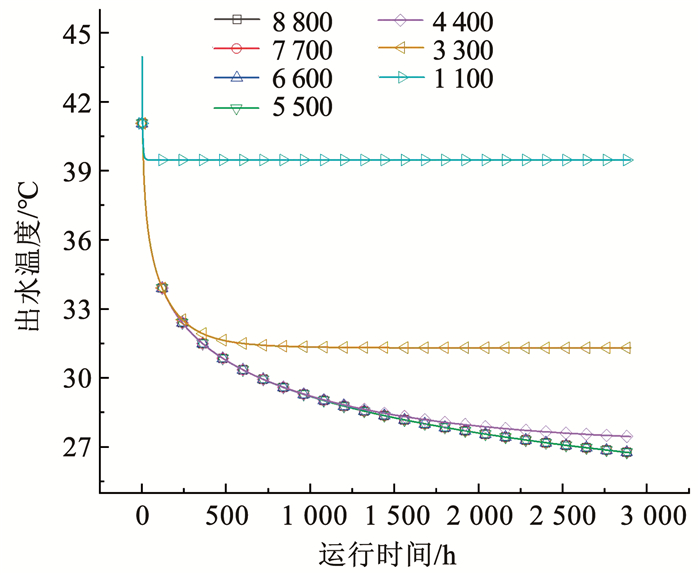
2 数值模型求解及验证 2.1 模型求解在非稳态数值传热模拟中,时间步长Δτ、纵向步长Δz及径向步长对模拟计算速度及结果的精确度均有一定影响。为了保证结果的准确性需要对其做无关性验证,由图 2可知Δτ可取900 s,此外,考虑径向较远处热流趋近于零,钻孔附近的热流及温度梯度较大,故以钻孔壁为界采用变步长,即径向步长按照等比级数变化(等比系数为1.2),径向离钻孔第1个节点距离为0.168 m, 径向共取40个节点,纵向步长Δz取10 m。由图 3可知节点数量可取7 700个,满足计算精度要求。其余模拟所需的基础物理参数见表 1,岩土热物性参数除特别说明外取下文中的案例1。
|
图 2 时间步长无关性验证 Fig. 2 Verification of time step independence |
|
图 3 节点数量无关性验证 Fig. 3 Verification of node number independence |
| 表 1 模拟所需的物理参数 Tab. 1 Physical parameters required for simulation |
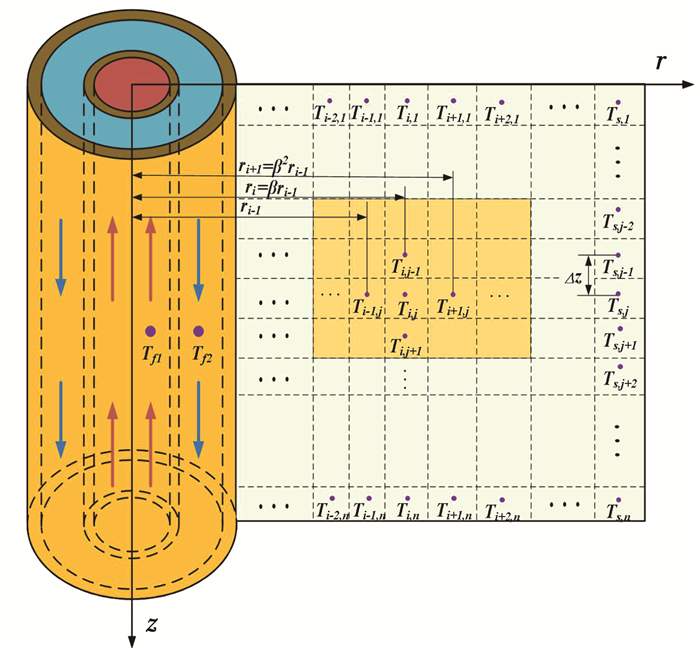
在中深层地埋管换热器与周围岩土层的耦合传热问题中,可将其看作圆柱体的二维瞬态导热。对于二维瞬态耦合传热问题,若采用隐式格式差分方法得到非边界处节点方程中的未知数通常有5个,采用迭代法求解耗时较长[16]。因此,本文基于微元体热平衡和交替时间步长法[17]建立节点方程,离散网格如图 4所示。
|
图 4 模型离散网格示意 Fig. 4 Schematic of discretization mesh for numerical model |
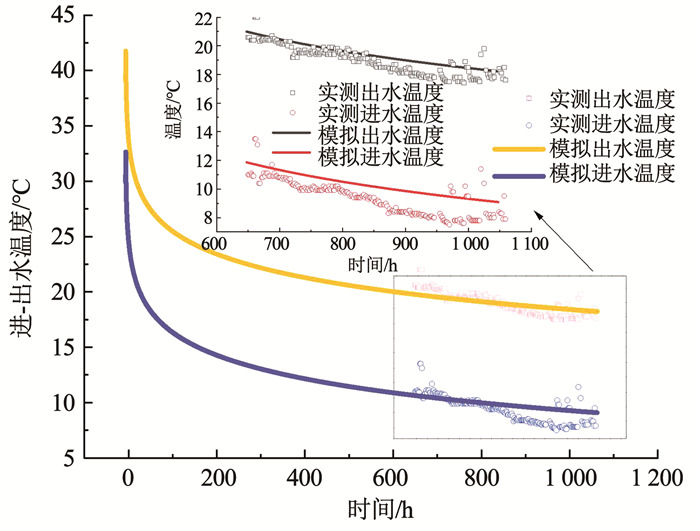
为了验证建立的数学模型及所编程序的准确性,作者所在团队于2019年11月至2020年1月期间对西安市某住宅工程进行了现场实测,测试参数主要包括中深层地埋管换热器进出水温度、机组及循环水泵耗电量、用户侧进出水温度及循环水泵耗电量,测试期间机组的平均COP达4.7,限于篇幅,其余内容详见文献[7]。其中,测试期间单孔地热井平均换热量为270 kW,循环水平均流量为25.5 m3/h,中深层地埋管换热器进出水温差约为9.2 ℃,将该地热井运行参数导入所编制的程序,进而得出模拟地源侧进出口温度,选取650 h后的测试数据与模拟值进行对比,地源侧进出口温度的模拟值与实测值对比如图 5所示。从图 5中出水温度可知,除个别波动点外,最大误差为6.01%,进而验证了数值传热模型及所编程序的正确性,为下文相关分析奠定了基础。
|
图 5 地源侧进、出口温度实际值与模拟值比对 Fig. 5 Comparison of actual and simulated temperature at inlet and outlet of ground source side |
考虑到中深层地热地埋管供热系统需长期运行,因此,为明确利用该系统供热的可持续性,需要对中深层套管式地埋管换热器长期取热的稳定性以及对其周围岩土的热扰进行相关研究。
3.1 中深层套管式地埋管换热器的稳定性 3.1.1 长期出水温度对中深层套管式地埋管换热器的长期出水温度进行为期15 a的模拟计算,此时的延米换热量为100 W/m,流量为28 m3/h,其余参数见表 1。
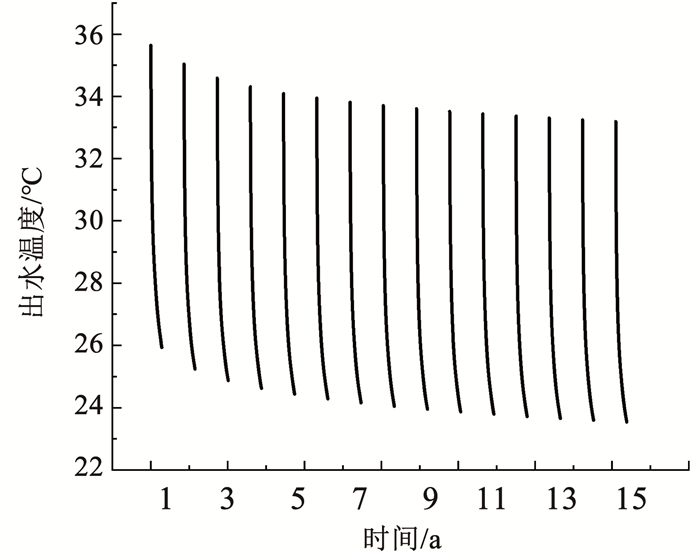
图 6所示为中深层套管式地埋管换热器在15 a运行期间的出水温度。从图 6中可以看出,在每个供热周期内的中深层套管式地埋管换热器的出水温度变化较大,以第1个供暖期为例,初始阶段的出水温度为35.6 ℃,采暖季结束后的出水温度为25.9 ℃。从整体看,中深层套管式地埋管换热器的出水温度随着运行年限的增加呈递减趋势,并且递减程度逐渐减小,第1 a、第5 a、第10 a和第15 a采暖季末期的中深层套管式地埋管换热器的出水温度分别为25.9、24.4、23.9、23.5 ℃。分别以第1 a、第5 a和第10 a的出水温度为基准,第5 a、第10 a和第15 a的出水温度在此基础上分别下降5.8%、2.0%和1.8%。此外,从图 6中也可以看出,从第11 a开始出水温度基本处于准稳态阶段,第11 a、第12 a、第13 a、第14 a和第15 a采暖季末期的中深层套管式地埋管换热器的出水温度分别为23.79、23.72、23.66、23.60、23.54 ℃,表明中深层套管式地埋管换热器长期运行下的出水温度较为稳定。
|
图 6 15 a内的中深层套管式地埋管换热器出水温度 Fig. 6 The oulet temperature of MDBHE within 15 a |
对距地埋管换热器外壁1 m,不同埋管深度的岩土温度进行为期15 a的模拟计算,此时的延米换热量为100 W/m,流量为28 m3/h,其余参数见表 1。
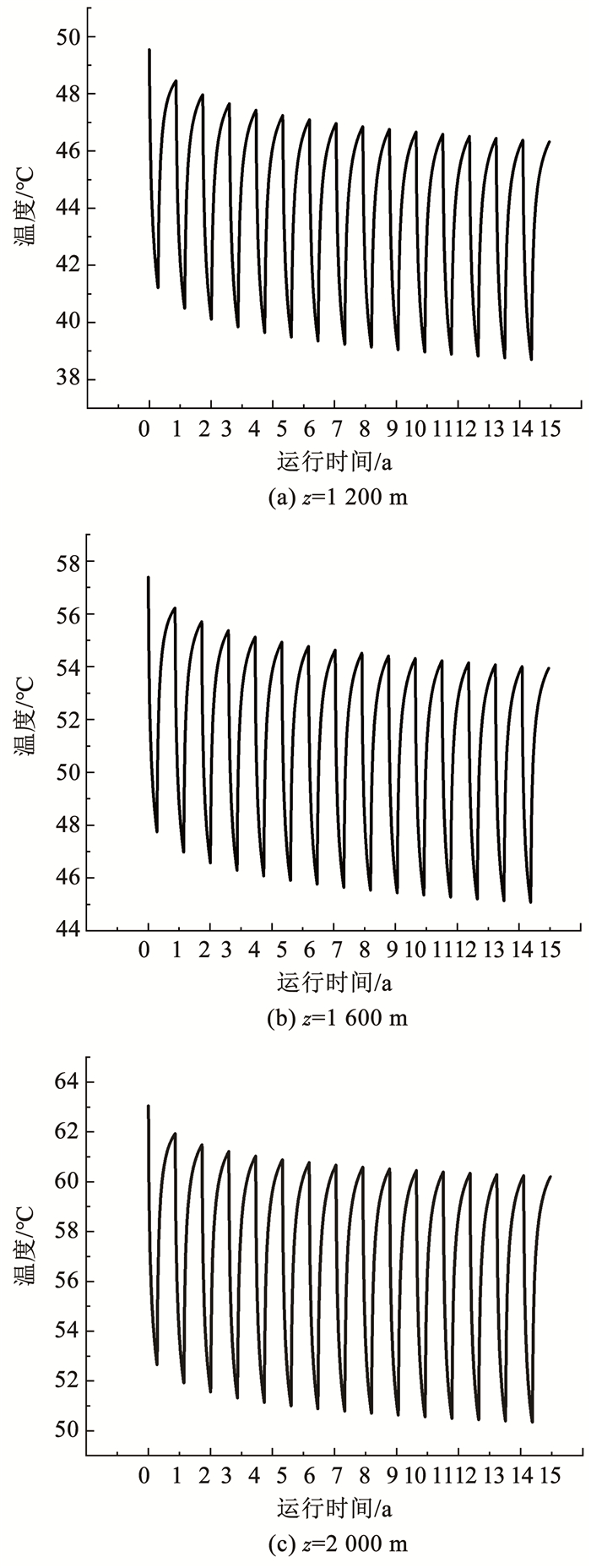
从图 7可以看出,在15 a运行期间,距钻孔壁1 m处不同深度岩土层的温度呈周期性变化,并且岩土经过热恢复期不能完全恢复到初始状态,与初始温度相比,岩土温度随运行年限的增加逐年下降。以z=1 800 m为例进行分析,与岩土初始温度相比,第1 a温降比例为2.03%,第5 a温降比例为4.30%,第10 a温降比例为5.37%,第13~15 a温降比例分别为5.78%,5.90%和6.01%,温降增幅逐年减小。分析原因:在运行参数不变的条件下,被取热后的岩土不能完全恢复到初始温度,会造成下一年地埋管换热器取热能力略有下降,进而对其周围岩土的热干扰作用减弱,经过长时间的周期循环这种现象会逐渐减弱,最后会趋于相对平衡,此外,经过为期15 a运行,最大温降比例仅为6.50%,说明中深层地埋管换热器取热稳定性较好,岩土具有较强的热恢复能力。
|
图 7 不同埋管深度下径向1 m处的岩土温度变化 Fig. 7 Temperature variation of rock and soil at 1 m in radial direction under different buried depths |
为分析中深层地埋管换热器取热对周围岩土的热扰,引入热影响半径r*。其中,Δtr, z, τ表示埋管深度相同时,径向边界温度与τ时刻半径为r处的温度的差值。当Δtr, z, τ到最小时所对应的径向距离即为最大热影响半径rmax*。
| $ \Delta t_{r, z, \tau}=t_{\mathrm{bnd}, z, 0}-t_{r^{*}, z, \tau} $ | (9) |
式中:tbnd, z, 0为τ=0时刻径向边界温度,℃;tr, z, τ为τ时刻半径r处的温度, ℃。
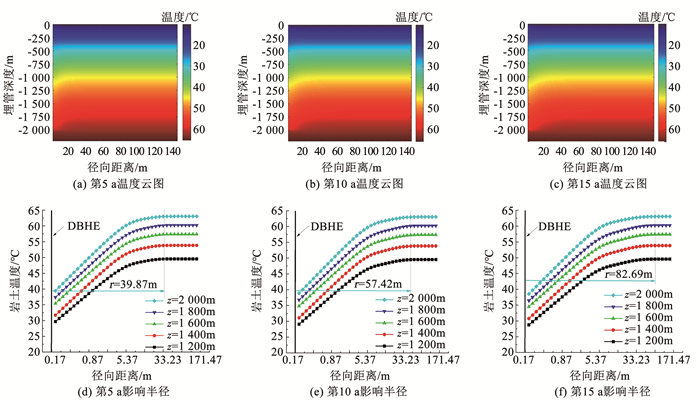
3.2.1 不同运行时间下热影响半径图 8所示为中深层地埋管换热器运行5、10、15 a后的岩土温度场以及其不同埋管深度处径向岩土温度的变化曲线。以图 8(f)为例进行分析,当运行15 a后,与径向边界171.47 m处的岩土温度相比,当中深层地埋管换热器的埋管深度分别为1 200、1 400、1 600、1 800、2 000 m时,距离其0.17 m处的岩土温降分别为20.79、23.07、22.91、23.81、24.51 ℃,相比而言z=1 200 m处的温降最小,表明中深层地埋管换热器的取热区域主要集中在1 400~2 000 m处的岩土。此外,随着运行时间的增加中深层地埋管换热器的热影响半径逐渐增大,第5、10、15 a的影响半径分别为39.87、57.42、82.69 m,以第10 a对应的热影响半径为基准,第15 a的热影响半径在其基础上增加44%。分析原因:由前文分析可知经取热后的岩土不能完全恢复到初始状态,并且,随着运行年限的增加,岩土温度逐渐降低,由于热传导的作用,周围未受影响的岩土会向地埋管中心进行热量传递,故热影响半径会随运行时间的增加而逐渐增大。
|
图 8 不同运行年限下温度场分布和不同埋管深度径向温度的变化 Fig. 8 Distribution of temperature field and variation of radial temperature at different buried depths under different operation periods |
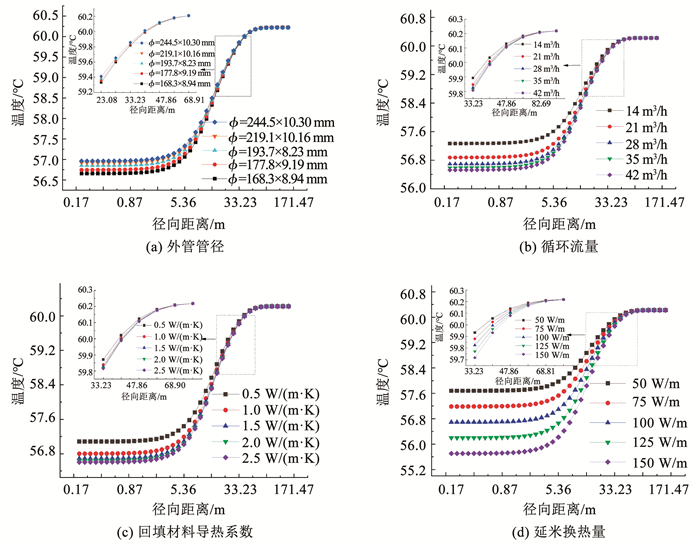
采用控制变量法分析主要设计参数和中深层地埋管换热器热影响半径之间的关系,其中,主要设计参数包括管径、工质循环流量、回填材料导热系数以及延米换热量。在不同设计参数下,系统运行10 a后z=2 000 m处径向岩土温度的分布如图 9所示。从图 9可以看出,管径、工质循环流量以及回填材料导热系数的变化对中深层地埋管换热器周围岩土层温度分布影响较小,相对于其他3种设计参数,延米换热量对中深层地埋管换热器周围岩土层温度分布影响较大,随着延米换热换热量的增大周围岩土层的温度越低。因此,在进行工程设计时应采用合理的延米换热量,文献[18]对延米换热量做了详细研究,并指出延米换热量不宜大于150 W/m。此外,从图中可以看出在一定范围内,上述4种设计参数虽对中深层地埋管换热器周围岩土具有一定的影响,但对其热半径的热影响范围有限,即中深层地埋管换热器的热影响半径趋于一致。
|
图 9 不同设计参数下运行10 a后径向岩土温度的分布 Fig. 9 Radial temperature distribution of rock and soil under different design parameters after 10 a operation |
本文主要分析岩土热物性参数和热影响半径之间的关系。岩土不同热物性参数见表 2,此时的延米换热量为100 W/m,流量为28 m3/h,其余参数见表 1。
| 表 2 岩土物理参数 Tab. 2 Physical parameters of rock and soil |
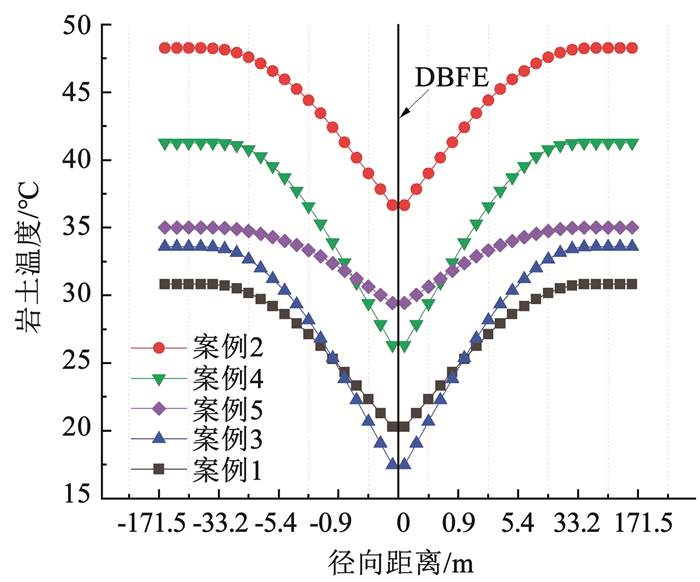
在表 2所示的岩土热物性参数下,图 10所示为z=500 m处岩土的径向温度分布。从图 10中可以看出,与径向边界171.47 m处的岩土温度相比,当岩土热物性参数分别取案例1~5时,距离中深层地埋管换热器0.17 m处的岩土温降分别为10.55、11.61、16.13、14.94、5.58 ℃,由此可知,中深层地埋管换热器取热对其周围岩土温度场的热扰主要与岩土本身热物性参数相关。
|
图 10 不同岩土热物性参数下径向岩土温度分布 Fig. 10 Radial temperature distribution along depth of DBHE under different geotechnical thermal physical parameters |
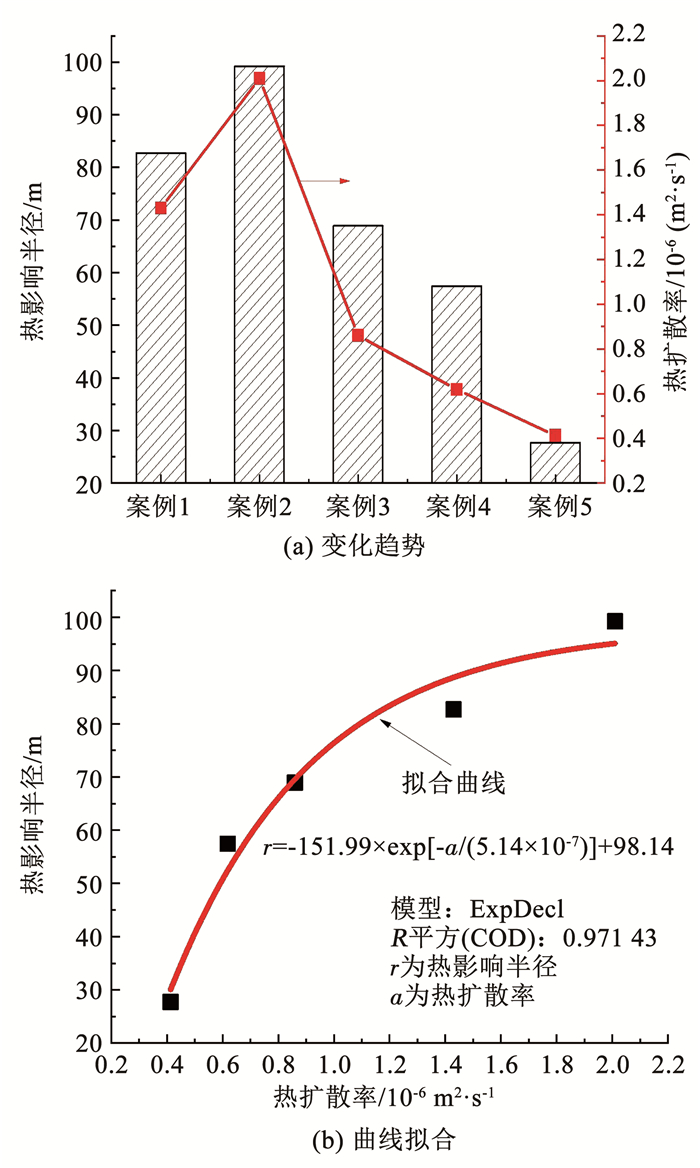
案例1~5的岩土单位体积平均热容分别为2.410×106、1.390×106、2.040×106、2.210×106、2.680×106 J/(m3·K),其中案例2的单位体积平均热容最小,案例5的单位体积平均热容最大。当z=2 000 m时,案例2的热影响半径最大,而案例5的热影响半径最小,其中,案例1~5的岩土平均热扩散率分别为1.43×10-6、2.01×10-6、8.60×10-7、6.19×10-7、4.13×10-7 m2/s,所对应的中深层地埋管换热器热影响半径分别为82.69、99.23、68.91、57.43、27.69 m。因此,中深层地埋管换热器热影响半径与岩土单位体积热容及热扩散率等物性参数相关性较大,岩土单位体积热容越小、热扩散率越大,热影响半径也越大。但随着热扩散率的增大,中深层地埋管换热器的半径增加的速率逐渐减小,当热扩散率由4.13×10-7 m2/s增加到6.19×10-7 m2/s时,热影响半径由27.69 m增加到57.43 m;而当热扩散率由1.43×10-6 m2/s增加到2.01×10-6 m2/s时,热影响半径由82.69 m增加到99.23 m,增加率为20%。
为进一步探究中深层地埋管换热器热影响半径与岩土热扩散率的关系,图 11所示为两者拟合关系式。由图 11(a)可知,两者并非简单的线性关系,具体表现为随岩土热扩散率的增加,中深层地埋管换热器的热影响半径在前期增加速率较快,而后期较慢,满足指数关系式的变化规律。从图 11(b)中可以看出,当热影响半径r和热扩散率a的关系式满足r=-151.99×exp[-a/(5.14×10-7)]+98.14时,此时的R2为0.97,能够较好的表述两者之间的关系。
|
图 11 岩土热扩散率与中深层地埋管热影响半径的关系 Fig. 11 Relationship between thermal diffusivity of rock and soil and heat-affected radius of MDBHE |
但应当指出:利用中深层地埋管换热器热影响半径确定钻孔间距并不是最好的方法,热影响半径和间距问题并不完全等价,最好的方法是直接求解多根中深层地埋管换热器之间耦合,而且要求解反问题,即算出取热量随间距的变化,当然难度和计算工作量较大。现有文献的报道多关于单根中深层地埋管换热器,但在实际工程中,延米换热量取值一般要小于150 W/m,单根中深层地埋管换热器不能满足现有公共建筑及住宅建筑的供暖需求,往往需要更多根中深层地埋管换热器来满足建筑总供热负荷。因此,为使研究成果更好的服务实际工程,应研究中深层地埋管换热器管群,分析管群的布管形式以及地埋管换热器之间的相互影响,但在现有研究背景下,本研究成果仍有一定的参考意义。
4 结论1) 中深层套管式地埋管换热器长期运行下的出水温度较为稳定。从第11 a开始出水温度基本处于准稳态阶段,第11 a、第12 a、第13 a、第14 a和第15 a采暖季末期的中深层套管式地埋管换热器的出水温度分别为23.79、23.72、23.66、23.60、23.54 ℃。
2) 中深层套管式地埋管换热器周围岩土热恢复能力较强。对距地埋管换热器外壁1 m位置处不同埋管深度的岩土温度进行为期15 a计算,结果显示经过15 a的运行,与初始岩土温度相比最大温降比例仅为6.50%。
3) 中深层套管式地埋管换热器的热影响半径随运行时间的增加而逐渐增大。运行5、10、15 a的影响半径分别为39.87、57.42、82.69 m,以第10 a对应的热影响半径为基准,5 a后的热影响半径在其基础上增加44%。
4) 相比于中深层套管式地埋管换热器外管管径、回填材料导热系数及工质循环流量,延米换热量对中深层换热器周围岩土的温度分布影响较大。但在一定范围内,上述设计参数和中深层套管式地埋管换热器热影响半径之间无明显关系。
5) 随岩土热扩散率的增加,中深层套管式地埋管换热器的热影响半径在前期增加速率较快,而后期较慢,当热扩散率由4.13×10-7 m2/s增加到6.19×10-7 m2/s时,热影响半径由27.69 m增加到57.43 m;而当热扩散率由1.43×10-6 m2/s增加到2.01×10-6 m2/s时,热影响半径由82.69 m增加到99.23 m,增长率为20%,满足指数关系式的变化规律。并且,热影响半径r和热扩散率a的关系式满足r=-151.99×exp[-a/(5.14×10-7)]+98.14,其中,R2=0.97。
| [1] |
满意, 姜国心, 杜甜甜, 等. 利用弃井开采中深层地热能名义取热量的模拟[J]. 山东建筑大学学报, 2019, 34(4): 20. MAN Yi, JIANG Guoxin, DU Tiantian, et al. Modeling of deep and middle geothermal energy utilization in abandoned oil wells[J]. Journal of Shandong Jianzhu University, 2019, 34(4): 20. DOI:10.12077/sdjz.2019.04.004 |
| [2] |
ZHU Jialing, HU Kaiyong, LU Xinli, et al. A review of geothermal energy resources, development, and applications in China: Current status and prospects[J]. Energy, 2015, 93: 466. DOI:10.1016/j.energy.2015.08.098 |
| [3] |
HEIN P, KOLDITZ O, GÖRKE U, et al. A numerical study on the sustainability and efficiency of borehole heat exchanger coupled ground source heat pump systems[J]. Applied Thermal Engineering, 2016, 100: 421. DOI:10.1016/j.applthermaleng.2016.02.039 |
| [4] |
CHEN Chaofan, SHAO Haibing, NAUMOV D, et al. Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger system for building heating[J]. Geothermal Energy, 2019, 7(1): 18. DOI:10.1186/s40517-019-0133-8 |
| [5] |
王沣浩, 蔡皖龙, 王铭, 等. 地热能供热技术研究现状及展望[J]. 制冷学报, 2021, 42(1): 14. WANG FengHao, CAI Wanlong, WANG Ming, et al. Status and outlook for research on geothermal heating technology[J]. Journal of Refrigeration, 2021, 42(1): 14. DOI:10.3969/j.issn.0253-4339.2021.01.014 |
| [6] |
唐晓音, 程璐瑶, 许威, 等. 西安地区中深层套管式地埋管换热性能数值模拟[J]. 地质科学, 2021, 56(3): 985. TANG Xiaoyin, CHENG Luyao, XU Wei, et al. Numerical study on factors that influence the heat transfer performance of mid-deep coaxial casing heat exchanger in the Xi'an area[J]. Chinese Journal of Geology, 2021, 56(3): 985. DOI:10.12017/dzkx.2021.051 |
| [7] |
LI Ji, XU Wei, LI Jianfeng, et al. Heat extraction model and characteristics of coaxial deep borehole heat exchanger[J]. Renewable Energy, 2021, 169: 738. DOI:10.1016/j.renene.2021.01.036 |
| [8] |
LIU Jun, WANG Fenghao, GAO Yuan, et al. Influencing factors analysis and operation optimization for the long-term performance of medium-deep borehole heat exchanger coupled ground source heat pump system[J]. Energy and Buildings, 2020, 226: 110385. DOI:10.1016/j.renene.2019.11.158 |
| [9] |
FANG Liang, DIAO Nairen, SHAO Zhukun, et al. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers[J]. Energy and Buildings, 2018, 167: 79. DOI:10.1016/j.enbuild.2018.02.013 |
| [10] |
贾林瑞, 崔萍, 方亮, 等. 中深层地埋管换热器传热过程对周围岩土体的热影响[J]. 暖通空调, 2020, 51(1): 101. JIA Linrui, CUI Ping, FANG Liang, et al. Thermal effect of heat transfer process of deep borehole heat exchangers on surrounding rock and soil[J]. HV&AC, 2020, 51(1): 101. |
| [11] |
CAI Wanlong, WANG Fenghao, LIU Jun, et al. Experimental and numerical investigation of heat transfer performance and sustainability of deep borehole heat exchangers coupled with ground source heat pump systems[J]. Applied Thermal Engineering, 2019, 149: 975. DOI:10.1016/j.applthermaleng.2018.12.094 |
| [12] |
SONG Xianzhi, WANG Gaosheng, SHI Yu, et al. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system[J]. Energy, 2018, 164: 1298. DOI:10.1016/j.energy.2018.08.056 |
| [13] |
PIECHOWSKIM. Heat and mass transfer model of a ground heat exchanger: Validation and sensitivity analysis[J]. International Journal of Energy Research, 1998, 22(11): 965. DOI:10.1002/(SICI)1099-114X(199809)22:113.0.CO;2-G |
| [14] |
刘晓燕, 赵军, 石成, 等. 土壤恒温层温度及深度研究[J]. 太阳能学报, 2007, 28(5): 494. LIU Xiaoyan, ZHAO Jun, SHI Cheng, et al. Study on soil layer of constant temperature[J]. Acta Energiae Solaris Sinica, 2007, 28(5): 494. DOI:10.3321/j.issn:0254-0096.2007.05.007 |
| [15] |
贾力, 方肇洪, 钱兴华. 高等传热学[M]. 北京: 高等教育出版社, 2003. JIA Li, FANG Zhaohong, QIAN Xinghua. Advanced heat transfer[M]. Beijing: Higher Education Press, 2003. |
| [16] |
邵珠坤. 深孔套管式地埋管换热器传热数值分析及其应用[D]. 济南: 山东建筑大学, 2018 SHAO Zhukun. Numerical analysis and application of heat transfer in deep hole coaxial tube ground heat exchanger[D]. Jinan: Shandong Jianzhu University, 2018 |
| [17] |
俞昌铭. 热传导及其数值分析[M]. 北京: 清华大学出版社, 1981. YU Changming. Heat conduction and its numerical analysis[M]. Beijing: Tsinghua University Press, 1981. |
| [18] |
孔彦龙, 陈超凡, 邵亥冰, 等. 深井换热技术原理及其换热量评估[J]. 地球物理学报, 2017, 60(12): 4741. KONG Yanlong, CHEN Chaofan, SHAO Haibing, et al. Principle and capacity quantification of deep-borehole heat exchangers[J]. Chinese Journal of Geophysics, 2017, 60(12): 4741. DOI:10.6038/cjg20171216 |
| [19] |
LIU Jun, WANG Fenghao, CAI Wanlong, et al. Numerical study on the effects of design parameters on the heat transfer performance of coaxial deep borehole heat exchanger[J]. International Journal of Energy Research, 2018, 43(12): 6337. DOI:10.1002/er.4357 |
| [20] |
杜甜甜, 满意, 姜国心, 等. 中深层地埋管换热器最佳钻孔间距的模拟研究[J]. 煤气与热力, 2019, 39(11): A21. DU Tiantian, MAN Yi, JIANG Guoxin, et al. Simulation study on optimal drilling spacing of medium and deep buried tube heat exchanger[J]. Gas & Heat, 2019, 39(11): A21. DOI:10.13608/j.cnki.1000-4416.2019.11.008 |
| [21] |
PAN Sheng, KONG Yanlong, CHEN Chaofan, et al. Optimization of the utilization of deep borehole heat exchangers[J]. Geothermal Energy, 2020, 8(1): 6. DOI:10.1186/s40517-020-0161-4 |
| [22] |
LIU Jun, WANG Fenghao, CAI Wanlong, et al. Numerical investigation on the effects of geological parameters and layered subsurface on the thermal performance of medium-deep borehole heat exchanger[J]. Renewable Energy, 2020, 149: 384. DOI:10.1016/j.renene.2019.11.158 |
 2022, Vol. 54
2022, Vol. 54


