2. 华东交通大学 土木建筑学院,南昌 330013
2. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China
闭式冷却塔作为石油化工领域的主要蒸发换热设备,其主要由交错管束组成,目前已经被大范围应用[1-4]。该换热设备内部外掠管束外的蒸发冷却换热过程是一个复杂的多相流换热过程,目前对于其换热机理的认识还不明确,为实际工程设计带来困难。
目前,对于外掠管束间蒸发冷却特性的研究方法,主要有实验、理论推导和数值模拟等。在实验及理论推导方面,Heyns等[5]和Zheng等[6]通过实验数据,拟合了传质和对流换热系数计算关联式,但是由于传热现象的复杂性,其计算结果存在很大差异。在数值模拟方面,Gan等[7-8]和Hasan等[9]基于DPM模型,研究了其传热传质问题,但这些研究主要考虑了显热换热,对于喷淋水蒸发的潜热换热并未考虑,从而造成计算结果差异较大。同时,Xie等[10]在文献[6-8]基础上,综合考虑喷淋水的蒸发传质,但是并没有考虑喷淋水膜流动对其传热传质过程的影响,也就是忽略了管壁喷淋水膜对传热特性的影响作用。同时,许多学者在不考虑传热基础上,也模拟分析了外掠管束间喷淋水的流动特性,如Zhao等[11]和Ding等[12]采用VOF模型,通过模拟分析,捕捉了喷淋水在管壁形成水膜及其在管壁的流动过程。其后,Karmakar等[13]基于OpenFOAM中VOF模型,建立了三维外掠管束间喷淋水膜-管壁换热分析模型,研究分析了管壁表面润湿性对其显热换热的影响。结果表明,当平衡接触角在2°~175°范围内时,管表面的显热换热速率明显降低。总而言之,上述这些研究,对于液膜在管壁的形成、喷淋水与湿空气间的热质交换,以及水蒸气在湿空气中的扩散等问题,并未进行充分考虑,这将影响计算方法的可靠性。
本文综合考虑液膜在管壁的形成、喷淋水与湿空气间的热质交换,以及水蒸气在湿空气中的扩散过程,采用欧拉-拉格朗日方法,基于DPM和wall film模型耦合原理,建立了外掠管束间湿空气-喷淋水的蒸发冷却及压降特性分析模型,通过文献数据,对模型进行验证;采用数值模拟方法,探究了外掠管束间,喷淋水-湿空气的热质传递、喷淋水-管壁间对流换热及湿空气压降特性沿盘管高度的变化规律。
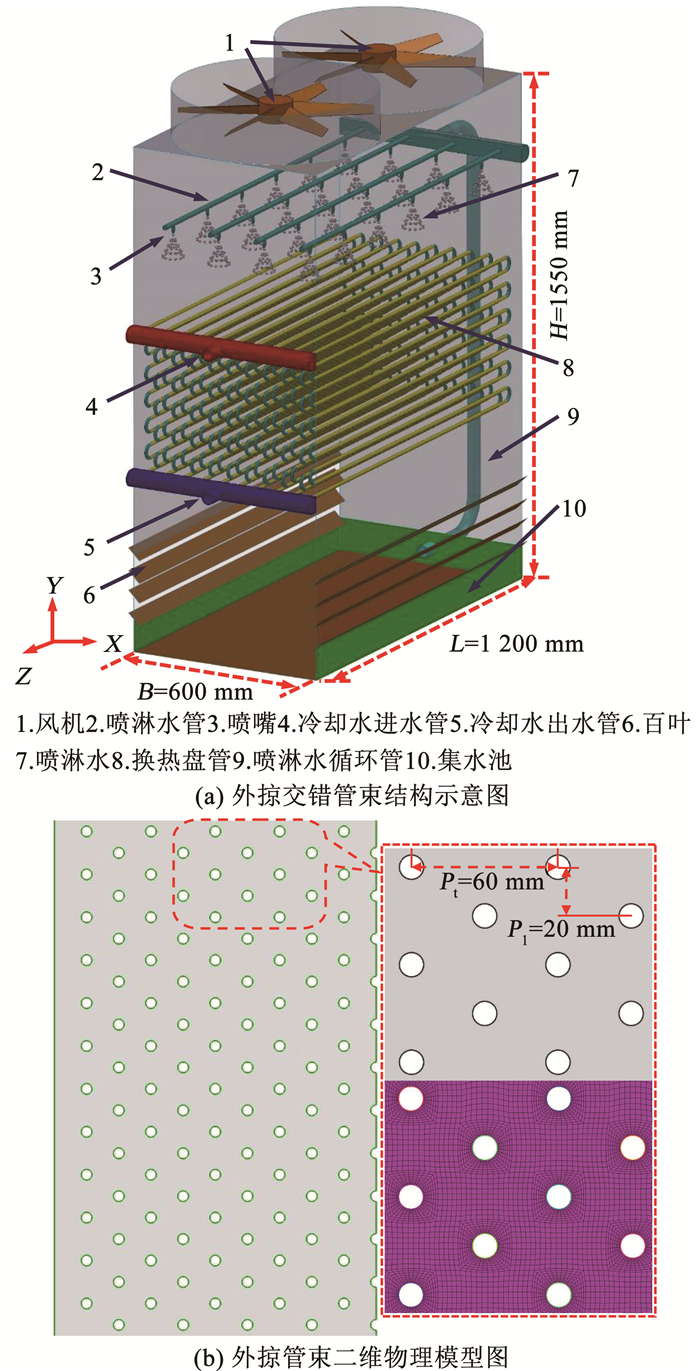
1 数理模型建立 1.1 物理模型简化本文依据文献[8],对密闭式冷却塔内交错排列外掠管束进行研究,如图 1(a)所示。表 1是交错管束具体结构参数。由于密闭式冷却塔几何长度不小于宽度的两倍(L≥2B),因此取垂直于盘管方向的密闭式冷却塔中间位置二维结构进行研究分析;考虑到其关于中心线对称,所以只对平面结构的1/2进行建模,如图 1(b)所示。
|
图 1 外掠交错管束几何模型 Fig. 1 Geometric model of staggered tube bundle |
| 表 1 交错管束结构参数 Tab. 1 Structural parameters of staggered tube bundle |
喷淋水从喷嘴喷出后,受到重力、阻力和浮力的共同作用,其满足动量守恒,同时也必须满足质量及能量守恒。对于单个喷淋水滴,其动量、质量及能量守恒方程分别如下:
动量守恒:
| $ m_{\mathrm{p}} \frac{\mathrm{d} \overrightarrow{\boldsymbol{u}}_{\mathrm{p}}}{\mathrm{d} t}=m_{\mathrm{p}} \overrightarrow{\boldsymbol{g}}-m_{\mathrm{p}} \frac{\overrightarrow{\boldsymbol{u}}-\overrightarrow{\boldsymbol{u}}_{\mathrm{p}}}{\tau_{\mathrm{p}}}-m_{\mathrm{p}} \overrightarrow{\boldsymbol{g}} \frac{\rho}{\rho_{\mathrm{p}}} $ | (1) |
质量守恒:
| $ m_{\mathrm{p}}(t)=m_{\mathrm{p}}(t-\Delta)-N_{\mathrm{i}, \mathrm{p}} A_{\mathrm{p}} M_{\mathrm{w}, \mathrm{i}} \Delta t $ | (2) |
能量守恒:
| $ m_{\mathrm{p}} c_{\mathrm{pp}} \frac{\mathrm{d} T_{\mathrm{p}}}{\mathrm{d} t}=h_{\mathrm{p}} A_{\mathrm{p}}\left(T_{\infty}-T_{\mathrm{p}}\right)-\frac{\mathrm{d} m_{\mathrm{p}}}{\mathrm{d} t} h_{\mathrm{fg}} $ | (3) |
式中:Ap为单个喷淋水滴表面积,m2;cpp为喷淋水比热容,J/kg·K;dmp/dt为喷淋水滴蒸发率,kg/s;
在式(2)中,喷淋水滴表面单位面积上摩尔蒸发速率可表示为
| $ N_{\mathrm{i}, \mathrm{p}}=k_{\mathrm{c}}\left(C_{\mathrm{i}, \mathrm{s}}-C_{\mathrm{i}, \infty}\right) $ | (4) |
式中:kc为喷淋水滴-湿空气界面水蒸汽传质系数,m/s;Ci, s和Ci, ∞分别为喷淋水滴表面和主流湿空气水蒸汽浓度,kmol/m3。
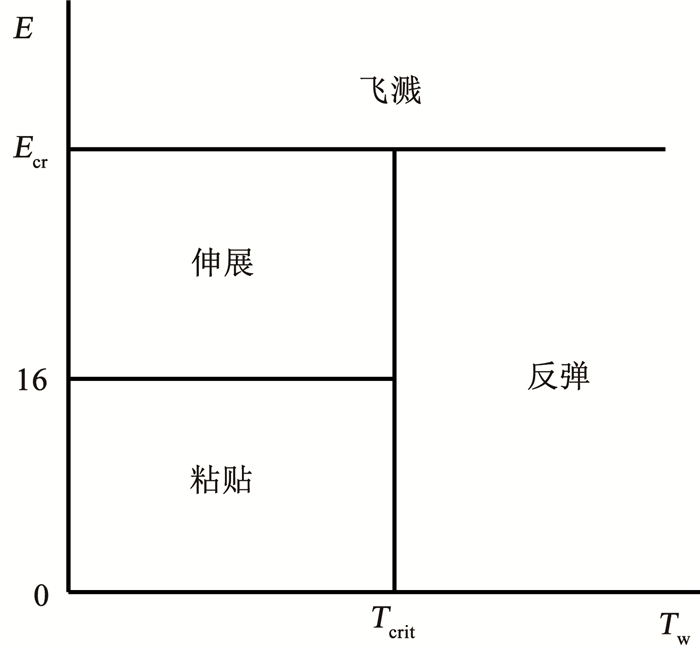
1.2.2 水膜形成分离及水膜传热传质过程数学描述喷淋水滴从喷嘴喷出后,在外掠交错管束间向下运动过程中,将会与盘管壁面发生碰撞;撞击管束壁面后,将会出现4种不同的状态,分别为:粘贴、扩散伸展、反弹、破裂,其撞击结果由喷淋水滴所具有的冲击能量和管束壁面温度决定,具体结果如图 2所示。根据文献[16-17],冲击能量E和临界壁面温度Tcrit被定义为
| $ E^{2}=\frac{\rho_{\mathrm{p}} u_{\mathrm{pn}}^{2} d_{\mathrm{p}}}{\sigma}\left(\frac{1}{\min \left(h_{\mathtt{δ}} / d_{\mathrm{p}}, 1\right)+\delta_{\mathrm{b} 1} / d_{\mathrm{p}}}\right) $ | (5) |
| $ T_{\text {crit }}=T_{\text {crit }}^{*} T_{\mathrm{sat}} $ | (6) |
|
图 2 喷淋水滴与壁面碰撞关系 Fig. 2 Relationship between spray water droplet and wall collision |
式中:upn为喷淋水滴垂直于壁面的速度分量,m/s;σ为喷淋水表面张力,N/m;hδ为管束表面微元体内水膜厚度,m;δbl为壁面水膜边界层厚度,m;Tsat为喷淋水饱和温度,K;Tcrit*为临界温度系数,其值在1.0~1.5之间。
水膜沿管束周向开始运动过程中,会受到体积力、壁面和湿空气对喷淋水膜剪切力的共同作用。对于微元体内喷淋水膜,其动量、质量及能量守恒方程分别如下:
动量守恒:
| $ \rho_{\mathrm{p}} h_{\delta} \frac{\mathrm{d} \overrightarrow{\boldsymbol{u}}_{\mathrm{film}}}{\mathrm{d} t}=\overrightarrow{\boldsymbol{\tau}}_{\mathrm{g}}+\overrightarrow{\boldsymbol{\tau}}_{\mathrm{w}}+\overrightarrow{\boldsymbol{G}}_{\mathrm{film}} $ | (7) |
质量守恒:
| $ m_{\mathrm{p}, \text { film }}(t)=m_{\mathrm{p}, \text { film }}(t-\Delta t)-N_{\mathrm{i}, \mathrm{film}} A_{\mathrm{p}, \text { film }} M_{\mathrm{w}, \mathrm{i}} \Delta t $ | (8) |
能量守恒:
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(m_{\mathrm{p}, \mathrm{film}} c_{\mathrm{pp}} T_{\mathrm{p}, \mathrm{film}}\right)=Q_{\mathrm{p}, \mathrm{cond}}+Q_{\mathrm{p}, \text { conv }}-N_{\mathrm{i}, \mathrm{film}} A_{\mathrm{p}, \text { film }} M_{\mathrm{w}, \mathrm{i}} h_{\mathrm{fg}} $ | (9) |
式中: Ap, film为管束表面微元内水膜表面面积,m2;
在式(8)、(9)中,Ni, film可表示为
| $ N_{\mathrm{i}, \mathrm{film}}=k_{\mathrm{film}}\left(C_{\mathrm{i}, \mathrm{s}}-C_{\mathrm{i}, \infty}\right) $ | (10) |
式中,kfilm为喷淋水膜-湿空气交界面水蒸汽传质系数,m/s。
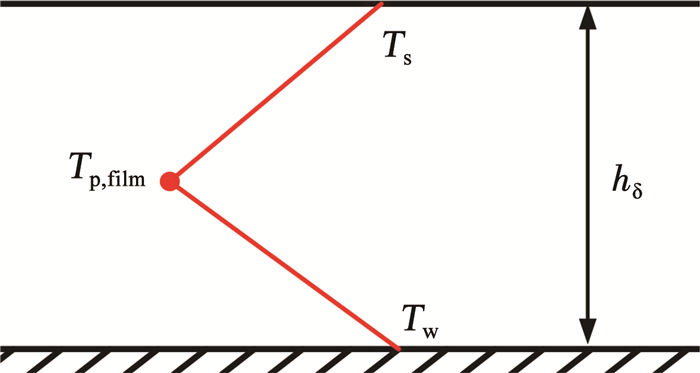
如图 3所示,由于喷淋水膜是有厚度的,因此其内部温度与表面温度不同,故用中间温度Tp, film作为水膜温度,K;Tw、Ts分别为管束和水膜表面温度,K。
|
图 3 喷淋水膜双线性温度分布的假设 Fig. 3 Assumption of a bilinear temperature profile of spray water film |
湿空气在外掠交错管束间向上流动过程中,微元体内湿空气动量、质量、能量和组分守恒方程分别如下:
动量守恒:
| $ \left\{\begin{array}{l} \frac{\partial}{\partial t}\left(\rho u_{x}\right)+\left[\frac{\partial}{\partial x}\left(\rho u_{x} u_{x}\right)+\frac{\partial}{\partial y}\left(\rho u_{x} u_{y}\right)\right]=\mu \nabla^{2} u_{x}+F_{x}+ \\ \frac{\partial}{\partial x}\left[2 u_{\mathrm{t}} \frac{\partial u_{x}}{\partial x}-\frac{2}{3} \mu_{\mathrm{t}}\left(\frac{\partial u_{x}}{\partial x}+\frac{\partial u_{y}}{\partial y}\right)\right]+\frac{\partial}{\partial y}\left[\mu_{\mathrm{t}}\left(\frac{\partial u_{x}}{\partial y}+\frac{\partial u_{y}}{\partial x}\right)\right] \\ \frac{\partial}{\partial t}\left(\rho u_{y}\right)+\left[\frac{\partial}{\partial x}\left(\rho u_{y} u_{x}\right)+\frac{\partial}{\partial y}\left(\rho u_{y} u_{y}\right)\right]=\mu \nabla^{2} u_{y}+F_{y}+ \\ \frac{\partial}{\partial y}\left[2 \mu_{\mathrm{t}} \frac{\partial u_{y}}{\partial y}-\frac{2}{3} \mu_{\mathrm{t}}\left(\frac{\partial u_{x}}{\partial x}+\frac{\partial u_{y}}{\partial y}\right)\right]+\rho g_{y}+\frac{\partial}{\partial x}\left[\mu_{\mathrm{t}}\left(\frac{\partial u_{x}}{\partial y}+\frac{\partial u_{y}}{\partial x}\right)\right] \end{array}\right. $ | (11) |
质量守恒:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x}\left(\rho u_{x}\right)+\frac{\partial}{\partial y}\left(\rho u_{y}\right)=S_{\mathrm{p}}+S_{\mathrm{film}} $ | (12) |
能量守恒:
| $ \begin{aligned} &\rho\left(\frac{\partial h}{\partial t}+u_{x} \frac{\partial h}{\partial x}+u_{y} \frac{\partial h}{\partial y}\right)=\nabla \cdot\left(k_{\text {eff }} \nabla T\right)- \\ &{\left[\frac{\partial}{\partial x}\left(h_{\mathrm{i}} J_{\mathrm{i}, x}\right)+\frac{\partial}{\partial y}\left(h_{\mathrm{i}} J_{\mathrm{i}, y}\right)\right]+S_{\mathrm{Q}, \mathrm{p}}+S_{\mathrm{Q}, \mathrm{film}}} \end{aligned} $ | (13) |
组分守恒:
| $ \begin{aligned} \frac{\partial}{\partial t}\left(\rho Y_{\mathrm{i}}\right) &+\left[\frac{\partial}{\partial x}\left(u_{x} \rho Y_{\mathrm{i}}\right)+\frac{\partial}{\partial y}\left(u_{y} \rho Y_{\mathrm{i}}\right)\right]=\\ &-\left(\frac{\partial}{\partial x} J_{\mathrm{i}, x}+\frac{\partial}{\partial y} J_{\mathrm{i}, y}\right)+S_{\mathrm{i}} \end{aligned} $ | (14) |
式中: Fx、Fy为喷淋水滴对湿空气的作用力; gy为湿空气的重力加速度在y方向的分量,m/s2;Ji, x、Ji, y分别为x和y方向水蒸汽的扩散通量,kg/m2·s;keff为湿空气有效导热率,W/(m·K);Sp、Sfilm分别为喷淋水滴和喷淋水膜蒸发进入湿空气的水蒸气质量流率,kg/(m3·s);SQ, p、SQ, film分别为水滴和水膜蒸发的水蒸汽进入空气的能量,kW/m3;Si为水蒸发速率,kg/m3s;ux、uy分别为x和y方向湿空气的速度分量,m/s;Yi为水蒸汽质量分数;μt为湍流动力黏度,Pa·s。
本文采用标准k-ε湍流模型,求解湍流动能k及耗散率ε,其可表示为
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho k)+u_{x} \frac{\partial \rho k}{\partial x_{x}}+u_{y} \frac{\partial \rho k}{\partial x_{y}}=\frac{\partial}{\partial x_{x}}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{x}}\right]+ \\ \frac{\partial}{\partial x_{y}}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{y}}\right]+G_{k}-\rho \varepsilon \end{gathered} $ | (15) |
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho \varepsilon)+u_{x} \frac{\partial \rho \varepsilon}{\partial x_{x}}+u_{y} \frac{\partial \rho \varepsilon}{\partial x_{y}}=\frac{\partial}{\partial x_{x}}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{x}}\right]+ \\ \frac{\partial}{\partial x_{y}}\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}} \frac{\partial \varepsilon}{\partial x_{y}}\right]+C_{1 \varepsilon} \frac{\varepsilon}{k} G_{k}-C_{2 \varepsilon} \rho \frac{\varepsilon^{2}}{k}\right. \end{gathered} $ | (16) |
式中:C1ε、C2ε为常数,分别取1.44和1.92;Gk为湿空气速度梯度产生的湍流动能;σk、σε分别为k和ε的湍流普朗特数,由实验得出,分别取1.0和1.3。
1.3 边界条件在确定了外掠交错管束间湿空气-喷淋水蒸发冷却传热传质及压降特性分析主微分方程之后,需要对方程添加边界条件,使其存在唯一解。根据实际工程,喷淋水滴和湿空气状态通常为已知量,可表示为:
| $ \begin{aligned} &\left.u_{\mathrm{p}, x}\right|_{y=1\ 300}=0 \\ &\left.u_{\mathrm{p}, y}\right|_{y=1\ 300}=u_{\mathrm{p}, \text { in }}=-2 \mathrm{~m} / \mathrm{s} \\ &\left.T_{\mathrm{p}}\right|_{y=1\ 300}=T_{\mathrm{p}, \text { in }} \\ &\left.d_{\mathrm{p}}\right|_{y=1\ 300}=d_{\mathrm{p}, \text { in }}=2 \mathrm{~mm} \end{aligned} $ | (17) |
式中:up, in为喷嘴出口喷淋水滴速度,m/s;Tp, in为喷嘴出口喷淋水的温度(不同的工况取值不同),K;dp, in为喷嘴出口喷淋水滴的直径,m。
在湿空气入口处,湿空气状态可表示为
| $ \begin{aligned} &\left.u_{\mathrm{air}, x}\right|_{y=0}=0 \mathrm{~m} / \mathrm{s} \\ &\left.u_{\mathrm{air}, y}\right|_{y=0}=u_{\mathrm{air}, \mathrm{in}} \\ &\left.T_{\mathrm{air}}\right|_{y=0}=T_{\mathrm{air}, \mathrm{in}} \\ &\left.P_{\mathrm{air}}\right|_{y=0}=0.101 \mathrm{~MPa} \\ &\left.Y_{i}\right|_{y=0}=\frac{p_{\mathrm{sat}} \mathrm{R} \mathrm{H}_{0}}{\mathrm{MR} T_{\mathrm{air}, \mathrm{in}} \rho_{\mathrm{in}}} \end{aligned} $ | (18) |
式中:uair, in为进口湿空气速度(不同工况取值不同),m/s;ρin为进口湿空气密度,kg/m3;Tair, in为进口湿空气温度(不同工况取值不同),K;RH0为进口湿空气的相对湿度(不同工况取值不同)。
同时,将管束壁面设置为wall film边界,将空气进口和出口设置为escape边界。
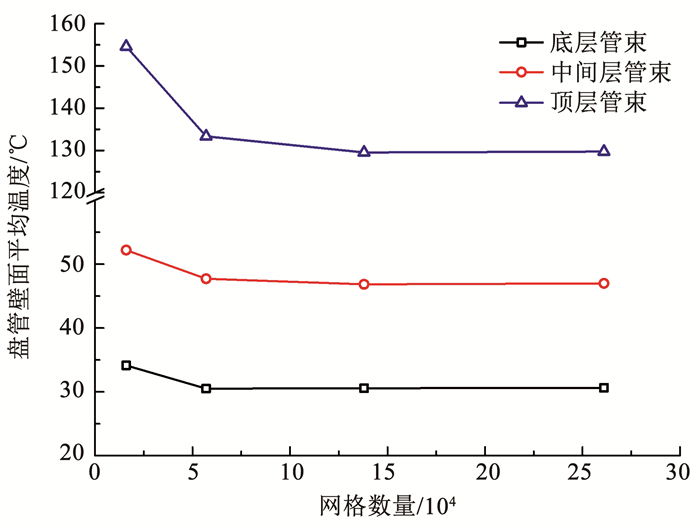
2 网格无关性及模型验证本文对计算模型采用了结构化网格,靠近管壁的区域划分了边界层,并进行了网格加密。选取4套数量如图 4所示的网格,比较了底层、中间层和顶层管束壁面温度变化,模拟结果如图 5所示。从中可以看出,当网格数量达到138 000时,各层管束壁面温度趋于稳定,说明其能够满足仿真精度要求。

|
图 4 外掠交错管束局部网格分布 Fig. 4 Local grid distribution of staggered tube bundles |
|
图 5 不同网格数量管束壁面温度变化 Fig. 5 Temperature variation of tube bundle wall with different mesh numbers |
为了保证外掠交错管束间湿空气-喷淋水蒸发冷却传热传质及压降特性模拟结果的准确性,本文将采用文献[8]实验数据进行验证。结果见文献[19],其误差在1%范围内。
3 结果与分析外掠交错管束间湿空气-喷淋水蒸发冷却传热传质主要包括,水膜与管束壁面对流换热,以及水膜和水滴与空气的传热传质过程。同时,外掠交错管束间湿空气-喷淋水传热传质过程的压降特性,是密闭式冷却塔动力设备,如风机选择的关键参数。因此,本文主要对外掠交错管束盘管高度方向,水膜与管束壁面对流换热,水膜和水滴与空气的传热传质以及外掠管束压降进行模拟分析。
外掠管束间水膜和水滴与空气的传热传质特性,可用外掠管束间水膜/水滴-湿空气传质系数β描述。根据文献[20],单层管束水膜/水滴-湿空气传质系数可表示为
| $ \beta=\frac{m_{\mathrm{a}}}{A_{\mathrm{w}}} \ln \left[1+\frac{i_{\mathrm{a}, \text { out }}-i_{\mathrm{a}, \text { in }}}{i_{\mathrm{a}}^{\prime}\left(t_{\mathrm{s}}\right)-i_{\mathrm{a}, \text { out }}}\right]=\frac{m_{\mathrm{a}}}{A_{\mathrm{w}}} \ln \left[1+\frac{\Delta i_{\mathrm{a}}}{\Delta i_{\mathrm{a}}^{\prime}}\right] $ | (19) |
式中:ma为湿空气质量流量,kg/s;Aw为管束表面积,m2;β为传质系数,kg/m2·s;i′a为单层管束周围喷淋水温度对应的饱和湿空气焓,kJ/kg;ia, in为与单层管束热质交换前湿空气的焓,kJ/kg;ia, out为与单层管束热质交换后湿空气的焓,kJ/kg;Δia为热质交换后湿空气焓ia, out与热质交换前湿空气焓ia, in的差,kJ/kg,简称湿空气焓差;Δi′a为饱和湿空气焓i′a与湿空气焓ia, out的差,kJ/kg,简称饱和湿空气焓差。
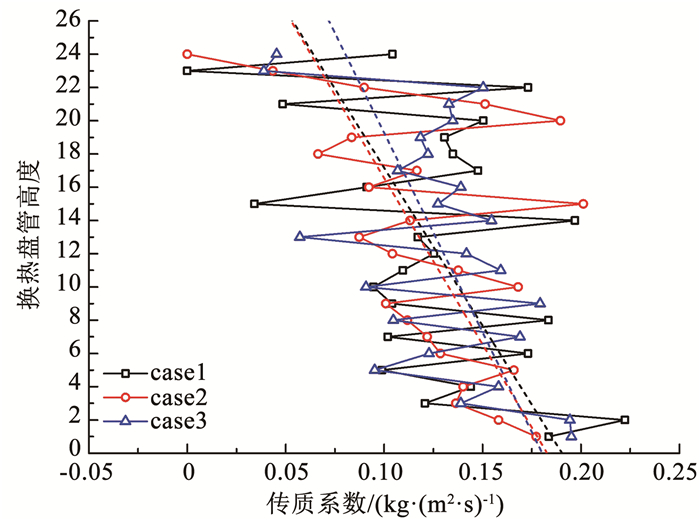
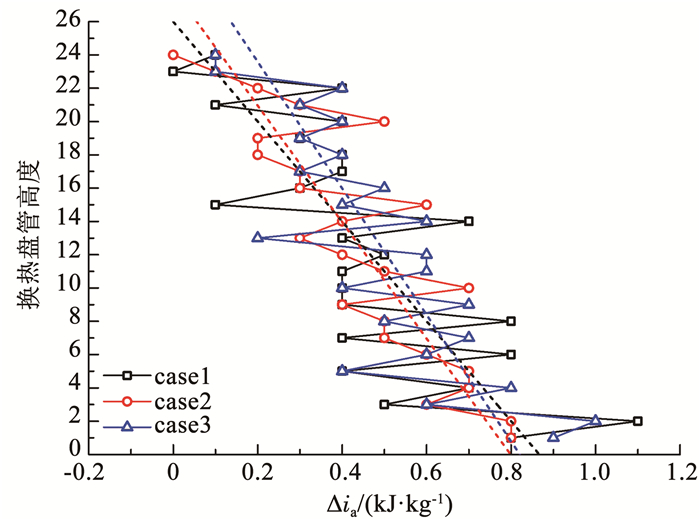
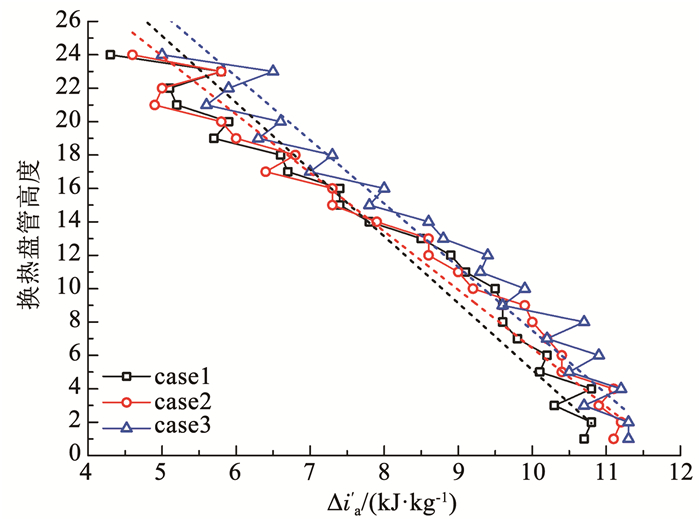
本文主要对3组典型工况的模拟结果进行了分析。根据式(19)得出外掠管束间水膜/水滴-空气传质系数沿盘管高度的变化,结果如图 6所示。结果表明,在同一工况下,传质系数沿盘管高度方向呈波动变化状态,但是沿盘管高度总体呈下降趋势。根据式(19)可知,外掠管束间水膜/水滴-空气传质系数主要受湿空气流量、管束壁面面积、湿空气焓差Δia以及饱和湿空气焓差Δi'a的影响。对于给定工况,湿空气流量和管束壁面面积是恒定的,湿空气焓差Δia和相应条件下饱和湿空气焓差Δi'a,是造成外掠管束间水膜/水滴-空气传质系数波动,以及其随盘管高度整体降低的主要原因。因此,为了进一步分析外掠管束间水膜/水滴-空气传质特性,图 7、8给出了外掠交错管束间湿空气焓差Δia和饱和湿空气焓差Δi'a随盘管高度的变化规律。结果表明,湿空气焓差Δia沿盘管高度方向也呈波动变化状态,这与传质系数变化趋势一致;同一工况下,饱和湿空气焓差Δi'a随着盘管高度的上升而降低,并且波动相对较小。由此可见,外掠交错管束间水膜/水滴-空气传质系数沿盘管高度方向的波动主要由湿空气焓差Δia波动引起,而沿盘管高度方向变化趋势是湿空气焓差Δia和对应条件下饱和湿空气焓差Δi'a共同作用的结果。
|
图 6 交错管束间传质系数沿盘管高度变化结果 Fig. 6 Variation of mass transfer coefficient between staggered tube bundles along coil height |
|
图 7 交错管束间湿空气焓差Δia沿盘管高度的变化 Fig. 7 Variation of enthalpy difference of wet air Δia between staggered tube bundles along coil height |
|
图 8 交错管束间饱和空气焓差Δi′a沿盘管高度的变化 Fig. 8 Variation of enthalpy difference of saturated air Δi′a between staggered tube bundles along coil height |
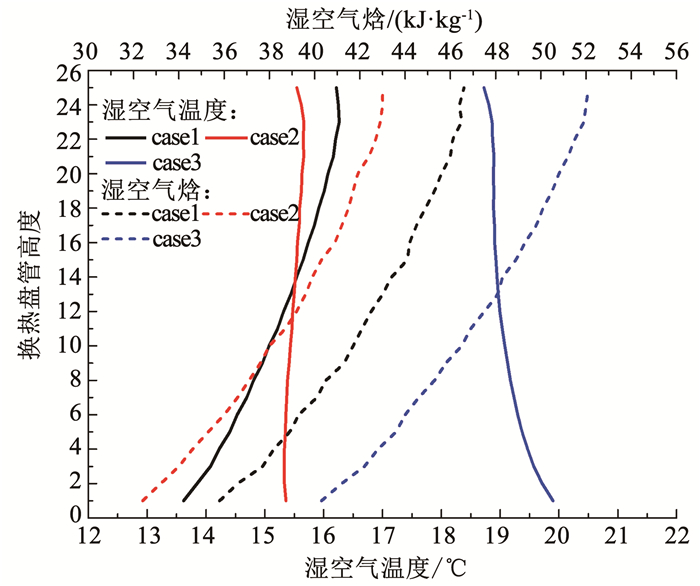
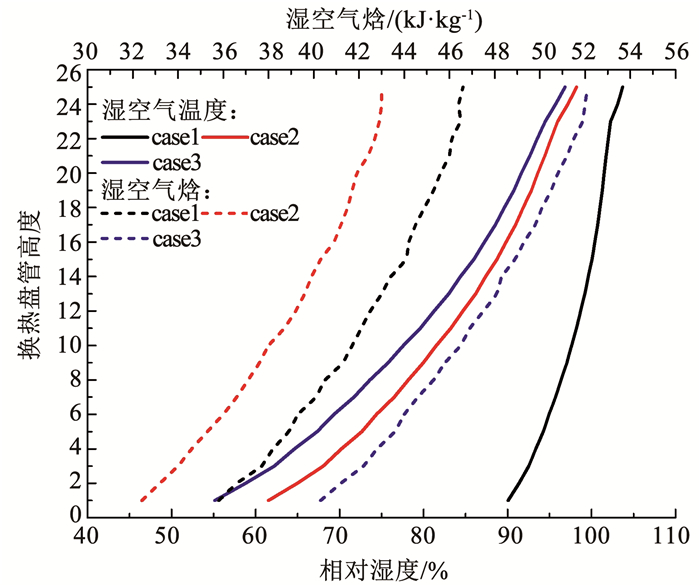
为进一步分析湿空气焓差Δia对外掠交错管束间水膜/水滴-空气传质性能的影响,本文又给出了湿空气焓与湿空气温度和相对湿度的关系。图 9给出了交错管束间湿空气焓与湿空气温度的变化关系。结果表明,湿空气焓随盘管高度上升而增大,但交错管束间湿空气温度随盘管高度的变化,在不同工况存在较大差异。对于工况1(case1)来讲,湿空气温度随盘管高度上升而增大;对于工况2(case2),湿空气温度受盘管高度的影响较小;在工况3(case3)中,湿空气温度将随盘管高度的增大而降低。这将说明,沿外掠管束盘管高度方向,湿空气的焓受其温度变化的影响较小,即湿空气温度并不是影响外掠交错管束间水膜/水滴-空气传质系数的主要因素。图 10是交错管束间湿空气焓与相对湿度的变化关系。结果表明,湿空气焓与相对湿度变化趋势保持一致,并随着盘管高度的增加均呈现增大趋势,表明湿空气的焓主要受相对湿度的影响较大。在同一工况下,外掠交错管束间水膜/水滴-空气传质系数随盘管高度的增加呈减小趋势,因此其传质系数将随湿空气相对湿度增大而减小。也就是说,沿着盘管高度方向,随着传热传质过程的进行,湿空气将越接近饱和,其蒸发传质性能将有所降低。
|
图 9 交错管束间湿空气焓与湿空气温度的变化关系 Fig. 9 Relationship between enthalpy of wet air and temperature of wet air between staggered tube bundles |
|
图 10 交错管束间湿空气焓与相对湿度的变化关系 Fig. 10 Relationship between enthalpy of wet air and relative humidity between staggered tube bundles |
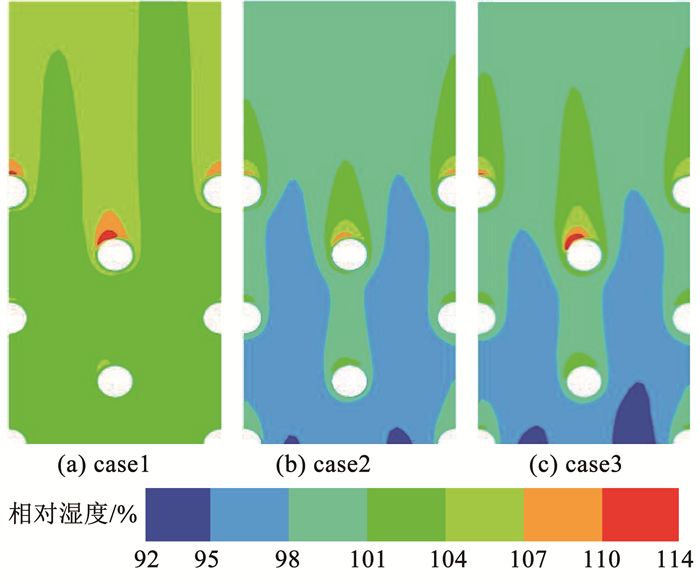
图 11是外掠交错管束间水滴蒸发量分布。结果表明,水的蒸发量与相对湿度成反比。在换热盘管下段区域,水蒸汽质量分数及相对湿度是整个换热器最低的区域,因此,换热盘管下段传质驱动力较大,使得水滴蒸发量较大,随着空气沿盘管高度方向运动,水蒸汽质量分数及相对湿度逐渐增大,传质驱动力逐渐减小,因此换热盘管上段水滴蒸发量小于换热盘管下段水滴蒸发量。同时可以看出,喷淋水蒸发过程主要发生在管壁和管束尾流区位置,但是管束尾流区空气流速非常低,这不利于喷淋水的蒸发冷却。因此,可以在管束间安装导流翅片或者减小管束横向间距来强化管束尾流区流场扰流作用,增强喷淋水的蒸发冷却作用,提高闭式冷却塔热工性能。图 12是外掠管束间顶层盘管局部相对湿度分布。图 13(c)是交错管束间顶层局部速度分布。结果显示,顶层盘管局部位置空气相对湿度已经达到100%,使得顶层盘管局部位置水的蒸发过程几乎停滞,严重影响顶层盘管区域传热传质效果。这是由于顶层盘管位置管束间相互干扰作用较弱,使得顶层盘管尾流区空气流动减慢,导致顶层盘管局部空气达到饱和。可以通过减小管束间距,增加管束间相互干扰作用,提高管束表面空气间的扰流强度,增强传热传质效果。

|
图 11 外掠交错管束间水滴蒸发量分布 Fig. 11 Distribution of water droplet evaporation between staggered tube bundles |
|
图 12 外掠管束间顶层盘管局部相对湿度分布 Fig. 12 Local relative humidity distribution of top coil between staggered tube bundles |
|
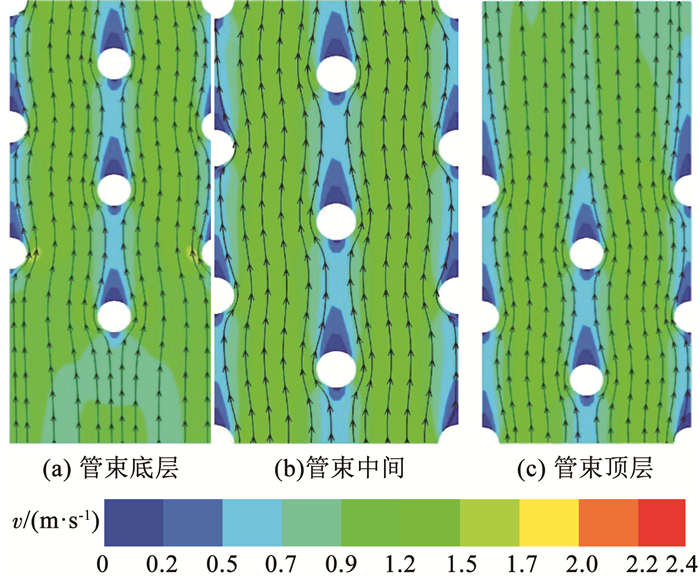
图 13 外掠交错管束间速度分布 Fig. 13 Velocity distribution between staggered tube bundles |
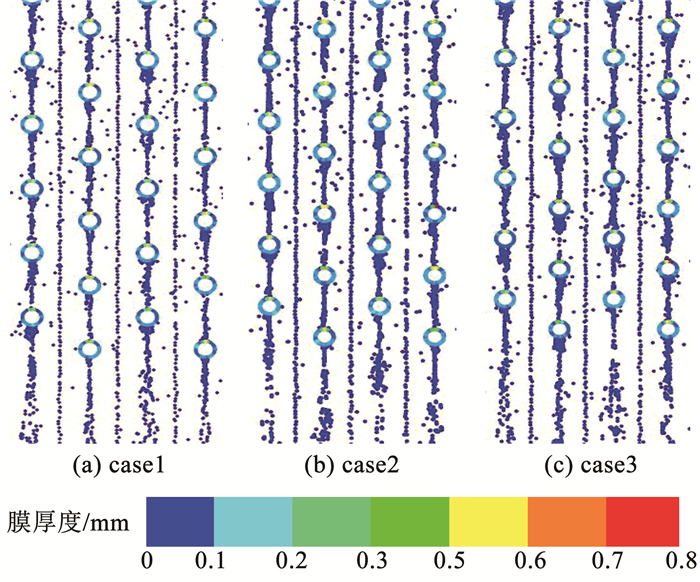
图 14是外掠交错管束间水膜厚度分布。可以看出,3组工况中管束表面水膜厚度相同,这表明喷淋水膜厚度与空气温度和喷淋水温度无关。同时,同一工况下,沿盘管高度方向喷淋水膜厚度变化不大,并且每排管束顶部位置喷淋水膜厚度最大。
|
图 14 外掠交错管束间水膜厚度分布 Fig. 14 Distribution of water film thickness between staggered tube bundles |
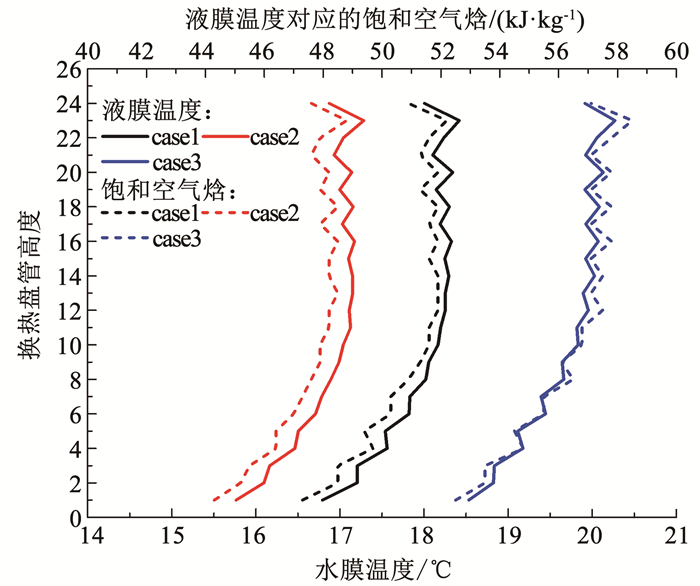
图 15是交错管束间水膜温度与饱和空气焓的关系。结果表明,外掠交错管束壁面水膜温度和表面饱和湿空气的焓,随排管高度呈增大趋势;外掠交错管束壁面水膜表面饱和湿空气焓与水膜温度成正相关。因此饱和空气焓沿盘管高度变化趋势和水膜温度变化趋势一样。
|
图 15 交错管束间水膜温度与饱和空气焓的关系 Fig. 15 Relationship between water film temperature and saturated air enthalpy between staggered tube bundles |
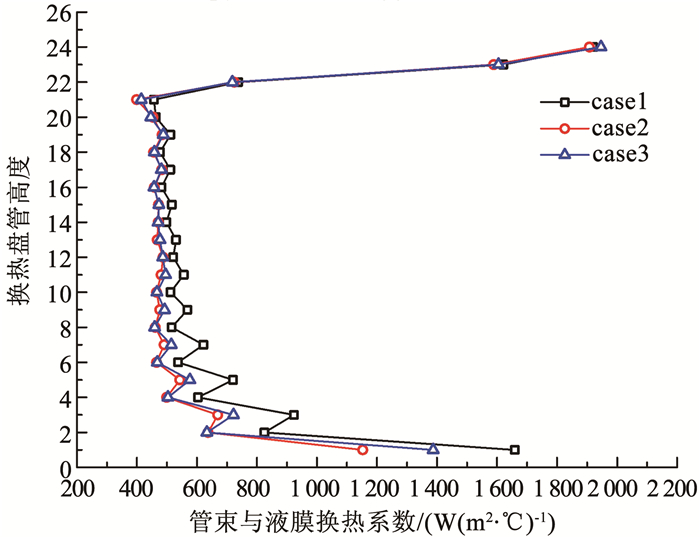
图 16是外掠交错管束水膜/水滴-管壁的对流换热系数沿盘管高度的变化曲线。结果表明,在同一工况下,沿盘管高度换热系数α变化不大;同时工况1、工况2和工况3之间的换热系数变化较小,这表明换热系数受进气温度、喷淋水温度及相对湿度的影响较小;图中可以看出,顶层和底层盘管的传热系数明显高于其他盘管的传热系数,这可能是顶层和底层盘管是空气进出换热盘管的过渡区造成的。同时,由于在换热器顶部空气出口3排和底部空气进口3排过渡段位置传热系数较大,因此,在换热面积不变的情况下,可将单个换热器分成多段布置,通过增加过渡段数量提高整体换热性能;但是,每段换热管束应保证6排以上,且分段不易过多,过渡段过多会导致压力损失增大。
|
图 16 交错管束间换热系数沿盘管高度的变化 Fig. 16 Variation of heat transfer coefficient between staggered tube bundles along coil height |
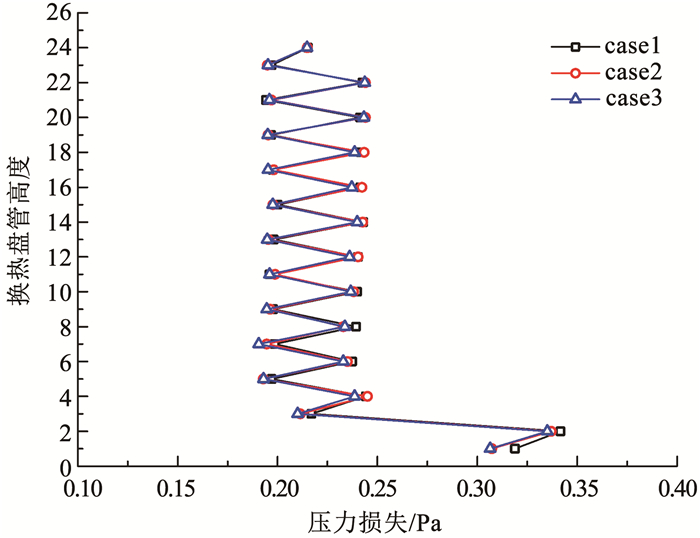
图 17是交错管束间压力损失沿盘管高度的变化。可以看出,在其他参数不变的情况下,沿盘管高度压力损失受进气温度、喷淋水流量和相对湿度的影响非常小;由于换热管束中间区域流场稳定,如图 13(b)所示,不同位置管束周围空气流态相似,因此交错管束间中间区域压力损失沿盘管高度变化不大;同时,换热盘管空气进口位置速度变化要比换热器中间区速度变化大,如图 13(a)所示,因此,换热盘管空气进口过渡段位置压力损失比中间区域的压力损失大。
|
图 17 交错管束间压力损失沿盘管高度的变化 Fig. 17 Variation of pressure loss between staggered tube bundles along coil height |
1) 建立外掠交错管束间水蒸发冷却传热传质模型,将预测的顶层和底层管束壁面温度与实验值进行了误差分析,其最大误差仅为1%范围内,验证了模型的准确性。
2) 交错管束间传质系数沿盘管高度方向呈波动状态变化,但总体呈下降趋势,这是湿空气焓差和饱和空气焓差的变化导致的,但是传质系数波动主要是由湿空气焓差造成。
3) 外掠交错管束间水膜温度并非保持恒定不变,而是随盘管高度的降低而降低,即沿下落方向液膜温度逐渐降低。交错管束间底部喷淋水滴蒸发量最大,沿盘管高度方向,喷淋水滴蒸发量降低。喷淋水蒸发过程主要发生在管束表面及管束尾流区,通过在管束间增加挡板或者减小管间距强化管束表面及尾流区流场扰流作用,增强喷淋水的蒸发冷却作用。
4) 交错管束间换热系数沿盘管高度变化较小,但在换热盘管空气进出口过渡区传热系数最大。交错管束间压力损失沿盘管高度变化较小,但在换热盘管空气进口过渡区压力损失最大。
| [1] |
JIN Zhijiang, CHEN Fuqiang, GAO Zhixin, et al. Effects of pitch and corrugation depth on heat transfer characteristics in six-start spirally corrugated tube[J]. International Journal of Heat and Transfer, 2017, 108: 1011. DOI:10.1016/j.ijheatmasstransfer.2016.12.091 |
| [2] |
LI M J, ZHANG H, ZHANG J, et al. Experimental and numerical study and comparison of performance for wavy fin and a plain fin with radiantly arranged winglets around each tube in fin-and-tube heat exchangers[J]. Applied Thermal Engineering, 2018, 133: 298. DOI:10.1016/j.applthermaleng.2018.01.012 |
| [3] |
GU Lingdong, MIN Jingchun, WU Xiaomin, et al. Airside heat transfer and pressure loss characteristics of bare and finned tube heat exchangers used for aero engine cooling considering variable air properties[J]. International Journal of Heat and Mass Transfer, 2017, 108(part_PB): 1839. DOI:10.1016/j.ijheatmasstransfer.2017.01.047 |
| [4] |
MA Hongqiang, CAI Weihua, CHEN Jie, et al. Numerical investigation on saturated boiling and heat transfer correlations in a vertical rectangular minichannel[J]. International Journal of Thermal Sciences, 2016, 102: 285. DOI:10.1016/j.ijthermalsci.2015.12.003 |
| [5] |
HEYNS J A, KRÖGER D G. Experimental investigation into the thermal-flow performance characteristics of an evaporative cooler[J]. Applied Thermal Engineering, 2010, 30(5): 492. DOI:10.1016/j.applthermaleng.2009.10.010 |
| [6] |
ZHENG Weiye, ZHU Dongsheng, ZHOU Guoyan, et al. Thermal performance analysis of closed wet cooling towers under both unsaturated and supersaturated conditions[J]. International Journal of Heat & Mass Transfer, 2012, 55(25/26): 7803. DOI:10.1016/j.ijheatmasstransfer.2012.08.006 |
| [7] |
GAN G, RIFFAT S B. Numerical simulation of closed wet cooling towers for chilled ceiling systems[J]. Applied Thermal Engineering, 1999, 19(12): 1279. DOI:10.1016/S1359-4311(99)00002-2 |
| [8] |
GAN G, RIFFAT S B, SHAO L, et al. Application of CFD to closed-wet cooling towers[J]. Applied Thermal Engineering, 2001, 21(1): 79. DOI:10.1016/S1359-4311(00)00048-X |
| [9] |
HASAN A, GAN Guohui. Simplification of analytical models and incorporation with CFD for the performance predication of closed-wet cooling towers[J]. International Journal of Energy Research, 2002, 26(13): 1161. DOI:10.1002/er.842 |
| [10] |
XIE Xiaocui, HE Chang, XU Tao, et al. Deciphering the thermal and hydraulic performances of closed wet cooling towers with plain, oval and longitudinal fin tubes[J]. Applied Thermal Engineering, 2017, 120: 203. DOI:10.1016/j.applthermaleng.2017.03.138 |
| [11] |
ZHAO Chuangyao, JI Wentao, JIN Puhang, et al. Hydrodynamic behaviors of the falling film flow on a horizontal tube and construction of new film thickness correlation[J]. International Journal of Heat and Mass Transfer, 2018, 119: 564. DOI:10.1016/j.ijheatmasstransfer.2017.11.086 |
| [12] |
DING Hongbing, XIE Peng, INGHAM D, et al. Flow behaviour of drop and jet modes of a laminar falling film on horizontal tubes[J]. International Journal of Heat and Mass Transfer, 2018, 124: 929. DOI:10.1016/j.ijheatmasstransfer.2018.03.111 |
| [13] |
KARMAKAR A, ACHARYA S. Wettability effects on falling film heat transfer over horizontal tubes in jet flow mode[C]//Proceedings of the ASME 2019 Heat Transfer Summer Conference collocated with the ASME 2019 13th International Conference on Energy Sustainability. Washington DC: ASME, 2019. DOI: 10.1115/HT2019-3532
|
| [14] |
GOSMAN A D, LOANNIDES E. Aspects of computer simulation of liquid-fueled combustors[J]. Journal of Energy, 1983, 7(6): 482. DOI:10.2514/3.62687 |
| [15] |
MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems[J]. Journal of Fluid Mechanics, 1972, 55(2): 193. DOI:10.1017/S0022112072001806 |
| [16] |
STANTON D W, RUTLAND C J. Modeling fuel film formation and wall interaction in diesel engines[J]. SAE Technical Paper Series, 1996, 808. DOI:10.4271/960628 |
| [17] |
O'ROURKE P J, AMSDEN A A. A spray/wall interaction submodel for the KIVA-3 wall film model[J]. SAE Technical Paper, 2000. DOI:10.4271/2000-01-0271 |
| [18] |
O'ROURKE P J, AMSDEN A A. A particle numerical model for wall film dynamics in port-injected engines[J]. SAE, 1996, 2000. DOI:10.4271/961961 |
| [19] |
MA H, LIU Y, HOU C, et al. Numerical investigation on the thermal-flow performance of humid air-water in the interspace outside staggered tube bundles[J]. International Journal of Heat and Mass Transfer, 2021, 166: 120784. DOI:10.1016/j.ijheatmasstransfer.2020.120784 |
| [20] |
HASAN A, SIREN K. Performance investigation of plain and finned tube evaporatively cooled heat exchangers[J]. Applied Thermal Engineering, 2003, 23(3): 325. DOI:10.1016/S1359-4311(02)00194-1 |
 2022, Vol. 54
2022, Vol. 54


