2. 烟台文化旅游职业学院,山东 烟台,264005
2. Yantai Vocational College of Culture and Tourism, Yantai 264005, Shandong, China
水陆两栖机器人可以在陆地、水下以及水陆交接的多变环境中,代替工作人员执行生态环境巡检、水下资源勘探、灾后搜救等复杂任务,因而研究高性能两栖机器人具有非常重要的社会意义和价值[1-2]。
为实现水陆两栖机器人的两栖运动功能,先前的学者已经进行了一些研究。Xing等[3]是在多足机器人腿的末端添加额外的喷水推进器,主要由分布在半球体上4个二自由度腿驱动,实现了水陆快速运动。但该推进结构冗余且体积较大,运动的灵活性较低。王常龙等[4]将轮子的轮毂做成螺旋桨,实现了轮桨复合功能,通过改变轮轴的方向完成了水陆两栖运动。但是,其螺旋桨结构暴露在外,叶片容易碰撞引起驱动失效或者损坏。两栖机器人进行水下巡检时,需要保持稳定的姿态以保证巡检的传感器件能够获得可靠的信息。而维持水下机器人稳定需要通过控制算法调节推力或改变重浮心的相对位置。何彦霖等[5]使用基于传统PID算法的神经网络自整定控制算法控制复合球型两栖机器人水下运行的姿态,解决了传统PID参数整定困难的问题,但响应速度较慢。Xu等[6]提出了一种基于控制力矩陀螺的内驱动控制方案,通过控制力矩陀螺可以改变重心和浮心的相对位置,以维持水下机器人的姿态平稳,但该方法需要预留力矩陀螺的安装空间,不利于机器人小型化。罗庆生等[7]使用自适应滑模控制来控制矢量多推进器水下机器人,但其无法解决低速条件下的自由度耦合问题。王涛等[8]基于干扰观测器对四倾转水下机器人进行姿态跟踪,但其推进器的倾转必须同步进行,这样降低了机器人的运动自由度。Jin等[9]提出了一种选择切换器来解决多推进器倾转时的耦合问题,但未考虑机器人推进器倾转带来的扰动,因此姿态控制精度较差。综上所述,现有的水陆两栖机器人在结构方面冗余复杂且存在损坏的风险,而在姿态控制器方面效率和精度较低。
针对具有可倾转推进器的水下机器人姿态稳定控制问题,本文首先将陆地轮式推进与可倾转喷水推进复合,将其安装在H型两栖机器人上,实现水陆两栖环境的基本行进功能,然后采用预约束建模方法和推力倾转角分离控制方法,将复杂的倾转模型简化为多个简单的模型,在此基础上建立了基于自抗扰理论[10]的姿态控制器,可以将建模误差和内外扰动统一处理为“总干扰”进行实时补偿,并对耦合自由度进行异步调节,以维持机器人姿态稳定。
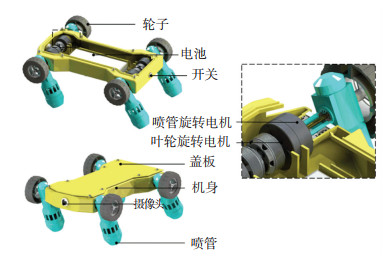
1 H型两栖机器人与复合推进结构H型两栖机器人整体方案如图 1所示,主要由机身和4个复合推进器组成。其构型与字母H类似,因此将其命名为H型两栖机器人。该机器人在水下运动时,4个喷管都可以360°转动,从而产生不同方向的推力和力矩以驱动机器人完成水下浮游运动,同时还可以控制喷管,提供轮子与水下壁面的贴紧力,使机器人机身附着于壁面,进行水下贴壁行走。在陆地运动时,通过控制4个轮子以不同的转速驱动机器人直行和转向;当机器人遇到使用轮驱动无法跨越的障碍时,可以控制4个喷管转动以支撑机身跨越障碍达到陆地爬行的效果。如图 2所示,H型两栖机器人能够完成水中浮游、水下贴壁行走、陆地轮驱动和陆地爬行4种运动模式。
|
图 1 H型两栖机器人的结构 Fig. 1 Structure of H-type amphibious robot |

|
图 2 H型两栖机器人的运动模式 Fig. 2 Motion mode of H-type amphibious robot |
H型两栖机器人所需驱动器的数量较多,因此将轮子与喷水推进器进行复合,使轮转动和喷水推进器叶轮转动共用一个驱动器,复合式推进器结构如图 3所示。

|
图 3 复合式推进器结构 Fig. 3 Composite propeller structure |
两栖推进器的运动动作有3个,分别为轮转动、螺旋桨转动、喷管转动。理论上需要3个驱动源,但可以将轮子的驱动器与喷管叶轮的驱动器进行复合使二者使用同一个驱动源。为实现二者的复合,无刷电机的输出在复合推进器中被分为2路,一路通过锥形齿轮连接至叶轮,直接带动叶轮转动以产生喷水推进力,2个锥齿轮齿数相同,叶轮的转速即为电机转速;另一路通过减速齿轮组和永磁离合装置连接到轮轴,永磁离合器处于常开状态。只有当喷管转动到水平对喷位置时,喷管内的磁铁受到机身上相应位置安装磁铁的排斥,从而推动离合装置接通,此时无刷电机驱动轮子转动。水下贴壁行走时轮子虽然不受电机驱动,但喷管产生的推力在机身方向的推力可以推动机器人向前行走。
2 H型两栖机器人预约束建模为了方便机器人运动学建模,建立了如图 4所示的固联于机器人的体坐标系和固联于地球的大地坐标系,体坐标系原点位于机器人的重心处[11]。

|
图 4 H型两栖机器人坐标系 Fig. 4 H-type amphibious robot coordinate system |
喷水推进器在水下的推力可以表达为[12]
| $ T_{i}=K_{\mathrm{F}} \rho\left(\frac{D}{1\ 000}\right)^{4} N_{I}^{2} $ | (1) |
式中:Ti为每个推进器的推力,KF为推力系数,ni为叶轮转速传动比,i=1、2、3、4。
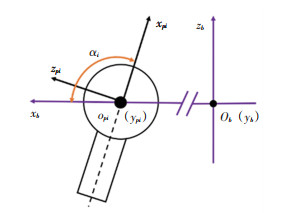
为了描述各个喷管的推力状态,引入如图 5所示的固联于各个喷管坐标系pi: {pi-xpiypizpi},其中xpi与喷管喷口的中心线重合并指向推力产生的方向;ypi与喷管转轴轴线重合并与机体坐标系y轴方向相同;zpi由右手定则判定;αi表示喷管中心线与机体坐标系下xb的夹角。
|
图 5 喷管坐标系 Fig. 5 Nozzle coordinate system |
则在喷管坐标系下,每个喷管所受的推力和力矩可以表达如下:
| $ \boldsymbol{\tau}_{p i}=\left[\begin{array}{l} \boldsymbol{F}_{p i} \\ \boldsymbol{M}_{p i} \end{array}\right]=\left[\begin{array}{llllll} F_{x p i} & F_{y p i} & F_{z p i} & M_{x p i} & M_{y p i} & M_{z p i} \end{array}\right] $ | (2) |
式中: Fpi和Mpi分别为每个喷管所受到的力和力矩。
将喷管坐标系下的力/力矩转换至机体坐标系下,便可以得到如下机器人所受的总力/力矩:
| $ \begin{aligned} &\boldsymbol{\tau}=\sum\limits_{i=1}^{4} \boldsymbol{\tau}_{i}= \\ &{\left[\begin{array}{l} T_{1} \cos \alpha_{1}+T_{2} \cos \alpha_{2}+T_{3} \cos \alpha_{3}+T_{4} \cos \alpha_{4} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \\ -\left(T_{1} \sin \alpha_{1}+T_{2} \sin \alpha_{2}+T_{3} \sin \alpha_{3}+T_{4} \sin \alpha_{4}\right) \\ \left(T_{1} \sin \alpha_{1}+T_{3} \sin \alpha_{3}-T_{2} \sin \alpha_{2}-T_{4} \sin \alpha_{4}\right) \cdot W \\ \left(T_{1} \sin \alpha_{1}+T_{2} \sin \alpha_{2}-T_{3} \sin \alpha_{3}-T_{4} \sin \alpha_{4}\right) \cdot L \\ \left(T_{1} \cos \alpha_{1}+T_{3} \cos \alpha_{3}-T_{2} \cos \alpha_{2}-T_{4} \cos \alpha_{4}\right) \cdot W \end{array}\right]} \end{aligned} $ | (3) |
式中:τi为每个喷管对机身所产生的推力/力矩;W,L分别为机器人长度和宽度的1/2。
2.2 预约束运动建模根据牛顿-欧拉方程, 六自由度水下机器人在体坐标系中的运动方程可描述为[13]:
| $ \boldsymbol{M} \dot{V}+\boldsymbol{C}(v) \boldsymbol{V}+\boldsymbol{D}(v) \boldsymbol{V}+\boldsymbol{G}(\eta)=\boldsymbol{\tau}+\boldsymbol{d} $ | (4) |
式中:M是惯性矩阵;C(v)为科氏力和离心力矩阵;D(v)为水动力阻尼矩阵;G(η)为重力项和浮力项矩阵;τ为机器人驱动力和力矩项矩阵;d为水下机器人受到外部扰动力和力矩项矩阵。
由式(3)、(4)可知,H型两栖机器人在水下运行时是一个非线性动力学系统,控制量有4个转角和4个转速,具有非线性、强耦合和多控制量等特点。为了方便研究,本文将机器人的运动进行分解,分别建立每个独立运动的动力学模型,从而将复杂的模型约束成多个简单模型,使某几个控制量可以合并成同一个控制量。将H型两栖机器人的运动分为沿自身xoz面的平动运动、沿着自身xoz面的俯仰运动和沿自身xoy面的偏转运动。
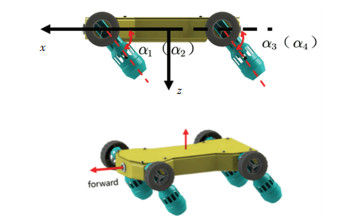
2.2.1 平动运动模式由H型两栖机器人的结构可知,当机器人的4个推进器推力相同,且4个喷管的同步转动时,如图 6所示机器人只受到自身xoz平面的力的作用并且合力矩为零,此时该机器人只能沿着自身xoz面进行平动运动,且自身姿态不会发生任何改变。
|
图 6 平动运动模式 Fig. 6 Translational motion mode |
此时4个喷管的推力被约束为1个变量,4个倾角也被约束为1个变量,即施加的约束为:T1=T2=T3=T4、α1=α2=α3=α4。因此控制量只有转速T和转角α,其动力学模型为
| $ \left\{\begin{array}{l} m \dot{v}_{x}+F_{p x}=\sum\limits_{i=1}^{4} T_{i} \cos \alpha_{i} \\ m{\dot{v}_{z}}+F_{p z}+\left(G-F_{f}\right)=\sum\limits_{i=1}^{4} T_{i} \sin \alpha_{i} \end{array}\right. $ | (5) |
式中:vx, vz分别为自身坐标系下x方向和z方向的速度;Fpx, Fpz分别为机器人在x方向和z方向所受的阻力矩;G为重力;Gf为浮力。
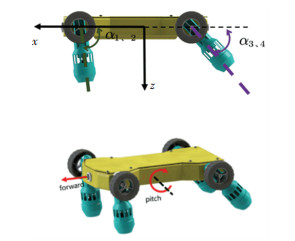
2.2.2 俯仰运动模式当H型两栖机器人的1、2号喷管保持相同的倾转角同步转动并保持相同的推力;3、4号喷管也保持相同的倾转角并保持相同的推力时,机器人的运动为在自身xoz面的平动运动和绕着y轴的转动的叠加,机器人可以在xoz平面进行转向,即俯仰运动如图 7所示。
|
图 7 俯仰运动模式 Fig. 7 Pitch motion mode |
为保证机器人在自身z轴方向不受力,该运动模式的约束为:T1=T2、T3=T4、α1=α2。此时的控制量为2个转角和2个推力,其动力学模型为
| $ \left\{\begin{array}{l} J_{y} \dot{\omega}+M_{p y}=\left(2 T_{1} \sin \alpha_{1}-2 T_{3} \sin \alpha_{3}\right) L \\ m \dot{v}+F_{p x}=2\left(T_{1} \cos \alpha_{1}+T_{3} \cos \alpha_{3}\right) \end{array}\right. $ | (6) |
式中:Jy为绕y轴的转动惯量;Mpy为阻力矩。
若H型两栖机器人在俯仰转向运动中始终满足2(T1sin α1+T3sin α3)=(G-Ff)sin θ,θ为机器人的俯仰角,即在机身坐标系的y轴方向机器人受力为零,则机器人可以做纯圆周运动,其理论转向轨迹为圆形轨迹。
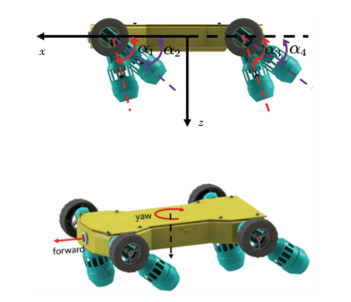
2.2.3 偏转运动模式当H型两栖机器人的1、3号喷管保持相同的倾转角同步转动并保持相同的推力;2、4号喷管也保持相同的倾转角并保持相同的推力时,机器人的运动为沿着x轴的前向运动和绕着z轴的转动的叠加,机器人可以在xoy平面进行转向,即进行偏转运动如图 8所示。
|
图 8 偏转转向模式 Fig. 8 Deflection steering mode |
此时4个喷管的推力被约束为2个变量(1、3号喷管1个;2、4号喷管1个),同理,4个倾角也被约束为2个变量。具体的运动约束为:α1=α3、α2=α4、T1=T3、T2=T4、2(T1sin α1+T2sin α2)=G。此时的控制量为2个转角和2个推力,其运动动力学模型为
| $ \left\{\begin{array}{l} J_{y} \dot{\omega}+M_{p z}=\left(T_{1} \sin \alpha_{1}-T_{2} \sin \alpha_{2}\right) * W \\ m \dot{v}+F_{p x}=2\left(T_{1} \cos \alpha_{1}+T_{2} \cos _{2}\right) \end{array}\right. $ | (7) |
式中:Jz为绕z轴的转动惯量;Mpz为z轴转动阻力矩。
3 姿态自抗扰控制 3.1 推力倾转角分离控制策略在每一时刻,上层控制器根据运动模型给出指令推力Tdi和指令转角αdi,然后推进器电机和喷管电机转动,喷管获得实际推力Ti和转角αi,旋转角度可由传感器直接观测,因此αdi=αi;而推力则无法直接观测,因此Tdi≠Ti。因此实际推力与指令推力有一定的误差,而且水下环境扰动较多,因此机器人实际姿态与理论姿态之间会有一定的偏差。为保持姿态的稳定,需要机器人所受地矢量驱动力进行调节进。
由式(3)可以看出,调节推力T或者倾转角都能够改变机器人所受的矢量力。由于推力和倾转角是以乘积的形式出现,因此如果对二者同时进行调节需要对二者的权重系数,不同的运动状态下权重系数可能是不同的,因此若对推力和倾转角度进行同时调节会导致控制系统过于复杂,不利于实际应用。
从机器人的结构特征来说,推力的变化需要叶轮转速的增加或者减少,相对于倾转角调节来说,其调整过程相对柔和,因此在应对由于小扰动下导致的姿态抖动问题时,对推力进行调节更加合理。
机器人的姿态控制方程可以写成如下式子:
| $ \left\{\begin{array}{l} \ddot{\phi}=\dot{\theta} \dot{\psi}\left(\frac{i_{y}-i_{z}}{i_{x}}\right)+\frac{W}{i_{x}} u_{1}+d_{\phi} \\ \ddot{\theta}=\dot{\phi} \dot{\psi}\left(\frac{i_{z}-i_{x}}{i_{y}}\right)+\frac{L}{i_{y}} u_{2}+d_{\theta} \\ \ddot{\psi}=\dot{\theta} \dot{\phi}\left(\frac{i_{x}-i_{y}}{i_{z}}\right)+\frac{W}{i_{z}} u_{3}+d_{\psi} \end{array}\right. $ | (8) |
式中:u1=T1sin α1+T3sin α3-T2sin α2-T4sin α4,u2=T1sin α1+T2sin α2-T3sin α3-T4sin α4,u3=T1cos α1+T3cos α3-T2cos α2-T4cos α4;[dϕdθdψ]分别为横滚、俯仰和偏转姿态上的干扰,包括阻力矩、回复力矩和干扰力矩。
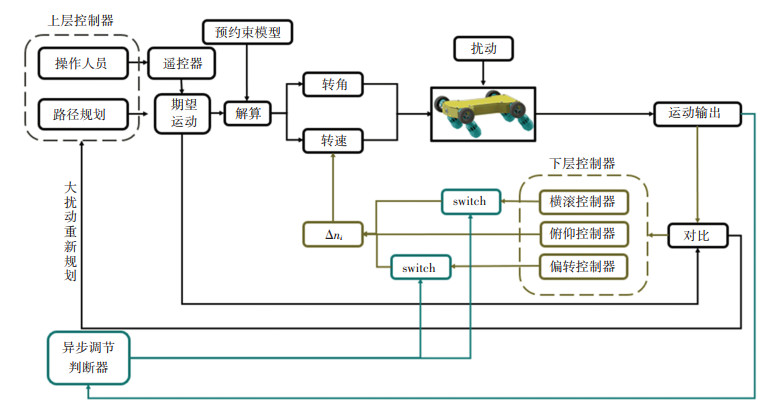
综上,基于推力调节的H型两栖机器人的姿态稳定框架如图 9所示。姿态调节的过程为:上层控制器根据当前的状态给机器人发送推力和转角信号,即初始的输出
|
图 9 推力与倾转角分离控制策略 Fig. 9 Thrust and tilt angle separation control strategy |
由公式(8)可以看出,横滚通道与偏转通道相互耦合,若对2个方向同时进行调整会对导致调整效果被抵消,因此横滚角与偏转角需要采用异步方式进行调节。两栖机器人的偏转角会对机器人的运行轨迹产生较大影响,且两栖机器人在横滚方向受到由重心与浮心位置不重合导致的恢复力矩作用,因此应该优先稳定偏转角,在偏转角已经限制在可接受范围内,并且横滚角超出允许值时转到横滚角调节。所以,异步调节开启的条件如下:eϕ>ed且eϕ>eψ,其中eϕ, eψ、ed分别为横滚角偏差、俯仰角偏差以及最大允许偏差。
由以上分析可知,H型两栖机器人的姿态受外部干扰、建模误差、未建模动态等扰动的影响。是否能有效处理扰动的影响是H型两栖机器人在水下保持姿态稳定的前提,而自抗扰控制相对于传统的反馈控制律可以在模型不准确的情况下利用扩张状态观测器有效地处理干扰扰动,因此本文采用自抗扰控制方法来保证机器人每一时刻姿态的稳定性。
3.2 控制模型建立令
| $ \left\{\begin{array}{l} \dot{\boldsymbol{X}}_{1}=\boldsymbol{X}_{2} \\ \dot{\boldsymbol{X}}_{2}=\boldsymbol{B} \boldsymbol{u}+\boldsymbol{D} \\ \boldsymbol{Y}=\left[\begin{array}{ll} y_{1}\ \ y_{2}\ \ y_{3} \end{array}\right]^{\mathrm{T}}=\boldsymbol{X}_{1} \end{array}\right. $ | (9) |
式中:u =[u1 u2 u3]T为控制输入信号;Y =[y1 y2 y3]T为输出向量;D =[d1 d2 d3]T为系统输入系数矩阵。D向量和B矩阵可以表达如下
| $ \boldsymbol{D}=\left[\begin{array}{l} \dot{\theta} \dot{\psi}\left(\frac{i_{y}-i_{z}}{i_{x}}\right)+d_{\phi} \\ \dot{\phi} \dot{\psi}\left(\frac{i_{z}-i_{x}}{i_{y}}\right)+d_{\theta} \\ \dot{\theta} \dot{\phi}\left(\frac{i_{x}-i_{y}}{i_{z}}\right)+d_{\psi} \end{array}\right] $ |
| $ \boldsymbol{B}=\left[\begin{array}{ccc} W / i_{x} & 0 & 0 \\ 0 & L / i_{y} & 0 \\ 0 & 0 & W / i_{z} \end{array}\right] $ |
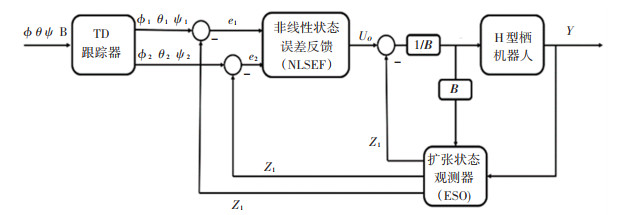
自抗扰控制算法是一种非线性控制算法,其吸取了PID控制算法“基于误差来消除误差”的控制思想,但在PID控制算法基本思想的基础上,增加了跟踪微分器TD、非线性反馈控制律和扩张状态观测器等3个环节[11]。典型的自抗扰控制结构如图 10所示。
|
图 10 自抗扰控制结构 Fig. 10 Active disturbance rejection control structure |
跟踪微分器不仅可为系统的期望输入信号安排过渡过程,而且也可获得高信噪比的期望输入信号的微分信息。本文设计的跟踪微分器如下:
| $ \left\{\begin{array}{l} \dot{\phi}_{1}=\dot{\phi}_{2} \\ \dot{\phi}_{2}=\text { fhan }\left(\dot{\phi}_{1}-\dot{\phi}_{0}, \dot{\phi}_{2}, r_{0}, h_{0}\right) \\ \dot{\theta}_{1}=\theta_{2} \\ \dot{\theta}_{2}=\text { fhan }\left(\theta_{1}-\theta_{0}, \theta_{2}, r_{0}, h_{0}\right. \\ \dot{\psi}_{1}=\psi_{2} \\ \psi_{2}=\text { fhan }\left(\psi_{1}-\psi_{0}, y_{2}, r_{0}, h_{0}\right) \end{array}\right. $ | (10) |
式中:ϕ0, θ0, ψ0, ϕ1, θ1, ψ1, ϕ2, θ2, ψ2分别为机器人的滚转角、俯仰角和偏航角的期望值、跟踪值和微分跟踪值;r0为跟踪微分器的快速因子;h0为跟踪微分器的滤波因子;fhan为最速控制综合函数。记fsg(x, d)=(sign(x+d)-sign(x-d))/2,则fhan的定义为对fh=fhan(x1, x2, r, h)有
| $ \left\{\begin{array}{l} d=r h^{3} \\ a_{0}=h x_{2} \\ y=x_{1}+a_{0} \\ a_{1}=\sqrt{d(d+8|y|)} \\ a_{2}=a_{0}+\operatorname{sign}(y)\left(a_{1}-d\right) / 2 \\ a=\left(a_{0}+y\right) \mathrm{fsg}(y, d)+a_{2}(1-\mathrm{fsg}(y, d)) \\ a=\left(a_{0}+y\right) \mathrm{fsg}(y, d)+a_{2}(1-\mathrm{fsg}(y, d)) \\ \mathrm{fh}=-r(a / d) \mathrm{fsg}(a, d)-r \cdot \operatorname{sign}(a)(1-\mathrm{fsg}(a, d)) \end{array}\right. $ |
状态观测器将影响被控对象输出的扰动作用扩张成新的状态变量,通过特殊的反馈机制观测被扩张的总扰动信号。将式(10)增广为
| $ \left\{\begin{array}{l} \dot{\boldsymbol{X}}_{1}=\boldsymbol{X}_{2} \\ \dot{\boldsymbol{X}}_{2}=\boldsymbol{X}_{3}+\boldsymbol{B} \boldsymbol{u} \\ \dot{\boldsymbol{X}}_{3}=\left[h_{1}(t)\ \ h_{2}(t)\ \ h_{3}(t)\right]^{\mathrm{T}} \\ \boldsymbol{Y}=\left[\begin{array}{ll} y_{1}\ \ y_{2}\ \ y_{3} \end{array}\right]^{\mathrm{T}} \end{array}\right. $ | (11) |
式中:X3= D为扩张后的扰动观测项;h1(t)、h2(t)、h3(t)分别为横滚、俯仰和偏航方向干扰函数。
非线性扩张状态观测器可对系统的总扰动进行估计,系统(7)非线性扩张状态观测器可设计为
| $ \left\{\begin{array}{l} \boldsymbol{e}=\left[e_{1}\ \ e_{2}\ \ e_{3}\right]^{\mathrm{T}}=\boldsymbol{Z}_{1}-\boldsymbol{Y} \\ \dot{\boldsymbol{Z}}_{1}=\boldsymbol{Z}_{2}-\boldsymbol{\beta}_{1} \boldsymbol{e} \\ \dot{\boldsymbol{Z}}_{2}=\boldsymbol{Z}_{3}-\boldsymbol{\beta}_{2}\left[\operatorname{fal}\left(e_{1}, \alpha_{01}, \delta\right) \quad \mathrm{fal}\left(e_{2}, \alpha_{01}, \delta\right) \quad \mathrm{fal}\left(e_{3}, \alpha_{01}, \delta\right)\right]^{\mathrm{T}}+\boldsymbol{B} \boldsymbol{u} \\ \dot{\boldsymbol{Z}}_{3}=-\boldsymbol{\beta}_{3}\left[\operatorname{fal}\left(e_{1}, \alpha_{02}, \delta\right) \quad \text { fal }\left(e_{2}, \alpha_{02}, \delta\right) \quad \operatorname{fal}\left(e_{3}, \alpha_{02}, \delta\right)\right]^{\mathrm{T}} \end{array}\right. $ | (12) |
式中:e为机器人的滚转角、俯仰角和偏航角的误差向量;Z1, Z2, Z3机器人的滚转角、俯仰角和偏航角的观测向量,微分观测向量和扰动观测向量;β1=diag[β11 β12 β13], β2=dia[β21 β22 β23], β3=diag[β31 β32 β33], 为非线性扩张状态观测器的增益矩阵;α01, α02为需要自行调节的观测器参数。非线性fal函数的形式如下:
| $ \operatorname{fal}(e, a, \delta)= \begin{cases}|e|^{a} \operatorname{sign}(e),\ \ |e|>\delta \\ e / \delta^{1-\alpha}, \ \ \ \ \ \ |e| \leqslant \delta\end{cases} $ |
根据跟踪微分器得出的给定信号和给定信号的微分与状态观测器观测到的系统输出和输出的导数的误差,进而进行控制和扰动补偿,基于“小误差大增益,大误差小增益”的设计思路,可以避免系统进入饱和状态,同时保持系统对误差敏感。非线性反馈控制器如下:
| $ \left\{\begin{array}{l} e_{1 \phi}=\phi_{1}-z_{1 \phi}, e_{2 \phi}=\phi_{2}-z_{2 \phi} \\ u_{1}=-\text { fhan }\left(e_{1 \phi}, c \cdot e_{2 \phi}, r, h\right)-z_{3 \phi} \\ e_{1 \theta}=\theta_{1}-z_{1 \theta}, e_{2 \theta}=\theta_{2}-z_{2 \theta} \\ u_{2}=-\text { fhan }\left(e_{1 \theta}, c \cdot e_{2 \theta}, r, h\right)-z_{3 \theta} \\ e_{1 \psi}=\psi_{1}-z_{1 \psi}, e_{2 \psi}=\psi_{2}-z_{2 \psi} \\ u_{3}=-\text { fhan }\left(e_{1 \psi}, c \cdot e_{2 \psi}, r, h\right)-z_{3 \psi} \end{array}\right. $ | (13) |
式中:[e1ϕ e1θ e1ψ]分别为横滚角、俯仰角和偏转角的误差;[e2ϕ e2θ e2ψ]分别为横滚角、俯仰角和偏转角的误差的导数;c为相应的控制参数。
3.3.4 异步调节器设计由于横滚角与偏转角的姿态相互耦合,若在时间上同步对2个姿态进行调节,可能在一个姿态角的调稳过程极有导致另外一个姿态角失稳,因此必须对这2个姿态角在时间上进行分别调节。异步调节器设计如下:
1)
| $ \left\{\begin{array}{l} \text {当 } e_{1 \phi}>e_{1 \psi} \text { 且 } e_{1 \phi}<a_{x} \text { 时, } \\ u_{1}=-\operatorname{fhan}\left(e_{1 \phi}, c \cdot e_{2 \phi}, r, h\right)-z_{3 \phi} \\ u_{3}=0 \\ \text {其他 } \\ u_{1}=0 \\ u_{3}=-\operatorname{fhan}\left(e_{1 \psi}, c \cdot e_{2 \psi}, r, h\right)-z_{3 \psi} \end{array}\right. $ | (14) |
式中:ax为平动模式下偏转角的最大允许误差。
在平动模式下,相对于横滚扰动机器人偏转角的扰动会导致机器人的运动更大程度的偏离期望运动,且由于流体的对机器人机身的回复力矩,机器人在横滚方向具有一定的自平衡能力,因此在该模式下应该优先调节偏转角。只有当偏转角度偏差小于允许误差且小于横滚角度偏差时再进行横滚角度调节。
2)
| $ \left\{\begin{array}{l} \text {当 } e_{1 \phi}>e_{1 \psi} \text { 且 } e_{1 \psi}<a_{y} \text { 时, } \\ u_{1}=-\operatorname{fhan}\left(e_{1 \phi}, c \cdot e_{2 \phi}, r, h\right)-z_{3 \phi} \\ u_{3}=0 ; \\ \text {其他 } \\ u_{1}=0 \\ u_{3}=-\operatorname{fhan}\left(e_{1 \psi}, c \cdot e_{2 \psi}, r, h\right)-z_{3 \psi} \end{array}\right. $ | (15) |
式中:ay为平动模式下偏转角的最大允许误差。
在俯仰模式下,2个姿态角的调节优先级与平动模式一致,只是由于机器人的期望姿态与平动模式不同,因此最大允许误差的数值是不同的。
3)
| $ \left\{\begin{array}{l} u_{1}=-\operatorname{fhan}\left(e_{1 \phi}, c \cdot e_{2 \phi}, r, h\right)-z_{3 \phi} \\ u_{3}=0 \end{array}\right. $ | (16) |
在偏转模式下,根据控制框架,偏转角度由喷管倾转角度进行控制,因此不要对其进行推力调节,在该模式下只调节横滚角。
4 姿态控制仿真和实验验证 4.1 姿态控制仿真由上文可知,自抗扰算法的可调参数较多。通过软件仿真不仅可以验证所提算法的有效性,而且还可获得具有较好调节效果的参数,为后续实验提供支持。为使理论模型更接近实际模型,首先在ADAMS中建立H型两栖机器人的实际模型,并给定关节约束;然后,借助ADAMS与Simulink间的数据交互接口实现在simulink中建立的自抗扰姿态控制器,控制ADAMS中的H型两栖机器人动力学模型。
ADAMS中的H型两栖机器人的重量为6.5 kg,长度2L=425 mm,宽度2W=220 mm。忽略喷管重量后的惯性张量(单位:kg·mm2)为:Ixx=23 132.4;Iyy=110 311.8;Izz=90 149.2,非对角部分为0。经过整定后的控制器参数如下:扩张状态观测器增益系数β1=β2=β3=[30 300 1 000];跟踪微分器参数h=0.001,r0=0.5;非线性控制参数c=3。参数确定后,对平动运动模式、俯仰运动模式、偏转运动模式分别进行仿真,每一个通道下对3个姿态角分别施加一个占空比为0.5 s的矩形脉冲,大小分别为5 N·m、8 N·m和15 N·m。
为了解决横滚角调节与偏转角调节互相耦合的问题,仿真时优先调节偏转角;当横滚角偏差与偏转角偏差满足e1>e3且e3 < 0.5°时,再开启横滚角调节,关闭偏转角调节。总的仿真时间为10 s,平动运动模式下保持3个姿态角都为0°;俯仰模式和偏转模式下使机器人在输入力的作用下分别沿自身y轴和z轴转动10°。同时,为了模拟平动运动模式下喷管转动带来的影响,本文使4个喷管同步以6(°)/s的速度转动。为了模拟俯仰运动模式下切换冲击,俯仰运动模式下在开始瞬间迅速使1、2号喷管转动到60°角的位置,而3、4号喷管转动到30°角的位置;偏转运动模式下在开始的一瞬间迅速使1、3号喷管转动到60°角的位置,2、4号喷管转动到30°角的位置。
如图 11所示分别为本文提出的姿态自抗扰控制和PID控制作用下的姿态跟踪轨迹曲线。如图 11所示,在受到给定扰动冲击时机器人的姿态都会偏离期望值,但在本文提出的姿态自抗扰控制器的作用下会在1 s内跟踪上期望值。相对于PID调节,本文提出的姿态自抗扰控制器作用下的最大偏离角度误差更小、轨迹跟踪曲线波动更小且能够在没有超调的情况下更快地恢复至平衡点附近。这说明了自抗扰控制中的跟踪微分器和非线性反馈控制器可以有效处理快速性和超调之间的矛盾,在受到冲击时本文提出的姿态自抗扰控制器相对于传统PID控制器具有更快的响应效果。图 11(b)和图 11(c)在开始时姿态会有一定的波动而图 11(a)始终保持稳定,这说明喷管匀速稳定的动作几乎不会对姿态产生影响,而快速的运动模式切换动作会对机器人的姿态产生一定的影响,但这种影响会在控制器的作用下快速恢复至平衡点。由于对横滚角和偏转角采用了分时异步调节机制,使得如图 11所示横滚角和偏转角会在跟踪值附近轻微波动,波动数值小于0.5°。

|
图 11 姿态自稳定控制仿真结果 Fig. 11 Simulation results of attitude self-stabilization control |
如图 12所示为扩张状态观测器观测的扰动观测效果。虽然图 12中观测值和实际施加的数值有一定的偏差,但是偏差值在极短的时间内趋近于零,观测值快速地跟踪上实际值。观测得到的波形与实际的冲击波形有一定的区别,这是由于矩形冲击施加的时间极短,且所有物理系统都具有延时性导致的。但是,实际值和跟踪值所包围的面积是相同的,即2种波形对系统的作用是相同的,这表明扩张状态观测器是在系统层面利用反馈对干扰进行观测的。

|
图 12 扰动观测效果 Fig. 12 Observation effect of disturbance |
图 13为异步调节器的状态,数值为1表示调节偏转角,数值为0表示横滚角调节。从图中可以看出,在z轴方向上的干扰作用后,横滚和偏转方向的姿态调节器会快速的开启和关闭,但偏转方向的总调节时间大于横滚方向,这是因为本次仿真设置为优先调节偏转角所致。从图 11的跟踪结果中可以看出,横滚角和偏转角会在期望值附近以微小的幅度波动且幅度不超过0.5°,这说明异步调节方式可以在产生可接受波动下有效地处理2个自由度的耦合问题。

|
图 13 异步调节器状态 Fig. 13 Asynchronous regulator state |
制作了如14所示的物理样机,并实验验证了样机结构和控制算法的可行性。实验样机的尺寸与ADAMS中的模型一致,采用ARDUINO2560进行控制,姿态传感器为MPU6050,叶轮使用1 800 kV的无刷电机驱动,喷管采用用舵机驱动。为了解决ARDUINO控制板无法多线程编程的问题,本文采用定时器中断的方式每隔0.01 s读取一次姿态传感器数据,并且使用串口总线控制舵机同步运动。

|
图 14 物理样机 Fig. 14 Physical prototype |
虽然仿真中已经整合出较优的控制器参数,但实验样机与仿真模型存在一定的误差,因此在实验样机进行水下运动之前首先设计三自由度实验平台测试出较优的控制器参数。三自由度实验平台如图 15所示。实验平台包括4个部分:固定支架、三自由度铰链、实验水池和H型两栖机器人本体。球铰允许最大±40°的横滚和俯仰运动,360°的偏转运动。固定支架置于水池上方,H型两栖机器人置于水池内部并完全浸入水中,支架和两栖机器人之间通过三自由度球铰连接,通过向水池底部的多空管道注水模拟扰动。

|
图 15 姿态控制实验平台 Fig. 15 Attitude control experimental platform |
进行姿态控制器验证时,使用自抗扰姿态控制器对机器人在水下运行的3种模式进行姿态控制,并采用所提的异步调节策略。使用MPU6050记录机身的姿态数据。为了验证喷管转角突变或者转速突变给姿态稳定带来的影响,每隔约2 s改变一次喷管的转角以及电机的转速,且异步调节的阈值设定为4°。多次实验后获得的具有较好控制效果的控制器参数为:扩张状态观测器增益系数β1=β2=β3=[30 300 1 500];跟踪微分器参数h=0.002,r0=0.5;非线性控制参数c=3。
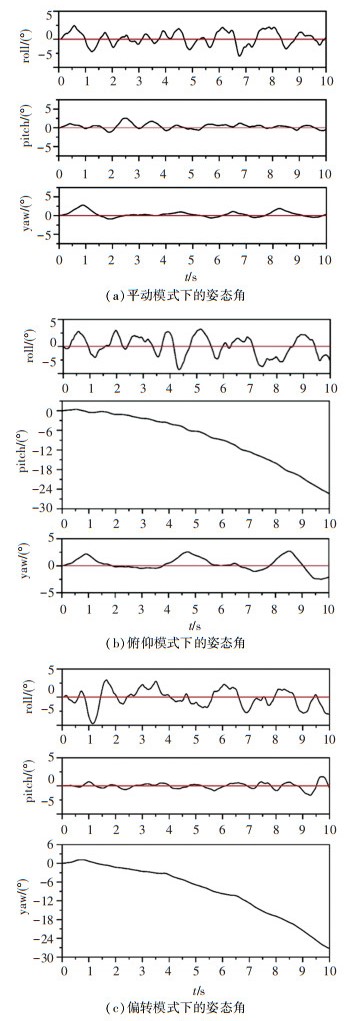
分别截取3种运动模式下10 s内的姿态曲线,并滤除漂移点后,可以得到如图 16所示为水下运动实验数据。从实验结果可以看出,在每种运动模式下自抗扰控制器都能够将机器人的姿态抖动幅度限制在5°内。横滚角的波动幅度相对于另外2个姿态角较大,但基本不会超过异步调节器的设定阈值。在每次手柄调节时由于控制量的变化不够稳定,导致该时间点姿态控制器计算出的调节量的根据是上一时刻的转角,进而导致调节不准,并且喷管的转动会带来震动。这2个因素都会引起机器人姿态角产生一定的抖动,但抖动仍可以稳定在5°内,并能很快恢复至平衡位置。
|
图 16 水下实验结果 Fig. 16 Underwater test results |
最后将机器人置于开方水域中进行水下航行实验,从图 17中可以看出,机器人能够稳定地运进行平动、俯仰和偏转运动。通过测量可以得到机器人在水下的最大直线速度为1.2 m/s,最小俯仰转向半径为0.2 m,最小偏转半径可以降低至0 m,具有较快的速度和较高的机动性。

|
图 17 水下运动实验 Fig. 17 Underwater motion experiment |
1) 为实现水陆两栖共存环境下的巡检工作,本文设计了一种轮泵复合式两栖驱动装置,进而创新设计了H型两栖机器人,并且最后的样机实验结果表明该机器人能够完成水下浮游、俯仰、偏转等预设运动。
2) 基于自抗扰控制策略和分层控制思想设计了该机器人姿态自稳定控制器,通过识别并补偿干扰来维持机体的姿态稳定,同时在2个耦合的自由度方向上采用异步调节,能够将姿态误差维持在5°以内。仿真和实验结果表明,本文提出的H型两栖机器人可以实现预设的运动,相对于其他水陆两栖机器人采用的PID控制算法,本文提出的基于自抗扰控制的姿态稳定算法可以更有效地维持机器人姿态稳定,并具有更快的稳定速度。
3) 本文研究内容对采用可倾转推进器的水下机器人的设计与控制具有一定的参考价值。
| [1] |
REN K, YU J. Research status of bionic amphibious robots: a review[J]. Ocean Engineering, 2021, 227: 108862. DOI:10.1016/j.oceaneng.2021.108862 |
| [2] |
RAFEEQ M, TOHA S F, AHMAD S, et al. Locomotion strategies for amphibious robots—a review[J]. IEEE Access, 2021, 9: 26323. DOI:10.1109/ACCESS.2021.3057406 |
| [3] |
XING H, GUO S, SHI L, et al. Design, modeling and experimental evaluation of a legged, multi-vectored water-jet composite driving mechanism for an amphibious spherical robot[J]. Microsystem Technologies, 2020, 26(2): 475. DOI:10.1007/s00542-019-04536-7 |
| [4] |
王常龙, 马新谋, 何自力, 等. 轮桨混合驱动两栖侦察车设计及轮桨分析[J]. 兵器装备工程学报, 2019, 40(2): 71. WANG Changlong, MA Xinmou, HE Zili, et al. Design and analysis of wheel propeller hybrid driving amphibious reconnaissance vehicle[J]. Journal of Ordnance Equipment Engineering, 2019, 40(2): 71. DOI:10.11809/bqzbgcxb2019.02.015 |
| [5] |
何彦霖, 董明利, 孙广开, 等. 复合式驱动小型两栖机器人水下运动控制研究[J]. 仪器仪表学报, 2019, 40(1): 219. HE Yanlin, DONG Mingli, SUN Guangkai, et al. Research on underwater motion control of hybrid driven small amphibious robot[J]. Acta Instrumenta Sinica, 2019, 40(1): 219. |
| [6] |
XU R, TANG G, HAN L, et al. Robust finite-time attitude tracking control of a CMG-based AUV with unknown disturbances and input saturation[J]. IEEE Access, 2019, 7: 56409. DOI:10.1109/ACCESS.2019.2914068 |
| [7] |
罗庆生, 刘星栋, 弓瑞, 等. 矢量喷水推进式水下机器人的建模仿真与验证[J]. 应用科技, 2017, 44(2): 7. LUO Qingsheng, LIU Xingdong, GONG Rui, et al. Modeling, simulation and verification of vector water jet propulsion underwater vehicle[J]. Applied Science and Technology, 2017, 44(2): 7. |
| [8] |
王涛, 吴超, 葛彤. 负浮力四倾转推进器水下机器人姿态跟踪控制[J]. 舰船科学技术, 2020, 42(3): 98. WANG Tao, WU Chao, GE Tong. Attitude tracking control of AUVs with negative buoyancy four tilt thrusters[J]. Ship Science and Technology, 2020, 42(3): 98. |
| [9] |
JIN S, KIM J, KIM J, et al. Six-degree-of-freedom hovering control of an underwater robotic platform with four tilting thrusters via selective switching control[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2370. DOI:10.1109/TMECH.2014.2378286 |
| [10] |
ZHONG S, HUANG Y, GUO L. A parameter formula connecting PID and ADRC[J]. Science China(Information Sciences), 2020, 63(09): 175. |
| [11] |
MAI T V, VAN M, HONG P B, et al. Study on dynamic behavior of unmanned surface vehicle-linked unmanned underwater vehicle system for underwater exploration[J]. Sensors, 2020, 20(5): 1329. DOI:10.3390/s20051329 |
| [12] |
徐文龙, 陈原, 郭登辉, 等. 轮泵复合式两栖驱动方法[J]. 哈尔滨工业大学学报, 2020, 52(7): 153. XU Wenlong, CHEN Yuan, GUO Denghui, et al. Compound amphibious driving method of wheel pump[J]. Journal of Harbin Institute of Technology, 2020, 52(7): 153. |
| [13] |
CHO G R, LI J H, PARK D, et al. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation[J]. Ocean Engineering, 2020, 201: 107131. DOI:10.1016/j.oceaneng.2020.107131 |
 2022, Vol. 54
2022, Vol. 54


