2. 中国建筑科学研究院 建筑机械分院,河北 廊坊 065000;
3. 德州海天机电科技有限公司,山东 德州 253000
2. Institute of Building Mechanization, China Academy of Building Research, Langfang 065000, Hebei, China;
3. Dezhou Haitian Electromechanical Technology Co., Ltd., Dezhou 253000, Shandong, China
装配式建筑因其“高效、经济、环保”的特点,成为建筑领域的发展热点,而预制混凝土构件的生产制作是装配式建筑的重要环节[1-2]。目前,国内外预制混凝土构件生产以人工操作螺旋布料机进行布料,布料路径完全由工人自主决定,作业过程中存在的布料路径重复、布料量不足或过多、混凝土浪费等现象,严重制约着预制混凝土构件标准化、自动化生产的发展。对布料路径进行规划可以缩短布料作业时间、减少混凝土浪费和改善生产车间环境等,可以有效地提高预制混凝土构件的生产效率。因此,开展预制混凝土构件布料路径规划研究有着重要的意义。
预制混凝土构件布料区域为规则边界的多边形,螺旋布料机在布料作业时需要遍历布料区域内的所有位置,以路程最短、时间最少、布料充足等为指标。因此,布料路径规划属于全覆盖路径规划研究范畴。全覆盖路径规划研究主要集中在扫地机器人[3-5]、搜寻机器人[6-10]、农业机器人[11-12]、激光切割[13-15]等领域[16-20]。主要思路为区域分解,然后利用优化算法求得最佳解,并做相关的改进。针对布料区域内混凝土浇筑量的问题,业内的研究方向主要集中在混凝土输送量的影响因素[21]、混凝土浇筑量的预报与测量[22-24]、浇筑量的补偿控制方法[25]等方面。
现阶段预制混凝土构件生产中自动化程度极低,在生产过程和生产方法上有着很大的进步空间[26]。由于螺旋布料机出料口状态可控,导致布料宽度不确定,为此,本文提出一种将布料区域分割为多个布料子区域的方法,螺旋布料机对布料子区域布料作业一次即可完成子区域的布料任务。随后建立布料路径规划模型,以非布料长度最短为目标进行求解,完成对布料区域的全覆盖路径规划。最后利用Matlab软件建立某螺旋布料机和某外墙挂板结构层的二维布料路径规划模型,进行布料路径规划。
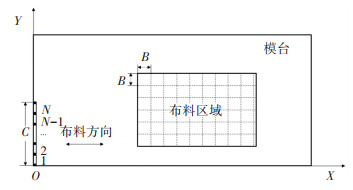
1 分割布料区域 1.1 布料区域网格划分图 1为PC构件厂内螺旋布料机出料口及模台简化后的俯视图,模台的左下角为坐标原点;布料机出料口的宽度为b(mm),相邻出料口的距离为s(mm),出料口开口方向为X轴正方向。在N个出料口都参与布料的状态下,最大布料宽度为C(mm),即单个出料口在模台Y轴方向上的布料宽度为C/N(mm);混凝土从出料口挤出并受重力落在模台上,取螺旋布料机静止状态下单个出料口在模台上的布料范围为边长是B=C/N(mm)的正方形区域,对布料区域进行网格划分。
|
图 1 出料口及模台简化俯视图 Fig. 1 Simplified top view of discharge port and mold table |
预制混凝土构件的布料区域是由直线段或曲线段组成的复杂多边形,同一预制混凝土构件的布料区域是连续的。螺旋布料机在一趟布料作业行程中,参与作业的出料口数量越多,布料面积就越大,布料总时间就会越短。为方便布料路径规划研究,需对布料区域进行分割,具体的分割步骤如下:
Step 1 在Y轴正方向上,与布料区域下边界宽度为螺旋布料机最大布料宽度C的位置处划分一条平行于X轴的分割线X1(布料区域的宽度大于螺旋布料机最大布料宽度C的情况下,否则在Y轴方向不进行分割线的划分)。
Step 2 在Y轴负方向上,与布料区域上边界宽度为螺旋布料机最大布料宽度C的位置处划分另一条平行于X轴的分割线X2(布料区域宽度大于2倍螺旋布料机最大布料宽度C的情况下)。
Step 3 在分割线X1和X2之间的Y轴正方向上,距离X1为C的整数倍,继续在布料区域内划分平行于X轴的分割线(布料区域宽度大于3倍螺旋布料机最大布料宽度C的情况下);当两条分割线之间的距离d小于最大布料宽度C时,不再进行分割线的划分。
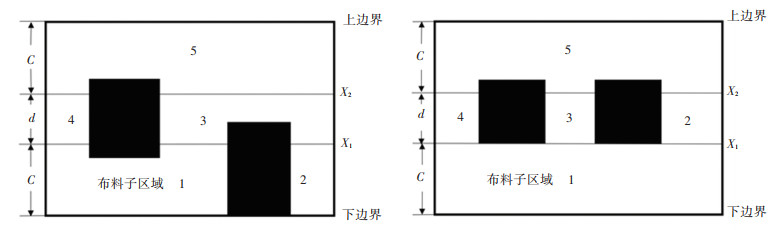
Step 4 在布料区域的上、下边界线和分割线中,如果相邻两条线之间的布料区域是连续的,就认定该区域为一个布料子区域;如果相邻两条线之间的布料区域会被非布料区域完全分割,该区域内就会包含多个布料子区域,且该区域内的布料子区域之间是不连续的。图 2为对某预制构件布料区域的分割情况。
|
图 2 布料区域分割 Fig. 2 Cloth segmentation |
通过此方法分割的布料子区域宽度不超过C,而宽度小于出料口宽度b的布料子区域,混凝土会落在边模上引起浪费,将不再认定为一个布料子区域,所以此分割原则下布料子区域的宽度在区间[b,C]内。
1.3 子区域布料作业规划在图 1中,螺旋布料机在初始位置时,出料口两端顶点D1, 0和DN, 0的坐标为:(0,0)和(0,C)。如图 3所示,利用矩形区域的4个顶点RA, i、RB, i、RC, i和RD, i来表示布料子区域Ri (i=1, 2, …, m,m为布料子区域的数量)在模台上的位置,坐标分别用(xi, 1,yi, 1)、(xi, 2,yi, 1)、(xi, 2,yi, 2)和(xi, 1,yi, 2)表示;布料子区域左边线下顶点DA, i和上顶点DD, i的坐标为:

|
图 3 布料子区域 Fig. 3 Cloth sub-area |
螺旋布料机对布料子区域的作业方式为:从布料起始位置(布料子区域的左边线或右边线)出发,沿X轴正方向或负方向进行布料作业,到达布料终止位置(布料子区域的左边线或右边线中某一边为布料起始位置后,另一边将自动作为布料终止位置)后,就表示完成了此子区域的布料任务。布料过程中会涉及部分出料口的开闭,到达布料终止位置后出料口会全部闭合。
取决于螺旋布料机出料口的几何设计,出料口开口数对应的布料宽度是:
1) 出料口的开口数为n(1≤n < N,n为自然数)时,布料宽度范围是[nb,(n+1)b+ns);
2) 出料口的开口数为N时,布料宽度范围是[Nb+(N-1)s,C]。
2 布料路径规划模型建立与求解螺旋布料机对预制混凝土构件的布料作业路径可分为两部分:一是螺旋布料机在布料子区域内浇筑混凝土时的布料长度L1,二是螺旋布料机未浇筑混凝土状态下遍历所有布料子区域时的非布料长度L2,其中布料长度L1是确定的。本节利用枚举法和动态规划算法,对螺旋布料机出料口和布料子区域集合建立布料路径规划模型的基础上,以非布料长度L2最短为目标对模型进行求解,从而完成了对布料区域的全覆盖路径规划。
2.1 布料路径规划模型建立1) 枚举布料作业顺序:
| $ q = m \times \left( {m - 1} \right) \times \cdots 2 \times 1 $ | (1) |
式中:m为布料子区域的数量,q表示m个布料子区域存在的枚举结果数。基于枚举法对布料子区域进行排列顺序枚举,枚举结果Ui(i =1, 2, …, q)代表螺旋布料机对布料子区域的作业顺序。
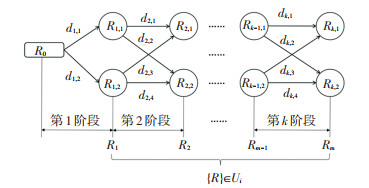
2) 相对最短非布料长度建模。动态规划是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推的方式去解决,从而获得问题的最优解[27-28]。图 4是多阶段决策过程示意图,m个布料子区域对应m个阶段,用k(取自然数1,2,…,m)表示,阶段变量R1,R2,…,Rm代表布料子区域。
|
图 4 多阶段决策过程示意图 Fig. 4 Schematic diagram of multi-stage decision-making process |
1) 第1阶段:起始状态集为s1={R0},允许决策集合为D1(s1)={R1, 1, R1, 2}。
状态变量R0:螺旋布料机出料口的初始位置。
D1, 1:螺旋布料机从初始位置到R1, 1的距离。
D1, 2:螺旋布料机从初始位置到R1, 2的距离。
2) 第2阶段:起始状态集为s2={R1, 1, R1, 2},允许决策集合为D2(s2)={R2, 1, R2, 2}。
状态变量R1, 1:R1布料子区域的左边线。
状态变量R1, 2:R1布料子区域的右边线。
D2, 1:螺旋布料机从布料子区域R1的右边线到布料子区域R2左边线的距离。
D2, 2:螺旋布料机从布料子区域R1的右边线到布料子区域R2右边线的距离。
D2, 3:螺旋布料机从布料子区域R1的左边线到布料子区域R2左边线的距离。
D2, 4:螺旋布料机从布料子区域R1的左边线到布料子区域R2右边线的距离。
3) 其他阶段的的定义规则与第2阶段相同,这里不做具体解释。
关于决策值Dk, j的计算如下:
| $ D_{k, j}=\left\{\begin{array}{l} \left|D_{N, i-1}^{\prime} D_{N, i}\right| \\ \left|D_{1, i-1}^{\prime} D_{1, i}\right| \end{array}, k=i=1, 2, \cdots, m, j=1, 2, 3, 4\right. $ | (2) |
式中,DN, i(i=1, 2, …, m)为编号为N的出料口在第i个布料子区域布料起始位置时的坐标(xi,yi+C),D1, i为编号为1的出料口在第i个布料子区域布料起始位置时的坐标(xi,yi);D′N, i为编号为N的出料口在第i个布料子区域布料终止位置时的坐标(x0, i,y0, i+C,D′1, i)为编号为1的出料口在第i个布料子区域布料终止位置时的坐标(x0, i,y0, i)。i=0时,螺旋布料机位于初始位置,此时:DN, 0=(0,C),D1, 0=(0,0),D′N, 0=(0,C),D′1, 0=(0,0)。将式(2)展开:
| $ \begin{aligned} &D_{k, 1}, D_{k, 3}= \\ &\left\{\begin{array}{l} \left|D_{N, i-1}^{\prime} D_{D, i}\right|, y_{0, i-1} \leqslant y_{i, 1} \text { 且 } y_{0, i-1}+C \leqslant y_{i, 2} \\ \left|x_{i, 1}-x_{0, i-1}\right|, y_{0, i-1}<y_{i, 1} \text { 且 } y_{0, i-1}+C>y_{i, 2} \\ \left|D_{1, i-1}^{\prime} D_{A, i}\right|, y_{0, i-1} \geqslant y_{i, 1} \text { 且 } y_{0, i-1}+C \geqslant y_{i, 2} \end{array}\right. \end{aligned} $ | (3) |
| $ \begin{aligned} &D_{k, 2}, d_{k, 4}= \\ &\left\{\begin{array}{l} \left|D_{N, i-1}^{\prime} D_{C, i}\right|, y_{0, i-1} \leqslant y_{i, 1} \text { 且 } y_{0, i-1}+C \leqslant y_{i, 2} \\ \left|x_{i, 1}-x_{0, i-1}\right|, y_{0, i-1}<y_{i, 1} \text { 且 } y_{0, i-1}+C>y_{i, 2} \\ \left|D_{1, i-1}^{\prime} D_{B, i}\right|, y_{0, i-1} \geqslant y_{i, 1} \text { 且 } y_{0, i-1}+C \geqslant y_{i, 2} \end{array}\right. \end{aligned} $ | (4) |
1) 相对最短非布料长度求解。动态规划求解中利用的递推关系为
| $ \begin{gathered} f_{k}\left(s_{k}\right)=\min _{u_{k} \in D_{k}\left(s_{k}\right)}\left\{D_{k, j}\left(s_{k}, u_{k}\left(s_{k}\right)\right)+f_{k+1}\left(u_{k}\left(s_{k}\right)\right)\right\}, \\ k=1, 2, \cdots, m \end{gathered} $ | (5) |
式中:Dk(sk)表示第k阶段从状态sk出发的允许决策集合,sk为第k阶段的状态变量,uk(sk)为sk的决策变量。
构建的目标函数为
| $ S_{i}=\mathop{\min}\limits _{{u_k} \in {D_k}\left({{s_k}}\right)} \sum\limits_{k=1}^{m} D_{k}\left(s_{k}, u_{k}\right), i=1, 2, \cdots, q $ | (6) |
式中,Si表示相对最短非布料长度,即枚举结果Ui构建的动态规划模型的最优解,根据计算反推得到最优决策函数序列{uk(i)}。
2) 最短非布料长度求解:
| $ L_{2}=min \left\{S_{i}\right\}, i=1, 2, \cdots, q $ | (7) |
式中,L2为螺旋布料机非布料状态下的最短非布料长度,对应的最优决策序列{Ui, uk(i)}为布料路径规划结果。
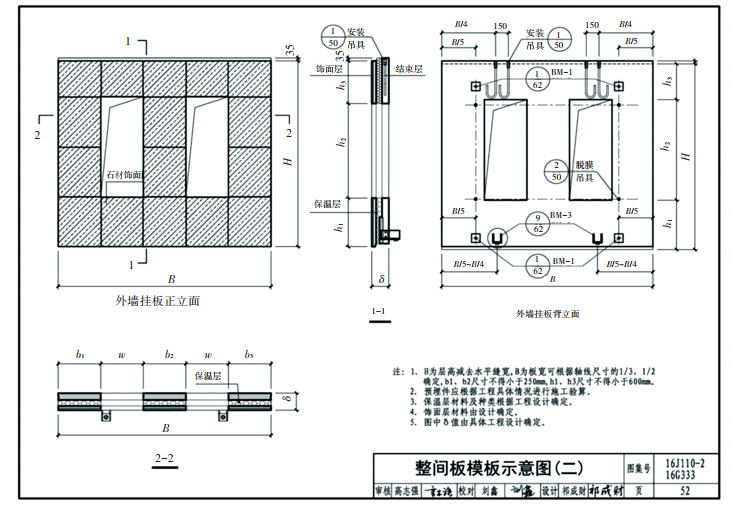
3 仿真实验某学校层高为4.4 m的实验楼外墙挂板设计采用如图 5所示的模板图[29],具体参数信息如表 1所示;山东某厂家生产的螺旋布料机在国内有着较高的市场占有率,某8出料口螺旋布料机的工作参数如表 2所示。利用Matlab软件,搭建该螺旋布料机和外墙挂板结构层的二维布料路径规划模型,做布料路径规划仿真。
|
图 5 外墙挂板模板图 Fig. 5 External wall hanging board template |
| 表 1 某实验楼外墙挂板相关参数 Tab. 1 Related parameters of external wall slabs of a laboratory building |
| 表 2 某螺旋布料机工作参数 Tab. 2 Working parameters of a spiral cloth machine |
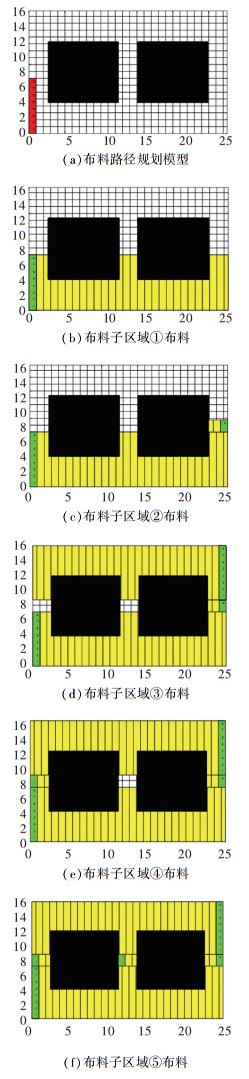
利用Matlab软件搭建的二维布料路径规划模型如图 6(a)所示,对外墙挂板结构层的布料路径规划结果如图 6(b)~(f)所示。该布料区域共被分割为了5个布料子区域,红色区域为螺旋布料机出料口的初始位置,8个出料口用数字1-8编号;绿色区域为对应布料子区域的布料起始位置,绿色区域上的数字代表参与该子区域布料作业的出料口编号,黄色区域为该子区域的布料过程。
|
图 6 预制混凝土外墙挂板布料路径规划仿真结果 Fig. 6 Simulation results of distribution path planning for precast concrete external wall hanging slabs |
按布料作业顺序对子区域编号,各布料子区域的参数汇总信息如表 3所示。
| 表 3 布料子区域参数 Tab. 3 Cloth sub-area parameters |
螺旋布料机出料口的布料量由移动速度v1(m/min) 和出料速度v2(m3/min)共同决定,为保证布料作业过程中布料时间t1 (s)最短,取中间出料口的出料速度v2中间(m3/min)或边缘出料口的出料速度v2边缘(m3/min)为最大出料速度v2max进行布料作业;若此工况下布料量过多,则取移动速度v1为最大移动速度v1max,通过调整出料口的出料速度来控制布料量。由于钢筋与预埋件对布料区域的混凝土需求量影响较小,在忽略该影响因素的条件下,螺旋布料机对该预制外墙挂板结构层5个布料子区域的布料参数计算结果如下:
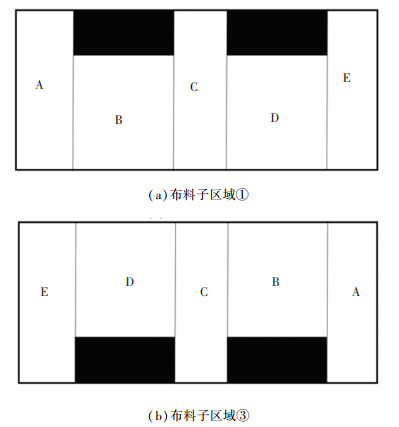
1) 布料子区域①。如图 7(a)所示,螺旋布料机对布料子区域①的布料作业共有5个工况,布料参数计算结果如表 4所示,布料时间t11为14.68 s。
|
图 7 布料子区域①和③ Fig. 7 Cloth sub-areas ① and ③ |
| 表 4 布料子区域①的布料参数 Tab. 4 Cloth parameters of cloth sub-area ① |
2) 布料子区域②。布料子区域②由8号出料口参与布料作业,为使得布料均匀,8号出料口应位于该区域的中间位置进行布料作业。螺旋布料机的移动速度v1为0.195 m/s,出料速度v2为最大值1.5 m3/min,布料时间t12为1.92 s。
3) 布料子区域③。布料子区域③的布料状况与布料子区域①情况相同,存在5个工况,如图 7(b)所示,布料参数计算结果如表 5所示,布料时间t13为14.68 s。
| 表 5 布料子区域③的布料参数 Tab. 5 Cloth parameters of cloth sub-area ③ |
4) 布料子区域④。布料子区域④由1号出料口参与布料作业,布料状况与布料子区域②相同。螺旋布料机的移动速度v1为0.195 m/s,出料速度v2为最大值1.5 m3/min,布料时间t14为1.92 s。
5) 布料子区域⑤。布料子区域⑤由1号出料口参与布料作业,布料状况与布料子区域②相同。螺旋布料机的移动速度v1为0.195 m/s,出料速度v2为最大值1.5 m3/min,布料时间t15为1.92 s。
3.3 规划结果分析未进行布料路径规划时,螺旋布料机的布料路径为牛耕法。取螺旋布料机非布料状态下的平均移动速度为
| 表 6 路径规划前后数据汇总 Tab. 6 Summary of data before and after path planning |
通过计算知,路径规划后布料总长度缩短了9.92%,布料总时间减少了8.44%。
4 结论1) 对布料区域网格划分的基础上,提出一种新的分割方法,将布料区域分割成多个布料子区域,螺旋布料机对子区域沿X轴方向布料一次即可完成该区域的浇筑任务,并对子区域内参与作业的出料口开口数做了计算。该分割方法简化了螺旋布料机的布料作业形式,为路径规划提供了一种思路。
2) 螺旋布料机的布料路径总长度分为布料长度和非布料长度,其中布料长度是确定值;利用枚举法和动态规划算法对螺旋布料机出料口和布料子区域集合建立了布料路径规划模型,并对多阶段决策过程中的决策值进行计算。最后以非布料长度最短为目标对模型进行求解,得到了最短的布料路径,完成了螺旋布料机对布料区域作业的全覆盖路径规划。
3) 根据此方法建立了某螺旋布料机和某预制混凝土外墙挂板结构层的二维布料路径规划模型,并对子区域的螺旋布料机布料移动速度、出料速度和布料时间做出计算。仿真结果表明,该方法缩短了布料总长度,减少了布料总时间,提高了预制构件的生产效率。
| [1] |
XIE Linlin, CHEN Yajiao, XIA Bo, et al. Importance-performance analysis of prefabricated building sustainability: a case study of Guangzhou[J]. Advances in Civil Engineering, 2020(1): 1. |
| [2] |
WANG He, ZHANG Yinqi, GAO Weijun, et al. Life cycle environmental and cost performance of prefabricated buildings[J]. Sustainability, 2020, 12(7): 2609. DOI:10.3390/su12072609 |
| [3] |
李楷, 陈永府, 金志勇, 等. 基于回溯法的全覆盖路径规划算法[J]. 计算机工程与科学, 2019, 41(7): 1227. LI Kai, CHEN Yongfu, JIN Zhiyong, et al. Full coverage path planning algorithm based on backtracking method[J]. Computer Engineering and Science, 2019, 41(7): 1227. DOI:10.3969/j.issn.1007-130X.2019.07.012 |
| [4] |
简毅, 高斌, 张月. 一种室内扫地机器人全遍历路径规划方法研究[J]. 传感器与微系统, 2018, 37(1): 32. JIAN Yi, GAO Bin, ZHANG Yue. Research on a full traversal path planning method for indoor sweeping robot[J]. Sensors and Microsystems, 2018, 37(1): 32. |
| [5] |
罗志远, 丰硕, 刘小峰, 等. 一种基于分步遗传算法的多无人清洁车区域覆盖路径规划方法[J]. 电子测量与仪器学报, 2020, 34(8): 43. LUO Zhiyuan, FENG Shuo, LIU Xiaofeng, et al. A multi-unmanned cleaning vehicle area coverage path planning method based on a step-by-step genetic algorithm[J]. Journal of Electronic Measurement and Instrument, 2020, 34(8): 43. |
| [6] |
朱大奇, 朱婷婷, 颜明重. 基于改进神经网络的多AUV全覆盖路径规划[J]. 系统仿真学报, 2020, 32(8): 1505. ZHU Daqi, ZHU Tingting, YAN Mingzhong. Multi-AUV full coverage path planning based on improved neural network[J]. Journal of System Simulation, 2020, 32(8): 1505. |
| [7] |
甘文洋, 朱大奇. 基于行为策略的AUV全覆盖信度函数路径规划算法[J]. 系统仿真学报, 2018, 30(5): 1857. GAN Wenyang, ZHU Daqi. AUV full coverage reliability function path planning algorithm based on behavior strategy[J]. Journal of System Simulation, 2018, 30(5): 1857. |
| [8] |
周林娜, 汪芸, 张鑫, 等. 矿区废弃地移动机器人全覆盖路径规划[J]. 工程科学学报, 2020, 42(9): 1220. ZHOU Linna, WANG Yun, ZHANG Xin, et al. Full coverage path planning of mobile robots in abandoned mining areas[J]. Chinese Journal of Engineering Science, 2020, 42(9): 1220. |
| [9] |
张丹红, 陈文文, 张华军, 等. A*算法与蚁群算法相结合的无人艇巡逻路径规划[J]. 华中科技大学学报(自然科学版), 2020, 48(6): 13. ZHANG Danhong, CHEN Wenwen, ZHANG Huajun, et al. Path planning for unmanned boat patrol combining A* algorithm and ant colony algorithm[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(6): 13. |
| [10] |
肖玉婷, 方勇纯, 梁潇, 等. 基于分块优化思想的多无人机覆盖路径规划[J]. 中国科学(技术科学), 2020, 50(4): 439. XIAO Yuting, FANG Yongchun, LIANG Xiao, et al. Multi-UAV coverage path planning based on block optimization ideas[J]. Science China (Technical Sciences), 2020, 50(4): 439. |
| [11] |
罗承铭, 熊陈文, 黄小毛, 等. 四边形田块下油菜联合收获机全覆盖作业路径规划算法[J]. 农业工程学报, 2021, 37(9): 140. LUO Chengming, XIONG Chenwen, HUANG Xiaomao, et al. Full coverage operation path planning algorithm of rape combine harvester under quadrilateral field[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(9): 140. |
| [12] |
王伟, 张彦斐, 宫金良, 等. 基于自适应升温模拟退火算法的农业机器人全区域覆盖策略[J]. 华南农业大学学报, 2021, 42(6): 126. WANG Wei, ZHANG Yanfei, GONG Jinliang, et al. Full area coverage strategy for agricultural robots based on adaptive heating simulated annealing algorithm[J]. Journal of South China Agricultural University, 2021, 42(6): 126. |
| [13] |
林砺宗, 李明智. 基于混合包络矩形的复杂轮廓激光切割路径规划[J]. 锻压技术, 2020, 45(4): 147. LIN Lizong, LI Mingzhi. Complex contour laser cutting path planning based on hybrid enveloping rectangle[J]. Forming & Stamping Technology, 2020, 45(4): 147. |
| [14] |
李世红, 袁跃兰, 刘绅绅, 等. 基于蚁群算法的激光切割工艺路径优化[J]. 锻压技术, 2019, 44(4): 69. LI Shihong, YUAN Yuelan, LIU Shenshen, et al. Laser cutting process path optimization based on ant colony algorithm[J]. Forming & Stamping Technology, 2019, 44(4): 69. |
| [15] |
王娜, 王海艳, 姜云春. 激光切割工艺路径的双向蚁群算法优化[J]. 锻压技术, 2020, 45(11): 30. WANG Na, WANG Haiyan, JIANG Yunchun. Two-way ant colony algorithm optimization of laser cutting process path[J]. Forming & Stamping Technology, 2020, 45(11): 30. |
| [16] |
梅伟, 赵云涛, 毛雪松, 等. 基于离散灰狼算法的喷涂机器人路径规划方法[J]. 计算机应用, 2020, 40(11): 3379. MEI Wei, ZHAO Yuntao, MAO Xuesong, et al. Path planning method of spray robot based on discrete gray wolf algorithm[J]. Journal of Computer Applications, 2020, 40(11): 3379. |
| [17] |
时梦楠, 崔博, 王佳俊, 等. 复杂施工条件下无人碾压机群协同全覆盖路径规划研究[J]. 水利学报, 2020, 51(12): 1544. SHI Mengnan, CUI Bo, WANG Jiajun, et al. Research on collaborative full coverage path planning of unmanned roller compactor group under complex construction conditions[J]. Journal of Hydraulic Engineering, 2020, 51(12): 1544. |
| [18] |
GALCERAN E, CARRERAS M. A survey on coverage path planning for robotics[J]. Robotics and Autonomous Systems, 2013, 61(12): 1258. |
| [19] |
LI Caihong, WANG Zhiqiang, FANG Chun, et al. An integrated algorithm of CCPP task for autonomous mobile robot under special missions[J]. International Journal of Computational Intelligence Systems, 2018, 11(1): 1357. |
| [20] |
卢俊华, 朱海飞, 梁经伦, 等. 双足爬壁机器人三维壁面环境全局路径规划[J]. 哈尔滨工业大学学报, 2020, 52(1): 148. LU Junhua, ZHU Haifei, LIANG Jinglun, et al. Global path planning of biped wall-climbing robot in three-dimensional wall environment[J]. Journal of Harbin Institute of Technology, 2020, 52(1): 148. |
| [21] |
周鹏, 郭菁菁, 李冬, 等. 混凝土布料机输送量影响因素研究[J]. 沈阳建筑大学学报(自然科学版), 2019, 3(4): 723. ZHOU Peng, GUO Jingjing, LI Dong, et al. Research on the influencing factors of the conveying capacity of concrete distributor[J]. Journal of Shenyang Jianzhu University (Natural Science Edition), 2019, 3(4): 723. |
| [22] |
周鹏, 郭菁菁, 李冬, 等. 基于神经网络的布料机输送预报与仿真研究[J]. 计算机仿真, 2021, 3(3): 476. ZHOU Peng, GUO Jingjing, LI Dong, et al. Research on prediction and simulation of distributor conveying based on neural network[J]. Computer Simulation, 2021, 3(3): 476. |
| [23] |
陈章华, 马月辉, 石彦辉. 混凝土布料机布料厚度测量系统[J]. 现代电子技术, 2020, 43(23): 76. CHEN Zhanghua, MA Yuehui, SHI Yanhui. Material thickness measurement system of concrete placing machine[J]. Modern Electronic Technology, 2020, 43(23): 76. |
| [24] |
LI D, ZHOU P, FAN L T, et al. Research on multi-agent control system for concrete distribution[J]. IOP Conference Series: Materials Science and Engineering, 2018, 399(1): 012029. |
| [25] |
李冬, 张成龙, 裴东锋, 等. 非稳态下混凝土浇筑重量补偿控制方法研究[J/OL]. 控制工程, https://doi.org/10.14107/j.cnki.kzgc.20200764 LI Dong, ZHANG Chenglong, PEI Dongfeng, et al. Research on the control method of concrete pouring weight compensation under unsteady state[J/OL]. Control Engineering, https://doi.org/10.14107/j.cnki.kzgc.20200764 |
| [26] |
SARA R, BENJAMIN K. State of practice of automation in precast concrete production[J]. Journal of Building Engineering, 2021, 43: 10227. |
| [27] |
杨嫒, 钱斌, 胡蓉, 等. 精确动态规划算法求解绿色单机调度问题[J]. 控制与决策, 2021, 36(8): 1891. YANG Ai, QIAN Bin, HU Rong, et al. Solving green single machine scheduling problem with accurate dynamic programming algorithm[J]. Control and Decision, 2021, 36(8): 189. |
| [28] |
周睿慜, 李辉. 改进动态规划算法的移动机器人路径规划[J]. 计算机工程与应用, 2020, 56(21): 20. ZHOU Ruimin, LI Hui. Improved dynamic programming algorithm for mobile robot path planning[J]. Computer Engineering and Applications, 2020, 56(21): 20. |
| [29] |
预制混凝土外墙挂板(一): 16J110-2、16G333[S]. 北京: 中国计划出版社, 2016: 52 Precast concrete exterior wall hanging board (1): 16J110-2, 16G333[S]. Beijing: China Planning Press, 2016: 52 |
 2022, Vol. 54
2022, Vol. 54


