面对日益激增的订单需求量和高昂的设备购置投入,半导体制造企业必须提高生产效率以应对高负荷的生产压力。半导体产品加工工艺复杂,其生产过程自动化水平高达95%以上。这些高度自动化加工设备内部结构十分复杂,在实际生产中,由于设备零部件连接松动、磨损、老化等原因[1],设备状态处于“完好”和“故障”之间的不可见状态[2]。在某公司的离子注入车间中,由于设备状态不确定[3]导致3台离子注入机在生产制造中表现出显著的时变效应,造成加工任务分配不均,生产调度计划失效率高等问题,成为衔接上下游生产的瓶颈工位。因此,研究考虑设备时变效应的晶圆加工序列决策调度方法,是解决具有时变效应调度问题的关键,也是该车间解决瓶颈工位问题的核心。
文献中量化设备不可见状态的经典方法是使用设备可靠性识别设备状态[4],设定设备的状态变化过程服从特定的规律[5-6]。但在实际生产中,设备状态的变化具有不确定性。机器学习模型需要大量数据的训练,以提取设备状态变化不确定性特征[7]。在数据缺失的情况下,可以使用隐式马尔可夫模型,其识别结果具有鲁棒性[8]。然而,以上研究主要聚焦于设备健康状态的监测,缺少通过和生产关键要素相关联而减少设备状态不确定因素对生产调度影响的深入研究。
设备状态退化使得加工时间具有可变特征,造成时变效应(time-changing effect),主要分为位置效应[9]、开始时间效应[10]和累积效应[11]。研究发现加工位置越靠后的工件,设计工时的延长时间越长。针对这一NP难问题[12],耿凯峰等[13]和Ding等[14]的研究中发现时间效应与调度决策相关,还假设与加工时设备状态的连续变化相关。Vimala Rani等[15]研究了半导体制造扩散炉中,晶圆的加工时间具有位置效应的动态调度问题。Zhang等[16]分析了大量历史数据后,使用非线性函数曲线拟合了晶圆批次加工工时的时变效应。Calderia等[17]设计模拟优化方法研究了晶圆的实际加工时间服从韦布尔分布的批量生产调度问题。Rostami等[18]则将具有时变效应的晶圆的加工时间当作设备状态识别的监测数据,进行维护决策。现有文献大多假设设备状态确定性变化引起的时变效应对生产调度计划的影响及其在半导体制造领域批量生产调度的应用,鲜少有文献研究设备状态不确定性导致的具有时变效应的晶圆加工序列的决策调度问题。
本文以半导体实际生产问题为驱动,研究了考虑设备状态不确定的平行机调度问题,旨在通过优化联合调度维护策略,减少设备状态不确定引起的时变效应对生产调度的影响。采用隐式马尔可夫模型识别设备状态,建立考虑设备时变效应的晶圆加工序列决策调度模型,将具有时变效应的工序调度和维护决策耦合在同一决策框架中,提出基于单机调度最优规则与多机调度优化知识库的集成调度优化知识的混合搜索算法进行求解。
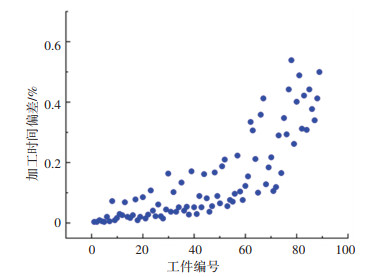
1 问题定义与建模 1.1 问题描述在某半导体工厂离子注入车间中,N组待加工晶圆拟在M台具有不同状态的离子注入机上加工。对于设备m,分析离子注入机的过往加工时间数据,具有显著的时变效应,这是由于连续工作引起的离子注入机清洁不当和加工环境温度的改变等原因造成的。计算实际加工时间与设计加工时间的偏差序列O,O = {om 1, om 2, …, omT},如图 1所示。由于数据点较为分散,使用传统的加工工时与设备状态连续变化相关拟合数据误差较大,基于对有限数据集的分析,使用隐式马尔科夫模型挖掘晶圆的加工工时与设备状态离散变化之间的量化关系。晶圆的加工时间偏差是隐式马尔可夫模型的观测序列,所以不考虑设备停机的影响。为了减少时变效应对调度作业的影响,花费b分钟的维修操作改善设备状态[19]。通过指派晶圆的加工顺序和进行合理的维护决策,最小化加工任务的最大完工时间。
|
图 1 离子注入机加工时间偏差 Fig. 1 Deviation of wafer processing time of ion implanter |
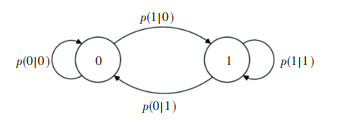
通过聚类分析,设备运行过程被划分为2个状态,如图 2所示,状态0(稳定状态)和状态1(不稳定状态)。隐式马尔可夫模型中的状态转移概率值是在调度作业中刻画设备状态的关键参数,设备m的状态转移概率Pm = {pm(0|0), pm(1|0), pm(1|1), pm(0|1)},满足pm(0|0) = 1-pm(1|0) 和pm(1|1) = 1-pm(0|1)。维护后,设备m的状态转移概率变为p′m(0|0)和p′m(1|1),并且p′m(0|0)>pm(0|0),p′m (1|1) < pm(1|1)。
|
图 2 设备状态间的状态转移概率 Fig. 2 Transition probabilities between machine states |
数据分析结果表明在设备处于不稳定状态时实际工时具有累计效应[20]。结合设备状态,当设备处于不稳定状态时,工件i在设备m的第j个位置的加工时间期望值是
| $ \begin{aligned} &\left(1-p_{m}(1 \mid 1)\right) t_{i}+p_{m}(1 \mid 1) t_{i j m}= \\ &\ \ \ \ \left(1-p_{m}(1 \mid 1)\right) t_{i}+p_{m} t_{i} d \end{aligned} $ | (1) |
式中:
假设同一批次的晶圆为1个工件,则有:1)每个工件有且仅有1次加工过程;2) 加工序列是连续的,并且每个加工位置上仅能安排1个工件;3)设备在同一时刻仅能加工1个工件;4)工件实际加工时间的偏差不允许超过阈值ω。
1.2 数学模型决策变量xijm和yjm均为0/1变量。如果工件i在设备m的任务序列中第j个被加工,则xijm取1,否则是0。如果设备m的任务序列中第j个被加工的工件前加入维护,则yjm取1,否则是0。
基于以上分析,建立的调度数学模型如下,
| $ Z=\min C_{\max } $ | (2) |
| $ \text { s.t. } \sum\limits_{i=1}^{|N|} x_{i j m} \leqslant 1, j \in N, m \in M $ | (3) |
| $ \sum\limits_{m=1}^{M} \sum\limits_{j=1}^{N} x_{i j m}=1, i \in N $ | (4) |
| $ x_{i j m} \leqslant \sum\limits_{h \in N, h \neq i} x_{h,(j-1), m}, j \in N $ | (5) |
| $ \begin{aligned} &\ \ \ \ \ \ \ \ C_{j m}+A\left(1-x_{i j m}\right) \geqslant C_{(j-1), m}+\left(1-y_{j m}\right) \cdot\\ &\min \left\{\left[p_{m}(0 \mid 0) x_{i j m} t_{i}+\left(1-p_{m}(0 \mid 0)\right) x_{i j m} t_{i j m}\right],[(1-\right.\\ &\left.\left.\left.p_{m}(1 \mid 1)\right) x_{i j m} t_{i}+p_{m}(1 \mid 1) x_{i j m} t_{i j m}\right]\right\}+b y_{j m}+\\ &y_{j m} \cdot \min \left\{\left[p^{\prime}{}_{m}(0 \mid 0) x_{i j m} t_{i}+\left(1-p^{\prime}{}_{m}(0 \mid 0)\right) x_{i j m} \cdot\right.\right.\\ &\left.\left.t_{i j m}\right],\left[\left(1-p^{\prime}{}_{m}(1 \mid 1)\right) x_{i j m} t_{i}+p^{\prime}{}_{m}(1 \mid 1) x_{i j m} t_{i j m}\right]\right\} \text {, }\\ &j \in N, m \in M \end{aligned} $ | (6) |
| $ C_{j m}+A\left(1-x_{i j m}\right) \geqslant t_{i}, j=1 $ | (7) |
| $ C_{j m}-C_{(j-1) m} \leqslant t_{i}(1+\omega)+A\left(1-x_{i j m}\right) $ | (8) |
| $ \begin{aligned} &x_{i j m} \in\{0,1\}, y_{j m} \in\{0,1\}, i=1,2, \cdots, N, \\ &j=1,2, \cdots, N, m=1,2, \cdots, M \end{aligned} $ | (9) |
式(2)中Z是目标函数值。式(3)和式(4)保证每个工件只能在1台设备被加工1次。式(5)保证每台设备上加工工件之间没有间隔。式(6)计算了从第2个位置开始每台设备每个位置的完工时间,其中min{[pm(0|0)xijmti+(1-pm(0|0))·xijmtijm], [(1-pm(1|1))xijmti+pm(1|1)xijmtijm]}计算了工件i在设备m的第j个位置加工时,当设备分别处于稳定状态和不稳定状态时工件i的期望加工时间,min{[p′m(0|0)xijmti+(1-p′m(0|0))xijmtijm], [(1-p′m(1|1))xijmti+p′m(1|1)xijmtijm]}则是插入维护操作后对应的期望加工时间,并且A是一个固定的正整数,
针对模型中的调度问题,考虑具有时变效应的加工工时的非线性约束增加了NP问题的求解难度,为了求解基于马尔可夫决策过程的联合调度模型,本文设计开发了一种基于单机调度最优规则与多机调度优化知识库的集成调度优化知识的混合搜索算法(Hybrid Search Algorithm with optimal scheduling knowledge, HSAOSK)。
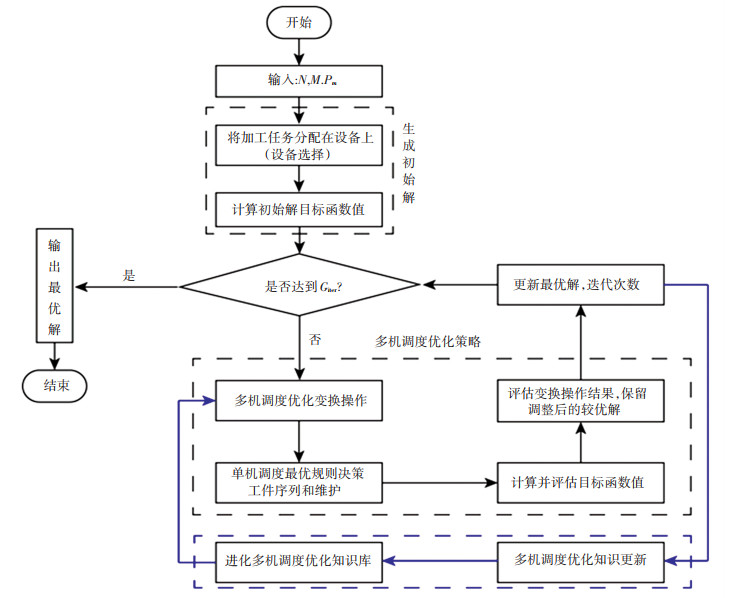
HSAOSK采用集成优化思路,构建单个设备可行解微观进化和平行机调度优化知识宏观进化的双层进化模型。根据设备选择规则,将加工任务分配到每台设备上,使用单机调度最优规则生成初始可行解并计算目标函数值。然后通过多机调度优化策略,使用基于统计知识的工件变换操作进行搜索,引入多机调度优化知识库通过减少搜索空间提升解的质量。具体的算法流程如图 3所示,其中Nab是可行解集的数量,Giter是最大迭代次数。
|
图 3 集成调度优化知识的混合搜索算法框架 Fig. 3 Framework of HSAOSK |
构造平行机调度序列,首先进行设备选择,将加工任务分配到具体的设备上。
本文使用|M|·|N|维矩阵表示平行机调度序列的解,每一个行向量代表一台设备,行向量组中的每一个元素表示在此台设备上进行加工的工件,空白位置使用0元素填充。如果以2台设备,8个工件为例,式(10)中的调度序列 S 代表 3、1、7、4、2依次在设备1上加工,而工件8、5、6则按顺序依次在设备2上加工,2台设备分别加工5个和3个工件,如图 4所示。
| $ \boldsymbol{S}=\left[\begin{array}{lll} 31\ 742\ 000 \\ 85\ 600\ 000 \end{array}\right] $ | (10) |

|
图 4 调度序列编码示意图 Fig. 4 Coding example of the schedule |
初始化时,基于设备状态进行设备选择构建初始解。由式(6)可知,工件在性能越好的设备上加工,时变效应越小。假设设备m1和m2的状态转移概率分别是pm1(0|0),pm1(1|1)和pm2(0|0),pm2(1|1),且pm1(0|0)>pm2(0|0),pm1(1|1) < pm2(1|1)。工件i分别在2台设备的第j个位置加工,则实际加工时间差为(pm1(0|0)-pm2(0|0))(d-1),已知(d-1)>0,则工件i在设备m1加工的时变效应较小。同理,当设备状态处于不稳定时,结论仍然成立。
设备的选择过程为:根据设备状态差异,首先生成一个随机数α符合[0, 1]均匀分布,定义表征搜索偏好的常数α0,且0≤α0≤1。当α≤α0时,选择pm(0|0)最大的设备;否则,选择所有设备中累计加工时间最短的设备。
2.2 目标函数值评估本文提出了最优调度顺序以及相应的维护方案,并结合向后递归算法,评估单台设备的最大完工时间。
2.2.1 单机调度最优规则向后递归算法(Backward Recursion Algorithm, BRA)是求解基于马尔可夫决策过程的动态优化问题的经典方法。单台设备使用向后递归算法的求解空间是4N-1ANN-1(N≥2),在平行机调度问题中,计算空间会呈指数倍增长,不符合实际需求。提出推论1,减少搜索空间。
推论1 在最优生产调度序列中,从第2个工件开始,所有工件的设计加工时间按照从小到大的规律排列。
证明 假设h、i和k分别是设备m最优生产调度序列中被第(r-1)、r和(r+1)个连续加工的3个工件,其中r≥2。如果交换工件i和工件k的加工顺序,第r个和第(r+1)个位置的完工时间会增加,即可证明推论的最优性。考虑到设备具有2个状态,只需在以下3种情况证明下述不等式成立:
| $ \begin{aligned} &\left(C_{i, r m}-C_{h, r-1, m}\right)+\left(C_{k,(r+1), m}-C_{i, r m}\right) \leqslant \\ &\left(C_{k, r m}-C_{h, r-1, m}\right)+\left(C_{i,(r+1) m}-C_{k, r m}\right) \end{aligned} $ | (11) |
设备m在加工完第(r-1)个工件和第r个工件后处于稳定状态。式(11)为
| $ \begin{aligned} &{\left[p_{m}(0 \mid 0)+\left(1-p_{m}(0 \mid 0)\right)\left(\frac{T}{T_{r}}\right)^{a}\right] t_{i}+} \\ &{\left[p_{m}(0 \mid 0)+\left(1-p_{m}(0 \mid 0)\right)\left(\frac{T}{T_{r}-t_{i}}\right)^{a}\right] t_{k} \leqslant} \\ &{\left[p_{m}(0 \mid 0)+\left(1-p_{m}(0 \mid 0)\right)\left(\frac{T}{T_{r}}\right)^{a}\right] t_{k}+} \\ &{\left[p_{m}(0 \mid 0)+\left(1-p_{m}(0 \mid 0)\right)\left(\frac{T}{T_{r}-t_{k}}\right)^{a}\right] t_{i}} \end{aligned} $ | (12) |
式中
| $ \frac{\left(\frac{T}{T_{r}}\right)^{a}-\left(\frac{T}{T_{r}-t_{k}}\right)^{a}}{\frac{t_{k}}{T}} \leqslant \frac{\left(\frac{T}{T_{r}}\right)^{-a}-\left(\frac{T}{T_{r}-t_{i}}\right)^{a}}{\frac{t_{i}}{T}} $ | (13) |
不等式(13)左侧是直线l1的斜率,直线l1分别穿过点
同理可证,设备m加工完第(r-1)个工件和第r个工件后处于任意状态,式(11)均成立。
综上,推论1成立。
基于推论1,单台设备的解空间由4N-1ANN-1(N≥2)减少到N。
2.2.2 维护决策的最优规则在最优调度序列中,插入维护作业改善设备状态。
推论2 设备m在加工完第(j-1)个工件后处于稳定状态时,第j个位置的最优维护决策,满足b < (p′m(0|0)-pm(0|0))(d-1)ti。
证明 假设Cjm是第j个位置插入维护的完工时间,C′jm是第j个位置没有维护操作的完工时间,则两个完工时间之间的差值是
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \varDelta C=C_{j m}-C^{\prime}{}_{j m}=b+p^{\prime}{}_{m}(0 \mid 0) t_{i}+(1- \\ &\left.p^{\prime}{}_{m}(0 \mid 0)\right) t_{i j}-p_{m}(0 \mid 0) t_{i}-\left(1-p_{m}(0 \mid 0)\right) t_{i j}= \\ &b-\left(p^{\prime}{}_{m}(0 \mid 0)-p_{m}(0 \mid 0)\right)(d-1) t_{i} \end{aligned} $ | (14) |
因为(d-1)>0,若b < (p′m(0|0)-pm(0|0))(d-1)tijm时,则ΔC < 0。此时插入维护作业可以减少完工时间。
同理可证设备m在加工完第(j-1)个工件后处于不稳定状态时的最优维护决策,满足b < (pm(1|1)-p′m(1|1))(d-1)ti。
2.2.3 最大完工时间评估联合单机最优调度和维护规则计算最优目标函数值,算法流程如下。
步骤1 将所有分配到设备m上的工件,基于推论1枚举所有可行的加工任务序列,集成集合S。
步骤2 使用二分搜索法在集合S中寻找加工任务序列sj,使得Z(sj) < Z(SPT)且Z(sj+1)>Z(SPT),建立子集Sjm= {s1m, s2m, …, sjm}。
步骤3 基于推论2对Sjm中的所有调度序列进行维护决策,并使用BRA分别计算插入维护决策后的每个生产调度序列的最大完工时间。
步骤4 m = m + 1,返回步骤1,直到计算完所有设备的最大完工时间,找出其中的最小值Z,算法终止。
2.3 基于统计知识的工件变换操作为了提高设备选择中工件变换操作的效率,提出了基于统计知识的强化策略。
将进化过程中每一次迭代获得的精英个体中最优调度、维护决策和设备状态等信息存储到平行机调度优化知识库中,采取统计方式对优化知识模型进行挖掘,将学习到的调度优化知识储存起来,用于指导进化后期迭代优化中的变换操作。在可行解的进化过程中,不断更新知识库,更新过程如下(其中工件的设计加工时间区间[vl, vh]被分为v等份,设备m在区间v的数量就是fmv):
步骤1 提取当下迭代过程中前10%的可行解,将其调度、维护决策和设备状态信息储存到优化知识库中。
步骤2 对每个可行解中的每台设备,根据调度序列中工件的设计加工时间,更新在该台设备上加工的工件中,t份区间里每个区间工件的数量。
步骤3 统计设备状态和各区间中的工件数量fmv,算法终止。
考虑到进化初期知识库信息的可信度有限,因此当达到迭代次数的1/5时,再应用储存的知识。定义pc为设备间交换工件的概率,进化后期调度优化变换操作如下:
步骤1 随机挑选一台设备m, m∈M。
步骤2 检查这台设备上加工工件的总数是否高于平行机组中每台设备的平均加工工件的数量(fmv),如果高于平均数量,则随机从该台设备上取出1个工件,插入到平行机组中设备加工工件数量最小的设备上。否则,转到步骤3。
步骤3 产生一个小于等于1的随机数R。如果R < pc,随机选择1个设备l,交换设备m和设备l上任意位置的2个工件。
步骤4 重新计算交换后的调度序列对应的最优维护决策,算法终止。
3 算例验证与分析使用小规模算例验证HSAOSK算法的有效性,并在大规模算例中分析其性能的优越性,最后选取模型中表征设备性能变化的状态转移概率讨论设备状态的不确定性对生产调度计划的影响。
将瓶颈工位3台离子注入机分别命名为设备1、设备2和设备3,收集了这3台设备的实际加工数据集,设备1为39组,设备2为34组,设备3为35组,作为1.1节中隐式马尔可夫模型的输入数据。使用Baum-Welch算法分别估计3台设备的状态转移概率[21],表 1为状态转移概率计算结果。
| 表 1 设备状态转移概率 Tab. 1 Transition probabilities for each machine |
根据工厂调研数据的统计结果,不同种类的工件在设备上的设计加工时间服从正态分布,均值是25,方差是3,单位为min。对离子注入机进行调整和清理操作的非更换零部件平均维修时间是b=10 min。
3.1 小规模算例验证HSAOSK算法参数设置时,种群规模过小会导致精度不足且解不稳定,过大造成算法性能下降;迭代次数过小影响算法收敛,过大降低算法效率;搜索偏好常数和交换工件的概率越小,搜索空间越大,导致算法性能下降,太大使得初始解差异太小陷入局部最优解。因此,分别使用HSAOSK算法和精确求解算法(BRA)求解相同的调度问题,调试HSAOSK算法参数取值,确定:Nab=40,Giter=400,α0=0.6,pc=0.7。随机生成20个算例,取平均值作为目标函数值,使用表 2评价算法的性能。当加工任务规模小于9个工件时,BRA可以计算求出精确解。
| 表 2 小规模算例 Tab. 2 Results of small scale instances |
HSAOSK算法的计算结果不仅与BRA算法相同,且所用时间更短,证明了该算法的有效性。
3.2 算法对比分析为了验证HSAOSK算法在大规模算例中的表现,考虑到文献中没有相关问题的基准算例,选取3种不同算法进行比较:标准搜索算法(SSA),含有单机调度最优规则的搜索算法(RSA)和含有单机调度最优规则的遗传算法(RGA)。分别求解不同规模的算例,且单个加工任务在实际生产中最多包含800个工件,如表 3所示。
| 表 3 大规模算例 Tab. 3 Performance of algorithms in large scale instances |
与遗传算法相比,搜索算法求解结果的质量均有所提升,搜索算法中性能较差的SSA算法相较RGA的优化结果提升了2.73%,说明搜索算法的优化框架更适合求解考虑设备时变效应的平行机调度问题。在搜索算法中,HASOSK算法的性能最优,验证了单机最优调度规则和多机调度优化知识库具有较强的搜索和寻优能力。
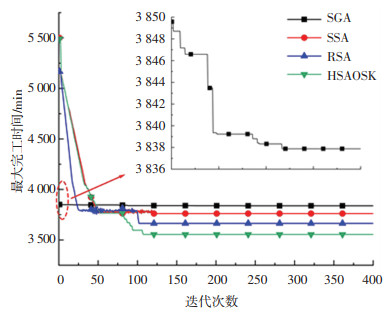
SSA的复杂度是O(n2),而加入单机最优调度规则后的其他3种算法的复杂度是O(nlogn),计算时间也验证了这一结果。其中,HASOSK求解时发挥了单机最优调度规则和多机调度优化知识减少搜索空间的作用,计算效率得到显著提升,如表 4所示。如图 5所示,在第100代左右就得到了目标函数值,验证了HASOSK的优越性。
| 表 4 大规模算例的计算时间 Tab. 4 Calculation time of algorithms in large scale instances |
|
图 5 不同算法的平均优化结果的迭代曲线对比 Fig. 5 Comparison of iteration curves of average optimal results of different algorithms |
HASOSK算法可以在有限的时间内,快速求解考虑设备时变效应的晶圆工序调度问题,为瓶颈工位3台设备提供更贴近生产实际的调度决策方案。为设备状态不确定性引起的时变效应对生产调度计划的影响预留出充足的缓冲时间,使得该工位上下游的工艺流程可以适时调整生产计划,避免晶圆的堆积。
3.3 敏感性分析设备状态转移概率是表征设备状态差异的重要参数,通过对比3台设备的加工数据,分析设备状态转移概率对联合调度决策的影响。
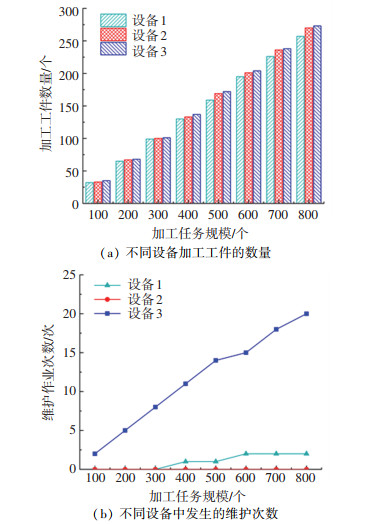
如图 6所示,每台设备加工工件的数量各不相同。其中设备3加工工件的数量最多,设备1的最少,并且差值随着加工任务规模的增加而增大。这是因为设备3保持在稳定状态的概率最大,相比于其他2台设备,在该设备上加工相同的工件,时变效应最小。随着加工任务规模的增大,设备1和设备3的维护作业次数都有所增加。其中,设备3插入更多维护作业的原因是为了使得设备以一个较大的概率处于稳定状态,从而减小时变效应。随着设备3加工工件数量增加,维护次数也显著增加。
|
图 6 设备状态转移概率的敏感性分析 Fig. 6 Sensitivity analysis of transition probability |
因此,在调度决策时,具有较高稳定状态转移概率的离子注入机将承担更多的加工任务,在可接受的维护成本下,减少因设备状态变化不确定导致的时变效应对调度的影响。一旦连续发生多次维护超过合理阈值,建议强制关闭设备进行检测,提高设备的基础稳定状态转移概率,避免由于设备状态较差使得加工任务显著的时变效应造成严重的生产延误。
4 结论1) 分析设备状态不确定性造成的时变效应对实际晶圆调度计划的影响,以过往加工数据为基础构造隐式马尔科夫模型,挖掘设备状态变化和加工时间之间的耦合关系,构建考虑设备时变效应的晶圆加工序列决策调度方法,实现对晶圆加工序列调度决策的有效表达。
2) 针对时变效应非线性约束的复杂性,提出HASOSK算法。算法在搜索算法的基础上,通过构建单机调度最优规则来强化单台设备的算法寻优能力,利用多机调度优化知识库来加强算法深度搜索的效率,实现晶圆加工序列的优化。
3) 实际数据算例分析结果表明,考虑设备时变效应的晶圆加工序列决策调度方法对实际生产具有有效性;HASOSK算法在大规模算例中具有良好的求解性能,表明了算法的有效性和可行性,能为具有时变效应的晶圆加工序列调度构建合理的调度计划。
4) 后续可以针对晶圆对设备状态敏感性的差异,进一步研究设备状态变化对晶圆工序决策调度计划的影响。
| [1] |
ALLAHVERDI A, MITTENTHAL J. Scheduling on a two-machine flowshop subject to random breakdowns with a makespan objective function[J]. European Journal of Operational Research, 1995, 81(2): 376. DOI:10.1016/0377-2217(93)E0318-R |
| [2] |
LEE J, LAPIRA E, BAGHERI B, et al. Recent advances and trends in predictive manufacturing systems in big data environment[J]. Manufacturing Letters, 2013, 1(1): 38. DOI:10.1016/j.mfglet.2013.09.005 |
| [3] |
RUSTOGI K, STRUSEVICH V. Single machine scheduling with a generalized job-dependent cumulative effect[M]. London: University of Greenwich, 2015: 105.
|
| [4] |
王金凤, 陈璐, 杨雯惠. 考虑设备可用性约束的单机调度问题[J]. 上海交通大学学报, 2021, 55(1): 103. WANG Jinfeng, CHEN Lu, YANG Wenhui. A single machine scheduling problem considering machine availability constraints[J]. Journal of Shanghai Jiao Tong University, 2021, 55(1): 103. DOI:10.16183/j.cnki.jsjtu.2019.173 |
| [5] |
陶辛阳, 夏唐斌, 奚立峰. 基于健康指数的预防性维护与多目标生产调度联合优化建模[J]. 上海交通大学学报, 2014, 48(8): 1170. TAO Xinyang, XIA Tangbin, XI Lifeng. Health-index-based joint optimization of preventive maintenance and multi-attribute production scheduling[J]. Journal of Shanghai Jiao Tong University, 2014, 48(8): 1170. DOI:10.16183/j.cnki.jsjtu.2014.08.020 |
| [6] |
ALSINA E F, CHICA M, TRAWINSKI K, et al. On the use of machine learning methods to predict component reliability from data-driven industrial case studies[J]. International Journal of Advanced Manufacturing Technology, 2017, 94(5/6/7/8): 2419. DOI:10.1007/s00170-017-1039-x |
| [7] |
LU Shibo, CHAI Hua, SABOO A, et al. Condition monitoring based on partial discharge diagnostics using machine learning methods: a comprehensive state-of-the-art review[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(6): 1861. DOI:10.1109/TDEI.2020.009070 |
| [8] |
KHALEGHEI A, MAKIS V. Model parameter estimation and residual life prediction for a partially observable failing system[J]. Naval Research Logistics, 2015, 62(3): 190. DOI:10.1002/nav.21622 |
| [9] |
WANG Ting, BALDACCI R, LIM A, et al. A branch-and-price algorithm for scheduling of deteriorating jobs and flexible periodic maintenance on a single machine[J]. European Journal of Operation Research, 2018, 271(3): 826. DOI:10.1016/j.ejor.2018.05.050 |
| [10] |
CHENG T C E, KRAVCHENKO S A, LIN M T. Scheduling step-deteriorating jobs to minimize the total completion time[J]. Computers & Industrial Engineering, 2020, 144. DOI:10.1016/j.cie.2020.106329 |
| [11] |
WU C C, LIN W C, ZHANG Xingong, et al. Tardiness minimisation for a customer order scheduling problem with sum-of-processing-time based learning effect[J]. Journal of the Operational Research Society, 2018, 70(3): 487. DOI:10.1080/01605682.2018.1447249 |
| [12] |
WU Huapin, HUANG Min. Improved estimation of distribution algorithm for the problem of single-machine scheduling with deteriorating jobs and different due dates[J]. Computational & Applied Mathematics, 2014, 33(3): 557. DOI:10.1007/s40314-013-0081-z |
| [13] |
耿凯峰, 叶春明. 考虑多时间因素的绿色可重入混合流水车间调度问题[J]. 计算机集成制造系统. [2021-08-18]. https://kns.cnki.net/kcms/detail/11.5946.TP.20210818.1625.014.html GENG Kaifeng, YE Chunming. Green re-entrant hybrid flow shop scheduling problem considering multiple time factors[J]. Computer Integrated Manufacturing Systems. [2021-08-18]. https://kns.cnki.net/kcms/detail/11.5946.TP.20210818.1625.014.html |
| [14] |
DING Junwen, SHEN Liji, LU Zhiping, et al. Parallel machine scheduling with completion-time-based criteria and sequence-dependent deterioration[J]. Computers & Operation Research, 2019, 103: 35. DOI:10.1016/j.cor.2018.10.016 |
| [15] |
RANI M V, MATHIRAJAN M. Meta-heuristics for dynamic real time scheduling of diffusion furnace in semiconductor manufacturing industry[J]. International Journal of Industrial and Systems Engineering, 2020, 34(3): 365. DOI:10.1504/IJISE.2020.105737 |
| [16] |
ZHANG Yi, PENG Peng, LIU Chongdang, et al. A sequential resampling approach for imbalanced batch process fault detection in semiconductor manufacturing[J]. Journal of Intelligent Manufacturing, 2020(12): 1. DOI:10.1007/s10845-020-01716-5 |
| [17] |
CALDERIA R H, GNANAVELBABU A. A simheuristic approach for the flexible job shop scheduling problem with stochastic processing times[J]. SIMULATION: Transactions of The Society for Modeling and Simulation International, 2021, 97(3): 215. DOI:10.1177/0037549720968891 |
| [18] |
ROSTAMI H, BLUE J, CHEN A, et al. Equipment deterioration modeling and cause diagnosis in semiconductor manufacturing[J]. International Journal of Intelligent Systems, 2021, 36(6): 2618. DOI:10.1002/int.22395 |
| [19] |
李小林, 司佳佳, 伊传传, 等. 考虑工件释放时间的柔性维护的单机调度问题[J]. 计算机集成制造系统. [2021-06-22]. https://kns.cnki.net/kcms/detail/11.5946.TP.20210621.1722.004.html LI Xiaolin, SI Jiajia, YI Chuanchuan, et al. Single machine scheduling problem considering job release times and flexible maintenance[J]. Computer Integrated Manufacturing System. [2021-06-22]. https://kns.cnki.net/kcms/detail/11.5946.TP.20210621.1722.004.html |
| [20] |
WU C C, HSU P H, LAI K J. Simulated-annealing heuristics for the single-machine scheduling problem with learning and unequal job release times[J]. Journal of Manufacturing Systems, 2011, 30(1): 54. DOI:10.1016/j.jmsy.2011.03.004 |
| [21] |
BAUM L E, PETRIE T, SOULES G, et al. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains[J]. The Annals of Mathematical Statistics, 1970, 41(1): 164. DOI:10.1214/aoms/1177697196 |
 2022, Vol. 54
2022, Vol. 54


