2. 河北工业大学 机械工程学院,天津 300401
2. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China
RV减速器具有传动比大、负载能力强、寿命长、运动精度高等优点,广泛应用于机器人关节处,RV减速器的可靠性会直接影响机器人的性能[1]。Yang等[2]考虑不确定性参数建立了RV减速器可靠性优化设计数学模型,并对RV减速器体积进行优化。Qian等[3]提出了一种基于Kriging模型的多失效模式下RV减速器时变可靠性分析方法。杜雪松等[4]基于强度退化理论,建立了RV减速器动态可靠度分析模型,并分析了RV减速器主要设计参数对可靠性的影响程度。于影等[5]建立了摆线针轮减速器优化设计模型,对RV减速器的优化设计提供理论依据。RV减速器属于高寿命、高可靠性产品,目前针对RV减速器可靠性的研究大多数停留在理论分析和仿真上,缺乏试验依据。
针对高可靠性产品,进行全寿命试验比较困难,常开展加速退化试验研究其可靠性。加速退化试验既能节省试验时间和成本,又能为产品的可靠性分析提供具体、可靠的试验数据。基于加速退化试验的可靠性建模方法有多种,当产品的性能退化趋势不明显时,通过对产品的性能退化量分布建模,从而求得产品的可靠性。吕瑛等[6]使用对数正态分布和威布尔分布对大功率开关的性能退化量建模,Sun等[7]使用威布尔分布和高斯-泊松联合分布对电容器的性能退化量建模,并对2种分布类型的准确性进行对比分析。若选用的分布函数类型不合适,会使可靠性分析结果不精确。当产品的性能退化轨迹可描述,基于随机过程建模的方法最为常用。其中,Wiener过程和Gamma过程使用最多,应用范围最广[8]。使用Gamma过程建模时,产品的性能退化量必须是独立的和非负的,并且服从Gamma分布,而Wiener过程对产品的性能退化数据没有具体的要求,因此,广泛应用于加速退化试验中。Wang等[9]基于Wiener退化过程对集成电路的可靠性进行分析。黄亮等[10]和王玺等[11]基于多阶段非线性Wiener过程对发动机性能衰减过程建模。针对复杂的性能退化模型,难以定义首次达到失效阈值时的精确解,Gao[12]等基于Wiener模型,结合计算机仿真进行求解。Zhai[13]等提出了一种带有IG漂移的Wiener退化模型,使Wiener模型建模过程更具有灵活性。
目前基于Wiener过程求解可靠性的方法很多,但是不能体现出个体的差异,并且估计Wiener模型参数过程复杂,所需样本量较多。对于RV减速器这种高可靠性产品来说,开展全寿命试验所需成本高、时间长,无法获得足够多的样本量。因此,本文制定并开展了RV减速器高应力加速退化试验,以传动精度作为评判RV减速器可靠性的标准,使用样本数据分离的极大似然法估计Wiener模型中的未知参数,再根据RV减速器传动精度退化规律,对各参数分布进行合理的假设。结合加速退化试验和传动精度退化建模的方法求得RV减速器可靠性函数,在体现个体差异的同时,实现了小样本条件下RV减速器的可靠性分析。
1 加速退化试验加速退化试验是在不改变产品失效机理的情况下,对产品施加高于正常工作条件下的应力,加快产品失效或性能退化的过程[14]。加速退化试验更注重产品的性能退化过程,通过对产品的性能退化轨迹或退化量建模,来评估产品的可靠性。
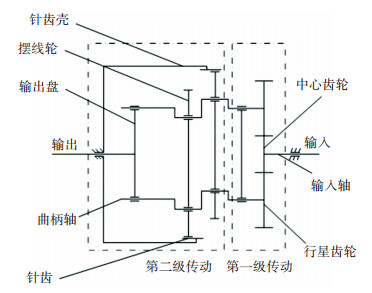
1.1 试验平台RV减速器是一种封闭式的两级传动机构,电机输入轴与双侧行星轮外啮合,完成第一级传动,双侧行星轮带动曲柄轴,曲柄轴通过轴承带动摆线轮实现偏心运动,完成第二级传动,如图 1所示。
|
图 1 RV减速器传动原理图 Fig. 1 Transmission schematic diagram of RV reducer |
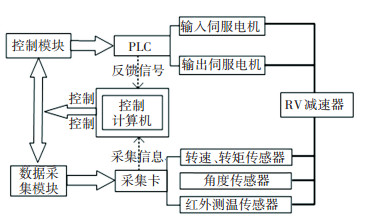
根据RV减速器工作原理,搭建加速退化试验平台,试验平台原理如图 2所示。
|
图 2 试验平台原理图 Fig. 2 Schematic diagram of test platform |
在RV减速器输入、输出端装有角度传感器、转速、转矩传感器,通过LabVIEW控制程序测试RV减速器的传动精度。RV减速器传动精度是输出端实际转角与理论转角之差,是RV减速器的重要性能指标,直接影响机器人运动精度。因此,本试验以RV减速器传动精度作为评判RV减速器可靠性的性能指标。
与RV减速器摆臂式寿命试验台相比,本次试验所用的试验台通过输出伺服电机对RV减速器施加负载扭矩,所提供的扭矩比较稳定,加速效果明显。摆臂式寿命试验台通过负重块对RV减速器提供负载扭矩,所能提供的负载扭矩呈正弦周期性变化,且变化幅度比较大,加速效果不显著。
1.2 摆线针轮传动强度校核进行高应力加速退化试验时,试验的最大加载值对结果影响较大。最大加载值是在不改变RV减速器失效机理的情况下,所能施加的最大应力水平。摆线针轮传动是RV减速器实现高负载、高精度的主要原因,文献[15]指出,摆线轮也是RV减速器最薄弱环节,因此,首先在2.5倍额定负载下对摆线针轮传动部分进行强度校核,为RV减速器加速退化试验确定最大加载值提供理论依据。
在工程应用中,为补偿制造误差、保证润滑状态,通常会对摆线轮齿廓进行修形。考虑摆线轮修形、轮齿的接触变形和针齿弯曲变形,对摆线针轮传动进行强度校核,具体分析过程如下:
修形后,摆线轮轮齿与针齿之间啮合法线方向的初始间隙Δ(φi)[16]为
| $ \begin{aligned} \Delta\left(\varphi_{i}\right)=&\Delta r_{\mathrm{rp}}\left(1-\frac{\sin \varphi_{i}}{\sqrt{1+K_{1}^{2}-2 K_{1} \cos \varphi_{i}}}\right)+ \\ &\frac{\Delta r_{\mathrm{p}}\left(1-K_{1} \cos \varphi_{i}-\sqrt{1-K_{1}^{2}} \sin \varphi_{i}\right)}{\sqrt{1+K_{1}^{2}-2 K_{1} \cos \varphi_{i}}} \end{aligned} $ | (1) |
式中:φi表示第i个针齿相对于转臂的转角; Δrp表示等距修形量; Δrrp表示移距修形量; K1表示短幅系数,K1=ezp/rp。
在负载转矩T的作用下,啮合点公法线上的总变形δi[17]为
| $ \delta_{i}=l_{i} \beta=\frac{\sin \varphi_{i}}{\sqrt{1+K_{1}^{2}-2 K_{1} \cos \varphi_{i}}} \delta_{\max } $ | (2) |
式中:β表示加载后,由于传力零件变形所引起的摆线轮的转角;li表示第i个针齿啮合点公法线或待啮合点的法线至摆线轮的距离;rc′表示摆线轮节圆半径;θi表示第i个针齿啮合点的公法线或待啮合点的法线与转臂之间的夹角;δmax表示啮合点公法线上最大变形,其值δmax=ωmax+fmax。
根据赫兹公式[18],接触变形ωmax为
| $ \begin{aligned} \omega_{\max }=& \frac{2 F_{\max }}{{\rm{ \mathsf{ π} }} L}\left[\frac{1-\mu_{1}^{2}}{E_{1}}\left(\frac{1}{3}+\ln \frac{4 R_{1}}{c}\right)+\right.\\ &\left.\frac{1-\mu_{2}^{2}}{E_{2}}\left(\frac{1}{3}+\ln \frac{4 R_{2}}{c}\right)\right] \end{aligned} $ | (3) |
式中:μ1,μ2表示摆线轮与针齿材料的泊松比;Fmax表示针齿与摆线轮啮合时的最大作用力;E1,E2表示摆线轮与针齿材料的弹性模量;c可通过式(4)求得
| $ c=1.60 \sqrt{\frac{F_{\max }}{L}} K_{\mathrm{D}}\left(\frac{1-\mu_{1}^{2}}{E_{1}}+\frac{1-\mu_{2}^{2}}{E_{2}}\right) $ | (4) |
式中:L表示针齿壳与针齿有效接触长度,KD表示当量曲率半径。
采用有限元法精确计算针齿最大弯曲变形[19],最大弯曲变形为
| $ f_{\max }=\frac{31}{64} \frac{F_{\max } L^{3}}{48 E J} $ | (5) |
式中:J表示惯性矩;J=πr/64,r为针齿半径。因此,可求得啮合点公法线上最大变形δmax。
在传递扭矩过程中,当某一位置的总变形δi大于初始间隙Δ(φi),即δi-Δ(φi)>0时,该处摆线轮与针齿进入啮合状态;反之,则该处摆线轮与针齿未进入啮合状态。则啮合力为
| $ F_{i}=\frac{\delta_{i}-\Delta\left(\varphi_{i}\right)}{\omega_{\max }} F_{\max } $ | (6) |
| $ F_{\max }=\frac{T_{\mathrm{C}}}{\sum\limits_{i=m}^{n}\left(\frac{l_{i}}{r^{\prime}{ }_{\mathrm{c}}}-\frac{\Delta\left(\varphi_{i}\right)}{\omega_{\max }}\right) l_{i}}=\frac{0.55 T}{\sum\limits_{i=m}^{n}\left(\frac{l_{i}}{r^{\prime}{ }_{\mathrm{c}}}-\frac{\Delta\left(\varphi_{i}\right)}{\omega_{\max }}\right) l_{i}} $ | (7) |
式中TC表示每个摆线轮传递的力矩,其中TC=0.55T。
修形后的摆线轮与针齿的最大啮合力处于有间隙啮合与无间隙啮合的最大啮合力之间,取二者均值作初始迭代条件,其值为
| $ F_{\max 0}=\frac{F_{1}+F_{2}}{2} $ | (8) |
无间隙啮合时的最大啮合力为[19]
| $ F_{1}=\frac{4 T_{\mathrm{C}}}{k z_{\mathrm{c}} r_{\mathrm{z}}}=\frac{2.2 T}{k z_{\mathrm{c}} r_{\mathrm{z}}} $ | (9) |
有间隙啮合时的最大啮合力为
| $ F_{2}=\frac{0.55 T}{r^{\prime}{}_\mathrm{c}}=\frac{0.55 T}{e z_{\mathrm{c}}} $ | (10) |
取式(8)为初值,代入式(1)~(10),当|Fmax-Fmax0|>0.01Fmax时,停止迭代,即可求得摆线轮和针齿啮合时各受力齿与摆线轮之间的最大啮合力Fmax,从而求得每个啮合齿的啮合力。
根据赫兹接触理论,计算摆线轮与针齿啮合时的啮合应力,求解过程为
| $ \sigma_{\mathrm{H}}=0.418 \sqrt{\frac{E_{\mathrm{d}} F_{i}}{b_{\mathrm{c}} p_{e i}}} $ | (11) |
式中:E1表示摆线轮弹性模量;E2为针齿弹性模量;Ed表示当量弹性模量,其中Ed=2E1E2/(E1+E2);bc表示针齿与摆线轮啮合时的有效接触长度;pei表示当量曲率半径,其值ρei=|ρi rrp/(ρi-rrp)|,ρi表示啮合点处摆线轮的曲率半径。
将修形后的摆线轮各参数代入式(1)~(11),可得摆线轮与针齿啮合时的啮合齿数、啮合力、啮合应力,计算结果如表 1所示。
| 表 1 摆线轮与针齿啮合时啮合力及应力 Tab. 1 Engagement force and stress when the cycloid wheel engages with the needle tooth |
从表 1可以看出,负载转矩为412 N·m时,共有16个针齿参与啮合,其中5号齿啮合力最大,为600.993 9 N,此处啮合应力为1 147.937 0 MPa,啮合应力最大。摆线轮的材料为20CrMnMo,其许用应力为1 268.000 0 MPa,针齿的材料为GCr15,许用应力为3 636.000 0 MPa。由表 1计算结果可知,高应力下摆线轮与针齿啮合过程中,最大啮合应力小于摆线轮和针齿的许用应力。
1.3 RV减速器高应力加速退化试验方案1) 选择加速应力。合适的加速应力,能够对试验起到良好的加速效果,通过对产品施加高于正常工作条件下的应力等级,加快产品失效或性能退化的过程,针对高可靠性产品,可选用负载[20]、温度[21]等作为加速应力。本试验选择负载作为加速应力,RV减速器输出端负载越大,减速器损坏越快,并且这种损坏逐渐累加,测试过程中不易受其他因素影响,操作方便,效果较好。
2) 选取试验最大加载值。试验的最大加载值是指在不改变RV减速器失效机理的情况下,所能施加的最大负载。根据摆线针轮传动部分的强度校核结果,本试验在2.5倍额定负载下进行。
3) 选择失效标准。以传动精度作为RV减速器可靠性评判标准,当RV减速器传动精度高于国标规定值时,即为失效。国标GB/T 37165—2018规定RV减速器传动精度不应高于60″,对某国产RV-20E减速器进行性能初测,其性能初值在40″左右,因此,假设减速器传动精度下降20″时视为失效,即失效阈值Df=20″。
对3台RV-20E减速器在高应力下开展加速退化试验,转速为1815 r/min,最大加载值为412 N·m(额定负载为167 N·m),3台减速器工况完全相同,定期加润滑脂并记录减速器传动精度,高应力下3台减速器性能退化数据如表 2所示。
| 表 2 RV减速器传动精度退化数据 Tab. 2 Transmission accuracy degradation data of RV reducer |
从表 2可以看出,在高应力下,3台RV减速器传动精度退化量不断增加,且退化速度较快,试验起到了良好的加速效果。其中,第2台减速器退化速度比其余2台较快,但退化趋势基本一致。在60到100 h内,传动精度出现了回弹现象,RV减速器经过前60 h的磨合,输入、输出启动扭矩不断变小,运行状态逐渐达到最佳,传动精度出现短暂的弹性回归。同时可以看出,传动精度退化量随时间增加而不断增大,呈递增趋势,这是由于RV减速器在试验过程中,随循环次数的增加,其内部零部件在较大的交变载荷的作用下,会逐渐出现磨损、疲劳剥落等现象,影响RV减速器整机的可靠性。但是由于个体差异及加工误差,3台减速器退化速度略有不同。本试验反映出了RV减速器传动精度退化过程,为RV减速器可靠性分析提供了真实、具体、可靠的试验数据。
2 RV减速器退化过程建模 2.1 转换工作时间根据疲劳等效理论,将高应力下RV减速器传动精度退化量转化为正常工作条件下的传动精度退化量,使用Wiener退化过程对RV减速器传动精度退化量建模。RV减速器疲劳等效公式[22]为
| $ L_{\mathrm{h}}=t \times \frac{N_{0}}{N_{\mathrm{m}}} \times\left(\frac{T_{0}}{T_{\mathrm{m}}}\right)^{\frac{10}{3}} $ | (12) |
式中:Lh表示折算后寿命时间,Nm表示平均输出转速,Tm表示平均负载转矩,N0表示额定输出转速,T0表示额定转矩,t表示高应力下时间。折算后,可得到RV减速器正常工作时间所对应的传动精度退化量变化趋势,如图 3所示。

|
图 3 折算后RV减速器传动精度退化量趋势图 Fig. 3 Trend of transmission accuracy degradation of RV reducer after conversion |
从图 3可以看出,3台减速器传动精度退化趋势相同,退化过程中传动精度退化量出现波动,传动精度退化量随试验时间的增加呈增加趋势,由于个体差异,3台减速器传动精度退化速度略有差异。在1 000 h到2 200 h范围内,3台减速器传动精度有不同程度的弹性回归,由于个体差异,弹性回归时间略有差异,在2 200 h传动精度退化量逐渐增加。
2.2 Wiener退化模型使用Wiener退化模型对3台减速器传动精度退化轨迹建模,Wiener退化过程是一个随机过程,可以很好地体现出产品个体差异以及退化量存在波动的特点[11]。Wiener退化过程模型为
| $ y(t)=\alpha+\mu t+\sigma B(t) $ | (13) |
式中:y(t)表示t时刻产品的性能退化量;α表示产品的性能退化量初始值;μ为漂移系数;σ为扩散系数;B(t)为标准Brown运动,并且具有以下性质:
1) B(0)= 0,B(t)∈(-∞, +∞);
2) t>0时,B(t)~N(0, t);
3) 独立增量性。
Brown运动是一个具有独立增量的连续随机过程,对任意时间间隔Δt,随机增量ΔB服从均值是零、方差是Δt的正态分布,即ΔB~N(0, Δt)。
当传动精度退化量大于失效阈值时,即y(t)≥Df,减速器失效,此时,RV减速器寿命T服从逆Gauss分布[23],概率密度函数为
| $ f(t)=\frac{D_{\mathrm{f}}-\alpha}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2} t^{3}}} \times \exp \left(-\frac{\left(D_{\mathrm{f}}-\alpha-\mu t\right)^{2}}{2 \sigma^{2} t}\right) $ | (14) |
可靠度函数为
| $ \begin{aligned} R(t)=&\varphi\left(\frac{D_{\mathrm{f}}-\alpha-\mu t}{\sigma \sqrt{t}}\right)-\exp \left(\frac{2 \mu\left(D_{\mathrm{f}}-\alpha\right)}{\sigma^{2}}\right) \times \\ &\varphi\left(\frac{-\left(D_{\mathrm{f}}-\alpha\right)-\mu t}{\sigma \sqrt{t}}\right) \end{aligned} $ | (15) |
将所有样本数据融合估计参数值时,每个样本点测试间隔应该相同,计算时受到很多限制,并且忽略了不同个体之间的差异。因此,对每台减速器的传动精度退化轨迹建模,体现个体间的差异,对各参数值分布做出假设,从而简化可靠性求解过程。t=0时刻产品性能退化量为0,由Wiener过程的独立增量性可知,此时
| $ \Delta y=y_{1}-0=\alpha+\mu t_{1}+\sigma B\left(t_{1}\right) $ | (16) |
式中B(t1)~N(0, t1)。因此Δy服从均值是α+μt1,方差是σ2Δt1的正态分布,即
| $ \Delta y \sim N\left(\alpha+\mu t_{1}, \sigma^{2} \Delta t_{1}\right) $ | (17) |
t>0时
| $ \begin{aligned} \Delta y_{i}=& y_{i+1}-y_{i}=\left(\alpha_{i+1}+\mu t_{i+1}+\sigma B\left(t_{i+1}\right)\right)-\\ &\left(\alpha_{i}+\mu t_{i}+\sigma B\left(t_{i}\right)\right)=\mu \Delta t_{i}+\sigma\left(B\left(t_{i+1}\right)-\right.\\ &\left.B\left(t_{i}\right)\right) \quad i=1,2,3, \cdots, N \end{aligned} $ | (18) |
式中Δti=ti+1-ti,i表示每个产品的测量次数。因为B(t)为标准布朗运动,并且当t>0时,B(t)~N(0, t),所以,B(ti+1)-B(ti)服从均值为零、方差为Δti的正态分布,则
| $ \Delta y_{i} \sim N\left(\mu \Delta t_{i}, \sigma^{2} \Delta t_{i}\right), i=1,2,3, \cdots, N $ | (19) |
可得Wiener退化轨迹的似然函数为
| $ \begin{array}{c} L(\alpha, \mu, \sigma)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2} t_{1}}} \times \exp \left[-\frac{\left(y_{1}-\alpha-\mu t_{1}\right)}{2 \sigma^{2} t_{1}}\right] \times \\ \prod\limits_{i=2}^{N} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2} \Delta t_{i}}} \cdot \exp \left[-\frac{\left(\Delta y_{i}-\mu \Delta t_{i}\right)}{2 \sigma^{2} \Delta t_{i}}\right] \end{array} $ | (20) |
对式(20)取对数,然后分别对α、μ和σ求偏导得
| $ \left\{\begin{array}{l} \frac{\partial \ln L}{\partial \mu}=\sum\limits_{i=1}^{N} \frac{\Delta y_{i}-\mu \Delta t_{i}}{\sigma^{2} \Delta t_{i}} \\ \frac{\partial \ln L}{\partial \sigma}=\sum\limits_{i=1}^{N}\left(-\frac{1}{\sigma}+\frac{\left(\Delta y_{i}-\mu \Delta t_{i}\right)^{2}}{\sigma^{3} \Delta t_{i}}\right) \\ \frac{\partial \ln L}{\partial \alpha}=\frac{y_{1}-\alpha-\mu t_{1}}{\sigma^{2} t_{1}} \end{array}\right. $ | (21) |
从而求得参数μ和σ的估计值为
| $ \left\{\begin{array}{l} \mu=\frac{1}{N} \sum\limits_{i=1}^{N} \frac{\Delta y_{i}}{\Delta t_{i}} \\ \sigma=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N} \frac{\left(\Delta y_{i}-\mu \Delta t_{i}\right)^{2}}{\Delta t_{i}}} \\ \alpha=y_{1}-\mu t_{1} \end{array}\right. $ | (22) |
基于每台减速器的性能退化数据,建立极大似然估计函数,求得每台减速器Wiener退化模型的未知参数,如表 3所示。
| 表 3 未知参数估计值 Tab. 3 Estimated values of unknown parameters |
当传动精度退化量大于失效阈值时,RV减速器寿命T服从逆Gauss分布,若此时根据表 3数据直接评估RV减速器可靠性,概率密度函数和可靠度函数为μ、σ和α的三重积分,求解过程十分复杂。从表 3数据可以看出,3台RV减速器Wiener退化模型中漂移系数μ差异较大,扩散系数σ相对稳定,可将相对稳定的参数设为定值,从而简化RV减速器求解过程,提高计算效率。
3 RV减速器可靠性分析3台减速器由于个体差异及装配误差影响,其性能退化量初值α有所不同,各产品参数估计值μ、σ也有差异。可将变异系数[24]小的未知参数取平均值,假设变异系数大的未知参数服从正态分布,既能保证计算精度,又能简化计算量,提高计算效率。变异系数是指根据每台RV减速器传动精度退化量,求得的Wiener退化模型中未知参数波动程度,与其均值以及方差有关。变异系数CV(X)可由式(23)求得:
| $ C_{V}(X)=\frac{\sqrt{\operatorname{Var}(X)}}{E(X)} $ | (23) |
式中: Var(X)表示未知参数的方差,E(X)表示未知参数的均值。若退化量初始值变异系数较大,可假设
| $ \left\{\begin{array}{l} \hat{\alpha}=\frac{1}{N} \sum\limits_{i=1}^{N} \alpha_{i} \\ \hat{\delta}{}_{\alpha}^{2}=\frac{1}{N-1} \sum\limits_{i=1}^{N}\left(\alpha_{i}-\hat{\alpha}\right)^{2} \end{array}\right. $ | (24) |
进而,可将式(12)概率密度函数改写为
| $ \begin{aligned} f(t)=& k \cdot \int_{\hat{\alpha}-3 \hat{\beta}_{\alpha}}^{\hat{\alpha}+3 \hat{\delta}_{\alpha}}\left(\frac{D_{\mathrm{f}}-\hat{\alpha}}{\sqrt{2 {\rm{ \mathsf{ π} }} \hat{\sigma}{}^{2} t^{3}}} \times \exp \left(-\frac{\left(D_{\mathrm{f}}-\hat{\alpha}-\hat{\mu} t\right)^{2}}{2 \hat{\sigma}{}^{2} t}\right)\right) \times \\ & p(\alpha) \mathrm{d} \alpha \end{aligned} $ | (25) |
可将式(14)可靠度函数改写为
| $ \begin{aligned} R(t)=& k \cdot \int_{\hat{\alpha}-3 \hat{\delta}_{\alpha}}^{\hat{\alpha}+3 \hat{\delta}_{\alpha}} \varphi\left(\left(\frac{D_{\mathrm{f}}-\hat{\alpha}-\hat{\mu} t}{\hat{\sigma} \sqrt{t}}\right)-\exp \left(\frac{2 \hat{\mu}\left(D_{\mathrm{f}}-\hat{\alpha}\right)}{\hat{\sigma}^{2}}\right) \times\right.\\ &\left.\varphi\left(\frac{-\left(D_{\mathrm{f}}-\hat{\alpha}\right)-\hat{\mu} t}{\hat{\sigma} \sqrt{t}}\right)\right) \times p(\alpha) \mathrm{d} \alpha \end{aligned} $ | (26) |
式中: k表示补偿系数,k=1/2(Ф(3)-1); p(α)是性能退化量初值α的概率密度函数,可由式(27)求得
| $ p(\alpha)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \hat{\delta}_{\alpha}}} \cdot \exp \left[-\frac{(\alpha-\hat{\alpha})^{2}}{2 \hat{\delta}{}_{\alpha}^{2}}\right] $ | (27) |
同理,当漂移系数μ或扩散系数σ的变异系数较大时,同样可以假设其服从正态分布,其余未知参数为定值,从而简化产品的可靠性求解过程,提高求解效率。
根据表 3,求得各未知参数的均值和方差,可得各参数的变异系数,如表 4所示。
| 表 4 参数估计值变异系数 Tab. 4 Coefficient of variation of parameter estimates |
从表 4中可以看出,漂移系数μ变异系数最大,退化量初始值α和扩散系数σ比较稳定,与图6中RV减速器传动精度退化趋势一致。3台减速器的传动精度退化初始值和扩散系数基本相同,但是,由于制造误差和加工误差,3台减速器传动精度退化速度略有不同,即3台减速器Wiener模型中的漂移系数μ有变异系数较大。因此,可将退化量初始值α和扩散系数σ设为定值,假设漂移系数μ服从正态分布,即μ~N(0.002 5, (7.937 3×10-4)2),
| $ \begin{aligned} f(t)=& k \times \int_{0.000\ 1}^{0.004\ 9}\left[\frac{D_{\mathrm{f}}-3.905\ 7}{\sqrt{2 {\rm{ \mathsf{ π} }} \times(0.011\ 4)^{2} \times t^{3}}} \times\right.\\ &\left.\exp \left(-\frac{\left(D_{\mathrm{f}}-3.905\ 7-0.002\ 5 \times t\right)^{2}}{2 \times(0.011\ 4)^{2} \times t}\right)\right] \times \\ & p(\mu) \mathrm{d} \mu \end{aligned} $ | (28) |
| $ \begin{aligned} R(t)=& k \times \int_{0.000\ 1}^{0.004\ 9}\left\{\varphi\left(\frac{D_{\mathrm{f}}-3.905\ 7-0.002\ 5 \times t}{0.011\ 4 \times \sqrt{t}}\right)-\right.\\ & {\left[\exp \left(\frac{2 \times 0.002\ 5 \times\left(D_{\mathrm{f}}-3.905\ 7\right)}{(0.011\ 4)^{2}}\right) \times\right.} \\ &\left.\left.\varphi\left(\frac{-\left(D_{\mathrm{f}}-3.905\ 7\right)-0.002\ 5 \times t}{0.011\ 4 \times \sqrt{t}}\right)\right]\right\} \times\\ & p(\mu) \mathrm{d} \mu \end{aligned} $ | (29) |
| $ p(\mu)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \hat{\delta}{}_{\mathtt{μ}}^{2}}} \cdot \exp \left[-\frac{(\mu-\hat{\mu})^{2}}{2 \hat{\delta}{}_{\mathtt{μ}}^{2}}\right] $ | (30) |
RV减速器性能退化缓慢,试验所需成本高,开展多台RV减速器试验困难,但是在小样本条件下对产品可靠性分析又比较困难。本方法使用样本数据分离的方法对RV减速器传动精度退化轨迹建模,根据RV减速器的试验轨迹特点,对各参数进行合理的假设,结合加速退化试验和传动精度退化量建模求解了RV减速器可靠性,充分体现了个体之间的差异,简化了可靠性求解过程,提高了求解效率。根据3台RV减速器的试验数据即可完成了RV减速器可靠性分析,解决了小样本条件下的RV减速器可靠性求解困难的问题。
对式(29)可靠性函数进行积分,可求得RV减速器的平均寿命,如式(31)所示:
| $ E(t)=\int_{0}^{+\infty} R(t) \mathrm{d} t $ | (31) |
令Df=20″,则可得到RV减速器的概率密度分布及可靠度,分别如图 4和图 5所示。

|
图 4 RV减速器失效概率密度图 Fig. 4 Failure probability density diagram of RV reducer |

|
图 5 RV减速器可靠度函数图 Fig. 5 Reliability function diagram of RV reducer |
由图 4和图 5可知,在前5 000 h内,RV减速器正常工作,RV减速器可靠性较高,5 000 h到7 000 h,减速器可靠性降低,失效概率大幅度增加,减速器性能逐渐超过减速器的使用要求。RV减速器在服役4 000 h以后,摆线轮与滚子轴承的可靠性衰退速度高于行星轮,并且在5 000 h到6 000 h,摆线轮与滚子轴承可靠性严重下降[5],导致减速器可靠性降低。这是由于摆线针轮传动部分以及滚子轴承等零部件在长时间的工作过程中,受力复杂并且润滑不良,出现磨损、疲劳脱落等情况影响RV减速器的性能。RV减速器投入使用的前一阶段很少会出现失效情况,工作一段时间后,各零部件疲劳强度随载荷循环次数的增加而逐渐下降,在服役后期衰退速度加快,最终失效。
4 结论1) 考虑摆线针轮修形对初始间隙的影响,利用赫兹接触理论建立了高应力下各接触齿啮合力的力分析模型,并对摆线轮传动部分进行强度校核,证明了在该应力下,摆线轮与针齿啮合过程中的最大啮合应力小于其许用应力。
2) 基于RV减速器高应力加速退化试验,使用样本数据分离的极大似然估计法建立了RV减速器传动精度退化轨迹,不仅能够体现个体差异,而且能准确描述RV减速器传动精度退化规律。
3) 结合高应力加速退化试验和传动精度退化量建模求解RV减速器可靠性的方法,得到的可靠性结果不仅符合实际情况,而且有效解决了小样本条件下RV减速器的可靠性分析问题。
| [1] |
吴锦辉, 陶友瑞. 工业机器人定位精度可靠性研究现状综述[J]. 中国机械工程, 2020, 31(18): 2180. WU Jinhui, TAO Yourui. A review of the status of research on the reliability of positioning accuracy of industrial robots[J]. China Mechanical Engineering, 2020, 31(18): 2180. DOI:10.3969/j.issn.1004-132X.2020.18.005 |
| [2] |
YANG Meide, ZHANG Dequan, CHENG Cheng, et al. Reliability based design optimization for RV reducer with experimental constraint[J]. Structural and Multidisciplinary Optimization, 2021(63): 2047. DOI:10.1007/s00158-020-02781-3 |
| [3] |
QIAN Huaming, LI Yanfeng, HUANG Hongzhong. Time variant reliability analysis for industrial robot RV reducer under multiple failure modes using kriging model[J]. Reliability Engineering & System Safety, 2020, 199: 1. DOI:10.1016/j.ress.2020.106936 |
| [4] |
杜雪松, 楼嘉彬, 黄玉成, 等. 考虑强度退化与失效相关性的RV减速器动态可靠性分析[J]. 机械传动, 2020, 44(2): 98. DU Xuesong, LOU Jiabin, HUANG Yucheng, et al. Dynamic reliability analysis of RV reducer considering strength degradation and failure correlation[J]. Mechanical Transmission, 2020, 44(2): 98. DOI:10.16578/j.issn.1004.2539.2020.02.014 |
| [5] |
于影, 于波, 陈建新, 等. 摆线针轮行星减速器的优化设计[J]. 哈尔滨工业大学学报, 2002, 34(4): 4. YU Ying, YU Bo, CHEN Jianxin, et al. Optimal design of cycloid planetary reducer[J]. Journal of Harbin Institute of Technology, 2002, 34(4): 4. DOI:10.3969/j.issn.1009-1971.2002.04.002 |
| [6] |
吕瑛, 王振宇, 赵岩, 等. 电子元器件加速退化寿命评估方法研究[J]. 计算机测量与控制, 2021, 29(11): 6. LV Ying, WANG Zhenyu, ZHAO Yan, et al. Research on accelerated degradation life evaluation method for electronic components[J]. Computer Measurement and Control, 2021, 29(11): 6. |
| [7] |
SUN Quan, TANG Yanzhen, FENG Jing, et al. Reliability assessment of metallized film capacitors using reduced degradation test sample[J]. Quality and Reliability Engineering International, 2013, 29(2): 259. DOI:10.1002/qre.1307 |
| [8] |
PANG Zhenan, SI Xiaosheng, HU Changhua, et al. A review on modeling and analysis of accelerated degradation data for reliability assessment[J]. Microelectronics Reliability, 2020, 107(5): 1. DOI:10.1016/j.microrel.2020.113602 |
| [9] |
WANG Xiaofei, WANG Bingxing, WU Wenhua, et al. Reliability analysis for accelerated degradation data based on the Wiener process with random effects[J]. Quality and Reliability Engineering, 2020(2): 1. DOI:10.1002/qre.2668 |
| [10] |
黄亮, 刘君强, 贡英杰. 基于Wiener过程的发动机多阶段剩余寿命预测[J]. 北京航空航天大学学报, 2018, 44(5): 1081. HUANG Liang, LIU Junqiang, GONG Yingjie. Multi-stage remaining life prediction of engine based on Wiener process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(5): 1081. DOI:10.13700/j.bh.1001-5965.2017.0383 |
| [11] |
王玺, 胡昌华, 任子强, 等. 基于非线性Wiener过程的航空发动机性能衰减建模与剩余寿命预测[J]. 航空学报, 2020, 41(2): 195. WANG Xi, HU Changhua, REN Ziqiang, et al. Modeling of aero-engine performance decay and remaining life prediction based on nonlinear Wiener process[J]. Journal of Aeronautics, 2020, 41(2): 195. DOI:10.7527/S1000.-6893.2019.23291 |
| [12] |
GAO Hongda, CUI Lirong, QIU Qingan. Reliability modeling for degradation-shock dependence systems with multiple species of shocks[J]. Reliability Engineering & System Safety, 2019, 185: 133. |
| [13] |
ZHAI Qingqing, CHEN Piao, HONG Lanqing, et al. A random-effects Wiener degradation model based on accelerated failure time[J]. Reliability Engineering & System Safety, 2018, 180: 94. DOI:10.1016/j.ress.2018.07.003 |
| [14] |
赵建印, 刘芳. 加速退化失效产品可靠性评估方法[J]. 哈尔滨工业大学学报, 2008, 40(10): 1669. ZHAO Jianyin, LIU Fang. Reliability assessment method for accelerated degradation failure products[J]. Journal of Harbin Institute of Technology, 2008, 40(10): 1669. DOI:10.3321/j.issn:0367-6234.2008.10.035 |
| [15] |
楼嘉彬, 杜雪松, 朱才朝. RV减速器可靠性优化设计方法[J]. 机械设计与制造, 2021(7): 210. LOU Jiabin, DU Xuesong, ZHU Caichao. RV reducer reliability optimization design method[J]. Machinery Design & Manufacture, 2021(7): 210. |
| [16] |
朱良斌, 肖正明, 杨凯, 等. 重载RV减速器的摆线针轮疲劳寿命预测[J/OL]. 机械科学与技术, 2021: 2. [2022-03-11]. https://doi.org/10.13433/j.cnki.1003-8728.20200612 ZHU Liangbin, XIAO Zhengming, YANG Kai, et al. Fatigue life prediction of cycloid pin wheel for heavy-duty RV reducer[J/OL]. Mechanical Science and Technology for Aerospace Engineering, 2021: 2. [2022-03-11]. https://doi.org/10.13433/j.cnki.1003-8728.20200612 |
| [17] |
陈振宇, 沈兆光, 杨玉虎. 摆线针轮行星传动机构啮合特性分析[J]. 机械设计, 2015, 32(10): 13. CHEN Zhenyu, SHEN Zhaoguang, YANG Yuhu. Analysis on meshing characteristics of cycloid pin gear planetary transmission mechanism[J]. Machine Design, 2015, 32(10): 13. DOI:10.3969/j.issn.1001-3997.2015.10.004 |
| [18] |
李力行. 摆线针轮行星传动的齿形修正及受力分析[J]. 大连铁道学院学报, 1984(4): 37. LI Lixing. Tooth profile modification and force analysis of cycloid pin gear planetary transmission[J]. Journal of Dalian Railway Institute, 1984(4): 37. |
| [19] |
郑钰馨, 奚鹰, 李梦如, 等. 基于密切值法的RV减速器传动受力影响分析[J]. 中国工程机械学报, 2017, 15(2): 156. ZHENG Yuxin, XI Ying, LI Mengru, et al. Influence analysis of RV reducer transmission force based on proximity value method[J]. Chinese Journal of Construction Machinery, 2017, 15(2): 156. |
| [20] |
王巧, 杜雪松, 宋朝省, 等. 谐波减速器加速寿命试验方法研究[J/OL]. 中国机械工程. [2022-03-11]. http://kns.cnki.net/kcms/detail/42.1294.TH.20220104.1324.016.html WANG Qiao, DU Xuesong, SONG Chaosheng, et al. Research on accelerated life test method of harmonic reducer[J]. China Mechanical Engineering. [2022-03-11]. http://kns.cnki.net/kcms/detail/42.1294.TH.20220104.1324.016.html |
| [21] |
KIM S J, MUN B M, BAE S J. A cost-driven reliability demonstration plan based on accelerated degradation tests[J]. Reliability Engineering & System Safety, 2018, 183: 226. DOI:10.1016/j.ress.2018.11.017 |
| [22] |
张跃明, 冀永虎, 纪姝婷, 等. RV减速器的寿命计算与加速寿命试验[J]. 机械设计与制造, 2020(8): 272. ZHANG Yueming, JI Yonghu, JI Shuting, et al. Life calculation and accelerated life test of RV reducer[J]. Machinery Design & Manufacture, 2020(8): 272. |
| [23] |
段雨男, 段富海, 曹慧. 考虑退化特性相关性的航空电连接器可靠性分析方法[J]. 大连理工大学学报, 2021, 61(5): 490. DUAN Yunan, DUAN Fuhai, CAO Hui. Reliability analysis method of avionics connectors considering the correlation of degradation characteristics[J]. Journal of Dalian University of Technology, 2021, 61(5): 490. DOI:10.7511/dllgxb202105007 |
| [24] |
张云, 姜楠, 王立平. 基于Wiener过程的数控转台极小子样可靠性分析[J]. 清华大学学报(自然科学版), 2019, 59(2): 92. ZHANG Yun, JIANG Nan, WANG Liping. Reliability analysis of turntable with minimal sample based on Wiener process[J]. Journal of Tsinghua University (Science and Technology), 2019, 59(2): 92. |
 2022, Vol. 54
2022, Vol. 54


